On the Modernisation of Weber’s Electrodynamics

Abstract

This work is an attempt to modernise Weber’s electrodynamics to make it compatible with the high-velocity regime, and with the existence of a limiting velocity, c. For this purpose, starting from the law of energy conservation and the mass–energy equivalence, new expressions for potential energy and for kinetic energy are derived jointly which are consistent with an ultimate velocity of the value of c. The new potential energy, already reported by Phipps, becomes Weber’s expression in the limit of low velocities. The new kinetic energy differs from the relativistic expression, but, like the latter, it also becomes the Newtonian expression in the limit of low velocities. New expressions for force and linear momentum are also derived which complete a new mechanics. Phipps’ potential energy and new kinetic energy are applied to the problem of two interacting charges in a radial motion and orbital motion. The new framework is also applied to the problem of a charge moving between the two plates of a charged capacitor, obtaining a result similar to that obtained by means of Maxwell–Lorentz electromagnetism and relativistic mechanics. The metaphysical considerations that clearly differentiate the conventional framework from the new framework proposed here are discussed.

1. Introduction

Probably, one of the most interesting questions in fundamental physics is how two electric charges interact when they are in relative motion. This subject was able to capture the attention of the most brilliant minds of the 19th and 20th centuries. At the beginning of the 19th century, Ampère [1], Gauss [2], Weber [3] and Riemann [4] (highly influential figures in science at that time) developed different electrodynamic theories extending the well-known Coulomb’s law. These were laws of instantaneous action-at-a-distance, in which the concept of “field” was completely absent. In this context, Weber developed his electrodynamic theory during the same period in which Maxwell was working on his equations. Maxwell, though he was a strong advocate of the field idea, studied Weber’s theory rigorously, praised it repeatedly, and analysed it in detail in the last chapter of his most famous work Treatise [5], considering it a promising alternative approach to his own.

Despite being in line with the most commonly recognised facts of electromagnetism and Maxwell’s endorsement, Weber’s electrodynamics gradually fell into oblivion. Today, Weber’s name only appears in textbooks in connection with the unit of magnetic flux in the International System of Units, as the only recognition of his research prowess. One of the reasons for this neglect, perhaps the main one, is that Weber’s theory was unable to predict the propagation of electromagnetic waves in a vacuum, as Maxwell’s theory was able to do. Interestingly, Weber and Kirchhoff had been the first to show that the electrical signal should travel through conducting wires in the form of travelling waves with velocity, c. However, the reasoning employed there was not valid in a vacuum, where there were no supporting electric charges. Another reason that undermined confidence in Weber’s electrodynamics was Helmholtz’s fierce criticism, arguing that the theory involved a violation of the law of energy conservation and predicted that, under certain configurations, charges could act as if they had a negative inertial mass, contrary to experiments. Weber vigorously refuted the first criticism in [6], and Maxwell, in his study of Weber’s electrodynamics, ruled that Weber’s electrodynamics did satisfy the law of energy conservation [5]. However, the doubts and misgivings about the theory would never disappear. The advent of the special relativity theory (SRT), which rejects the absolute simultaneity of two distant events, dealt a mortal blow to the concept of action-at-a-distance and condemned as heretical all theories that relied on it. Interestingly, however, in recent years, the concept of action-at-a-distance has been making an increasingly strong comeback in the field of quantum physics [7,8].

Weber’s electrodynamics, like Gauss’s and Riemann’s, were expressed in terms of the interaction force between two charged particles in relative motion. However, unlike other theories, Weber’s force satisfies Newton’s law of action and reaction in its strongest form and, as such, is compatible with the conservation of linear and angular momentum. It can be derived from a generalised velocity-dependent potential energy and is compatible with the law of energy conservation. From it can be derived Coulomb’s law, Faraday’s law of induction and Ampère’s expression for the force between current elements.

The most detailed and rigorous current treatise on Weber’s electrodynamics is the one written by Assis [9]. A comprehensive review of the state of the art on this topic, including the most relevant and the most recent contributions, can be found in [10]. New and recent work extending the experimental verification of the predictions of Weber’s electrodynamic theory can be found in [11,12,13,14,15,16,17,18,19,20,21,22,23,24].

Weber’s potential energy equation can be written as [9].

$$U_W=\frac{q_1{q}_2}{4\pi {\epsilon }_0}\frac{1}{r}\left(1-\frac{{\dot{r}}^2}{2c^2}\right)$$

(1)

In this expression, U_W is the potential energy generated by q₁ and q₂, ε₀ is the vacuum’s permittivity, c is the velocity of light in the vacuum, r is the distance separating the two charges, and the dot stands for the time derivation, $\dot{r}\equiv dr/dt$, so $\dot{r}$ represents the radial relative velocity. Notice that Equation (1) is fully relational; that is, it is dependent only on the two interacting charges, on the distance between them (r) and on their radial relative velocity ($\dot{r}$).

In order to overcome Helmholtz’s objection to Weber’s law (the ‘negative mass behaviour’ for all velocities of a value less than that of c), Phipps proposed [25] a new expression for electrodynamic potential energy:

$$U_P=\frac{q_1{q}_2}{4\pi {\epsilon }_0}\frac{1}{r}{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}$$

(2)

It is obvious that both Equations (1) and (2) implicitly contemplate a radial relative velocity that we can call critical. In Weber’s expression, this critical velocity takes the value of $\sqrt{2}c$, whereas in Phipps’ expression, it takes the value of c. From a strictly mathematical point of view, in Weber’s expression the value of $\sqrt{2}c$ needs not be a limiting value, so that higher values are conceivable (although the sign of the energy would change from attractive to repulsive or vice versa). In Phipps’ expression, on the other hand, the value of c is a full-fledged limiting value, because higher values would imply non-real (complex) quantities. This is a difference to be taken into account.

It is easy to show that Weber’s expression can be seen as an approximate version of Phipps’ expression, valid only for situations where $\dot{r}/c\ll 1$ (low velocities). It is sufficient to take Maclaurin’s development of Phipps’ expression, retaining only the terms up to second order in $\dot{r}/c$; the expression thus obtained coincides exactly with the one proposed by Weber.

The forces deriving from the above potential energies can be found by taking into account that

$$\overrightarrow{F}=-\frac{dU}{dr}\widehat{r}=-\frac{dU}{dt}\frac{dt}{dr}\widehat{r}=-\frac{1}{\dot{r}}\frac{dU}{dt}\widehat{r}$$

(3)

where $\widehat{r}\equiv \overrightarrow{r}/r$ is the unit vector in the direction of $\overrightarrow{r}$, and the vector connecting the two charges: from q₂ to q₁.

Applying Equation (3) to Equations (1) and (2) gives the following expressions for the respective forces:

$${\overrightarrow{F}}_W=\frac{q_1{q}_2}{4\pi {\epsilon }_0}\frac{\widehat{r}}{r^2}\left(1-\frac{{\dot{r}}^2}{2c^2}+\frac{r \ddot{r}}{c^2}\right)$$

(4)

$${\overrightarrow{F}}_P=\frac{q_1{q}_2}{4\pi {\epsilon }_0}\frac{\widehat{r}}{r^2}\left[{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}+\frac{r \ddot{r}}{c^2}{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{-\frac{1}{2}}\right]$$

(5)

Note that, in both cases, these are central forces, always directed along the line joining the two interacting charges.

On the other hand, the central forces can also be calculated from the kinetic energy, by means of:

$$\overrightarrow{F}=\widehat{r}\cdot \frac{1}{\dot{r}}\frac{dT}{dt}$$

(6)

Thus, for the central forces, the total energy is conserved, i.e.,

$$\frac{d}{dt}\left(U+T\right)=\frac{dU}{dt}+\frac{dT}{dt}=0$$

(7)

as is easily inferred by taking into account Equations (3) and (6), according to which $dU/dt=-\dot{r}\cdot F$ and $dT/dt=\dot{r}\cdot F$. The conservation of energy is completely independent of the expression adopted for kinetic energy, provided that the latter is correctly defined.

Therefore, in the studies carried out by different authors using Weber’s or Phipps’ electrodynamic potential energy, the Newtonian expression of kinetic energy has been used, due to the confidence that the existence of a limiting velocity was already guaranteed by the expression of the potential energy. However, there seems to be sufficient evidence that this strategy is not sufficient to reproduce some experimental results involving high velocities, and to yield predictions consistent with those of SRT [26,27]. Therefore, some authors have tentatively used other expressions for kinetic energy, such as the one deduced by Schrödinger [28] or the well-known relativistic expression [29]. Some works in this direction are those conducted in [30,31], although the results obtained have not been considered fully satisfactory. The theoretical effort to renew the expression for kinetic energy did not accompany the modernising attempt that led to the introduction of Phipps’ expression. The tentative or heuristic search for the most convenient expression for kinetic energy to be used in conjunction with Phipps’ expression for potential energy could prove tedious and, in the end, lack convincing power. Interesting work in this direction can be found in [32]. However, it would be ideal to find a deductive procedure which, starting on a firm basis, would allow the simultaneous derivation of the expressions of potential and kinetic energies. The basis of our deduction could be the law of energy conservation and the mass–energy equivalence.

In this work, based on these principles and following a reasoning similar to that adopted by Wesley in [33] to derive Weber’s potential energy, we shall show that it is possible to deduce jointly the expression of Phipps’ potential energy and the expression of kinetic energy that is compatible with it.

From the new expression for kinetic energy, we will derive new expressions for (linear) momentum and force (fundamental law of dynamics) applicable to the study of the radial motion of two interacting charges. We will then extend the study to the orbital motion of these charges, proposing new expressions for kinetic energy, linear momentum, angular momentum and force. Finally, an attempt will be made to solve, in the new framework, the problem of a charge moving perpendicularly to the plates of a charged capacitor.

All the proposed expressions will be analysed to check whether or not in the limit of low velocities and low energy, they are reduced to the expressions known in Newtonian mechanics. The results obtained in the new framework will also be contrasted with the predictions obtained in the Maxwell–Lorentz and SRT framework, in particular, to check that c is a limiting velocity.

2. New Mechanics for New Electrodynamics

2.1. Derivation of Potential and Kinetic Energies

Considering two charges, q₁ and q₂, with respective masses m₁ and m₂, interacting with each other and isolated from the rest of the universe, both particles will, in general, move around their common centre of mass. To facilitate the calculations, we can adopt the reduced mass procedure. By this procedure, the two-particle problem is reduced to that of a single particle with charge q₁ and mass (μ) calculated via

$$\mu =\frac{m_1\cdot m_2}{m_1+m_2}$$

(8)

moving with respect to the other particle, of charge q₂, which is in this case ‘fixed’, at a distance, r.

Supposing charge q₁ starts to move and acquires kinetic energy (T), by virtue of the mass–energy equivalence, the inertial mass of the system should be increased by the value $T/c^2$. If the initial energy of the system is E, then the total mass of the charge in motion should be $\mu +T/c^2=\mu +(E-U_C)/c^2$, where $U_C$ is the Coulomb potential energy, which is given by

$$U_C=\frac{q_1 q_2}{4\pi {\epsilon }_0 r}$$

(9)

Assuming that the acting force, F, can be calculated as a derivative of the momentum with respect to time, i.e.,

$$F=\frac{d}{dt}\left[\left(\mu +\frac{E-U_C}{c^2}\right)\cdot \dot{r}\right]$$

(10)

as charge q₁ moves away from the fixed q₂ charge, the rate to increase its kinetic energy by, $dT/dt=d(E-U_C)/dt=-d{U}_C/dt$, will be equal to the rate at which the force does work on charge q₁. Thus,

$$-\frac{d{U}_C}{dt}=\dot{r}\cdot F=\dot{r}\cdot \frac{d}{dt}\left[\left(\mu +\frac{E-U_C}{c^2}\right)\cdot \dot{r}\right]$$

(11)

and from here

$$\frac{d{U}_C}{dt}=\frac{{\dot{r}}^2}{c^2}\cdot \frac{d{U}_C}{dt}-\dot{r}\cdot \left(\mu +\frac{E-U_C}{c^2}\right)\cdot \frac{d\dot{r}}{dt}$$

(12)

In order to simplify the latter expression, we define the function γ as

$$\gamma \equiv {\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{-\frac{1}{2}}$$

(13)

the derivative of which, with respect to time, gives

$$\frac{d\gamma }{dt}={\gamma }^3\cdot \frac{\dot{r}}{c^2}\cdot \frac{d\dot{r}}{dt}$$

(14)

and here,

$$\dot{r}\cdot \frac{d\dot{r}}{dt}=\frac{c^2}{{\gamma }^3}\cdot \frac{d\gamma }{dt}$$

(15)

Then, by inserting the latter result in Equation (12) and manipulating it algebraically, we obtain

$$\frac{d{U}_C}{dt}\cdot \left(1-\frac{{\dot{r}}^2}{c^2}\right)=-\left(\mu +\frac{E-U_C}{c^2}\right)\cdot \frac{c^2}{{\gamma }^3}\cdot \frac{d\gamma }{dt}$$

(16)

which we can rewrite as

$$d{U}_C\cdot {\gamma }^{-2}=\left(U_C-E-\mu c^2\right)\cdot {\gamma }^{-3}\cdot d\gamma$$

(17)

Additionally, from here,

$$\frac{d{U}_C}{(U_C-E-\mu c^2)}=\frac{d\gamma }{\gamma }$$

(18)

Integrating this first-order ordinary differential equation between the corresponding limits of integration:

$${\displaystyle {\int }_{U_{C0}}^{U_C}\frac{d{U}_C}{(U_C-E-\mu c^2)}}={\displaystyle {\int }_{{\gamma }_0}^{\gamma }\frac{d\gamma }{\gamma }}$$

(19)

the following is obtained:

$$\frac{U_C-E-\mu c^2}{U_{C0}-E-\mu c^2}=\frac{\gamma }{{\gamma }_0}$$

(20)

Restricting it to the case where initial energy is only potential, then $U_{C0}=E$ and ${\gamma }_0=1$, so that Equation (20) becomes

$$E=U_C+\mu c^2(\gamma -1)$$

(21)

Equation (21) is the expression of the law of energy conservation, and it includes Coulomb’s potential energy and the well-known relativistic expression for kinetic energy.

Now dividing Equation (21) by γ, and adding E to the two members of the equality, we obtain

$$E+E/\gamma =E+U_C/\gamma +\mu c^2(1-1/\gamma )$$

(22)

which we can regroup as

$$E=U_C/\gamma +(\mu c^2+E)(1-1/\gamma )$$

(23)

If, in view of this equation, we now define the new electrodynamic potential energy, U, and its corresponding kinetic energy, T, as

$$U=U_C/\gamma$$

(24)

$$T=(\mu c^2+E)(1-1/\gamma )$$

(25)

then

$$U=\frac{q_1 q_2}{4\pi {\epsilon }_0 r}\cdot {\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}$$

(26)

$$T=(\mu c^2+E)\cdot \left[1-{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}\right]$$

(27)

On the one hand, Equation (26) coincides with the expression for the electrodynamic potential energy proposed by Phipps, Equation (2). On the other hand, Equation (27) is the new expression for the kinetic energy compatible with Phipps’ potential energy. This expression differs from the relativistic expression and has a different upper bound. Indeed, if $\dot{r}\to c$, then $T\to (\mu c^2+E)$, instead of $T\to \infty$, which is the case with the relativistic expression. A further difference is that in Equation (27), to the intrinsic inertial energy, $\mu c^2$, the inertial contribution from the total energy of the system, E, must now be added, which is not the case in the relativistic expression.

2.2. Limit of Low Radial Velocities and Low Energies

In the limit of low radial velocities, from Equation (26), Weber’s potential energy expression is recovered:

$$U\approx \frac{q_1 q_2}{4\pi {\epsilon }_0 r}\cdot \left(1-\frac{{\dot{r}}^2}{2c^2}\right)$$

(28)

Assuming further that $\mu c^2\gg E$, Equation (27) recovers the Newtonian expression for kinetic energy:

$$T\approx \mu c^2\cdot \left[1-\left(1-\frac{{\dot{r}}^2}{2c^2}\right)\right]=\frac{1}{2}\mu \cdot {\dot{r}}^2$$

(29)

Thus, it can be concluded that it is consistent to use the Newtonian expression for kinetic energy together with Weber’s potential energy, but with Phipps’ potential energy, Equation (27) must be used, if the mass–energy equivalence is to be guaranteed.

2.3. Discussion

In the conventional approach, electrostatic potential energy (Coulomb’s law) does not depend on $\dot{r}$. The dependence on velocity only resides in kinetic energy, both in the classical (Newtonian) and relativistic (SRT) frameworks. Therefore, in the latter case, all the mathematics to prevent velocities from exceeding the limiting value of c must be contained in the kinetic energy expression. The solution provided by the SRT is that the kinetic energy increases with increasing velocity, tending to be infinity as the velocity approaches the value of c.

In Weber’s or Phipps’ electrodynamics, the situation is not the same, since both potential energy and kinetic energy depend on $\dot{r}$. This double dependence might seem an unnecessary complexity in view of the success of the alternative (Coulomb-based) approach, but it could be justified if it could explain the same known phenomena without having to accept the epistemologically harder points of SRT, such as time dilations and space contractions.

According to Equation (27), the maximum value of the kinetic energy is $(\mu c^2+E)$ and not infinity, as is the case for relativistic kinetic energy. Particle accelerators may seem to be excellent proof that SRT is the correct choice. However, this is not the case. With Phipps’ electrodynamics, the potential energy tends to be zero as $\dot{r}\to c$; i.e., the force on the interacting particles tends to be zero as $\dot{r}\to c$, so they can no longer gain energy. Our belief that particles travelling inside particle accelerators have very high energies is due to the proven difficulty of slowing them down. However, since any deceleration must be caused by an electromagnetic force, if these were of the Weberian type (such as Phipps’ force), they would be extraordinarily weak (and therefore be highly ineffective at slowing down) until the particles are travelling at speeds much slower than the speed of light. This ignored inefficiency of the forces to achieve deceleration would create the appearance that the particles actually had very high initial energy values. The mathematics of these two competing theoretical models are very different, but both are perfectly self-consistent.

In light of our demonstration, the energy balances of Equations (21) and (23) are mathematically equivalent, although metaphysically speaking they respond to very different approaches. However, we insist, only if Phipps’ electrodynamics (together with the new expression for kinetic energy) can explain the totality of known electromagnetic phenomena, its apparently greater complexity would be justified, because it would be achieved without the need to appeal to the space-time approaches of SRT.

3. The Two-Body Problem in the New Framework

3.1. Radial Motion

Supposing the system consisting of two charges (q₁ and q₂) and a reduced mass, μ, given by Equation (8), interacting with each other according to Phipps’ potential energy, Equation (26), and which are radially displaced relative to each other, according to the expression of the kinetic energy given by Equation (27), for this system, using the reduced mass procedure, the law of energy conservation will require that

$$\frac{q_1 q_2}{4\pi {\epsilon }_0 r}{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}+(\mu c^2+E)\cdot \left[1-{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}\right]=E$$

(30)

which can be rewritten as

$$\frac{q_1 q_2}{4\pi {\epsilon }_0 r}{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}+\mu c^2\cdot \left[1-{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}\right]=E\cdot {\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}$$

(31)

additionally simplifying

$$\frac{q_1 q_2}{4\pi {\epsilon }_0 r}+\mu c^2\cdot \left[{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{-\frac{1}{2}}-1\right]=E$$

(32)

which turns out to be the same expression that would have been obtained using Coulomb’s potential energy and the relativistic kinetic energy.

Solving for $\dot{r}$, it follows that

$$\dot{r}=\pm c{\left[1-{\left(1+\frac{E-\alpha /r}{\mu c^2}\right)}^{-2}\right]}^{\frac{1}{2}}$$

(33)

where $\alpha =q_1{q}_2/(4\pi {\epsilon }_0)$.

Except in those mathematical situations that revert to a complex (non-real) $\dot{r}$, $\dot{r}\le c$ is fulfilled, which is what would be expected according to SRT. However, if we analyse the interaction between two charges of the same mass, with velocities ${\overrightarrow{v}}_1$ and ${\overrightarrow{v}}_2$ with respect to a reference frame bound to the centre of mass, we obtain $\left|{\overrightarrow{v}}_1\right| = \left|{\overrightarrow{v}}_2\right| =c/2$, and not $\left|{\overrightarrow{v}}_1\right| = \left|{\overrightarrow{v}}_2\right| =c$, as would be expected from SRT [34]. With Weber’s and Phipps’ electrodynamics (see [26,35,36,37]), it is not possible to obtain, simultaneously, $\dot{r}=c$ and $\left|{\overrightarrow{v}}_1\right| = \left|{\overrightarrow{v}}_2\right| =c$.

The price to pay for accepting the reorganisation implied by the definitions contained in Equations (24) and (25) is that, in addition to adopting a new expression for kinetic energy, we must also modify the expressions for force and momentum. The new expression for kinetic energy, given by Equation (27), requires an expression for force that is different from the Newtonian one ($\overrightarrow{F}=\mu \ddot{r} \widehat{r}$). We can find it simply by appealing to the definition of Equation (6):

$$\overrightarrow{F}=\frac{1}{\dot{r}}\cdot \frac{dT}{dt}\widehat{r}=-\frac{(\mu c^2+E)}{2\dot{r}}\cdot {\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{-\frac{1}{2}}\cdot \left(\frac{-2 \dot{r} \ddot{r}}{c^2}\right)\widehat{r}=\left(\mu +E/c^2\right)\cdot {\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{-\frac{1}{2}}\cdot \ddot{r} \widehat{r}$$

(34)

An expression for the kinetic energy similar to that described by Equation (27) was already reported by Li in [32], where it was derived from a postulated expression for the force, which is equal to that of Equation (34). In contrast, in this work, Equation (34) has not been postulated, but has been derived from the kinetic energy expression, which is also not postulated, but deduced from the mass–energy equivalence.

Additionally, the expression of momentum, $\overrightarrow{p}$, will have to change. Keeping the definition $\overrightarrow{F}=d\overrightarrow{p}/dt$ as essential, then $d\overrightarrow{p}=\overrightarrow{F}dt$, so that, taking into account Equation (34), it follows that

$$d\overrightarrow{p}=\left(\mu +E/c^2\right)\cdot {\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{-\frac{1}{2}}\cdot d\dot{r} \widehat{r}$$

(35)

which when integrated turns out to be

$$\overrightarrow{p}=c\left(\mu +E/c^2\right)\cdot \arcsin \left(\dot{r}/c\right)\widehat{r}$$

(36)

A similar expression was also reported by Li in [32]. Note that $p=0$ when $\dot{r}=0$, and that $p=(\pi /2)\left(\mu c+E/c\right)$ when $\dot{r}=c$. Note, also, that since the definition $\overrightarrow{F}=d\overrightarrow{p}/dt$ is preserved, then Newton’s third law of action and reaction is also satisfied in an isolated system with no external forces acting on it (momentum is conserved).

In the limit of low radial velocities and low energies ($\mu c^2\gg E$), Equation (34), referring to the force, can be simplified to

$$\overrightarrow{F}\approx \mu \cdot \left(1+\frac{{\dot{r}}^2}{2c^2}\right)\cdot \ddot{r} \widehat{r}\approx \mu \ddot{r} \widehat{r}$$

(37)

which is the well-known expression of Newton’s second law.

In the same limit again, from Equation (36), referring to the momentum, the Newtonian expression will also be recovered:

$$\overrightarrow{p}\approx c \mu \cdot \left(\dot{r}/c\right) \widehat{r}=\mu \dot{r} \widehat{r}$$

(38)

The dynamic analysis of the motion is achieved by equating the expression of Phipps’ force, given by Equation (5), with the new expression of the second law of dynamics, Equation (34). The result is greatly simplified and leads to

$$\frac{q_1 q_2}{4\pi {\epsilon }_0 r^2}\left(1-\frac{{\dot{r}}^2}{c^2}+\frac{r \ddot{r}}{c^2}\right)=\left(\mu +\frac{E}{c^2}\right) \ddot{r}$$

(39)

It can be seen that in the low-energy limit ($E/c^2\ll \mu$), this expression is similar, except for a factor of ½ in the second term on the left, to the expression that would be obtained using Weber’s force and Newton’s second law. One reason why Weber’s electrodynamics together with Newtonian dynamics give predictions close to those of the relativistic ones, even though both are valid only for low velocities, is that the dynamical equations derived from this combination are very similar to those that arise (after simplification) using Phipps’ electrodynamics and the new mechanics together. In many cases, the difference lies in a factor of ½, which corrects for the fact that for Weber the limiting velocity is $\sqrt{2}c$, whereas for Phipps (and SRT) it is c.

Introducing in Equation (39) the expression of E taken from Equation (32), and regrouping the terms with $\ddot{r}$, we obtain

$$\frac{q_1 q_2}{4\pi {\epsilon }_0 r^2}=\mu {\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{-\frac{3}{2}} \ddot{r}$$

(40)

which is the well-known expression for relativistic rectilinear accelerated motion [29].

For ease of comparison, the expressions resulting from the energy balance and dynamic analysis using three scenarios of interest are summarised in

Table 1. Expressions describing radial motion in the scenarios of interest. The constant $\alpha =q_1{q}_2/(4\pi {\epsilon }_0)$.

Framework	Energy Analysis	Dynamic Analysis
Coulomb + Newton	$\frac{\alpha }{r}+\frac{\mu {\dot{r}}^2}{2}=E$	$\frac{\alpha }{r^2}=\mu \ddot{r}$
Weber + Newton	$\frac{\alpha }{r}\left(1-\frac{{\dot{r}}^2}{2c^2}\right)+\frac{\mu {\dot{r}}^2}{2}=E$	$\frac{\alpha }{r^2}\left(1-\frac{{\dot{r}}^2}{2c^2}+\frac{r \ddot{r}}{c^2}\right)=\mu \ddot{r}$
Phipps + New Mechanics	$\frac{\alpha }{r}+\mu c^2\cdot \left[{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{-\frac{1}{2}}-1\right]=E$ In the limit $\dot{r}\ll c$, the Newton + Coulomb expression is recovered.	$\frac{\alpha }{r^2}\left(1-\frac{{\dot{r}}^2}{c^2}+\frac{r \ddot{r}}{c^2}\right)=\left(\mu +\frac{E}{c^2}\right)\ddot{r}$ In the limit $E/c^2\ll \mu$, $\frac{\alpha }{r^2}\left(1-\frac{{\dot{r}}^2}{c^2}+\frac{r \ddot{r}}{c^2}\right)= \mu \ddot{r}$

: (a) Coulomb’s law and Newton’s mechanics, (b) Weber’s law and Newton’s mechanics, and (c) Phipps’ law and the new mechanics proposed in this work.

3.2. Orbital Motion

In this case, admitting that the moving charge (q₁) could move around the ‘fixed’ charge (q₂), expressed in polar coordinates, the law of energy conservation implies that

$$\frac{q_1 q_2}{4\pi {\epsilon }_0 r}{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}+(\mu c^2+E)\cdot \left[1-{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}\right]+(\mu c^2+E)\cdot \left[1-{\left(1-\frac{r^2{\dot{\phi }}^2}{c^2}\right)}^{\frac{1}{2}}\right]=E$$

(41)

where the expression for translational kinetic energy, given by Equation (27), has been extended to the angular case, simply by changing $\dot{r}$, the radial velocity, by $r\dot{\phi }$, the transversal velocity (a demonstration of this expression can be found in the Appendix A of this paper).

As a simplification,

$$\frac{q_1 q_2}{4\pi {\epsilon }_0 r}{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}+(\mu c^2+E)\cdot \left[2-{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}-{\left(1-\frac{r^2{\dot{\phi }}^2}{c^2}\right)}^{\frac{1}{2}}\right]=E$$

(42)

Similarly, the following expression could be proposed for the momentum:

$$\overrightarrow{p}=\left(\mu +E/c^2\right)c\arcsin (\dot{r}/c) \widehat{r}+\left(\mu +E/c^2\right)c\arcsin (r\dot{\phi }/c) \widehat{\phi }$$

(43)

where $\widehat{r}$ and $\widehat{\phi }$ are the unit vectors in the radial and transversal directions, respectively (as shown in Appendix B, $\overrightarrow{p}$ is parallel to $\overrightarrow{v}$).

Additionally, following a similar reasoning, for the angular momentum we could propose the expression

$$\overrightarrow{L}=\overrightarrow{r}\times \overrightarrow{p}=\left(\mu +E/c^2\right)c r\arcsin (r\dot{\phi }/c) \widehat{z}$$

(44)

where $\widehat{z}$ is the unit vector normal to the plane formed by $\widehat{r}$ and $\widehat{\phi }$, i.e., $\widehat{z}=\widehat{r}\times \widehat{\phi }$.

The expression of the force (the new second law of dynamics) shall be calculated as the time derivative of the momentum:

$$\begin{array}{l}\overrightarrow{F}=\left(\mu +\frac{E}{c^2}\right)\left[\ddot{r}{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{-\frac{1}{2}}-c\dot{\phi }\arcsin \left(\frac{r\dot{\phi }}{c}\right)\right]\widehat{r}+\\ +\left(\mu +\frac{E}{c^2}\right)\left[\left(\dot{r}\dot{\phi }+r\ddot{\phi }\right){\left(1-\frac{r^2{\dot{\phi }}^2}{c^2}\right)}^{-\frac{1}{2}}+c\dot{\phi }\arcsin \left(\frac{\dot{r}}{c}\right)\right]\widehat{\phi }\end{array}$$

(45)

where it has been considered that

$$\frac{d\widehat{r}}{dt}=\dot{\phi }\widehat{\phi }$$

(46)

$$\frac{d\widehat{\phi }}{dt}=-\dot{\phi }\widehat{r}$$

(47)

Since the force is central, the transversal component in Equation (45) must be zero.

In the limit of (radial and transversal) low velocities and low energy, Equation (42), which expresses the conservation of energy, is simplified, and it allows a recovery of the classical expression. Namely,

$$\frac{q_1 q_2}{4\pi {\epsilon }_0 r}\left(1-\frac{{\dot{r}}^2}{2c^2}\right)+\mu c^2\cdot \left[2-\left(1-\frac{{\dot{r}}^2}{2c^2}\right)-\left(1-\frac{r^2{\dot{\phi }}^2}{2c^2}\right)\right]\simeq E$$

(48)

Additionally, from here, simplifying and, subsequently, neglecting the only term in ${\left(\dot{r}/c\right)}^2$,

$$\frac{q_1 q_2}{4\pi {\epsilon }_0 r}+\frac{\mu {\dot{r}}^2}{2}+\frac{\mu r^2{\dot{\phi }}^2}{2}\simeq E$$

(49)

At the same limit, Equation (43), referring to momentum, and Equation (44), referring to angular momentum, are reduced to the well-known Newtonian expressions:

$$\overrightarrow{p}\simeq \mu \dot{r} \widehat{r}+\mu r \dot{\phi } \widehat{\phi }$$

(50)

$$\overrightarrow{L}\simeq \mu r^2\dot{\phi } \widehat{z}$$

(51)

Finally, at the same limit, the expression of the new second law of dynamics, Equation (45), is simplified to

$$\overrightarrow{F}\simeq \mu \left[\ddot{r}\left(1+\frac{{\dot{r}}^2}{2c^2}\right)-r{\dot{\phi }}^2\right]\widehat{r}+\mu \left[\left(\dot{r}\dot{\phi }+r\ddot{\phi }\right)\left(1+\frac{r^2{\dot{\phi }}^2}{2c^2}\right)+\dot{\phi }\dot{r}\right]\widehat{\phi }$$

(52)

Additionally, neglecting the terms in ${\left(\dot{r}/c\right)}^2$ and ${\left(r\dot{\phi }/c\right)}^2$, it turns out that

$$\overrightarrow{F}\approx \mu \left(\ddot{r}-r{\dot{\phi }}^2\right)\widehat{r}+\mu \left(2\dot{r}\dot{\phi }+r\ddot{\phi }\right)\widehat{\phi }$$

(53)

which coincides with the Newtonian expression.

From Equation (44), it follows that

$$\frac{r\dot{\phi }}{c}=\sin \left(\frac{L}{(\mu +E/c^2)cr}\right)$$

(54)

Substituting Equation (54) into Equation (42), which gives the total energy, we obtain

$$E=\frac{q_1 q_2}{4\pi {\epsilon }_0 r}{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}+(\mu c^2+E)\left[2-{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}-\cos \left(\frac{L}{(\mu +E/c^2)cr}\right)\right]$$

(55)

which is the expression of the total energy as a function of the variables r, $\dot{r}$ and L. Manipulating this algebraically, it follows that

$$\frac{{\dot{r}}^2}{c^2}=1-{\left\{\frac{E-(\mu c^2+E)\cdot \left[2-\cos \left(\frac{L}{(\mu +E/c^2)cr}\right)\right]}{\frac{\alpha }{r}-(\mu c^2+E)}\right\}}^2$$

(56)

where, again, $\alpha =q_1{q}_2/(4\pi {\epsilon }_0)$. Obviously, by ensuring $L=0$, we recover Equation (33), for the radial motion.

Restricting this to the case of a uniform circular motion, $\dot{r}=0$, $\ddot{r}=0$ and $\ddot{\phi }=0$, then, for Phipps’ electrodynamics coupled with the new mechanics, the radial component of the force satisfies

$$\frac{q_1 q_2}{4\pi {\epsilon }_0 r^2}=-\left(\mu +\frac{E}{c^2}\right)c\dot{\phi }\arcsin \left(\frac{r\dot{\phi }}{c}\right)$$

(57)

Now, taking into account the definition of angular momentum, given by Equation (44), and that $dL/dt=0$, because the force is central, then

$$(r{\dot{\phi }}^2)\cdot {\left(1-\frac{r^2{\dot{\phi }}^2}{c^2}\right)}^{-\frac{1}{2}}+c\dot{\phi }\arcsin \left(\frac{r\dot{\phi }}{c}\right)=0$$

(58)

Thus,

$$\frac{q_1 q_2}{4\pi {\epsilon }_0 r^2}=\left(\mu +\frac{E}{c^2}\right)\cdot (r{\dot{\phi }}^2)\cdot {\left(1-\frac{r^2{\dot{\phi }}^2}{c^2}\right)}^{-\frac{1}{2}}$$

(59)

which coincides, when $E/c^2\ll \mu$, with the centripetal force expression provided in the Maxwell–Lorentz and SRT framework [29].

Table 2. Expressions describing the orbital motion in the scenarios of interest. $\alpha =q_1{q}_2/(4\pi {\epsilon }_0)$.

Framework	Energy Analysis	Dynamic Analysis
Coulomb + Newton	$\frac{\alpha }{r}+\frac{\mu {\dot{r}}^2}{2}+\frac{\mu r^2{\dot{\phi }}^2}{2}=E$	$\frac{\alpha }{r^2}=\mu \left(\ddot{r}-r{\dot{\phi }}^2\right)$ $2\dot{r}\dot{\phi }+r\ddot{\phi }=0$
Weber + Newton	$\frac{\alpha }{r}\left(1-\frac{{\dot{r}}^2}{2c^2}\right)+\frac{\mu {\dot{r}}^2}{2}+\frac{\mu r^2{\dot{\phi }}^2}{2}=E$	$\frac{\alpha }{r^2}\left(1-\frac{{\dot{r}}^2}{2c^2}+\frac{r \ddot{r}}{c^2}\right)=\mu \left(\ddot{r}-r{\dot{\phi }}^2\right)$ $2\dot{r}\dot{\phi }+r\ddot{\phi }=0$
Phipps + New mechanics	$\begin{array}{l}\frac{\alpha }{r}{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}+\\ +(\mu c^2+E)\cdot \left[2-{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}-{\left(1-\frac{r^2{\dot{\phi }}^2}{c^2}\right)}^{\frac{1}{2}}\right]\\ =E\end{array}$ In the limit of low velocities and $E/c^2\ll \mu$, $\frac{\alpha }{r}\left(1-\frac{{\dot{r}}^2}{2c^2}\right)+\frac{\mu }{2}\left({\dot{r}}^2+r^2{\dot{\phi }}^2\right)\simeq E$ Neglecting the terms of the second order in $\dot{r}/c$, the Coulomb + Newton expression is recovered.	$\begin{array}{l}\frac{\alpha }{r^2}\left(1-\frac{{\dot{r}}^2}{c^2}+\frac{r \ddot{r}}{c^2}\right)=\\ =\left(\mu +\frac{E}{c^2}\right)\left[\ddot{r}-c\dot{\phi }\arcsin \left(\frac{r\dot{\phi }}{c}\right)\cdot {\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{\frac{1}{2}}\right]\end{array}$ $\dot{r}\dot{\phi }+r\ddot{\phi }+c\dot{\phi }\arcsin \left(\frac{\dot{r}}{c}\right)\cdot {\left(1-\frac{r^2{\dot{\phi }}^2}{c^2}\right)}^{\frac{1}{2}}=0$ In the limit of low velocities and $E/c^2\ll \mu$, $\frac{\alpha }{r^2}\left(1-\frac{{\dot{r}}^2}{c^2}+\frac{r \ddot{r}}{c^2}\right)\simeq \mu \left[\ddot{r}-r{\dot{\phi }}^2\left(1-\frac{{\dot{r}}^2}{2c^2}\right)\right]$ $\dot{r}\dot{\phi }+r\ddot{\phi }+\dot{r}\dot{\phi }\left(1-\frac{r^2{\dot{\phi }}^2}{2c^2}\right)\simeq 0$ Neglecting the terms of the second order, the Coulomb + Newton expressions are recovered.

shows the equations resulting from the energy balance and the application of the new second law of dynamics for the three scenarios of interest.

4. The Capacitor Problem in the New Framework

The potential energies of Weber and Phipps, Equations (1) and (2), are valid for the two-body problem (two mutually interacting particles, isolated from the rest of the universe). In this case, it is obvious that both expressions guarantee the existence of an ultimate velocity ($\sqrt{2}c$ in the Weber case, and c in the Phipps case). It is expected that this feature would hold in other situations where many particles are involved. Unfortunately, this is not always the case.

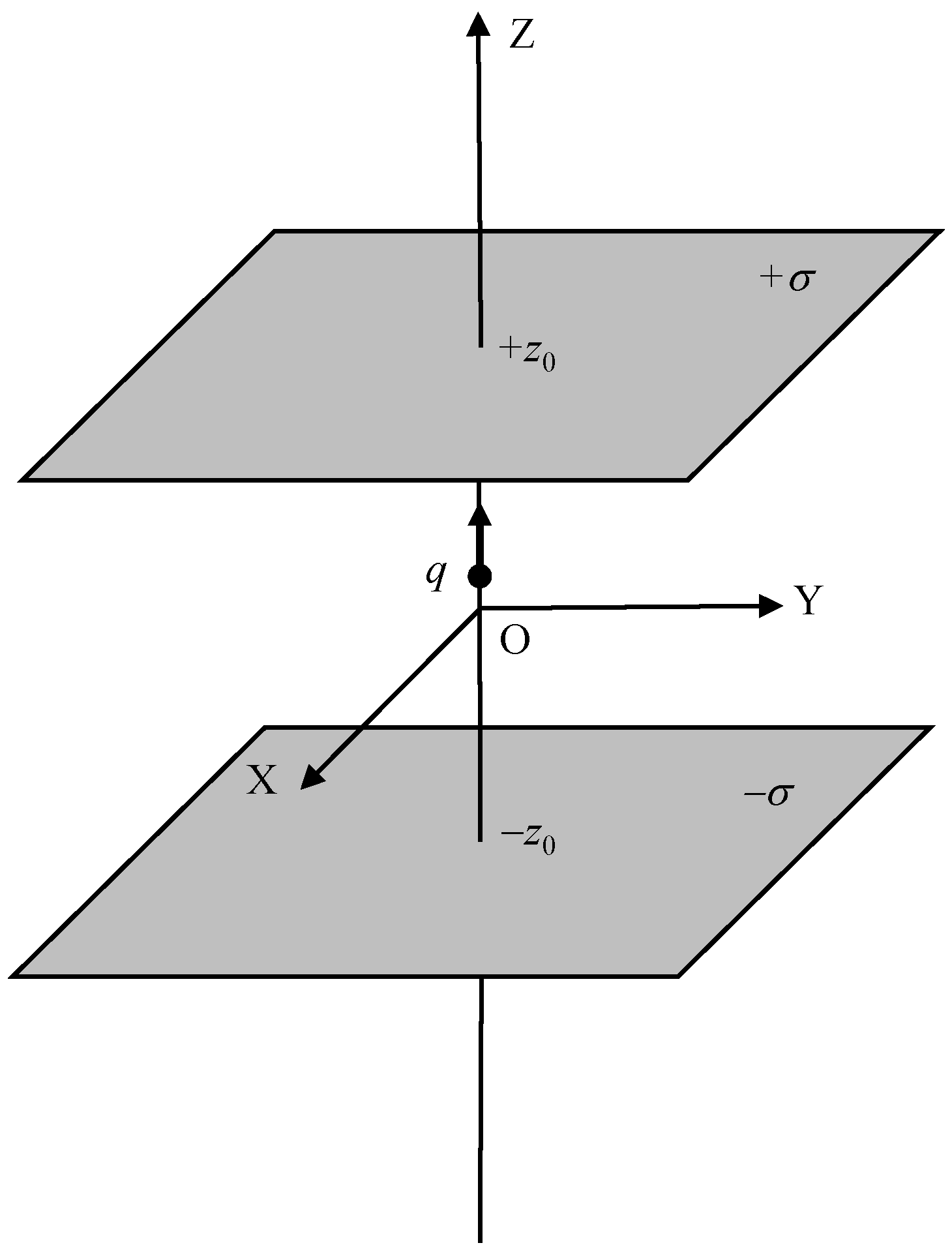
We will now discuss the motion of a charge, q, moving orthogonally to the infinite plates of an ideal capacitor with surface charge densities, $\pm \sigma$. The plates are situated at $\pm z_0$, with respect to a frame inside the capacitor, at an equal distance from both plates, i.e., at the centre of mass of the system (Figure 1).

4.1. Relativistic Solution

According to the conventional framework (the Maxwell–Lorentz and SRT framework), there is no electric field outside the capacitor, but inside there is a uniform electric field given by $\overrightarrow{E}=-(\sigma /{\epsilon }_0)\widehat{z}$, which means that there is a voltage difference between the two infinite plates given by $V_0=2\sigma z_0/{\epsilon }_0=2z_{0}E$.

Taking into account the law of energy conservation, the total mechanical energy of a particle of mass (m) and charge (q) can be expressed as

$$E=q\frac{V_0}{2}\frac{z}{z_0}+m{c}^2\left[{\left(1-\frac{v^2}{c^2}\right)}^{-\frac{1}{2}}-1\right]$$

(60)

where the relativistic expression of kinetic energy is considered, being $v=\dot{z}$ the velocity of the charge with respect to the chosen reference frame. Assuming that at the midpoint between the plates, $z=0$, a charge (q), with mass (m) and zero initial velocity is placed, the energy at any z between 0 and z₀ is expressed as

$$-\frac{q{V}_0}{2m{c}^2}\frac{z}{z_0}={\left(1-\frac{v^2}{c^2}\right)}^{-\frac{1}{2}}-1$$

(61)

from which, isolating v, we obtain

$$v=\pm c{\left[1-{\left(1-\frac{q{V}_0}{2m{c}^2}\frac{z}{z_0}\right)}^{-2}\right]}^{\frac{1}{2}}$$

(62)

It can be seen from this expression that no matter how high a value V₀ might be, v cannot exceed the value of c (i.e., if $V_0\to \infty$, then $v\to c$), in accordance with the postulations of the SRT.

The force felt by the test charge outside the capacitor would be zero, since there is no electric field outside. Inside the capacitor, however, the charge would feel a force given by

$$\overrightarrow{F}=-\frac{q{V}_0}{2z_0}\widehat{z}=\frac{d}{dt}\left[mv{\left(1-\frac{v^2}{c^2}\right)}^{-\frac{1}{2}}\widehat{z}\right]=m{\left(1-\frac{v^2}{c^2}\right)}^{-\frac{3}{2}}a \widehat{z}$$

(63)

where a is the acceleration at which the charge would move rectilinearly, according to SRT [18].

4.2. Solution with the New Electrodynamics

In previous works [26,37], this problem was solved using Weber’s and Phipps’ electrodynamical potential energies. In both cases, it was found that the solution obtained did not guarantee the existence of an upper limit to the velocity, unless an expression for kinetic energy different from the Newtonian one, such as the relativistic expression or something similar, was used. In the same sense, to overcome the above drawback, in a previous work [27] by the author, the need to use effective potential energy, $U^{*}$, was shown, so that

$$U^{*}\equiv U-\dot{r}\cdot \frac{\partial U}{\partial \dot{r}}$$

(64)

Applying this expression to Phipps’ potential energy yields to obtain the following effective potential energy,

$$U_P^{*}=\frac{q_1{q}_2}{4\pi {\epsilon }_0}\frac{1}{r}{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{-\frac{1}{2}}$$

(65)

Integrating this interaction energy for all fixed charges located on the capacitor plates, the following expression is obtained for the net potential energy of the test charge, q:

$$U= \left\{\begin{array}{l}\mathrm{sgn}(z) q\frac{V_0}{2}{\left(1-\frac{v^2}{c^2}\right)}^{\frac{1}{2}}, |z| > z_0\\ q\frac{V_0}{2}\frac{z}{z_0}{\left(1-\frac{v^2}{c^2}\right)}^{\frac{1}{2}}, |z| \le z_0\end{array}\right.$$

(66)

In the zone between the plates, $\left|z\right| \le z_0$, the conservation of energy requires that

$$E=q\frac{V_0}{2}\frac{z}{z_0}{\left(1-\frac{v^2}{c^2}\right)}^{\frac{1}{2}}+(m{c}^2+E)\left[1-{\left(1-\frac{v^2}{c^2}\right)}^{\frac{1}{2}}\right]$$

(67)

where the new expression for the kinetic energy, given by Equation (27), is used, now being $\dot{r}=v$, because this is the velocity, relative to the centre of mass, in the direction of the resultant force acting on the charge (responsible for kinetic work), and $\mu =m$, because the mass of the capacitor (which we can assume to be concentrated at its centre of mass) is much larger than that of the test charge.

By rearranging terms, Equation (67) can be rewritten as

$$E=\frac{q{V}_{0}z}{2z_0}+m{c}^2\left[{\left(1-\frac{v^2}{c^2}\right)}^{-\frac{1}{2}}-1\right]$$

(68)

which coincides exactly with the relativistic result given by Equation (60). Naturally, Equations (61) and (62) are also derived from this.

For the outer zone ($\left|z\right| > z_0$), the conservation of energy translates into

$$E=\mathrm{sgn}(z) q\frac{V_0}{2}{\left(1-\frac{v^2}{c^2}\right)}^{\frac{1}{2}} +(m{c}^2+E)\left[1-{\left(1-\frac{v^2}{c^2}\right)}^{\frac{1}{2}} \right]$$

(69)

which is simplified to

$$E=\mathrm{sgn}(z) q\frac{V_0}{2} +m{c}^2\left[{\left(1-\frac{v^2}{c^2}\right)}^{-\frac{1}{2}}-1 \right]$$

(70)

which is the same result that would be obtained assuming that the electric potential is constant in the zone outside the plates (it would not be the case if we integrate Phipps’ potential energy directly).

Although the new framework proposed here succeeds in reproducing the same result as that obtained using Maxwell–Lorentz and SRT, there are profound differences between the two approaches. In SRT, the reason for the existence of a limiting velocity is that if the particle velocity with respect to an inertial observer is v, as $v\to c$, we see that $T\to \infty$, so the particle acceleration tends to be zero, giving a limiting velocity, even though the electric force does not cease. With the model proposed here, however, T does not tend to be infinity as $v\to c$, but it is the electric force (through the electrodynamic potential) that tends to be zero as $v\to c$, preventing subsequent acceleration. Thus, although the two models yield similar energetic results, there are profound metaphysical differences between them, and they cannot be considered equivalent. The advantage of this new electrodynamic route is that the simple space-time framework of Newtonian mechanics can still be used.

On the other hand, Phipps’ effective force, i.e., the force derived from Phipps’ effective potential energy, Equation (5), turns out to be

$${\overrightarrow{F}}_P^{*}=\frac{q_1{q}_2}{4\pi {\epsilon }_0}\frac{\widehat{r}}{r^2}\left[{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{-\frac{1}{2}}-\frac{r \ddot{r}}{c^2}{\left(1-\frac{{\dot{r}}^2}{c^2}\right)}^{-\frac{3}{2}}\right]$$

(71)

Integrating this elementary force over all the fixed charges on the capacitor plates, we find the following net force acting on the test charge, q. After integration we obtain

$$\overrightarrow{F}= \left\{\begin{array}{l}\mathrm{sgn}(z) \frac{q{V}_{0}a}{2c^2}{\left(1-\frac{v^2}{c^2}\right)}^{-\frac{1}{2}}\widehat{z}, |z| > z_0\\ \frac{q{V}_0}{2z_0}\left[-{\left(1-\frac{v^2}{c^2}\right)}^{\frac{1}{2}}+\frac{az}{c^2}{\left(1-\frac{v^2}{c^2}\right)}^{-\frac{1}{2}}\right]\widehat{z}, |z| \le z_0\end{array}\right.$$

(72)

An alternative and faster way to find the force is to apply $\overrightarrow{F}=-(\dot{U}/v)\widehat{z}$ to the net potential energy, U, given by Equation (66).

Equating both branches of Equation (72) with Equation (34), considering $\ddot{r}=a$ and $\mu =m$, we obtain two equalities. The first one is only valid whenever $a=0$. The second one turns out to be

$$\frac{q{V}_0}{2z_0}\left[-{\left(1-\frac{v^2}{c^2}\right)}^{\frac{1}{2}}+\frac{az}{c^2}{\left(1-\frac{v^2}{c^2}\right)}^{-\frac{1}{2}}\right]=\left(m+\frac{E}{c^2}\right){\left(1-\frac{v^2}{c^2}\right)}^{-\frac{1}{2}}a$$

(73)

and inserting Equation (68) into Equation (73), after algebraic manipulation and simplification, we obtain

$$-\frac{q{V}_0}{2z_0}=m{\left(1-\frac{v^2}{c^2}\right)}^{-\frac{3}{2}}a$$

(74)

This result is in line with the prediction of the Maxwell–Lorentz and SRT framework, Equation (63).

4.3. Why Does the Effective Potential Energy Work?

It is not obvious why the calculation in the previous section should use the effective potential energy and not the potential energy directly, as in the case of the interaction of two charges. Some possible options were discussed in the paper [27]. The reason may lie in the fact that in the capacitor problem it is necessary to integrate, in application of the superposition principle, and this, in the case of velocity-dependent potentials, could introduce additional complexity.

From a mathematical point of view, however, the mission of the effective potential energy seems clear: it allows to recover, after the integration process of the potential energy, a functional dependence on velocity similar to that of Phipps.

Assuming that the potential energies U and U* are given by

$$U=\frac{\alpha }{r}\cdot f(\dot{r})$$

(75)

$$U^{*}=\frac{\alpha }{r}\cdot f^{*}(\dot{r})$$

(76)

in the capacitor problem, in order to know the potential energy felt by the test charge, basically the following calculation has to be carried out: $-\dot{r} {\displaystyle \int \left(U^{*}/{\dot{r}}^2\right) }d\dot{r}$. Thus, if the objective is that, after the integration process required by the principle of superposition, the result is an expression with the same dependence on velocity as Phipps’ expression, then it must be fulfilled that

$$f=-\dot{r}{\displaystyle \int \frac{f^{*}}{{\dot{r}}^2} }d\dot{r}$$

(77)

Deriving the last equation with respect to $\dot{r}$, it is found that

$$\frac{d}{d\dot{r}}\left(-\frac{f}{\dot{r}}\right)=\frac{f^{*}}{{\dot{r}}^2}$$

(78)

Additionally, operating

$$f-\dot{r}\cdot \left(df/d\dot{r}\right)=f^{*}$$

(79)

Thus, taking into account the definitions given in Equation (75) and Equation (76), it is concluded that

$$U^{*}=U-\dot{r}\cdot \left(\frac{\partial U}{\partial \dot{r}}\right)$$

(80)

which coincides exactly with Equation (64).

Thus, the definition given for U^* guarantees that, after the integration process which the superposition principle forces, functional dependence on the velocity of Phipps’ expression is recovered. The question is whether or not this effective potential energy, U^*, is merely a mathematical subterfuge or hides some subtle physical meaning. We leave the study of this possibility for another paper.

5. Conclusions

In this work, it is shown that it is possible to derive together the expressions for Phipps’ electrodynamic potential energy and its corresponding kinetic energy on the basis of the principles of energy conservation and mass–energy equivalence. In the limit of low energies and low velocities, it is known that this potential energy becomes Weber’s potential energy, and it has now been proven that the new expression for kinetic energy becomes the classical Newtonian expression.

The sum of Phipps’ potential and new kinetic energies turns out to be equivalent to the sum of the Coulomb potential energy and the SRT kinetic energy. However, the equivalence ends there, because the new approach shares the space-time framework of classical Newtonian mechanics and not the relativistic space-time framework, or its Lorentz transformations.

With the new electrodynamic framework proposed in this work, the problem of two interacting charges, in radial or orbital relative motion, is tackled. For these studies, new expressions for linear momentum, angular momentum, force and kinetic energy are proposed which are shown to be reduced to Newtonian expressions in the limit of low velocities and low energy. All the results obtained are consistent with the existence of a limiting velocity of the value of c, and they are in agreement with the predictions obtained by the Maxwell–Lorentz and SRT framework.

However, the new framework proposed is not sufficient to solve the problem of the motion of a charge between the plates of a charged capacitor. In order to also guarantee the existence of a limiting velocity in this case, it is necessary to resort to the so-called ‘effective potential energy’, which has already been introduced in a previous work. Considering this concept, the capacitor problem can be successfully solved and the same result as that achieved from the Maxwell–Lorentz and SRT framework can be reproduced.

In general, it can be concluded that, in the elementary cases studied, the results of the energy analysis and the dynamic analysis obtained with this new electrodynamic framework and the Maxwell–Lorentz and SRT framework coincide, even though both theoretical models are not metaphysically equivalent. This work opens the door to the consideration that Phipps’ electrodynamic approach and the conventional approach (Maxwell–Lorentz and SRT) could be just two different ways to describe the same reality.