Magnetic Field as an Important Tool in Exploring the Strongly Correlated Fermi Systems and Their Particle–Hole and Time-Reversal Asymmetries
Abstract
:1. Introduction
2. The Effective Mass M*
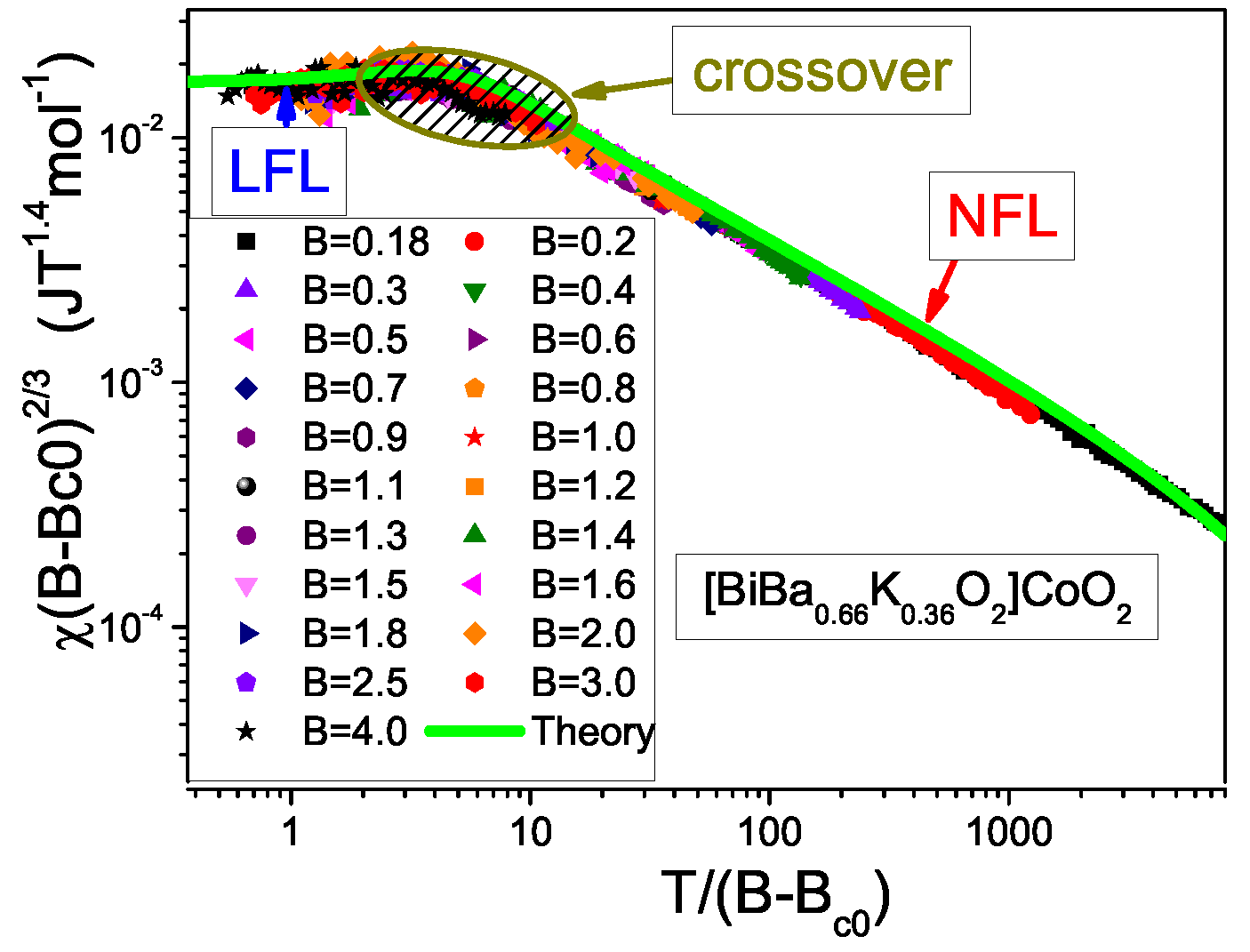
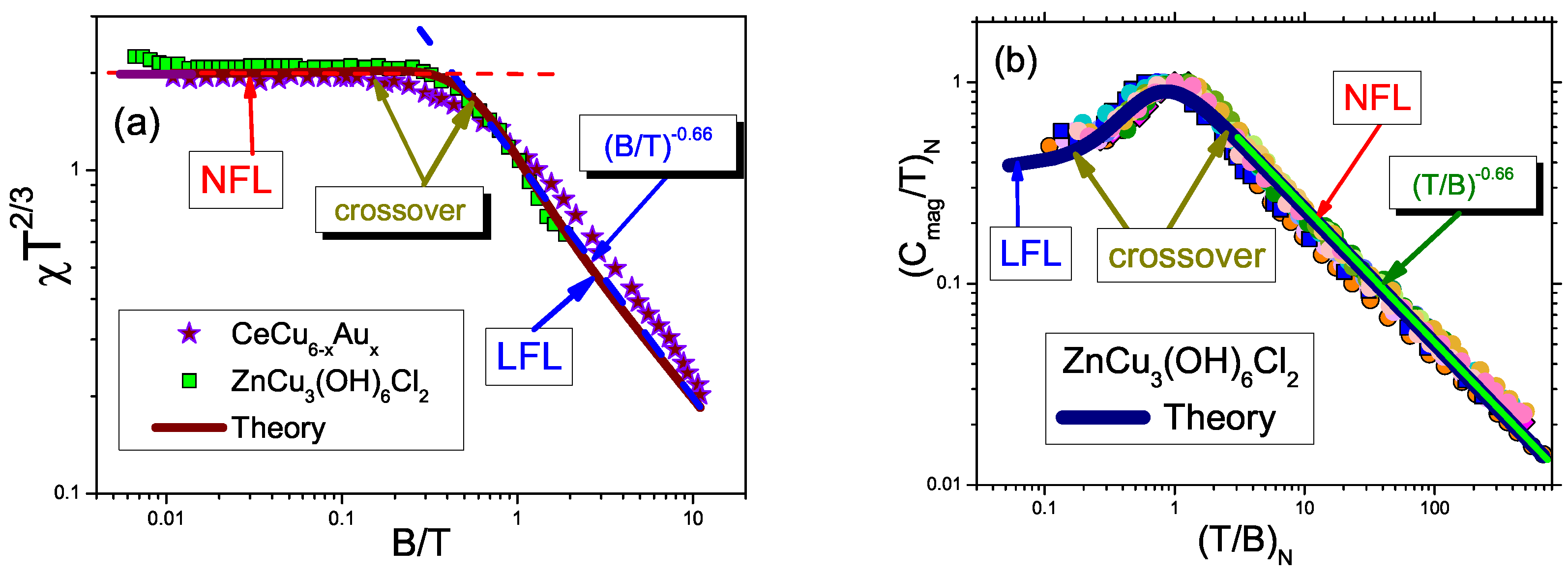
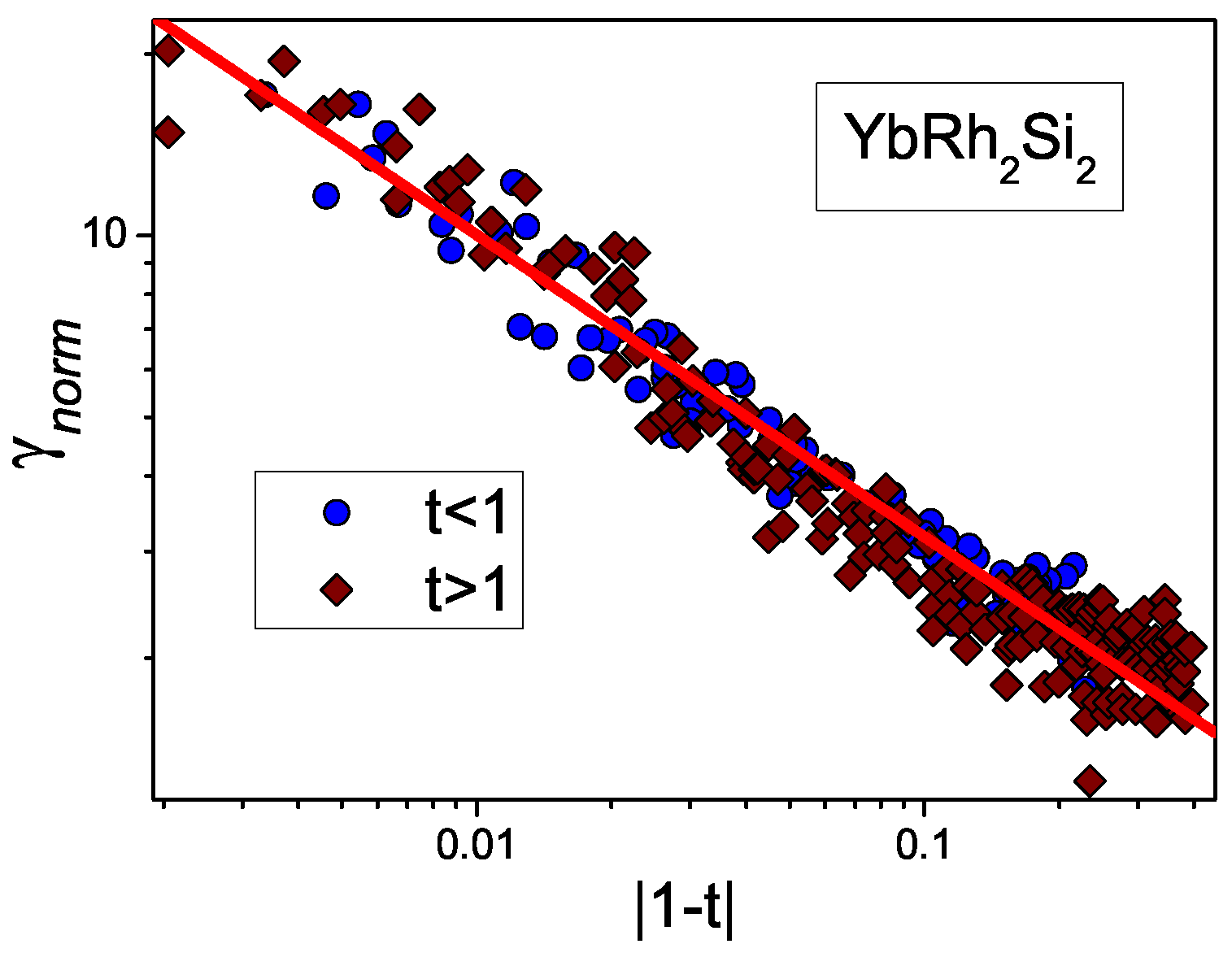
3. The Scaling of the Effective Mass
4. Flat Bands and Particle–Hole Asymmetry
5. Thermopower under the Application of Magnetic Fields
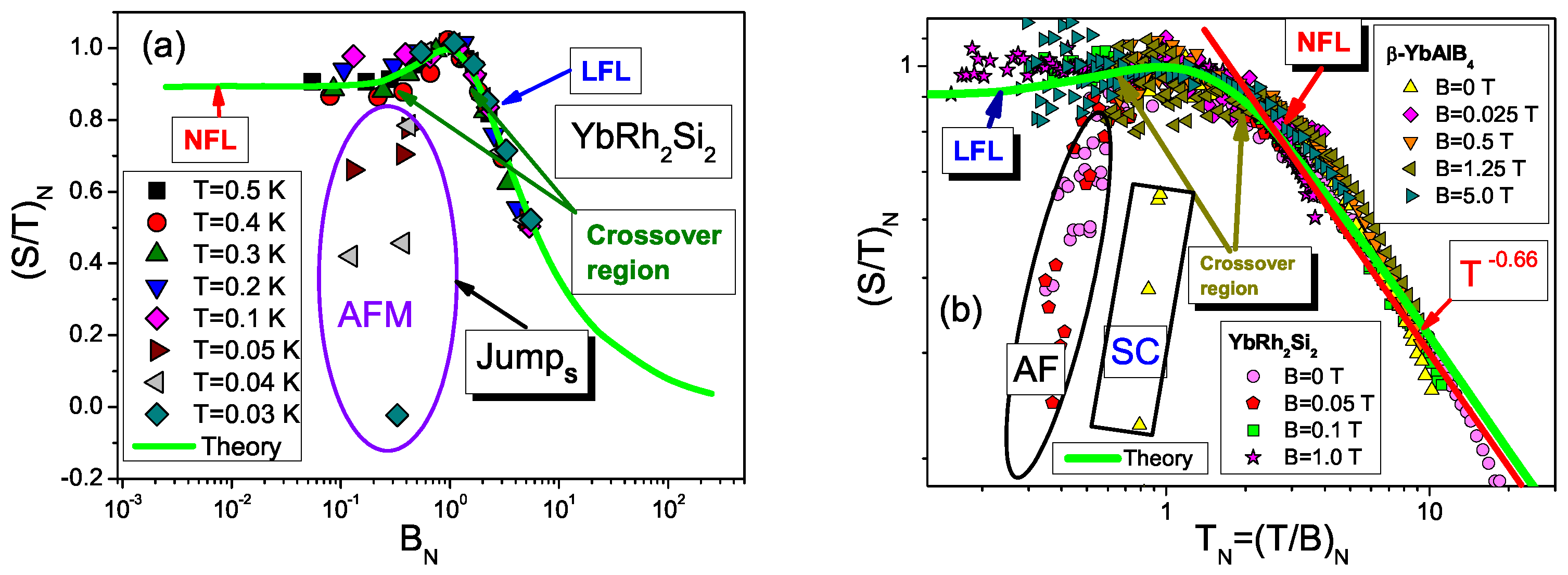
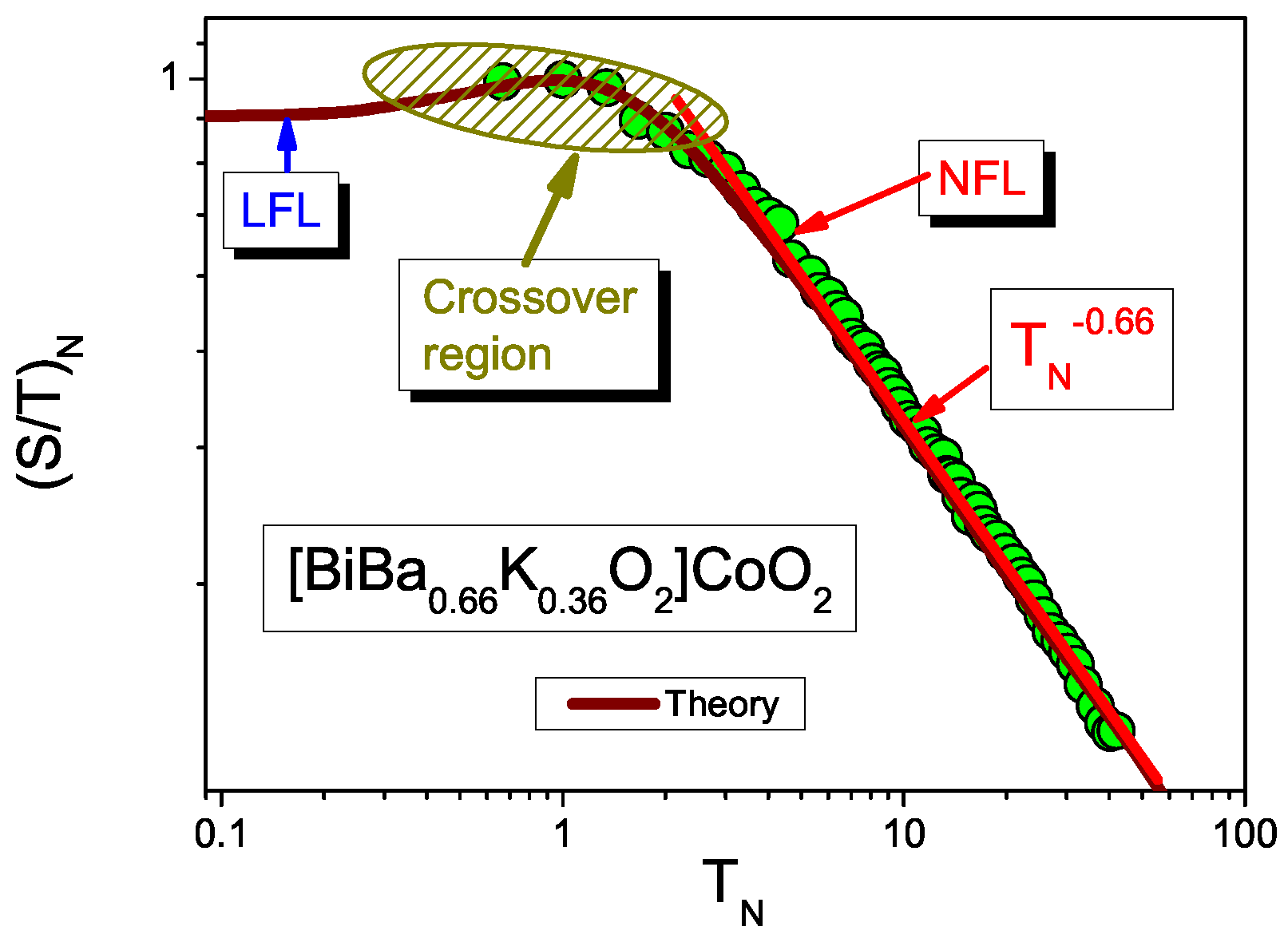
5.1. Scaling
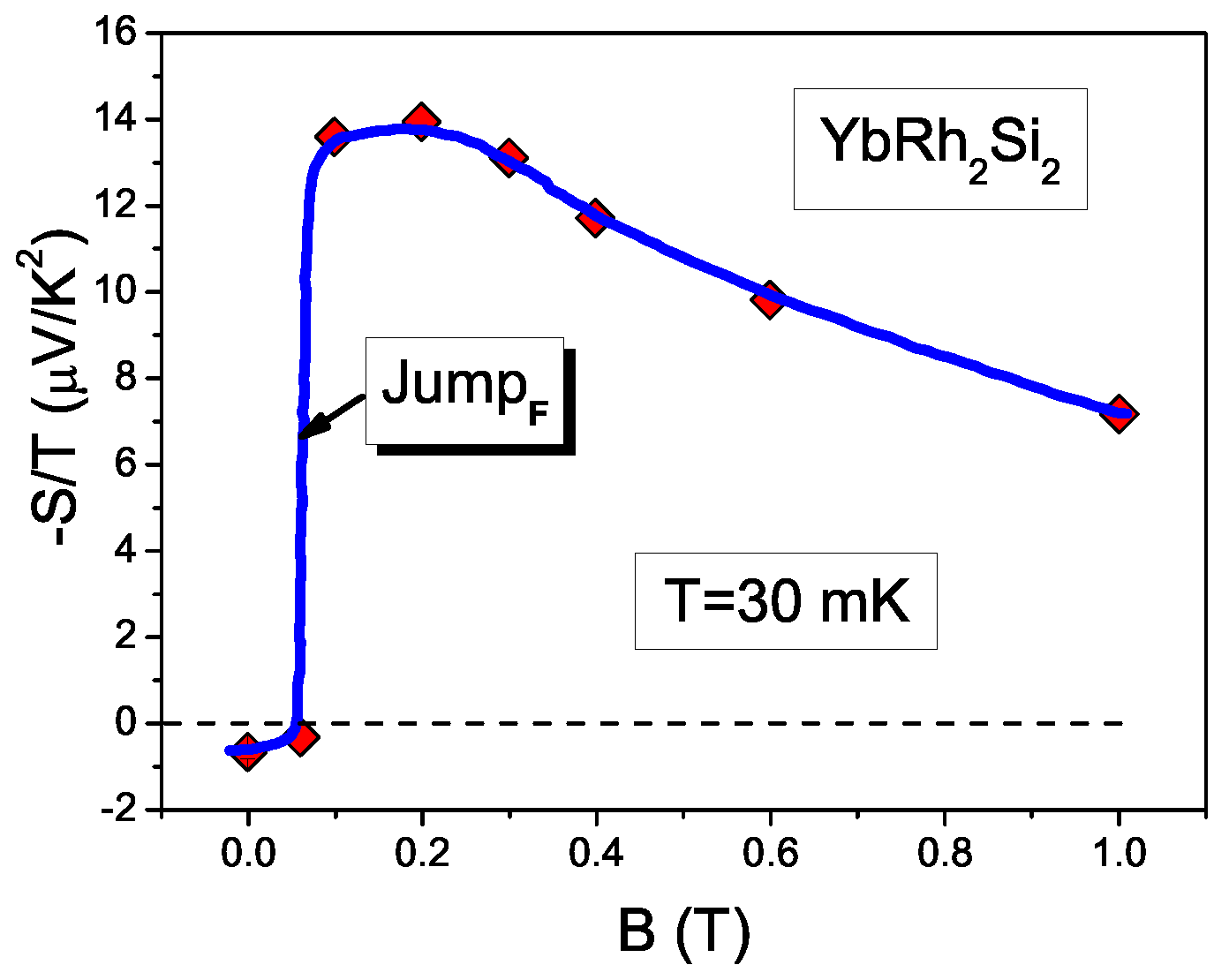
5.2. Flat Bands and Jumps in the AF Phase Transition
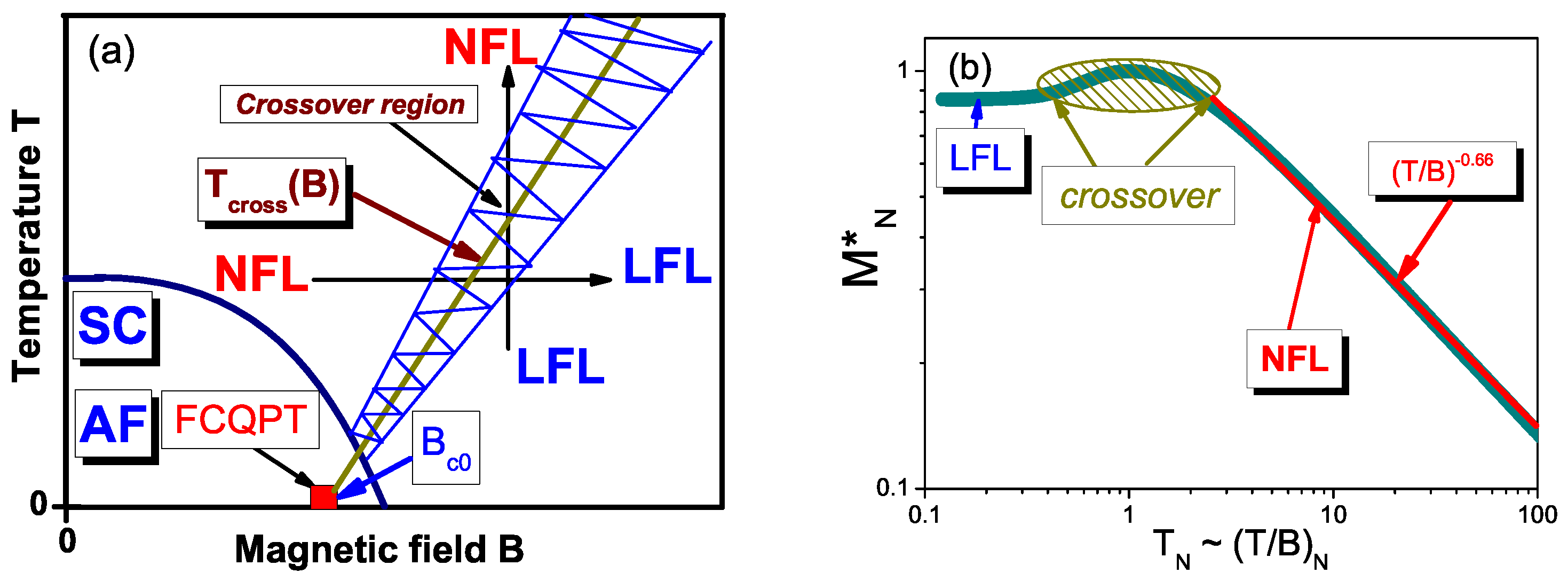
6. The Tricritical Point in the B − T Phase Diagram of YbRh2Si2

Schematic Phase Diagram
7. Magnetic Field to Probe the Nature of Quantum Phase Transition
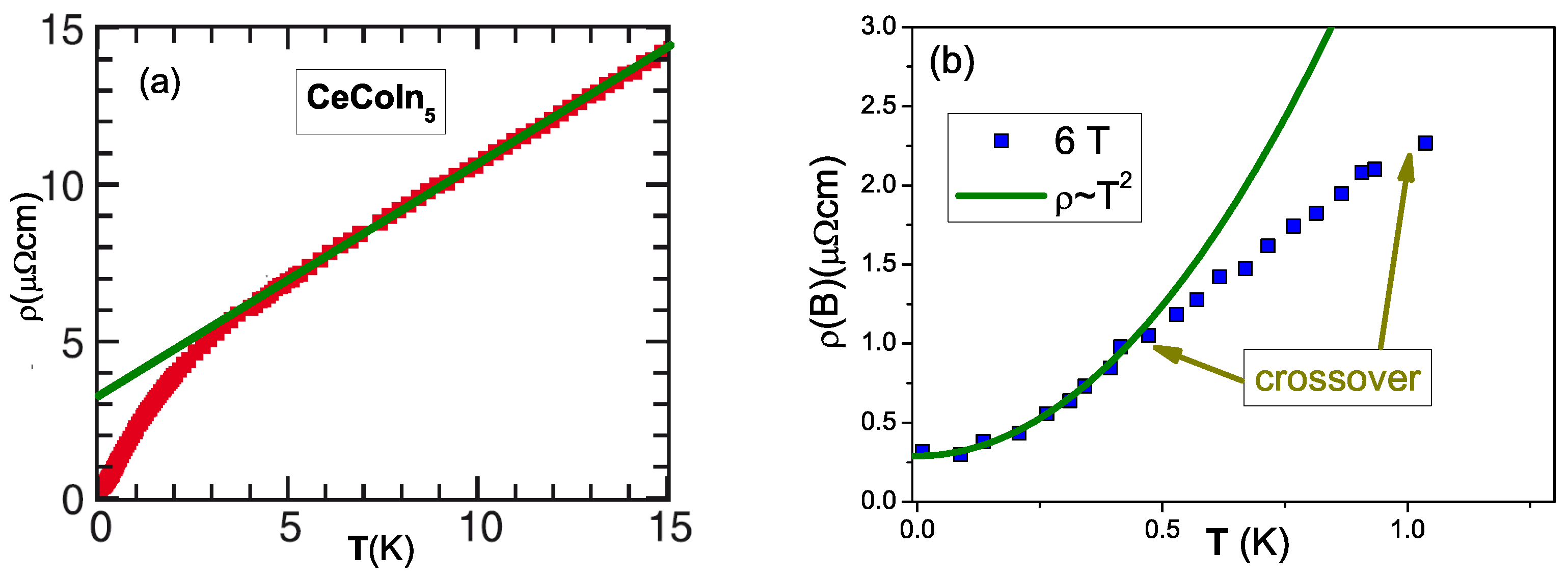
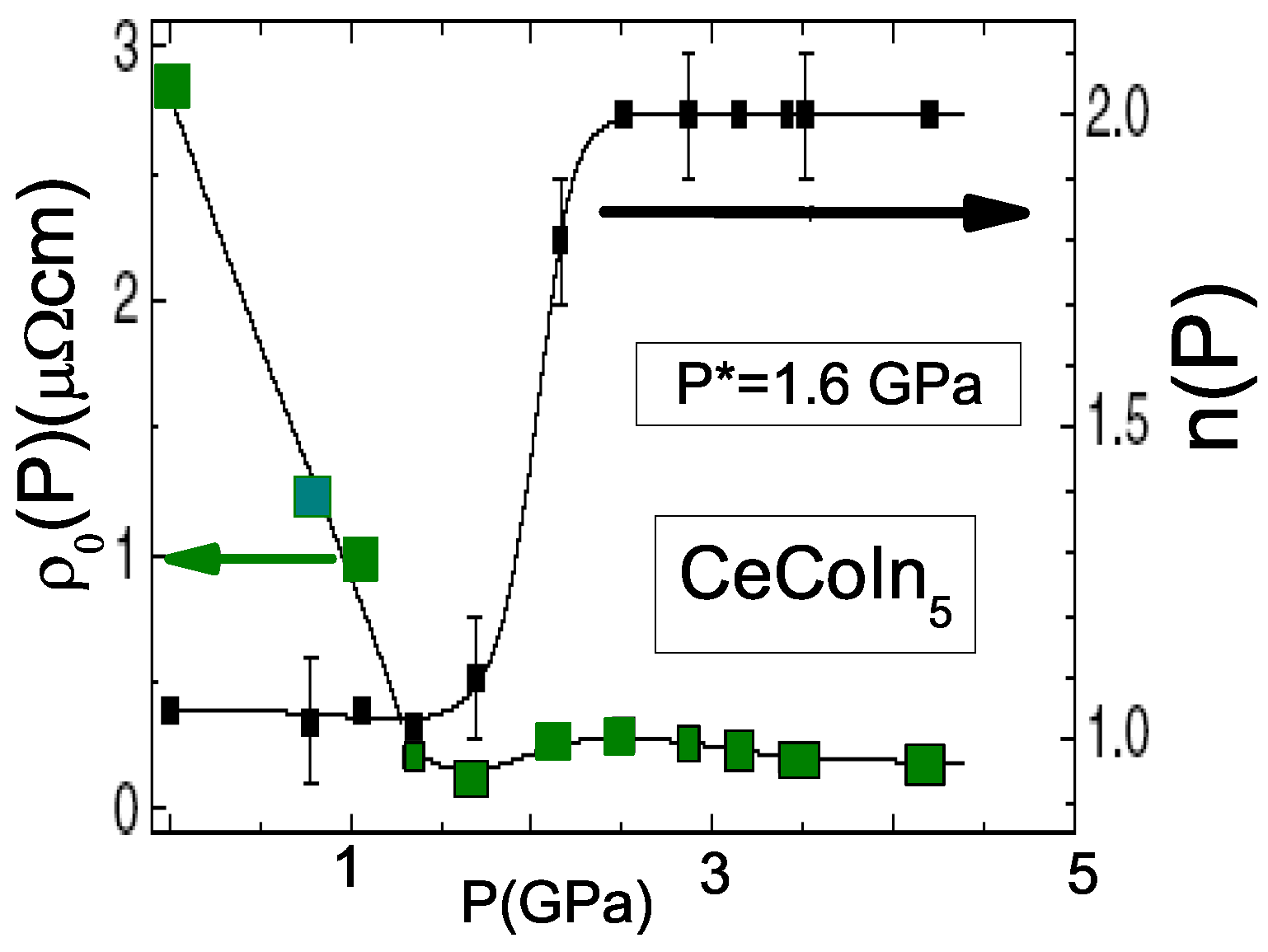
7.1. Residual Resistivity
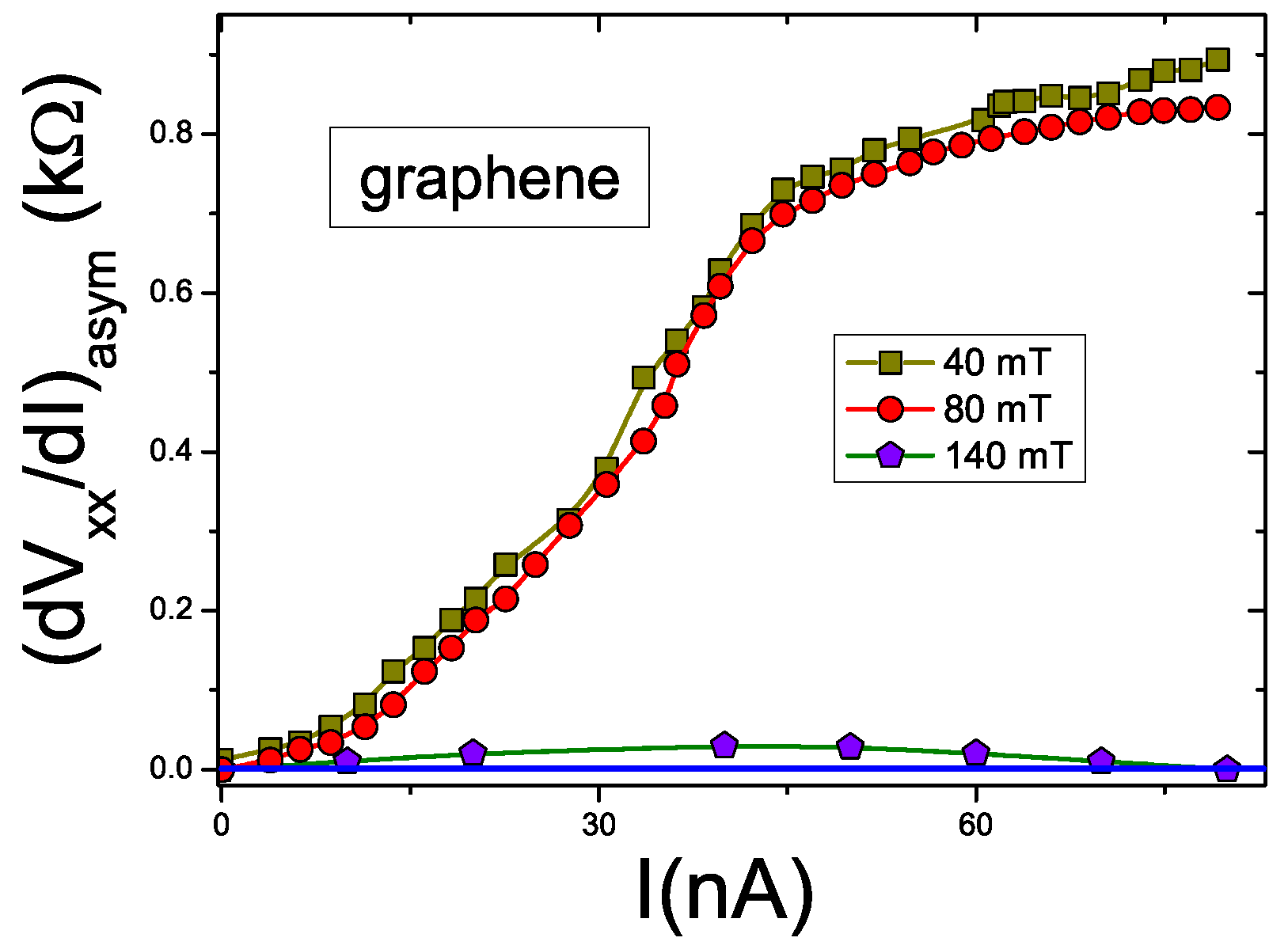
7.2. Asymmetric Tunneling Differential Conductivity
7.3. Hall Effect
8. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Landau, L.D. Theory of Fermi liquid. Sov. Phys. JETP 1956, 30, 920. [Google Scholar]
- Lifshitz, E.M.; Pitaevskii, L.P. Statistical Physics, Part 2; Butterworth-Heinemann: Oxford, UK, 1999. [Google Scholar]
- Abrikosov, A.A. Fundamentals of the Theory of Metals; North-Holland: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Senthil, T.; Vojta, M.; Sachdev, S. Weak magnetism and non-Fermi liquids near heavy-fermion critical points. Phys. Rev. B 2004, 69, 035111. [Google Scholar] [CrossRef] [Green Version]
- Coleman, P.; Schofield, A.J. Quantum criticality. Nature 2005, 433, 226. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coleman, P.; Pèpin, C.; Si, Q.; Ramazashvili, R. How do Fermi liquids get heavy and die? J. Phys. Condens. Matter 2001, 13, R723. [Google Scholar] [CrossRef] [Green Version]
- Löhneysen, H.V.; Rosch, A.; Vojta, M.; Wölfle, P. Fermi-Liquid Instabilities at Magnetic Quantum Phase Transitions. Rev. Mod. Phys. 2007, 79, 1015. [Google Scholar] [CrossRef] [Green Version]
- Gegenwart, P.; Si, Q.; Steglich, F. Quantum criticality in heavy-fermion metals. Nat. Phys. 2008, 4, 186. [Google Scholar] [CrossRef] [Green Version]
- Stockert, O.; Steglich, F. Unconventional Quantum Criticality in Heavy-Fermion Compounds. Annu. Rev. Condens. Matter Phys. 2011, 2, 79. [Google Scholar] [CrossRef]
- Sachdev, S. Quantum magnetism and criticality. Nat. Phys. 2008, 4, 173. [Google Scholar] [CrossRef]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43–50. [Google Scholar] [CrossRef] [Green Version]
- Törmä, P.; Peotta, S.; Bernevig, B.A. Superconductivity, superfluidity and quantum geometry in twisted multilayer systems. Nat. Rev. Phys. 2022, 4, 528. [Google Scholar] [CrossRef]
- Regnault, N.; Xu, Y.; Li, M.-R.; Ma, D.-S.; Jovanovic, M.; Yazdani, A.; Parkin, S.S.P.; Felser, C.; Schoop, L.M.; Ong, N.P.; et al. Catalogue of flat-band stoichiometric materials. Nature 2022, 603, 824. [Google Scholar] [CrossRef]
- Shaginyan, V.R.; Msezane, A.Z.; Popov, K.G.; Stephanovich, V.A. Universal Behavior of Two-Dimensional He 3 at Low Temperatures. Phys. Rev. Lett. 2008, 100, 096406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shaginyan, V.R.; Amusia, M.Y.; Msezane, A.Z.; Popov, K.G. Scaling behavior of heavy fermion metals. Phys. Rep. 2010, 492, 31. [Google Scholar] [CrossRef] [Green Version]
- Amusia, M.Y.; Popov, K.G.; Shaginyan, V.R.; Stephanovich, V.A. Theory of Heavy-Fermion Compounds; Springer Series in Solid-State Sciences; Springer: Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2015; Volume 182. [Google Scholar]
- Amusia, M.Y.; Shaginyan, V.R. Strongly Correlated Fermi Systems: A New State of Matter; Springer Tracts in Modern Physics; Springer Nature: Cham, Switzerland, 2020; Volume 283. [Google Scholar]
- Khodel, V.A.; Shaginyan, V. Superfluidity in system with fermion condensate. J. Exp. Theor. Phys. Lett. 1990, 51, 553. [Google Scholar]
- Volovik, G.E. A new class of normal Fermi liquids. J. Exp. Theor. Phys. Lett. 1991, 53, 222. [Google Scholar]
- Khodel, V.A.; Shaginyan, V.R.; Khodel, V.V. New approach in the microscopic Fermi systems theory. Phys. Rep. 1994, 249, 1. [Google Scholar] [CrossRef]
- Volovik, G.E. From Standard Model of particle physics to room-temperature superconductivity. Phys. Scr. 2015, 164, 014014. [Google Scholar] [CrossRef] [Green Version]
- Volovik, G.E. Springer Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2007; Volume 718, p. 31. [Google Scholar]
- Khodel, V.A.; Clark, J.W.; Zverev, M.V. Topology of the Fermi surface beyond the quantum critical point. Phys. Rev. 2008, 78, 075120. [Google Scholar] [CrossRef] [Green Version]
- Shaginyan, V.R.; Msezane, A.Z.; Japaridze, G.S.; Stephanovich, V.A. Violation of the Time-Reversal and Particle-Hole Symmetries in Strongly Correlated Fermi Systems: A Review. Symmetry 2020, 12, 1596. [Google Scholar] [CrossRef]
- Clark, J.W.; Khodel, V.A.; Zverev, M.V. Anomalous low-temperature behavior of strongly correlated Fermi systems. Phys. Rev. 2005, 71, 012401. [Google Scholar] [CrossRef] [Green Version]
- Kadowaki, K.; Woods, S.B. Universal relationship of the resistivity and specific heat in heavy-Fermion compounds. Solid State Commun. 1986, 58, 507. [Google Scholar] [CrossRef]
- Khodel, V.A.; Clark, J.W.; Zverev, M.V. Topological disorder triggered by interaction-induced flattening of electron spectra in solids. Phys. Rev. 2020, 102, 201108(R). [Google Scholar] [CrossRef]
- Maksimovic, N.; Eilbott, D.H.; Cookmeyer, T.; Wan, F.; Rusz, J.; Nagarajan, V.; Haley, S.C.; Maniv, E.; Gong, A.; Faubel, S.; et al. Evidence for a delocalization quantum phase transition without symmetry breaking in CeCoIn5. Science 2022, 375, 76. [Google Scholar] [CrossRef] [PubMed]
- Shaginyan, V.R. Dissymmetrical tunnelling in heavy fermion metals. J. Exp. Theor. Phys. Lett. 2005, 81, 222. [Google Scholar] [CrossRef] [Green Version]
- Shaginyan, V.R.; Msezane, A.Z.; Japaridze, G.S. Peculiar Physics of Heavy-Fermion Metals: Theory versus Experiment. Atoms 2022, 10, 67. [Google Scholar] [CrossRef]
- Shaginyan, V.R.; Popov, P.G.; Artamonov, S.A. Hall coefficient in heavy fermion metals. J. Exp. Theor. Phys. Lett. 2005, 82, 215. [Google Scholar] [CrossRef] [Green Version]
- Shaginyan, V.R.; Msezane, A.Z.; Popov, K.G.; Clark, J.W.; Zverev, M.V.; Khodel, V.A. Magnetic field dependence of the residual resistivity of the heavy-fermion metal CeCoIn5. Phys. Rev. B 2012, 86, 085147. [Google Scholar] [CrossRef] [Green Version]
- Paschen, S.; Lühmann, T.; Wirth, S.; Gegenwart, P.; Trovarelli, O.; Geibel, C.; Steglich, F.; Coleman, P.; Si, Q. Hall-effect evolution across a heavy-fermion quantum critical point. Nature 2004, 432, 881. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.Y.; Xu, D.F.; Niu, X.H.; Jiang, J.; Peng, R.; Xu, H.C.; Wen, C.H.P.; Ding, Z.F.; Huang, K.; Shu, L.; et al. Direct observation of how the heavy-fermion state develops in CeCoIn5. Phys. Rev. 2017, 96, 045107. [Google Scholar] [CrossRef] [Green Version]
- Pfitzner, M.; Wölfle, P. Quasiparticle interaction in a nearly localized Fermi liquid: Application to 3He and heavy-fermion systems. Phys. Rev. B 1986, 33, 2003. [Google Scholar] [CrossRef]
- Oliveira, L.N.; Gross, E.K.U.; Kohn, W. Density-functional theory for superconductors. Phys. Rev. Lett. 1988, 60, 2430. [Google Scholar] [CrossRef]
- Shaginyan, V.R. Density functional theory of fermion condensation. Phys. Lett. A 1998, 249, 237. [Google Scholar] [CrossRef]
- Oeschler, N.; Hartmann, S.; Pikul, A.; Krellner, C.; Geibel, C.; Steglich, F. Low-temperature specific heat of YbRh2Si2. Physica B 2008, 403, 1254. [Google Scholar] [CrossRef]
- Tokiwa, Y.; Radu, T.; Geibel, C.; Steglich, F.; Gegenwart, P. Divergence of magneicGrüneisen ratio at the field-induced quantum critical point in YbRh2Si2. Phys. Rev. Lett. 2009, 102, 066401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schröder, A.; Aeppli, G.; Coldea, R.; Adams, M.; Stockert, O.; Löhneysen, H.V.; Bucher, E.; Ramazashvili, R.; Coleman, P. Onset of antiferromagnetism in heavy-fermion metals. Nature 2000, 407, 351. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Helton, J.S.; Matan, K.; Shores, M.P.; Nytko, E.A.; Bartlett, B.M.; Qiu, Y.; Nocera, D.G.; Lee, Y.S. Dynamic Scaling in the Susceptibility of the Spin-1/2 Kagome Lattice Antiferromagnet Herbertsmithite. Phys. Rev. Lett. 2010, 104, 147201. [Google Scholar] [CrossRef] [Green Version]
- Murayama, H.; Tominaga, T.; Asaba, T.; Silva, A.O.; Sato, Y.; Suzuki, H.; Ukai, Y.; Suetsugu, S.; Kasahara, Y.; Okuma, R.; et al. Universal scaling of specific heat in the S=1/2 quantum kagome antiferromagnet herbertsmithite. Phys. Rev. B 2022, 106, 174406. [Google Scholar] [CrossRef]
- Gourgout, A.; Grissonnanche, G.; Lalibertè, F.; Ataei, A.; Chen, L.; Verret, S.; Zhou, J.-S.; Mravlje, J.; Georges, A.; Doiron-Leyraud, N.; et al. Seebeck Coefficient in a Cuprate Superconductor: Particle-Hole Asymmetry in the Strange Metal Phase and Fermi Surface Transformation in the Pseudogap Phase. Phys. Rev. X 2022, 12, 011037. [Google Scholar] [CrossRef]
- Paul, A.K.; Ghosh, A.; Chakraborty, S.; Roy, U.; Dutta, R.; Watanabe, K.; Taniguchi, T.; Panda, A.; Agarwala, A.; Mukerjee, S.; et al. Interaction-driven giant thermopower in magic-angle twisted bilayer graphene. Nat. Phys. 2022, 18, 691. [Google Scholar] [CrossRef]
- Stepanov, P. Thermopower probes electronic flat bands. Nat. Phys. 2022, 18, 608. [Google Scholar] [CrossRef]
- Hartmann, S.; Oeschler, N.; Krellner, C.; Geibel, C.; Paschen, S.; Steglich, F. Thermopower Evidence for an Abrupt Fermi Surface Change at the Quantum Critical Point of YbRh2Si2. Phys. Rev. Lett. 2010, 104, 096401. [Google Scholar] [CrossRef]
- Friedemann, S.; Wirth, S.; Kirchner, S.; Si, Q.; Hartmann, S.; Krellner, C.; Geibel, C.; Westerkamp, T.; Brando, M.; Steglich, F. Break Up of Heavy Fermions at an Antiferromagnetic Instability. J. Phys. Soc. Jpn. 2011, 80, SA002. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.-S.; Pépin, C. Thermopower as a signature of quantum criticality in heavy fermions. Phys. Rev. 2010, 81, 205108. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.-S.; Pépin, C. Thermopower as a fingerprint of the Kondo breakdown quantum critical point. Phys. Rev. 2011, 83, 073104. [Google Scholar] [CrossRef] [Green Version]
- Lifshitz, E.M.; Landau, L.D.; Pitaevskii, L.P. Electrodynamics of Continuous Media; Elsevier: New York, NY, USA, 1984. [Google Scholar]
- Behnia, K.; Jaccard, D.; Flouquet, J. On the thermoelectricity of correlated electrons in the zero-temperature limit. J. Phys. Condens. Matt. 2004, 16, 5187. [Google Scholar] [CrossRef] [Green Version]
- Miyake, K.; Kohno, H. Theory of Quasi-Universal Ratio of Seebeck Coefficient to Specific Heat in Zero-Temperature Limit in Correlated Metals. J. Phys. Soc. Jpn. 2005, 74, 254. [Google Scholar] [CrossRef] [Green Version]
- Zlatić, V.; Monnier, R.; Freericks, J.K.; Becker, K.W. Relationship between the thermopower and entropy of strongly correlated electron systems. Phys. Rev. 2007, 76, 085122. [Google Scholar] [CrossRef] [Green Version]
- Shaginyan, V.R.; Msezane, A.Z.; Japaridze, G.S.; Popov, K.G.; Clark, J.W.; Khodel, V.A. Scaling behavior of the thermopower of the archetypal heavy-fermion metal YbRh2Si2. Front. Phys. 2016, 11, 117102. [Google Scholar] [CrossRef] [Green Version]
- Nozières, P. Properties of Fermi liquids with a finite range interaction. J. Phys. 1992, 2, 443. [Google Scholar] [CrossRef]
- Limelette, P.; Saulquin, W.; Muguerra, H.; Grebille, D. From quantum criticality to enhanced thermopower in strongly correlated layered cobalt oxide. Phys. Rev. 2010, 81, 115113. [Google Scholar] [CrossRef] [Green Version]
- Gegenwart, P.; Custers, J.; Geibel, C.; Neumaier, K.; Tayama, T.; Tenya, K.; Trovarelli, O.; Steglich, F. Magnetic-Field Induced Quantum Critical Point in YbRh2Si2. Phys. Rev. Lett. 2002, 89, 056402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mokashi, A.; Li, S.; Wen, B.; Kravchenko, S.V.; Shashkin, A.A.; Dolgopolov, V.T.; Sarachik, M.P. Critical Behavior of a Strongly Interacting 2D Electron System. Phys. Rev. Lett. 2012, 109, 096405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Machida, Y.; Tomokuni, K.; Ogura, C.; Izawa, K.; Kuga, K.; Nakatsuji, S.; Lapertot, G.; Knebel, G.; Brison, J.-P.; Flouquet, J. Thermoelectric Response Near a Quantum Critical Point of YbAlB4 and YbRh2Si2: A Comparative Study. Phys. Rev. Lett. 2012, 109, 156405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taupin, M.; Paschen, S. Are Heavy Fermion Strange Metals Planckian? Crystals 2022, 12, 251. [Google Scholar] [CrossRef]
- Köhler, U.; Oeschler, N.; Steglich, F.; Maquilon, S.; Fisk, Z. Energy scales of Lu1-xYbxRh2Si2 by means of thermopower investigations. Phys. Rev. 2008, 77, 104412. [Google Scholar] [CrossRef]
- Lifshitz, E.M.; Pitaevskii, L.P. Statistical Physics, Part 1; Butterworth-Heinemann: Oxford, UK, 1996. [Google Scholar]
- Krellner, C.; Hartmann, S.; Pikul, A.; Oeschler, N.; Donath, J.G.; Geibel, C.; Steglich, F.; Wosnitza, J. Violation of Critical Universality at the Antiferromagnetic Phase Transition of YbRh2Si2. Phys. Rev. Lett. 2009, 102, 196402. [Google Scholar] [CrossRef] [Green Version]
- Bianchi, A.; Movshovich, R.; Oeschler, N.; Gegenwart, P.; Steglich, F.; Thompson, J.D.; Pagliuso, P.G.; Sarrao, J.L. First-Order Superconducting Phase Transition in CeCoIn5. Phys. Rev. Lett. 2002, 89, 137002. [Google Scholar] [CrossRef] [Green Version]
- Paglione, J.; Tanatar, M.; Hawthorn, D.G.; Boaknin, E.; Hill, R.W.; Ronning, F.; Sutherland, M.; Taillefer, L.; Petrovic, C.; Canfield, P.C. Field-induced quantum critical point in CeCoIn5. Phys. Rev. Lett. 2003, 91, 246405. [Google Scholar] [CrossRef] [Green Version]
- Seyfarth, G.; Brison, J.P.; Knebel, G.; Aoki, D.; Lapertot, G.; Flouquet, J. Multigap Superconductivity in the Heavy-Fermion System CeCoIn5. Pys. Rev. Lett. 2008, 101, 046401. [Google Scholar] [CrossRef]
- Tokiwa, Y.; Bauer, E.D.; Gegenwart, P. Zero-Field Quantum Critical Point in CeCoIn5. Phys. Rev. Lett. 2013, 111, 107003. [Google Scholar] [CrossRef] [Green Version]
- Paglione, J.; Tanatar, M.A.; Hawthorn, D.G.; Ronning, F.; Hill, R.W.; Sutherland, M.; Taillefer, L.; Petrovic, C. Nonvanishing energy scales at the quantum critical point of CeCoIn5. Phys. Rev. Lett. 2006, 97, 106606. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sidorov, V.A.; Nicklas, M.; Pagliuso, P.G.; Sarrao, J.L.; Bang, Y.; Balatsky, A.V.; Thompson, J.D. Superconductivity and quantum criticality in CeCoIn5. Phys. Rev. Lett. 2002, 89, 157004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Polshyn, H.; Yankowitz, M.; Chen, S.; Zhang, Y.; Watanabe, K.; Taniguchi, T.; Dean, C.R.; Young, A.F. Large linear-in-temperature resistivity in twisted bilayer graphene. Nat. Phys. 2019, 15, 1011. [Google Scholar] [CrossRef] [Green Version]
- Shrestha, K.; Zhang, S.; Greene, L.H.; Lai, Y.; Baumbach, R.E.; Sasmal, K.; Maple, M.B.; Park, W.K. Spectroscopic evidence for the direct involvement of local moments in the pairing process of the heavy-fermion superconductor CeCoIn5. Phys. Rev. 2021, 103, 224515. [Google Scholar] [CrossRef]
- Wirth, S.; Prots, Y.; Wedel, M.; Ernst, S.; Kirchner, S.; Fisk, Z.; Thompson, J.D.; Steglich, F.; Grin, Y.J. Structural Investigations of CeIrIn5 and CeCoIn5 on Macroscopic and Atomic Length Scales. Phys. Soc. Jpn. 2014, 83, 061009. [Google Scholar] [CrossRef] [Green Version]
- Park, W.K.; Greene, L.H.; Sarrao, J.L.; Thompson, J.D. Andreev reflection at the normal-metal/heavy-fermion superconductor CeCoIn5 interface. Phys. Rev. B 2005, 72, 052509. [Google Scholar] [CrossRef] [Green Version]
- Seiro, S.; Jiao, L.; Kirchner, S.; Hartmann, S.; Friedemann, S.; Krellner, C.; Geibel, C.; Si, Q.; Steglich, F.; Wirth, S. Evolution of the Kondo lattice and non-Fermi liquid excitations in a heavy-fermion metal. Nat. Commun. 2018, 9, 3324. [Google Scholar] [CrossRef] [Green Version]
- Pristàš, G.; Reiffers, M.; Bauer, E.; Jansen, A.G.M.; Maude, D.K. Suppression of asymmetric differential resistance in the non-Fermi-liquid system YbCu5−xAlx (x = 1.3–1.75) in high magnetic fields. Phys. Rev. B 2008, 78, 235108. [Google Scholar] [CrossRef]
- Khodel, V.A.; Zverev, M.V.; Clark, J.W. Damping effects and the metal-insulator transition in the two-dimensional electron gas. J. Exp. Theor. Phys. Lett. 2005, 81, 315. [Google Scholar] [CrossRef] [Green Version]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaginyan, V.R.; Msezane, A.Z.; Artamonov, S.A. Magnetic Field as an Important Tool in Exploring the Strongly Correlated Fermi Systems and Their Particle–Hole and Time-Reversal Asymmetries. Magnetism 2023, 3, 180-203. https://doi.org/10.3390/magnetism3030015
Shaginyan VR, Msezane AZ, Artamonov SA. Magnetic Field as an Important Tool in Exploring the Strongly Correlated Fermi Systems and Their Particle–Hole and Time-Reversal Asymmetries. Magnetism. 2023; 3(3):180-203. https://doi.org/10.3390/magnetism3030015
Chicago/Turabian StyleShaginyan, Vasily R., Alfred Z. Msezane, and Stanislav A. Artamonov. 2023. "Magnetic Field as an Important Tool in Exploring the Strongly Correlated Fermi Systems and Their Particle–Hole and Time-Reversal Asymmetries" Magnetism 3, no. 3: 180-203. https://doi.org/10.3390/magnetism3030015
APA StyleShaginyan, V. R., Msezane, A. Z., & Artamonov, S. A. (2023). Magnetic Field as an Important Tool in Exploring the Strongly Correlated Fermi Systems and Their Particle–Hole and Time-Reversal Asymmetries. Magnetism, 3(3), 180-203. https://doi.org/10.3390/magnetism3030015






