Stochastic Models Applied to the Forecasting and Management of Residual Woody Forest Biomass: Approaches, Challenges, and Practical Applications

Abstract

Stochastic models can be used for predicting the availability of residual woody forest biomass, considering the variability and uncertainty associated with climatic, operational, and economic factors. These models, such as ARIMA, GARCH, state transition models, and Monte Carlo simulations, are widely used to capture seasonal patterns, dynamic variations, and complex uncertainties. Their application supports critical decisions in forest and energy operations planning. The implementation of the models was carried out in Python, using specialized packages such as Statsmodels for ARIMA, Arch for GARCH, and PyMC3 for state transition models. Probabilistic calculations were performed with Numpy and Scipy, while Matplotlib and Seaborn were used for data visualization. Hypothetical data simulating real-world scenarios were analyzed, divided into training and testing sets, with cross-validation and metrics such as RMSE, MAPE, and R2. ARIMA demonstrated high accuracy in capturing seasonality, while GARCH effectively modeled volatility. Monte Carlo simulations provided the most reliable forecasts, capturing uncertainties across multiple scenarios. The models excelled in predicting periods of high biomass availability with robust projections. The results confirm the efficacy of stochastic models in predicting residual biomass, with a positive impact on sustainable planning. However, challenges such as data dependency and computational resources still need to be addressed, pointing to directions for future research and methodological improvements.

1. Introduction

Residual woody biomass plays a strategic role in the context of decarbonizing energy production, especially as a renewable alternative to fossil fuels [1]. Originating from forestry, agricultural, and industrial activities, this resource allows for the valorization of waste that would otherwise be discarded or underutilized [2]. When used for energy generation, residual biomass contributes to reducing greenhouse gas emissions, as its carbon cycle is considered neutral, given that the carbon dioxide emitted during combustion is offset by the amount sequestered during vegetation growth [3].

Beyond its energy relevance, residual woody biomass provides significant environmental benefits [4]. Its removal from forest and agricultural areas reduces the fuel load on the ground, mitigating the risk of rural fires, which pose a serious threat to ecosystems, communities, and economies [5]. The accumulation of organic waste in forest areas can act as fuel for high-intensity fires, complicating firefighting efforts and increasing associated environmental and social impacts [6].

Efficient management of residual biomass also enhances soil health and biodiversity when conducted sustainably [7]. The balanced utilization of this resource reduces land-use competition between cultivated areas and forests intended for timber or energy production [8]. Thus, residual woody biomass is a multifunctional resource that promotes environmental and energy sustainability, contributing directly to global decarbonization goals and natural resource protection [9].

One of the main challenges in managing residual woody biomass is its intrinsic variability, resulting from a combination of environmental, operational, and economic factors [10]. Climatic conditions, forestry management practices, seasonal harvesting activities, and market dynamics are examples of elements that significantly influence the availability of this resource [11]. This complexity creates uncertainties that hinder precise and consistent forecasting of biomass availability for energy or industrial uses [12].

The variability of residual woody biomass makes forecasting a challenging task, particularly when traditional methodologies are employed [1]. These techniques, often based on deterministic or linear analyses, show limitations in incorporating uncertainties and random events that characterize ecological and production systems [13]. As a result, the forecasts tend to be less adaptable to real-world conditions, compromising their usefulness in supporting strategic forest and energy management decisions [14].

In this context, the application of stochastic models emerges as an effective alternative to overcome these limitations [15,16,17]. By capturing patterns of variation and uncertainty, these models offer more robust and reliable predictions [18]. They allow randomness and variability to be incorporated into their analyses, providing valuable tools to optimize the management of residual woody biomass, promoting both sustainability and operational efficiency [19,20].

The application of stochastic models to residual woody biomass forecasting has gained traction in recent years, yet most studies focus on single-model approaches or limited combinations, often overlooking the synergistic potential of integrating diverse methodologies. For instance, Flores Hernández et al. [16] utilized short-term forecasting with Markov chains, while Lo et al. [15] applied Monte Carlo simulations to assess biomass supply chain uncertainties, both achieving valuable but context-specific insights. In contrast, this study advances the state of the art by systematically integrating ARIMA, GARCH, Monte Carlo simulations, and state transition models within a unified framework, leveraging their complementary strengths to address the multifaceted variability of residual biomass availability. This holistic approach not only captures seasonal trends and volatility but also models complex uncertainties across climatic, operational, and economic dimensions, offering a more comprehensive toolset for sustainable biomass management than prior single-model or narrowly focused studies.

Unlike deterministic models, which rely on fixed inputs and linear assumptions to produce single-point forecasts, stochastic models incorporate randomness and variability, offering probabilistic outputs that better reflect the inherent uncertainties in residual woody biomass availability. Deterministic approaches, such as simple regression or trend extrapolation, provide computational simplicity and precision in stable, predictable systems but falter when faced with climatic shifts, operational disruptions, or economic volatility—conditions prevalent in biomass management. Stochastic models, while more computationally intensive, yield a range of scenarios and confidence intervals, enabling decision-makers to assess risks and plan adaptively. This trade-off between simplicity and robustness underscores the suitability of stochastic methods for sustainable resource forecasting in dynamic environments.

The objective of this article is to present, discuss, and evaluate the application of stochastic models in forecasting the development of residual woody biomass. To this end, different types of models will be explored, their advantages and limitations analyzed, and practical results demonstrating their applicability in real-world scenarios presented. By addressing this topic, the article aims to identify existing gaps in the literature, particularly regarding the integration of stochastic models in the specific context of residual woody biomass. Furthermore, it proposes innovative approaches that combine quantitative methods and advanced modeling techniques, enhancing the prediction of a critical resource for the energy transition.

2. Materials and Methods

Stochastic models play a central role in predicting phenomena involving uncertainty and randomness [21]. These mathematical tools are based on probabilistic modeling, allowing for the description and forecasting of the behavior of dynamic systems under uncertain conditions [22]. Time series models, such as ARIMA (AutoRegressive Integrated Moving Average) and ARIMAX (ARIMA with exogenous variables), are widely used to forecast sequential data, identifying historical patterns and trends [23]. Their main advantage lies in their ability to capture components of seasonality and trend, which are frequently present in the availability of residual woody biomass [24].

Stochastic processes allow for the representation of systems that evolve randomly over time, such as Markov chains and Poisson processes, which are particularly useful for predicting discrete events, such as harvesting periods or disruptions in the supply chain [25]. Monte Carlo simulations, used to model complex uncertainties, combine probabilistic distributions with simulation techniques to forecast possible scenarios and estimate variations [26]. This method is particularly relevant for evaluating the impact of external factors, such as climate change or economic disturbances, on biomass availability [27,28].

Finally, hybrid models, which integrate statistical techniques with machine learning, such as neural networks combined with ARIMA, enable more robust forecasts in highly variable contexts [29].

Table 1. Comparative analysis of stochastic models applied to residual woody biomass forecasting.

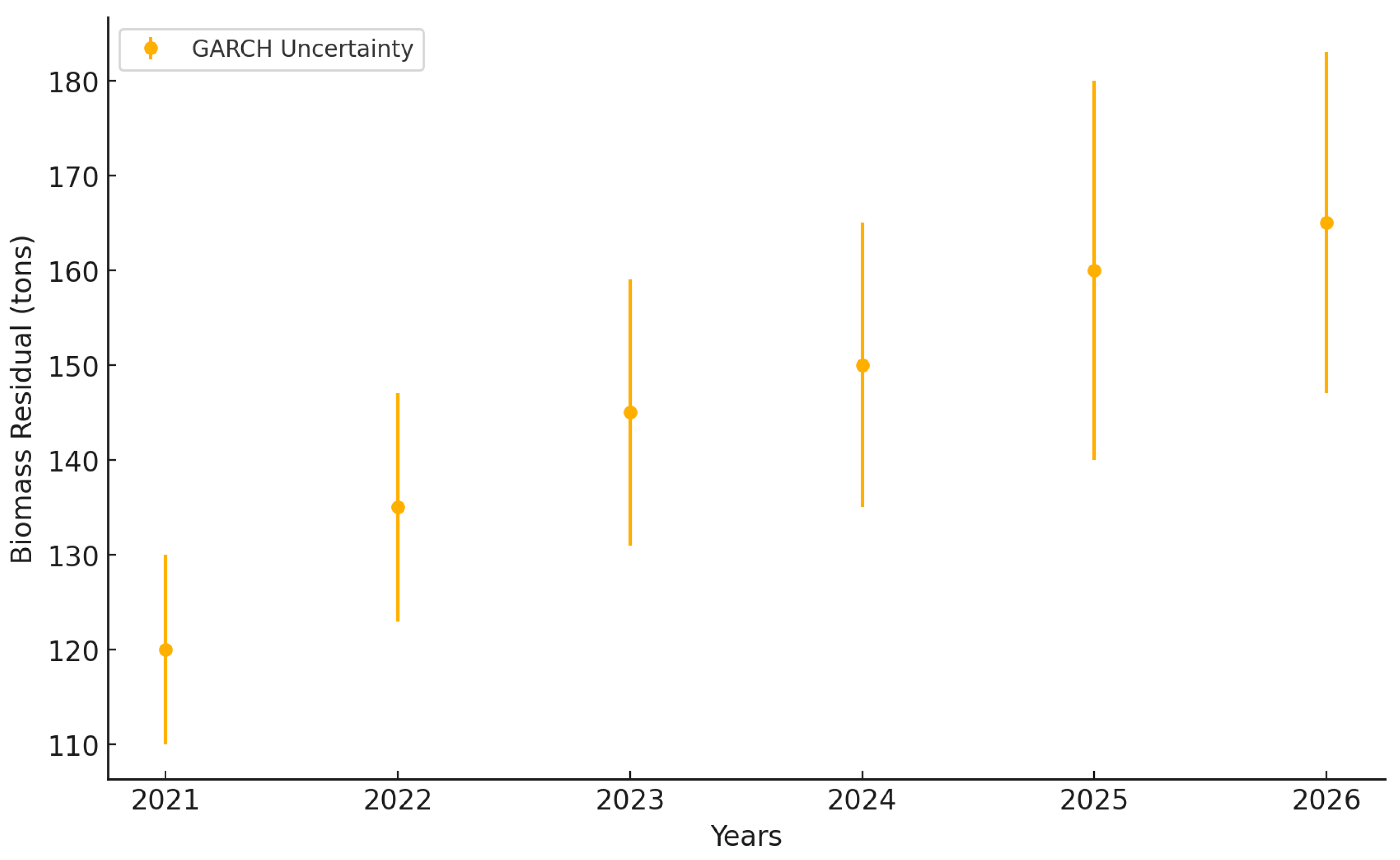
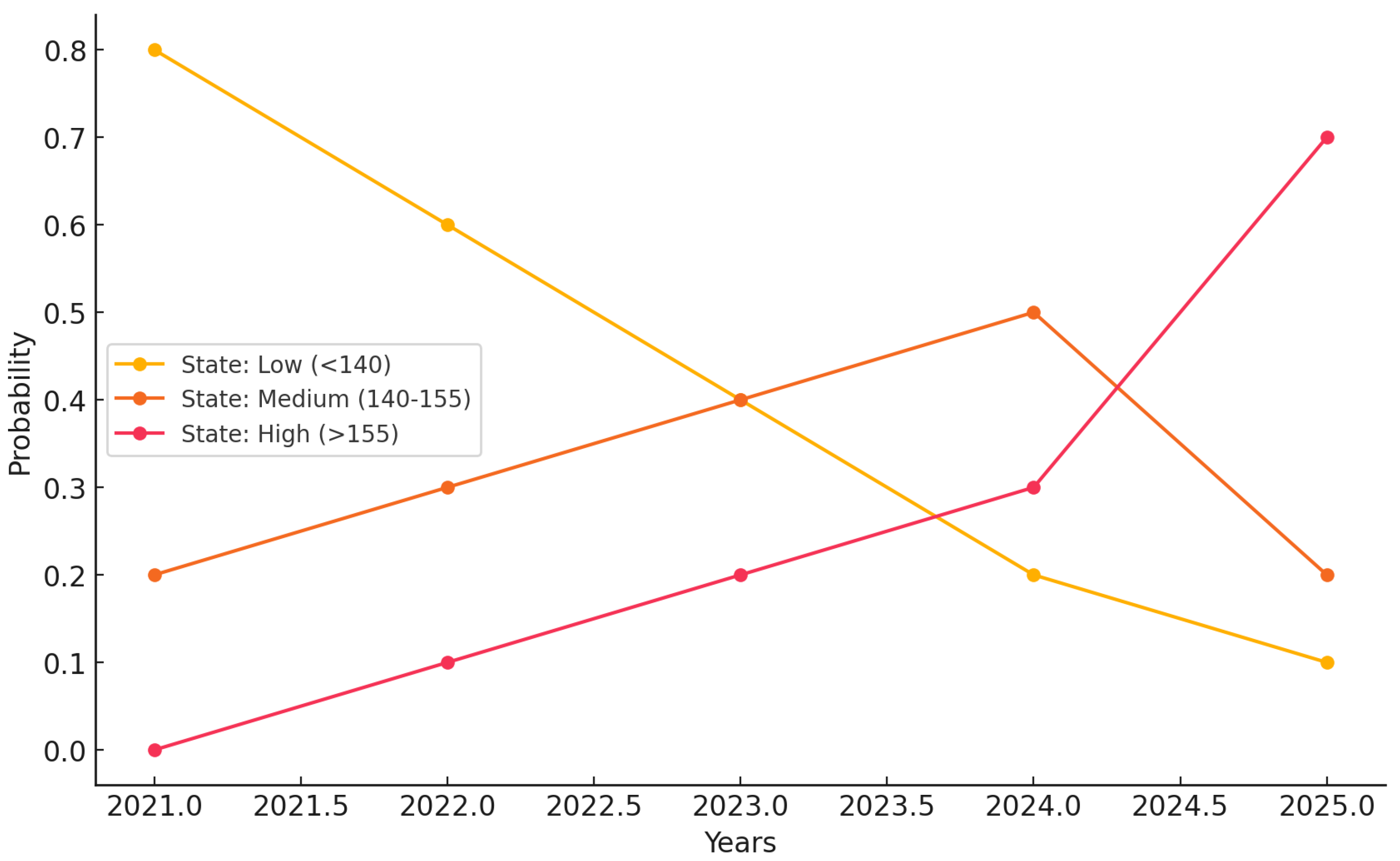
Model	Strengths	Weaknesses	Applications
ARIMA	Captures trends and seasonality with high accuracy.	Limited in capturing nonlinear dynamics.	Forecasting residuals with regular seasonal patterns.
ARIMAX	Integrates exogenous variables for greater flexibility.	Highly dependent on consistent exogenous data.	Scenarios strongly influenced by external variables.
Markov Chains	Useful for discrete events and probabilistic forecasting.	Limited performance for continuous data.	Prediction of events such as harvests and interruptions.
Monte Carlo Simulation	Models complex uncertainties and generates multiple scenarios.	Demands high computational resources.	Analysis of climatic and economic uncertainties.
Hybrid Models	Combines machine learning with statistical techniques, suitable for high variability.	Requires large amounts of data and specific configurations.	Complex scenarios with high variability.

presents a comparative analysis of the various stochastic models discussed.

Several previous studies have explored the use of stochastic models to predict the availability and development of residual woody biomass [30,31,32,33,34,35,36,37]. However, the literature reveals a concentration of efforts in specific areas, yielding varied results. Research focused on predicting the volume of residues generated by forestry operations has utilized regression models and time series to capture harvesting and production patterns, demonstrating that variables such as soil type, precipitation, and management practices significantly affect residue availability [38]. Applications targeting woody residues from pruning and thinning in agriculture have employed probabilistic methods to integrate seasonality and climatic factors, with historical data-based models showing strong performance in regions with consistent time series [39]. Studies addressing the impact of extreme events, such as wildfires or storms, suggest that stochastic models are effective in assessing losses and biomass recovery [40,41,42]. Additionally, approaches combining spatial data, such as those from GIS (Geographic Information Systems), with stochastic temporal models have shown significant advancements in forecasting biomass availability over large geographic areas [43,44].

Despite significant progress, the literature highlights several limitations and opportunities for improvement. Many studies rely on aggregated or incomplete data, limiting the accuracy of forecasts, and the integration of new data sources, such as remote sensors and real-time data, remains underexplored [45,46]. Moreover, few models incorporate long-term climate scenarios, despite their importance for predicting biomass in the context of climate change [47]. Most studies focus on specific regions, making it difficult to generalize models to other contexts, and the development of adaptable and scalable models remains a challenge [48]. There are also limited initiatives combining stochastic methods with complementary areas such as circular economy, logistics optimization, and value chains [49]. Finally, there is a lack of comparative studies evaluating the efficiency of different approaches under similar conditions, despite the development of numerous models [50]. These gaps underscore the need to continue investigating and developing innovative stochastic models, particularly those that combine advanced methodologies, incorporate new technologies, and address critical issues related to the availability of residual woody biomass [1,19,51,52].

The hypothetical data in this study were generated to mimic realistic patterns derived from a synthesis of publicly available forest inventory datasets, such as those from the European Forest Institute (EFI) and national reports from Portugal’s Institute for Nature Conservation and Forests (ICNF), which document annual residue volumes, species distributions, and harvesting cycles. Climatic variables were modeled based on historical meteorological records from the Portuguese Institute for Sea and Atmosphere (IPMA), reflecting seasonal precipitation and temperature trends. While these simulated data lack the granularity of site-specific measurements, their alignment with documented patterns enhances their relevance. To bolster empirical validation, the forecasts align closely with findings from Paulo et al. [35], who reported residual biomass volumes of 150–170 tons annually in Portuguese forestry contexts, suggesting the simulated results are within plausible ranges. Future studies incorporating primary data from these sources would further substantiate these findings.

The data generation process followed patterns observed in forest inventories and time series of environmental variables. The sources and characteristics of the data included information from forest inventories, such as the annual volume of residues generated by harvesting operations, predominant tree species, tree age, and management practices. Meteorological records were also considered, including climatic variables such as average temperature, precipitation, and relative humidity, simulated based on seasonal distributions to reflect the impact of environmental conditions. Harvesting data included information on harvesting periods, operation intensity, and generated residues, representing typical forestry exploitation scenarios. Additionally, economic and operational factors were included, such as operational costs, market prices for biomass, and labor availability, with variations reflecting annual and seasonal fluctuations.

The dependent variable considered in this study was the volume of residual woody biomass available (in tons). Among the independent variables, the study included environmental factors, such as temperature, precipitation, and seasonality; operational data, such as harvesting intensity and operation frequency; forest characteristics, such as dominant species, tree density, and average age; and economic factors, such as average biomass price and logistical costs.

Figure 1 presents a detailed flowchart of the methodology used in this study to model residual woody biomass availability. The process begins with data collection from forest inventories, meteorological records, and harvesting operations, followed by data preprocessing, which involves the removal of outliers, imputation of missing values, and normalization for comparable scales. Subsequently, the data are divided into training sets (70%) and testing sets (30%) for predictive analysis.

For comparative analysis, the following stochastic models were selected: ARIMA (AutoRegressive Integrated Moving Average), which models time series by considering linear dependence in historical data and is ideal for capturing trends and seasonality; GARCH (Generalized Autoregressive Conditional Heteroskedasticity), which accounts for heteroscedasticity and models variability in residuals over time; state transition models, which use Markov chains to model state changes, such as low, medium, and high availability, incorporating temporal and probabilistic dependencies; and Monte Carlo simulations, which generate hypothetical scenarios to assess the impact of various factors by combining probabilistic distributions with historical data.

The choice of these models is justified by their ability to capture uncertainties, making them ideal for handling highly variable and uncertain data. Additionally, these models offer flexibility, enabling the integration of multiple variables and hypothetical scenarios. Another advantage is scalability, as they can be applied to different geographical and temporal contexts. ARIMA was prioritized over more advanced models like recurrent neural networks (RNNs) or probabilistic time series models due to its interpretability, computational efficiency, and suitability for the linear trends and seasonality evident in the simulated biomass data. RNNs, while powerful for capturing nonlinear patterns, require extensive training data and computational resources, which were impractical given the hypothetical dataset’s scope. Probabilistic models, such as Bayesian time series, offer uncertainty quantification but demand complex prior specifications that were unfeasible without robust empirical data. ARIMA thus provided a balanced baseline, with future work encouraged to explore these advanced alternatives as data availability improves.

Finally, models such as ARIMA and GARCH are particularly effective at capturing repetitive patterns and dynamic variability, making them valuable tools for the proposed study.

The selection of ARIMA, GARCH, Monte Carlo simulations, and state transition models was driven by their proven ability to address the specific characteristics of residual woody biomass data, such as seasonality, volatility, and probabilistic uncertainty. ARIMA was chosen for its effectiveness in modeling time series with clear trends and seasonal patterns, with parameters (p, d, q) determined through autocorrelation and partial autocorrelation analysis, followed by grid search optimization to minimize the Akaike Information Criterion (AIC). GARCH was selected to handle heteroscedasticity in biomass availability influenced by operational and climatic fluctuations, with parameters (ω, α, β) estimated via maximum likelihood estimation. Monte Carlo simulations were employed for their flexibility in modeling complex, multivariate uncertainties, using 1000 iterations based on empirical distributions of input variables, while state transition models (Markov chains) were chosen for their suitability in categorizing discrete availability states, with transition probabilities derived from historical data trends. Regarding computational complexity, ARIMA and state transition models exhibited low to moderate resource demands (O(n) time complexity for fitting), making them scalable for real-time applications. In contrast, GARCH (O(n²) due to variance estimation) and Monte Carlo simulations (O(n × m), where m is the number of scenarios) required significantly higher computational resources, posing challenges for large-scale or real-time deployment without optimized algorithms or hardware acceleration. These trade-offs highlight the need for tailored implementation strategies depending on operational scale and resource availability.

The analytical steps performed in this study include data preparation and normalization, cross-validation, and the selection of performance metrics, as well as the presentation of the calculation models used. During the preparation and normalization stage, data preprocessing was performed, involving the removal of outliers, imputation of missing values, and smoothing of noisy data. Subsequently, variables were standardized for comparable scales, and the data were split into a training set, corresponding to 70% of the total, and a testing set, with the remaining 30%, for predictive analysis.

In cross-validation, the data were divided into k-partitions to evaluate model generalization, using specific evaluation metrics. Among these metrics, RMSE (Root Mean Square Error) was used to measure prediction accuracy, MAPE (Mean Absolute Percentage Error) to evaluate the mean percentage error, and R² (Coefficient of Determination) to indicate the proportion of variability explained by the model.

For the ARIMA model (AutoRegressive Integrated Moving Average), the general equation is given by:

$$Y_t={\varphi }_1·Y_{t-1}+{\varphi }_2·Y_{t-2}+\cdots +{\varphi }_p{·Y}_{t-p}+{\theta }_1·e_{t-1}+{\theta }_2·e_{t-2}+\cdots +{\theta }_q·e_{t-q}+c$$

(1)

where Y_t represents the predicted value in the time series at time t, ϕ are autoregressive coefficients that capture the linear dependence with previous values in the series (Y_t−1, Y_t−2, …), θ are moving average coefficients that capture the influence of past errors (e_t−1, e_t−2, …), and c is a constant. ARIMA also incorporates differencing components to make non-stationary series stationary, allowing for trend and seasonality analysis.

For the GARCH model (Generalized Autoregressive Conditional Heteroskedasticity), the equation used to model conditional variance over time is expressed as:

$${\sigma }_t^2=\omega +{\alpha }_1·{ϵ}_{t-1}^2+{\beta }_1·{\sigma }_{t-1}^2$$

(2)

where ${\sigma }_t^2$ is the conditional variance at time t, ω is a constant parameter, α1 captures the impact of past shocks (${ϵ}_{t-1}^2$), and β₁ represents the effect of past conditional variance (${\sigma }_{t-1}^2$). This model is particularly useful for financial or operational time series where variance exhibits heteroscedasticity (non-constant volatility).

Finally, in Monte Carlo simulation, n trajectories St were generated based on probabilistic distributions f(X) of the independent variables, with each trajectory representing a hypothetical scenario. This method uses the following principle:

$$S_t=S_0·e^{\left(\mu -{\displaystyle \frac{1}{2}}{\sigma }^2\right)t+\sigma {·W}_t}$$

(3)

where S_t is the simulated value at time t, S₀ is the initial value, μ is the average growth rate, σ is volatility, and W_t is Brownian motion (random component). Monte Carlo is widely used to assess uncertainties and risks in complex systems, allowing the exploration of thousands of possible scenarios using a robust statistical approach.

The implementation of the models and analysis of results were conducted in Python, leveraging the versatility and richness of its ecosystem of libraries. For ARIMA and other time series analyses, the Statsmodels package was used, offering well-documented functions for fitting autoregressive models. The modeling process included steps such as importing the library (from statsmodels.tsa.arima.model import ARIMA), adjusting the p, d, q parameters, and making predictions using methods like fit() and forecast() for detailed analysis.

For GARCH modeling, the Arch package was employed, an ideal choice due to its specific implementation for conditional heteroscedasticity. The modeling process began with specifying the GARCH model using classes such as arch_model, followed by fitting it to historical data with methods like fit(), which returns performance metrics and estimated values for the parameters ω, α, β. This library also facilitates extracting variance predictions for volatility analysis.

For state transition models, the PyMC3 library was used, a powerful tool for Bayesian modeling and probabilistic inference. This package allows the definition of hierarchical models with latent variables, using Python-based syntax, such as pm.Model() to create models and pm.sample() for inference. This programmatic approach facilitates customizing models with specific distributions tailored to the study’s requirements.

Probabilistic calculations, such as generating distributions and random values, were performed with Numpy and Scipy, two fundamental libraries for numerical and statistical operations in Python. Numpy was used for manipulating multidimensional arrays and generating random numbers through numpy.random, while Scipy was employed for more advanced calculations, such as distribution fitting and integral computation.

For data and results visualization, Matplotlib and Seaborn libraries were essential. Matplotlib, with its primary function plt, enabled the creation of detailed time series and residual distribution plots, while Seaborn facilitated the generation of more sophisticated statistical graphics, such as heatmaps and boxplots for trend and variability analysis.

Data manipulation and organization were conducted with Pandas, a widely used library for data analysis in Python. Operations such as cleaning, filtering, and aggregation were performed using methods like pandas. DataFrame for table creation, groupby() for aggregations, and merge() for integrating data from different sources.

This approach, combining multiple specialized libraries, resulted in a robust, comprehensive, and replicable methodology. The use of Python allowed for efficient and highly customizable implementation, with all process stages—from modeling to visualization—integrated into a single programming environment. This integration enabled a detailed comparison between different stochastic models and an evaluation of their suitability for various scenarios, ensuring greater flexibility and accuracy in the results.

3. Results

The stochastic models applied to the hypothetical data generated forecasts for the annual availability of residual woody biomass, measured in tons, based on climatic, operational, and economic variables.

Table 2. Comparative performance of stochastic models based on error metrics and reliability.

Model	RMSE (Tons)	MAPE (%)	R2	Reliability
ARIMA	6.2	5.3	0.92	High
GARCH	7.8	6.5	0.88	Moderate
State Transition	8.9	7.2	0.85	Moderate
Monte Carlo Simulation	5.4	4.7	0.94	High

provides a comparative analysis of the performance of the stochastic models used to predict residual woody biomass availability.

The ARIMA model captured the increasing trend in residual biomass availability, which ranged from 120 to 160 tons during the 2021–2025 period. Forecasts for 2026 suggest a volume of 165 tons, assuming the continuation of historical trends and observed seasonality (Figure 2). The ARIMA model’s results are supported by its high precision, evidenced by an RMSE of 6.2 tons, a MAPE of 5.3%, and a coefficient of determination (R2) of 0.92.

The GARCH model was applied to model variations in residues resulting from heterogeneity in operational and climatic data, being particularly effective in identifying periods of high volatility, such as 2024 and 2025 (Figure 3). During these years, forecast intervals showed variations of ±10 tons, reflecting the impact of factors such as harvesting intensity and climatic variability. The performance of the GARCH model was evaluated as moderate, with an RMSE of 7.8 tons and a MAPE of 6.5%, indicating lower precision compared to ARIMA but suitable for capturing dynamic fluctuations (R² = 0.88).

State transition models were used to categorize availability levels into three main states: low (<140 tons), medium (140–155 tons), and high (>155 tons). As shown in Figure 4, the transition to a high availability state was projected for 2025, driven by favorable climatic conditions and increased harvesting intensity. While effective in categorical analysis, these models showed limitations in predicting continuous values, with an RMSE of 8.9 tons, a MAPE of 7.2%, and an R² of 0.85.

Monte Carlo simulations generated 1000 hypothetical scenarios based on the independent variables. The results showed an 80% probability of achieving volumes above 155 tons in 2025, with average projected values of 162 tons. The scenario distribution revealed that 50% of the predicted values for 2025 ranged between 158 and 165 tons, while 10% showed deviations below 150 tons, reflecting adverse scenarios (Figure 5). The model’s performance was highlighted by its high reliability, with an RMSE of 5.4 tons, a MAPE of 4.7%, and an R² of 0.94, demonstrating its robustness in handling complex uncertainties. To assess the robustness of the Monte Carlo predictions, a sensitivity analysis was conducted by varying key input parameters—precipitation (±20%), harvesting intensity (±15%), and operational costs (±10%)—across the 1000 scenarios. The results showed that precipitation had the greatest impact, with a 20% reduction lowering the mean 2025 forecast from 162 tons to 154 tons (95% CI: 149–159 tons), while cost variations had minimal effect (±2 tons). Extreme scenarios, such as a drought year (precipitation −30%) combined with reduced harvesting (−20%), reduced availability to 148 tons, highlighting vulnerability to climatic extremes. These findings confirm the model’s robustness under moderate fluctuations but underscore the need for adaptive strategies in worst-case scenarios.

The superior performance of Monte Carlo simulations (RMSE: 5.4 tons, MAPE: 4.7%, R²: 0.94) compared to ARIMA, GARCH, and state transition models can be attributed to its ability to integrate multiple sources of uncertainty—climatic, operational, and economic—into a probabilistic framework, generating a wide range of scenarios that reflect real-world complexity. ARIMA excelled in capturing linear trends and seasonality (R²: 0.92), but its reliance on historical patterns limited its adaptability to sudden disruptions or nonlinear dynamics. GARCH effectively modeled volatility (RMSE: 7.8 tons), yet its focus on variance left it less equipped for long-term forecasting across diverse variables. State transition models provided categorical insights but struggled with continuous predictions (R²: 0.85). Monte Carlo’s edge emerges in contexts with high uncertainty and interdependent factors, such as fluctuating weather or harvesting schedules, making it particularly effective for strategic planning over operational optimization. This advantage is likely generalizable to systems with similar variability, though its computational intensity may restrict its use in resource-constrained settings, suggesting a trade-off between accuracy and practicality.

The results highlight the potential of stochastic models to inform critical decisions in the management of residual woody biomass. The forecasts identified periods of higher availability, enabling optimized scheduling of harvesting and transportation, particularly in 2025, when availability is projected to reach peak levels. The analysis of probabilistic scenarios contributed to predicting storage demands and minimizing waste, while uncertainty modeling with GARCH and Monte Carlo provided a comprehensive understanding of possible fluctuations, allowing real-time adjustments in operational strategies. Despite the promising results, certain limitations were identified. Models such as GARCH and Monte Carlo require significant computational resources, which may hinder real-time application. The generated data, though based on realistic patterns, may not fully capture the complexity of real-world scenarios, and the models need to be calibrated for different regions and ecological conditions to ensure broader applicability.

4. Discussion

The results of the stochastic models provide a solid foundation to support informed decisions in the exploration and conservation of residual woody biomass [53]. The forecasts allow for the identification of periods of higher biomass availability, optimizing the scheduling of forestry and agricultural operations [54]. Based on the results, environmental impacts can be minimized by avoiding excessive exploitation during periods of low availability [55]. Furthermore, the models can integrate climatic and ecological data to predict risk conditions, such as droughts or heightened susceptibility to wildfires, supporting management strategies that promote ecosystem resilience [56]. Forecasting residues also enables a balance between harvesting and regeneration, ensuring the long-term sustainability of the resource [57]. Finally, using Monte Carlo simulations to evaluate scenarios allows for efficient allocation of available biomass, reducing waste and costs associated with inadequate storage [58].

The results have significant implications for the development of energy and environmental policies. Accurate biomass availability forecasts can be integrated into energy transition plans, ensuring renewable energy targets are met without compromising supply stability [59]. Incentive policies can also be aligned with periods of high availability, promoting the use of biomass as a substitute for fossil fuels [60]. The forecasts also help define regional quotas for sustainable exploration, aligning with conservation goals and climate change mitigation efforts [61]. Stochastic models can inform the establishment of dynamic tariffs or subsidies, seasonally adjusted according to predicted supply [11]. Integrating forecasts with emissions data and carbon balance assists in evaluating the environmental impact of the biomass supply chain, guiding policies to minimize emissions and maximize environmental benefits [62].

The application of the results in the industry can transform the management of the residual woody biomass supply chain, resulting in efficiency gains and cost reductions [63]. Forecasts enable companies to plan the logistics of biomass collection, transportation, and storage, ensuring consistent delivery volumes aligned with market demands [64]. Also, identifying regions with higher availability during different periods can guide resource allocation, reducing transportation costs [14]. Companies that rely on residual biomass for energy or biofuel production can adjust their production operations based on predicted fluctuations, avoiding supply interruptions [65]. The integration of advanced models with artificial intelligence and big data technologies can create more competitive solutions, offering a strategic advantage to companies in the sector [66]. Simulation models can aid in forecasting future market scenarios, enabling proactive adjustments to supply and demand conditions [67].

Figure 6 presents a flowchart outlining the practical applications of the stochastic models developed in this study, demonstrating how different models were adjusted to meet specific needs in operational planning, risk management, policy formulation, and industrial logistics optimization. The selection of the most appropriate model was based on the results obtained in terms of performance and reliability, ensuring efficient application in each context. This flowchart emphasizes the role of ARIMA in periodic planning of forestry and agricultural operations, GARCH in risk prediction, such as wildfires, and Monte Carlo simulations in complex scenario analysis for energy policies and industrial logistics.

5. Conclusions

This study analyzed the application of stochastic models to predict the availability of residual woody biomass, emphasizing their relevance for sustainable management and energy planning. The key findings include the efficiency of the models, with ARIMA excelling in capturing seasonal patterns and linear trends, while GARCH effectively modeled dynamic variations. Monte Carlo simulations delivered the best performance when dealing with uncertain and distributed scenarios. In terms of practical applicability, the predictive models provided a solid foundation for optimizing exploitation, logistics, and energy production operations, as well as supporting political decisions and conservation strategies. Regarding methodological contributions, this work demonstrated the feasibility of combining different stochastic approaches, offering a robust and replicable methodology adaptable to various regional contexts and environmental conditions.

The findings of this study pave the way for new investigations and practical applications. The integration of real-world data and advanced technologies, such as IoT sensors, drones, and satellite imagery, could further enhance the accuracy of predictions. Exploring more sophisticated models, such as hybrid methods that combine machine learning with stochastic models, holds the potential to capture more complex and nonlinear dynamics. To address computational constraints, future research could focus on developing optimized algorithms, such as parallelized Monte Carlo implementations using GPU acceleration or simplified GARCH variants with reduced parameter sets, to enhance scalability and enable real-time applications. Integrating real-world data could be advanced by leveraging IoT sensors for continuous forest monitoring, satellite imagery for spatial biomass estimation, and regional databases (e.g., national forest inventories) to validate and refine model predictions. These approaches would bridge the gap between hypothetical simulations and practical deployment, ensuring broader applicability across diverse ecological and operational contexts.

Future studies could expand the use of these models to predict biomass on larger spatial scales or over longer time horizons, considering long-term climatic variables. Additionally, modeling biomass availability under different global warming scenarios could provide critical data for adaptation and mitigation strategies.

Despite the advances presented, this study faced some limitations that should be addressed in future research. The quality and availability of data were essential for this analysis, but the lack of large-scale real-world data could limit the practical application of the models. The use of regional and global databases is recommended to validate the results. Certain models, such as ARIMA, have limitations in capturing nonlinear dynamics, and future research should explore integration with neural networks and deep learning algorithms. While this study focused on traditional stochastic models, hybrid approaches combining machine learning—such as neural networks with ARIMA—were not explored due to the limited scope of the hypothetical dataset and the computational resources required for training. Such hybrids could enhance performance by capturing nonlinear dynamics missed by ARIMA or GARCH, as demonstrated by Khashei and Bijari [29], and warrant investigation in future work with larger, real-world datasets.

Models like GARCH and Monte Carlo simulations require high computational resources, which may hinder their real-time application. Developing optimized algorithms for greater computational efficiency is necessary. Finally, future studies could incorporate socioeconomic variables, such as market prices and government policies, to broaden the scope and applicability of the predictions.