Extending the Local Convergence of a Seventh Convergence Order Method without Derivatives
Abstract
:1. Introduction
2. Local Convergence
- (1)
- has a smallest zero for some function , which is continuous and non-decreasing (function). Let .
- (2)
- has a smallest zero for some (function) and function defined by:
- (3)
- has a smallest zero for some (functions) , , , , and function defined by:
- (4)
- has a smallest zero for some function defined by:
- (a1)
- for all and some , .
- Let .
- (a2)
- and
- for all some , , and s, z given by the first two substeps of method (4).
- (a3)
- , where .
- (i)
- Pointis a simple solution of equation.
- (ii)
- has a smallest solution.Let .
- (iii)
- for all and some function .Let .Then, the only solution of the equation in the set is .
3. Attraction Basins
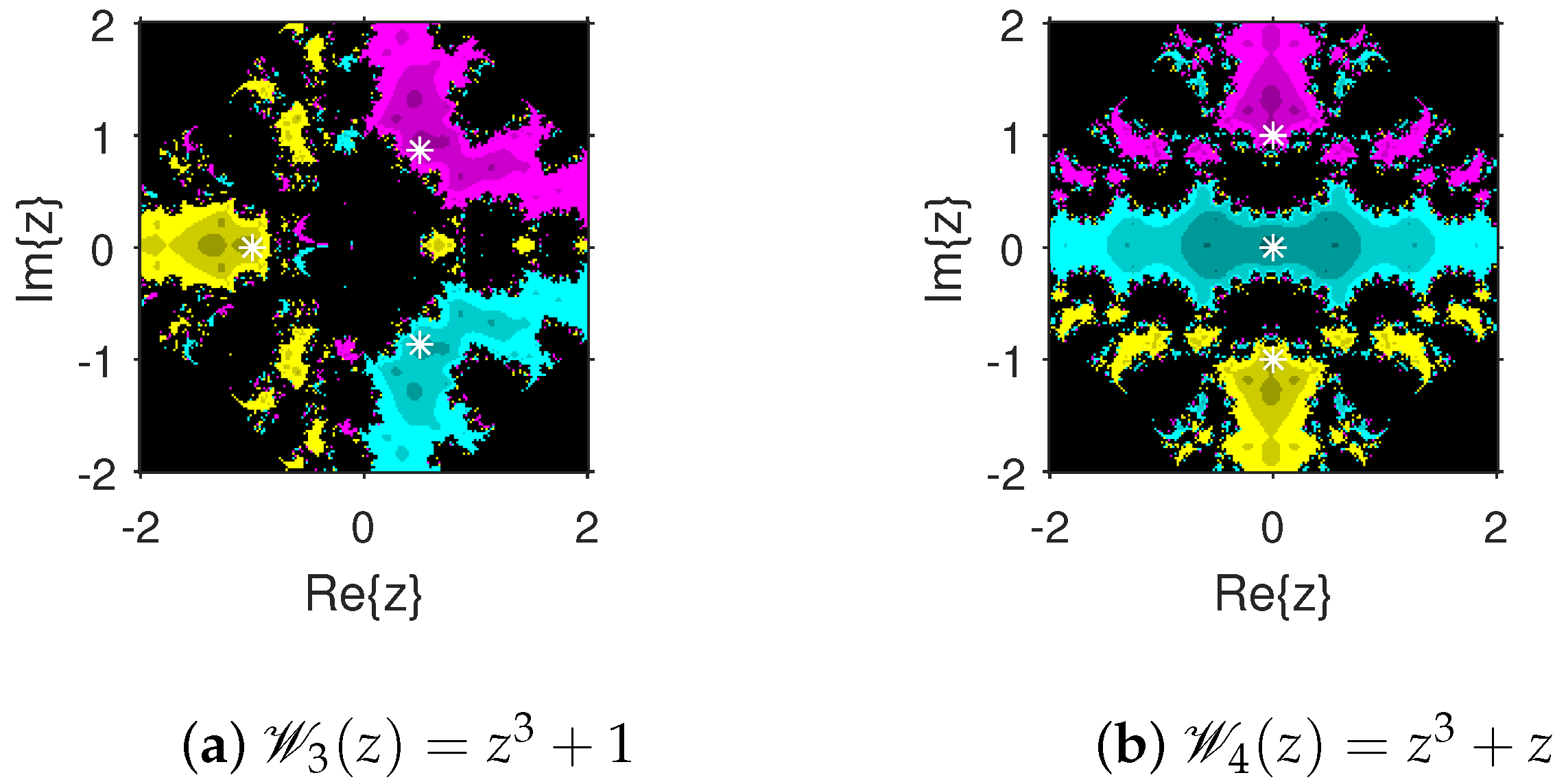
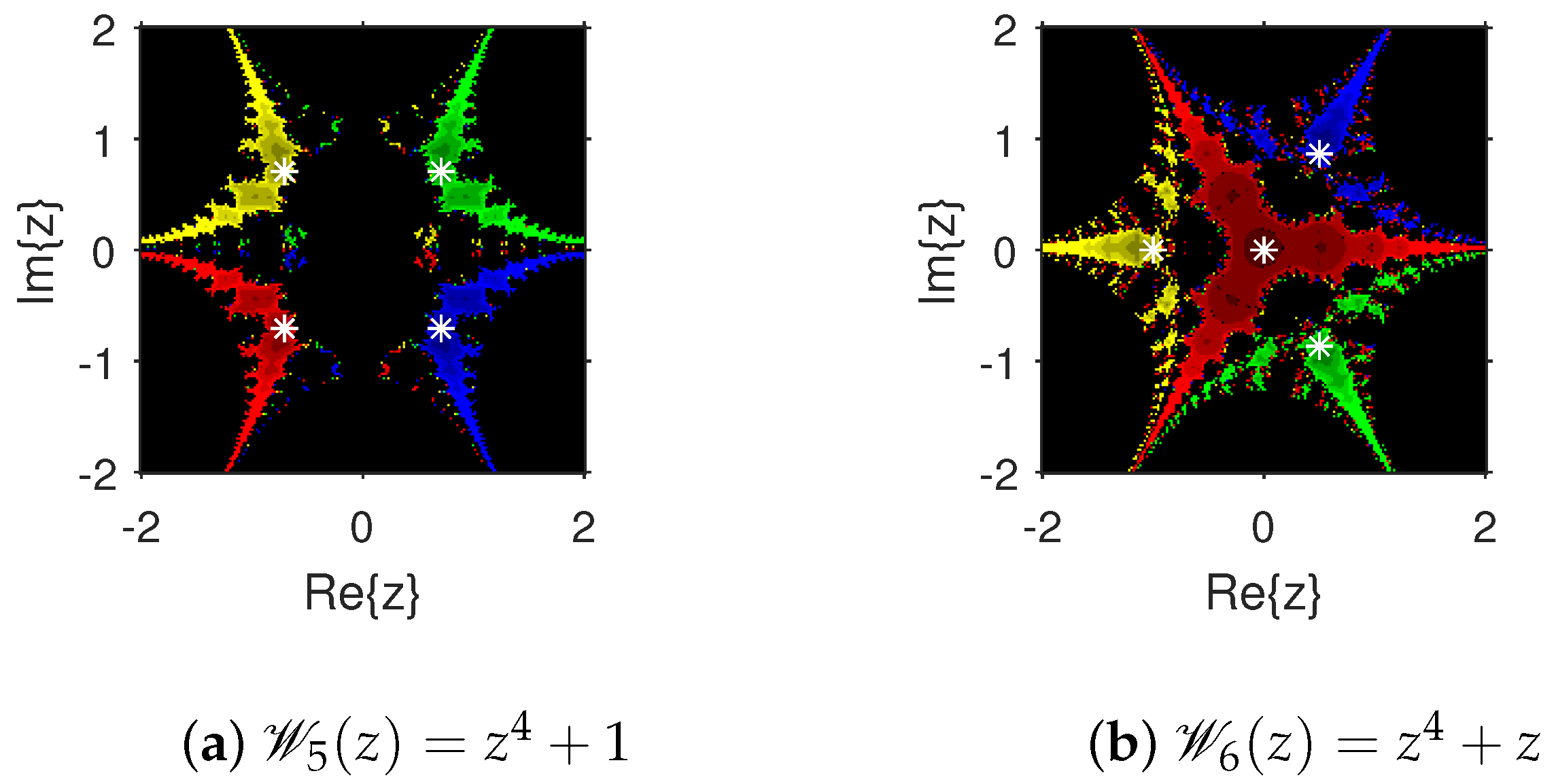
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ortega, J.M.; Rheinholdt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Traub, J.F. Iterative Methods for Solution of Equations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- Sharma, J.R.; Arora, H. An efficient derivative free iterative method for solving systems of nonlinear equations. Appl. Anal. Discr. Math. 2013, 7, 390–403. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Zhang, T. A family of steffensen type methods with seventh-order convergence. Numer. Algor. 2013, 62, 429–444. [Google Scholar]
- Argyros, I.K. Computational Theory of Iterative Methods, Series: Studies in Computational Mathematics; Chui, C.K., Wuytack, L., Eds.; Elsevier: New York, NY, USA, 2007. [Google Scholar]
- Argyros, I.K.; George, S. On the complexity of extending the convergence region for Traub’s method. J. Complex. 2020, 56, 101423. [Google Scholar] [CrossRef]
- Argyros, I.K. Unified Convergence Criteria for Iterative Banach Space Valued Methods with Applications. Mathematics 2021, 9, 1942. [Google Scholar] [CrossRef]
- Argyros, I.K.; Magreñán, Á.A. A Contemporary Study of Iterative Methods; Elsevier: New York, NY, USA, 2018. [Google Scholar]
- Argyros, I.K. The Theory and Applications of Iterative Methods, 2nd ed; Engineering Series; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Argyros, I.K.; Sharma, D.; Argyros, C.I.; Parhi, S.K.; Sunanda, S.K. Extended iterative schemes based on decomposition for nonlinear models. J. Appl. Math. Comput. 2021. [Google Scholar] [CrossRef]
- Behl, R.; Bhalla, S.; Magreñán, Á.A.; Moysi, A. An optimal derivative free family of Chebyshev-Halley’s method for multiple zeros. Mathematics 2021, 9, 546. [Google Scholar] [CrossRef]
- Cordero, A.; Hueso, J.L.; Martinez, E.; Torregrosa, J.R. A modified Newton-Jarratts composition. Numer. Algor. 2010, 55, 87–99. [Google Scholar] [CrossRef]
- Ezquerro, J.A.; Hernandez, M.A.; Romero, N.; Velasco, A.I. On Steffensen’s method on Banach spaces. J. Comput. Appl. Math. 2013, 249, 9–23. [Google Scholar] [CrossRef]
- Grau-Sanchez, M.; Grau, A.; Noguera, M. Frozen divided difference scheme for solving systems of nonlinear equations. J. Comput. Appl. Math. 2011, 235, 1739–1743. [Google Scholar] [CrossRef]
- Hernandez, M.A.; Rubio, M.J. A uniparametric family of iterative processes for solving nondifferentiable equations. J. Math. Anal. Appl. 2002, 275, 821–834. [Google Scholar] [CrossRef] [Green Version]
- Kantorovich, L.V.; Akilov, G.P. Functional Analysis; Silcock, H.L., Translator; Pergamon Press: Oxford, UK, 1982. [Google Scholar]
- Liu, Z.; Zheng, Q.; Zhao, P. A variant of Steffensen’s method of fourth-order convergence and its applications. Appl. Math. Comput. 2010, 216, 1978–1983. [Google Scholar] [CrossRef]
- Magreñán, Á.A.; Argyros, I.K.; Rainer, J.J.; Sicilia, J.A. Ball convergence of a sixth-order Newton-like method based on means under weak conditions. J. Math. Chem. 2018, 56, 2117–2131. [Google Scholar] [CrossRef]
- Magreñán, Á.A.; Gutiérrez, J.M. Real dynamics for damped Newton’s method applied to cubic polynomials. J. Comput. Appl. Math. 2015, 275, 527–538. [Google Scholar] [CrossRef]
- Ren, H.; Wu, Q.; Bi, W. A class of two-step Steffensen type methods with fourth-order convergence. Appl. Math. Comput. 2009, 209, 206–210. [Google Scholar] [CrossRef]
- Sharma, D.; Parhi, S.K. On the local convergence of higher order methods in Banach spaces. Fixed Point Theory. 2021, 22, 855–870. [Google Scholar] [CrossRef]
- Sharma, J.R.; Arora, H. A novel derivative free algorithm with seventh order convergence for solving systems of nonlinear equations. Numer. Algor. 2014, 67, 917–933. [Google Scholar] [CrossRef]
- Sharma, J.R.; Arora, H. Efficient derivative-free numerical methods for solving systems of nonlinear equations. Comp. Appl. Math. 2016, 35, 269–284. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, T.; Qian, W.; Teng, M. Seventh-order derivative-free iterative method for solving nonlinear systems. Numer. Algor. 2015, 70, 545–558. [Google Scholar] [CrossRef]
- Rall, L.B. Computational Solution of Nonlinear Operator Equations; Robert E. Krieger: New York, NY, USA, 1979. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Argyros, I.K.; Sharma, D.; Argyros, C.I.; Parhi, S.K. Extending the Local Convergence of a Seventh Convergence Order Method without Derivatives. Foundations 2022, 2, 338-347. https://doi.org/10.3390/foundations2020023
Argyros IK, Sharma D, Argyros CI, Parhi SK. Extending the Local Convergence of a Seventh Convergence Order Method without Derivatives. Foundations. 2022; 2(2):338-347. https://doi.org/10.3390/foundations2020023
Chicago/Turabian StyleArgyros, Ioannis K., Debasis Sharma, Christopher I. Argyros, and Sanjaya Kumar Parhi. 2022. "Extending the Local Convergence of a Seventh Convergence Order Method without Derivatives" Foundations 2, no. 2: 338-347. https://doi.org/10.3390/foundations2020023
APA StyleArgyros, I. K., Sharma, D., Argyros, C. I., & Parhi, S. K. (2022). Extending the Local Convergence of a Seventh Convergence Order Method without Derivatives. Foundations, 2(2), 338-347. https://doi.org/10.3390/foundations2020023







