Management of Coastline Variability in an Endangered Island Environment: The Case of Noirmoutier Island (France)
Abstract
:1. Introduction
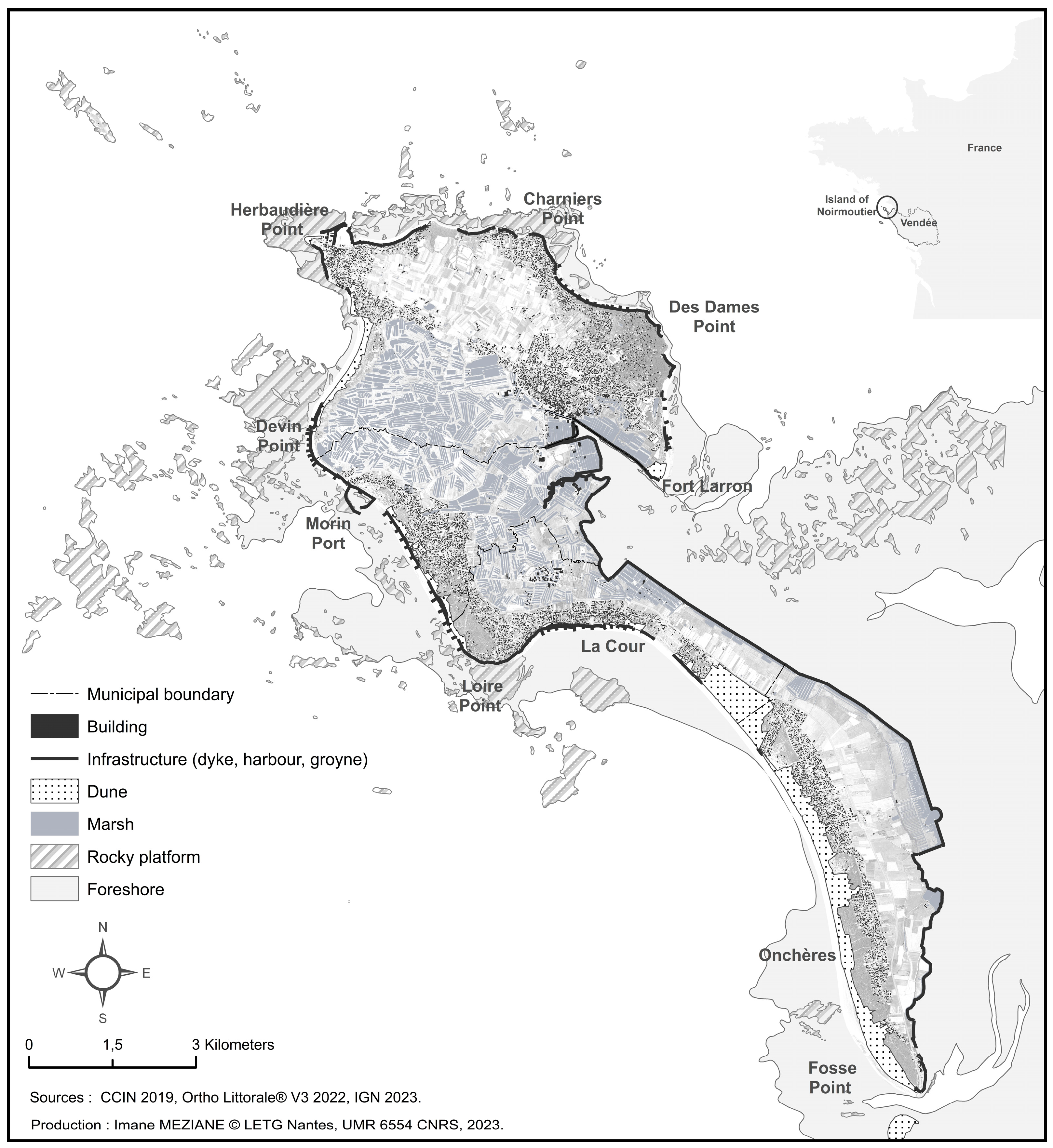
2. Characterisation of the Study Area
2.1. Outline of the Study Area
2.2. Regulatory Context
3. Methodology
3.1. Data Presentation
3.2. Choice of Shoreline Position Marker
3.3. Methodology for Calculating the Historical Evolution of the Shoreline
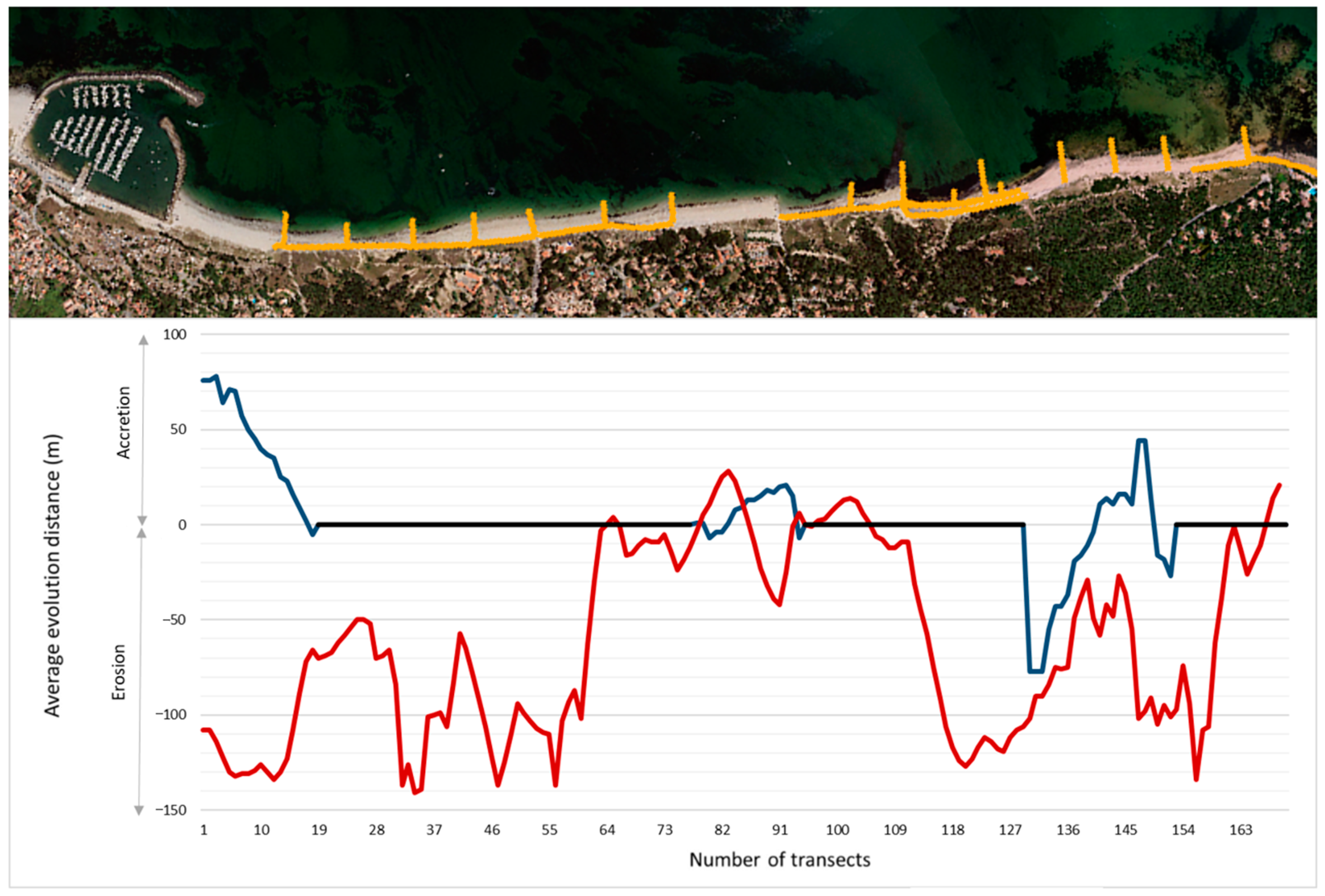
3.3.1. Kinematic Analysis of the Shoreline by Transects
3.3.2. Surface Analysis of the Shoreline Evolution
3.3.3. Cartographic Representation of the Historic Shoreline Evolution
3.3.4. Estimation of Error
3.4. Shoreline Projection Methodology
3.4.1. Mapping of the Projected Shorelines
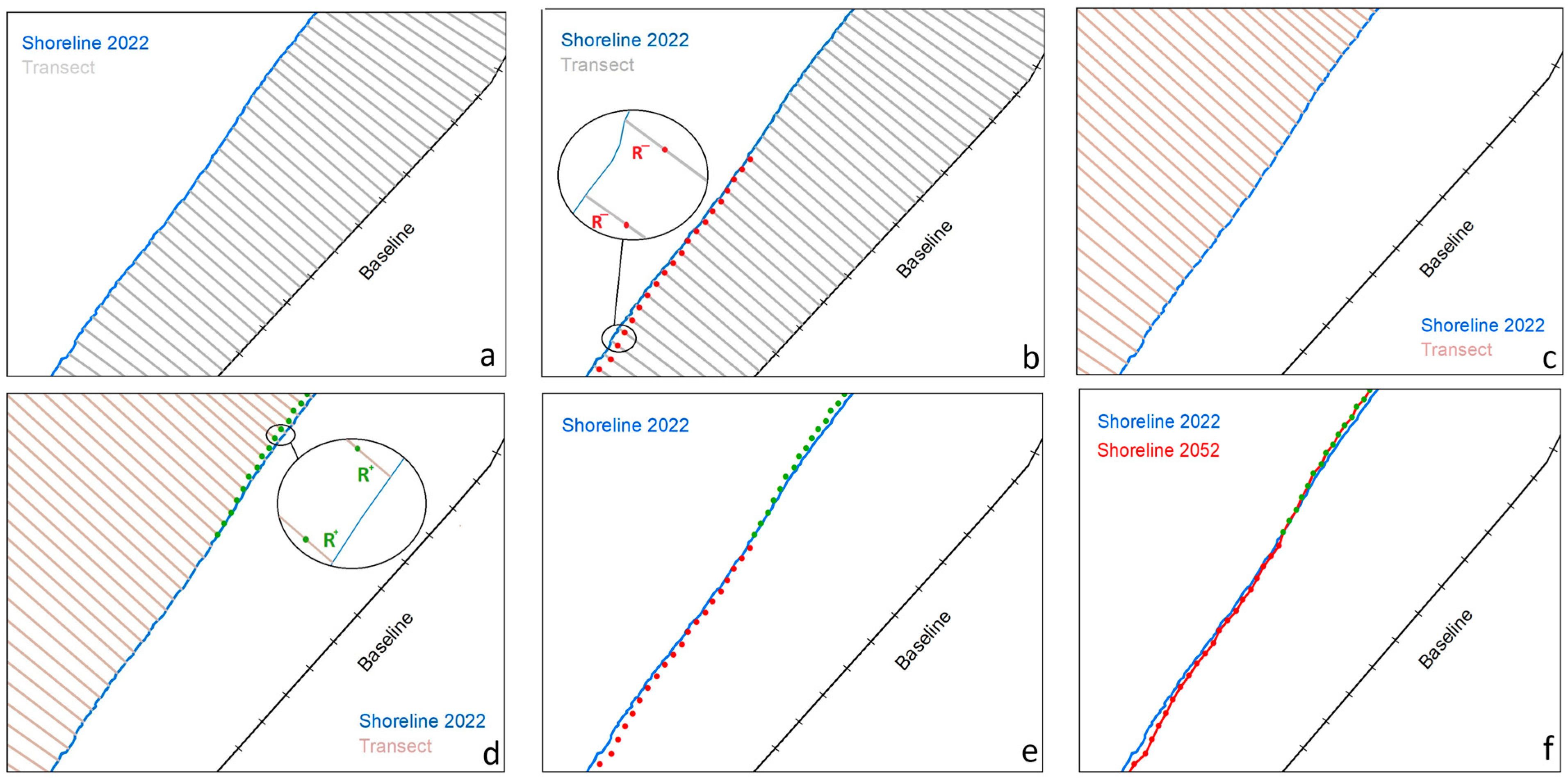
- Generation of transects: transects spaced 20 m apart were generated using DSAS, from the baseline to the 2022 reference shoreline.
- Projection of points on the land: after generating the transects, points were plotted along them towards land, spaced at a specific distance, using the ArcGIS ‘Create Point on Lines’ extension. The distance corresponded to the negative values of the projected retreat “R−” over a period of 30 years, as calculated by the Durand and Heurtefeux equation.
- Creation of transects oriented towards the sea: transects were also created for the reference 2022 shoreline, this time oriented towards the sea. These were spaced in the same way as the transects towards land.
- Projection of points towards the sea: the positive values of the projected retreat “R+” over 30 years were used to project points towards the sea along these transects.
- Overlay of points: Once all points are created, they are overlaid to obtain a complete visualisation of the projected shoreline at the 30-year horizon.
- Digitisation of the shoreline position in 2052: the shoreline position in 2052 was digitised by connecting the points created.
3.4.2. Estimation of Error
- Data error for the four variables used in the Durand and Heurtefeux equation [59] (Table 5): the calculation of uncertainty associated with the position of the shoreline was based on the results of the error in the overall position of the shoreline, as shown previously in Table 3. In addition, uncertainty relating to variable E20 was derived from work carried out by Ferret [63]. With regard to uncertainty related to slope, this value was deduced from the error present in the Lidar 2022 DTM data provided by the Vendée department. Finally, to estimate the uncertainty of variable E21 relating to future sea level rise, the IPCC assessments were used as a reference.
- Error relating to the shoreline projection based on the results of the comparison between the digitised and projected shorelines for 2022 (Table 6): the aim of the methodology was to quantify the past evolution of the shoreline and project it to the 2022 horizon, a year for which the position of the shoreline is known. The method consisted of first calculating an average evolutionary trend over a period of 26 years (1974–2000). The parameters used in the Durand and Heurtefeux formula, comprising extrapolation, slope, and rise in sea level since 1950 and predicted for 2022, were used for a 22-year projection of the shoreline based on the position of the shoreline in 2000. The uncertainty was then evaluated according to the mean annual difference between the two shoreline positions (digitised and projected in 2022) and normalised by the number of years used in the projection.
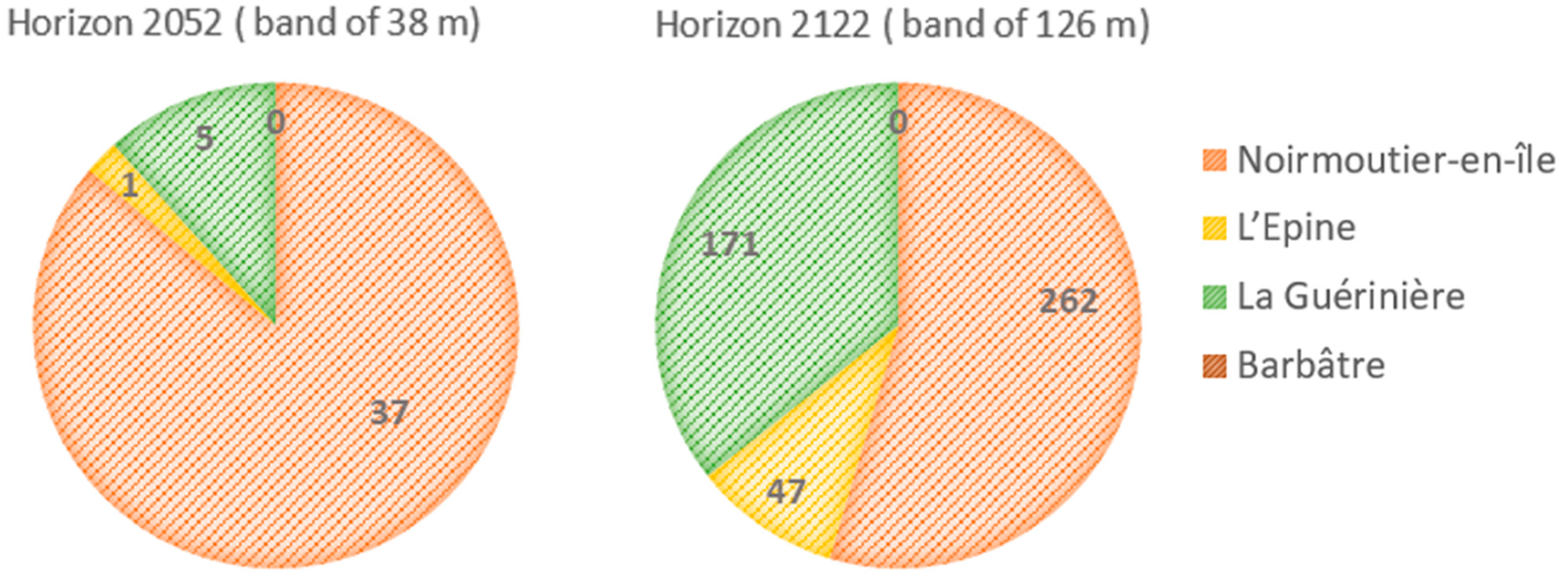
3.4.3. Proximity of Stakes to the Projected Shorelines
4. Results
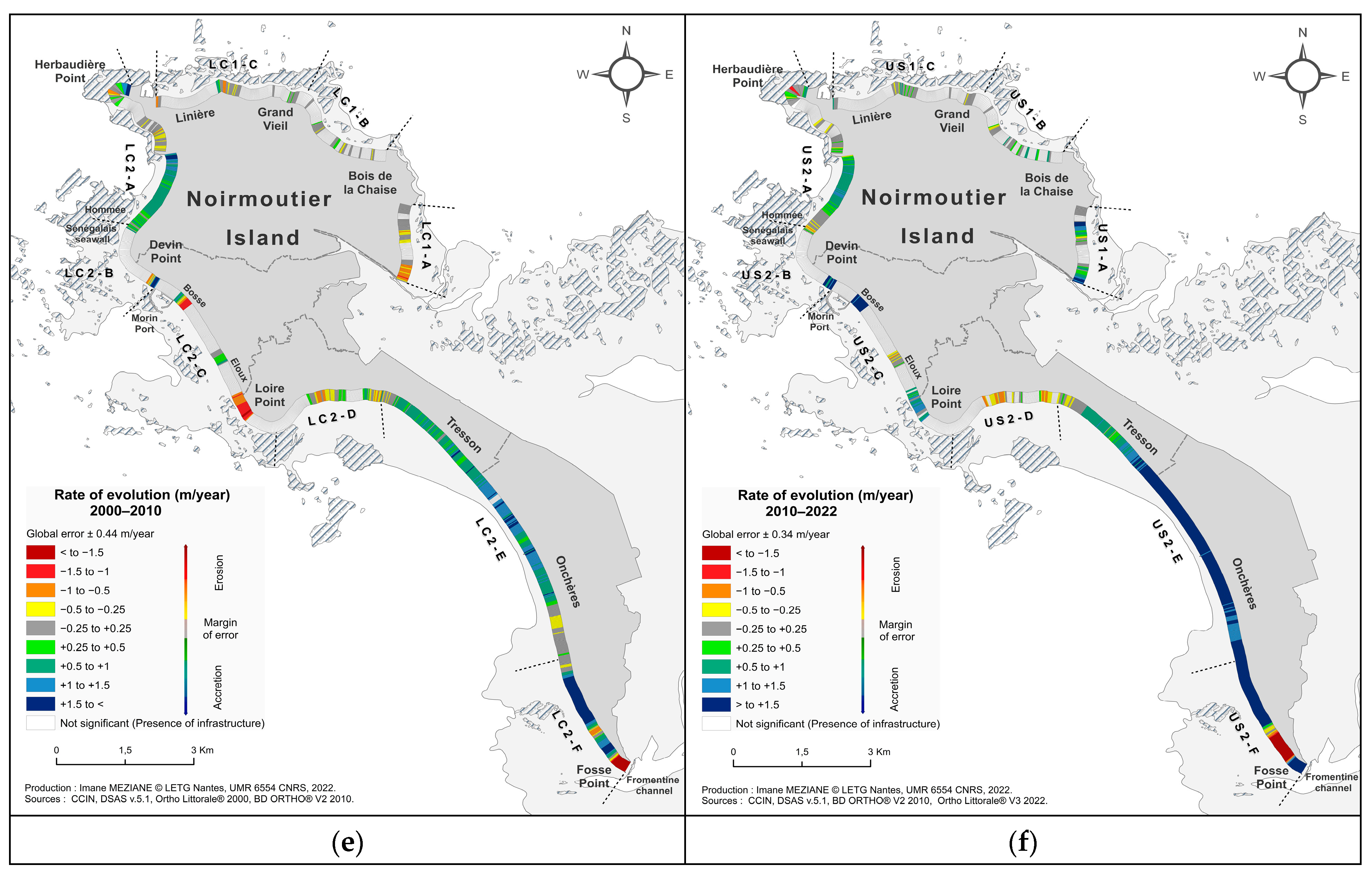
4.1. Analysis of the Shoreline Linear Evolution
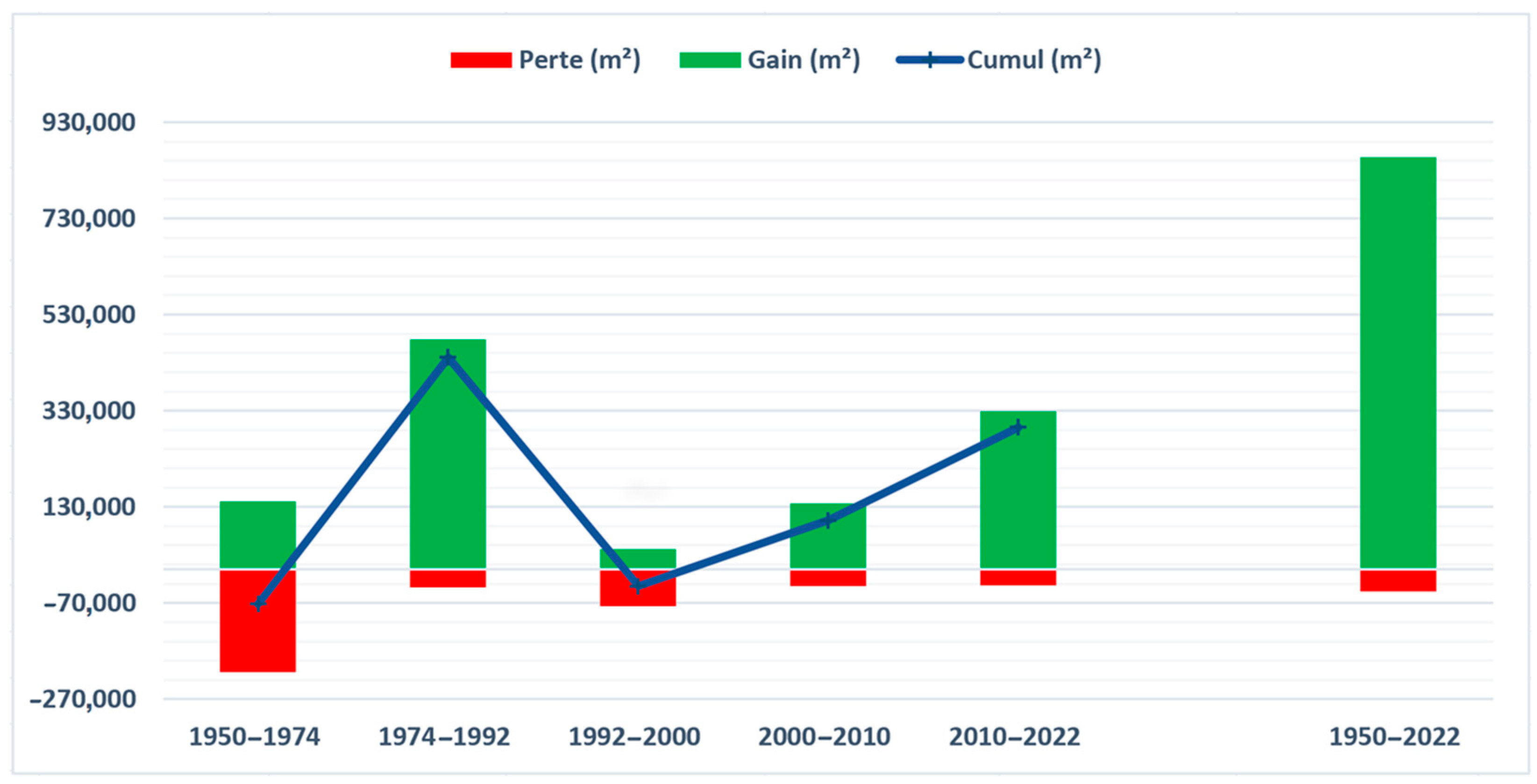
4.2. Analysis of the Shoreline Surface Evolution
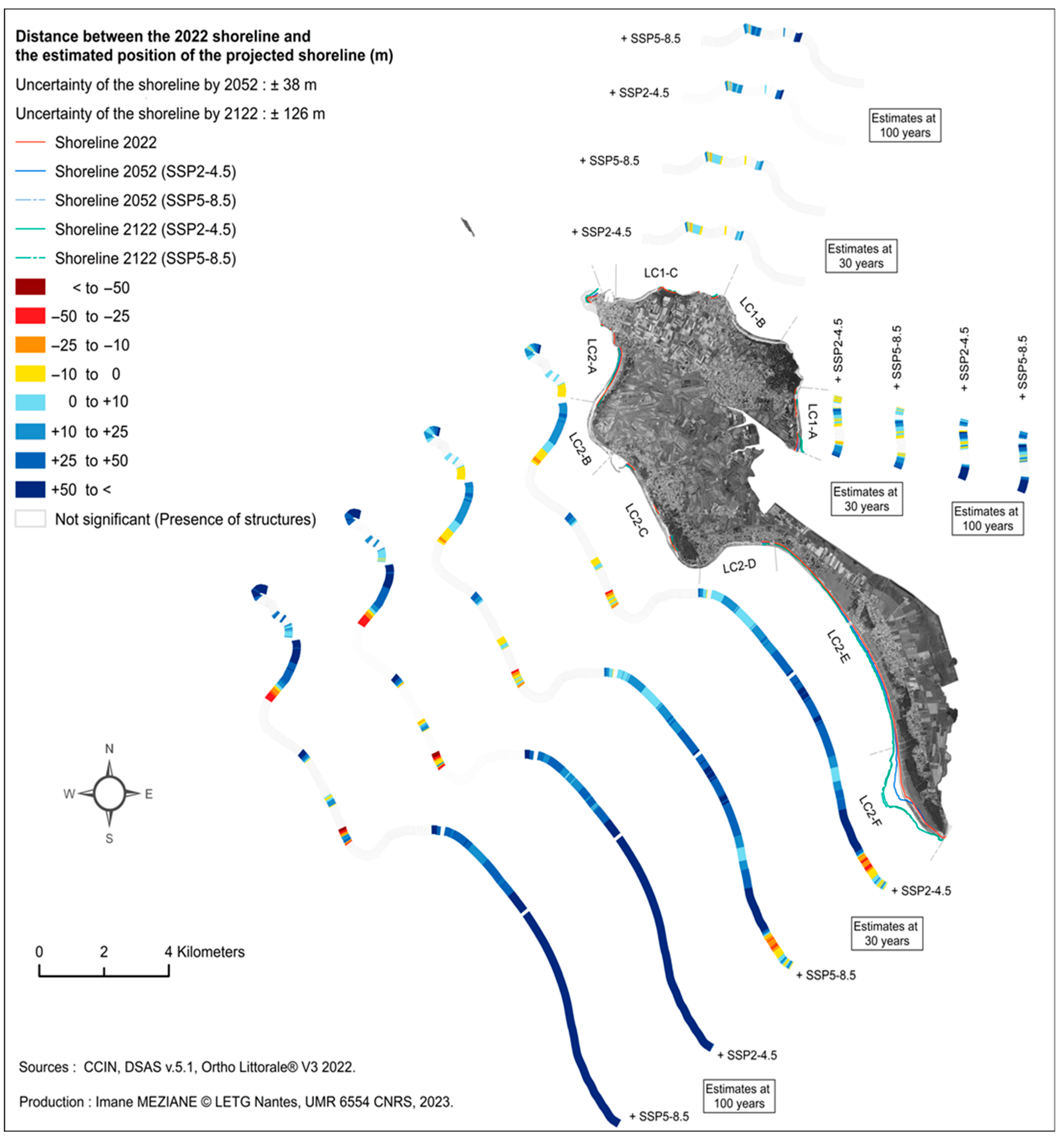
4.3. Prospective Analysis of the Shoreline over 30 Years and 100 Years
4.3.1. Comparison of the Two Projection Tests
4.3.2. Prospective Mapping of the Noirmoutier Island Shoreline in 2052 and 2122
5. Discussion
5.1. Methodological Choices
5.1.1. Choice of Method for Estimating Surface Uncertainty in the Shoreline Evolution
5.1.2. Choice of Shoreline Projection Method
5.1.3. Choice of Historic Period
5.1.4. Uncertainty Relating to the Estimation of Future Sea Level Rise (E21)
5.1.5. Uncertainty Relating to Slope Estimation
5.1.6. Choice of Using Lmax in the Durand and Heurtefeux Method
5.1.7. Inclusion or Exclusion of Coastal Protection Structures for Mapping
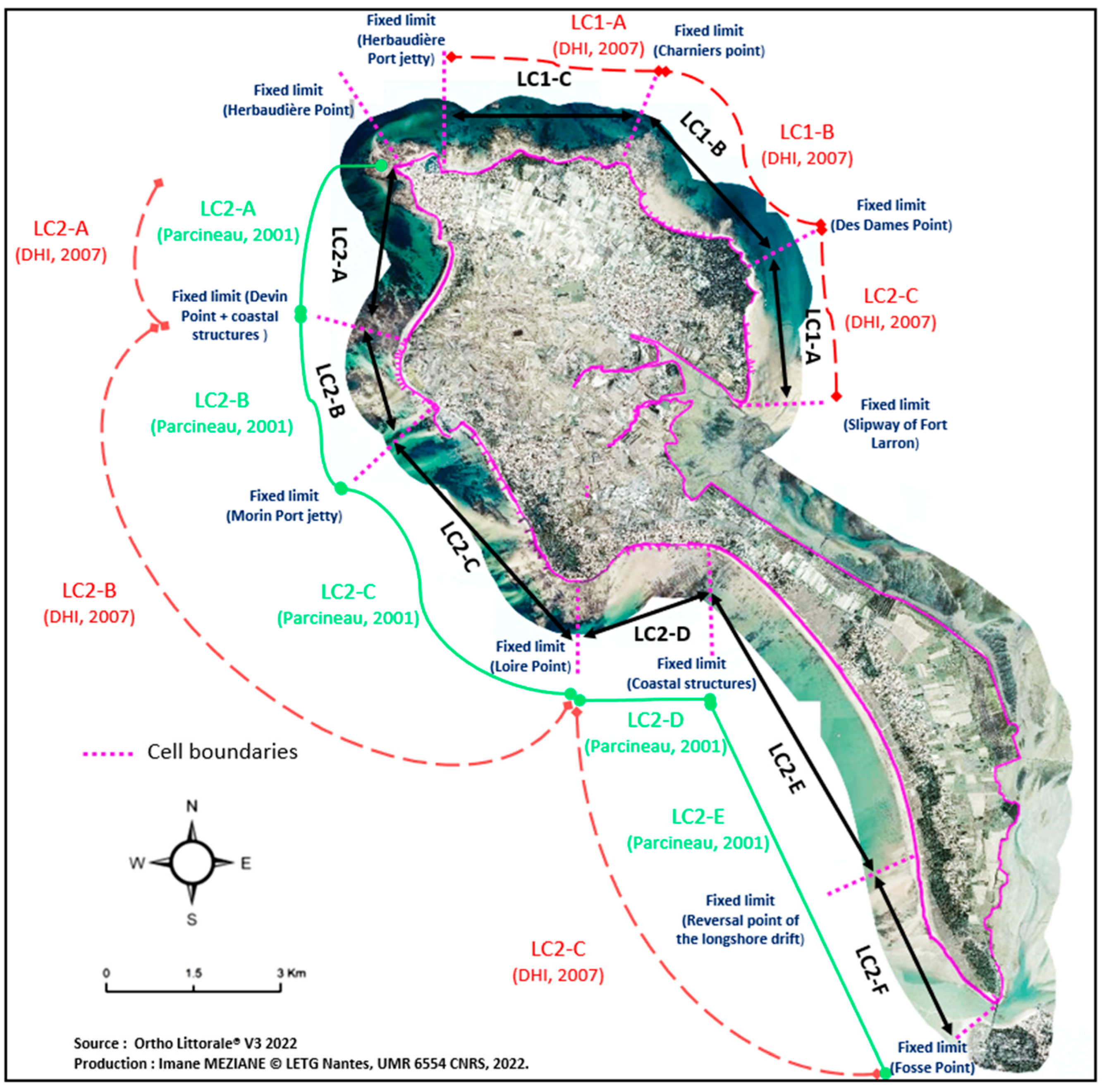
5.2. Most Impacted Sectors
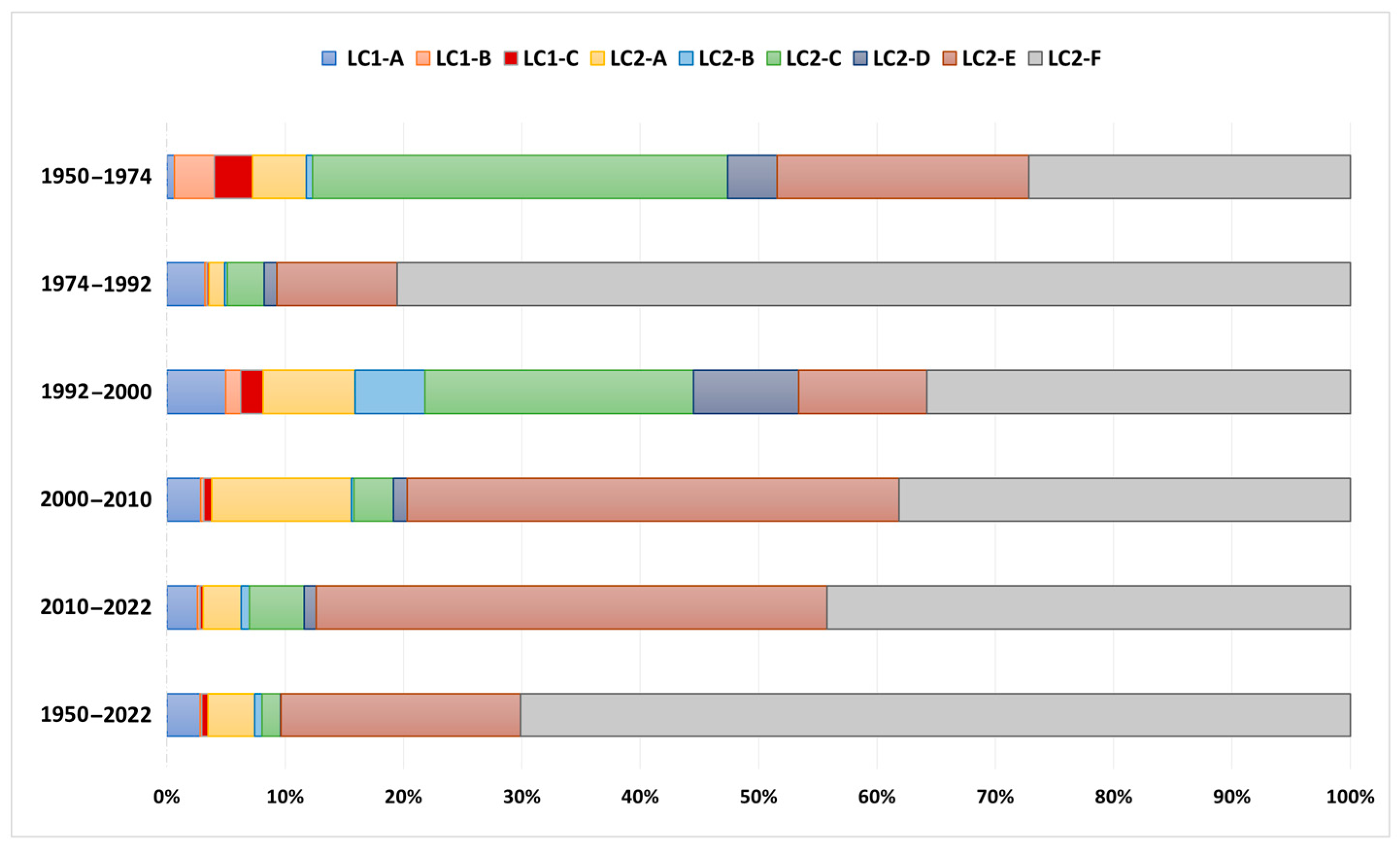
- The significant contribution of certain cells to the total balance. For instance, LC2-E showed a remarkable contribution to the overall balance, especially during the periods from 2000 to 2010 and 2010 to 2022. Indeed, each coastal cell exhibits a distinct behaviour that evolves at its own pace.
- Variations in contributions among different coastal cells over time. For example, LC2-F made a major contribution during the period 1974–1992, and its smallest contribution remains significant during the earlier period from 1950 to 1974. Other cells have minor contributions.
- These variations stem from both storm cycle variations and sand replenishment, as well as coastal defense development. For instance, LC1-B has seen a diminishing contribution over time, attributed in this case to an increase in protected coastline length. Thus, each case requires a thorough analysis of natural forces and human interventions.
5.3. Operational Use of Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Paskoff, R. Côte en Danger, Collection Pratiques de la Géographie; Masson: Paris, France, 1993; Volume 250. [Google Scholar]
- Onerc. Le Littoral Dans le Contexte du Changement Climatique, la Documentation Française. 2015; Volume 180. Available online: https://www.ecologie.gouv.fr/sites/default/files/documents/ONERC_Rapport_2015_Littoral_WEB.pdf (accessed on 13 April 2024).
- Meur-ferec, C.; Morel, V. L’érosion sur la frange côtière: Un exemple de gestion des risques. Nat. Sci. Soc. 2004, 12, 263–273. [Google Scholar] [CrossRef]
- Callaghan, D.P.; Roshanka, R.; Andrew, S. Quantifying the storm erosion hazard for coastal planning. Coast. Eng. 2009, 56, 90–93. [Google Scholar] [CrossRef]
- Oppenheimer, M.; Glavovic, B.C.; Hinkel, J.; van de Wal, R.; Magnan, A.K.; Abd-Elgawad, A.; Cai, R.; Cifuentes-Jara, M.; Deconto, R.M.; Ghosh, T.; et al. Sea level rise and implications for low-lying islands, coasts and communities. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; Pörtner, H.-O., Roberts, D.C., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegría, A., Nicolai, M., Okem, A., et al., Eds.; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2019. [Google Scholar]
- Rahman, M.K.; Crawford, T.W.; Islam, S. Shoreline Change Analysis along Rivers and Deltas: A Systematic Review and Bibliometric Analysis of the Shoreline Study Literature from 2000 to 2021. Geosciences 2022, 12, 410. [Google Scholar] [CrossRef]
- Buchou, S. Quel Littoral Pour Demain? Vers un Nouvel Aménagement des Territoires Côtiers Adapté Au changement Climatique. Rapport Remis à Monsieur le Premier Ministre. 2019, Volume 108. Available online: https://www.lereportersablais.com/wp-content/uploads/2019/11/Rapport_Buchou_Extrait.pdf (accessed on 2 May 2023).
- Apostolopoulos, D.; Nikolakopoulos, K. A review and meta-analysis of remote sensing data, GIS methods, materials and indices used for monitoring the coastline evolution over the last twenty years. Eur. J. Remote Sens. 2021, 54, 240–265. [Google Scholar] [CrossRef]
- Bruun, P. Sea level rise as a cause of shore erosion. J. Waterw. Harb. Div. 1962, 88, 117–130. [Google Scholar] [CrossRef]
- Luijendijk, A.; Hagenaars, G.; Ranasinghe, R.; Baart, F.; Donchyts, G.; Aarninkhof, S. The State of the World’s Beaches. Sci. Rep. 2018, 8, 6641. [Google Scholar] [CrossRef] [PubMed]
- Cooper, A.; Masselink, G.; Coco, G.; Short, A. Sandy beaches can survive sea-level rise. Nat. Clim. Chang. 2020, 10, 993–995. [Google Scholar] [CrossRef]
- Fattal, P.; Robin, M.; Paillart, M.; Maanan, M.; Mercier, D.; Lamberts, C.; Costa, S. Effets des tempêtes sur une plage aménagée et à forte protection côtière: La plage des Éloux (côte de Noirmoutier, Vendée, France). Norois 2010, 215, 101–114. [Google Scholar] [CrossRef]
- Debaine, F.; Robin, M. A new GIS modelling of coastal dune protection services against physical coastal hazards. Ocean Coast. Manag. 2012, 63, 43–54. [Google Scholar] [CrossRef]
- DHI. Analyses Météocéaniques au Large de Noirmoutier; DHI: Trentino, Italy, 2023; pp. 29–50. [Google Scholar]
- CEREMA. Dynamique et Évolution du littoral, Fascicule 6 de la pointe de Chémoulin à la pointe de Suzac, Collection: Connaissances. 2019. Available online: https://doc.cerema.fr/Default/digital-viewer/c-16157 (accessed on 8 May 2023).
- DHI; GEOS. Etude de Connaissance des Phénomènes D’érosion sur le LITTORAL vendéen. Rapport Final de la Tranche Ferme 2007. Volume 356. Available online: https://www.pays-de-la-loire.developpement-durable.gouv.fr/IMG/pdf/_50198_Erosion_du_littoral_vendeen_TF_FINAL.pdf (accessed on 22 April 2023).
- Parcineau, L. Noirmoutier, Une île à Fleur D’eau: Évolution et Défense du Littoral de la Côte Ouest de l’île de Noirmoutier du 18e Siècle à Nos Jours 1. Master’s Thesis, Nantes University, Nantes, France, 1991. [Google Scholar]
- Carter, R.W.G. Coastal Environments; Academic Press: Cambridge, MA, USA, 1988; p. 617. [Google Scholar]
- Bray, M.; Carter, D.; Hooke, J. Littoral cell definition and budgets for central southern England. J. Coast. Res. 1995, 11, 381–400. [Google Scholar]
- Frihy, O.E.; Shereet, S.M.; El Banna, M.M. Pattern of beach erosion and scour depth along the rosetta promontory and their effect on the existing protection works, Nile Delta, Egypt. J. Coast. Res. 2008, 244, 857–866. [Google Scholar] [CrossRef]
- Anfuso, G.; Pranzini, E.; Vitale, G. An integrated approach to coastal erosion problems in northern Tuscany (Italy): Littoral morphological evolution and cell distribution. Geomorphology 2011, 129, 204–214. [Google Scholar] [CrossRef]
- Boak, E.H.; Turner, I.L. Shoreline definition and detection: A review. J. Coast. Res. 2005, 214, 688–703. [Google Scholar] [CrossRef]
- Moore, L.J. Shoreline mapping techniques. J. Coast. Res. 2000, 16, 111–124. [Google Scholar]
- UNESCO-CSI. Environment and Development in Coastal Regions and in Small Islands. Available online: http://www.unesco.org/csi/pub/info/info410.htm (accessed on 15 May 2023).
- Zemmour, A. Étude de l’évolution des Littoraux Dunaires de la Côte d’Opale à Différentes Échelles de temps: Analyse de leur Capacité de Régénération Post-Tempête. Thèse de Doctorat, Université du Littoral Côte d’Opale, Wimereux, France, 2019. Available online: https://theses.hal.science/tel-02270709 (accessed on 23 March 2022).
- Dolan, R.; Fenster, M.S.; Holme, S.J. Temporal Analysis of Shoreline Recession and Accretion. J. Coast. Res. 1991, 7, 723–744. [Google Scholar]
- Crowell, M.; Leatherman, S.P.; Buckley, M.K. Historical shoreline change: Error analysis and mapping accuracy. J. Coast. Res. 1991, 7, 839–852. [Google Scholar]
- Durand, P. Approche Méthodologique Pour L’analyse de L’évolution des Littoraux Sableux par Photo-Interprétation. Exemple des Plages Situées Entre les Embouchures de l’Aude et de l’Hérault (Languedoc, France). Photo-Interprétation, 2000/1-2, 3-18. Available online: http://geoprodig.cnrs.fr/items/show/190158 (accessed on 2 July 2023).
- Morton, R.A.; Miller, T.L. National Assessment of Shoreline Change—Part 2: Historical Shoreline Changes and Associated Coastal Land Loss along the US Southeast Atlantic Coast; U.S. Geological Survey Open-File Report; U.S. Geological Survey: Reston, VA, USA, 2005; p. 1401. Available online: http://pubs.usgs.gov/ (accessed on 30 September 2023).
- Hapke, C.J.; Reid, D.; Richmond, B.M.; Ruggiero, P.; List, J. National Assessment of Shoreline Change: Part 3: Historical Shoreline Changes and Associated Coastal Land Loss Along the Sandy Shorelines of the California Coast; U.S. Geological Survey Open-File Report; U.S. Geological Survey: Reston, VA, USA, 2006; Volume 79, p. 1219.
- Genz, A.S.; Fletcher, C.H.; Dunn, R.A.; Frazer, L.N.; Rooney, J.J. The Predictive Accuracy of Shoreline Change Rate Methods and Alongshore Beach Variation on Maui, Hawaii. J. Coast. Res. 2007, 231, 87–105. [Google Scholar] [CrossRef]
- Del Río, L.; Gracia, F.J.; Benavente, J. Shoreline change patterns in sandy coasts. A case study in SW Spain. Geomorphology 2012, 196, 252–266. [Google Scholar] [CrossRef]
- Juigner, M.; Robin, M.; Paul, F.; Maanan, M.; Debaine, F.; Le Guern, C.; Gouguet, L.; Baudouin, V. Cinématique d’un trait de côte sableux en Vendée entre 1920 et 2010. Méthode et analyse. Dyn. Environnementales Méthode Anal. 2012, 30, 29–39. [Google Scholar]
- Grenier, A.; Dubois, J.M.M. Evolution littorale récente par télédétection: Synthèse méthodologique. Pho-Interprétation 1990, 6, 3–16. [Google Scholar]
- Anfuso, G.; Bowman, D.; Danese, C.; Pranzini, E. Transect based analysis versus area based analysis to quantify shoreline displacement: Spatial resolution issues. Environ. Monit. Assess. 2016, 188, 568. [Google Scholar] [CrossRef] [PubMed]
- Himmelstoss, E.A.; Henderson, R.E.; Kratzmann, M.G.; Farris, A.S. Digital Shoreline Analysis System (DSAS) Version 5.1 User Guide; U.S. Geological Survey Open-File Report; U.S. Geological Survey: Reston, VA, USA, 2021; Volume 104, p. 1091. [CrossRef]
- Houser, C.; Hapke, C.; Hamilton, S. Controls on coastal dune morphology, shoreline erosion and barrier island response to extreme storms. Geomorphology 2008, 100, 223–240. [Google Scholar] [CrossRef]
- Moussaid, J.; Fora, A.A.; Zourarah, B.; Maanan, M.; Maanan, M. Using automatic computation to analyze the rate of shoreline change on the Kenitra coast, Morocco. Ocean Eng. 2015, 102, 71–77. [Google Scholar] [CrossRef]
- Cellone, F.; Carol, E.; Tosi, L. Coastal erosion and loss of wetlands in the middle Río de la Plata estuary (Argentina). Appl. Geogr. 2016, 76, 37–48. [Google Scholar] [CrossRef]
- Audère, M.; Robin, M. Assessment of the vulnerability of sandy coasts to erosion (short and medium term) for coastal risk mapping (Vendée, W France). Ocean Coast. Manag. 2021, 201, 105452. [Google Scholar] [CrossRef]
- Apostolopoulos, D.N.; Avramidis, P.; Nikolakopoulos, K.G. Estimating Quantitative Morphometric Parameters and Spatiotemporal Evolution of the Prokopos Lagoon Using Remote Sensing Techniques. J. Mar. Sci. Eng. 2022, 10, 931. [Google Scholar] [CrossRef]
- Chrisben Sam, S.; Gurugnanam, B. Coastal transgression and regression from 1980 to 2020 and shoreline forecasting for 2030 and 2040, using DSAS along the southern coastal tip of Peninsular India. Geod. Geodyn. 2022, 13, 585–594. [Google Scholar] [CrossRef]
- Sheik, M.; Chandrasekar. A shoreline change analysis along the coast between Kanyakumari and Tuticorin, India, using digital shoreline analysis system. Geo-Spat. Inf. Sci. 2011, 14, 282–293. [Google Scholar] [CrossRef]
- Juigner, M.; Robin, M.; Debaine, F.; Hélen, F. A generic index to assess the building exposure to shoreline retreat using box segmentation: Case study of the Pays de la Loire sandy coast (west of France). Ocean Coast. Manag. 2017, 148, 40–52. [Google Scholar] [CrossRef]
- Juigner, M.; Robin, M. Caractérisation de la morphologie des massifs dunaires de la région Pays de la Loire (France) face au risque de submersion marine. VertigO Revue Electr. Sci. Environ. 2018, 18, 2. [Google Scholar] [CrossRef]
- Kerguillec, R.; Audère, M.; Baltzer, A.; Debaine, F.; Fattal, P.; Juigner, M.; Launeau, P.; Le Mauff, B.; Luquet, F.; Maanan, M.; et al. Monitoring and management of coastal hazards: Creation of a regional observatory of coastal erosion and storm surges in the pays de la Loire region (Atlantic coast, France). Ocean Coast. Manag. 2019, 181, 104904. [Google Scholar] [CrossRef]
- Robin, M.; Juigner, M.; Luquet, F.; Audère, M. Assessing surface changes between shorelines from 1950 to 2011: The case of a 169-km sandy coast, Pays de la Loire (W France). J. Coast. Res. 2019, 88, 122–134. [Google Scholar] [CrossRef]
- Fletcher, C.; Rooney, J.; Barbee, M.; Lim, S.C.; Richmond, B. Mapping shoreline change using digital orthophoto-grammetry on Maui, Hawaii. J. Coast. Res. Spec. Issue 2003, 38, 106–124. [Google Scholar]
- Dada, O.A.; Li, G.; Qiao, L.; Ding, D.; Ma, Y.; Xu, J. Seasonal shoreline behaviours along the arcuate Niger Delta coast: Complex interaction between fluvial and marine processes. Cont. Shelf Res. 2016, 122, 51–67. [Google Scholar] [CrossRef]
- Blanc, J.J.; Froget, C.H. Mesure et méthode d’étude quantitative de l’érosion des littoraux meubles, exemple de la Camargue. Bull. L’association Française L’étude Quat. 1981, 18, 47–52. [Google Scholar] [CrossRef]
- Pilkey, O.H.; Young, R.S.; Bush, D.M.; Thieler, E.R. Predicting the behavior of beaches: Alternatives to models. In Proceedings of the 2nd International Symposium, Littoral 94, Lisbon, Association EUROCOAST, Lisbon, Portugal, 26–29 September 1994; pp. 53–60. [Google Scholar]
- Crowell, M.; Douglas, B.C.; Leatherman, S.P. On forecasting future U.S. shoreline positions: A test of algorithms. J. Coast. Res. 1997, 13, 1245–1255. [Google Scholar]
- Douglas, B.C.; Crowell, M.; Leatherman, S.P. Considerations for shoreline position and prediction. J. Coast. Res. 1998, 14, 1025–1033. [Google Scholar]
- Durand, P. L’évolution des Plages de L’ouest du Golfe du Lion au 20ème Siècle. Cinématique du Trait de Côte, Dynamique Sédimentaire et Analyse Prévisionnelle. Ph.D. Thesis, Université Lumière Lyon II, Lyon, France, 1999; p. 461.
- Durand, P. Erosion et protection du littoral de Valras-Plage (Languedoc, France). Un exemple de déstabilisation an-thropique d’un système sableux. Géomorphologie Relief Process. Environ. 2001, 1, 55–68. [Google Scholar] [CrossRef]
- Douglas, B.C.; Crowell, M. Long-Term Shoreline Position Prediction and Error Propagation. J. Coast. Res. 2000, 16, 145–152. [Google Scholar]
- Sabatier, F.; Suanez, S. Evolution of the Rhône Delta coast since the end of the 19th century. Géomorphologie Relief Process. Environ. 2003, 4, 283–300. [Google Scholar] [CrossRef]
- Dubois, R.N. How does a barrier shoreface respond to a sea-level rise? J. Coast. Res. 2002, 18, iii–v. [Google Scholar]
- Durand, P.; Heurtefeux, H. Impact de l’élévation du niveau marin sur l’évolution future d’un cordon littoral lagunaire: Une méthode d’évaluation. Exemple des étangs de Vic et de Pierre Blanche (littoral méditerranéen, France). Z. Geomorphol. N.F. 2006, 50, 221–244. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Callaghan, D.; Stive, M.J. Estimating coastal recession due to sea level rise: Beyond the Bruun rule. Clim. Chang. 2012, 110, 561–574. [Google Scholar] [CrossRef]
- Collectif (BRGM/Cerema). Recommandations Pour L’élaboration de la Carte Locale D’exposition au Recul du Trait de Côte; Co-Edition BRGM et Cerema, août 2022; BRGM: Orleans, France, 2022; p. 95. ISBN 978-2-7159-2791-9/978-2-37180-566-8. [Google Scholar]
- Garner, G.G.; Hermans, T.; Kopp, R.E.; Slangen, A.B.A.; Edwards, T.L.; Levermann, A.; Nowikci, S.; Palmer, M.D.; Smith, C.; Fox-Kemper, B.; et al. IPCC AR6 Sea Level Projections. Version 20210809. 2021. Available online: https://sealevel.nasa.gov/ipcc-ar6-sea-level-projection-tool (accessed on 13 March 2023).
- Ferret, Y. Reconstruction de la série marégraphique de Saint-Nazaire. Rapport No.27, Shom/DOPS/HOM/MAC. 2016. Available online: https://www.pays-de-la-loire.developpement-durable.gouv.fr/IMG/pdf/_50198_Erosion_du_littoral_vendeen_TF_FINAL.pdf (accessed on 11 August 2023).
- Audère, M. Spatialisation des Enjeux Côtiers sous l’emprise de l’aléa Érosion Observé et Scénarisé en Fonction des Changements Climatiques en Région Pays de la Loire. Ph.D. Thesis, Nantes Université, Nantes, France, 2022. Available online: https://www.theses.fr/2022NANU2027 (accessed on 22 May 2023).
- SAFEGE CETIIS. Etude Hydrosédimentaire de la Côte Ouest de Noirmoutier: Rapport Final; SAFEGE CETIIS: Barcelona, Spain, 2004; p. 104. [Google Scholar]
- Bernier, P.; Gruet, Y. Environnement Littoral. Sédimentation et Biodiversité de l’Estran. Île de Noirmoutier (Vendée). 2011. Available online: https://www.persee.fr/doc/geoly_0245-9825_2011_hos_10_1 (accessed on 1 July 2023).
- Le Cozannet, G.; Bulteau, T.; Castelle, B.; Ranasinghe, R.; Wöppelmann, G.; Rohmer, J.; Bernon, N.; Idier, D.; Louisor, J.; Salas-Y-Mélia, D. Quantifying uncertainties of sandy shoreline change projections as sea level rises. Sci. Rep. 2019, 9, 42. [Google Scholar] [CrossRef] [PubMed]
- List, J.H.; Sallenger, A.H.; Hansen, M.E.; Jaffe, B.E. Accelerated relative sea-level rise and rapid coastal erosion: Testing a causal relationship for the Louisiana barrier islands. Mar. Geol. 1997, 140, 347–365. [Google Scholar] [CrossRef]
- Cooper, J.A.G.; Pilkey, O.H. Sea-level rise and shoreline retreat: Time to abandon the Bruun Rule. Glob. Planet. Chang. 2004, 43, 157–171. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Stive, M.J.F. Rising seas and retreating coastlines. Clim. Chang. 2009, 97, 465–468. [Google Scholar] [CrossRef]
- Stive, M.J.F.; Ranasinghe, R.; Cowell, P. Sea level rise and coastal erosion. In Handbook of Coastal and Ocean Engineering; Kim, Y., Ed.; World Scientific: Singapore, 2010; p. 1023. [Google Scholar]
- Yates-Michelin, M.; Le Cozannet, G.; Krien, Y.; Lenôtre, N. Amélioration de la Méthode RNACC: Caractérisation des Incertitudes Relatives à la Quantification des Impacts de l‘Elévation du Niveau Marin. Rapport Final BRGM/RP-59405-FR. 2011, p. 142. Available online: https://infoterre.brgm.fr/rapports/RP-59405-FR.pdf (accessed on 3 August 2023).
- Holman, R.A.; Sallenger, A.H. Set-up and swash on a natural beach. J. Geophys. Res. 1985, 90, 945–953. [Google Scholar] [CrossRef]
- Nielsen, P.; Hanslow, D.J. Wave runup distributions on natural beaches. J. Coast. Res. 1991, 7, 1139–1152. [Google Scholar]
- Stockdon, H.F.; Holman, R.A.; Howd, P.A.; Sallenger, A.H., Jr. Empirical parameterization of setup, swash, and runup. Coast. Eng. 2006, 53, 573–588. [Google Scholar] [CrossRef]
- Cariolet, J.-M. Quantification du runup sur une plage macrotidale à partir des conditions morphologiques et hydrodynamiques. Geomorphol. Process. Environ. 2011, 17, 95–109. [Google Scholar] [CrossRef]
- MEDDE. Guide Méthodologique: Plan de Prévention des Risques Littoraux. Ministère de l’Écologie, du Développement Durable, et de l’Energie, Direction Générale de la Prévention des Risques, La Défense. 2014; p. 169. Available online: https://www.ecologie.gouv.fr/sites/default/files/documents/Guide_m%C3%A9thodo_PPRL_%202014.pdf (accessed on 1 January 2023).
- Héquette, A.; Ruz, M.-H.; Zemmour, A.; Marin, D.; Cartier, A.; Sipka, V. Alongshore variability in coastal dune erosion and post-storm recovery, northern coast of France. J. Coast. Res. 2019, 88, 25–45. [Google Scholar] [CrossRef]

| Category | Class | Type | Number | Cumulative Length (km) |
|---|---|---|---|---|
| Protective structures | Structure replacing the shoreline | Coastal dyke | 18 | 21.9 |
| Retaining wall | 11 | 1.7 | ||
| Stone revetment | 35 | 8.9 | ||
| Erosion control structure | Breakwater | 2 | 0.3 | |
| Groyne | 74 | 4 | ||
| Other coastal developments | Access | Entrance, path, submersible causeway, etc. | 1 | 3.8 |
| Slipway | 7 | 0.3 | ||
| Constructions | Building, blockhouse, fortification, etc. | 2 | 0.1 | |
| Individual protection | 16 | 2.4 | ||
| Port and navigation infrastructure | Jetty | 6 | 2.3 | |
| Miscellaneous | Other or unidentified | 17 | 1.3 | |
| Total | 189 | 47 | ||
| Date | Type of Data | Source | Scale |
|---|---|---|---|
| 1950 | BD ORTHO® HISTORIY | GEOPAL (IGN) | 1/25,000 |
| 1974 | Aerial photo | CCIN (IGN) | 1/30,000 |
| 1992 | Aerial photo | CCIN (IGN) | 1/30,000 |
| 2000 | Ortho Littorale® | Géolittoral (IGN) | 1/25,000 |
| 2006 | BD ORTHO® V2 | CCIN (IGN) | 1/25,000 |
| 2010 | BD ORTHO® V2 | CCIN (IGN) | 1/25,000 |
| 2016 | BD ORTHO® | CCIN (GEOVENDEE) | 1/25,000 |
| 2020 | Ortho Littorale® V3 | CEREMA (GEOFIT) | 1/25,000 |
| 2022 | Ortho Littorale® V3 | CCIN (Department) | 1/25,000 |
| (m) = (Epixel 2 + Eortho 2 + Edig 2) 0.5 | ||||||
|---|---|---|---|---|---|---|
| Year | 1950 | 1974 | 1992 | 2000 | 2010 | 2022 |
| Epixel—Pixel error (m) | 0.5 | 1 | 0.58 | 0.5 | 0.5 | 0.5 |
| Eortho—Orthorectification error (m) | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 |
| Edig—Digitisation error (m) | 1.68 | 2.00 | 1.91 | 1.60 | 0.50 | 0.23 |
| Overall error (m) | 3.33 | 3.61 | 3.46 | 3.29 | 2.92 | 2.88 |
| B. Calculation of period error(m) = ( 2 a + 2 b) 0.5 and E (m/an) = ()/I, where a = date a and b = date b | ||||||
| Period (year) | 1950–1974 | 1950–2022 | 1974–1992 | 1992–2000 | 2000–2010 | 2010–2022 |
| I—Interval (year) | 24 | 72 | 18 | 8 | 10 | 12 |
| —Overall error (m) | 4.91 | 4.40 | 5.00 | 4.78 | 4.40 | 4.10 |
| —Periodic error (m/year) | 0.20 | 0.06 | 0.28 | 0.60 | 0.44 | 0.34 |
| Littoral Cells (LCs) | 1950–1974 | 1950–2022 | 1974–1992 | 1992–2000 | 2000–2010 | 2010–2022 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cl (m) | Esp2 (m2) | Cl (m) | Esp2 (m2) | Cl (m) | Esp2 (m2) | Cl (m) | Esp2 (m2) | Cl (m) | Esp2 (m2) | Cl (m) | Esp2 (m2) | |
| LC1-A | 1856 | 9107 | 778 | 3425 | 1008 | 5039 | 868 | 4147 | 680 | 2988 | 523 | 2147 |
| LC1-B | 2433 | 11,940 | 332 | 1463 | 1402 | 7013 | 302 | 1442 | 227 | 999 | 151 | 618 |
| LC1-C | 3373 | 16,557 | 625 | 2751 | 3091 | 15,457 | 736 | 3517 | 359 | 1579 | 325 | 1335 |
| LC2-A | 2796 | 13,723 | 643 | 2832 | 3870 | 19,352 | 802 | 3832 | 632 | 2777 | 417 | 1710 |
| LC2-B | 701 | 3440 | 414 | 1824 | 254 | 1268 | 255 | 1217 | 98 | 433 | 136 | 556 |
| LC2-C | 4480 | 21,990 | 1523 | 6707 | 3268 | 16,341 | 914 | 4363 | 673 | 2957 | 668 | 2738 |
| LC2-D | 643 | 3157 | 925 | 4075 | 936 | 4683 | 1470 | 7022 | 887 | 3898 | 545 | 2236 |
| LC2-E | 7235 | 35,510 | 2938 | 12,938 | 5218 | 26,091 | 4487 | 21,430 | 2429 | 10,680 | 2105 | 8632 |
| LC2-F | 3087 | 15,153 | 3171 | 13,964 | 3170 | 15,851 | 3182 | 15,197 | 3180 | 13,980 | 3256 | 13,352 |
| Overall coastline studied | 26,604 | 130,577 | 11,349 | 49,979 | 22,218 | 111,095 | 13,016 | 62,167 | 9164 | 40,290 | 8125 | 33,324 |
| Variables | Uncertainty of shoreline position (pixel error, orthorectification error, digitisation error) | This study | Uncertainty | 1950–2022 | 1992–2022 | Uncertainty by projection horizon | 2052 | 2122 |
| 6 cm/an | 15 cm/an | 450 cm | 600 cm | |||||
| Uncertainty related to the average annual sea level rise since 1950 (E20) | Ferret (2016) [63] | 1950–2014 | 2052 | 2122 | ||||
| 0.022 cm/an | 0.66 cm | 2.2 cm | ||||||
| Uncertainty about slope (DTM error) | Lidar provided by the Vendée department (2022) | 2022 | 2052 | 2122 | ||||
| 15 cm | 15 cm | 15 cm | 15 cm | |||||
| Uncertainty related to the estimation of future sea level rise (E21) | IPPC (2022) SSP2-4.5 (median) | Projection | 2052 | 2122 | 2052 | 2122 | ||
| 21 cm | 23 cm | 9 cm | 33 cm | |||||
| IPPC (2022) SSP5-8.5 (secure) | 64 cm | 90 cm | 10 cm | 30 cm | ||||
| Littoral Cells (LCs) | Mean Deviation (m) | Annualised Mean (m) | Max (m) | Min (m) | Standard Deviation (m) | Total (m) | Total Number of Transects |
|---|---|---|---|---|---|---|---|
| LC1-A | 15.29 | 0.59 | 39.49 | 1.06 | 11.34 | 886.65 | 58 |
| LC1-B | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 |
| LC1-C | 3.31 | 0.13 | 10.06 | 0.40 | 2.65 | 109.32 | 33 |
| LC2-A | 11.39 | 0.44 | 49.82 | 0.06 | 10.85 | 1685.64 | 148 |
| LC2-B | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 |
| LC2-C | 6.13 | 0.24 | 24.76 | 0.03 | 5.60 | 337.12 | 55 |
| LC2-D | 18.26 | 0.70 | 29.49 | 1.39 | 7.86 | 255.69 | 14 |
| LC2-E | 22.48 | 0.86 | 54.64 | 0.07 | 12.10 | 8316.74 | 370 |
| LC2-F | 110.09 | 4.23 | 270.23 | 0.05 | 85.44 | 15,082.25 | 137 |
| Overall coastline studied | 32.73 | 1.26 | 270.23 | 0.03 | 50.71 | 26,673.41 | 815 |
| 2052 | 2122 | |
|---|---|---|
| Data error (m) | 4.50 | 6.01 |
| Projection test error (m) | 37.76 | 125.88 |
| Overall error (m) | 38.03 | 126.02 |
| A. Distance between the 2022 and 2052 Shorelines According to the SP5-8.5 Scenario. | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| The average distance of evolution (m) over 30 years (2022–2052) | |||||||||||
| Test | Observation period | LC1-A | LC1-B | LC1-C | LC2-A | LC2-B | LC2-C | LC2-D | LC2-E | LC2-F | |
| 1 | 1992–2022 (presence of longitudinal coastal structures) | +58 | / | +33 | +10.83 | −7.71 | +3.05 | +12.04 | +28.33 | +76.46 | |
| 2 | 1950–1974 (absence of longitudinal coastal structures) | +7.46 | +10.49 | +4.34 | +7.7 | +13.53 | −20.4 | +3.46 | −4.82 | +45.17 | |
| B. Distance between the 2022 and the 2122 shoreline according to the SP5-8.5 scenario. | |||||||||||
| The average distance of evolution (m) over 100 years (2022–2122) | |||||||||||
| Test | Observation period | LC1-A | LC1-B | LC1-C | LC2-A | LC2-B | LC2-C | LC2-D | LC2-E | LC2-F | |
| 1 | 1950–2022 (presence of longitudinal coastal structures) | +62.52 | / | +30.03 | +36.55 | −34.81 | +10.18 | +62.86 | +70.07 | +351 | |
| 2 | 1950–1974 (absence of longitudinal coastal structures) | +36.61 | +46.3 | +26.43 | +33.65 | +53.91 | −51.95 | +37.07 | −7.08 | +181 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meziane, I.; Robin, M.; Fattal, P.; Rahmani, O. Management of Coastline Variability in an Endangered Island Environment: The Case of Noirmoutier Island (France). Coasts 2024, 4, 482-507. https://doi.org/10.3390/coasts4030025
Meziane I, Robin M, Fattal P, Rahmani O. Management of Coastline Variability in an Endangered Island Environment: The Case of Noirmoutier Island (France). Coasts. 2024; 4(3):482-507. https://doi.org/10.3390/coasts4030025
Chicago/Turabian StyleMeziane, Imane, Marc Robin, Paul Fattal, and Oualid Rahmani. 2024. "Management of Coastline Variability in an Endangered Island Environment: The Case of Noirmoutier Island (France)" Coasts 4, no. 3: 482-507. https://doi.org/10.3390/coasts4030025
APA StyleMeziane, I., Robin, M., Fattal, P., & Rahmani, O. (2024). Management of Coastline Variability in an Endangered Island Environment: The Case of Noirmoutier Island (France). Coasts, 4(3), 482-507. https://doi.org/10.3390/coasts4030025






