Correlation of the Isotropic NMR Chemical Shift with Oxygen Coordination Distances in Periodic Solids
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. NMR of Na with in Oxygen Coordination
3.2. NMR of Al with in Oxygen Coordination
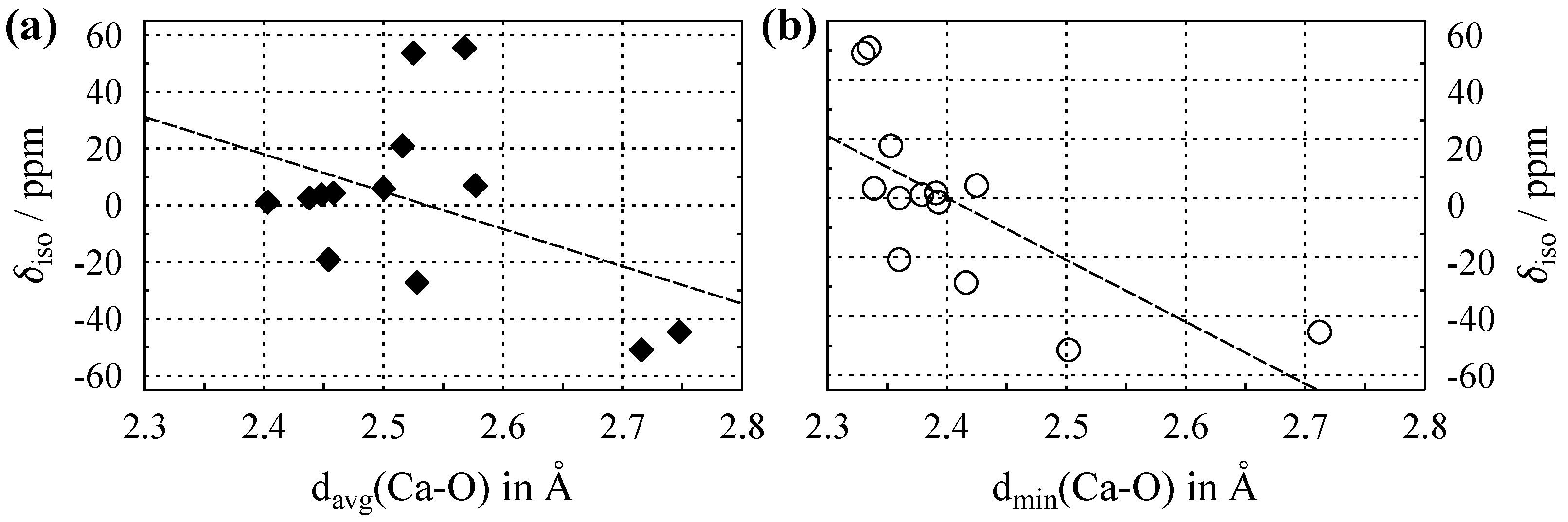
3.3. NMR of Ca with in Oxygen Coordination
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CN | Coordination Number |
| ICSD | Inorganic Crystal Structure Database |
| MDPI | Multidisciplinary Digital Publishing Institute |
| NMR | Nuclear Magnetic Resonance |
| XRD | X-ray Diffraction |
Appendix A. Chemical Shifts and Structural Parameters for 23Na
| Compound | ICSD Code (year) | Space Group (no.) | CN | /Å (Na–O) | /Å (Na–O) | /ppm | Ref. |
|---|---|---|---|---|---|---|---|
| NaAlO | 14780 (2020) | (33) | 5 | 2.459 | 2.298 | 26.2 | [24] |
| NaGeO | 1622 (1978) | (36) | 5 | 2.398 | 2.291 | 22.6 | [14] |
| NaBO | 10061 (1979) | (15) | 5 | 2.394 | 2.302 | 19.6 | [14] |
| 6 | 2.480 | 2.349 | 14.4 | ||||
| NaCO | 56906 (1981) | (14) | 6 | 2.405 | 2.320 | 17.9 | [25] |
| NaBO | 34645 (1963) | (167) | 7 | 2.512 | 2.461 | 1.8 | [14] |
| NaSO | 28056 (1975) | (70) | 6 | 2.432 | 2.334 | [24] | |
| NaGeO | 68507 (1990) | (88) | 6 | 2.542 | 2.325 | [14] | |
| NaHCO | 18183 (1965) | (14) | 6 | 2.437 | 2.385 | [26] | |
| NaGeO | 189269 (2013) | (165) | 7 | 2.611 | 2.442 | [14] | |
| NaNO | 68707 (1990) | (44) | 6 | 2.471 | 2.451 | [25] | |
| -NaVO | 29450 (1984) | (62) | 6 | 2.435 | 2.369 | [25] | |
| NaIO | 14287 (1970) | (88) | 8 | 2.566 | 2.535 | [26] | |
| NaClO | 200405 (1978) | (63) | 8 | 2.564 | 2.386 | −20.4 | [26] |
Appendix B. Chemical Shifts and Structural Parameters for 27Al
| Compound | ICSD Code (year) | Space Group (no.) | CN | /Å (Al–O) | /Å (Al–O) | /ppm | Ref. |
|---|---|---|---|---|---|---|---|
| -LiAlO | 430184 (2016) | (92) | 4 | 1.758 | 1.752 | 81.8 | [27] |
| -NaAlO | 14780 (2020) | (33) | 4 | 1.768 | 1.733 | 80.1 | [28] |
| -AlO | 82504 (1996) | (12) | 4 | 1.773 | 1.697 | 80 | [29] |
| 6 | 1.929 | 1.819 | 10.5 | ||||
| AlPO(OH) ·HO (senegalite) | 100542 (1979) | (33) | 5 | 1.848 | 1.788 | 36 | [30] |
| 6 | 1.900 | 1.819 | 1.7 | ||||
| AlSiO (andalusite) | 172728 (2006) | (58) | 5 | 1.823 | 1.804 | 35 | [31] |
| 6 | 1.920 | 1.823 | 10 | ||||
| AlPO(OH) (augelite) | 426641 (2014) | (12) | 5 | 1.831 | 1.752 | 30.9 | [30] |
| 6 | 1.889 | 1.827 | 0.3 | ||||
| AlVO | 55870 (2004) | (2) | 5 | 1.829 | 1.805 | 27.2 | [32] |
| -AlO | 51687 (2001) | (167) | 6 | 1.914 | 1.854 | 18.8 | [33] |
| YAlO | 88261 (1999) | (62) | 6 | 1.910 | 1.901 | 10.7 | [34] |
| KAlPO | 2888 (1973) | (14) | 6 | 1.889 | 1.842 | −16.6 | [35] |
Appendix C. Chemical Shifts and Structural Parameters for 43Ca
| Compound | ICSD Code (year) | Space Group (no.) | CN | /Å (Ca–O) | /Å (Ca–O) | /ppm | Ref. |
|---|---|---|---|---|---|---|---|
| CaZrO | 97463 (2003) | (62) | 8 | 2.568 | 2.335 | 55.5 | [36] |
| CaAlO | 14270 (1970) | (15) | 7 | 2.525 | 2.330 | 53.7 | [37] |
| CaTiO | 153172 (2005) | (62) | 8 | 2.516 | 2.353 | 21.0 | [38] |
| CaMgSiO | 100736 (1981) | (113) | 8 | 2.577 | 2.425 | 7 | [39] |
| CaBO | 62430 (1987) | (60) | 8 | 2.500 | 2.339 | 6 | [22] |
| CaCO ·2HO | 30783 (1980) | (87) | 8 | 2.458 | 2.391 | 4.4 | [40] |
| CaCO ·3HO | 159351 (1981) | (2) | 8 | 2.448 | 2.379 | 3.8 | [41] |
| CaWO | 5510 (2019) | (88) | 8 | 2.438 | 2.360 | 2.6 | [36] |
| CaMoO | 60556 (1985) | (88) | 8 | 2.403 | 2.393 | 1.1 | [36] |
| CaSO·2HO | 161622 (2008) | (15) | 8 | 2.454 | 2.360 | −19.1 | [38] |
| CaCO (aragonite) | 32100 (1986) | (62) | 9 | 2.528 | 2.416 | −27.2 | [42] |
| CaAlO | 202616 (1988) | (194) | 12 | 2.748 | 2.712 | −44.6 | [37] |
| Ca(NO) | 52351 (1931) | (205) | 12 | 2.716 | 2.502 | −50.9 | [38] |
References
- Bloch, F. Nuclear Induction. Phys. Rev. 1946, 70, 460–474. [Google Scholar] [CrossRef]
- Abragam, A. The Principles of Nuclear Magnetism; Oxford University Press: Oxford, UK, 1961; ISBN 978-0-19-852014-6. [Google Scholar]
- Ernst, R.R.; Bodenhausen, G.; Wokaun, A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions; Clarendon Press: Oxford, UK, 1987; ISBN 0-19-855647-0. [Google Scholar]
- MacKenzie, K.J.D.; Smith, M.E. Multinuclear Solid-State NMR of Inorganic Materials; Pergamon Materials Series v. 6; Pergamon: Oxford, UK, 2002; ISBN 0-08-043787-7. [Google Scholar]
- Harris, R.K. NMR crystallography: The use of chemical shifts. Solid State Sci. 2004, 6, 1025–1037. [Google Scholar] [CrossRef]
- Taulelle, F. NMR crystallography: Crystallochemical formula and space group selection. Solid State Sci. 2004, 6, 1053–1057. [Google Scholar] [CrossRef]
- Bryce, D.L. NMR crystallography: Structure and properties of materials from solid-state nuclear magnetic resonance observables. IUCrJ 2017, 4, 350–359. [Google Scholar] [CrossRef] [Green Version]
- Commission on NMR Crystallography and Related Methods. Available online: https://www.iucr.org/iucr/commissions/nmr-crystallography (accessed on 7 July 2022).
- Andrew, E.R. Magic angle spinning in solid state n.m.r. spectroscopy. Phil. Trans. R. Soc. A 1981, 299, 505–520. [Google Scholar]
- Herzfeld, J.; Berger, A.E. Sideband intensities in NMR spectra of samples spinning at the magic angle. J. Chem. Phys. 1980, 73, 6021–6030. [Google Scholar] [CrossRef]
- Hodgkinson, P.; Emsley, L. The reliability of the determination of tensor parameters by solid-state nuclear magnetic resonance. J. Chem. Phys. 1997, 107, 4808–4816. [Google Scholar] [CrossRef]
- Vosegaard, T. Single-crystal NMR spectroscopy. Prog. Nucl. Magn. Reson. Spectr. 2021, 123, 51–72. [Google Scholar] [CrossRef]
- Xue, X.; Stebbins, J.F. 23Na NMR chemical shifts and local Na coordination environments in silicate crystals, melts and glasses. Phys. Chem. Miner. 1993, 20, 297–307. [Google Scholar] [CrossRef]
- George, A.M.; Sen, S.; Stebbins, J.F. 23Na chemical shifts and local structure in crystalline, glassy, and molten sodium borates and germanates. Solid State Nucl. Magn. Reson. 1997, 10, 9–17. [Google Scholar] [CrossRef]
- Haouas, M.; Taulelle, F.; Martineau, C. Recent advances in application of 27Al NMR spectroscopy to materials science. Prog. Nucl. Magn. Reson. Spectr. 2016, 94–95, 11–36. [Google Scholar] [CrossRef] [PubMed]
- Gambuzzi, E.; Pedone, A.; Menziani, M.C.; Angeli, F.; Florian, P.; Charpentier, T. Calcium environment in silicate and aluminosilicate glasses probed by 43Ca MQMAS NMR experiments and MD-GIPAW calculations. Solid State Nucl. Magn. Reson. 2015, 68–69, 31–36. [Google Scholar] [CrossRef] [PubMed]
- Fayon, F.; Farnan, I.; Bessada, C.; Coutures, J.; Massiot, D.; Coutures, J.P. Empirical Correlations between 207Pb NMR Chemical Shifts and Structure in Solids. J. Am. Chem. Soc. 1997, 119, 6837–6843. [Google Scholar] [CrossRef]
- Hoppe, R. Effective coordination numbers (ECoN) and mean Active ionic radii (MEFIR). Z. Kristallog.-Cryst. Mater. 1979, 150, 23–52. [Google Scholar] [CrossRef]
- Zeman, O.E.O.; Steinadler, J.; Hochleitner, R.; Bräuniger, T. Determination of the Full 207Pb Chemical Shift Tensor of Anglesite, PbSO4, and Correlation of the Isotropic Shift to Lead-Oxygen Distance in Natural Minerals. Crystals 2019, 9, 43. [Google Scholar] [CrossRef] [Green Version]
- Cohen, M.H.; Reif, F. Quadrupole effects in nuclear magnetic resonance studies of solids. Solid State Phys. 1957, 5, 321–438. [Google Scholar] [CrossRef]
- Engelhardt, G.; Koller, H. A simple procedure for the determination of the quadrupole interaction parameters and isotropic chemical shifts from magic angle spinning NMR spectra of half-integer spin nuclei in solids. Magn. Reson. Chem. 1991, 29, 941–945. [Google Scholar] [CrossRef]
- Gervais, C.; Laurencin, D.; Wong, A.; Pourpoint, F.; Labram, J.; Woodward, B.; Howes, A.P.; Pike, K.J.; Dupree, R.; Mauri, F.; et al. New perspectives on calcium environments in inorganic materials containing calcium-oxygen bonds: A combined computational-experimental 43Ca NMR approach. Chem. Phys. Lett. 2008, 464, 42–48. [Google Scholar] [CrossRef]
- Pearson, K. Note on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar]
- Koller, H.; Engelhardt, G.; Kentgens, A.P.M.; Sauer, J. 23Na NMR spectroscopy of solids: Interpretation of quadrupole interaction parameters and chemical shifts. J. Phys. Chem. 1994, 98, 1544–1551. [Google Scholar] [CrossRef]
- Skibsted, J.; Nielsen, N.C.; Bildsøe, H.; Jakobsen, H.J. Satellite transitions in MAS NMR spectra of quadrupolar nuclei. J. Magn. Reson. 1991, 95, 88–117. [Google Scholar] [CrossRef]
- Tabeta, R.; Saito, H. 23Na chemical shifts of some inorganic and organic compounds in the solid state as determined by the magic angle spinning and high power NMR methods. Chem. Lett. 1984, 13, 293–296. [Google Scholar] [CrossRef] [Green Version]
- Bräuniger, T.; Groh, B.; Moudrakovski, I.L.; Indris, S. Local electronic structure in γ-LiAlO2 studied by single-crystal 27Al NMR and DFT calculations. J. Phys. Chem. A 2016, 120, 7839–7846. [Google Scholar] [CrossRef]
- Müller, D.; Gessner, W.; Samoson, A.; Lippmaa, E.; Scheler, G. Solid-state aluminium-27 nuclear magnetic resonance chemical shift and quadrupole coupling data for condensed AlO4 tetrahedra. J. Chem. Soc. Dalton Trans. 1986, 6, 1277–1281. [Google Scholar] [CrossRef]
- O’Dell, L.A.; Savin, S.L.P.; Chadwick, A.V.; Smith, M.E. A 27Al MAS NMR study of a sol-gel produced alumina: Identification of the NMR parameters of the θ-Al2O3 transition alumina phase. Solid State Nucl. Magn. Reson. 2007, 31, 169–173. [Google Scholar] [CrossRef] [PubMed]
- Bleam, W.F.; Dec, S.F.; Frye, J.S. 27Al Solid-state Nuclear Magnetic Resonance Study of Five-Coordinate Aluminum in Augelite and Senegalite. Phys. Chem. Miner. 1989, 16, 817–820. [Google Scholar] [CrossRef]
- Alemany, L.B.; Massiot, D.; Sherriff, B.L.; Smith, M.E.; Taulelle, F. Observation and accurate quantification of 27Al MAS NMR spectra of some Al2SiO5 polymorphs containing sites with large quadrupole interactions. Chem. Phys. Lett. 1991, 177, 301–306. [Google Scholar] [CrossRef]
- Nielsen, U.G.; Boisen, A.; Brorson, M.; Jacobsen, C.J.H.; Jakobsen, H.J.; Skibsted, J. Aluminum orthovanadate (AlVO4): Synthesis and characterization by 27Al and 51V MAS and MQMAS NMR spectroscopy. Inorg. Chem. 2002, 41, 6432–6439. [Google Scholar] [CrossRef]
- Vosegaard, T.; Jakobsen, H.J. 27Al Chemical Shielding Anisotropy. J. Magn. Reson. 1997, 128, 135–137. [Google Scholar] [CrossRef]
- Florian, P.; Gervais, M.; Douy, A.; Massiot, D.; Coutures, J.-P. A Multi-nuclear Multiple-Field Nuclear Magnetic Resonance Study of the Y2O3—Al2O3 Phase Diagram. J. Phys. Chem. B 2001, 105, 379–391. [Google Scholar] [CrossRef]
- Müller, D.; Grunze, I.; Hallas, E.; Ladwig, G. Hochfeld-27Al-NMR-Untersuchungen zur Aluminiumkoordination in kristallinen Aluminiumphosphaten. Z. Anorg. Allg. Chem. 1983, 500, 80–88. [Google Scholar] [CrossRef]
- Lin, Z.; Smith, M.E.; Sowrey, F.E.; Newport, R.J. Probing the local structural environment of calcium by natural-abundance solid-state 43Ca NMR. Phys. Rev. B 2004, 69, 224107. [Google Scholar] [CrossRef] [Green Version]
- MacKenzie, K.J.D.; Schmücker, M.; Smith, M.E.; Poplett, I.J.F.; Kemmitt, T. Evolution of crystalline aluminates from hybrid gel-derived precursors studied by XRD and multinuclear solid state MAS NMR IV: Calcium dialuminate, CaAl4O7 and calcium hexaaluminate, CaAl12O19. Thermochim. Acta 2000, 363, 181–188. [Google Scholar] [CrossRef]
- Widdifield, C.M.; Moudrakovski, I.; Bryce, D.L. Calcium-43 chemical shift and electric field gradient tensor interplay: A sensitive probe of structure, polymorphism, and hydration. Phys. Chem. Chem. Phys. 2014, 16, 13340–13359. [Google Scholar] [CrossRef] [Green Version]
- Dupree, R.; Howes, A.P.; Kohn, S.C. Natural abundance solid state 43Ca NMR. Chem. Phys. Lett. 1997, 276, 399–404. [Google Scholar] [CrossRef]
- Bowers, G.M.; Kirkpatrick, R.J. Natural Abundance 43Ca NMR as a Tool for Exploring Calcium Biomineralization: Renal Stone Formation and Growth. Cryst. Growth Des. 2011, 11, 5188–5191. [Google Scholar] [CrossRef]
- Wong, A.; Howes, A.P.; Dupree, R.; Smith, M.E. Natural abundance 43Ca NMR study of calcium-containing organic solids: A model study for Ca-binding biomaterials. Chem. Phys. Lett. 2006, 427, 201–205. [Google Scholar] [CrossRef]
- Huang, Y.-C.; Mou, Y.; Tsai, T.W.-T.; Wu, Y.-J.; Lee, H.-K.; Huang, S.-J.; Chan, J.C.C. Calcium-43 NMR Studies of Polymorphic Transition of Calcite to Aragonite. J. Phys. Chem. B 2012, 116, 14295–14301. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steinadler, J.; Zeman, O.E.O.; Bräuniger, T. Correlation of the Isotropic NMR Chemical Shift with Oxygen Coordination Distances in Periodic Solids. Oxygen 2022, 2, 327-336. https://doi.org/10.3390/oxygen2030023
Steinadler J, Zeman OEO, Bräuniger T. Correlation of the Isotropic NMR Chemical Shift with Oxygen Coordination Distances in Periodic Solids. Oxygen. 2022; 2(3):327-336. https://doi.org/10.3390/oxygen2030023
Chicago/Turabian StyleSteinadler, Jennifer, Otto E. O. Zeman, and Thomas Bräuniger. 2022. "Correlation of the Isotropic NMR Chemical Shift with Oxygen Coordination Distances in Periodic Solids" Oxygen 2, no. 3: 327-336. https://doi.org/10.3390/oxygen2030023
APA StyleSteinadler, J., Zeman, O. E. O., & Bräuniger, T. (2022). Correlation of the Isotropic NMR Chemical Shift with Oxygen Coordination Distances in Periodic Solids. Oxygen, 2(3), 327-336. https://doi.org/10.3390/oxygen2030023







