The Reliability Inference for Multicomponent Stress–Strength Model under the Burr X Distribution
Abstract
1. Introduction
2. The Likelihood Function Based on Sample from G System
3. The Maximum Likelihood Estimators
3.1. Case 1: Equal Scale Parameters
3.1.1. Point Estimators under Equal Scale Parameters
3.1.2. Approximated Confidence Interval for
3.2. Case 2: Different Scale Parameters
| Algorithm 1: Parametric bootstrap procedure under . |
|
3.2.1. Point Estimators under Different Parameters
3.2.2. Approximated Confidence Interval for
4. Inference Based on Pivotal Quantity
4.1. Case 1:
| Algorithm 2: Pivotal-quantity-based estimation method under . |
|
4.2. Case 2:
- and are probability independent;
- and are probability independent.
| Algorithm 3: Pivotal-quantity-based estimation method under . |
|
5. Inference of
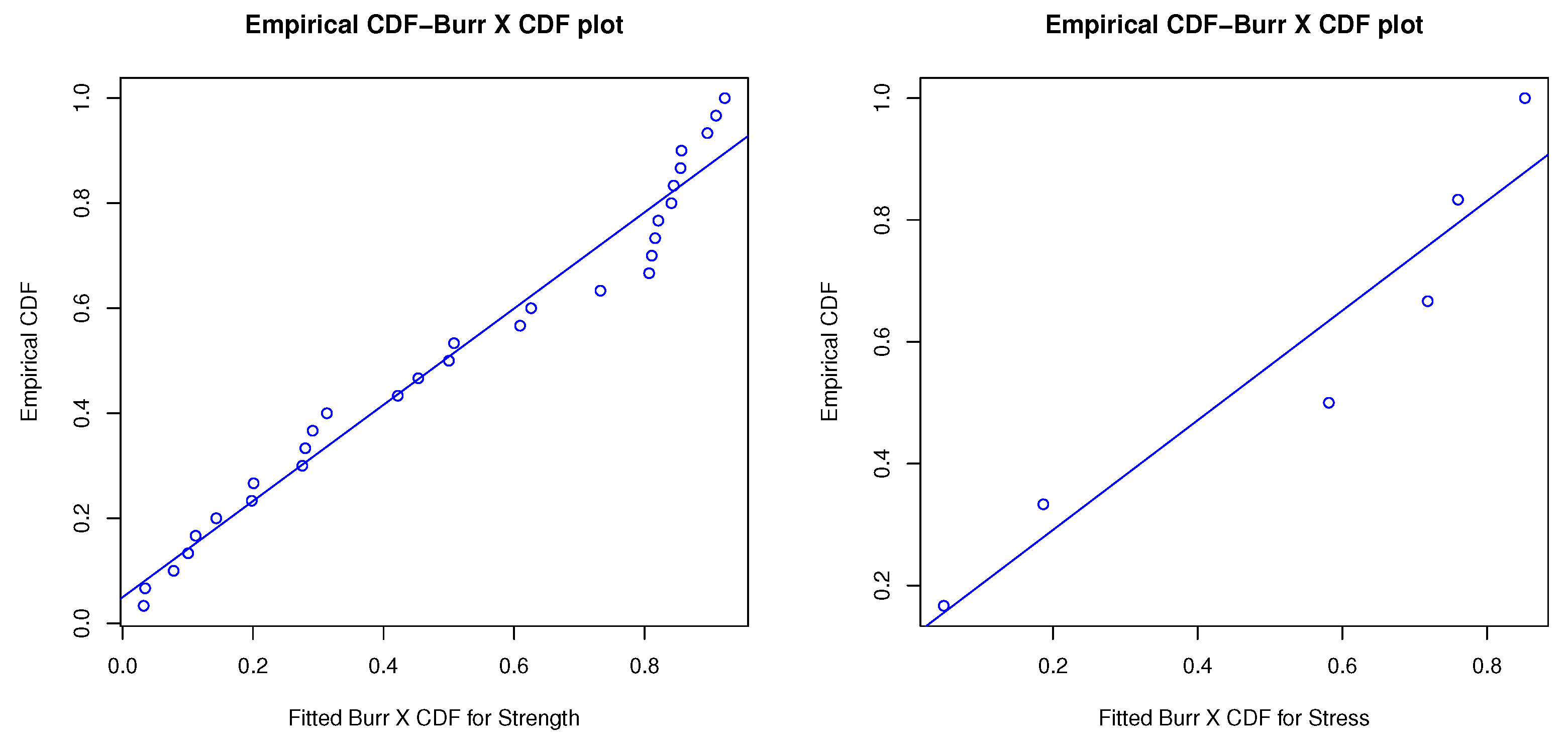
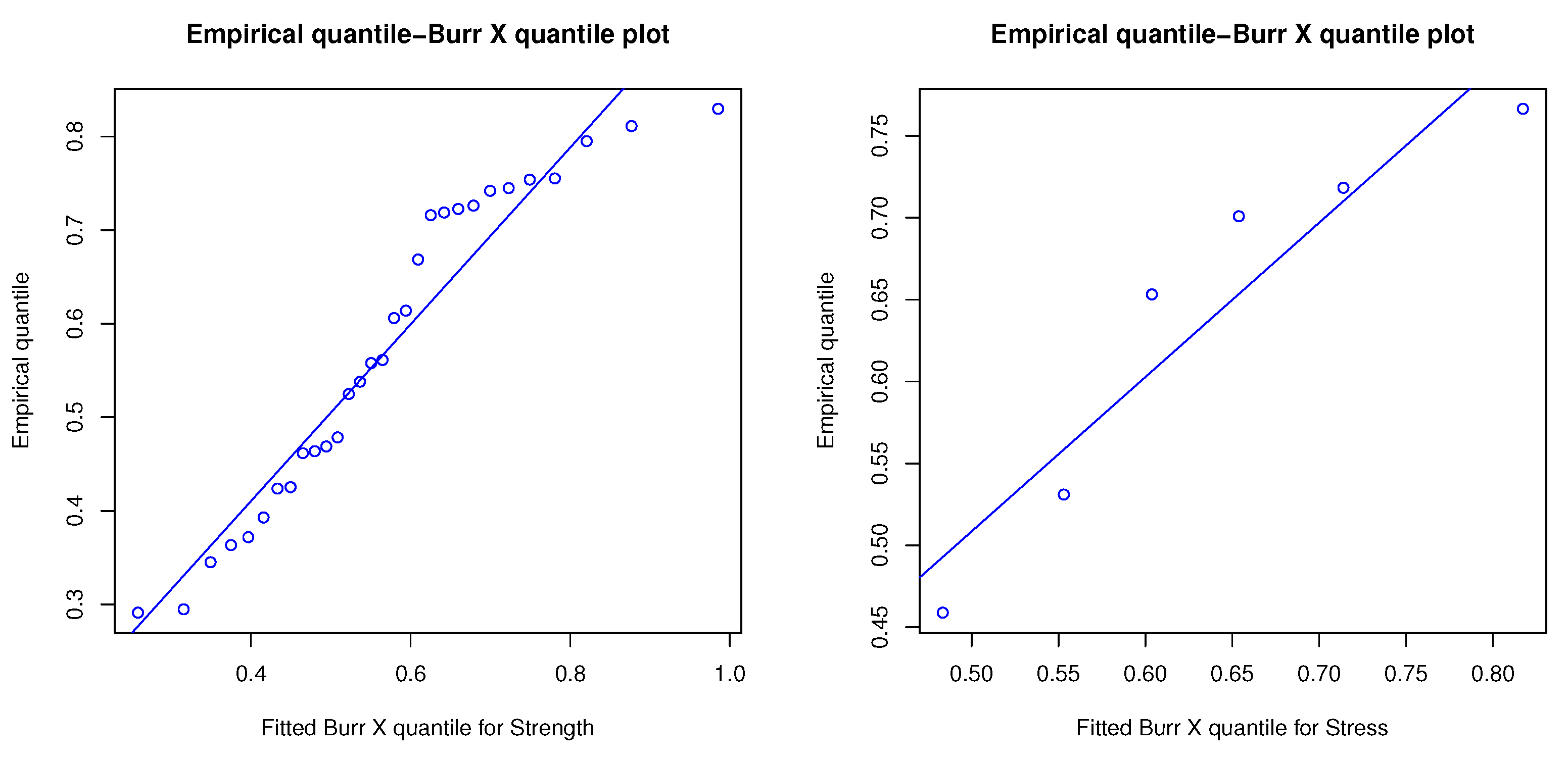
6. Practical Data Application
7. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Verification of Theorem 2
Appendix B. The Verification of Theorem 3
Appendix C. The Verification of Theorem 4
Appendix D. The Verification of Lemma 1
Appendix E. The Verification of Corollary 1
Appendix F. Complete Shasta Reservoir Water Capacity per Month
| Date | Storage AF | Date | Storage AF | Date | Storage AF |
|---|---|---|---|---|---|
| 01/1981 | 3,453,500 | 09/1982 | 3,486,400 | 05/1984 | 4,294,400 |
| 02/1981 | 3,865,200 | 10/1982 | 3,433,400 | 06/1984 | 4,070,000 |
| 03/1981 | 4,320,700 | 11/1982 | 3,297,100 | 07/1984 | 3,587,400 |
| 04/1981 | 4,295,900 | 12/1982 | 3,255,000 | 08/1984 | 3,305,500 |
| 05/1981 | 3,994,300 | 01/1983 | 3,740,300 | 09/1984 | 3,240,100 |
| 06/1981 | 3,608,600 | 02/1983 | 3,579,400 | 10/1984 | 3,155,400 |
| 07/1981 | 3,033,000 | 03/1983 | 3,725,100 | 11/1984 | 3,252,300 |
| 08/1981 | 2,547,600 | 04/1983 | 4,286,100 | 12/1984 | 3,105,500 |
| 09/1981 | 2,480,200 | 05/1983 | 4,526,800 | 01/1985 | 3,118,200 |
| 10/1981 | 2,560,200 | 06/1983 | 4,471,200 | 02/1985 | 3,240,400 |
| 11/1981 | 3,336,700 | 07/1983 | 4,169,900 | 03/1985 | 3,445,500 |
| 12/1981 | 3,492,000 | 08/1983 | 3,776,200 | 04/1985 | 3,546,900 |
| 01/1982 | 3,556,300 | 09/1983 | 3,616,800 | 05/1985 | 3,225,400 |
| 02/1982 | 3,633,500 | 10/1983 | 3,458,000 | 06/1985 | 2,856,300 |
| 03/1982 | 4,062,000 | 11/1983 | 3,395,400 | 07/1985 | 2,292,100 |
| 04/1982 | 4,472,700 | 12/1983 | 3,457,500 | 08/1985 | 1,929,200 |
| 05/1982 | 4,507,500 | 01/1984 | 3,405,200 | 09/1985 | 1,977,800 |
| 06/1982 | 4,375,400 | 02/1984 | 3,789,900 | 10/1985 | 2,083,100 |
| 07/1982 | 4,071,200 | 03/1984 | 4,133,600 | 11/1985 | 2,173,900 |
| 08/1982 | 3,692,400 | 04/1984 | 4,342,700 | 12/1985 | 2,422,100 |
Appendix G. R Codes for the Estimation Methods
References
- Eryilmaz, S. Phase type stress-strength models with reliability applications. Commun. Stat.—Simul. Comput. 2018, 47, 954–963. [Google Scholar] [CrossRef]
- Kundu, D.; Raqad, M.D. Estimation of R = P(Y < X) for three-parameter Weibull distribution. Stat. Probab. Lett. 2009, 79, 1839–1846. [Google Scholar]
- Krishnamoorthy, K.; Lin, Y. Confidence limits for stress-strength reliability involving Weibull models. J. Stat. Plan. Inference 2010, 140, 1754–1764. [Google Scholar] [CrossRef]
- Mokhlis, N.A.; Ibrahim, E.J.; Ibrahim, E.J. Stress-strength reliability with general form distributions. Commun. Stat.—Theory Methods 2017, 46, 1230–1246. [Google Scholar] [CrossRef]
- Surles, J.G.; Padgett, W.J. Inference for P(Y < X) in the Burr Type X Model. J. Appl. Stat. Sci. 1998, 7, 225–238. [Google Scholar]
- Wang, B.; Geng, Y.; Zhou, J. Inference for the generalized exponential stress-strength model. Appl. Math. Model. 2018, 53, 267–275. [Google Scholar] [CrossRef]
- Bhattacharyya, G.K.; Johnson, R.A. Estimation of reliability in multicomponent stress-strength model. Am. Stat. Assoc. 1947, 69, 966–970. [Google Scholar] [CrossRef]
- Dey, S.; Mazucheli, J.; Anis, M.Z. Estimation of reliability of multicomponent stress-strength for a Kumaraswamy distribution. Commun. Stat.—Theory Methods 2017, 46, 1560–1572. [Google Scholar] [CrossRef]
- Kayal, T.; Tripathi, Y.M.; Dey, S.; Wu, S.J. On estimating the reliability in a multicomponent stress-strength model based on Chen distribution. Commun. Stat.—Theory Methods 2020, 49, 2429–2447. [Google Scholar] [CrossRef]
- Kizilaslan, F. Classical and Bayesian estimation of reliability in a multicomponent stress-strength model based on the proportional reversed hazard rate model. Math. Comput. Simul. 2017, 136, 36–62. [Google Scholar] [CrossRef]
- Kizilaslan, F. Classical and Bayesian estimation of reliability in a multicomponent stress-strength model based on a general class of inverse exponentiated distributions. Stat. Pap. 2018, 59, 1161–1192. [Google Scholar] [CrossRef]
- Kizilaslan, F.; Nadar, M. Estimation of reliability in a multicomponent stress-strength model based on a bivariate Kumaraswamy distribution. Stat. Pap. 2018, 59, 307–340. [Google Scholar] [CrossRef]
- Nadar, M.; Kizilaslan, F. Estimation of reliability in a multicomponent stress-strength model based on a Marshall-Olkin bivariate Weibull distribution. IEEE Trans. Reliab. 2016, 65, 370–380. [Google Scholar] [CrossRef]
- Rao, G.S. Estimation of reliability in multicomponent stress-strength model based on Rayleigh distribution. ProbStat Forum 2012, 5, 150–161. [Google Scholar]
- Rao, G.S. Estimation reliability in multicomponent stress-strength based on generalized Rayleigh distribution. J. Mod. Appl. Stat. Methods 2014, 13, 367–379. [Google Scholar] [CrossRef]
- Rao, G.S.; Aslam, M.; Kundu, D. Burr type XII distribution parametric estimation and estimation of reliability of multicomponent stress-strength. Commun. Stat.—Theory Methods 2015, 44, 4953–4961. [Google Scholar] [CrossRef]
- Shawky, A.I.; Khan, K. Reliability estimation in multicomponent stress-strength based on inverse Weibull distribution. Processes 2022, 10, 226. [Google Scholar] [CrossRef]
- Lio, Y.L.; Tsai, T.-R.; Wand, L.; Cecilio Tejada, I.P. Inferences of the Multicomponent Stress-Strength Reliability for Burr XII Distributions. Mathematics 2022, 10, 2478. [Google Scholar] [CrossRef]
- Sauer, L.; Lio, Y.; Tsai, T.-R. Reliability inference for the multicomponent system based on progressively type II censoring samples from generalized Pareto distributions. Mathematics 2020, 8, 1176. [Google Scholar] [CrossRef]
- Wang, L.; Lin, H.; Ahmadi, K.; Lio, Y. Estimation of stress-strength reliability for multicomponent system with Rayleigh data. Energies 2021, 14, 7917. [Google Scholar] [CrossRef]
- Burr, I.W. Cumulative frequency functions. Ann. Math. Stat. 1942, 13, 215–232. [Google Scholar] [CrossRef]
- Belili, M.C.; Alshangiti, A.M.; Gemeay, A.M.; Zeghdoudi, H.; Karakaya, K.; Bakr, M.E.; Balogun, O.S.; Atchade, M.N.; Hussam, E. Two-paramter family of distributions: Properties, estimation, and applications. AIP Adv. 2023, 13, 105008. [Google Scholar] [CrossRef]
- Yousof, H.M.; Afify, A.Z.; Hamedani, G.G.; Aryal, G. The Burr X generator of distributions for lifetime data. J. Stat. Theory Appl. 2017, 16, 288–305. [Google Scholar] [CrossRef]
- Jamal, F.; Nasir, M.A. Generalized Burr X family of distributions. Int. J. Math. Stat. 2018, 19, 55–73. [Google Scholar]
- Jaheen, Z.F. Empirical Bayes estimation of the reliability and failure rate functions of the Burr type X failure model. J. Appl. Stat. Sci. 1996, 3, 281–288. [Google Scholar]
- Ahmad, K.E.; Fakhry, M.E.; Jaheen, Z.F. Empirical Bayes estimation of P(Y < X) and characterization of Burr-type X model. J. Stat. Plan. Inference 1997, 64, 297–308. [Google Scholar]
- Akgul, F.G.; Senoglu, B. Inferences for stress-strength reliability of Burr type X distributions based on ranked set sampling. Commun. Stat.—Simul. Comput. 2022, 51, 3324–3340. [Google Scholar] [CrossRef]
- Efron, B. Jackknife, Bootstrap, Other Resampling Plans. In CBMS-NSF Regional Conference Series in Applied Mathematics; SIAM: Philadelphia, PA, USA, 1982; Volume 38. [Google Scholar]
- Hall, P. Theoretical comparison of bootstrap confidence intervals. Annu. Stat. 1988, 16, 927–953. [Google Scholar] [CrossRef]
- Xu, J.; Long, J.S. Using the Delta Method Tonconstruct Confidence Intervals for Predicted Probabilities, Rates, and Discrete Changes; Lecture Notes; Indiana University: Bloomington, IN, USA, 2005. [Google Scholar]
- Weerahandi, S. Generalized Inference in Repeated Measures: Exact Methods in MANOVA and Mixed Models; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Cherstvy, A.G.; Thapa, S.; Wagner, C.E.; Metzler, R. Non-Gaussian, non-ergodic, and non-Fickian diffusion of tracers in mucin hydrogels. Soft Matter 2019, 15, 2526–2551. [Google Scholar] [CrossRef]
- Thapa, S.; Park, S.; Kim, Y.; Jeon, J.-H.; Metzler, R.; Lomholt, M.A. Bayesian inference of scaled versus fractional Brownian motion. J. Phys. A Math. Theor. 2022, 55, 194003. [Google Scholar] [CrossRef]
- Krog, J.; Lomholt, M.A. Bayesian inference with information content model check for Langevin equations. Phys. Rev. E 2017, 96, 062106. [Google Scholar] [CrossRef] [PubMed]
- Viveros, R.; Balakrishnan, N. Interval estimation of parameters of life from progressively censored data. Technometrics 1994, 36, 84–91. [Google Scholar] [CrossRef]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data, 2nd ed.; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Stephens, M.A. Tests for the exponential distribution. In Goodness-of-Fit Techniques; D’Agostino, R.B., Stephens, M.A., Eds.; Marcel Dekker: New York, NY, USA, 1986; pp. 421–459. [Google Scholar]

| ACI | GCI | BCI |
| ACI | GCI | BCI |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lio, Y.; Chen, D.-G.; Tsai, T.-R.; Wang, L. The Reliability Inference for Multicomponent Stress–Strength Model under the Burr X Distribution. AppliedMath 2024, 4, 394-426. https://doi.org/10.3390/appliedmath4010021
Lio Y, Chen D-G, Tsai T-R, Wang L. The Reliability Inference for Multicomponent Stress–Strength Model under the Burr X Distribution. AppliedMath. 2024; 4(1):394-426. https://doi.org/10.3390/appliedmath4010021
Chicago/Turabian StyleLio, Yuhlong, Ding-Geng Chen, Tzong-Ru Tsai, and Liang Wang. 2024. "The Reliability Inference for Multicomponent Stress–Strength Model under the Burr X Distribution" AppliedMath 4, no. 1: 394-426. https://doi.org/10.3390/appliedmath4010021
APA StyleLio, Y., Chen, D.-G., Tsai, T.-R., & Wang, L. (2024). The Reliability Inference for Multicomponent Stress–Strength Model under the Burr X Distribution. AppliedMath, 4(1), 394-426. https://doi.org/10.3390/appliedmath4010021







