Abstract
Devising a financial trading strategy that allows for long-term gains is a very common problem in finance. This paper aims to formulate a mathematically rigorous framework for the problem and compare and contrast the results obtained. The main approach considered is based on Dynamic Bayesian Networks (DBNs). Within the DBN setting, a long-term as well as a short-term trading strategy are considered and applied on twelve equities obtained from developed and developing markets. It is concluded that both the long-term and the medium-term strategies proposed in this paper outperform the benchmark buy-and-hold (B&H) trading strategy. Despite the clear advantages of the former trading strategies, the limitations of this model are discussed along with possible improvements.
1. Introduction
In this paper, Dynamic Bayesian Networks (DBNs) are used to study the problem of obtaining and testing a financial strategy whose return is higher than the buy and hold strategy for a given equity. A Bayesian Network (BN) is a graphical and compact representation of a joint probability density function (PDF) that makes use of conditional independence and can be used to model a system under one time instance. DBNs extend the BN to more than one time period, which is to say that DBNs are a temporally driven extension of BNs.
Some benefits of using DBNs over other models, such as basic time series models, are the following. Firstly, DBNs have the capacity to incorporate what are known as hidden (or latent) variables, which either govern, or are thought to govern, the observations of the observable random variable. These hidden variables are random variables whose true value cannot be measured directly, sometimes due to instrumental inadequacies, and other times simply because the existence of these variables is hypothesized. Examples of such hidden variables are the intelligence of an individual (which cannot be measured precisely using any instrument) or the state (bull or bear) of a financial market (whose existence itself is hypothetical). Secondly, since they are an offshoot of BNs, DBNs allow for compact representations of an otherwise possibly cumbersome joint distribution. Russell and Norvig [1] argue that due to conditional independence, representing a joint distribution as a DBN may eliminate any redundant terms, which, in turn, also makes parameter estimation simpler. Murphy [2] state that another benefit of DBNs is the ease with which variations to the model at hand can be introduced. DBNs can be used to alternatively represent both basic Hidden Markov Models (HMMs), and HMMs with variations, such as HMMs with a mixture-of-Gaussian outputs, Auto-regressive HMMs, Input–Output HMMs and Hierarchical HMMs. DBNs can also be used to represent Kalman Filter Models where, contrary to HMMs, the hidden state is continuous rather than discrete. Lastly, DBNs also have the capacity to answer questions about different types of reasoning or inference, such as diagnostic inference (from effects to causes), causal inference (from causes to effects), intercausal inference (between causes of the same effect), and mixed inference (a mixture of any two of the above types of inference).
In this research paper, we use the price–earnings (PE) ratio in the models discussed. In the literature, various papers can be found which apply the said PE ratio to examine investment strategies. Most notably, one can mention Basu [3]. This ratio has also been used in a vast range of literature including that of Lleo [4] and Angelini [5]. Chang and Tian [6] also use BNs to model the qualitative and quantitative relationships between several variables that affect the dynamics of the S&P 500 stock index, with the aim of optimizing trading decisions, namely when to open a short position and when to invest in a long position. Damiano et al. [7] base their work on a previous study, that of Tayal [8], which employs HHMMs to analyze financial data. The results obtained by Tayal are reproduced in Damiano et al.’s paper, and further insight is given. Damiano et al. [7] conclude that probabilistic inference allows the identification of two distinct states in high-frequency data that are mainly marked by buying and selling pressure.
Historically, Paul Dagum is thought to have kick-started the development of DBNs in the early 1990s, namely, in the work by Dagum et al. [9] in 1992 and by Dagum et al. [10] in 1995. Ever since, DBNs have been used in various areas, namely, in finance and economics. However, other areas include (but are not limited to) speech recognition (Murphy [2], Zweig, Russell [11], and Nefian et al. [12]), biology(Yao et al. [13], Raval et al. [14], Murphy and Mian [15]), robotics (Prembida et al. [16], Patel et al. [17]), image processing (Delage et al. [18]), and fault detection (Cozar et al. [19]). Parameter estimation techniques of DBNs are discussed by Benhamou et al. [20], whereas Murphy [21] works on the theoretical foundations of DBNs.
The rest of this paper is structured as follows. Section 2 introduces the theoretical underpinnings of DBNs. In Section 3, DBNs are applied to twelve equities from both developed and developing markets, and the return on investment is presented. The reason for considering both developed and developing markets is to test model robustness under different economic conditions and growth patterns. Finally, in the concluding section, the key points and results obtained are highlighted.
2. Theoretical Framework
This model is based on the work by Wang [22] and exploits two behavioral finance phenomena—behavioral volatility and mean reversion. Behavioral volatility refers to the phenomenon whereby market-related events such as irrational trades executed by inexperienced traders cause the trading price of a stock to deviate away from its ‘true’ value. Events like these continually affect market price either until the effects caused cancel each other out, or until rational investors balance these effects out with their rational trades. This phenomenon is known as mean reversion. The theory of mean reversion is applicable not only to the price of a stock, but to any price-related metric, such as the price–earnings (PE) ratio (share price divided by the earnings per share). As a result, one can decide to buy (or sell) a stock only when some metric that follows the mean reversion theory is far away from the mean, knowing that the ‘true’ value of the metric will be returned to at some point in the future.
A Directed Graphical Model (DGM) is a representation of a probabilistic model that uses conditional independence assumptions through a directed graph, where the vertices (note that the terms “state”, “random variable”, “node” and “vertex” may be used interchangeably) of the graph represent random variables and the arcs represent conditional dependence between pairs of random variables. An arc from vertex A to vertex B represents the statement “A causes B” (Murphy [2]). DGMs are convenient due to their compactness in exhibiting some joint probability distribution—for N binary random variables, the general closed form of the joint probability distribution of these random variables may need parameters, whereas the graphical model may give the same information using fewer parameters due to the omission of terms via conditional independence statements.
A Bayesian Network is a DGM that represents a set of random variables and their conditional dependencies through a directed acyclic graph (DAG), denoted by . Each vertex in represents a random variable , and each directed edge in represents the conditional dependence a random variable has on another. A conditional probability distribution is associated to each node , and the joint probability distribution on the vertex set is given by . The generalization of a BN to multiple time slices gives rise to the definition of a DBN. A Dynamic Bayesian Network is defined to be a pair , where is the BN representing the prior probability (or the initial state probability), that is, the probability distribution of the random variables at time 0, and is a two-slice temporal BN which describes transition probabilities from time to time t for any node X in the vertex set of the DAG , denoted by . The joint probability distribution of the vertex set over all time slices is given by:
where refers to the set of all vertices indexed from time up to time . A DBN can be parametrized by its transition matrix and its prior distribution . If the transition probabilities are assumed to be constant for all time slices (), then they are said to be homogeneous and have a much more compact joint distribution function. When representing a DBN pictorially, two or three time slices are typically shown—the initial time slice and the subsequent one or two—since its structure is assumed to replicate throughout time.
An important property of DAGs is that “nodes can be ordered such that parents come before children. This is called a topological ordering, and it can be constructed from any DAG.” (Murphy [23]). Given such an ordering, the Ordered Markov property (or Local Markov property) is defined to be the “assumption that a node only depends on its parents, not on all its predecessors in the ordering” (Murphy [23]). This assumption is in fact a generalization of the Markov property for Markov chains.
2.1. Inference for DBNs
The objective in inference is to infer the value of the latent states given the observations of the observable states, that is, inferring the marginals . If , the process is known as filtering (or ‘now-casting’); if , then this is smoothing; and if , then one would be performing prediction (or forecasting). A commonly used inference algorithm for DBNs is the forward–backward algorithm. In this algorithm, dynamic programming is implemented through two steps, known as passes, that run in a counter-directional manner—one runs forward in time, whilst the other runs backward. Note that it is assumed that the transition probability matrix, emission probability matrix, and prior probabilities are all known. In the forward pass, the value of is found in a recursive manner. In the backward pass, the value of is also found recursively but moving in counter chronological order (from time T to time 2). After the forward and backward passes are complete, the value for can finally be obtained:
where .
2.2. Learning DBNs
In this context, learning refers to the parameter estimation process. In parameter estimation, learning can be tackled either through a Maximum Likelihood (ML) approach or through the Maximum A Posteriori (MAP) approach. If using ML, then the data are used to obtain parameter estimates via the solution of the optimization problem: , where is the set of parameters to be estimated. Typically, contains the transition matrix and parameters pertaining to the probability distribution used in the emission matrix. On the other hand, if using the MAP method, the optimization problem above is adjusted slightly to become where is the parameter prior distribution. The approach to solving the optimization problems above is through an adaptation of the Expectation–Maximization (EM) algorithm known as the Baum–Welch algorithm, proven to give a local optimum to the optimization problems above (Baum et al. [24], Dempster et al. [25]). It uses the forward–backward algorithm as a subroutine. Hence, in cases where the model parameters are unknown, the Baum–Welch algorithm is first used to estimate (or learn) the model parameters. Then, the forward–backward algorithm is used to infer the posterior marginals.
2.3. Application of Theory
The main hypothesis of the model is that the stock price of a firm is not always equal to the firm’s ‘true’ intrinsic value. Utilizing the phenomena of behavioral volatility and mean reversion, temporary effects that cause stock metrics to deviate from their ‘true’ value are classified into two: short-term effects (length of a few days) and medium-term effects (length of several weeks).
It is hypothesized that the fundamental value of a company i at time t, denoted by , is directly proportional to its annual earnings at time t, denoted by , with the fundamental PE ratio, denoted by , acting as the constant of proportionality:
On the other hand, the observed PE ratio (openly available on the public domain), denoted by , is given by where denotes the actual trading price of a company i at time t.
Note that from this point onward, the index i is dropped, as the analysis on stocks is performed univariately. The model equation that results from the above is given by:
where , is a discrete-time Markov chain modeling the medium-term noise effects, and is a random variable modeling the short-term noise effects. Due to the above model equation, the model used is only applicable for firms that have positive earnings throughout the period under study. Furthermore, one must note that is an observable quantity (since both and are); however, and are not. It is assumed that both and are discrete-valued; hence, and where M and N represent the number of possible latent states of and , respectively.
The conditional independence assumptions used in this model are presented next:
For and , the matrix is defined to be the transition probability matrix, where
Note that and . For , and , the matrix is defined to be the emission probability matrix at time t, where
where . For and , the vectors and are defined to be the initial probability vectors that contain the initial probability distributions, where
Note that , and . These prior distributions serve to incorporate any expert knowledge that the researcher may have available. A graphical representation of the model described above can be found in Figure 1.
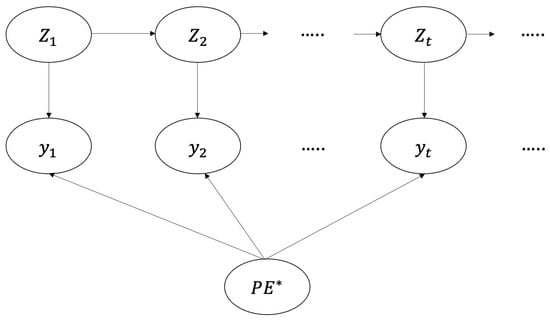
Figure 1.
Representation of the model described above using a DBN, where is observable and and are latent, discrete variables.
Having laid out the principles needed for inference, the aim of the analysis now makes itself clearer—that of inferring the value of so as to estimate the fundamental price of a stock and formulate a trading strategy based on this knowledge. Furthermore, inferring the value of is also useful, as it can be used to test an alternative trading strategy. In this context, the data used will be split into a training and a test set. The set of model parameters is given by . The space of possible parameters is given by the set:
Learning and inference then follow. Since the parameters in are unknown, they will first need to be estimated (learning procedure). As mentioned, the algorithm used to obtain the MAP estimates is the Baum–Welch algorithm. After the unknown model parameters are estimated, the forward–backward algorithm is used on the parameter estimates to infer the constant value of for the training set and test set, and to infer the value of through smoothing for the training set, and through filtering for the test set:
- Filtering probabilities:
- Smoothing probabilities: , where
2.4. Inference with Known Parameters
As per the forward pass of the forward–backward algorithm, the following definitions are made and equations derived for the filtering probabilities:
After defining the filtering probabilities, the smoothing probabilities are given through the estimate denoted by :
Next, as per the backward pass of the forward–backward algorithm, the definition of is to be given so as to be able to obtain the values for :
Therefore, as per the forward–backward algorithm, one has:
What remains to be derived are the expressions for :
For :
With expressions found for both the smoothing and filtering probabilities, the most probable values of the latent variables and are found through marginalization:
To find the estimate for the latent state , smoothing is used on the training, set whilst filtering is applied on the test set:
where and denote the training set and test set, respectively.
2.5. Learning Unknown Parameters
The optimization problem in learning is given by and is solved using the Baum–Welch algorithm (note that in the forthcoming expressions, should technically be written with a hat superscript () since it is a set of parameter estimates):
- (1)
- Set .
- (2)
- Set
- (3)
- while do
- (i)
- Calculate probabilities
- (ii)
- Solve the constrained maximization problemwhere .
- (iii)
- Increment j
An expression in closed form can be obtained for by using the smoothing probabilities:
In the argument of the maximization problem above, is the logarithm of the prior distribution , where since the independence of priors is assumed. Within this prior distribution, two types of expert knowledge can be included—prior knowledge of the ballpark value of and prior knowledge of the persistence of the medium-term noise effects, which are encoded through the prior and the prior , respectively.
The prior for the vector is represented by the Dirichlet distribution:
The values for intuitively correspond to the degree of belief an expert has on the event that is the ‘true’ value for . For this analysis, . The prior for the matrix is also derived from the Dirichlet distribution where and
Since is the transition matrix for the hidden Markov chain , then the diagonal entries of represent the probability that a particular state persists (stays as is in the next time point). The greater the value of (or, correspondingly, ), the greater that state’s persistence. In this analysis, the off-diagonal entries (the reader is suggested to refer to Wang [22] for more information on the values of the off-diagonals) are set to 0.
Taking all the above into consideration, the logarithm of the prior becomes
where
The constant is only included for completeness’ sake—it is rendered irrelevant when maximizing in the Baum–Welch algorithm.
With the priors set, the constrained optimization problem is now fully defined. Note that only the equality constraints in (6) will be considered, as the inequality constraints will end up being satisfied still. Therefore, the method of Lagrange multipliers can be used to solve this optimization problem. The expressions for the estimators of the four variables in question are given below:
where
3. Methodology of Analysis and Results
Twelve equities were chosen to be analyzed in this paper (see Table 1)—nine from a developed market (US) and three from emerging markets (Brazil and China). The training set contains data from the 1st of January 2011 to the 31st of December 2019 whilst the test set contains data from the 1st of January 2020 to the 30st of September 2020. Using a 12-month rolling Sharpe ratio as a point of reference, all equities displayed average or above average returns (with respect to an S&P benchmark) in the test period, with the exception of the two underperforming Brazilian equities [26]. Two datasets were collected for each stock for the above-mentioned period—daily price data and quarterly earnings per share data.

Table 1.
Table of results, showing the return on investment as a percentage of the sum invested. Values in brackets are negative.
After the preliminary data cleaning and preparation phase, the initial values of vectors and are set next. Priors of the vector and matrix are set as discussed earlier; the prior for is set to be the discrete uniform distribution, and the initial value of is set to 5. Parameter learning is then performed before inference of the latent states and . Simulation of the trading strategies follows. The trading strategies proposed by Wang [22] and used in this paper will be compared to the benchmark B&H strategy. For both the proposed trading strategies, let denote the amount of cash available at time t; let denote the units of a security held at time t; let represent the size of the training set; and let T represent the size of the dataset (sum of sizes of training and test sets). Both the long-term and the medium-term trading strategies can be described by three possible courses of action (labeled (i), (ii) and (iii) below) at time t; that is, courses of action (i) through (ii) are common to both trading strategies:
(i) If and , then buy the security using all the available cash . Hence, and .
(ii) If and , then sell all the units held . Hence, and .
(iii) If neither (i) or (ii) are satisfied, do not execute any trades. Hence, and .
Note that is considered to be a baseline and depends on the trading strategy. The threshold value acts as a sensitivity gauge defining how much the investor wants to allow to deviate from the baseline before triggering a particular course of action in the trading strategies. This is clear from how the courses of action are defined. The total profit at the end of the trading period is given by .
The first trading strategy is the so-called ‘long-term strategy’, where trading is performed with respect to the constant value of , so . The alternative strategy is the ‘medium-term strategy’, where trading is performed with respect to the dynamic values of , where each is dynamically estimated through filtering. Therefore, for the medium-term strategy, .
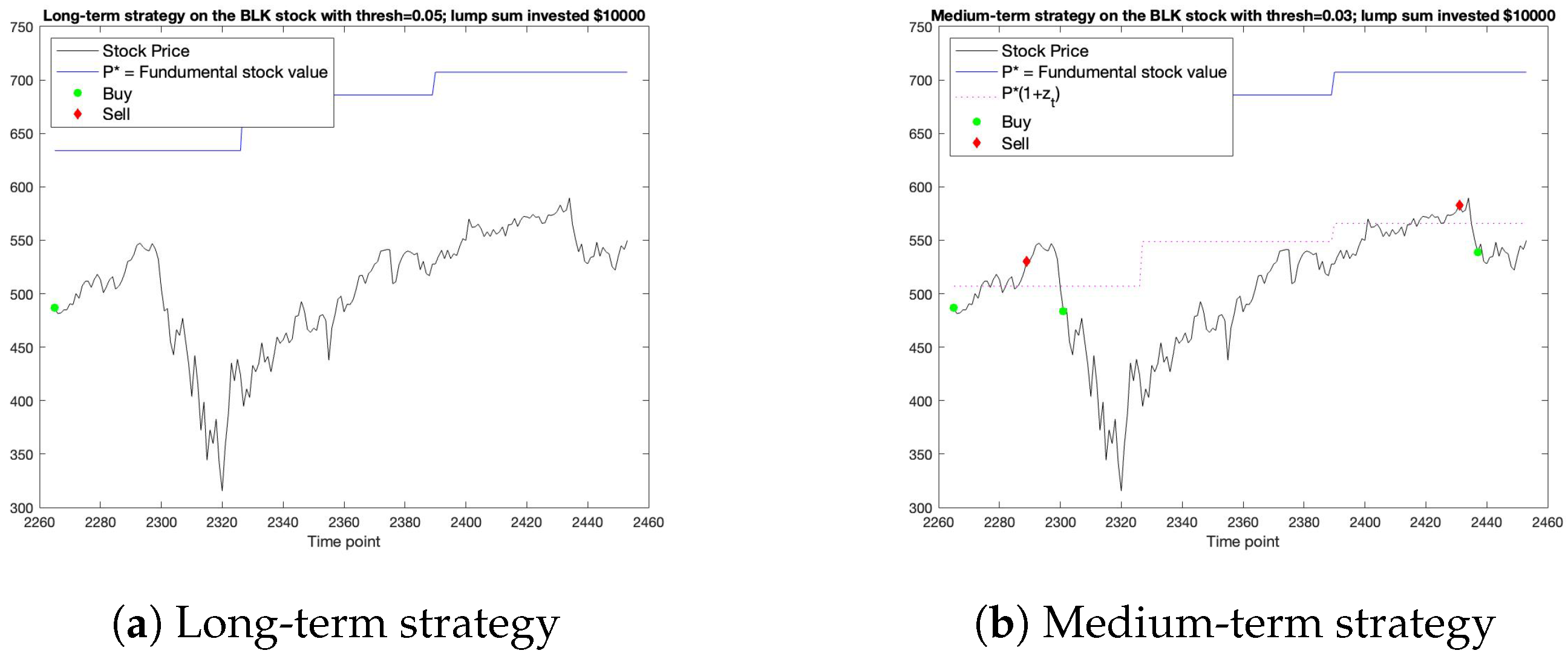
The results on the BLK and ITUB stocks are presented in graphical detail in this paper. Firstly, the long-term strategy on the BLK stock data suggests that the investor buys the stock at time point and holds the stock for the rest of the period. Clearly, this strategy coincides with the B&H strategy and, as a result, profit from the long-term-strategy would be equal to profit from the B&H strategy which is equal to USD1298.04, equaling a 12.98% return on the initial investment of USD 10,000. On the other hand, the medium-term strategy suggests that the investor buys the stock at time points 2265, 2301 and 2437, sells it at time points 2289 and 2431, and holds it for the rest of the time points. This would yield a profit of USD 3391.85; equalling a 33.92% return on the initial investment of USD 10,000 in the nine-month period that the testing set covers. This means that the medium-term strategy beats the B&H strategy by 20.94%. Figure 2 illustrates the long-term strategy and medium-term strategy.
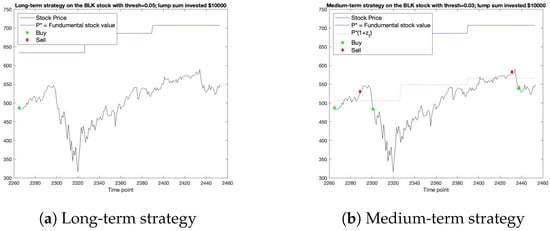
Figure 2.
Simulated strategies for the BLK stock.
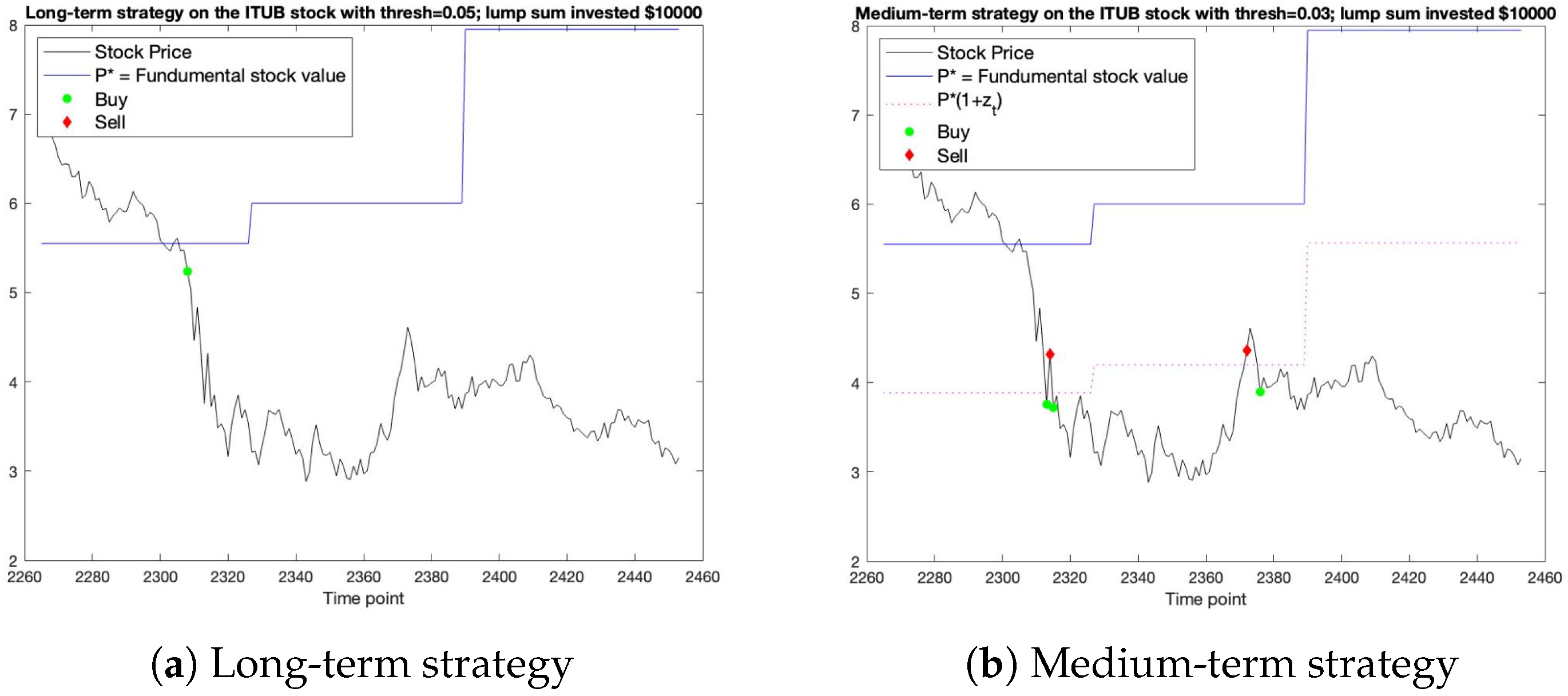
Next, we discuss the ITUB stock data. The long-term strategy suggests that the investor buys the stock at time point 2308 and holds the stock for the rest of the period. Implementing this strategy would yield a loss of USD 3986.16, which equates to a 39.86% loss on the initial investment of USD 10,000. The buy-and-hold strategy, however, would yield a greater loss of USD 5584.67. In contrast, the medium-term strategy suggests that the investor buys the stock at time points 2313, 2315 and 2376, sells it at time points 2314 and 2372, and holds it for the rest of the time points. This would actually yield a profit of USD 909.81. Although this is only a 9.1% return on the initial investment of USD 10,000, the medium-term strategy provides the investor with a strategy whereby he or she can make a profit in a period when the stock is actually crashing. Figure 3 illustrates the long-term strategy and medium-term strategy, respectively.
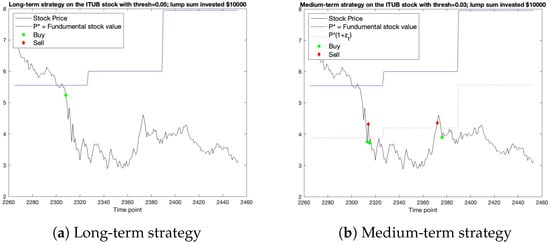
Figure 3.
Simulated strategies for the IUTB stock.
More generally, we see in Table 1 that the medium strategy has been consistently superior (for various thresholds) for BLK, COST, HD, ITUB, MA, MCD, NVDA and UNH. For ITUB, for all but one threshold, the strategy turns a slight profit even though a loss is registered for other strategies. The long-term strategy has been consistently superior for NTES and SAN. Neither strategy has offered any advantages on ADBE, while for AAPL, the success of the medium-term strategy depends on the choice of threshold. Some further analysis on these results will be given in the conclusion.
4. Conclusions
Through the use of DBNs, the model for stock movement by Wang [22] is built for our existing equity dataset. This model includes two latent states—one modeling the medium-term noise effects, and the other modeling the true fundamental PE ratio of a firm, the latter assumed to be constant throughout the period under study. The forward–backward algorithm and the Baum–Welch algorithm (variant of the EM algorithm) are used to perform parameter learning and inference. Based on this fitted model, the long- and medium-term strategies are applied to the twelve stocks studied here, with nine of these stocks trading on a developed market and the rest on an emerging one. Overall, both the long-term and medium-term strategies outperform the benchmark B&H trading strategy 17 and 31 times, respectively, out of a total of 48 experiment runs for each strategy (four for each of the twelve stocks). The strategies proposed by Wang only lose out to the B&H four and three times, respectively. Furthermore, the outperformance of these trading strategies is substantial. Whereas the average profit over all stocks when using the B&H is 20.83%, the average profit over all stocks and over all thresholds for the long-term strategy is 27.78% and that for the medium-term strategy is 36.23%. Lastly, it results that these trading strategies provide the investor with trading suggestions that, in certain cases, can even turn a loss under the B&H strategy into a profit as was shown to be the case for the ITUB stock. This stock was on a downfall, but the medium-term strategy still yielded a profit on the sum invested. All these results are as displayed in Table 1.
As with any statistical model, the model implemented in this work has room for improvement. The first and most significant limitation is the fact that only stocks that had a positive EPS during the period under study can be modeled by the model. This is due to the left-hand side of the model equation, that is, Equation (1). In certain times such as during pandemics or during recessions, it may be considerably difficult to find a firm who has not registered a loss in at least one quarter for the period under study. A second limitation is the lack of use of expert knowledge. In real-world investing, expertise in the field is considered highly valuable, and only seasoned investors are generally advised to trade actively. Since the model in this paper allows for the incorporation of expert knowledge, it is indeed a limitation that such knowledge is not made use of. Another limitation related to expert knowledge is the limitation that no trading fees or commissions are taken into account in this analysis. Although the proposed model allows for commissions to be considered in the trading strategies, no knowledge on the actual values of fees or commissions charged was available at the time of writing, and hence, such expenses could not be taken into account. It is well known that certain trading fees can sometimes tally up when executing numerous trades in such a way that a profit can turn into a loss when these fees are brought to the fore, which would make the buy-and-hold strategy more profitable.
Improvements on the above-mentioned limitations can add value to the model and should be considered in future works. In addition, another improvement that makes the model here more applicable in real-life scenarios is the incorporation of some variable that measures the liquidity of a stock. This is because the suggestions provided by the trading strategies on when to buy and sell a stock are rendered useless if the stock itself is not liquid. Prices may change by the time the stock becomes liquid enough for an actual trading opportunity to arise, and if the price changes significantly, that obviously renders the suggestion itself useless. In this study, liquidity was not envisaged to be of concern since all 12 stocks considered are large-cap stocks.
The choice of historical data used is always an important decision due to the fact that the length of the time series plays a major role. In principle, longer time series are preferred to shorter ones, but if the historical data contain changes in regime, this may inhibit the model in its forecasting performance. Furthermore, future regime changes that may occur in the test period may also impact the model’s forecasting performance.
Finally, other improvements that can be implemented in future studies are further and deeper experimentation and testing, and the possibility of short-selling stock. To begin with, experimentation at a portfolio level can be implemented with the stocks studied here to understand how the profits change when a group of stocks are considered together—for instance, samples of nine stocks from the twelve studied here can be taken to form portfolios, and the ’optimal’ portfolio can be identified. Apart from this, more time can be spent on cross-validation in future studies to further improve on the suggestions provided by the trading strategies in this work. Also, the properties of all the estimators used could be derived in future works, to better understand their behavior. Finally, this strategy does not allow the short-selling of stock; extensions to the model which allow for this could be proposed.
Author Contributions
All the three authors worked equally hard to write this paper. K.L. took care of the coding in MATLAB and the results section, M.A.C. and D.P.S. took care of the methodology and theoretical content of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All the data is openly available from Yahoo Finance at https://finance.yahoo.com/.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BN | Bayesian Network |
| DAG | Directed Acyclic Graph |
| DBN | Dynamic Bayesian Network |
| DGM | Directed Graphical Model |
| EM | Expectation–Maximization |
| HNN | Hidden Markov Model |
| Probability Density Function | |
| MAP | Maximum A Posteriori |
| ML | Maximum Likelihood |
References
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Murphy, K. Dynamic Bayesian Networks: Representation, Inference and Learning. Ph.D. Dissertation, University of California, Berkeley, CA, USA, 2002. [Google Scholar]
- Basu, S. Investment Performance of common stocks in relation to their price-earnings ratios: A Test of the efficient market hypothesis. J. Financ. 1977, 23, 663–673. [Google Scholar]
- Lleo, S.; Ziemba, W.T. A Tale of Two Indexes: Predicting Equity Market Downturns in China. SSRN 2020. [Google Scholar] [CrossRef]
- Angelini, N.; Bormetti, G.; Marmi, S.; Nardini, F. Value Matters: Predictability of Stock Index Returns. SSRN 2012. [Google Scholar] [CrossRef]
- Chang, K.C.; Tian, Z. Market analysis and trading strategies with Bayesian networks. In Proceedings of the 18th International Conference on Information Fusion, FUSION 2015, Washington, DC, USA, 6–9 July 2015; pp. 1922–1929. [Google Scholar]
- Damiano, L.; Peterson, B.; Weylandt, M. Regime Switching and Technical Trading with Dynamic Bayesian Networks in High-Frequency Stock Markets. 2017. Available online: https://luisdamiano.github.io/work/gsoc17_rs_technical_trading.pdf (accessed on 28 April 2024).
- Tayal, A. Regime Switching and Technical Trading with Dynamic Bayesian Networks in High-Frequency Stock Markets; University of Waterloo: Waterloo, ON, Canada, 2009. [Google Scholar]
- Dagum, P.; Galper, A.; Horvitz, E. Dynamic Network Models for Forecasting. In Proceedings of the Eighth Conference on Uncertainty in Artificial Intelligence, Stanford, CA, USA, 17–19 July 1992; pp. 41–48. [Google Scholar]
- Dagum, P.; Galper, A.; Horvitz, E. Uncertain Reasoning and Forecasting. Int. J. Forecast. 1995, 11, 73–87. [Google Scholar] [CrossRef]
- Zweig, Z.; Russell, S. Speech Recognition with Dynamic Bayesian Networks. 1998. Available online: http://www.cse.msu.edu/~cse841/papers/zweig.pdf (accessed on 28 April 2024).
- Nefian, A.; Liang, L.; Pi, X.; Liu, X.; Murphy, K. Dynamic Bayesian Networks for Audio-Visual Speech Recognition. EURASIP J. Adv. Signal Process. 2002, 11, 783042. [Google Scholar] [CrossRef]
- Yao, X.Q.; Zhu, H.; She, Z. A dynamic Bayesian network approach to protein secondary structure prediction. BMC Bioinform. 2008, 9, 49. [Google Scholar] [CrossRef] [PubMed]
- Raval, A.; Ghahramani, Z.; Wild, D.L. A Bayesian network model for protein fold and remote homologue recognition. Bioinformatics 2002, 18, 788–801. [Google Scholar] [CrossRef] [PubMed]
- Murphy, K.; Mian, S. Modelling Gene Expression Data Using Dynamic Bayesian Networks. 1996. Available online: https://www.cs.ubc.ca/~murphyk/Papers/ismb99.pdf (accessed on 28 April 2024).
- Prembida, C.; Souza, F.A.A.; Faria, D.R. Dynamic Bayesian network for semantic place classification in mobile robotics. Auton. Robot. 2016, 5, 1161–1172. [Google Scholar] [CrossRef]
- Patel, M.; Miro, J.V.; Dissanayake, G. Dynamic Bayesian Networks for Learning Interactions Between Assistive Robotic Walker and Human Users. 2010. Available online: https://opus.lib.uts.edu.au/bitstream/10453/16294/1/2010000382.pdf (accessed on 28 April 2024).
- Delage, E.; Lee, H.A.Y. A Dynamic Bayesian Network Model for Autonomous 3D Reconstruction from a Single Indoor Image. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; Volume 2, pp. 2418–2428. [Google Scholar] [CrossRef]
- Cozar, J.; Puerta, J.; Gamez, J.A. An Application of Dynamic Bayesian Networks to Condition Monitoring and Fault Prediction in a Sensored System: A Case Study. Int. J. Comput. Intell. Syst. 2017, 10, 176. [Google Scholar] [CrossRef]
- Benhamou, E.; Atif, J.; Laraki, R. A New Approach to Learning in Dynamic Bayesian Networks (DBNs). SSRN Electron. J. 2018. [Google Scholar] [CrossRef]
- Murphy, K. An Introduction to Graphical Models. 2001. Available online: https://www.cs.ubc.ca/~murphyk/Bayes/bnintro.html (accessed on 28 April 2024).
- Wang, H. Bayesian Probabilistic Inference on Firm-Level Stock Price Dynamics. Ph.D. Dissertation, Suranaree University of Technology, Nakhon Ratchasima, Thailand, 2016. [Google Scholar]
- Murphy, K. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Baum, L.E.; Petries, T.; Soules, G.; Weiss, N. A Maximization Technique Occurring in the Statistical Analysis of Probabilistic Functions of Markov Chains. Ann. Math. Stat. 1970, 41, 167–171. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data Via the EM Algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–22. [Google Scholar] [CrossRef]
- PortfoliosLab. Available online: https://portfolioslab.com/ (accessed on 28 April 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).