Exploring the Influence of Oblateness on Asymptotic Orbits in the Hill Three-Body Problem
Abstract
:1. Introduction
2. Equations of Motion
3. Equilibrium Points and Zero-Velocity Curves
4. Analytical Solution of Asymptotic Motion at the Equilibrium Points
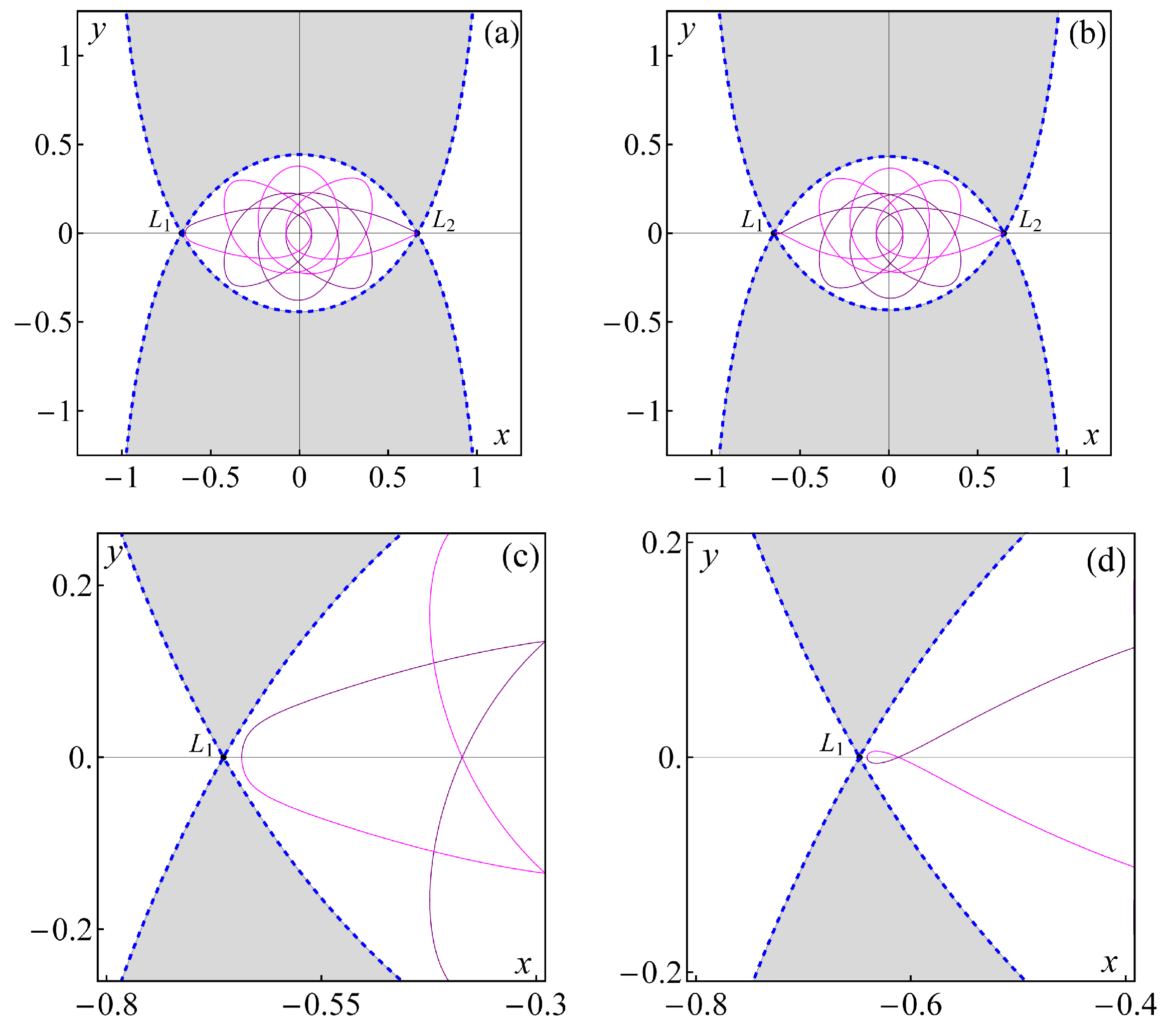
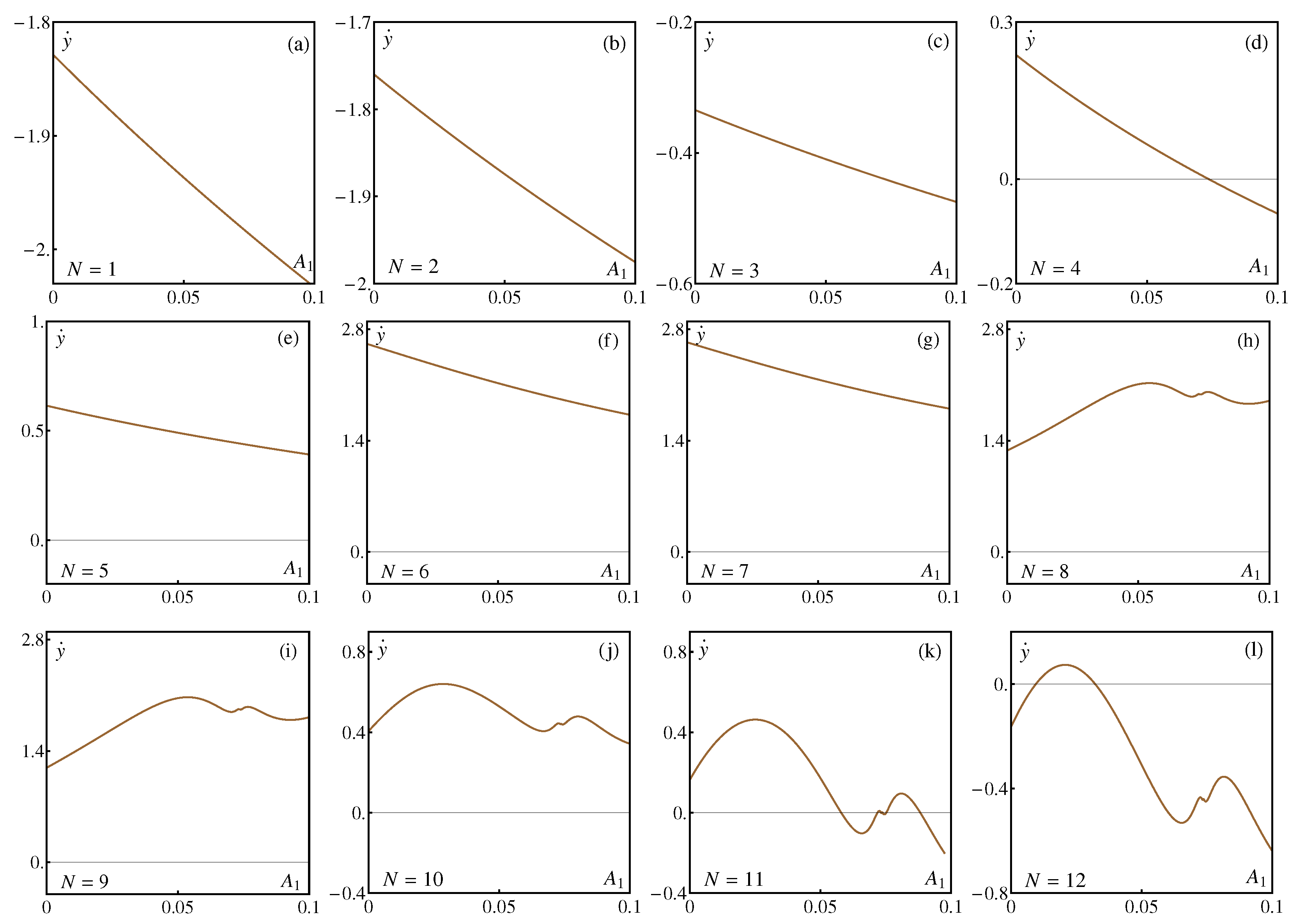
5. Numerical Results for Asymptotic Orbits at the Equilibrium Points
5.1. Homoclinic Orbits
5.2. Heteroclinic Orbits
6. Discussion and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Musielak, Z.; Quarles, B. Three Body Dynamics and Its Applications to Exoplanets; Springer Briefs in Astronomy; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Gao, F.B.; Zhang, W. A study on periodic solutions for the circular restricted three-body problem. Astron. J. 2014, 148, 116. [Google Scholar] [CrossRef]
- Voyatzis, G.; Antoniadou, K.I. On quasi-satellite periodic motion in asteroid and planetary dynamics. Celest. Mech. Dyn. Astron. 2018, 130, 59. [Google Scholar] [CrossRef]
- Voyatzis, G.; Tsiganis, K.; Antoniadou, K.I. Inclined asymmetric librations in exterior resonances. Celest. Mech. Dyn. Astr. 2018, 130, 29. [Google Scholar] [CrossRef]
- Burgos-Garcia, J.; Bengochea, A. Horseshoe orbits in the restricted four-body problem. Astrophys. Space Sci. 2017, 362, 212. [Google Scholar] [CrossRef]
- Pathak, N.; Abouelmagd, E.I.; Thomas, V.O. On higher order resonant periodic orbits in the photo-gravitational planar restricted three-body problem with oblateness. J. Astronaut. Sci. 2019, 66, 475–505. [Google Scholar] [CrossRef]
- Gao, F.; Wang, R. Bifurcation analysis and periodic solutions of the HD 191408 system with triaxial and radiative perturbations. Universe 2020, 6, 35. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, Y.; Shi, Y.; Xu, S. Libration points and periodic orbit families near a binary asteroid system with different shapes of the secondary. Acta Astronaut. 2020, 177, 15–29. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, S. Equilibrium points and associated periodic orbits in the gravity of binary asteroid systems: (66391) 1999 KW4 as an example. Celest. Mech. Dyn. Astr. 2018, 130, 32. [Google Scholar]
- Hill, G.W. Researches in the lunar theory. Amer. J. Math. 1878, 1, 5–26. [Google Scholar] [CrossRef]
- Hénon, M. Numerical exploration of the restricted problem V. Hill’s case: Periodic orbits and their stability. Astron. Astrophys. 1969, 1, 223–238. [Google Scholar]
- Hénon, M. Vertical stability of periodic orbits in the restricted problem II. Hill’s case. Astron. Astrophys. 1974, 30, 317–321. [Google Scholar]
- Zagouras, C.; Markellos, V.V. Three-dimensional periodic solutions around equilibrium points in Hill’s problem. Celest. Mech. 1985, 35, 257–267. [Google Scholar] [CrossRef]
- Batkhin, A.B.; Batkhina, N.V. Hierarchy of periodic solutions families of spatial Hill’s problem. Sol. Syst. Res. 2009, 43, 178–183. [Google Scholar] [CrossRef]
- Kalantonis, V. Numerical investigation for periodic orbits in the Hill three-body problem. Universe 2020, 6, 72. [Google Scholar] [CrossRef]
- Aydin, C. The Conley-Zehnder indices of the spatial Hill three-body problem. Celest. Mech. Dyn. Astr. 2023, 135, 32. [Google Scholar] [CrossRef]
- Xu, X. Determination of the doubly symmetric periodic orbits in the restricted three-body problem and Hill’s lunar problem. Celest. Mech. Dyn. Astr. 2023, 135, 8. [Google Scholar] [CrossRef]
- Markellos, V.V.; Roy, A.E.; Velgakis, M.J.; Kanavos, S.S. A photogravitational Hill problem and radiation effects on Hill stability of orbits. Astrophys. Space Sci. 2000, 271, 293–301. [Google Scholar] [CrossRef]
- Kanavos, S.S.; Markellos, V.V.; Roy, A.E.; Perdios, E.A.; Douskos, C.N. The photogravitational Hill problem: Numerical exploration. Earth Moon Planets 2002, 91, 223–241. [Google Scholar] [CrossRef]
- Tsirogiannis, G.A.; Perdios, E.A.; Markellos, V.V. Improved grid search method: An efficient tool for global computation of periodic orbits: Application to Hill’s problem. Celest. Mech. Dyn. Astr. 2009, 103, 49–78. [Google Scholar] [CrossRef]
- Vincent, A.E.; Tsirogiannis, G.A.; Perdiou, A.E.; Kalantonis, V.S. Out-of-plane equilibrium points in the photogravitational Hill three-body problem. Symmetry 2024, 16, 1374. [Google Scholar] [CrossRef]
- Markellos, V.V.; Roy, A.E.; Perdios, E.A.; Douskos, C.N. A Hill problem with oblate primaries and effect of oblateness on Hill stability of orbits. Astrophys. Space Sci. 2001, 278, 295–304. [Google Scholar] [CrossRef]
- Kalantonis, V.S.; Markellos, V.V.; Perdios, E.A. Computing periodic orbits of the three-body problem: Effective convergence of Newton’s method on the surface of section. Astrophys. Space Sci. 2005, 298, 441–451. [Google Scholar] [CrossRef]
- Perdiou, A.E.; Markellos, V.V.; Douskos, C.N. The Hill problem with oblate secondary: Numerical exploration. Earth Moon Planets 2005, 97, 127–145. [Google Scholar] [CrossRef]
- Perdiou, A.E. Multiple periodic orbits in the Hill problem with oblate secondary. Earth Moon Planets 2008, 103, 105–118. [Google Scholar] [CrossRef]
- De Bustos, M.T.; Lopez, M.A.; Martinez, R.; Vera, J.A. On the periodic solutions emerging from the equilibria of the Hill Lunar problem with oblateness. Qual. Theory Dyn. Syst. 2018, 17, 331–344. [Google Scholar] [CrossRef]
- Moneer, E.M.; Alanazi, M.; Elaissi, S.; Allawi, Y.; Dubeibe, F.L.; Zotos, E.E. Orbital dynamics in the Hill problem with oblateness. Results Phys. 2023, 53, 106936. [Google Scholar] [CrossRef]
- Bouaziz, F.; Ansari, A.A. Perturbed Hill’s problem with variable mass. Astron. Nachr. 2021, 342, 666–674. [Google Scholar] [CrossRef]
- Abouelmagd, E.I.; Kalantonis, V.S.; Perdiou, A.E. A quantized Hill’s dynamical system. Adv. Astron. 2021, 2021, 9963761. [Google Scholar] [CrossRef]
- Abouelmagd, E.I.; Alhowaity, S.; Diab, Z.; Guirao, J.L.G.; Shehata, M.H. On the periodic solutions for the perturbed spatial quantized Hill problem. Mathematics 2022, 10, 614. [Google Scholar] [CrossRef]
- Ansari, A.A.; Alhowaity, S.; Abouelmagd, E.I.; Sahdev, S.K. Analysis of equilibrium points in quantized Hill system. Mathematics 2022, 10, 2186. [Google Scholar] [CrossRef]
- Vincent, A.E.; Abouelmagd, E.I.; Perdios, E.A.; Kalantonis, V.S. Numerical exploration of the quantized Hill problem dynamics. Chaos Soliton Fract. 2024, 181, 114688. [Google Scholar] [CrossRef]
- Abouelmagd, E.I. New model for Hill’s problem in the framework of continuation fractional potential. Math. Comput. Appl. 2024, 29, 34. [Google Scholar] [CrossRef]
- Abouelmagd, E.I.; Alshaery, A.A.; Gao, F. New dynamical system for circular satellites relative motion. Chaos Soliton Fract. 2024, 182, 114879. [Google Scholar] [CrossRef]
- Ibrahim, M.K.; Rabeh, T.; Abouelmagd, E.I. Dynamical properties of perturbed Hill’s system. Math. Comput. Appl. 2024, 29, 66. [Google Scholar] [CrossRef]
- Deprit, A.; Henrard, J. Symmetric doubly asymptotic orbits in the restricted three-body problem. Astron. J. 1965, 70, 271–274. [Google Scholar] [CrossRef]
- Perdios, E.A.; Markellos, V.V. Symmetric doubly–asymptotic periodic orbits at collinear equilibria. Astrophys. Space Sci. 1990, 166, 129–149. [Google Scholar] [CrossRef]
- Perdios, E.A. Non-symmetric doubly-asymptotic orbits at the outer collinear equilibrium point L3. Astrophys. Space Sci. 1993, 199, 185–188. [Google Scholar] [CrossRef]
- Perdios, E.A.; Ragos, O.; Perdiou, A.E.; Vrahatis, M.N. Symmetric doubly asymptotic orbits in the photogravitational restricted three-body problem. Nonlinear Anal. 2001, 47, 3443–3448. [Google Scholar] [CrossRef]
- Kalantonis, V.S.; Douskos, C.N.; Perdios, E.A. Numerical determination of homoclinic and heteroclinic orbits at collinear equilibria in the restricted three-body problem with oblateness. Celest. Mech. Dyn. Astr. 2006, 94, 135–153. [Google Scholar] [CrossRef]
- Perdios, E.A.; Ragos, O. Asymptotic and periodic motion around collinear equilibria in Chermnykh’s problem. Astron. Astrophys. 2004, 414, 361–371. [Google Scholar] [CrossRef]
- Sharma, R.K.; Subba Rao, P.V. Stationary solutions and their characteristic exponents in the restricted three–body problem when the more massive primary is an oblate spheroid. Celest. Mech. 1976, 13, 137–149. [Google Scholar] [CrossRef]
- Abouelmagd, E.I.; Alhothuali, M.S.; Guirao, J.L.G.; Malaikah, H.M. The effect of zonal harmonic coefficients in the framework of the restricted three body problem. Adv. Space Res. 2015, 55, 1660–1672. [Google Scholar] [CrossRef]
- Zotos, E.E.; Suraj, M.S.; Aggarwal, R.; Mittal, A. Orbit classification in the Copenhagen problem with oblate primaries. Astron. Nachr. 2019, 340, 760–770. [Google Scholar] [CrossRef]
- Suraj, M.S.; Alhowaity, S.S.; Aggarwal, R.; Asique, M.C.; Mittal, A.; Jain, M. On the topology of basins of convergence linked to libration points in the modified R3BP with oblateness. New Astron. 2022, 94, 101776. [Google Scholar] [CrossRef]
- Szebehely, V. Theory of Orbits; Academic Press: New York, NY, USA, 1967. [Google Scholar]
- Papadakis, K.E. The planar Hill problem with oblate primary. Astrophys. Space Sci. 2004, 293, 271–287. [Google Scholar] [CrossRef]




| N | C | |||
|---|---|---|---|---|
| 7 | ||||
| 7 | ||||
| 7 | ||||
| 8 | ||||
| 8 |
| N | C | |||
|---|---|---|---|---|
| 4 | ||||
| 11 | ||||
| 11 | ||||
| 11 | ||||
| 11 | ||||
| 11 | ||||
| 11 | ||||
| 11 | ||||
| 12 | ||||
| 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalantonis, V.S. Exploring the Influence of Oblateness on Asymptotic Orbits in the Hill Three-Body Problem. AppliedMath 2025, 5, 30. https://doi.org/10.3390/appliedmath5010030
Kalantonis VS. Exploring the Influence of Oblateness on Asymptotic Orbits in the Hill Three-Body Problem. AppliedMath. 2025; 5(1):30. https://doi.org/10.3390/appliedmath5010030
Chicago/Turabian StyleKalantonis, Vassilis S. 2025. "Exploring the Influence of Oblateness on Asymptotic Orbits in the Hill Three-Body Problem" AppliedMath 5, no. 1: 30. https://doi.org/10.3390/appliedmath5010030
APA StyleKalantonis, V. S. (2025). Exploring the Influence of Oblateness on Asymptotic Orbits in the Hill Three-Body Problem. AppliedMath, 5(1), 30. https://doi.org/10.3390/appliedmath5010030






