Evaluation of Alternative Models for Respiration Rate of Ready-to-Eat Strawberry (cv. ‘Ágata’) †
Abstract
1. Introduction
2. Material and Methods
2.1. Strawberries
2.2. Experimental Setup
2.3. Respiration Rate Assessment
2.4. Statistical Analysis, Respiration Rate Modelling and Selection
2.5. Validation Experiments
3. Results and Discussion
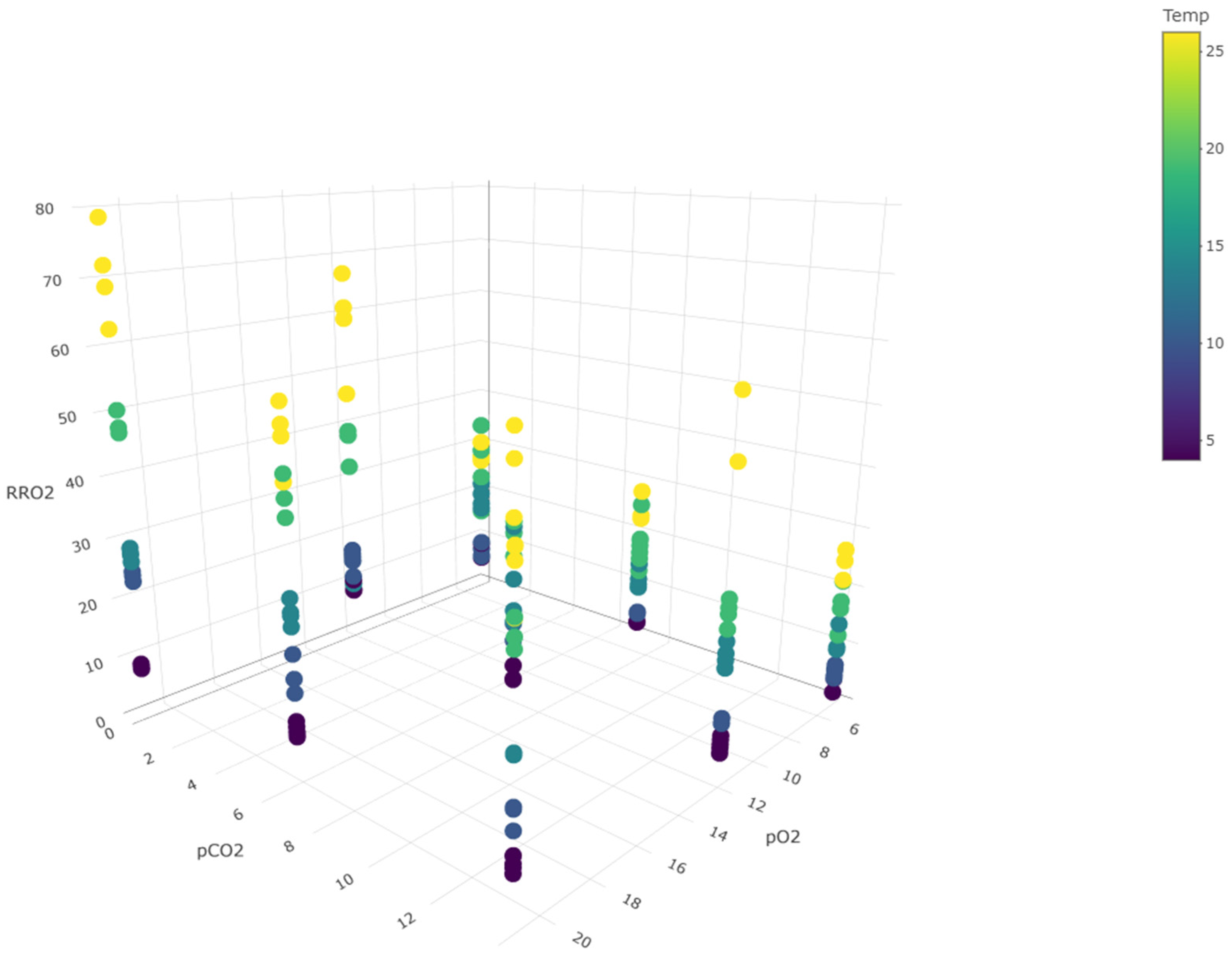
3.1. Gaseous Composition and Temperature Influence on Respiration Rate
3.2. RRO2 Models: Influence of O2, CO2 and Temperature
3.3. Model Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Giampieri, F.; Tulipani, S.; Alvarez-Suarez, J.M.; Quiles, J.L.; Mezzetti, B.; Battino, M. The strawberry: Composition, nutritional quality, and impact on human health. Nutrition 2012, 28, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Parvez, S.; Wani, I.A. Postharvest Biology and Technology of Strawberry. In Postharvest Biology and Technology of Temperate Fruits; Mir, S., Shah, M., Mir, M., Eds.; Springer Cham: Gewerbestrasse, Switzerland, 2018; pp. 331–348. [Google Scholar] [CrossRef]
- Mezzetti, B.; Balducci, F.; Capocasa, F.; Zhong, C.-F.; Cappelletti, R.; Di Vittori, L.; Mazzoni, L.; Giampieri, F.; Battino, M. Breeding Strawberry for Higher Phytochemicals Content and Claim It: Is It Possible? Int. J. Fruit Sci. 2016, 16, 194–206. [Google Scholar] [CrossRef]
- Rashvand, M.; Matera, A.; Altieri, G.; Genovese, F.; Fadiji, T.; Opara, U.L.; Mohamadifar, M.A.; Feyissa, A.H.; Di Renzo, G.C. Recent advances in the potential of modeling and simulation to assess the performance of modified atmosphere packaging (MAP) systems for the fresh agricultural product: Challenges and development. Trends Food Sci. Technol. 2023, 136, 48–63. [Google Scholar] [CrossRef]
- Schudel, S.; Shrivastava, C.; Rebeaud, S.G.; Karafka, L.; Shoji, K.; Onwude, D.; Defraeye, T. Combining experiments and mechanistic modeling to compare ventilated packaging types for strawberries from farm to retailer. Food Packag. Shelf Life 2022, 34, 100944. [Google Scholar] [CrossRef]
- Talasila, P.C.; Chau, K.V.; Brecht, J.K. Effects of Gas Concentrations and Temperature on O2 Consumption of Strawberries. Trans. Am. Soc. Agric. Eng. 1992, 35, 221–224. [Google Scholar] [CrossRef]
- Hertog, M.L.A.T.M.; Boerrigter, H.A.M.; Boogaard, G.J.P.M.; Tijskens, L.M.M.; van Schaik, A.C.R. Predicting keeping quality of strawberries (cv. `Elsanta’) packed under modified atmospheres: An integrated model approach. Postharvest Biol. Technol. 1999, 15, 1–12. [Google Scholar] [CrossRef]
- Barrios, S.; Lema, P.; Lareo, C. Modeling respiration rate of strawberry (cv. San Andreas) for Modified Atmosphere Packaging Design. Int. J. Food Prop. 2014, 17, 2039–2051. [Google Scholar] [CrossRef]
- Fonseca, S.C.; Oliveira, F.A.; Brecht, J.K. Modelling respiration rate of fresh fruits and vegetables for modified atmosphere packages: A review. J. Food Eng. 2002, 52, 99–119. [Google Scholar] [CrossRef]
- Badillo, G.M.; Segura-Ponce, L.A. Classic and Reaction-Diffusion Models Used in Modified Atmosphere Packaging (MAP) of Fruit and Vegetables. Food Eng. Rev. 2020, 12, 209–228. [Google Scholar] [CrossRef]
- Hertog, M.L.A.T.M.; Peppelenbos, H.W.; Evelo, R.G.; Tijskens, L.M.M. A dynamic and generic model of gas exchange of respiring produce: The effects of oxygen, carbon dioxide and temperature. Postharvest Biol. Technol. 1998, 14, 335–349. [Google Scholar] [CrossRef]
- Peleg, M.; Corradini, M.G.; Normand, M.D. Kinetic models of complex biochemical reactions and biological processes. Chem. Ing. Tech. 2004, 76, 413–423. [Google Scholar] [CrossRef]
- Irazoqui, M. Experimental respiration data used for model calibration. Universidad de la República: Montevideo, Uruguay, 2024; unpublished data. [Google Scholar]
- Barbosa, N.C.; Vieira, R.A.M.; de Resende, E.D. Modeling the respiration rate of Golden papayas stored under different atmosphere conditions at room temperature. Postharvest Biol. Technol. 2018, 136, 152–160. [Google Scholar] [CrossRef]
- Tano, K.; Kamenan, A.; Arul, J. Respiration and transpiration characteristics of selected fresh fruits and vegetables. Agron. Afr. 2005, 17, 103–115. [Google Scholar] [CrossRef]
- Geysen, S.; Verlinden, B.E.; Conesa, A.; Leuven, K.U. Modelling Respiration of Strawberry (cv. ‘Elsanta’) as a Function of Temperature, Carbon Dioxide, Low and Superatmospheric Oxygen Concentrations. Respiration 2005, 5, 12–16. [Google Scholar]
- Jalali, A.; Linke, M.; Geyer, M.; Mahajan, P.V. Shelf life prediction model for strawberry based on respiration and transpiration processes. Food Packag. Shelf Life 2020, 25, 100525. [Google Scholar] [CrossRef]
- Matar, C.; Gaucel, S.; Gontard, N.; Guilbert, S.; Guillard, V. Predicting shelf life gain of fresh strawberries ‘ Charlotte cv’ in modified atmosphere packaging. Postharvest Biol. Technol. 2018, 142, 28–38. [Google Scholar] [CrossRef]

| Description | Equation * | Equation Number |
|---|---|---|
| Model 1—Langmuir adsorption (L) | (3) | |
| Model 2—Michaelis–Menten with no CO2 Inhibition (MM) | (4) | |
| Model 3—Michaelis–Menten with competitive CO2 Inhibition (CMM) | (5) | |
| Model 4—Michaelis–Menten with uncompetitive CO2 Inhibition (UMM) | (6) | |
| Model 5—Michaelis–Menten with non-competitive CO2 Inhibition (NMM) | (7) | |
| Model 6—Michaelis–Menten with competitive-uncompetitive CO2 Inhibition (MixMM) | (8) | |
| Model 7—Generalized linear (GLM) | (9) | |
| Model 8—Quadratic (QM) | (10) |
| Parameters | Value | Parameters | Value | Parameters | Value | |
|---|---|---|---|---|---|---|
| Quadratic model | 0.67 ± 3.55 (0.849) | 0.64 ± 0.40 (0.111) | −0.91 ± 0.40 (0.023) | |||
| −0.22 ± 0.428 (0.429) | −0.031 ± 0.013 (0.177) | 0.030 ± 0.017 (0.0778) | ||||
| 0.0325 ± 0.0073 (1.78 × 10−5) | 0.044 ± 0.022 (0.0492) | 0.026 ± 0.020 (0.194) | ||||
| 0.098 ± 0.012 (2.40 × 10−13) | −0.0046 ± 0.0014 (0.00106) | |||||
| R2 | 0.914 | |||||
| RMSE | 4.90 | |||||
| AIC | 1052.6 | |||||
| Parameters | Langmuir | Parameters | UMM | NMM | MixMM | |
| Power model | 2.18 ± 0.36 (7.88 × 10−9) | 2.18 ± 0.36 (7.88 × 10−9) | 1.98 ± 0.31 (1.83 × 10−9) | 2.13 ± 0.37 (3.59 × 10−8) | ||
| 1.237 ± 0.046 (<2 × 10−16) | 1.237 ± 0.046 (<2 × 10−16) | 1.232 ± 0.046 (<2 × 10−16) | 1.235 ± 0.046 (<2 × 10−16) | |||
| 0.0613 ± 0.0087 (3.97 × 10−11) | 16.3 ± 2.3 (3.97 × 10−11) | 13.0 ± 1.6 (3.51 × 10−13) | 15.4 ± 2.9 (3.20 × 10−7) | |||
| 0.0468 ± 0.0080 (2.52 × 10−8) | 21.4 ± 3.6 (2.52 × 10−8) | --- | 191.3 (0.699) | |||
| --- | 43.9 ± 6.3 (1.01 × 10−10) | --- | ||||
| --- | --- | 24 ± 10 (0.016) | ||||
| R2 | 0.911 | R2 | 0.911 | 0.911 | 0.912 | |
| RMSE | 4.96 | RMSE | 4.96 | 4.98 | 4.96 | |
| AIC | 1043.0 | AIC | 1043.0 | 1044.3 | 1044.8 | |
| Arrhenius model | 1.77 × 1011 (0.166) | 1.77 × 1011 (0.166) | 1.51 × 1011 (0.168) | 1.74 × 1011 (0.170) | ||
(kJ/mol) | 52.4 ± 1.7 (<2 × 10−16) | (kJ/mol) | 52.4 ± 1.7 (<2 × 10−16) | 52.3 ± 1.8 (<2 × 10−16) | 52.39 ± 0.24 (<2 × 10−16) | |
| 0.0641 ± 0.0092 (8.57× 10−11) | 15.6 ± 2.2 (8.57× 10−11) | 12.5 ± 1.6 (1.11 × 10−12) | 15.2 ± 2.9 (4.46 × 10−7) | |||
| 0.0460 ± 0.0080 (4.12 × 10−8) | 21.7 ± 3.8 (4.12 × 10−8) | --- | 406 (0.855) | |||
| --- | 44.0 ± 6.6 (2.89 × 10−10) | --- | ||||
| --- | --- | 23.1 ± 9.1 (0.012) | ||||
| R2 | 0.907 | R2 | 0.907 | 0.906 | 0.907 | |
| RMSE | 5.09 | RMSE | 5.09 | 5.11 | 5.09 | |
| AIC | 1051.7 | AIC | 1051.7 | 1053.6 | 1044.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Irazoqui, M.; Barrios, S.; Lema, P. Evaluation of Alternative Models for Respiration Rate of Ready-to-Eat Strawberry (cv. ‘Ágata’). Biol. Life Sci. Forum 2024, 40, 54. https://doi.org/10.3390/blsf2024040054
Irazoqui M, Barrios S, Lema P. Evaluation of Alternative Models for Respiration Rate of Ready-to-Eat Strawberry (cv. ‘Ágata’). Biology and Life Sciences Forum. 2024; 40(1):54. https://doi.org/10.3390/blsf2024040054
Chicago/Turabian StyleIrazoqui, Magdalena, Sofía Barrios, and Patricia Lema. 2024. "Evaluation of Alternative Models for Respiration Rate of Ready-to-Eat Strawberry (cv. ‘Ágata’)" Biology and Life Sciences Forum 40, no. 1: 54. https://doi.org/10.3390/blsf2024040054
APA StyleIrazoqui, M., Barrios, S., & Lema, P. (2024). Evaluation of Alternative Models for Respiration Rate of Ready-to-Eat Strawberry (cv. ‘Ágata’). Biology and Life Sciences Forum, 40(1), 54. https://doi.org/10.3390/blsf2024040054