On the Modeling of Isolation and Vibration Control Using Laminated Composite Materials †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fabrication of Specimens
2.2. Numerical Modal Analysis in SOLIDWORKS
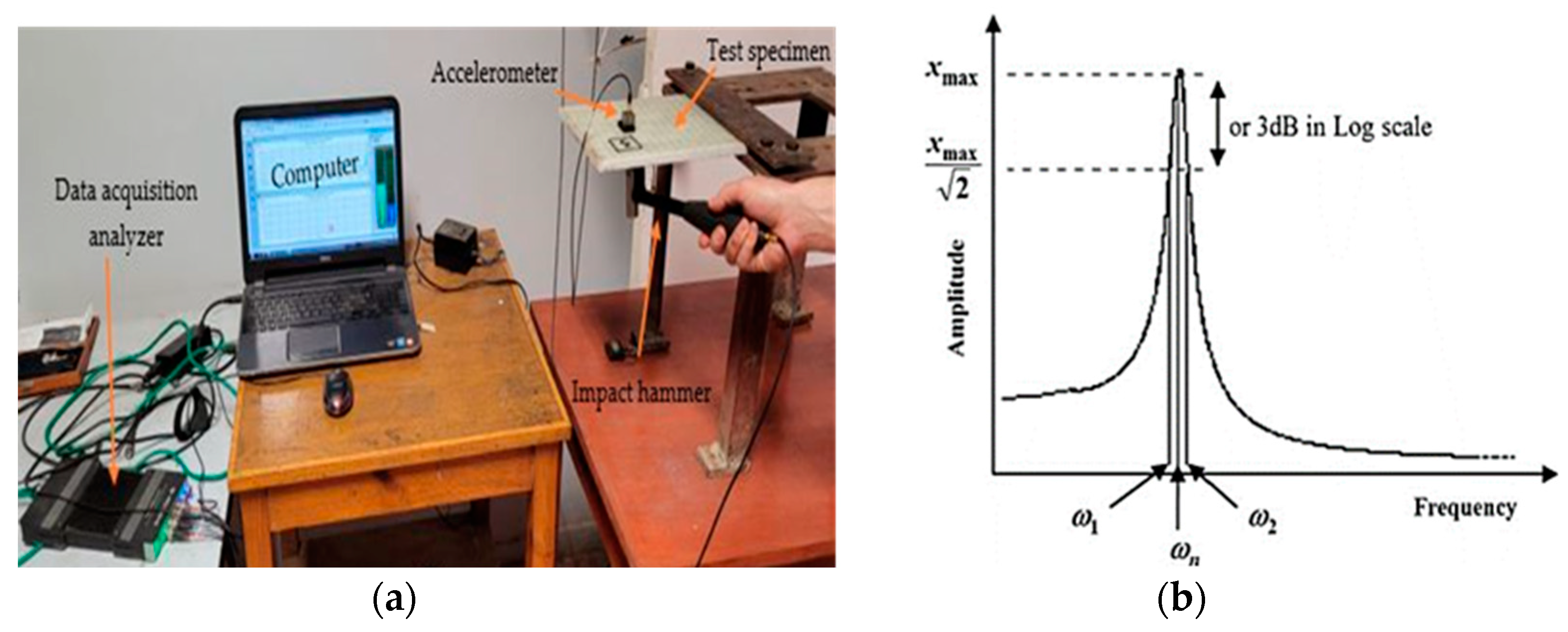
2.3. Experimental Modal Analysis
3. Results and Discussion
3.1. Numerical Analysis Results from SOLIDWORKS
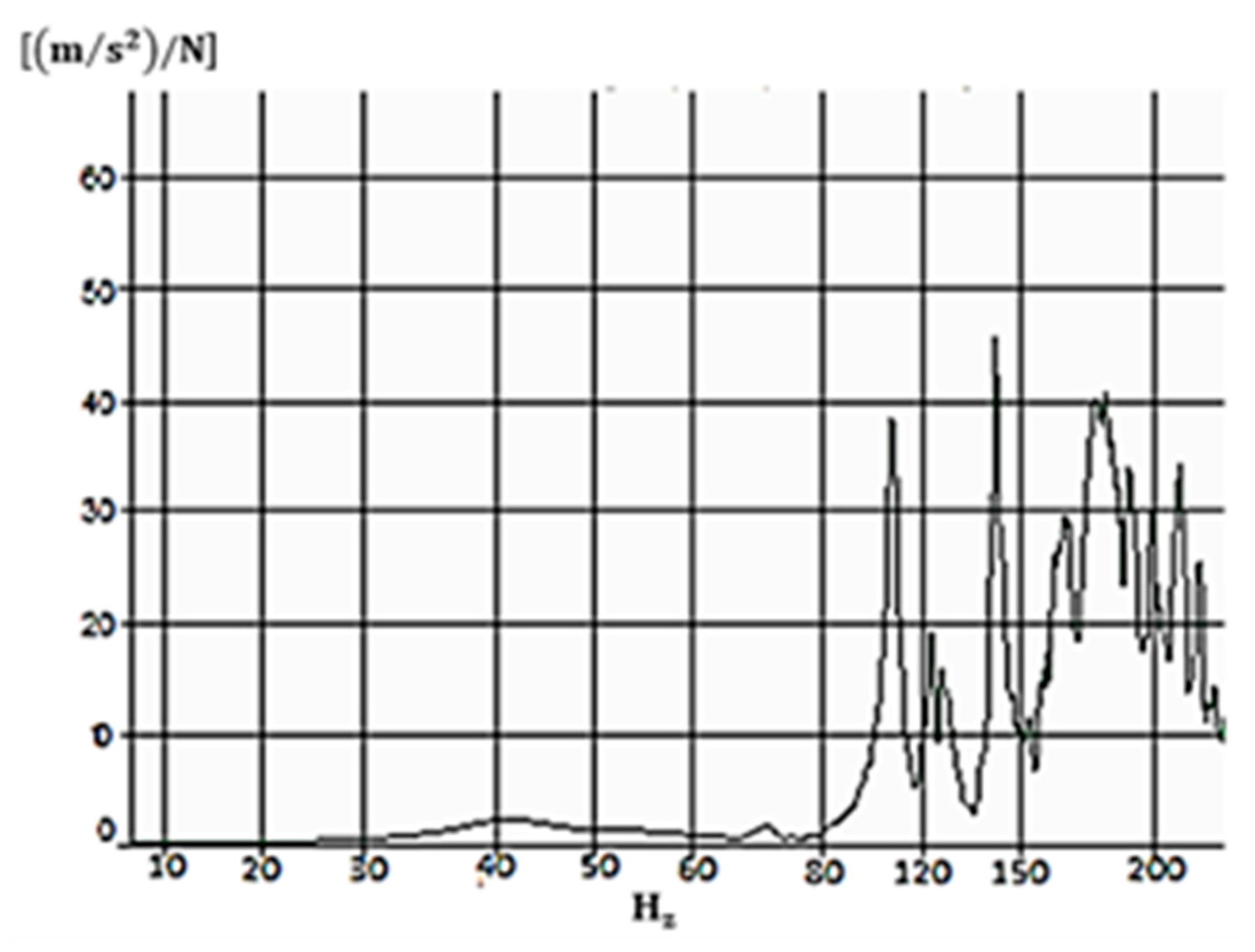
3.2. Experimental Modal Analysis Results
3.3. Comparison of Results
3.4. Optimum Configurations Results
1.528 A2 + 0.956 B2 + 0.44 C2 + 1.299 D2 + 1.101 E2 − 0.909 AB − 0.634 AC +
0.133 AD − 2.64 BC
0.171 C2 − 0.024 D2 − 0.257 E2 + 0.167 AB + 0.379 AC + 0.807 AD + 0.36 BC
4. Conclusions
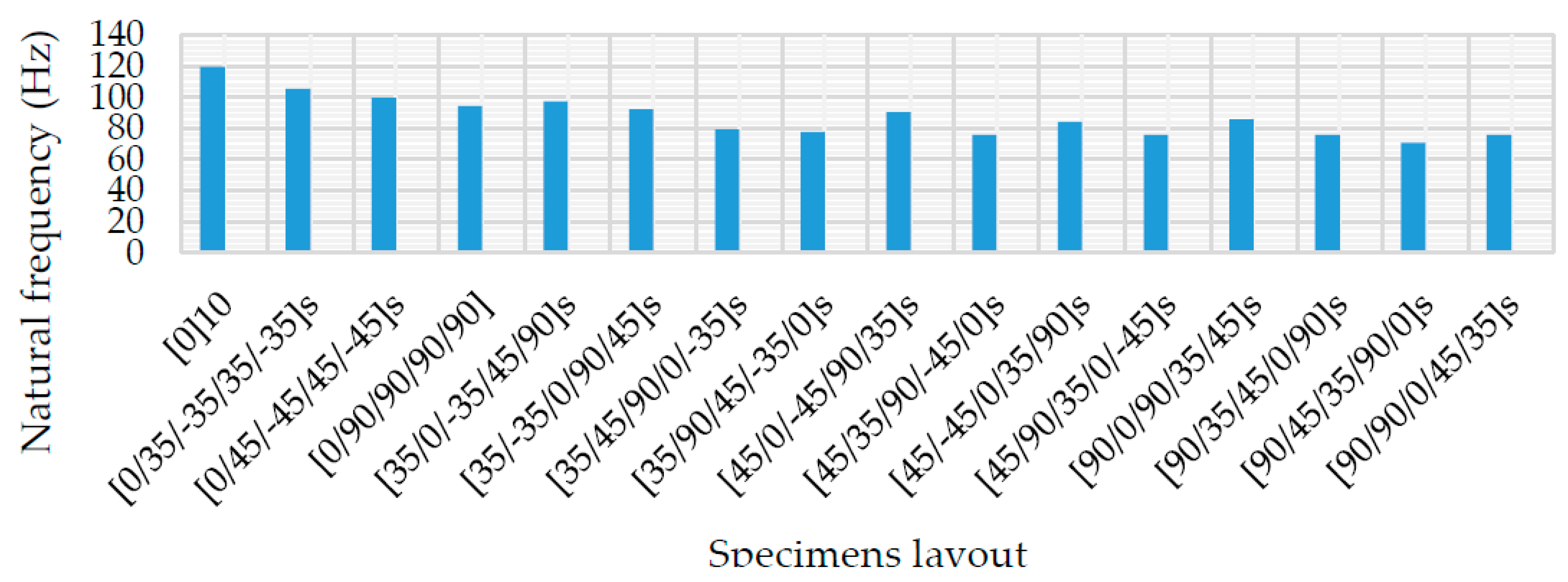
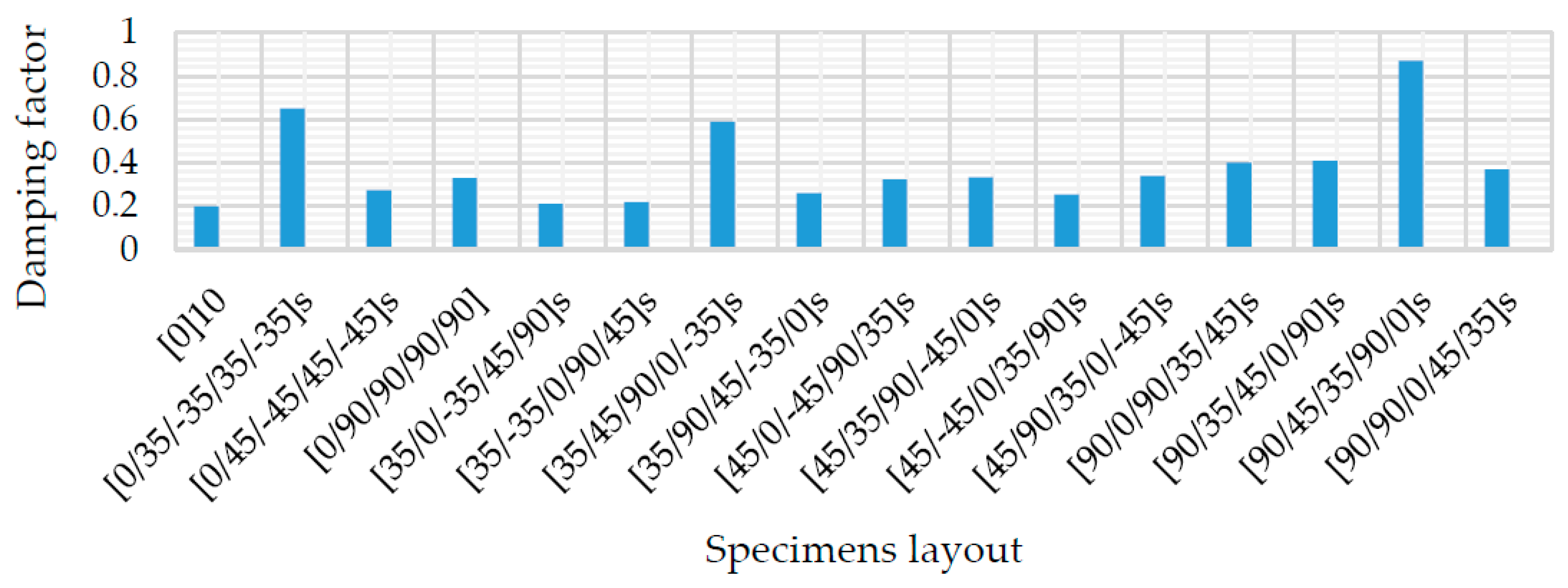
- The stacking sequence combination of [0]10 has the highest natural frequency and minimum damping ratio. However, the combination of [90/±45/±35/90/0]s has the lowest natural frequency and maximum damping ratio.
- The dynamic characteristics, such as natural frequency and damping capacity of the composite isolator, are sensitive to the outer lamina orientation, the frequency decreases while the damping increases by increasing the outer laminas angles from 0° to 90°.
- The optimum layouts for minimum frequency and maximum damping factor were identified using the Taguchi technique as follows [90/90/90/0/0]s and [90/±45/±35/90/±35]s, respectively.
- The experimental testing verified the numerical results, which prove that the suggested finite element model of the composite plate provides an efficient tool for the dynamic analysis of the composite structure.
- The verification test conducted at the optimum combination had shown a great agreement between the Taguchi method and FEM results, with a prediction error of 3.8% and 4% for frequency and damping, respectively.
- The Taguchi technique is a very efficient and practical tool for modeling and optimizing laminated composite plates to achieve the desired vibration control levels.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Verma, A.; Singh, V. Mechanical, Microstructural and Thermal Characterization of Epoxy-Based Human Hair-Reinforced Composites. J. Test. Eval. 2019, 47, 1193–1215. [Google Scholar] [CrossRef]
- Jain, N.; Singh, V.K.; Chauhan, S. Review on effect of chemical, thermal, additive treatment on mechanical properties of basalt fiber and their composites. J. Mech. Behav. Mater. 2017, 26, 205–211. [Google Scholar] [CrossRef]
- Verma, A.; Negi, P.; Singh, V.K. Experimental Analysis on Carbon Residuum Transformed Epoxy Resin: Chicken Feather Fiber Hybrid Composite. Polym. Compos. 2018, 40, 2690–2699. [Google Scholar] [CrossRef]
- Verma, A.; Negi, B.; Singh, V. Physical and Thermal Characterization of Chicken Feather Fiber and Crumb Rubber Reformed Epoxy Resin Hybrid Composite. Adv. Civ. Eng. Mater. 2018, 7, 538–557. [Google Scholar] [CrossRef]
- Verma, A.; Negi, P.; Singh, V.K. Experimental investigation of chicken feather fiber and crumb rubber reformed epoxy resin hybrid composite: Mechanical and microstructural characterization. J. Mech. Behav. Mater. 2018, 27, 1–24. [Google Scholar] [CrossRef]
- Verma, A.; Joshi, K.; Gour, A.; Singh, V. Mechanical Properties and Microstructure of Starch and Sisal Fiber Bio Composite Modified with Epoxy Resin. Mater. Perform. Charact. 2017, 6, 500–520. [Google Scholar]
- Verma, A.; Singh, C.; Singh, V.; Jain, N. Fabrication and Characterization of Chitosan coated Sisal Fiber—Phytagel modified Soy Protein based Green Composite. J. Compos. Mater. 2019, 53, 2481–2504. [Google Scholar] [CrossRef]
- Pandit, M.; Mukhopadhayay, S.H.M. Free Vibration Analysis of Laminated Composite Rectangular Plate Using Finite Element Method. J. Reinf. Plast. Compos. 2007, 26, 69–80. [Google Scholar] [CrossRef]
- Kumar, K.S.; Siva, I.; Jeyaraj, P.; Jappes, J.W.; Amico, S.C.; Rajini, N. Synergy of fiber length and content on free vibration and damping behavior of natural fiber reinforced polyester composite beams. Mater. Des. 2014, 56, 379–386. [Google Scholar]
- Sahoo, S.; Panda, S.; Singh, V. Experimental and numerical investigation of static and free vibration responses of woven glass/epoxy laminated composite plate. J. Mater.: Des. App. 2017, 231, 1–16. [Google Scholar] [CrossRef]
- Erkling, A.; Bulut, M.; Yeter, E. The Natural Frequency and Damping Properties of Glass/Carbon/Kevlar fibers. Sci. Eng. Compos. Mater. 2014, 22, 565–571. [Google Scholar]
- Lavate, R.S.; Patil, A.T.; Patil, A.M.; Hargude, N.V. Dynamic Response Analysis of Fiber Reinforced Composite Beam. J. Mech. Civ. Eng. 2013, 6, 38–47. [Google Scholar]
- Alexander, J.; Kumar, H.; Augustine, B. Frequency Response of Composite Laminates at Various Boundary Conditions. In Proceedings of the National Conference on “Advances In Modelling And Analysis Of Aerodynamic Systems (AMAAS-2013)”, Rourkela, India, 1–2 March 2013; pp. 11–15. [Google Scholar]
- Lee, S.K.; Kim, M.W.; Park, C.J.; Chol, M.J.; Kim, G.; Cho, J.-M.; Choi, C.-H. Effect of fiber orientation on acoustic and vibration response of a carbon fiber/epoxy composite plate: Natural vibration mode and sound radiation. Int. J. Mech. Sci. 2016, 117, 162–173. [Google Scholar] [CrossRef]
- Samal, P.K.; Pruthvi, I.; Suresh, B. Effect of fiber orientation on vibration response of glass epoxy composite beam. Mater. Today Proc. 2020, 43, 1519–1525. [Google Scholar] [CrossRef]
- Daoud, H.; Rebière, J.-L.; Makni, A.; Taktak, M.; El Mahi, A.; Haddar, M. Numerical and Experimental Characterization of the Dynamic Properties of Flax Fiber Reinforced Composites. Int. J. Appl. Mech. 2016, 8, 1650068. [Google Scholar] [CrossRef]
- Mahmoudi, S.; Kervoelen, A.; Robin, G.; Duigou, L.; Daya, E.; Cadou, J. Experimental and numerical investigation of the damping of flax–epoxy composite plates. Compos. Struct. 2018, 208, 426–433. [Google Scholar] [CrossRef]
- Rueppel, M.; Rion, J.; Dransfeld, C.; Fischer, C.; Masania, K. Damping of carbon fiber and flax fiber angle-ply composite laminates. Compos. Sci. Technol. 2017, 146, 1–9. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, H.; Chen, C.; Zhang, Z. Structure and modal analysis of carbon fiber reinforced polymer raft frame. J. Low Freq. Noise Vib. Act. Control 2018, 37, 577–589. [Google Scholar]
- Khodadadi, A.; Liaghat, G.; Shahgholian-Ghahfarokhi, D.; Chizari, M.; Wang, B. Numerical and experimental investigation of impact on bilayer aluminum-rubber composite plate. Thin-Walled Struct. 2020, 149, 106673. [Google Scholar] [CrossRef]
- Taherzadeh-Fard, A.; Liaghat, G.; Ahmadi, H.; Razmkhah, O.; Charandabi, S.C.; Zarezadeh-Mehrizi, M.A.; Khodadadi, A. Experimental and numerical investigation of the impact response of elastomer layered fiber metal laminates (EFMLs). Compos. Struct. 2020, 245, 112264. [Google Scholar] [CrossRef]
- Khodadadi, A.; Liaghat, G.; Bahramian, A.R.; Ahmadi, H.; Anani, Y.; Asemani, S.; Razmkhah, O. High velocity impact behavior of Kevlar/rubber and Kevlar/epoxy composites: A comparative study. Compos. Struct. 2019, 216, 159–167. [Google Scholar] [CrossRef]
- Khodadadi, A.; Liaghat, G.; Ahmadi, H.; Bahramian, A.R.; Razmkhah, O. Impact response of Kevlar/rubber composite. Compos. Sci. Technol. 2019, 184, 107880. [Google Scholar] [CrossRef]


| Run No. | Input Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1st Ply (A) | 2nd Ply (B) | 3rd Ply (C) | 4th Ply (D) | 5th Ply (E) | ||||||
| Coded | Actual | Coded | Actual | Coded | Actual | Coded | Actual | Coded | Actual | |
| 1 | 1 | 0° | 1 | 0° | 1 | 0° | 1 | 0° | 1 | 0° |
| 2 | 1 | 0° | 2 | ±35° | 2 | ±35° | 2 | ±35° | 2 | ±35° |
| 3 | 1 | 0° | 3 | ±45° | 3 | ±45° | 3 | ±45° | 3 | ±45° |
| 4 | 1 | 0° | 4 | 90° | 4 | 90° | 4 | 90° | 4 | 90° |
| 5 | 2 | ±35° | 1 | 0° | 2 | ±35° | 3 | ±45° | 4 | 90° |
| 6 | 2 | ±35° | 2 | ±35° | 1 | 0° | 4 | 90° | 3 | ±45° |
| 7 | 2 | ±35° | 3 | ±45° | 4 | 90° | 1 | 0° | 2 | ±35° |
| 8 | 2 | ±35° | 4 | 90° | 3 | ±45° | 2 | ±35° | 1 | 0° |
| 9 | 3 | ±45° | 1 | 0° | 3 | ±45° | 4 | 90° | 2 | ±35° |
| 10 | 3 | ±45° | 2 | ±35° | 4 | 90° | 3 | ±45° | 1 | 0° |
| 11 | 3 | ±45° | 3 | ±45° | 1 | 0° | 2 | ±35° | 4 | 90° |
| 12 | 3 | ±45° | 4 | 90° | 2 | ±35° | 1 | 0° | 3 | ±45° |
| 13 | 4 | 90° | 1 | 0° | 4 | 90° | 2 | ±35° | 3 | ±45° |
| 14 | 4 | 90° | 2 | ±35° | 3 | ±45° | 1 | 0° | 4 | 90° |
| 15 | 4 | 90° | 3 | ±45° | 2 | ±35° | 4 | 90° | 1 | 0° |
| 16 | 4 | 90° | 4 | 90° | 1 | 0° | 3 | ±45° | 2 | ±35° |
| E11 (Pa) | E22 (Pa) | E33 (Pa) | G12 (Pa) | G13 (Pa) | G23 (Pa) | V12 | V13 | V23 | ρ (g/m3) |
|---|---|---|---|---|---|---|---|---|---|
| 4.46 × 1010 | 1.21 × 1010 | 1.21 × 1010 | 4.1 × 109 | 4.1 × 109 | 4.18 × 109 | 0.264 | 0.264 | 0.445 | 2.03 × 106 |
| Run No. | Specimen Layout | Numerical Natural Frequency (Hz) | Experimental Natural Frequency (Hz) | Damping Factor ζ |
|---|---|---|---|---|
| 1 | [0]10 | 121.43 | 119.56 | 0.2 |
| 2 | [0/±35/±35/±35/±35]s | 106.3 | 105.5 | 0.65 |
| 3 | [0/±45/±45/±45/±45]s | 101.03 | 99.7 | 0.274 |
| 4 | [0/90/90/90/90]s | 96.328 | 94.23 | 0.33 |
| 5 | [±35/0/±35/±45/90]s | 98.457 | 97.64 | 0.21 |
| 6 | [±35/±35/0/90/±45]s | 93.811 | 92.33 | 0.22 |
| 7 | [±35/±45/90/0/±35]s | 80.505 | 79.32 | 0.59 |
| 8 | [±35/90/±45/±35/0]s | 78.725 | 77.69 | 0.26 |
| 9 | [±45/0/±45/90/±35]s | 91.47 | 90.64 | 0.325 |
| 10 | [±45/±35/90/±45/0]s | 76.228 | 75.82 | 0.332 |
| 11 | [±45/±45/0/±35/90]s | 85.14 | 84.17 | 0.254 |
| 12 | [±45/90/±35/0/±45]s | 76.322 | 75.91 | 0.34 |
| 13 | [90/0/90/±35/±45]s | 86.414 | 85.84 | 0.4 |
| 14 | [90/±35/±45/0/90]s | 76.581 | 76 | 0.41 |
| 15 | [90/±45/±35/90/0]s | 71.352 | 70.94 | 0.87 |
| 16 | [90/90/0/±45/±35]s | 76.233 | 75.96 | 0.37 |
| Factor | Frequency Results | Damping Results | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Average η by Factor Level (dB) | Average η by Factor Level (dB) | |||||||||
| 1 | 2 | 3 | 4 | Rank | 1 | 2 | 3 | 4 | Rank | |
| A | −40.5 | −38.84 | −38.28 | −37.78 * | 1 | 10.662 | 9.252 | 9.847 | 13.6132 * | 2 |
| B | −39.88 | −38.83 | −38.47 | −38.22 * | 2 | 8.989 | 11.446 | 12.773 * | 10.166 | 4 |
| C | −39.37 | −38.78 | −38.73 | −38.54 * | 3 | 8.386 | 13.031 * | 9.895 | 12.063 | 1 |
| D | −38.78 * | −38.95 | −38.81 | −38.85 | 5 | 11.384 | 11.174 | 9.254 | 11.562 * | 5 |
| E | −38.58 * | −38.88 | −38.98 | −38.96 | 4 | 11.187 | 13.319 * | 9.576 | 9.292 | 3 |
| Optimum Condition | Combination of Input Parameters | Verification Test Result | Model Prediction | Prediction Error (%) | |
|---|---|---|---|---|---|
| Min Freq. | A4B4C4D1E1 | [90/90/90/0/0]s | 68.578 | 65.978 | 3.8 |
| Max Damping | A4B3C2D4E2 | [90/±45/±35/90/±35]s | 0.97 | 0.93 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghoneam, S.; Hamada, A.; Elkholy, A. On the Modeling of Isolation and Vibration Control Using Laminated Composite Materials. Phys. Sci. Forum 2022, 4, 31. https://doi.org/10.3390/psf2022004031
Ghoneam S, Hamada A, Elkholy A. On the Modeling of Isolation and Vibration Control Using Laminated Composite Materials. Physical Sciences Forum. 2022; 4(1):31. https://doi.org/10.3390/psf2022004031
Chicago/Turabian StyleGhoneam, Sobhy, Ahmed Hamada, and Ahmed Elkholy. 2022. "On the Modeling of Isolation and Vibration Control Using Laminated Composite Materials" Physical Sciences Forum 4, no. 1: 31. https://doi.org/10.3390/psf2022004031
APA StyleGhoneam, S., Hamada, A., & Elkholy, A. (2022). On the Modeling of Isolation and Vibration Control Using Laminated Composite Materials. Physical Sciences Forum, 4(1), 31. https://doi.org/10.3390/psf2022004031





