A Framework to Model the Wind-Induced Losses in Buildings during Hurricanes
Abstract
:1. Introduction
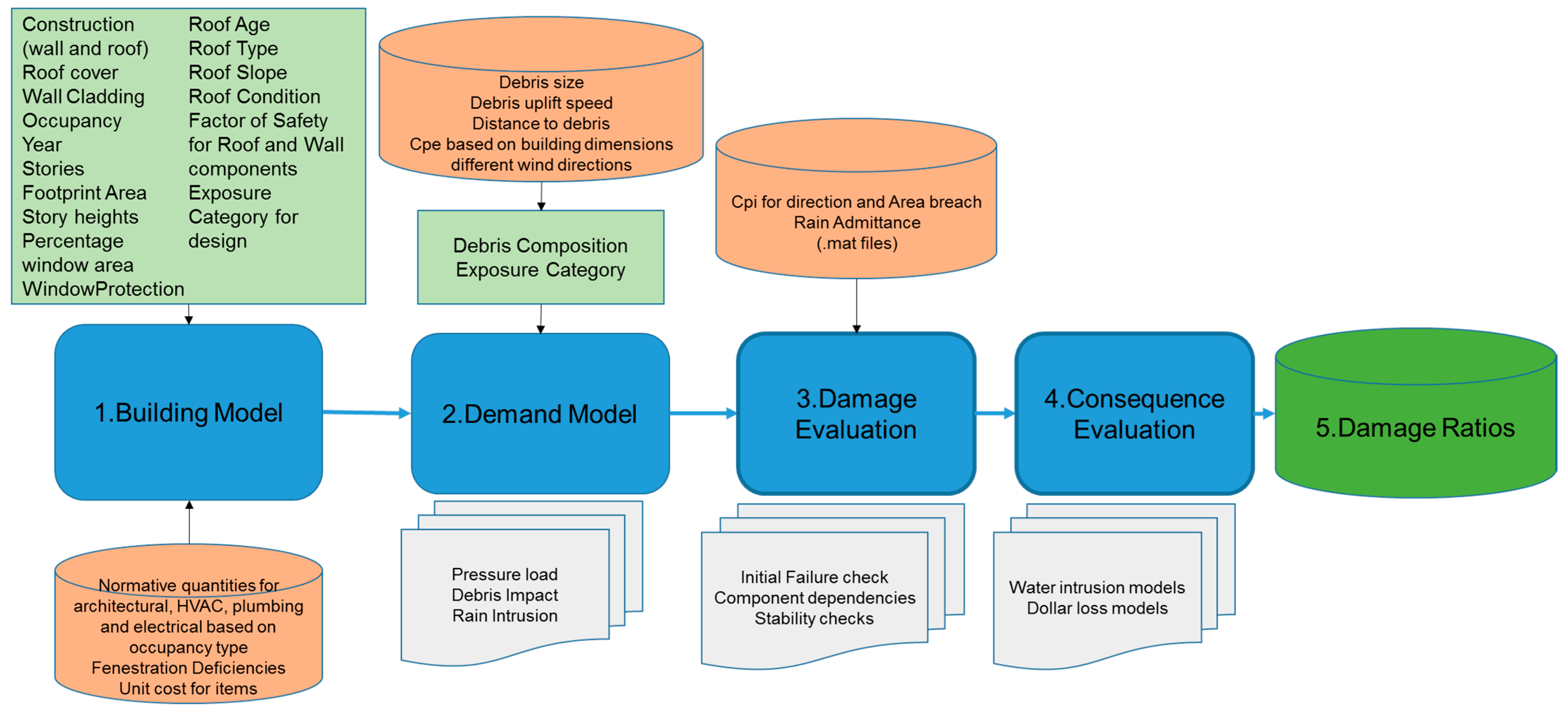
2. Materials and Methods
2.1. Building Model
2.1.1. Variables in the Building Model
Mean Resistance Capacity for Wind Uplift
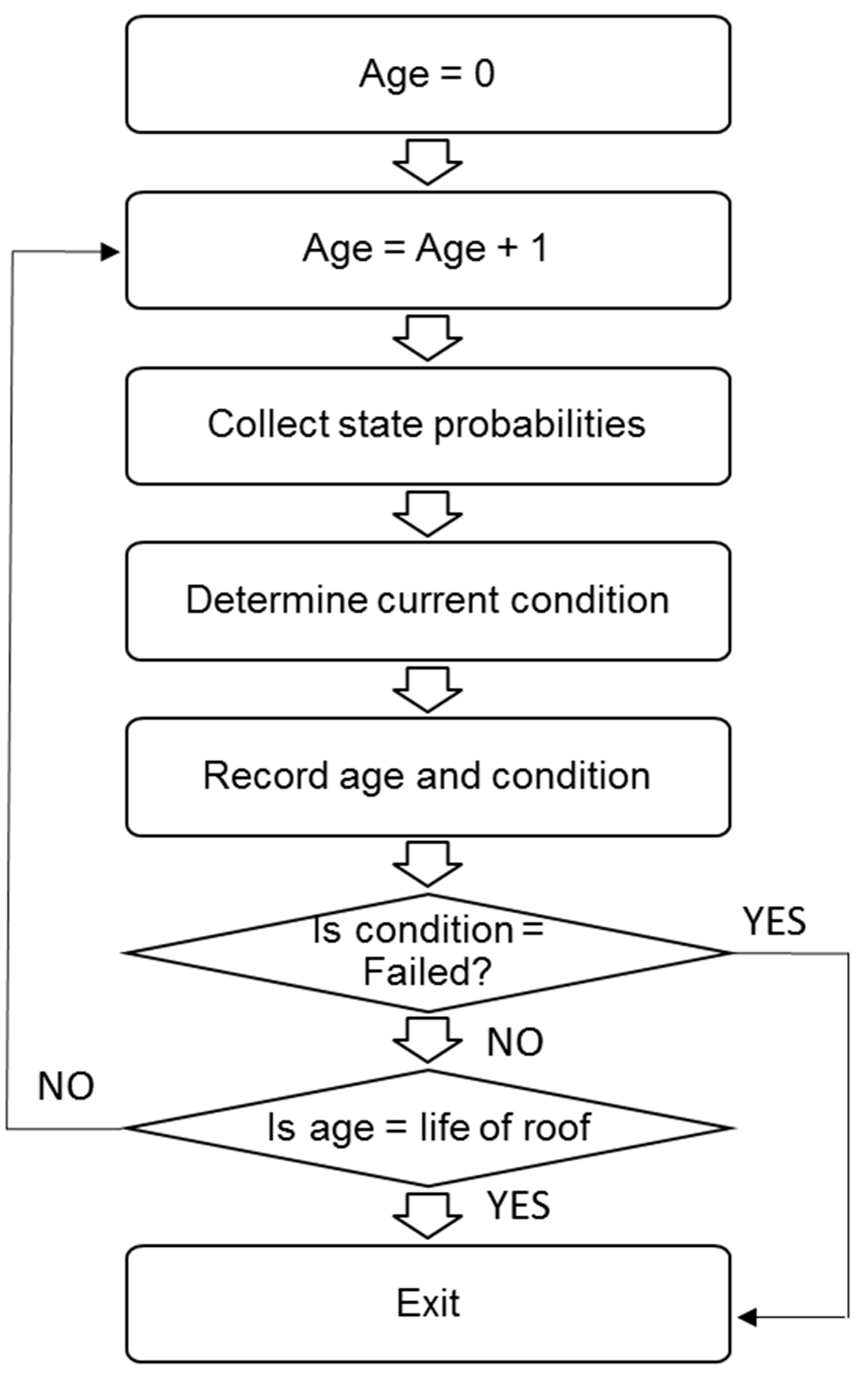
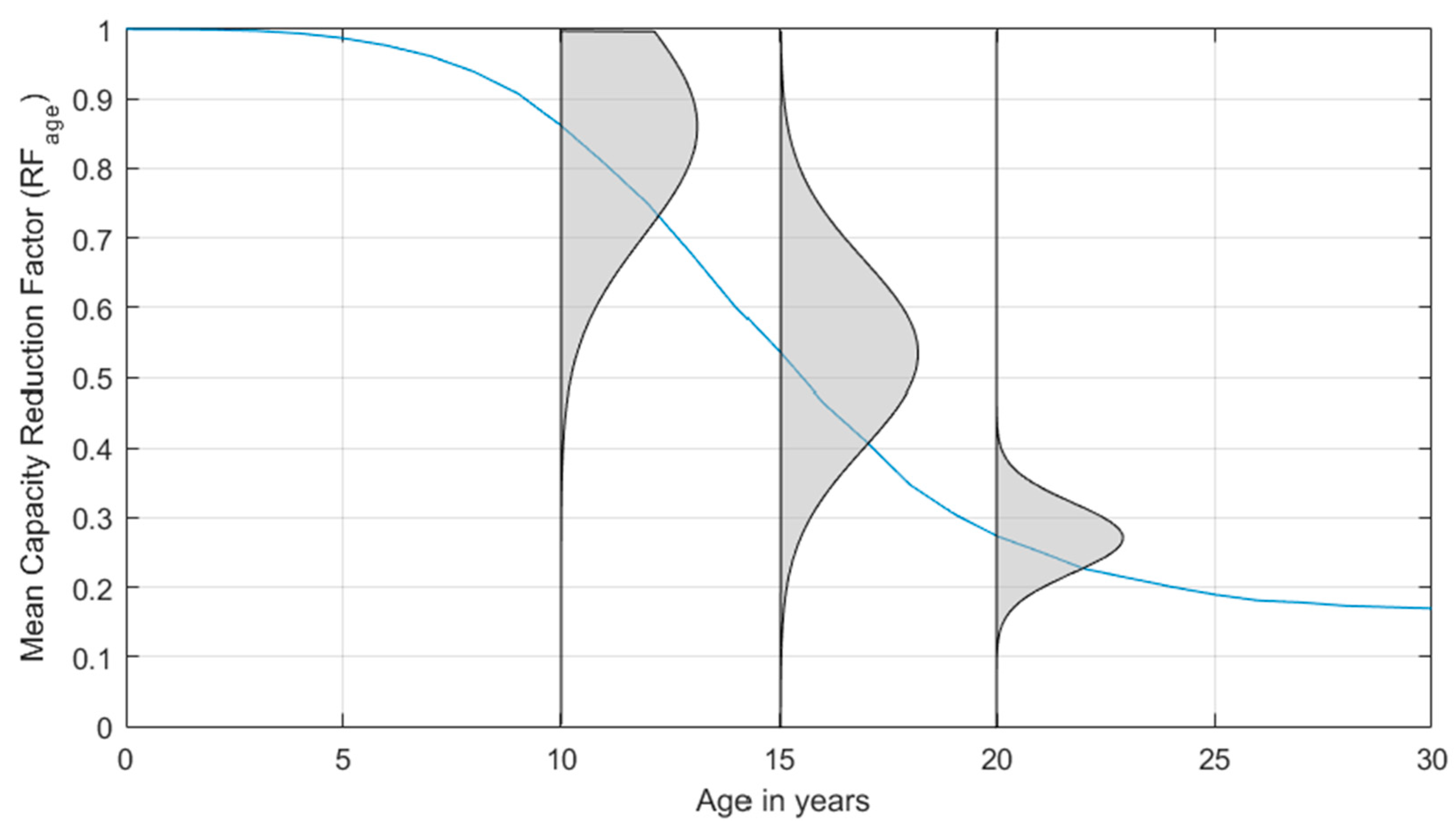
Roof Aging and Condition
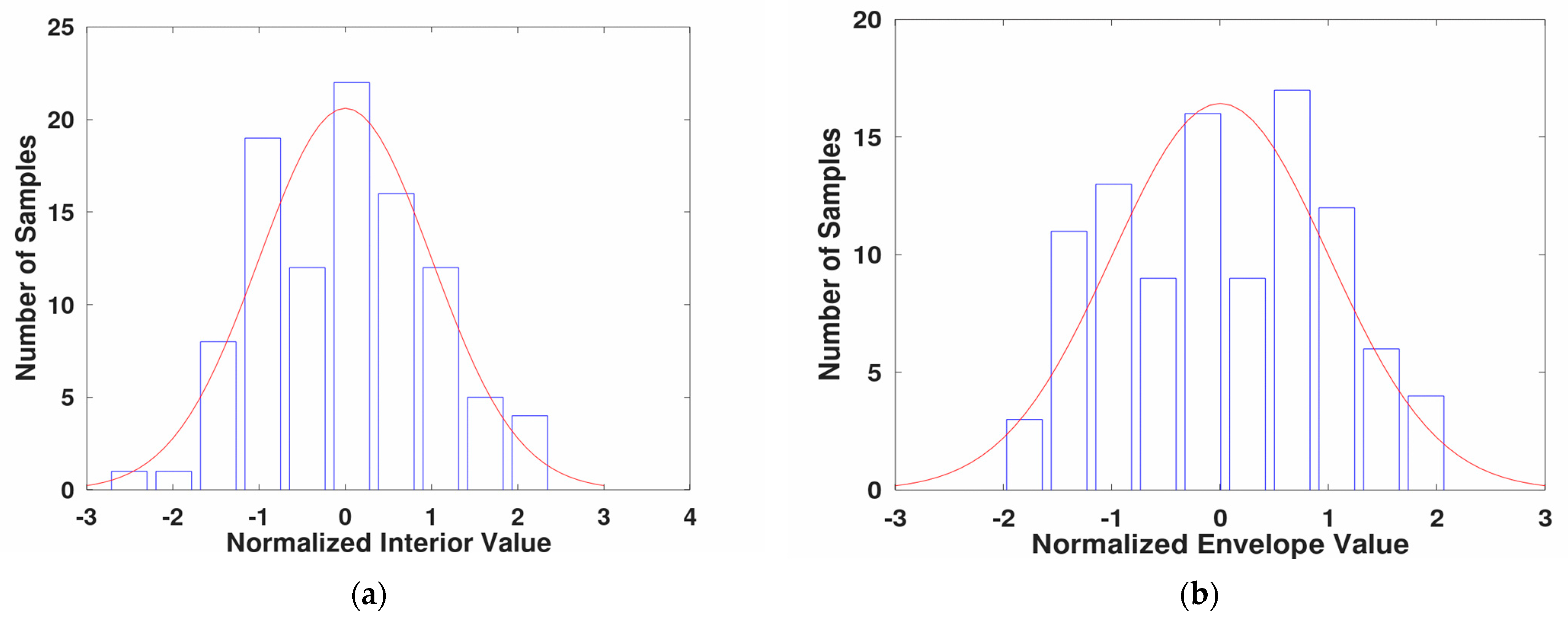
Interior Value
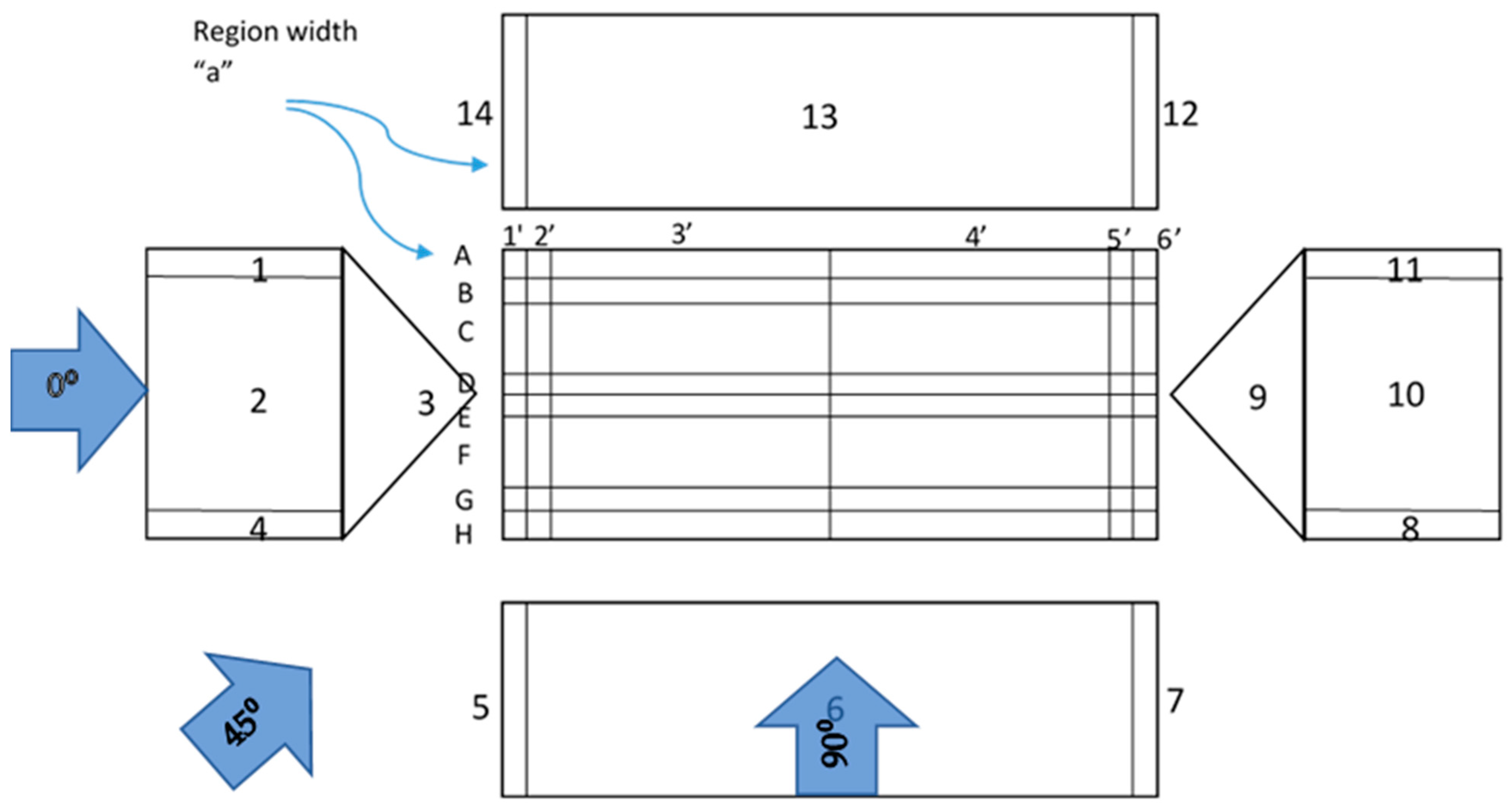
2.2. Demand Model
2.2.1. Wind Pressure Load
2.2.2. Debris Impact
2.2.3. Rain Intrusion
Impinging Rain
Distribution of Rain across the Surface of a Building
Area of Envelope Failure
Deficiency in Windows and Doors
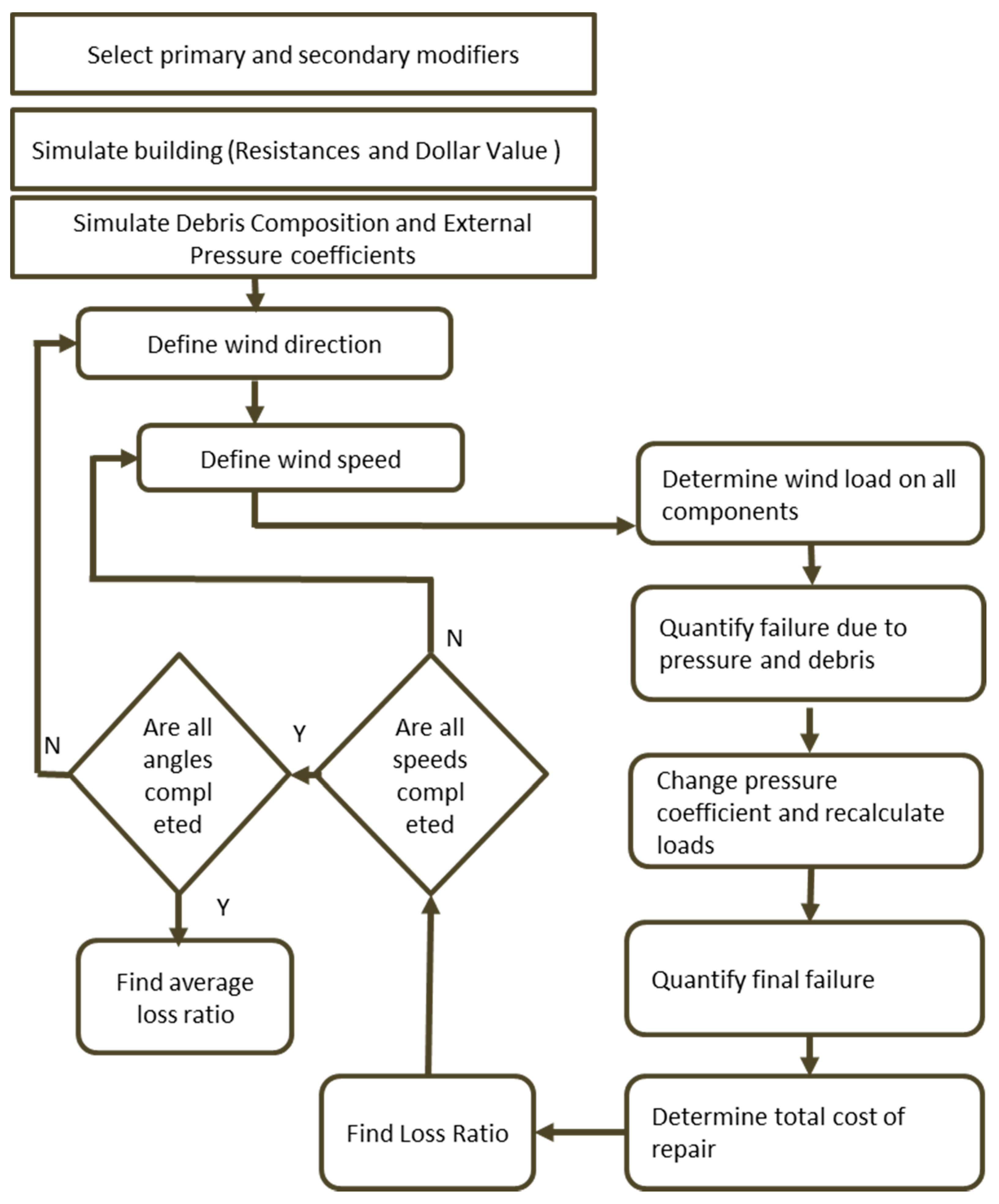
2.3. Damage Evaluation
- Initial failure check: each component of the building is checked for failure for a given wind speed and wind direction. Any component that is failed is recorded. Dependency of the roof cover on the roof deck is considered in this check along with the dependency of the roof sheathing on roof-to-wall connections.
- Recalculate the loads on the components and check for equilibrium: the loads on the components are recalculated, using the new internal pressure. Using the new loads, each component is checked for failure. Since the internal pressure depends on the area and location of failure of the envelope, we need to recalculate load, internal pressure and area of failure until there is an equilibrium, which means there is no more failure of any components. At this point, the maximum damage that can happen to the building due to wind pressure and debris will be obtained. This amount of damage for all the components that are modeled is recorded for the particular wind speed. These values will be further used in the next steps to estimate dollar losses.
2.4. Consequence Evaluation
2.4.1. Quantity of Water Entering the Building
2.4.2. Dollar Loss
2.5. Damage Ratio Calculation
3. Results
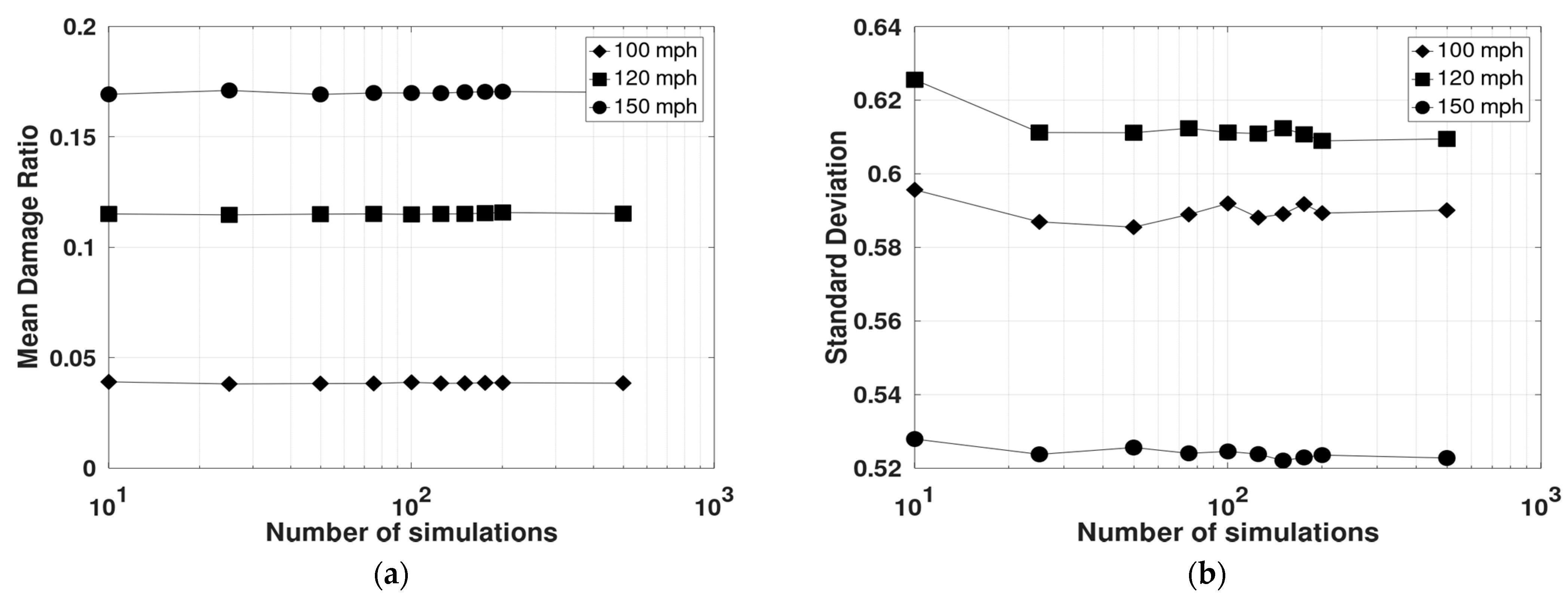
3.1. Convergence of Simulations
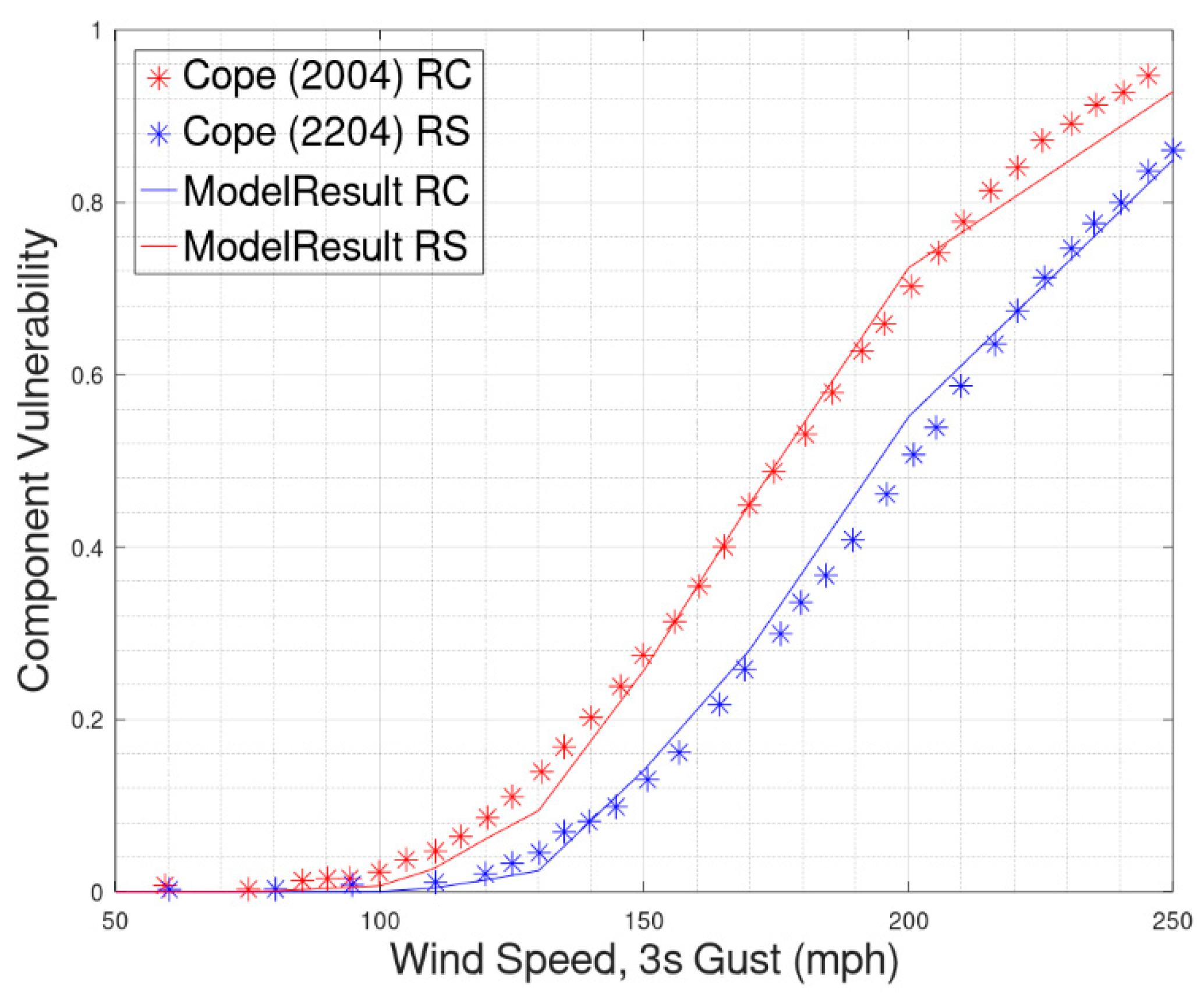
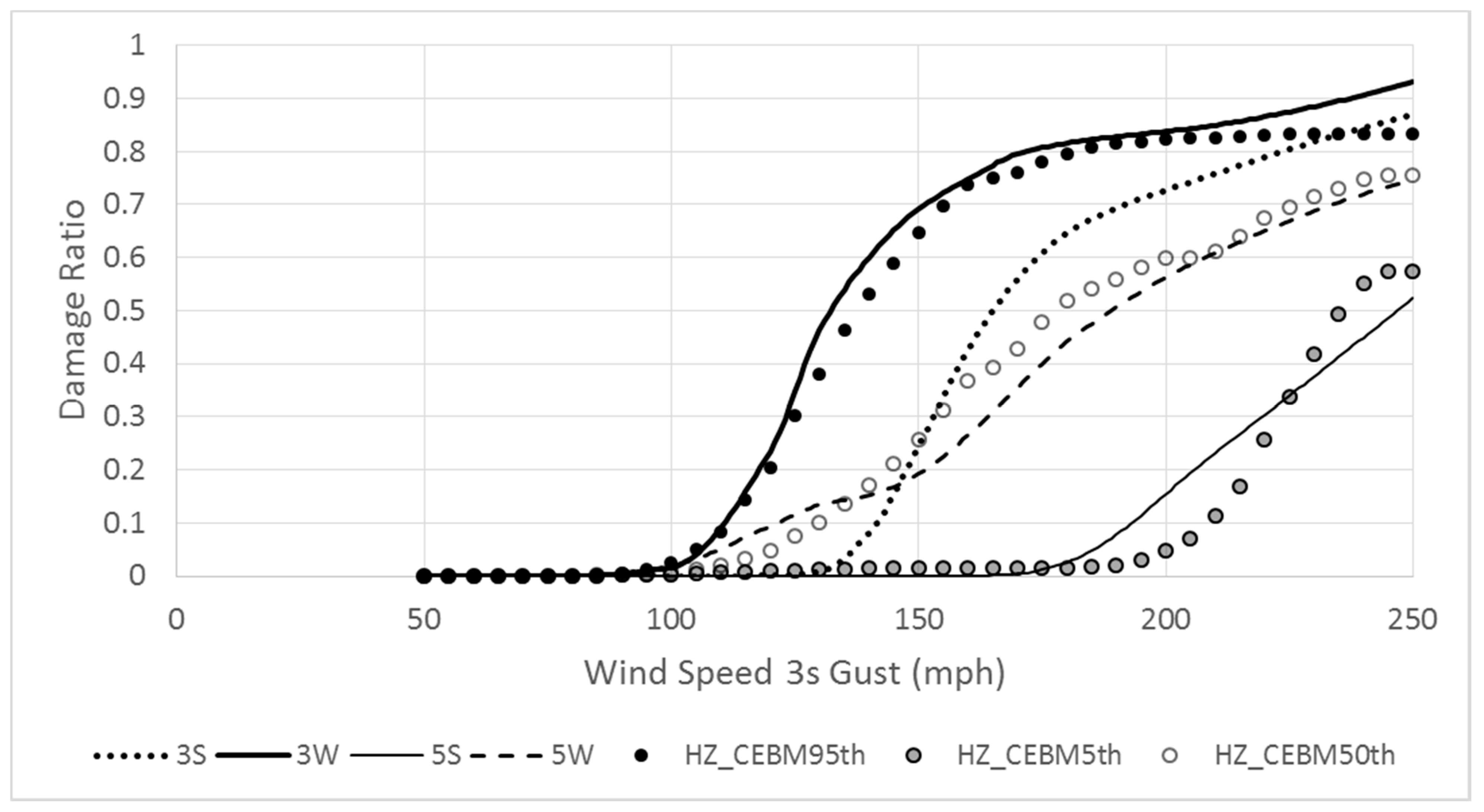
3.2. Case Study 1: Residential Building
3.3. Case Study 2: Commercial Buildings Based on HAZUS Models
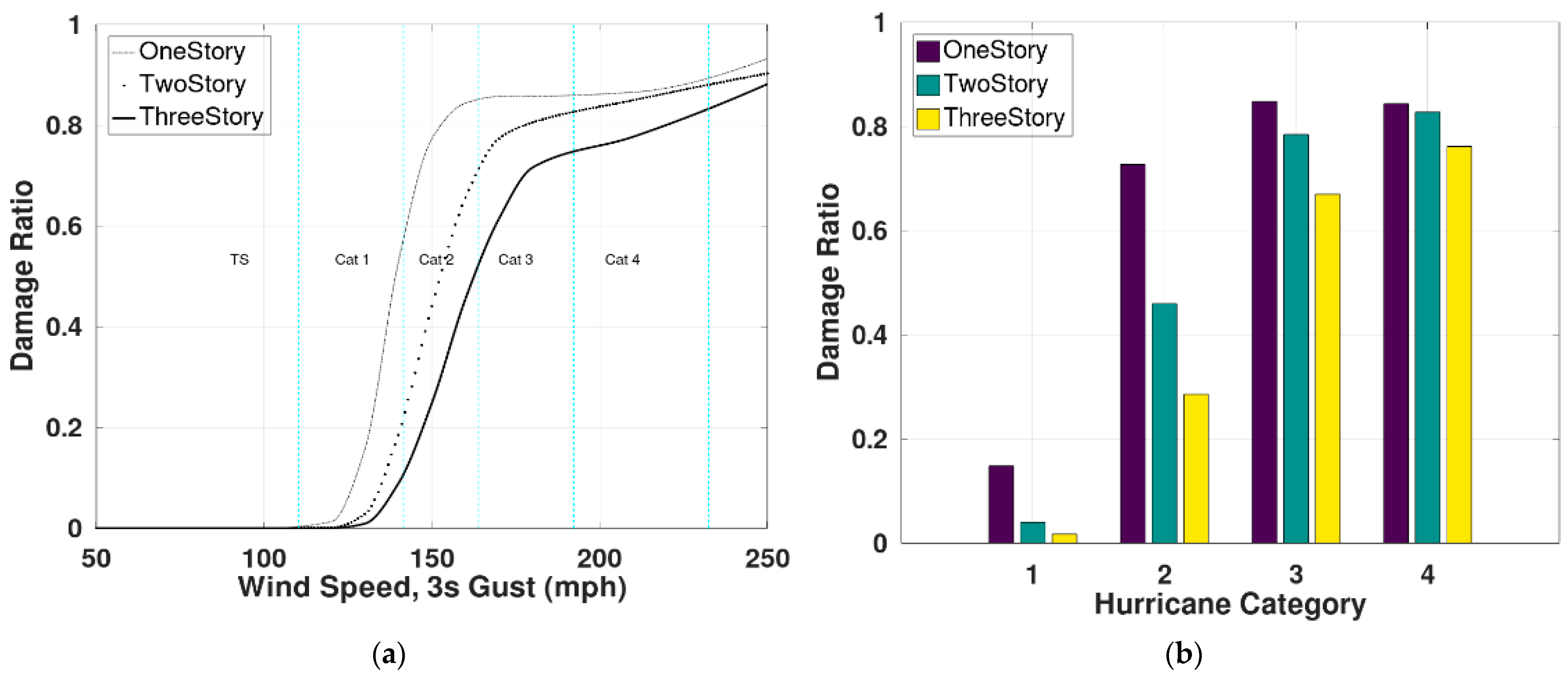
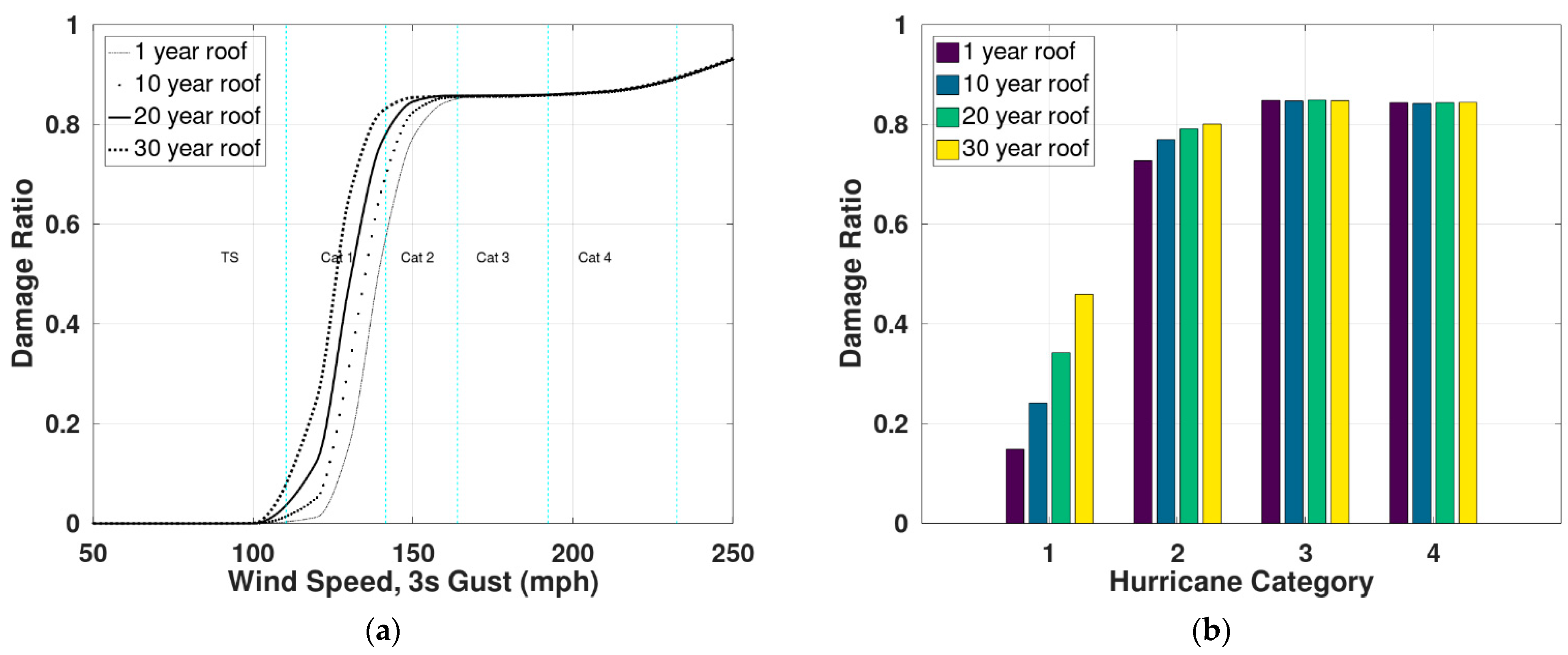
3.4. Case Study 3: Influence of Primary and Secondary Modifiers
4. Discussion
- A framework for generating vulnerability functions to assist insurance loss modeling has been proposed, which, unlike conventional models, does not rely on the fragility of components. Results were validated using the residential building examples from FPHLM and a commercial building example from HAZUS. The influence of primary modifiers (story and construction) and secondary modifiers (window protection, roof age, and debris composition) on overall loss was also explored.
- A Markovian approach-based roof aging model is introduced, which is able to predict the increase in vulnerability with aging. Further study based on claims data is necessary to validate the results of the model or to calibrate the model as necessary. The state transition probabilities used in the analysis can also be modified if new data are available from in-service roofs.
- Damage ratio was found to decrease with an increase in the number of stories by about 50% for Cat1 hurricanes for each added story. Floor area does not influence losses significantly.
- Reinforced concrete buildings are about twice as resilient as masonry for Cat1 hurricanes.
- The model also shows that window protection can help to mitigate losses induced by debris impact in different debris environments. It can reduce losses for Cat2 hurricanes by 100% and Cat3 by 66%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Attribute Name | Residential (Case Study 1) | Strong (Case Study 2) | Weak (Case Study 2) |
|---|---|---|---|
| Occupancy | Single Family | Office | Office |
| Construction | Wood | Concrete | Concrete |
| Year | 1997 | 1997 | 1997 |
| Number of Stories | 1 | 3,5 | 3,5 |
| Floor Area | 2464 | 10,000 | 10,000 |
| Aspect Ratio | 1.64 | 3 | 3 |
| Roof Geometry | Gable | Flat, with basic slope | Flat, with basic slope |
| Roof Slope | 5/12 | 1/12 | 1/12 |
| Roof Maintenance | Excellent | Excellent | Excellent |
| Hurricane Bracing | Adequate | Adequate | Adequate |
| Opening Protection | No | Large Debris | No |
| Height Ground | 10 | 12 | 12 |
| Height Typical | 0 | 10 | 10 |
| Height Top | 0 | 10 | 10 |
| Exposure Category for Design | C | C | C |
| Exposure Category for Load | C | C | C |
| Design Speed | 100 | 100 | 100 |
| Debris Percentage Small | 90 | 90 | 90 |
| Debris Percentage Medium | 5 | 5 | 5 |
| Debris Percentage Large | 5 | 5 | 5 |
| Wall Cladding Type | Vinyl Siding | Brick Veneer | Brick Veneer |
| Percentage Window Area First Floor | 10 | 20 | 20 |
| Percentage Window Area Typical Floor | 0 | 20 | 20 |
| Percentage Window Area Top Floor | 0 | 20 | 20 |
| Roof Factor of Safety in Main region | 1.5 | 1.5 | 1.0 |
| Roof Factor of Safety in Corner region | 1.2 | 1.5 | 1.0 |
| Roof Factor of Safety in Edge region | 1.2 | 1.5 | 1.0 |
| Roof Cover Capacity Distribution | Lognormal | Gaussian | Gaussian |
| Roof Insulation Capacity Distribution | NA | Gaussian | Gaussian |
| Roof Deck Capacity Distribution | Lognormal | Gaussian | Gaussian |
| Roof cover COV | 0.4 | 0.1 | 0.1 |
| Roof Sheathing COV | 0.4 | 0.1 | 0.1 |
| Wall FS Main | 1.2 | 2 | 1.5 |
| Wall FS Corner | 1.2 | 2 | 1.5 |
| Wall Capacity Distribution | Gaussian | Gaussian | Gaussian |
| Wall COV | 0.4 | 0.1 | 0.1 |
| Window Capacity Distribution | Gaussian | Gaussian | Gaussian |
| Window COV | 0.2 | 0.1 | 0.1 |
| Window FS | 1.16 | 2 | 1.5 |
| Attribute Description | Numerical Values | Units |
|---|---|---|
| Distance to source of debris | [10,35] | feet |
| Debris uplift wind speed limits | Small [80,110] Medium [130,160] Large [140,170] | mph |
| Debris C value | 0.8, 0.496, 0.9 | |
| Momentum capacity of unprotected window | 0.025 | kgm/s |
| Momentum capacity of protected window | 62.37 | kgm/s |
| Item | Unit of Measurement | Normative Quantity (50th Percentile) | Unit Rate as Per RSMeans 2013 ($) |
|---|---|---|---|
| Interior partition length | 100 LF per 1 gsf | 1 E-3 | 10/ft |
| Ceramic Tile floors | SF per 1 gsf | 0.042 | 4.3/sf |
| Ceiling Lay in Tile | % | 95 | 1.8/sf |
References
- Rosowsky, D.V. Projecting the Effects of a Warming Climate on the Hurricane Hazard and Insured Losses: Methodology and Case Study. Struct. Saf. 2021, 88, 102036. [Google Scholar] [CrossRef]
- Pachauri, R.K.; Allen, M.R.; Barros, V.R.; Broome, J.; Cramer, W.; Christ, R.; Church, J.A.; Clarke, L.; Dahe, Q.; Dasgupta, P. Climate Change 2014: Synthesis Report. In Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.-F. The Representative Concentration Pathways: An Overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Why Hurricane Risk Modelling Has to Change|Swiss Re. Available online: https://www.swissre.com/risk-knowledge/mitigating-climate-risk/why-hurricane-risk-modelling-has-to-change.html (accessed on 11 January 2022).
- Pinelli, J.-P.; Roueche, D.; Kijewski-Correa, T.; Plaz, F.; Prevatt, D.; Zisis, I.; Elawady, A.; Haan, F.; Pei, S.; Gurley, K. Overview of Damage Observed in Regional Construction during the Passage of Hurricane Irma over the State of Florida. In Forensic Engineering 2018: Forging Forensic Frontiers; American Society of Civil Engineers: Reston, VA, USA, 2018; pp. 1028–1038. [Google Scholar]
- Zhou, Z.; Gong, J.; Hu, X. Community-Scale Multi-Level Post-Hurricane Damage Assessment of Residential Buildings Using Multi-Temporal Airborne LiDAR Data. Autom. Constr. 2019, 98, 30–45. [Google Scholar] [CrossRef]
- Tilon, S.; Nex, F.; Kerle, N.; Vosselman, G. Post-Disaster Building Damage Detection from Earth Observation Imagery Using Unsupervised and Transferable Anomaly Detecting Generative Adversarial Networks. Remote Sens. 2020, 12, 4193. [Google Scholar] [CrossRef]
- Herseth, A.; Ashley, E. FEMA Mitigation Assessment Team Program: Observations and Recommendations since Hurricane Andrew. In Advances in Hurricane Engineering: Learning from Our Past; American Society of Civil Engineers: Washington, DC, USA, 2013; pp. 630–645. [Google Scholar]
- Mehta, K.C. Wind Induced Damage Observations and Their Implications for Design Practice. Eng. Struct. 1984, 6, 242–247. [Google Scholar] [CrossRef]
- Keith, E.L.; Rose, J.D. Hurricane Andrew—Structural Performance of Buildings in South Florida. J. Perform. Constr. Facil. 1994, 8, 178–191. [Google Scholar] [CrossRef]
- Clark, K.M. The Use of Computer Modeling in Estimating and Managing Future Catastrophe Losses. The Geneva Papers on Risk and Insurance. Issues Pract. 2002, 27, 181–195. [Google Scholar]
- Vickery, P.J.; Skerlj, P.F.; Lin, J.; Twisdale Jr, L.A.; Young, M.A.; Lavelle, F.M. HAZUS-MH Hurricane Model Methodology. II: Damage and Loss Estimation. Nat. Hazards Rev. 2006, 7, 94–103. [Google Scholar] [CrossRef] [Green Version]
- Cope, A.D. Predicting the Vulnerability of Typical Residential Buildings to Hurricane Damage; University of Florida: Gainesville, FL, USA, 2004. [Google Scholar]
- Pinelli, J.-P.; Simiu, E.; Gurley, K.; Subramanian, C.; Zhang, L.; Cope, A.; Filliben, J.J.; Hamid, S. Hurricane Damage Prediction Model for Residential Structures. J. Struct. Eng. 2004, 130, 1685–1691. [Google Scholar] [CrossRef]
- Hamid, S.; Kibria, B.G.; Gulati, S.; Powell, M.; Annane, B.; Cocke, S.; Pinelli, J.-P.; Gurley, K.; Chen, S.-C. Predicting Losses of Residential Structures in the State of Florida by the Public Hurricane Loss Evaluation Model. Stat. Methodol. 2010, 7, 552–573. [Google Scholar] [CrossRef]
- Hamid, S.S.; Pinelli, J.-P.; Chen, S.-C.; Gurley, K. Catastrophe Model-Based Assessment of Hurricane Risk and Estimates of Potential Insured Losses for the State of Florida. Nat. Hazards Rev. 2011, 12, 171–176. [Google Scholar] [CrossRef]
- Pan, F. Damage Prediction of Low-Rise Buildings under Hurricane Winds. Ph.D. Thesis, Louisiana State University and Agricultural and Mechanical College, Baton Rouge, LA, USA, 2014. [Google Scholar]
- Mehta, K.C.; Smith, D.A.; McDonald, J.R. Procedure for Predicting Wind Damage to Buildings. J. Struct. Div. 1981, 107, 2089–2096. [Google Scholar] [CrossRef]
- Sparks, P.R.; Schiff, S.D.; Reinhold, T.A. Wind Damage to Envelopes of Houses and Consequent Insurance Losses. J. Wind Eng. Ind. Aerodyn. 1994, 53, 145–155. [Google Scholar] [CrossRef]
- Sparks, P.R. Relationship between Residential Insurance Losses and Wind Conditions in Hurricane Andrew. In Hurricanes of 1992-Andrew and Iniki One Year Later; CiNii: Tokyo, Japan, 1993; pp. 111–124. [Google Scholar]
- Bhinderwala, S. Insurance Loss Analysis of Single Family Dwellings Damaged in Hurricane Andrew. Ph.D. Thesis, Clemson University, Clemson, SC, USA, 1995. [Google Scholar]
- Stathopoulos, T. Wind Loads on Low-Rise Buildings: A Review of the State of the Art. Eng. Struct. 1984, 6, 119–135. [Google Scholar] [CrossRef]
- Levitan, M.L.; Mehta, K.C. Texas Tech Field Experiments for Wind Loads Part 1: Building and Pressure Measuring System. J. Wind Eng. Ind. Aerodyn. 1992, 43, 1565–1576. [Google Scholar] [CrossRef]
- Holmes, J.D. Mean and Fluctuating Internal Pressures Induced by Wind. In Wind Engineering; Elsevier: Amsterdam, The Netherlands, 1980; pp. 435–450. [Google Scholar]
- Ginger, J.D.; Holmes, J.D.; Kim, P.Y. Variation of Internal Pressure with Varying Sizes of Dominant Openings and Volumes. J. Struct. Eng. 2010, 136, 1319–1326. [Google Scholar] [CrossRef]
- Kopp, G.A.; Oh, J.H.; Inculet, D.R. Wind-Induced Internal Pressures in Houses. J. Struct. Eng. 2008, 134, 1129–1138. [Google Scholar] [CrossRef]
- Stathopoulos, T. Computational Wind Engineering: Past Achievements and Future Challenges. J. Wind Eng. Ind. Aerodyn. 1997, 67, 509–532. [Google Scholar] [CrossRef]
- Surry, D.; Stathopoulos, T. An Experimental Approach to the Economical Measurement of Spatially-Averaged Wind Loads. J. Wind Eng. Ind. Aerodyn. 1978, 2, 385–397. [Google Scholar] [CrossRef]
- Mehta, K.C.; Minor, J.E.; Reinhold, T.A. Wind Speed-Damage Correlation in Hurricane Frederic. J. Struct. Eng. 1983, 109, 37–49. [Google Scholar] [CrossRef]
- Kareem, A. Structural Performance and Wind Speed-Damage Correlation in Hurricane Alicia. J. Struct. Eng. 1985, 111, 2596–2610. [Google Scholar] [CrossRef]
- Kareem, A.; Stevens, J.G. Window Glass Performance and Analysis in Hurricane Alicia. In Hurricane Alicia: One Year Later; ASCE: Reston, VA, USA, 1985; pp. 178–186. [Google Scholar]
- Smith, W.R. Building Homes to Withstand Hurricane Damage. For. Prod. J. 1961, 11, 176–177. [Google Scholar]
- Ginger, J.D.; Holmes, J.D.; Kopp, G.A. Effect of Building Volume and Opening Size on Fluctuating Internal Pressures. Wind Struct. 2008, 11, 361–376. [Google Scholar] [CrossRef]
- Vickery, B.J. Internal Pressures and Interactions with the Building Envelope. J. Wind. Eng. Ind. Aerodyn. 1994, 53, 125–144. [Google Scholar] [CrossRef]
- Seong, S.H.; Peterka, J.A. Digital Generation of Non-Gaussian Spiky Excitations Using Spectral Representation with Additive Phase Structure. J. Eng. Mech. 2012, 138, 1236–1248. [Google Scholar] [CrossRef]
- Kumar, K.S.; Stathopoulos, T. Synthesis of Non-Gaussian Wind Pressure Time Series on Low Building Roofs. Eng. Struct. 1999, 21, 1086–1100. [Google Scholar] [CrossRef]
- Vickery, B.J.; Bloxham, C. Internal Pressure Dynamics with a Dominant Opening. J. Wind. Eng. Ind. Aerodyn. 1992, 41, 193–204. [Google Scholar] [CrossRef]
- Khanduri, A.C.; Morrow, G.C. Vulnerability of Buildings to Windstorms and Insurance Loss Estimation. J. Wind Eng. Ind. Aerodyn. 2003, 91, 455–467. [Google Scholar] [CrossRef]
- Stathopoulos, T. PDF of Wind Pressures on Low-Rise Buildings. J. Struct. Div. 1980, 106, 973–990. [Google Scholar] [CrossRef]
- Grayson, J.M. Building Envelope Failure Assessment of Residential Developments Subjected to Hurricane Wind Hazards. Ph.D. Thesis, Clemson University, Clemson, SC, USA, 2014. [Google Scholar]
- Grayson, M.; Pang, W.; Schiff, S. Three-Dimensional Probabilistic Wind-Borne Debris Trajectory Model for Building Envelope Impact Risk Assessment. J. Wind Eng. Ind. Aerodyn. 2012, 102, 22–35. [Google Scholar] [CrossRef]
- Grayson, J.M.; Pang, W.; Schiff, S. Building Envelope Failure Assessment Framework for Residential Communities Subjected to Hurricanes. Eng. Struct. 2013, 51, 245–258. [Google Scholar] [CrossRef]
- Lin, N.; Vanmarcke, E. Windborne Debris Risk Analysis—Part I. Introduction and Methodology. Wind. Struct. 2010, 13, 191. [Google Scholar] [CrossRef] [Green Version]
- Lin, N.; Letchford, C.; Holmes, J. Investigation of Plate-Type Windborne Debris. Part I. Experiments in Wind Tunnel and Full Scale. J. Wind Eng. Ind. Aerodyn. 2006, 94, 51–76. [Google Scholar] [CrossRef]
- Twisdale, L.A.; Vickery, P.J. Comparison of Debris Trajectory Models for Explosive Safety Hazard Analysis; Applied Research Associates Inc.: Raleigh, NC, USA, 1992. [Google Scholar]
- Twisdale, L.A.; Vickery, P.J.; Steckley, A.C. Analysis of Hurricane Windborne Debris Risk for Residential Structures. Raleigh (NC); Applied Research Associates Inc.: Albuquerque, NM, USA, 1996. [Google Scholar]
- Yazdani, N.; Green, P.S.; Haroon, S.A. Large Wind Missile Impact Capacity of Residential and Light Commercial Buildings. Pract. Period. Struct. Des. Constr. 2006, 11, 206–217. [Google Scholar] [CrossRef]
- Tachikawa, M. A Method for Estimating the Distribution Range of Trajectories of Wind-Borne Missiles. J. Wind Eng. Ind. Aerodyn. 1988, 29, 175–184. [Google Scholar] [CrossRef]
- Holmes, J.D.; Baker, C.J.; Tamura, Y. Tachikawa Number: A Proposal. J. Wind Eng. Ind. Aerodyn. 2006, 94, 41–47. [Google Scholar] [CrossRef]
- Tachikawa, M. Trajectories of Flat Plates in Uniform Flow with Application to Wind-Generated Missiles. J. Wind Eng. Ind. Aerodyn. 1983, 14, 443–453. [Google Scholar] [CrossRef]
- Reed, T.D.; Rosowsky, D.V.; Schiff, S.D. Uplift Capacity of Light-Frame Rafter to Top Plate Connections. J. Archit. Eng. 1997, 3, 156–163. [Google Scholar] [CrossRef]
- Ahmed, S.S.; Canino, I.; Chowdhury, A.G.; Mirmiran, A.; Suksawang, N. Study of the Capability of Multiple Mechanical Fasteners in Roof-to-Wall Connections of Timber Residential Buildings. Pract. Period. Struct. Des. Constr. 2011, 16, 2–9. [Google Scholar] [CrossRef]
- Shanmugam, B.; Nielson, B.G.; Schiff, S.D. Multi-Axis Treatment of Typical Light-Frame Wood Roof-to-Wall Metal Connectors in Design. Eng. Struct. 2011, 33, 3125–3135. [Google Scholar] [CrossRef]
- Mishra, S.; Vanli, O.A.; Alduse, B.P.; Jung, S. Hurricane Loss Estimation in Wood-Frame Buildings Using Bayesian Model Updating: Assessing Uncertainty in Fragility and Reliability Analyses. Eng. Struct. 2017, 135, 81–94. [Google Scholar] [CrossRef]
- Kakareko, G.; Jung, S.; Vanli, O.A. Hurricane Risk Analysis of the Residential Structures Located in Florida. Sustain. Resilient Infrastruct. 2020, 5, 395–409. [Google Scholar] [CrossRef]
- Pita, G.; Pinelli, J.-P.; Cocke, S.; Gurley, K.; Mitrani-Reiser, J.; Weekes, J.; Hamid, S. Assessment of Hurricane-Induced Internal Damage to Low-Rise Buildings in the Florida Public Hurricane Loss Model. J. Wind Eng. Ind. Aerodyn. 2012, 104, 76–87. [Google Scholar] [CrossRef]
- Blocken, B.; Carmeliet, J. Overview of Three State-of-the-Art Wind-Driven Rain Assessment Models and Comparison Based on Model Theory. Build. Environ. 2010, 45, 691–703. [Google Scholar] [CrossRef]
- Bitsuamlak, G.T.; Chowdhury, A.G.; Sambare, D. Application of a Full-Scale Testing Facility for Assessing Wind-Driven-Rain Intrusion. Build. Environ. 2009, 44, 2430–2441. [Google Scholar] [CrossRef]
- Blocken, B.; Carmeliet, J. A Review of Wind-Driven Rain Research in Building Science. J. Wind Eng. Ind. Aerodyn. 2004, 92, 1079–1130. [Google Scholar] [CrossRef]
- Choi, E.C. Simulation of Wind-Driven-Rain around a Building. J. Wind Eng. Ind. Aerodyn. 1993, 46, 721–729. [Google Scholar] [CrossRef]
- Choi, E.C. Wind-Driven Rain and Driving Rain Coefficient during Thunderstorms and Non-Thunderstorms. J. Wind Eng. Ind. Aerodyn. 2001, 89, 293–308. [Google Scholar] [CrossRef]
- Baheru, T.; Chowdhury, A.G.; Pinelli, J.-P.; Bitsuamlak, G. Distribution of Wind-Driven Rain Deposition on Low-Rise Buildings: Direct Impinging Raindrops versus Surface Runoff. J. Wind Eng. Ind. Aerodyn. 2014, 133, 27–38. [Google Scholar] [CrossRef]
- Lounis, Z.; Lacasse, M.A.; Vanier, D.J.; Kyle, B.R. Towards Standardization of Service Life Prediction of Roofing Membranes. In Roofing Research and Standards Development: Fourth Volume; ASTM International: West Conshohocken, PA, USA, 1999. [Google Scholar]
- Coffelt, D.P.; Hendrickson, C.T.; Healey, S.T. Inspection, Condition Assessment, and Management Decisions for Commercial Roof Systems. J. Archit. Eng. 2010, 16, 94–99. [Google Scholar] [CrossRef]
- Coffelt, D.P., Jr.; Hendrickson, C.T. Case Study of Occupant Costs in Roof Management. J. Archit. Eng. 2012, 18, 341–348. [Google Scholar] [CrossRef]
- Henderson, D.; Williams, C.; Gavanski, E.; Kopp, G.A. Failure Mechanisms of Roof Sheathing under Fluctuating Wind Loads. J. Wind Eng. Ind. Aerodyn. 2013, 114, 27–37. [Google Scholar] [CrossRef]
- Alduse, B.P.; Jung, S.; Vanli, O.A. Condition-Based Updating of the Fragility for Roof Covers under High Winds. J. Build. Eng. 2015, 2, 36–43. [Google Scholar] [CrossRef]
- Baskaran, A.; Current, J.; Martín-Pérez, B.; Tanaka, H. Quantification of Uplift Resistance of Adhesive-Applied Low-Slope Roof Configurations Subjected to Tensile Loading Test Protocol. J. Mater. Civ. Eng. 2011, 23, 903–914. [Google Scholar] [CrossRef] [Green Version]
- Molleti, S.; Ko, S.K.P.; Baskaran, B.A. Effect of Fastener-Deck Strength on the Wind-Uplift Performance of Mechanically Attached Roofing Assemblies. Pract. Period. Struct. Des. Constr. 2010, 15, 27–39. [Google Scholar] [CrossRef]
- Baskaran, A.; Murty, B.; Wu, J. Calculating Roof Membrane Deformation under Simulated Moderate Wind Uplift Pressures. Eng. Struct. 2009, 31, 642–650. [Google Scholar] [CrossRef] [Green Version]
- Dixon, C.R.; Masters, F.J.; Prevatt, D.O.; Gurley, K.R.; Brown, T.M.; Peterka, J.A.; Kubena, M.E. The Influence of Unsealing on the Wind Resistance of Asphalt Shingles. J. Wind Eng. Ind. Aerodyn. 2014, 130, 30–40. [Google Scholar] [CrossRef] [Green Version]
- Madanat, S.; Mishalani, R.; Ibrahim, W.H.W. Estimation of Infrastructure Transition Probabilities from Condition Rating Data. J. Infrastruct. Syst. 1995, 1, 120–125. [Google Scholar] [CrossRef]
- Jiang, Y.; Saito, M.; Sinha, K.C. Bridge Performance Prediction Model Using the Markov Chain; National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 1988. [Google Scholar]
- Xia, R.; Zhou, J.; Zhang, H.; Liao, L.; Zhao, R.; Zhang, Z. Quantitative Study on Corrosion of Steel Strands Based on Self-Magnetic Flux Leakage. Sensors 2018, 18, 1396. [Google Scholar] [CrossRef] [Green Version]
- Abdelmaksoud, A.M.; Balomenos, G.P.; Becker, T.C. Parameterized Logistic Models for Bridge Inspection and Maintenance Scheduling. J. Bridge. Eng. 2021, 26, 04021072. [Google Scholar] [CrossRef]
- FEMA. Next-Generation Methodology for Seismic Performance Assessment of Buildings; Applied Technology Council for the Federal Emergency Management Agency: Washington, DC, USA, 2012; p. 2.
- FEMA. Vol. 1 of Seismic Performance Assessment of Buildings FEMA P-58-1; Federal Emergency Management Agency (FEMA): Washington, DC, USA, 2012.
- Means, R.S. RS Means Building Construction Cost Data, 72nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013; pp. 861–871. [Google Scholar]






| Variable | Description | Units |
|---|---|---|
| DR | Damage Ratio | - |
| P0 | Estimated mean capacity of the component | psf |
| Factor of Safety of a component | - | |
| P | Nominal load on the component determined based on ASCE 7 | psf or lb |
| RFage | Reduction factor for age of the component | - |
| Cn | Normalized Condition for age | - |
| Standard deviation of capacity | psf | |
| Wind pressure | psf | |
| kz | Topographic factor from ASCE 7 | - |
| Wind speed | mph | |
| GCpe | External pressure coefficient | - |
| GCpi | Internal pressure coefficient | - |
| z | Height to the location where wind speed is calculated | ft |
| zg | Nominal Height to the atmospheric boundary layer | ft |
| α | Power law exponent based on ASCE 7 | - |
| Tachikawa number | - | |
| Air density | lb/ft3 | |
| Acceleration due to gravity | ft/s2 | |
| hm | Thickness of the debris | ft |
| ρm | Density of the debris | lb/ft3 |
| Dimensionless horizontal displacement | - | |
| Debris flight distance | - | |
| wd | Speed of debris | ft/s |
| Coefficient based on shape of debris | - | |
| RAF | Rain Admittance Factor | - |
| Vi | Volume of rain water | ft3 |
| Intensity of rain | - | |
| Afw | Area of failed window | ft2 |
| di | Deficiency in window | - |
| Fij | Factor for rain water calculation | - |
| Angle of attack of wind | deg. | |
| Arc | Actual failed area of roof cover | ft2 |
| Ars | Actual failed area of roof sheathing | ft2 |
| Apfrc | Area of failed roof cover projected in the vertical plane | ft2 |
| Apfrs | Area of failed roof sheathing projected in the vertical plane | ft2 |
| Rrc | Factor to address secondary rainwater penetration for roof | - |
| Di | Quantity of Damage to the ith component | ft2 or number |
| Qi | Quantity of the ith component in the building | ft2 or number |
| Ci | Cost of repair of the ith component in the building | Dollar |
| Nc | Total number of components in the building | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alduse, B.; Pang, W.; Tadinada, S.K.; Khan, S. A Framework to Model the Wind-Induced Losses in Buildings during Hurricanes. Wind 2022, 2, 87-112. https://doi.org/10.3390/wind2010006
Alduse B, Pang W, Tadinada SK, Khan S. A Framework to Model the Wind-Induced Losses in Buildings during Hurricanes. Wind. 2022; 2(1):87-112. https://doi.org/10.3390/wind2010006
Chicago/Turabian StyleAlduse, Bejoy, Weichiang Pang, Sashi Kanth Tadinada, and Shiraj Khan. 2022. "A Framework to Model the Wind-Induced Losses in Buildings during Hurricanes" Wind 2, no. 1: 87-112. https://doi.org/10.3390/wind2010006
APA StyleAlduse, B., Pang, W., Tadinada, S. K., & Khan, S. (2022). A Framework to Model the Wind-Induced Losses in Buildings during Hurricanes. Wind, 2(1), 87-112. https://doi.org/10.3390/wind2010006






