Study on Phase Characteristics of Wind Pressure Fields around a Prism Using Complex Proper Orthogonal Decomposition
Abstract
:1. Introduction
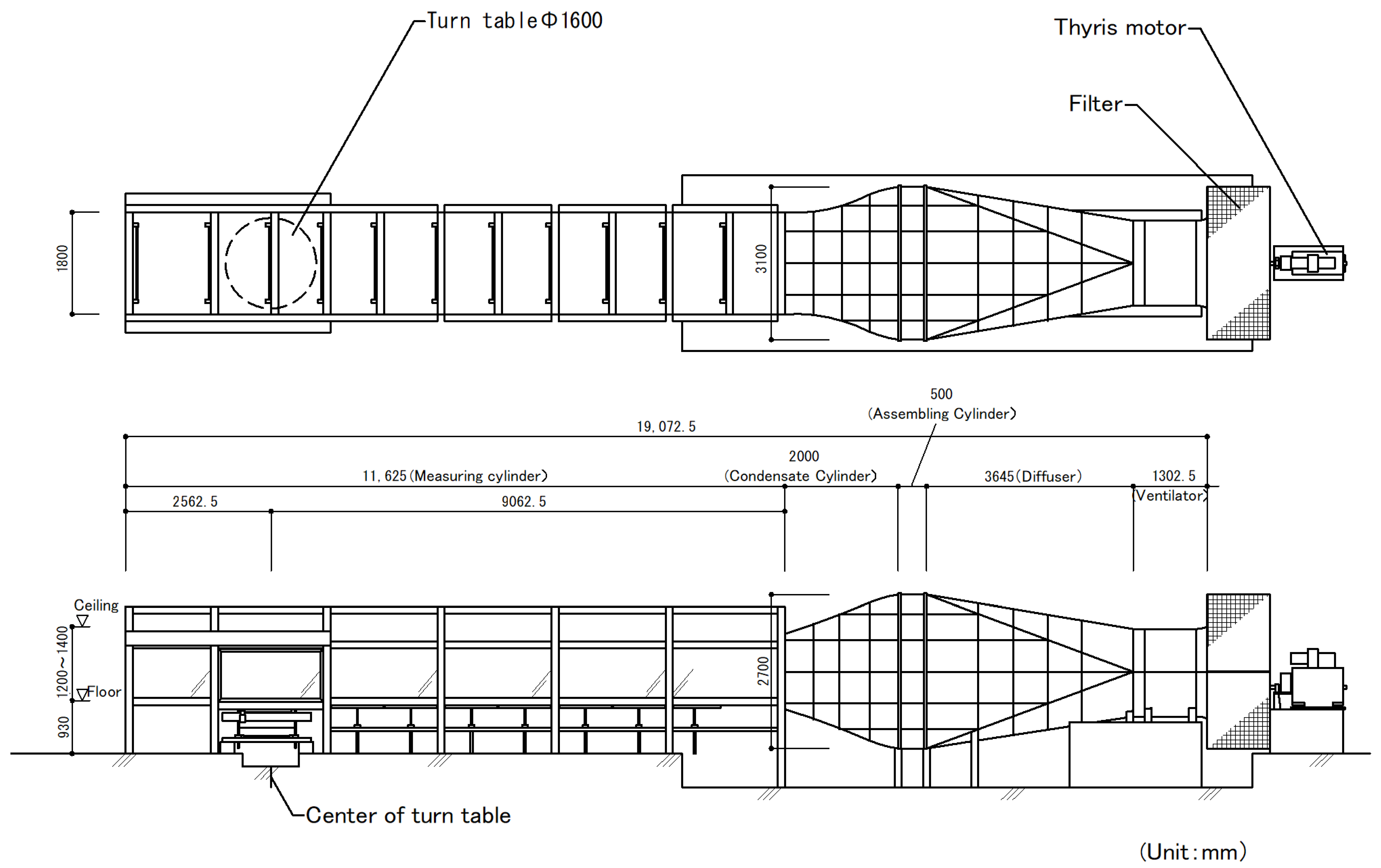
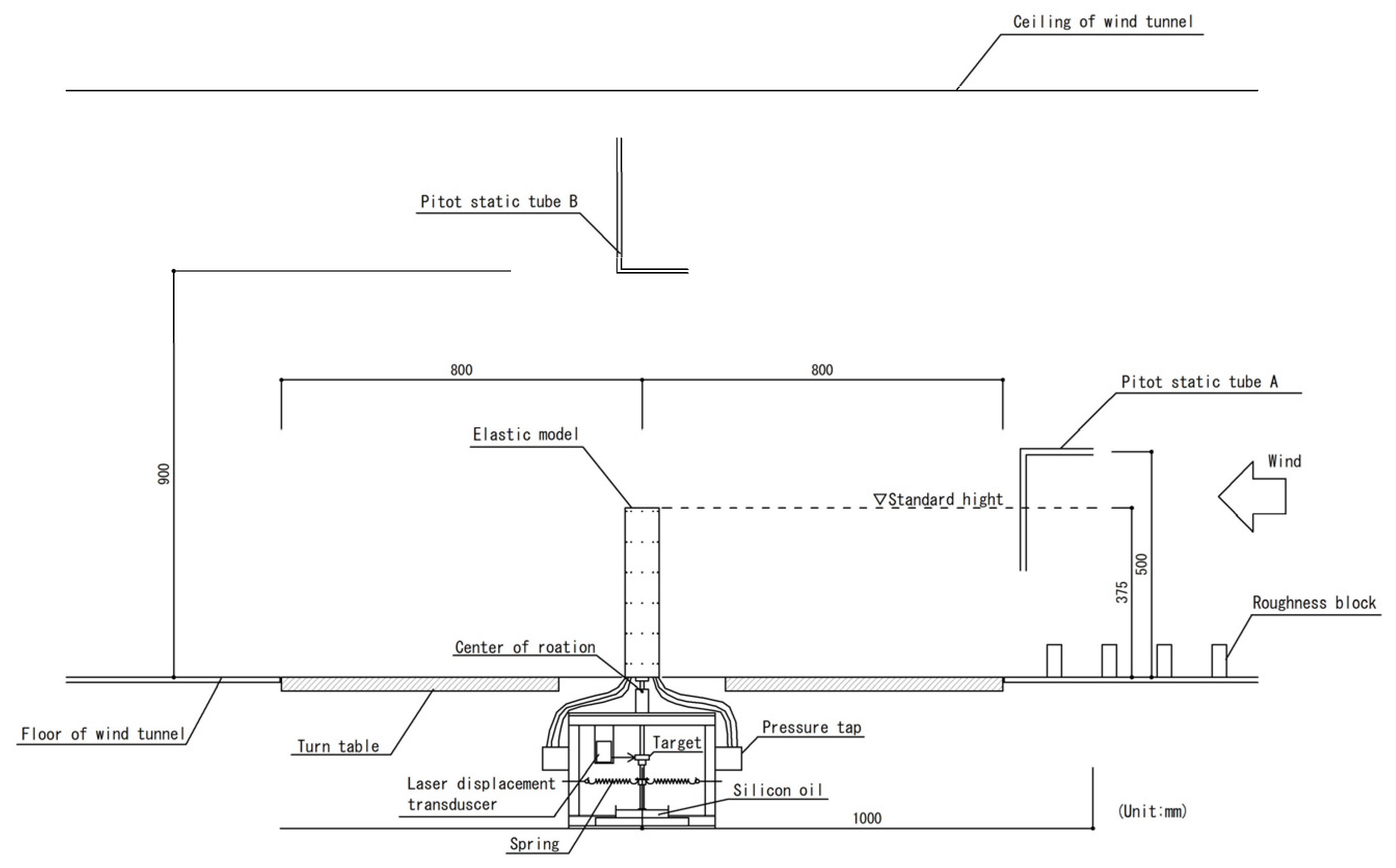
2. Wind Tunnel Experiment
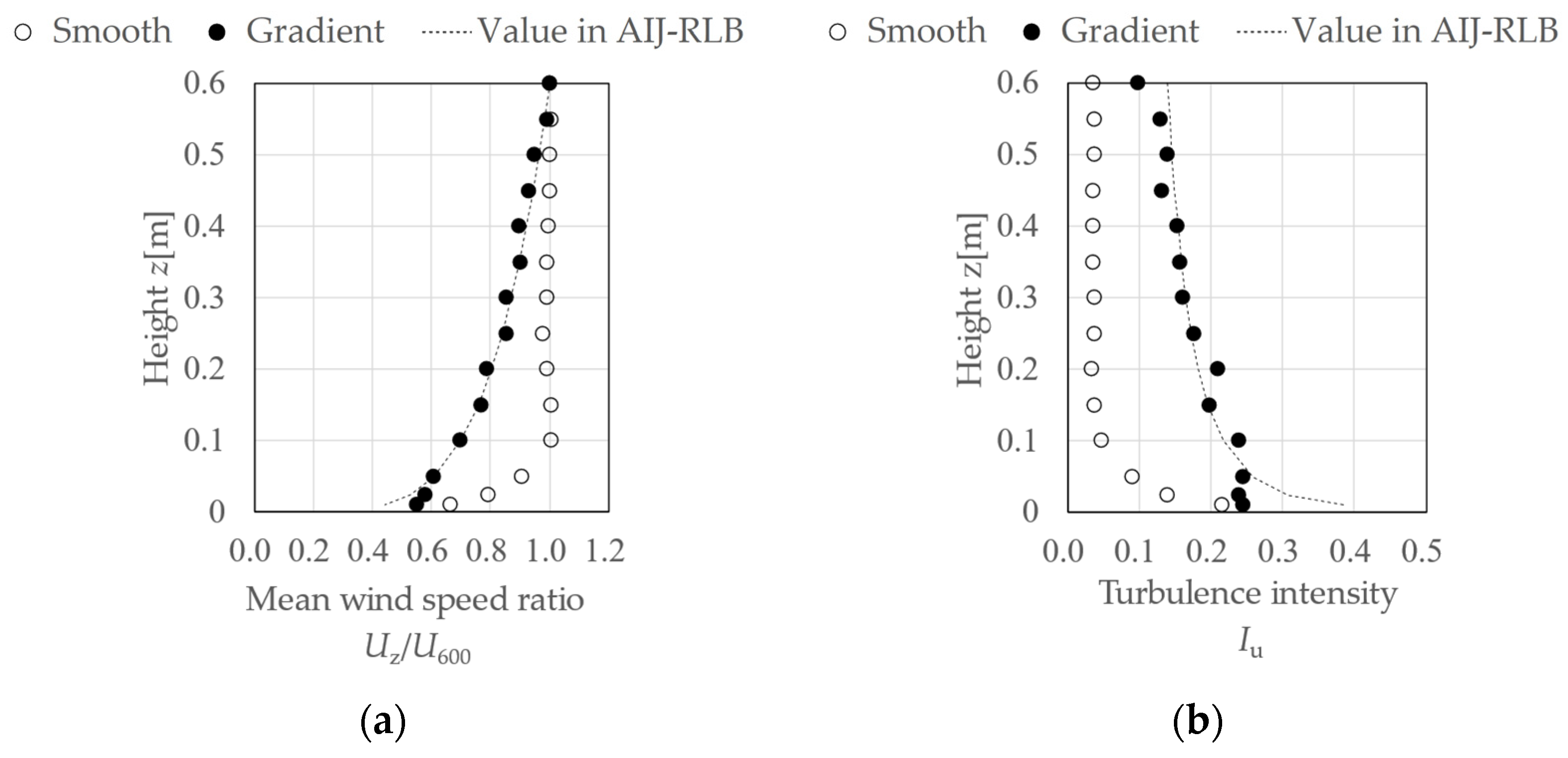
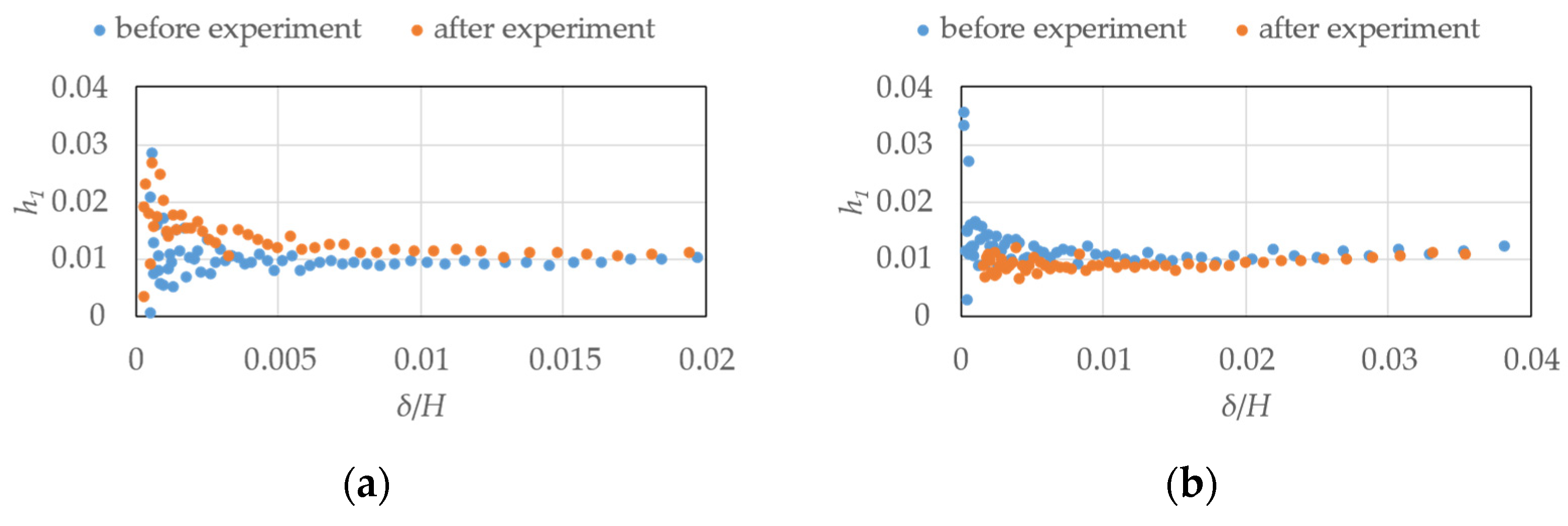
2.1. Wind Tunnel Flow
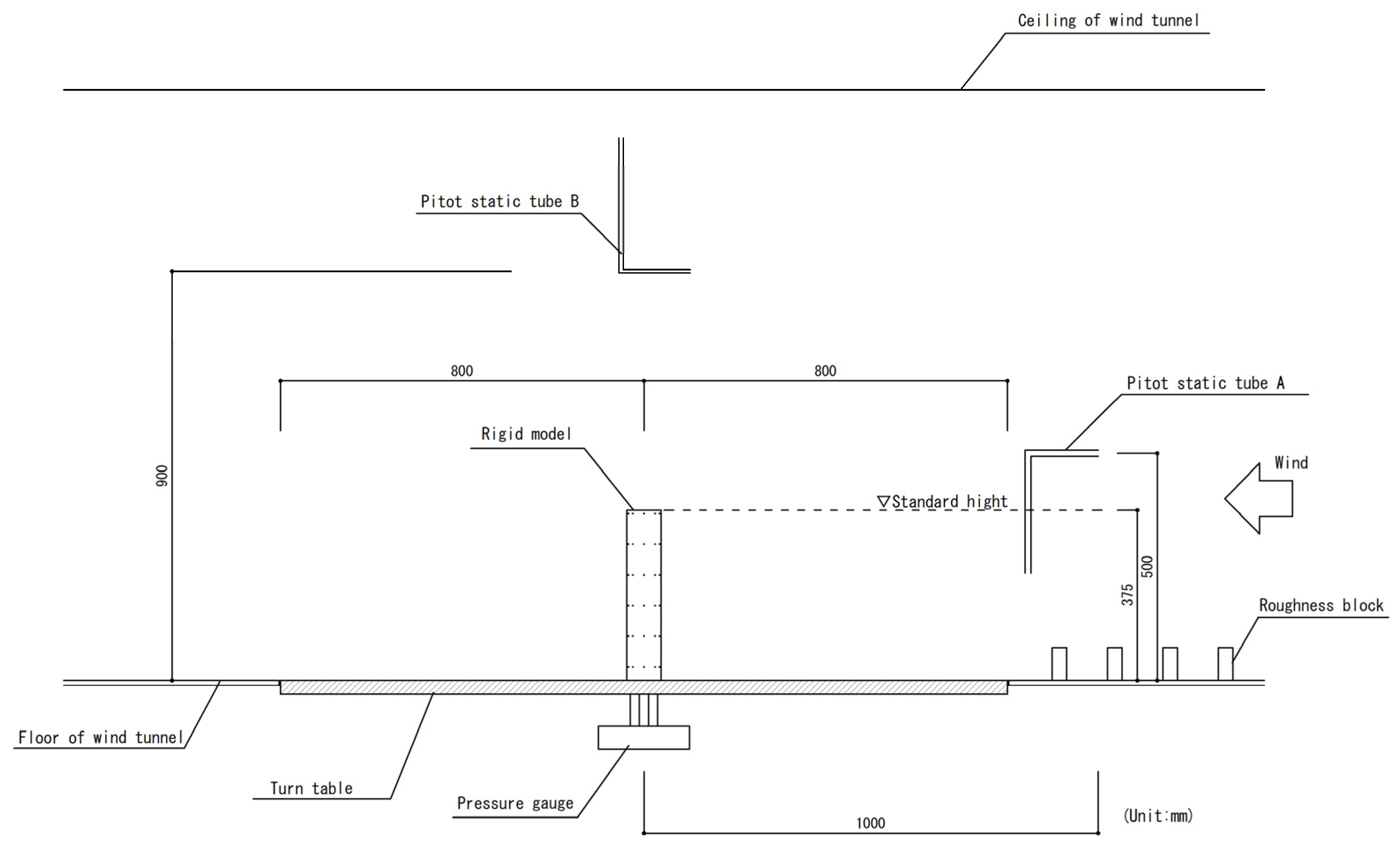
2.2. Experiments Using a Rigid Model
2.3. Experiments Using an Elastic Model
3. Complex Proper Orthogonal Decomposition
3.1. Evaluation Method
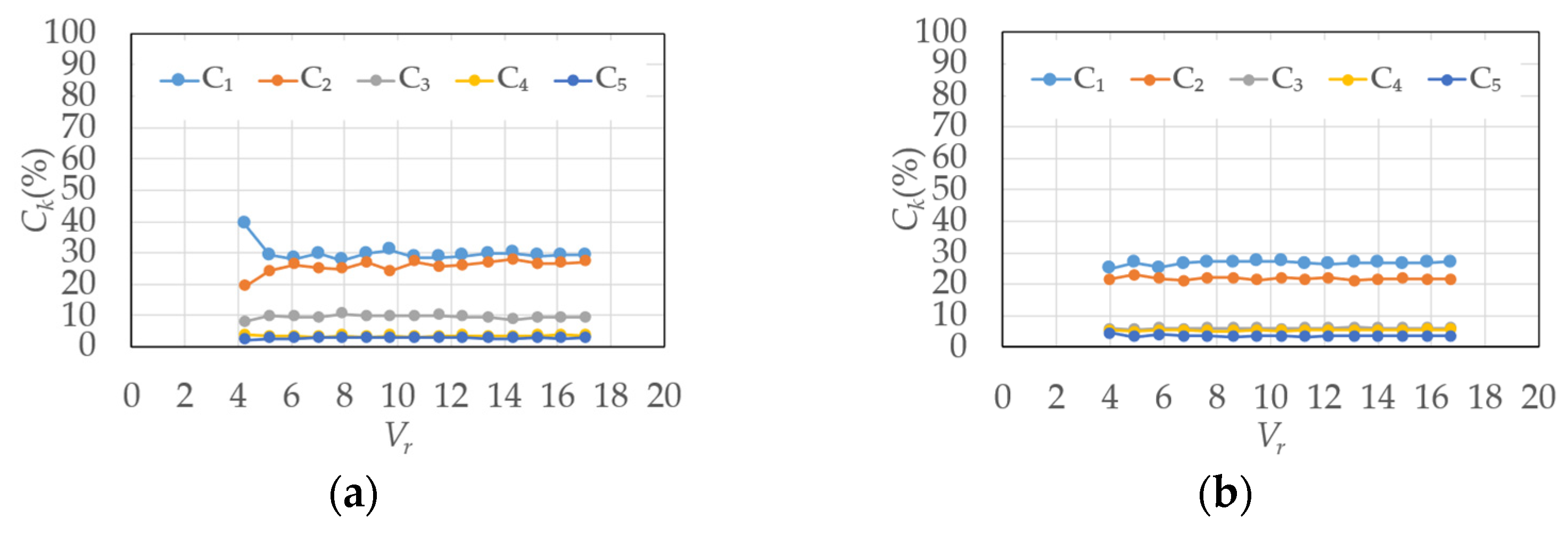
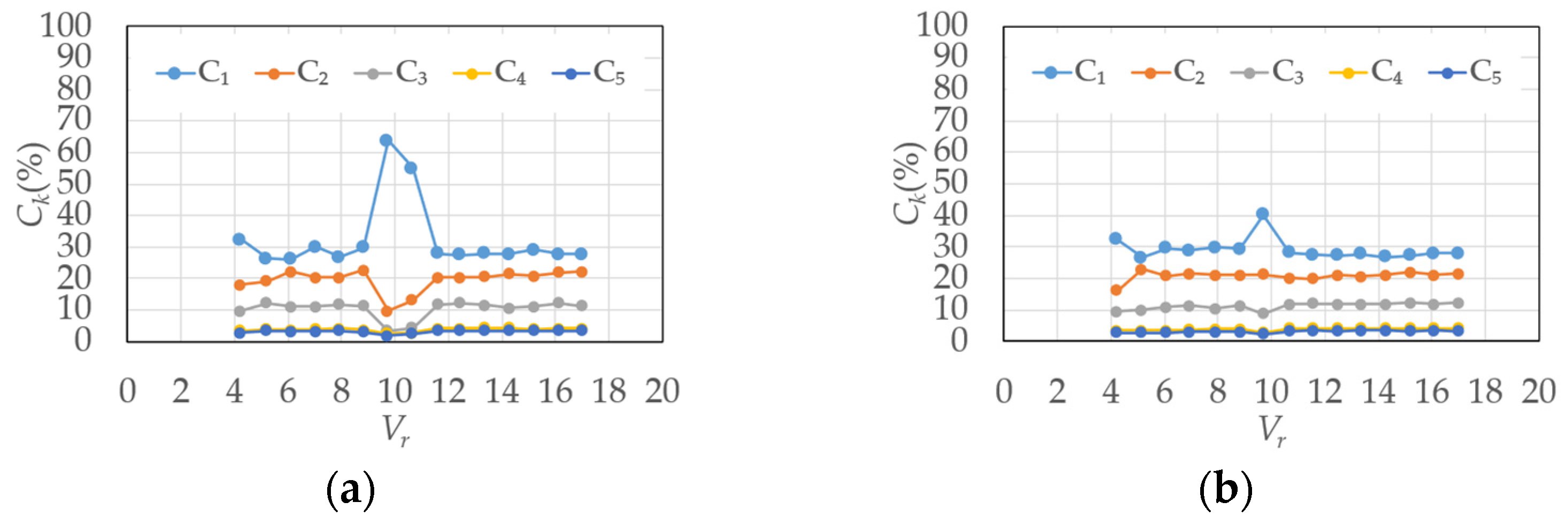
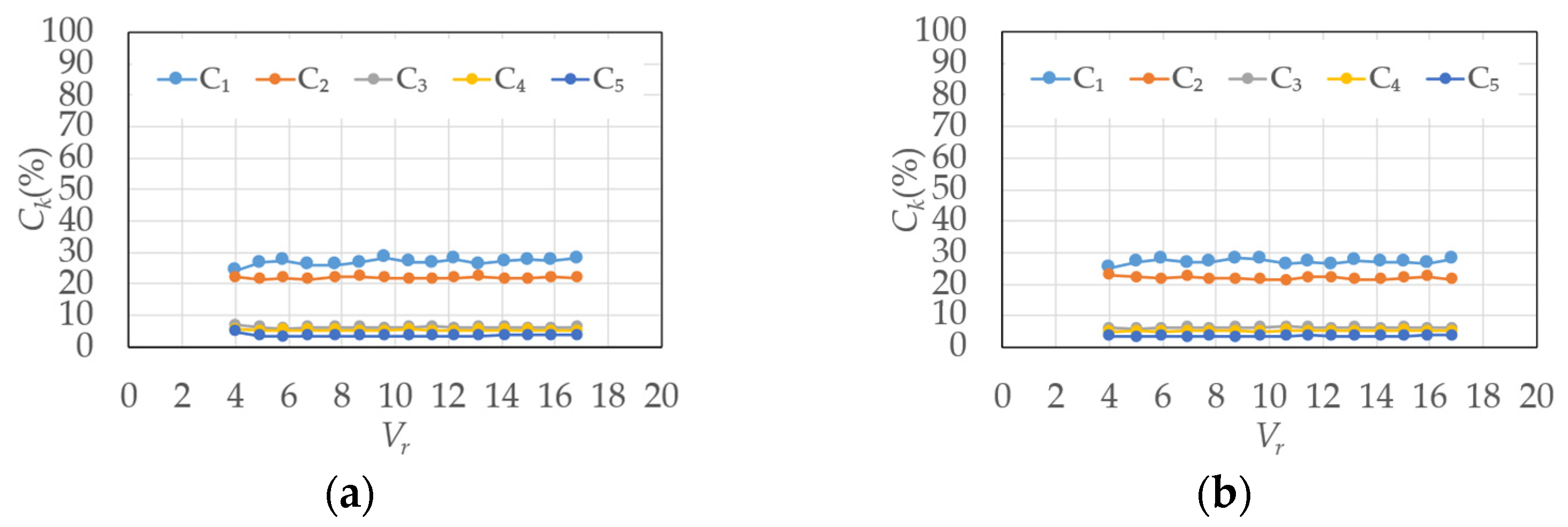
3.2. Contribution Ratio
3.3. Eigenmodes
4. Evaluation of Phase Characteristics
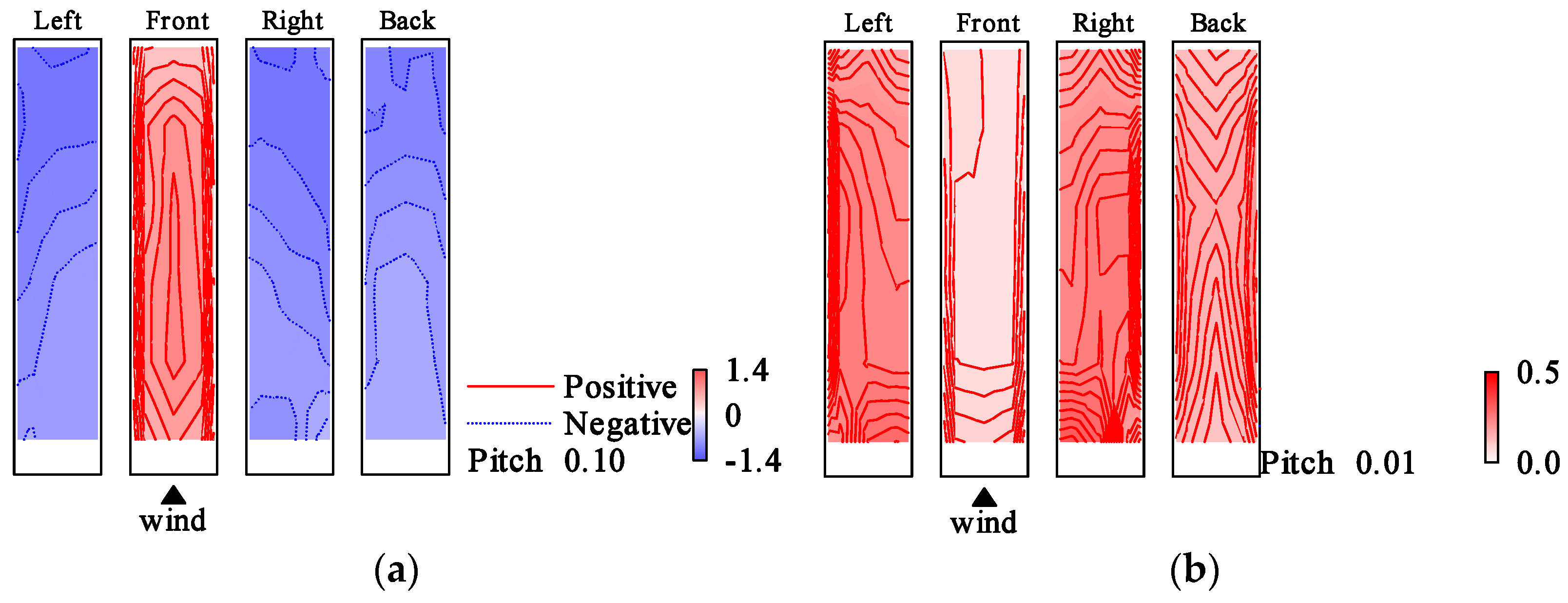
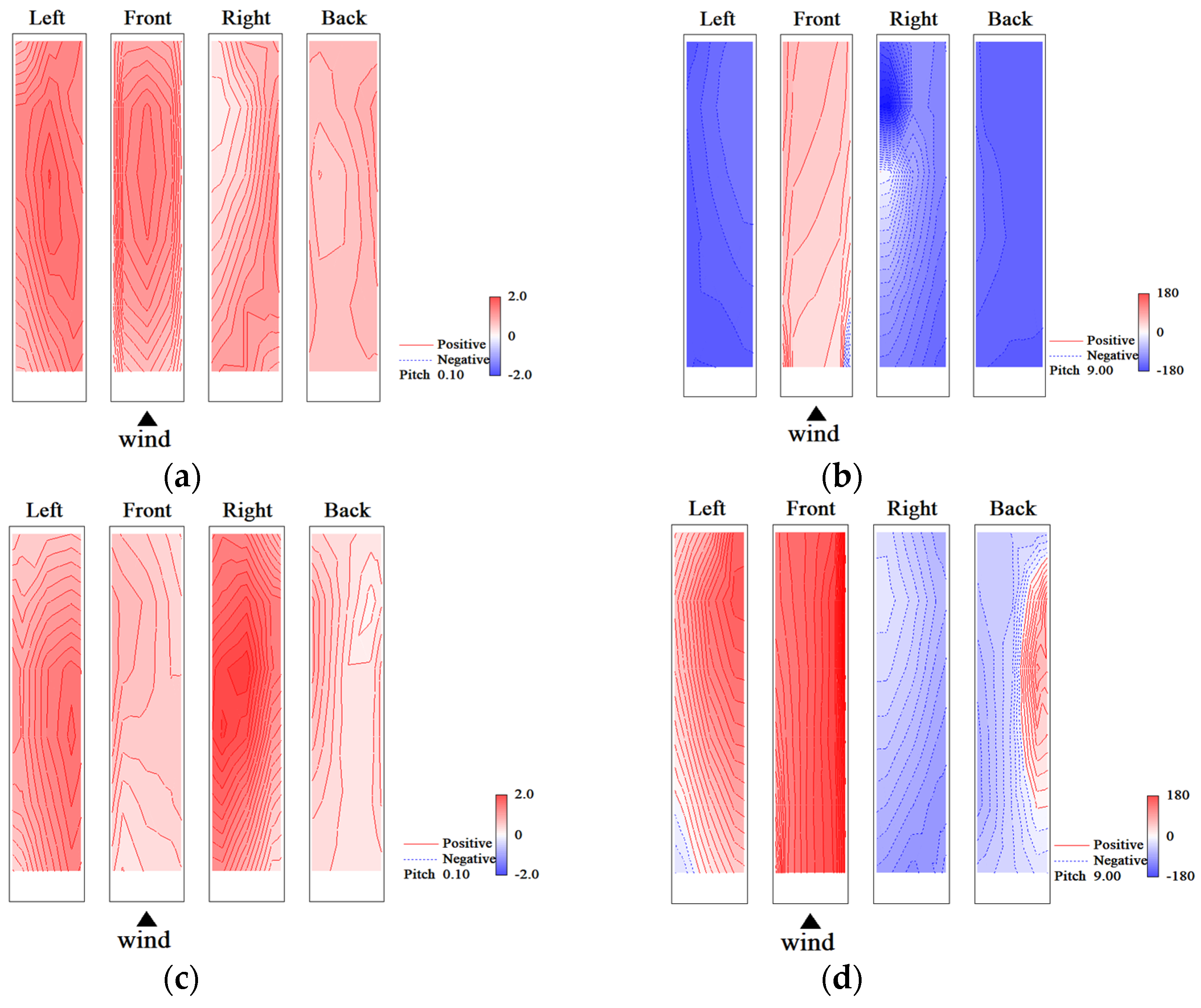
4.1. Symmetricity of Fluctuating Wind Pressure Mode
4.1.1. Inner Product
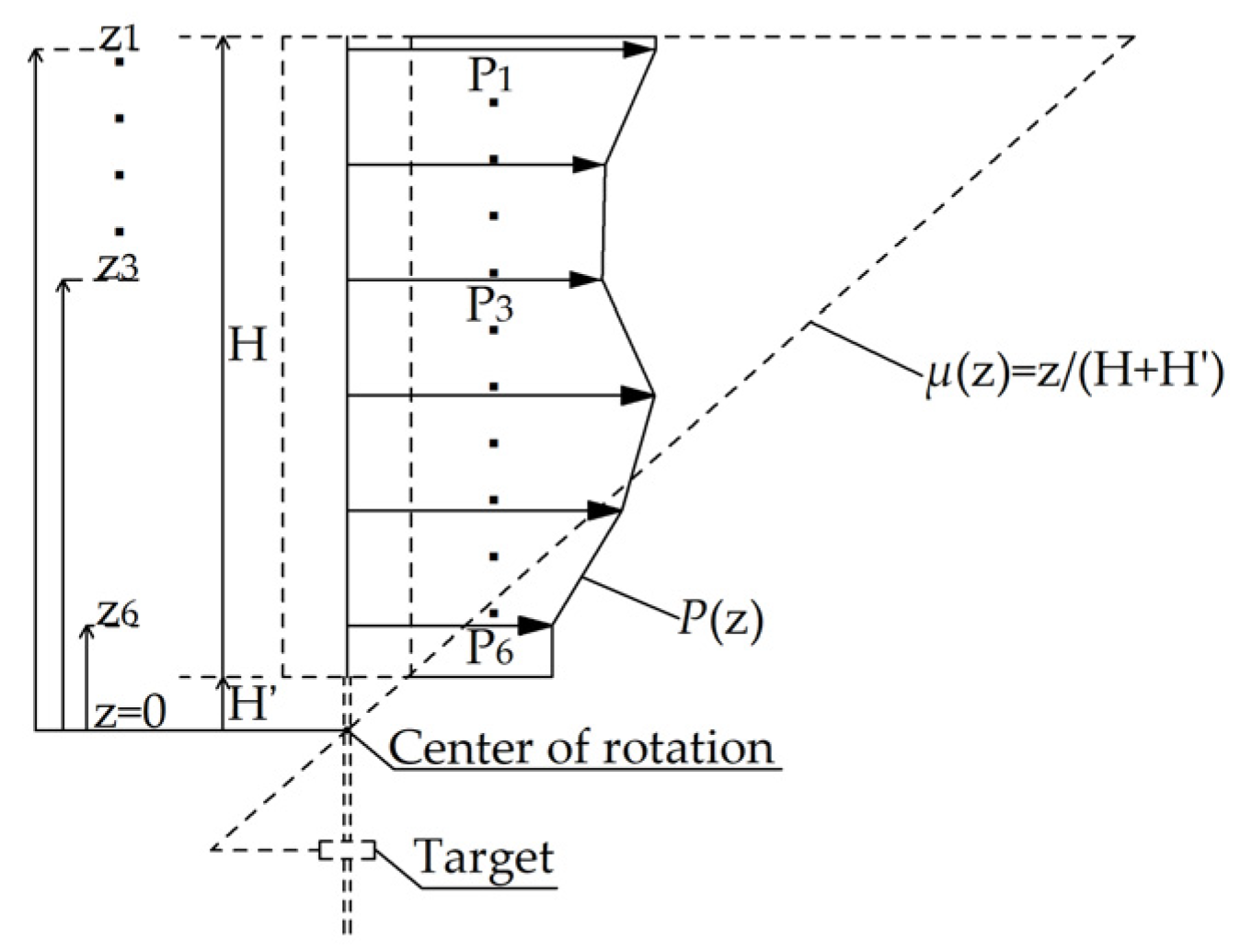
4.1.2. Element Exchange Vector
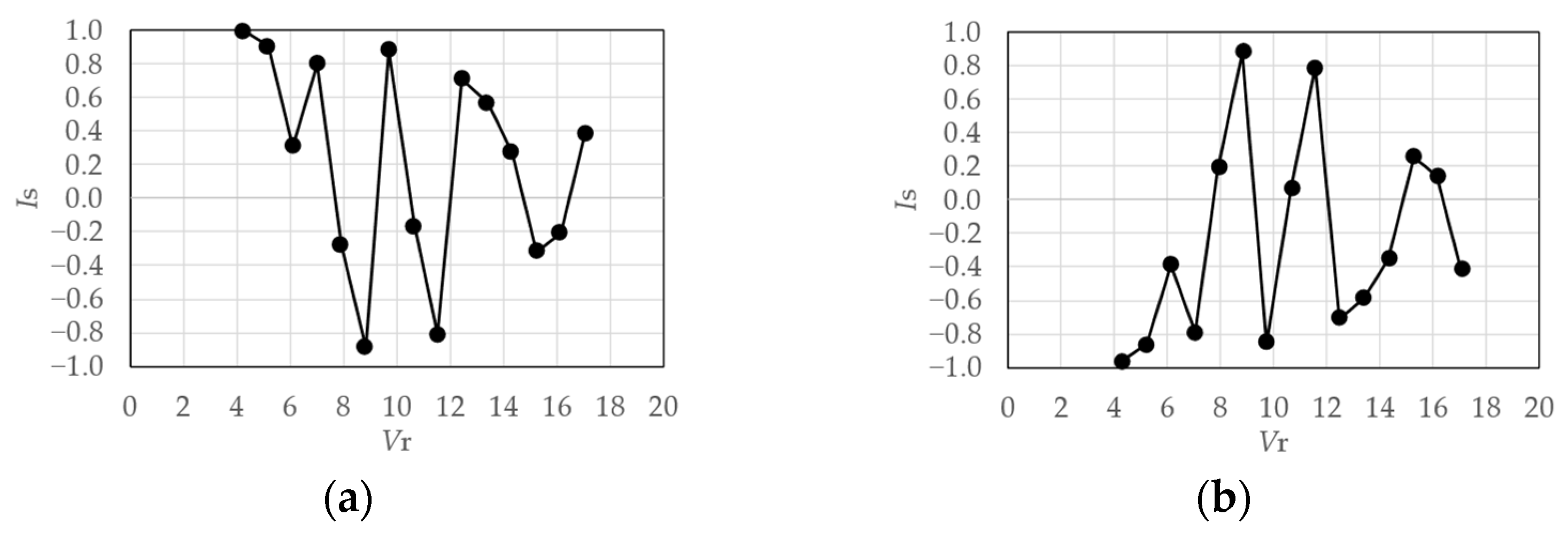
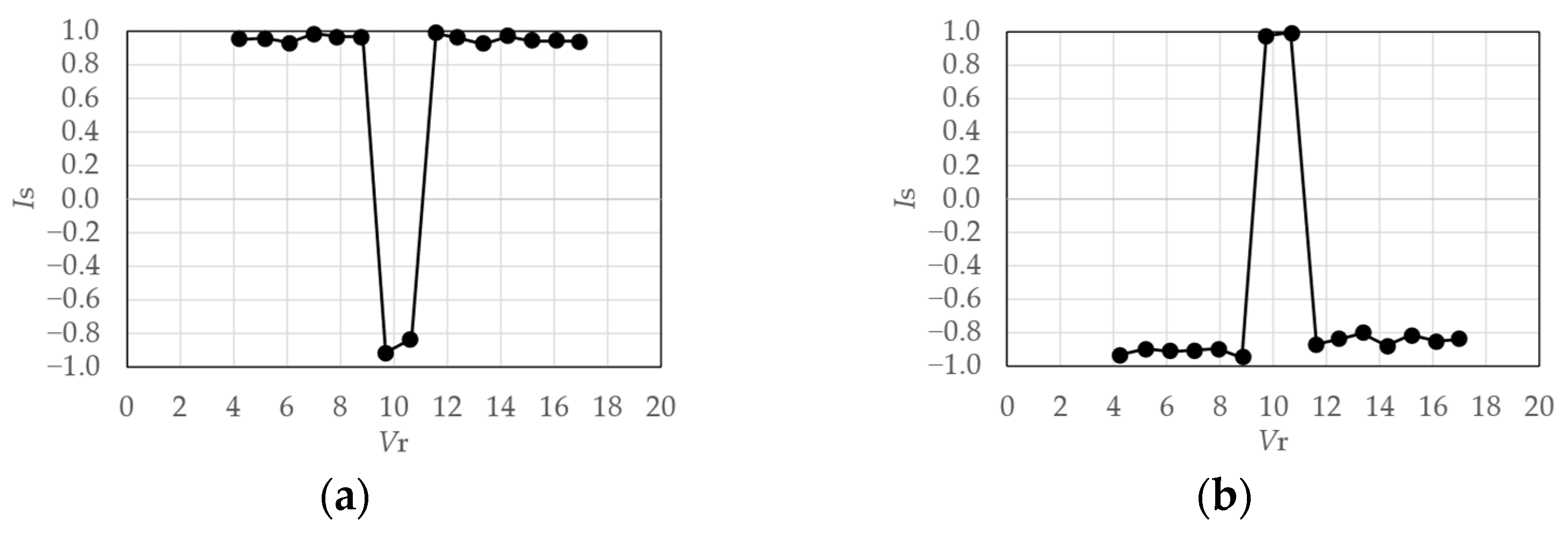
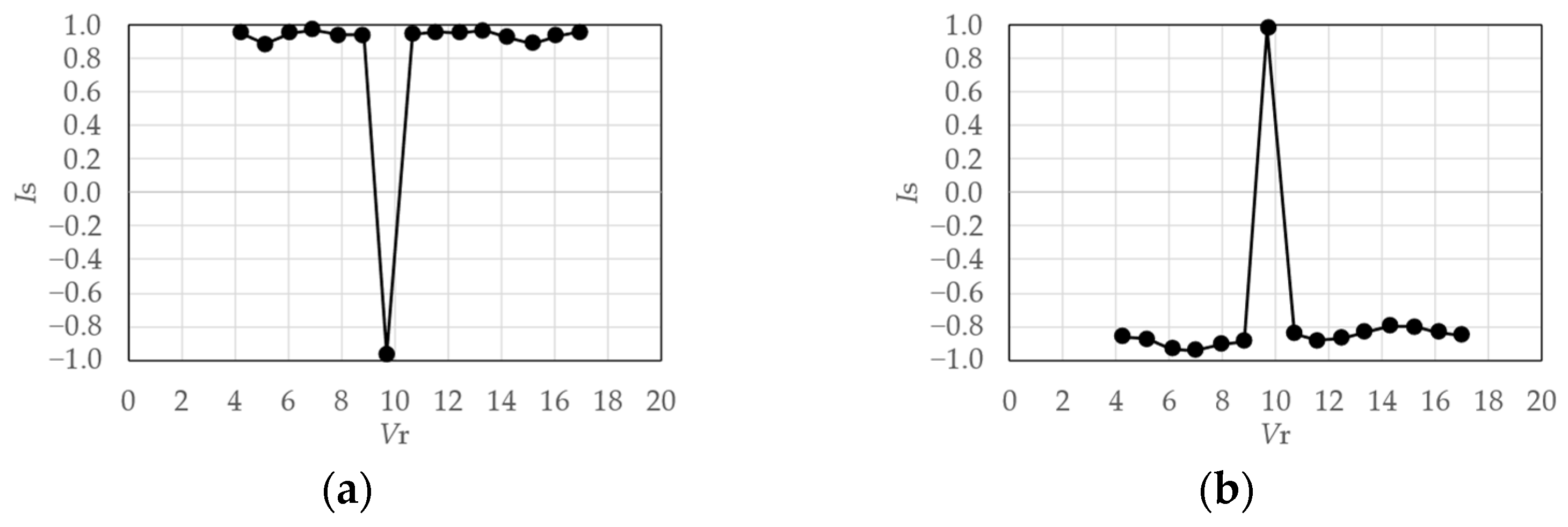
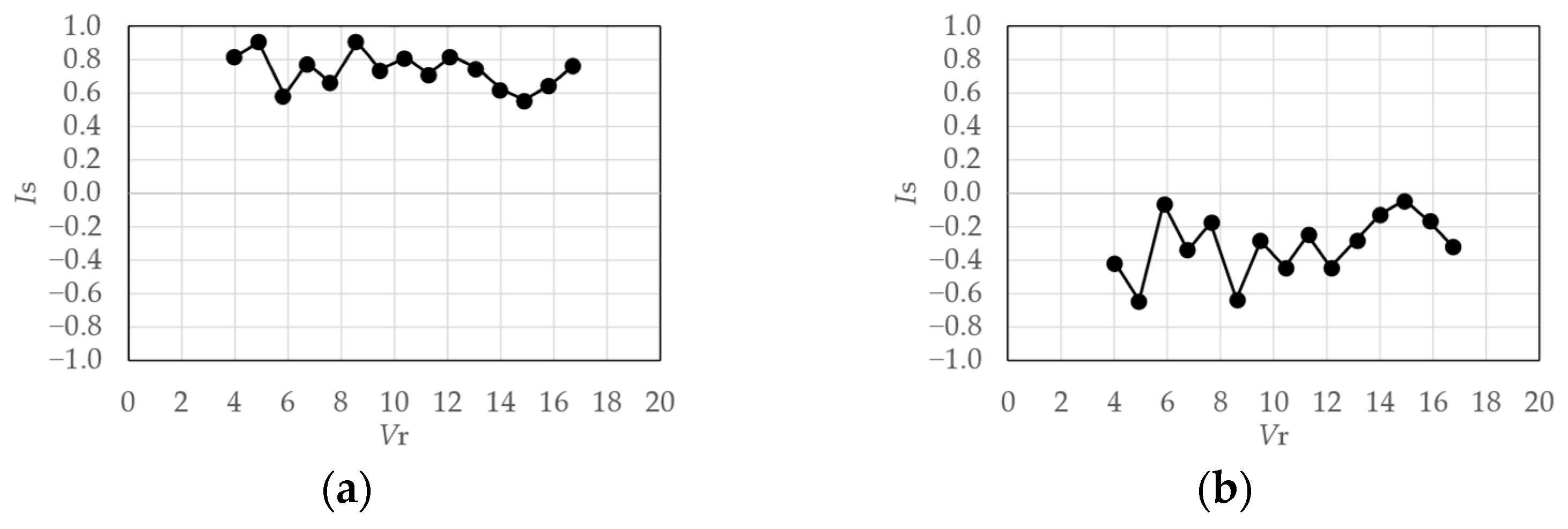
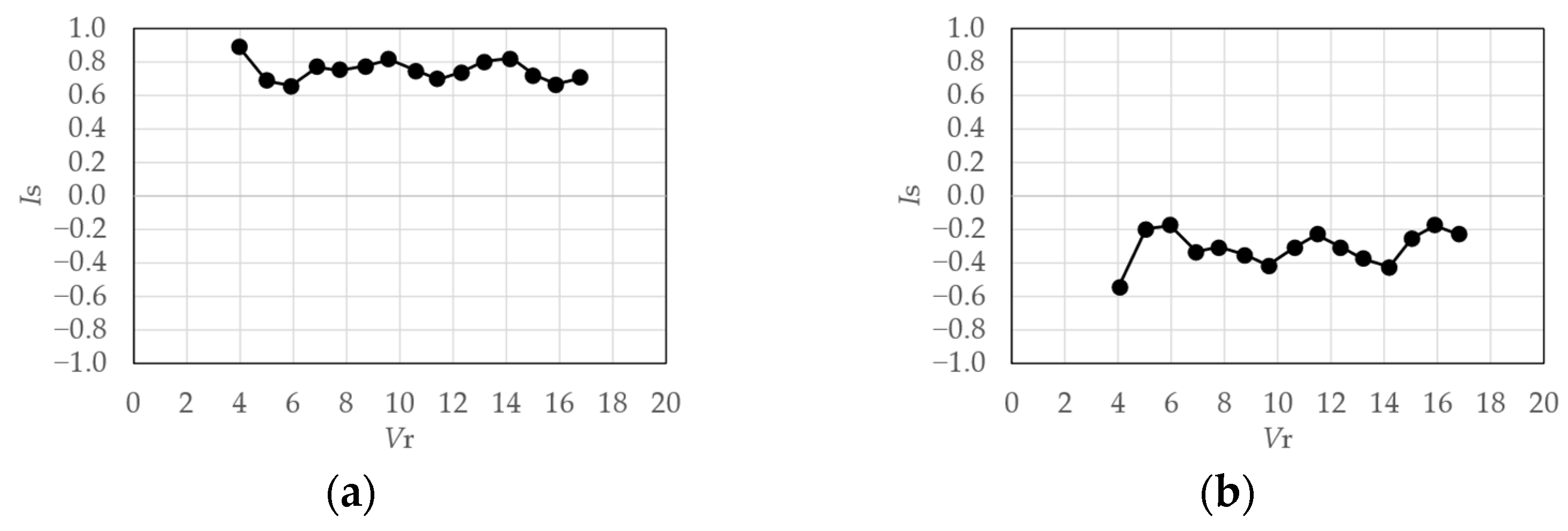
4.1.3. Symmetry Index
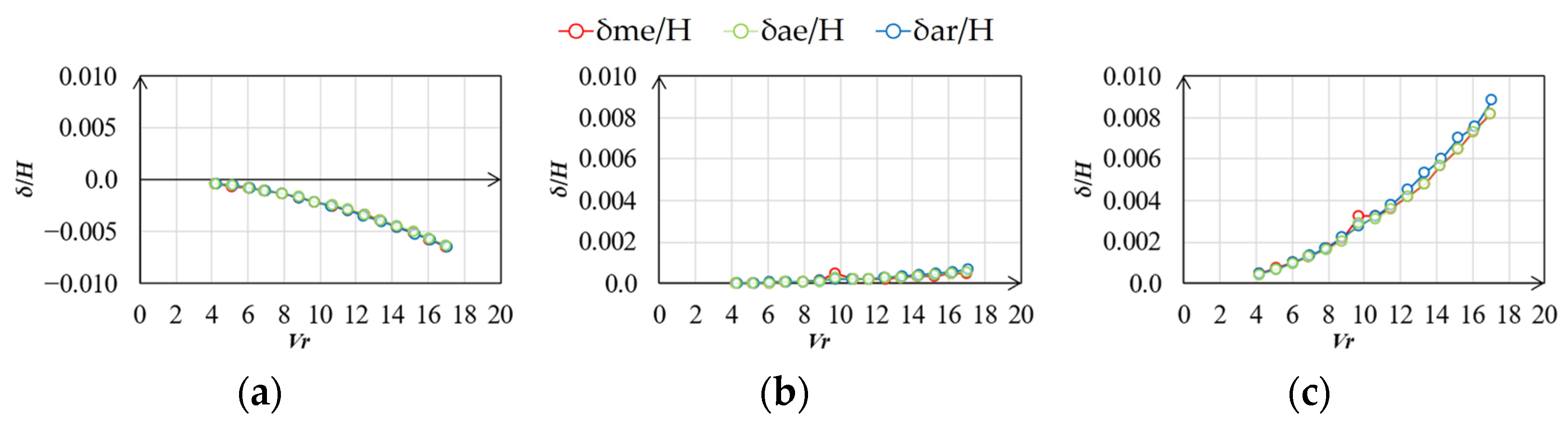
4.1.4. Evaluation Results
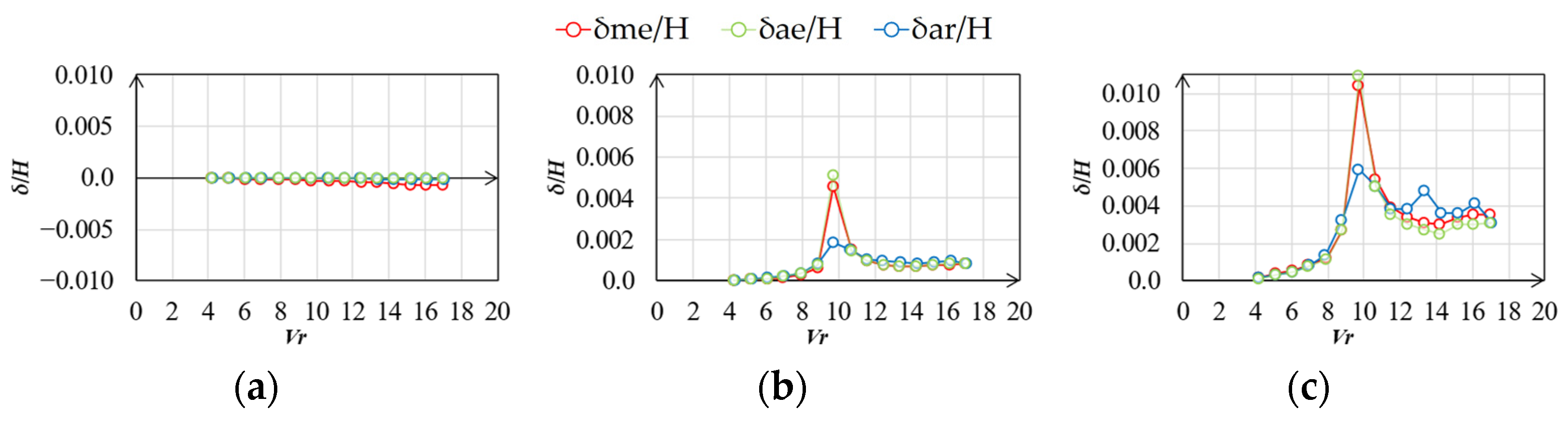
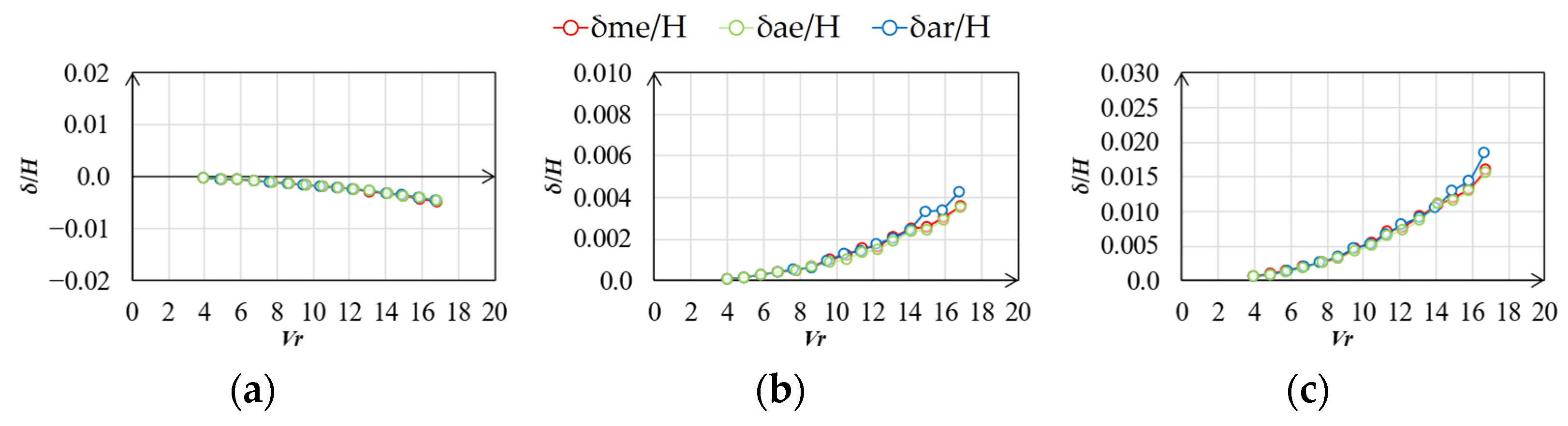
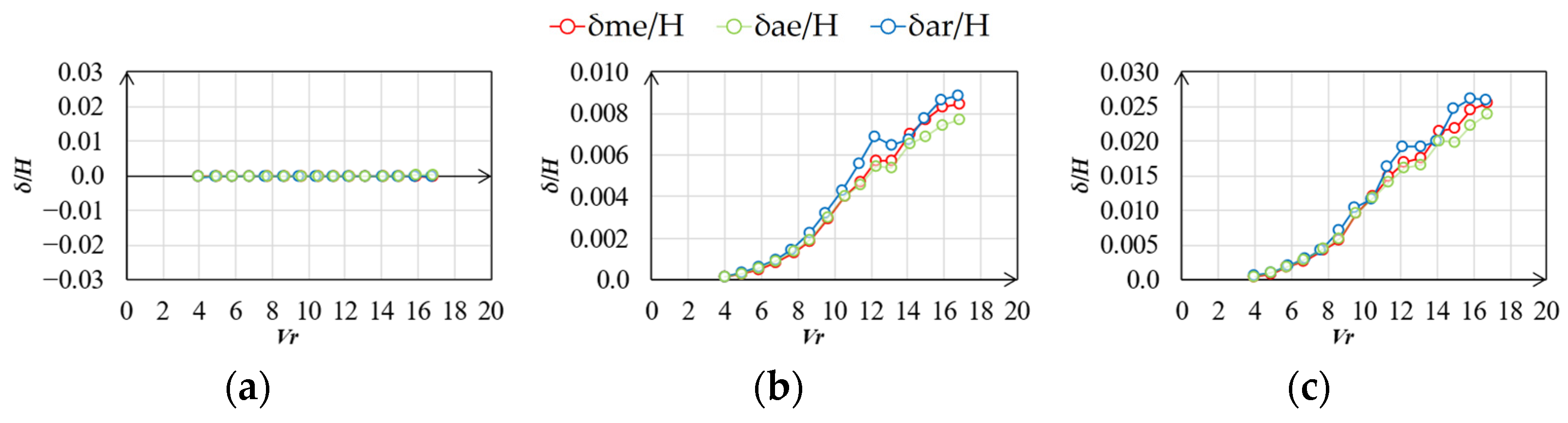
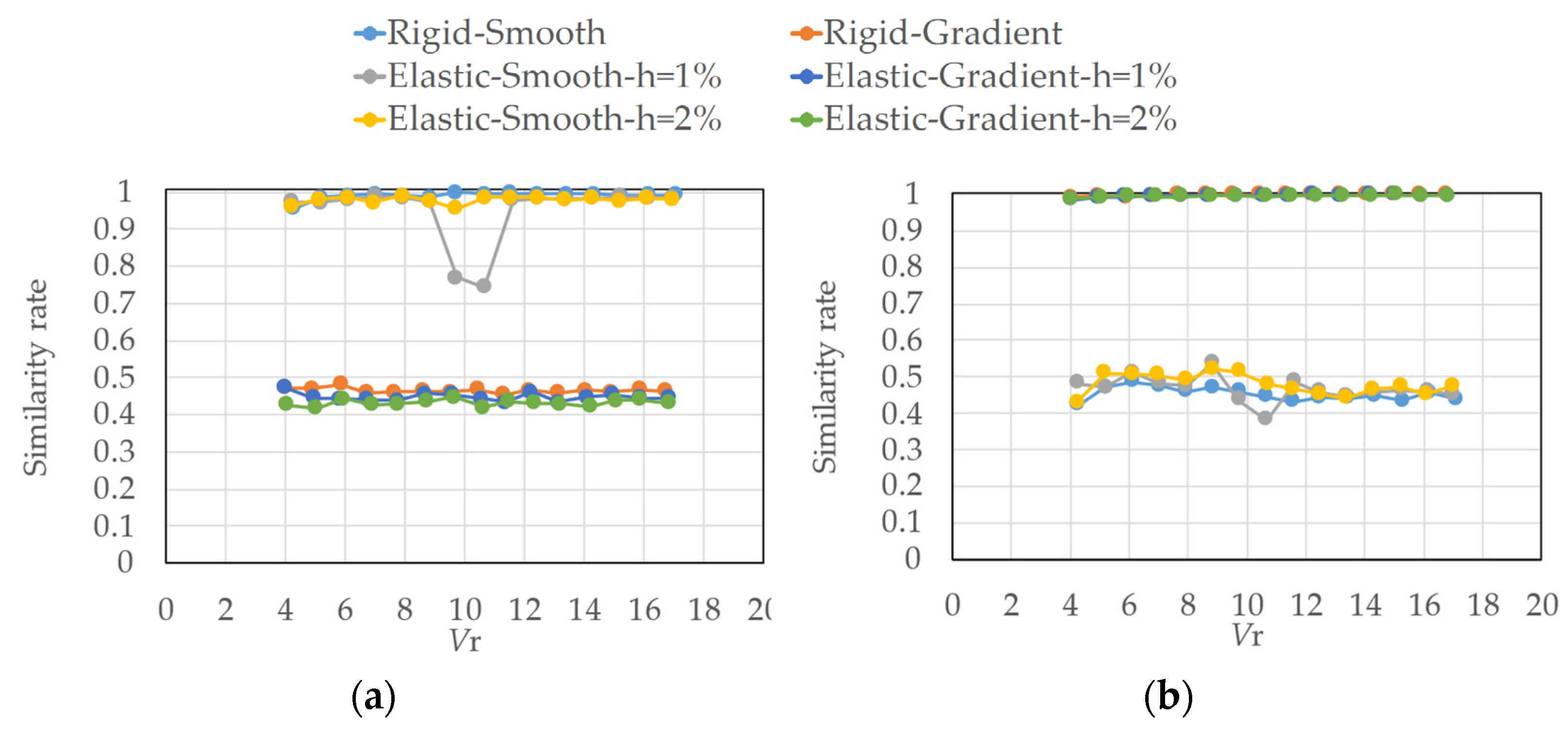
4.2. Similarity Rate of Fluctuating Wind Pressure Fields
5. Recomposition of Fluctuating Wind Pressure Fields
5.1. Principal Coordinate
5.2. Correlation of Wind Pressure Field
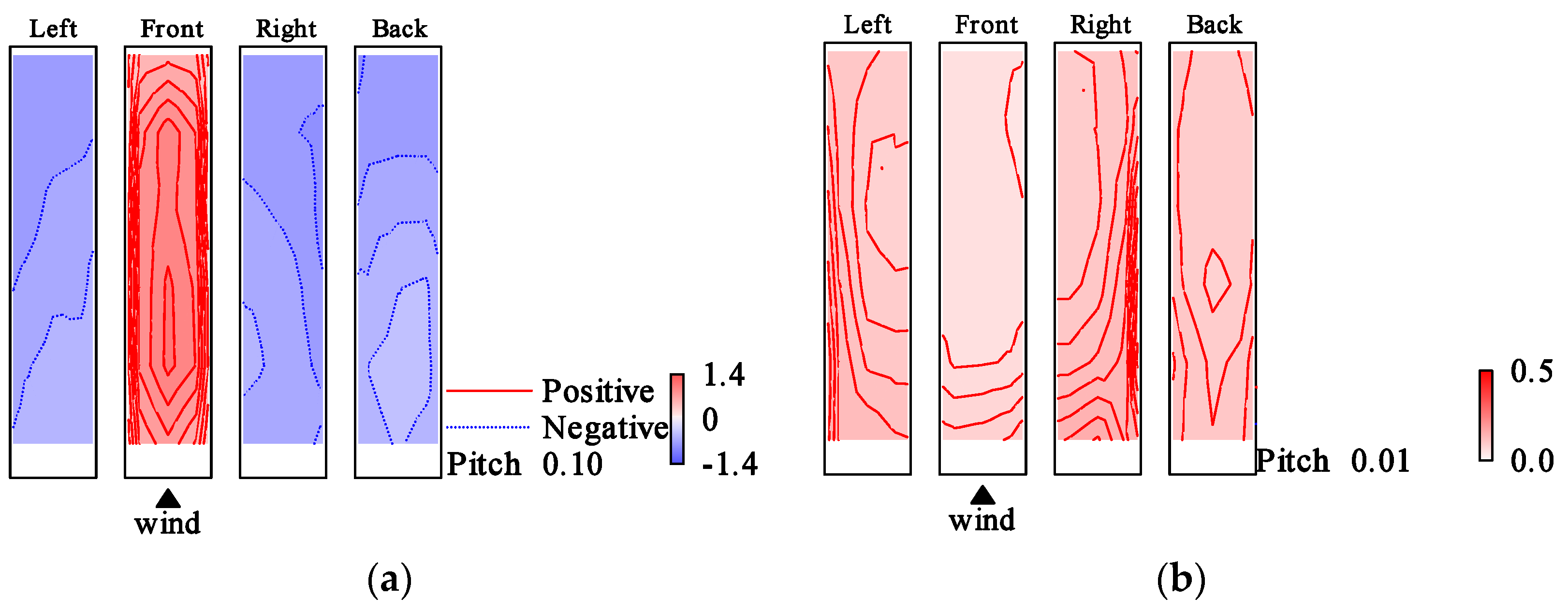
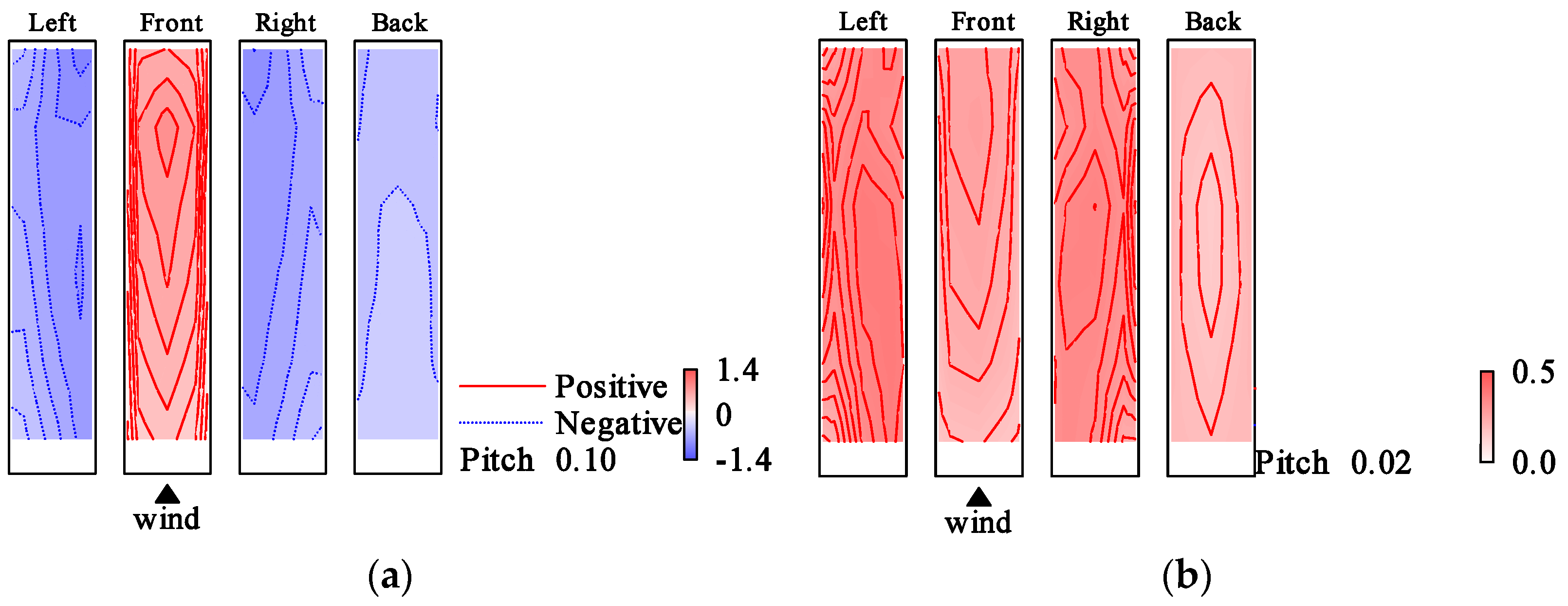
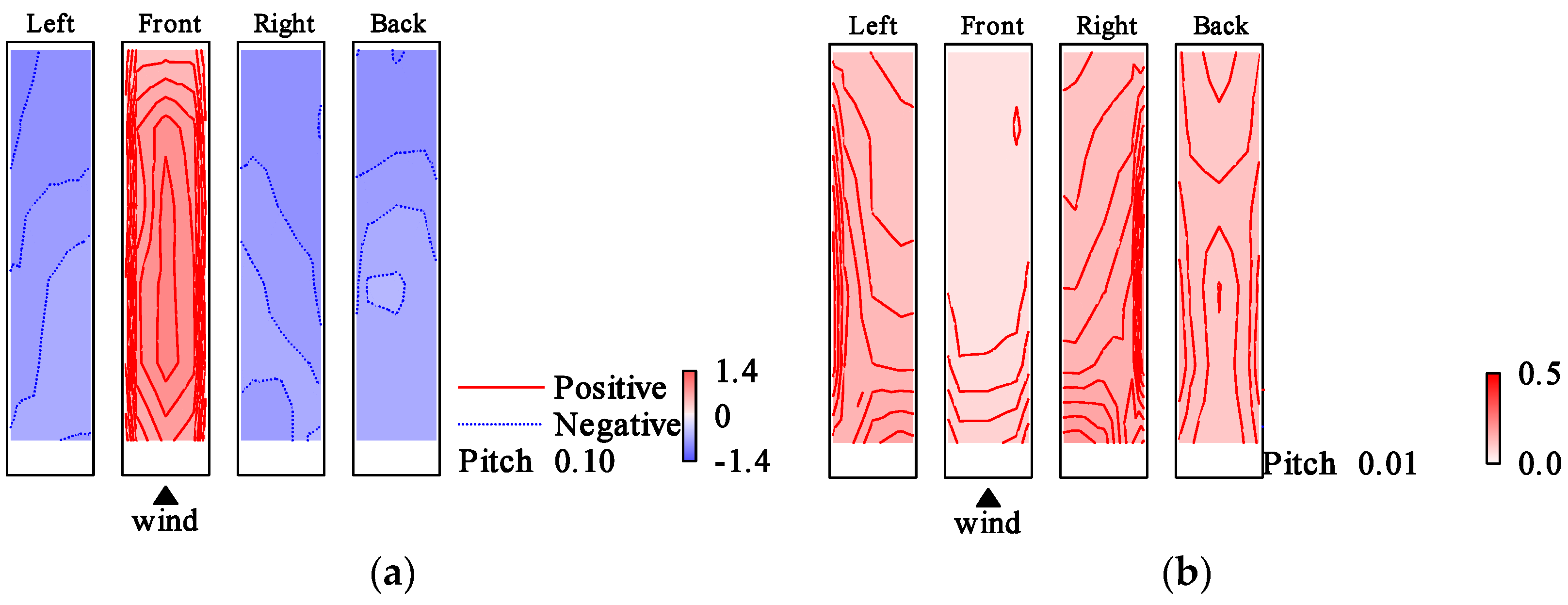
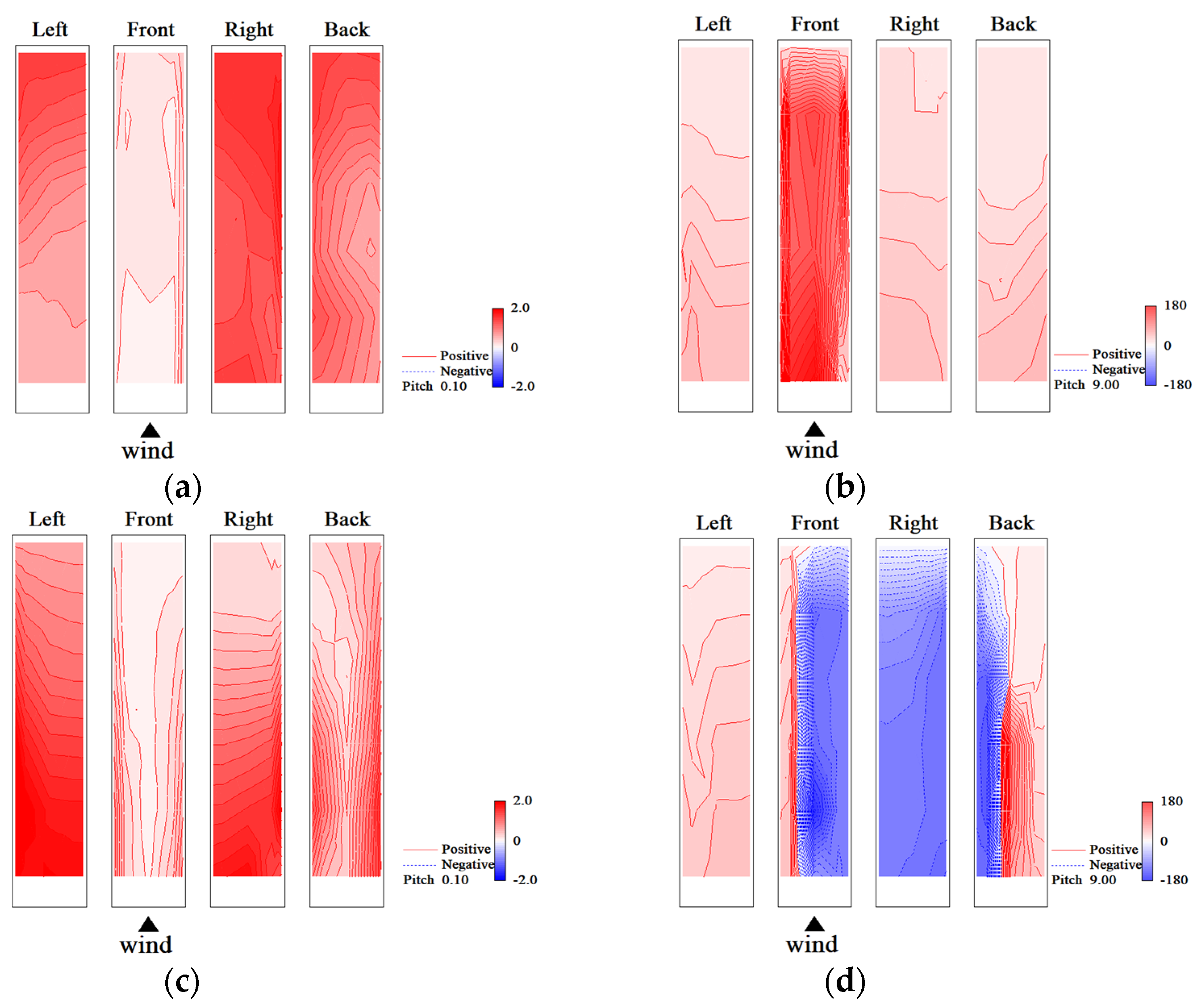
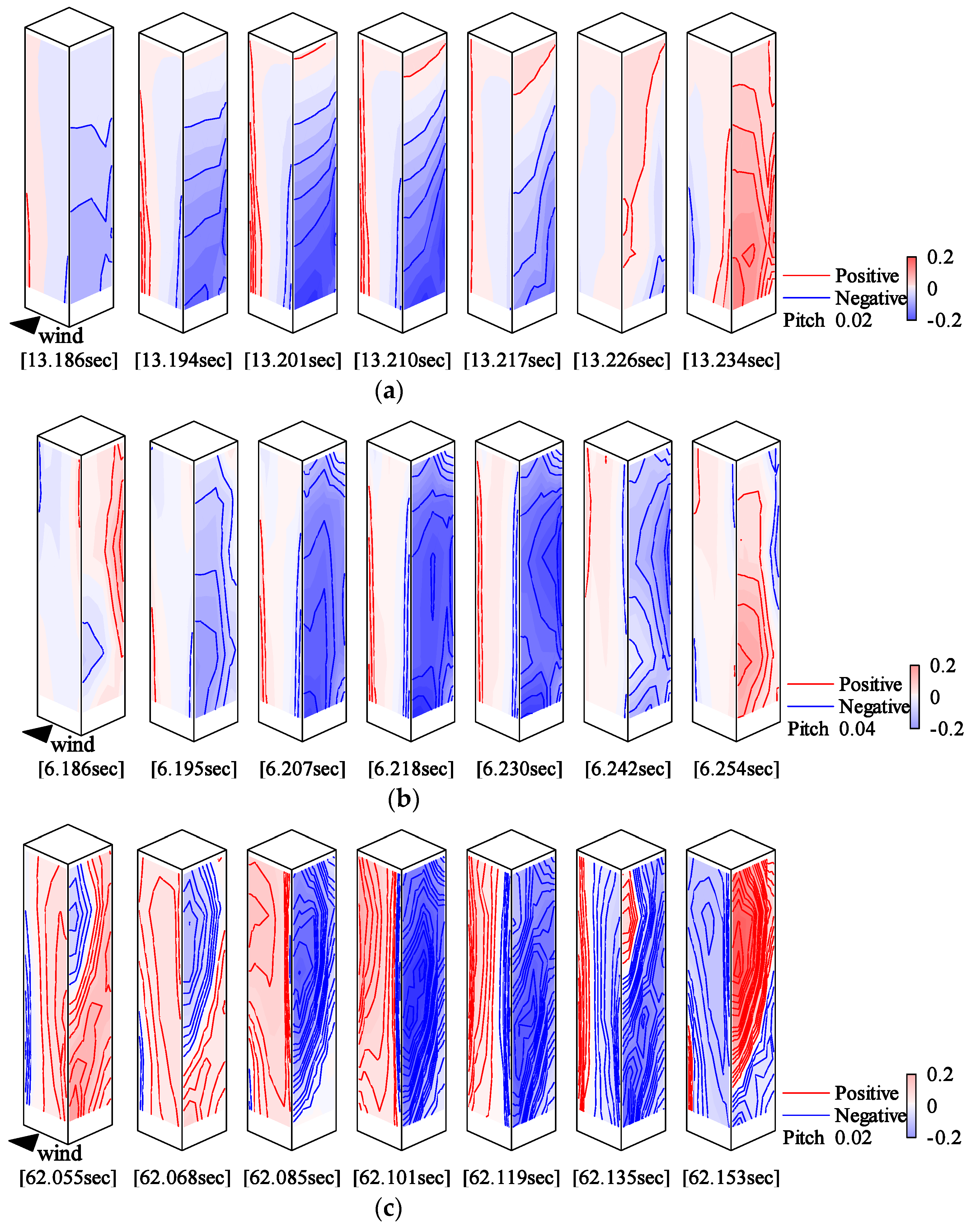
5.3. Wind Pressure Fields of Symmetric Mode
- Typical measurement case of Type 1: Rigid model, smooth flow, Vr = 9.7.
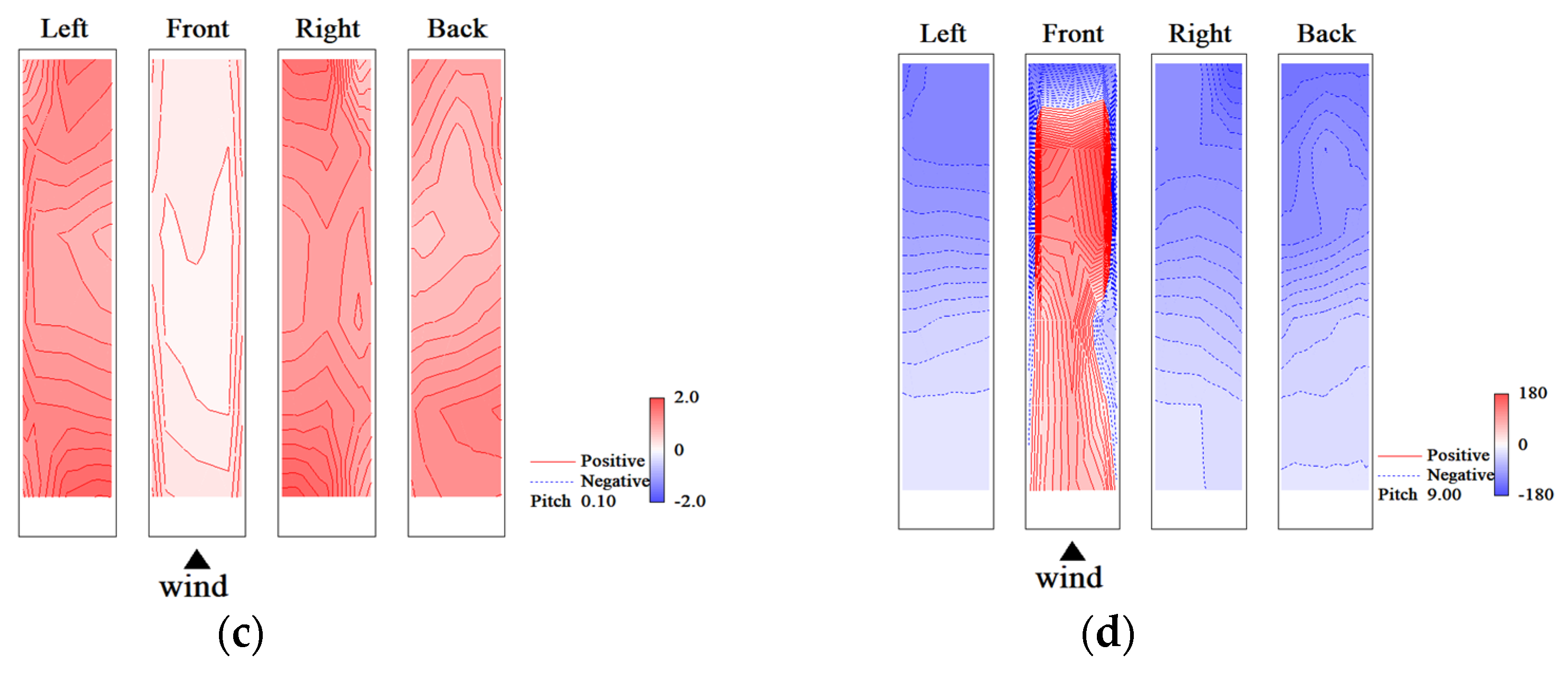
- Typical measurement case of Type 2: Elastic model, smooth flow, Vr = 9.7, h = 1%
- Typical measurement case of Type 3: Elastic model, gradient flow, Vr = 9.6, h = 1%
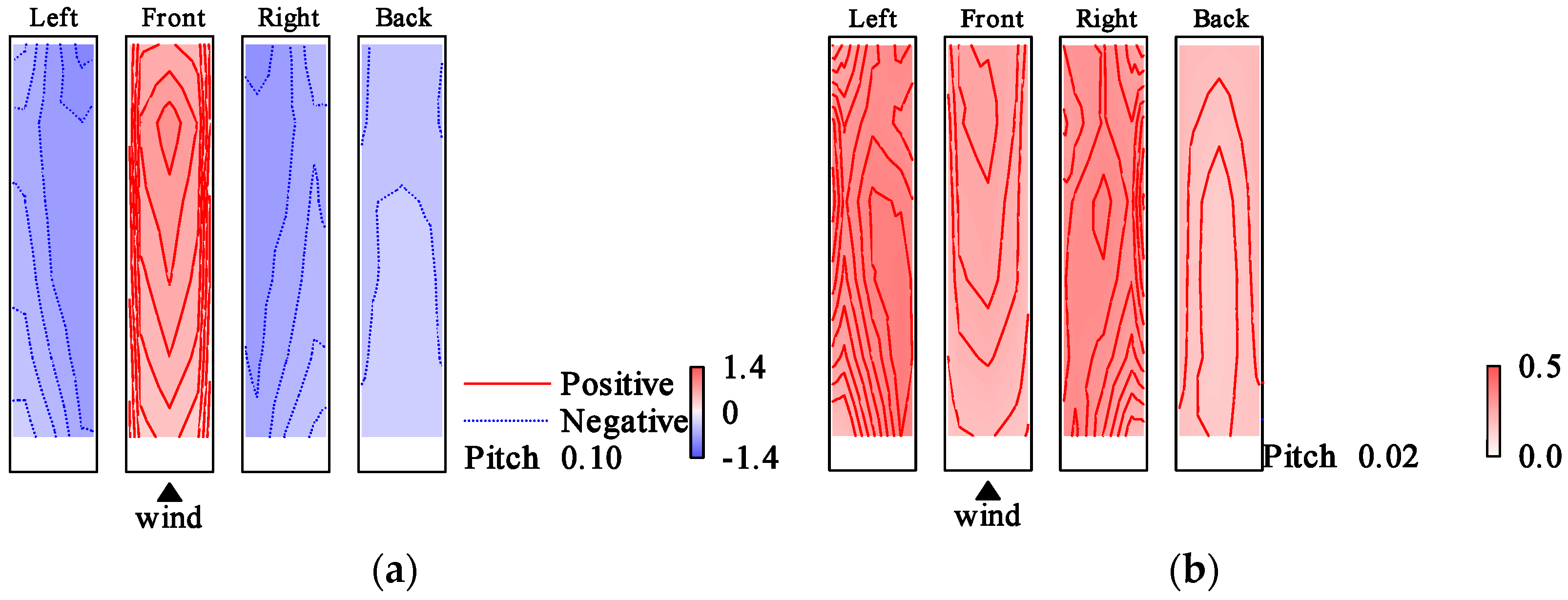
5.4. Wind Pressure Fields of Anti-Symmetric Mode
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Han, X.L.; Li, Q.S.; Zhou, K.; Li, X. Comparative study between field measurements of wind pressures on a 600-m-high skyscraper during Super Typhoon Mangkhut and wind tunnel test. Eng. Struct. 2022, 272, 114958. [Google Scholar] [CrossRef]
- Pomaranzi, G.; Amerio, L.; Schito, P.; Lamberti, G.; Gorlé, C.; Zasso, A. Wind tunnel pressure data analysis for peak cladding load estimation on a high-rise building. J. Wind Eng. Ind. Aerodyn. 2022, 220, 104855. [Google Scholar] [CrossRef]
- Park, S.; Yeo, D. Effects of aerodynamic pressure tap layout and resolution on estimated response of high-rise structures: A case study. Eng. Struct. 2021, 234, 111811. [Google Scholar] [CrossRef]
- Lu, B.; Li, Q.S. Investigation of the effects of wind veering and low-level jet on wind loads of super high-rise buildings by large eddy simulations. J. Wind Eng. Ind. Aerodyn. 2022, 227, 105056. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X. Evaluation of wind loads on high-rise buildings at various angles of attack by wall-modeled large-eddy simulation. J. Wind Eng. Ind. Aerodyn. 2022, 229, 105160. [Google Scholar] [CrossRef]
- Li, S.H.; Kilpatrick, J.; Browne, M.T.L.; Yakymyk, W.; Refan, M. Uncertainties in prediction of local peak wind pressures on mid- and high-rise buildings by considering gumbel distributed pressure coefficients. J. Wind Eng. Ind. Aerodyn. 2020, 206, 104364. [Google Scholar] [CrossRef]
- Lamberti, G.; Gorlé, C. Sensitivity of LES predictions of wind loading on a high-rise building to the inflow boundary condition. J. Wind Eng. Ind. Aerodyn. 2020, 206, 104370. [Google Scholar] [CrossRef]
- Hubova, O.; Macak, M.; Konecna, L.; Ciglan, G. External pressure coefficients on the atypical high-rise building–Computing simulation and measurements in wind tunnel. Procedia. Eng. 2017, 190, 488–498. [Google Scholar] [CrossRef]
- Tamura, Y.; Ueda, H.; Kikuchi, H.; Hibi, K.; Suganuma, S.; Bienkiewicz, B. Proper orthogonal decomposition study of approach wind-building pressure correlation. J. Wind Eng. Ind. Aerodyn. 1997, 72, 421–431. [Google Scholar] [CrossRef]
- Li, F.; Gu, M.; Ni, Z.; Shen, S. Wind pressures on structures by proper orthogonal decomposition. J. Civ. Eng. Archit. 2012, 6, 238–243. [Google Scholar]
- Kim, B.; Tse, K.T.; Tamura, Y. POD analysis for aerodynamic characteristics of tall linked buildings. J. Wind Eng. 2018, 181, 126–140. [Google Scholar] [CrossRef]
- Jeong, S.H.; Bienkiewicz, B.; Ham, H.J. Proper orthogonal decomposition of building wind pressure specified at non-uniformly distributed pressure taps. J. Wind Eng. 2000, 87, 1–14. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, X.; Zhou, D.; Ren, H. Investigation of local severe suction on the side walls of a high-rise building by standard, spectral and conditional POD. Build. Environ. 2022, 217, 109047. [Google Scholar] [CrossRef]
- Zhou, L.; Tse, K.T.; Hu, G.; Li, Y. Mode interpretation of interference effects between tall buildings in tandem and side-by-side arrangement with POD and ICA. Eng. Struct. 2021, 243, 112616. [Google Scholar] [CrossRef]
- Mohammadi, A.; Morton, C.; Martinuzzi, R.J. Benefits of Spectral Proper Orthogonal Decomposition in Separation of Flow Dynamics in the Wake of a Cantilevered Square Cylinder. Available online: https://ssrn.com/abstract=4269011 (accessed on 31 December 2022).
- Bourgeois, J.A.; Sattari, P.; Martinuzzi, R.J. Coherent vortical and straining structures in the finite wall-mounted square cylinder wake. Int. J. Heat Fluid Flow 2012, 35, 130–140. [Google Scholar] [CrossRef]
- Dongmei, H.; Shiqing, H.; Xuhui, H.; Xue, Z. Prediction of wind loads on high-rise building using a BP neural network combined with POD. J. Wind Eng. Ind. Aerodyn. 2017, 170, 1–17. [Google Scholar] [CrossRef]
- Huang, G.; Peng, L.; Kareem, A.; Song, G. Data-driven simulation of multivariate nonstationary winds: A hybrid multivariate empirical mode decomposition and spectral representation method. J. Wind Eng. Ind. Aerodyn. 2020, 197, 104073. [Google Scholar] [CrossRef]
- Tan, Z.X.; Zhu, L.D.; Zhu, Q.; Xu, Y.L. Modelling of distributed aerodynamic pressures on bridge decks based on proper orthogonal decomposition. J. Wind Eng. Ind. Aerodyn. 2018, 172, 181–195. [Google Scholar] [CrossRef]
- Tan, Z.X.; Xu, Y.L.; Zhu, L.D.; Zhu, Q. POD-based modelling of distributed aerodynamic and aeroelastic pressures on bridge decks. J. Wind Eng. Ind. Aerodyn. 2018, 179, 524–540. [Google Scholar] [CrossRef]
- Sheidani, A.; Salavatidezfouli, S.; Stabile, G.; Rozza, G. Assessment of URANS and LES methods in predicting wake shed behind a vertical axis wind turbine. J. Wind Eng. Ind. Aerodyn. 2023, 232, 105285. [Google Scholar] [CrossRef]
- Cao, Y.; Ping, H.; Tamura, T.; Zhou, D. Wind peak pressures on a square-section cylinder: Flow mechanism and standard/conditional POD analyses. J. Wind Eng. Ind. Aerodyn. 2022, 222, 104918. [Google Scholar] [CrossRef]
- Zhao, N.; Jiang, Y.; Peng, L.; Chen, X. Fast simulation of nonstationary wind velocity fields by proper orthogonal decomposition interpolation. J. Wind Eng. Ind. Aerodyn. 2021, 219, 104798. [Google Scholar] [CrossRef]
- Andersen, M.S.; Bossen, N.S. Modal decomposition of the pressure field on a bridge deck under vortex shedding using POD, DMD and ERA with correlation functions as Markov parameters. J. Wind Eng. Ind. Aerodyn. 2021, 215, 104699. [Google Scholar] [CrossRef]
- Ma, K.; Hu, C.; Zhou, Z. Investigation on vortex-induced vibration of twin rectangular 5:1 cylinders through wind tunnel tests and POD analysis. J. Wind Eng. Ind. Aerodyn. 2019, 187, 97–107. [Google Scholar] [CrossRef]
- Asami, Y.; Terazaki, H. Fluctuating wind pressure properties on rectangular prism. In the case of using complex proper orthogonal decomposition. Rep. Taisei Technol. Cent. 1997, 30, 135–138. (In Japanese) [Google Scholar]
- Asami, Y. Characteristics of Fluctuating Wall Pressure of High-Rise-Buildings. In Proceedings of the 18th National Symposium on Wind Engineering, Tokyo, Japan, 1 December 2004; pp. 341–346. (In Japanese). [Google Scholar]
- Gabor, D. Theory of communications. J. Inst. Electr. Eng. 1946, 93, 429–457. [Google Scholar] [CrossRef]
- Taniguchi, T.; Taniike, Y. Study on complex POD analysis for the estimation of coherent structures. J. Wind Eng. 2006, 31, 123–130. (In Japanese) [Google Scholar] [CrossRef]
- Chauve, M.P.; Gal, P.L. Complex bi-orthogonal decomposition of a chain of coupled wakes. Physica D. 1992, 58, 407–413. [Google Scholar] [CrossRef]
- Harlander, U.; Larcher, T.V.; Wang, Y.; Egbers, C. PIV- and LDV-measurements of baroclinic wave interactions in a thermally driven rotating annulus. Exp. Fluids 2011, 51, 37–49. [Google Scholar] [CrossRef]
- Pfeffer, R.L.; Ahlquist, J.; Kung, R.; Chang, Y.; Li, G. A study of baroclinic wave behavior over bottom topography using complex principal component analysis of experimental data. J. Atmos. Sci. 1990, 47, 67–81. [Google Scholar] [CrossRef]
- Feeny, B.F. A complex orthogonal decomposition for wave motion analysis. J. Sound Vib. 2008, 310, 77–90. [Google Scholar] [CrossRef]
- Froitzheim, A.; Ezeta, R.; Huisman, S.G.; Merbold, S.; Sun, C.; Lohse, D.; Egbers, C. Statistics, plumes and azimuthally travelling waves in ultimate Taylor–Couette turbulent vortices. J. Fluid Mech. 2019, 876, 733–765. [Google Scholar] [CrossRef] [Green Version]
- Georgiou, I.T.; Papadopoulos, C.I. Developing POD over the Complex Plane to form a Data Processing Tool for Finite Element Simulations of Steady State Structural Dynamics. In Proceedings of the International Mechanical Engineering Congress and Exposition, Chicago, IL, USA, 5–10 November 2006. [Google Scholar]
- Nakamura, R.; Taniguchi, T. Study of the three-dimensional fluctuating pressure field above a flat plate roof. In Proceedings of the 7th International Symposium on Computational Wind Engineering, Seoul, Republic of Korea, 18–22 June 2018. [Google Scholar]
- Architectural Institute of Japan. Recommendations for Loads on Buildings; Architectural Institute of Japan: Tokyo, Japan, 2015. [Google Scholar]




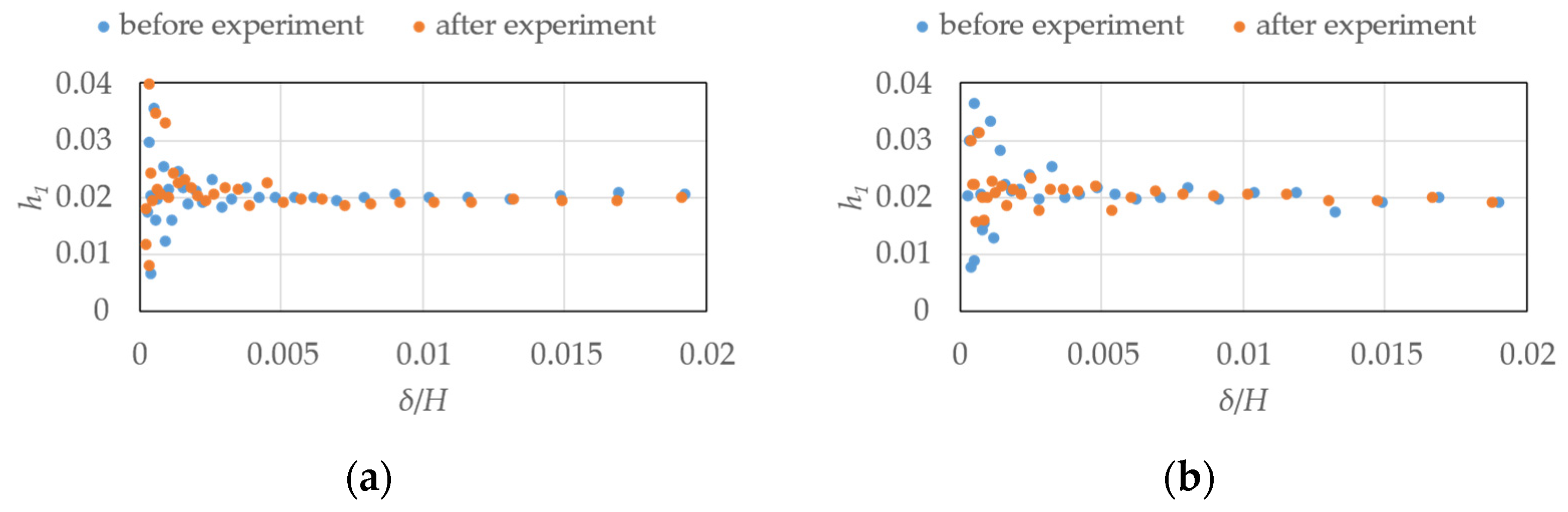
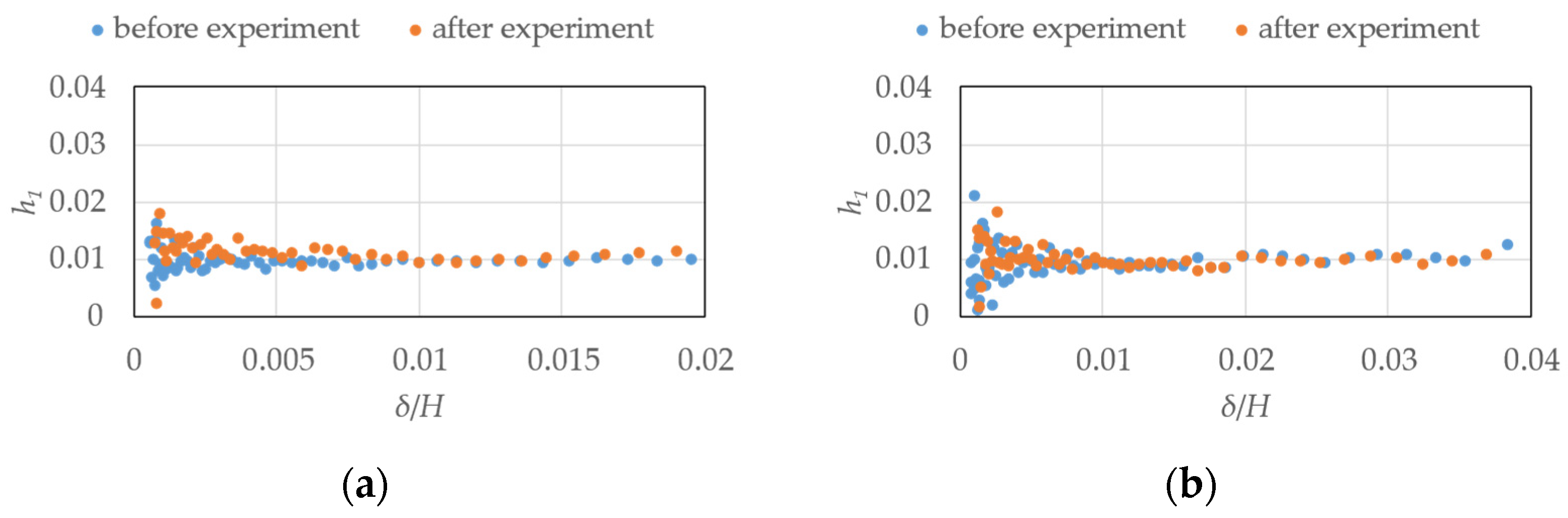
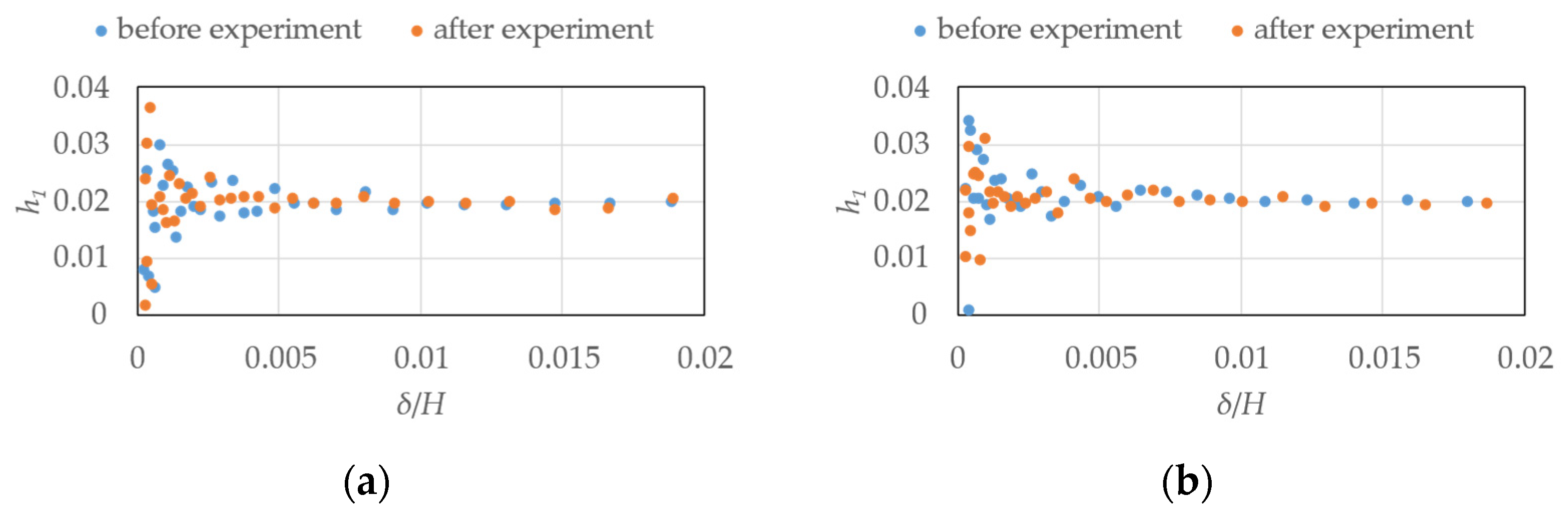













| Structural Specification | Target Building | Experimental Model | ||
|---|---|---|---|---|
| Natural frequency (Hz) | 0.25 | 8.34 | ||
| Wind speed at reference height (m/s) | 31.0–126.9 | 2.6–10.6 | ||
| Reduced wind velocity Vr | 4.1–16.9 | 4.1–16.9 | ||
| Building density (kg/m3) | 300 | 307 | ||
| Generalized mass (kg) | 13,500,000 | 0.216 | ||
| Damping ratio h (%) | Smooth flow | Along wind | 1 | 1.08 |
| Across wind | 1.02 | |||
| Gradient flow | Along wind | 1.04 | ||
| Across wind | 0.96 | |||
| Smooth flow | Along wind | 2 | 2.03 | |
| Across wind | 1.97 | |||
| Gradient flow | Along wind | 1.97 | ||
| Across wind | 2.00 | |||
| Type of Fluctuating Wind Pressure Field | Model | Flow | h | Vr |
|---|---|---|---|---|
| Type 1 (Smooth flow without resonance) | Rigid | Smooth | - | All measured Vr |
| Elastic | 1% | Except 9.7 and 10.7 | ||
| 2% | All measured Vr | |||
| Type 2 (Smooth flow with resonance) | Elastic | Smooth | 1% | 9.7, 10.7 |
| Type 3 (Gradient flow) | Rigid | Gradient | - | All measured Vr |
| Elastic | 1% | |||
| 2% |
| Type of Fluctuating Wind Pressure Field | 1 | 2 | 3 | ||
|---|---|---|---|---|---|
| 1 | Smooth flow without resonance | - | 0.701 | 0.632 | |
| 2 | Smooth flow with resonance | 0.907 | - | 0.352 | |
| 3 | Gradient flow | 0.547 | 0.670 | - | |
| ) | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murakami, T.; Nishida, Y.; Taniguchi, T. Study on Phase Characteristics of Wind Pressure Fields around a Prism Using Complex Proper Orthogonal Decomposition. Wind 2023, 3, 35-63. https://doi.org/10.3390/wind3010004
Murakami T, Nishida Y, Taniguchi T. Study on Phase Characteristics of Wind Pressure Fields around a Prism Using Complex Proper Orthogonal Decomposition. Wind. 2023; 3(1):35-63. https://doi.org/10.3390/wind3010004
Chicago/Turabian StyleMurakami, Tomoyuki, Yuichiro Nishida, and Tetsuro Taniguchi. 2023. "Study on Phase Characteristics of Wind Pressure Fields around a Prism Using Complex Proper Orthogonal Decomposition" Wind 3, no. 1: 35-63. https://doi.org/10.3390/wind3010004
APA StyleMurakami, T., Nishida, Y., & Taniguchi, T. (2023). Study on Phase Characteristics of Wind Pressure Fields around a Prism Using Complex Proper Orthogonal Decomposition. Wind, 3(1), 35-63. https://doi.org/10.3390/wind3010004





