Consistency in Young’s Modulus of Powders: A Review with Experiments
Abstract
:1. Introduction
| Material | E [GPa] | Device, Methodology and Comments |
|---|---|---|
| Lactose | 4.6 | Device: Instrumented Frogerais OA machine; cylindrical die 1 cm2 × 1 cm. Methodology: maximal stress of 250 MPa; strain rate = 0.005 ; linear part of unloading curve [28]. |
| Avicel PH 101 | 3.0–12.9 | Device: Lloyd testing machine (JJ Lloyd T30 K). Methodology: compression of compacts; tablets with diameter from 5 to 13 mm; crosshead rate of 1 mm/min; Eo by Spriggs [25]. |
| Starch 1500 | 1.5–4.1 | |
| Calcium phosphate | 6.3–928 | |
| Avicel PH-101 | 0.25–25.0 | Device: high-speed compaction simulator (Phoenix Calibration & Services Ltd.); 8 mm instrumented die. Methodology: maximal stress of 250 MPa; compaction speed of 0.1 mm/s; linear part of unloading curve [24]. |
| Eudragit L100–55 | 1.6 ± 0.2 | Device: diametrical compression of a single particle; probe with a diameter of 50 m. Methodology: maximal stress = load required to cause fracture; displacement speed of 2 m/ms; compression till nominal strain of or [19]. |
| Eudragit L100 | 1.2 ± 0.5 | |
| Eudragit S100 | 0.6 ± 0.1 | |
| Advantose S100 | 0.9 ± 0.4 | |
| Calcium carbonate | 0.3 ± 0.1 | |
| Starlac | 1.8 ± 0.9 | |
| Granulated sugar | 0.0013–0.12 | Device: triaxial apparatus; Methodology: Young’s modulus in unloading cycles: combination of Poisson’s ratio, determined by triaxial test (pressures of 100, 200 and 300 kPa, compression rate of 0.51 mm/min), and oedometric modulus, determined by an oedometer (11 to 360 kPa); hygroscopic moisture between 0.1 and 14% [38]. |
| Confectioners’ sugar | 0.00053–0.23 | |
| Barley flour | 0.00020–0.023 | |
| Maize flour | 0.00032–0.094 | |
| Soja flour | 0.00054–0.043 | |
| Wheat flour | 0.00050–0.055 | |
| CRM 116 limestone | 3.0–3.7 | Device: uniaxial tester. Methodology: Low pressure (10–130 kPa); cyclic compression; ignores Poisson effect [29]. |
| Silica | 0.034–0.196 | |
| Alumina | 5.8–5.2 | |
| MCC Vivapur 12 | 0.1–2.6 | Device: Stylcam 200R (Medelpharm). Methodology: double compaction method; Precompression up to 90 % of main compression; main compression with elastic behavior [26]. |
| Anhydrous calcium phosphate | 0.9–6.5 | |
| Avicel PH200 | 0.5–2.2, 3.2 | Device: Stylcam 200R (Medelpharm). Methodology: double compaction method; precompression up to 90% of main compression; Young’s modulus from main compression, with linear (elastic) behavior; apparent Young’s modulus from precompression as a function of porosity and applied pressure [27]. |
| Anhydrous calcium phosphate | 1.8–5.8, 11.1 | |
| Ibuprofen DTP | 1.2–2.6, 4.3 | |
| Mannitol | 1.6–5.0, 190 | |
| Lactose monohydrate | 4.38–5.37 | Device: compaction simulator Styl’One Evolution (Medelpharm); diameter of 11.28 mm. Methodology: fourfold compaction; precompression of 100 MPa or 200 MPa, two more compressions at pressure lower than the first one; main compression with displacement between 50 and 100 m; strain rates between 0.001 and 1 s−1 [22]. |
| MCC Vivapur 200 | 1.43–2.52 | |
| Starch | 0.63–1.11 | |
| Anhydrous calcium phosphate | 7.34–10.00 | |
| MCC Vivapur 102 | 0.56–1.36 | Device: parallelepiped die compaction (1.56 × 5.4 × 4.0 cm); Methodology: elastic behavior considered linear, isotropic and density-dependent; pressure from 5 to 35 MPa [21] |
| API A | 1.8–2.7 | Device: servo-hydraulic compaction simulator (HB100). Methodology: elastic properties were determined using a cyclic compression approach ranging from 50 MPa to 300 MPa at 50 MPa increments. The compression data was acquired from the reloading region of a reloaded compact [39]. |
| API B | 2.5–4.5 | |
| Mannitol | 1.4–7.4 | |
| Avicel PH102 | 0.9–2.7 |
2. Theoretical Background: Linear Elasticity
2.1. Elastic Modulus of Powders Determined under Compression Methodologies
2.1.1. Uniaxial Compression
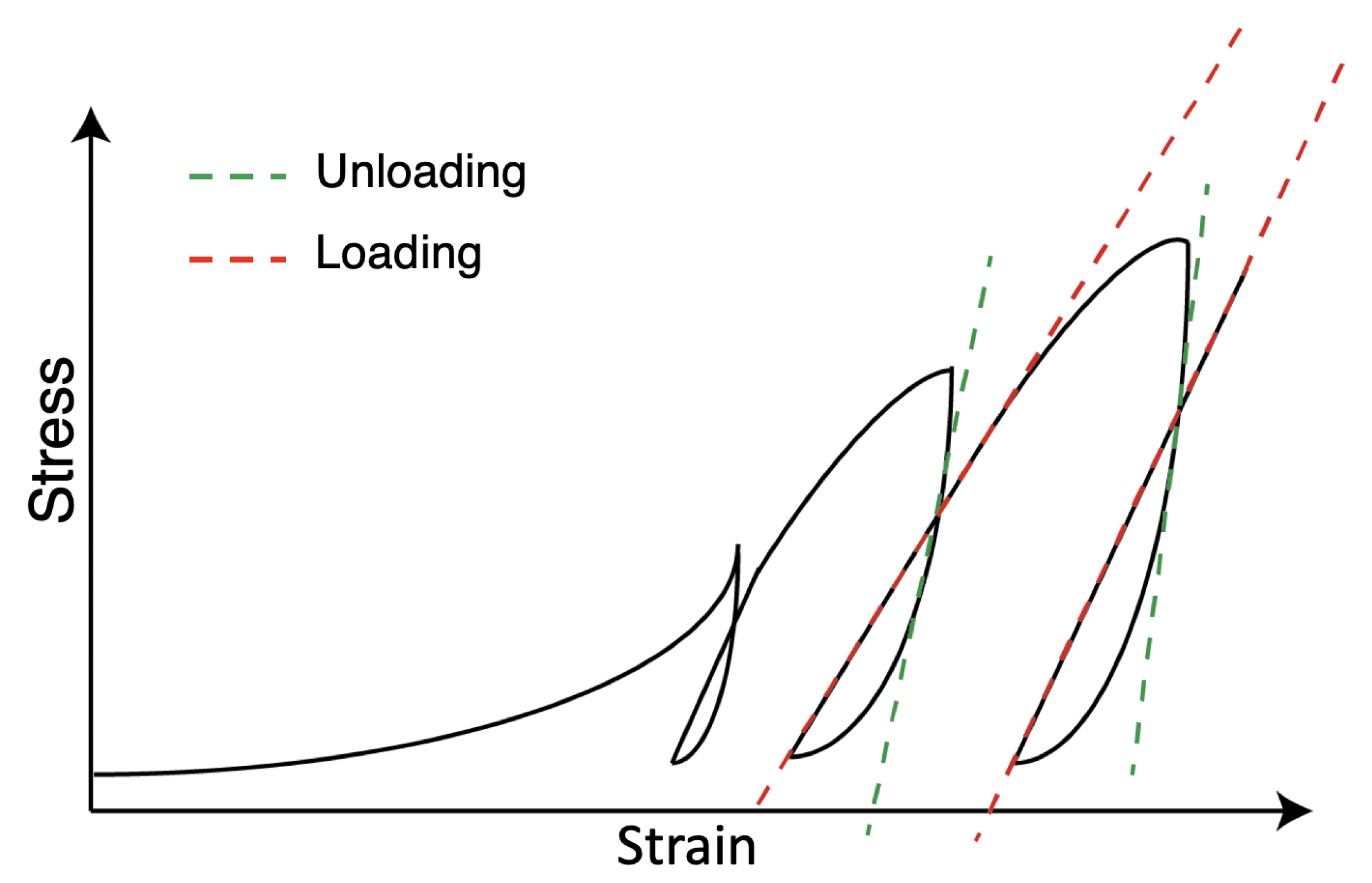
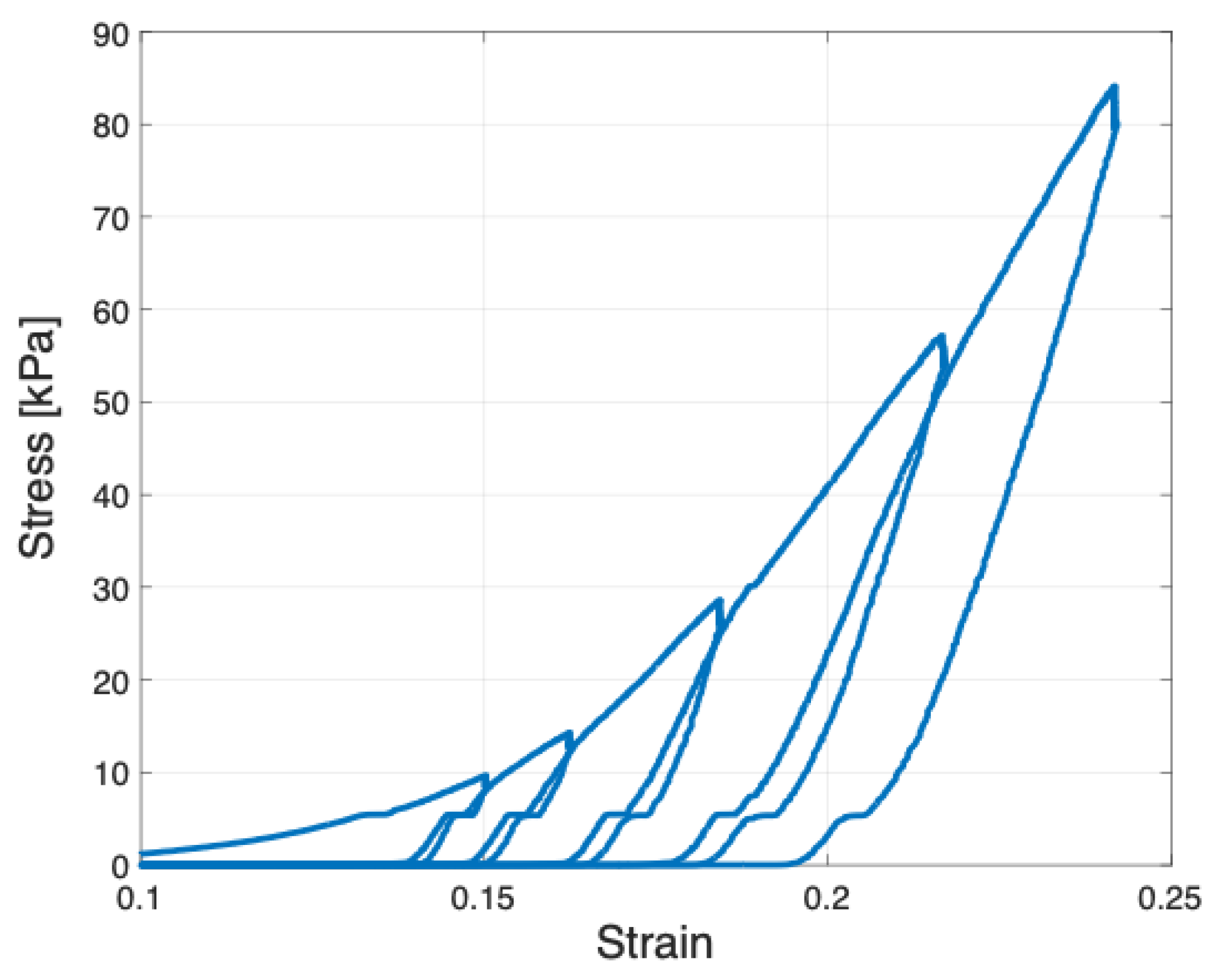
2.1.2. Cyclic Compression at Low Pressure (50 N)
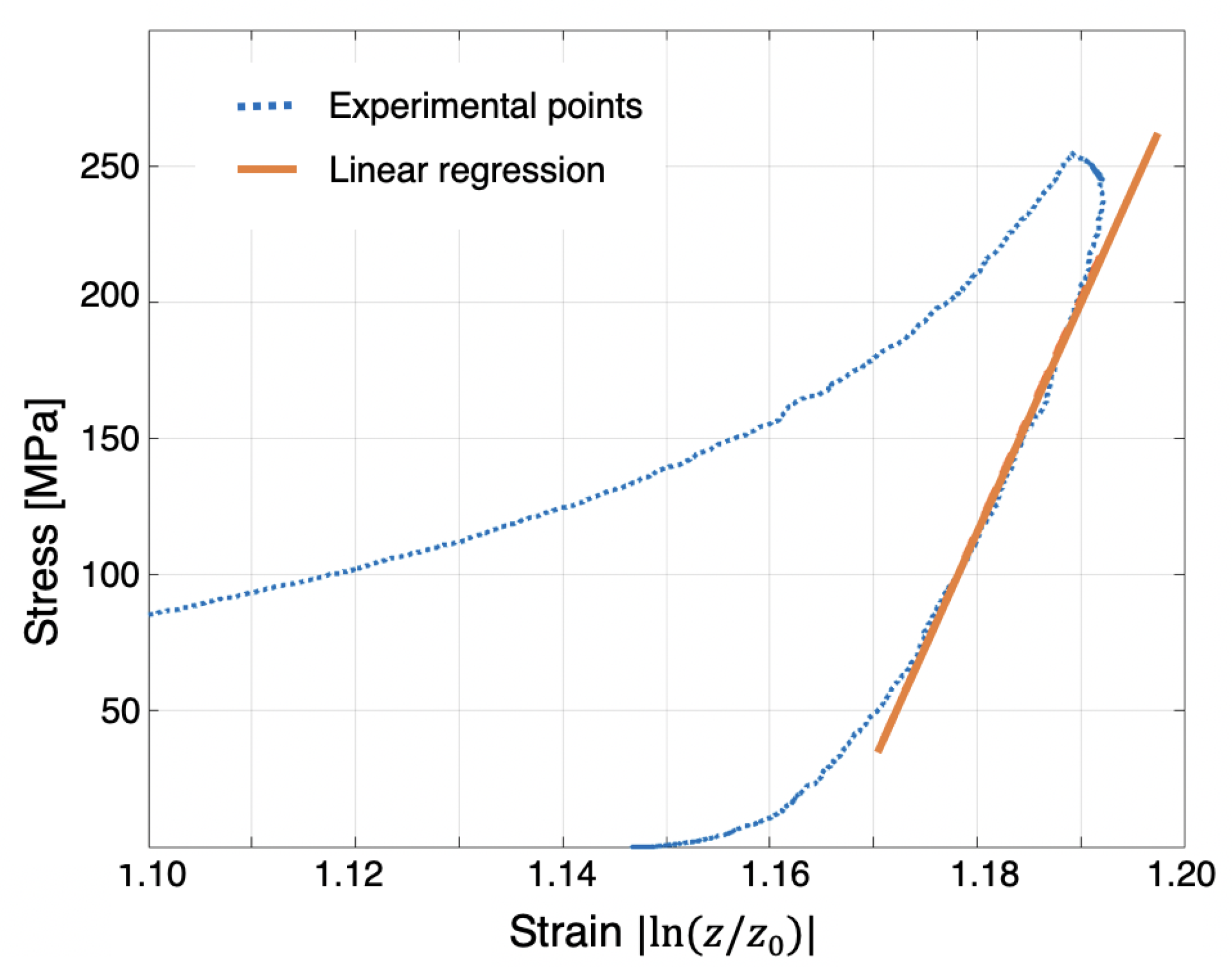
2.1.3. Cyclic Compression at High Pressure
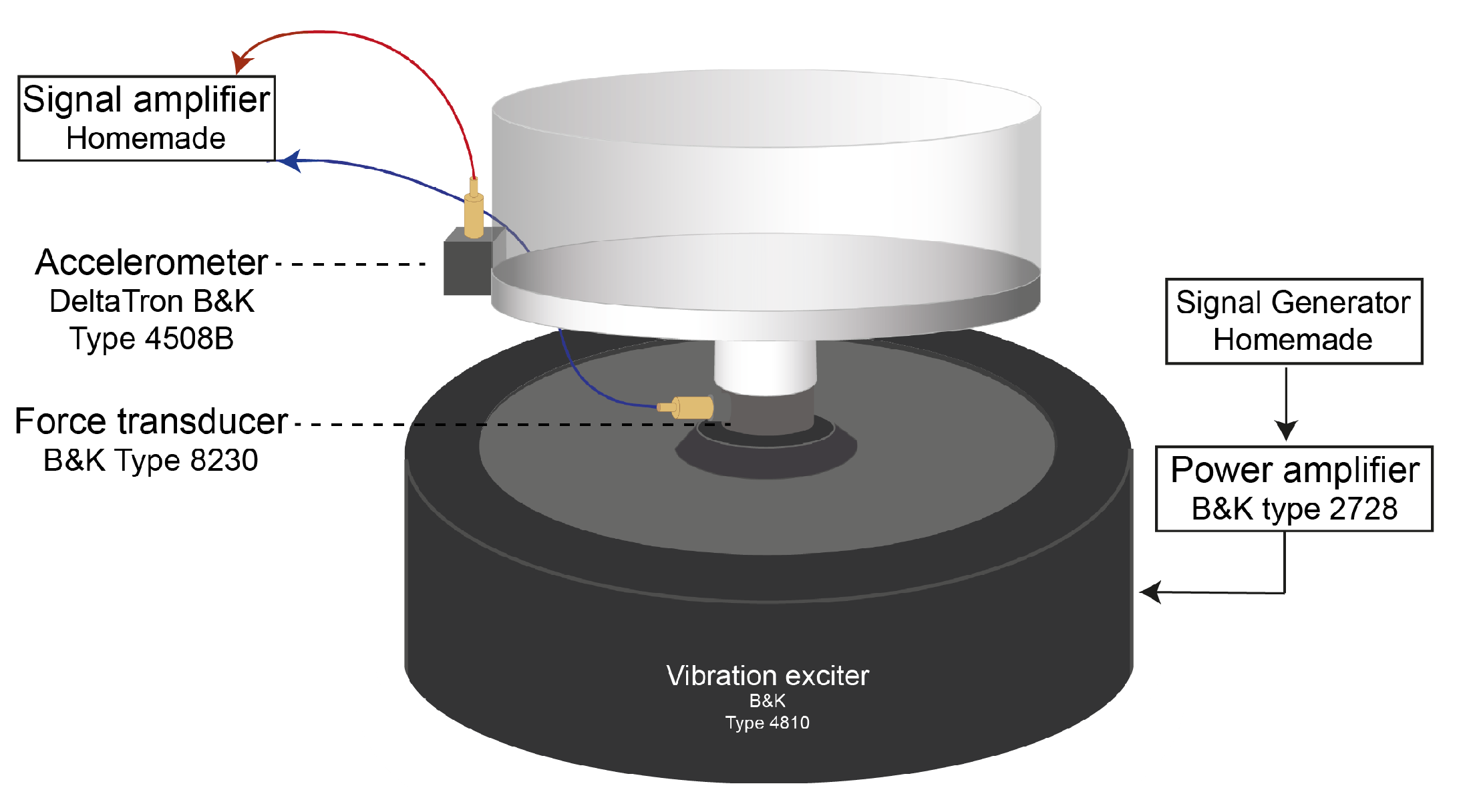
2.2. Elastic Modulus Determined under Vibration Methodologies
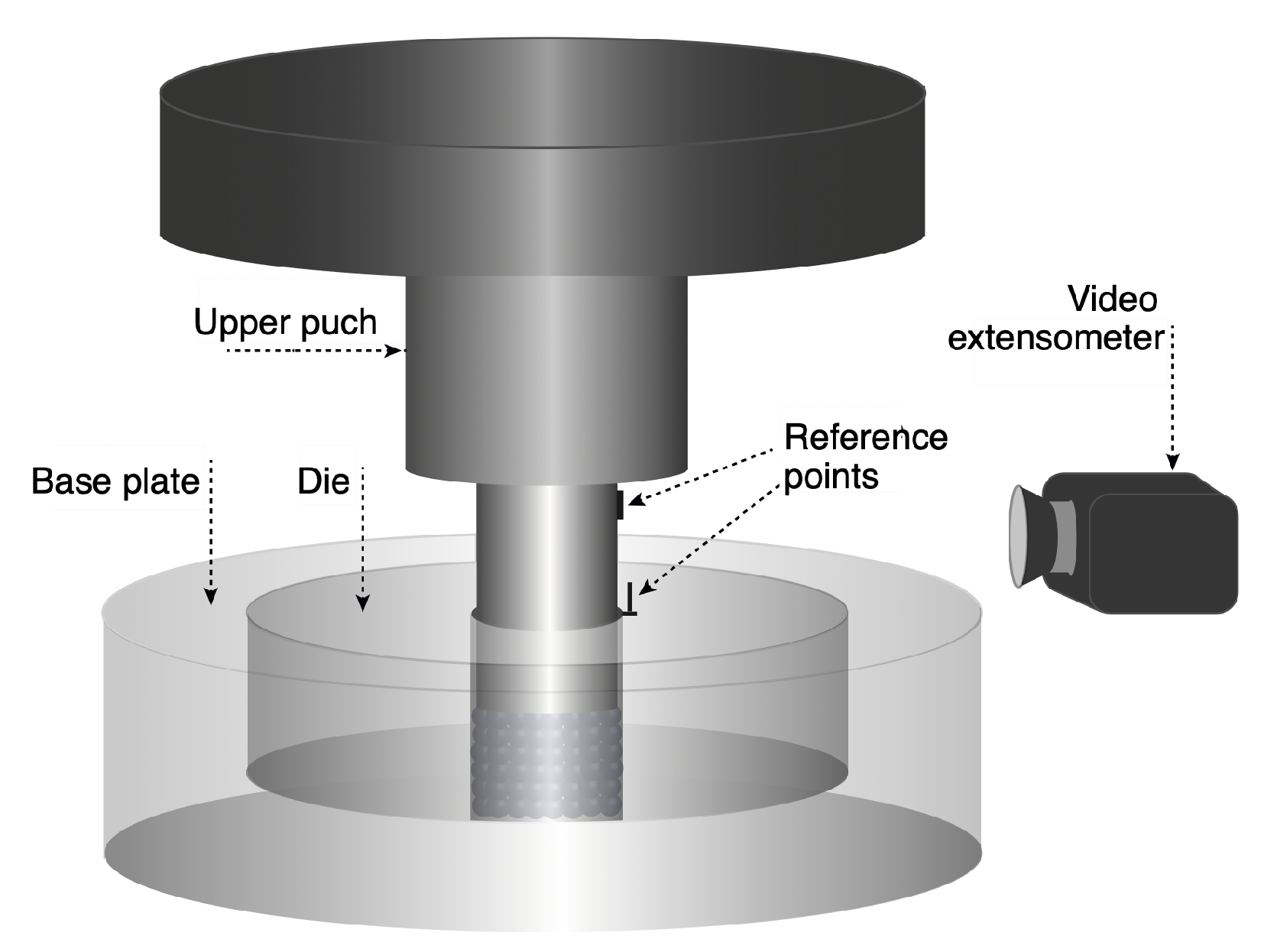
3. Materials and Methods
Industrial Powders
4. The Protocols
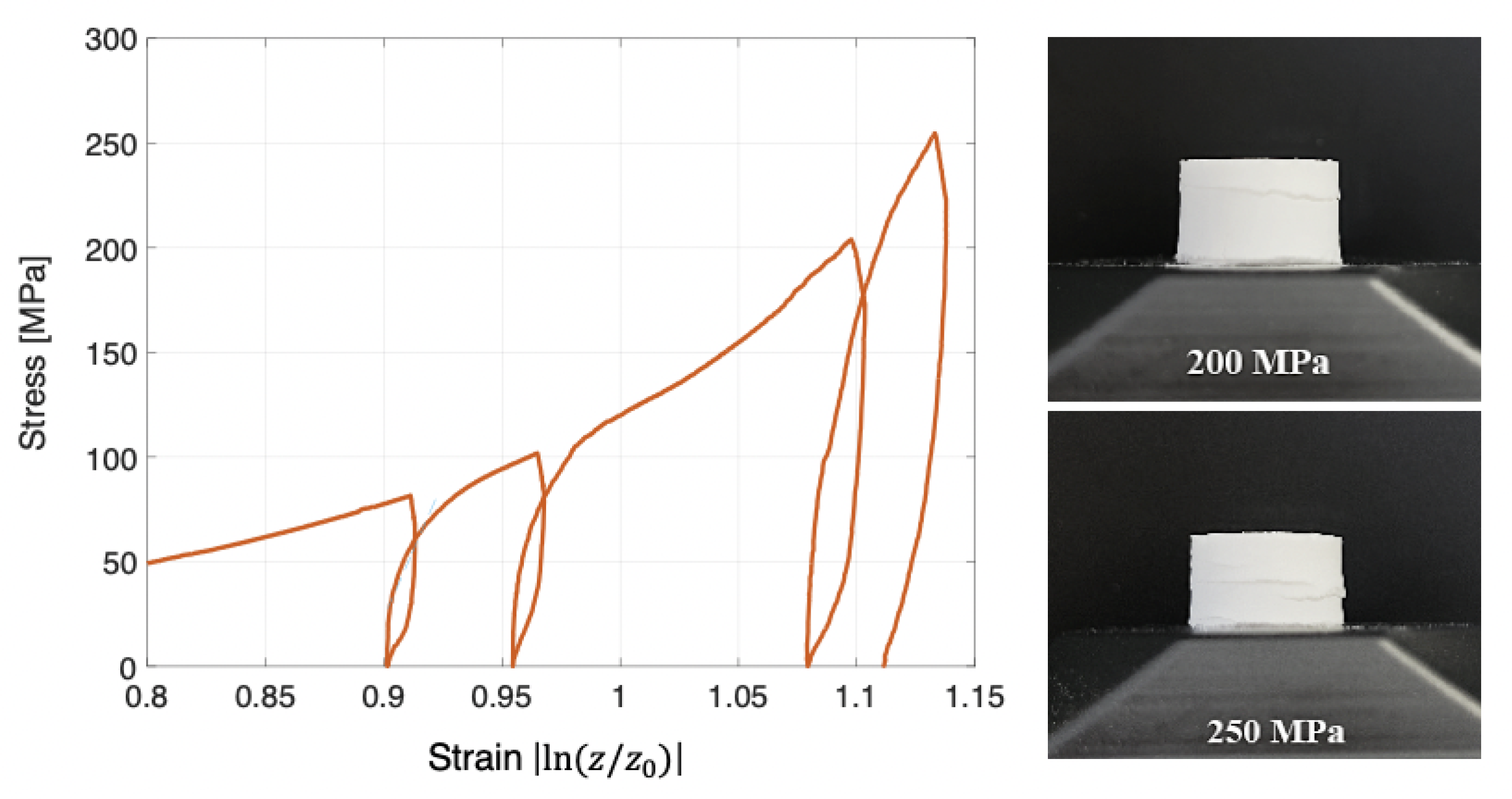
4.1. Single and Cyclic Compression at High Pressure, 250 MPa
4.2. Porosity
4.3. Resonance Frequency of the Powder Bed
5. Results and Discussions
5.1. Porosity
5.2. Poisson’s Ratio
5.3. Single Compression at High Pressure (250 MPa),
5.4. Cyclic Compression at High Pressure (250 MPa),
5.5. Vibration,
5.6. Exploring the Complexity: Consistency and Challenges in Young’s Modulus Determination for Powders
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Powders SEM Micrographs

Appendix B. Powders Tabletting for Porosity Quantification

References
- Jaeger, H.M.; Nagel, S.R.; Behringer, R.P. Granular solids, liquids, and gases. Rev. Mod. Phys. 1996, 68, 1259. [Google Scholar] [CrossRef]
- Herrmann, H.J.; Luding, S.; Hovi, J.P. (Eds.) Physics of Dry Granular Media; Kluwer Academic Publishers: London, UK, 1998. [Google Scholar] [CrossRef]
- Jop, P.; Forterre, Y.; Pouliquen, O. A constitutive law for dense granular flows. Nature 2006, 441, 727–730. [Google Scholar] [CrossRef] [PubMed]
- Andreotti, B.; Forterre, Y.; Pouliquen, O. Les Milieux Granulaires: Entre Fluide et Solide; EDP Sciences: Les Ulis, France, 2011. [Google Scholar]
- Midi, G. On dense granular flows. Eur. Phys. J. E 2004, 14. [Google Scholar] [CrossRef] [PubMed]
- Jenike, A.W.; Shield, R.T. On the Plastic Flow of Coulomb Solids Beyond Original Failure. J. Appl. Mech. 1959, 26, 4012119. [Google Scholar] [CrossRef]
- Nedderman, R.M. Statics and Kinematics of Granular Materials; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar] [CrossRef]
- Schulze, D. Powders and Bulk Solids; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Leturia, M.; Benali, M.; Lagarde, S.; Ronga, I.; Saleh, K. Characterization of flow properties of cohesive powders: A comparative study of traditional and new testing methods. Powder Technol. 2014, 253, 406–423. [Google Scholar] [CrossRef]
- Salehi, H.; Barletta, D.; Poletto, M. A comparison between powder flow property testers. Particuology 2017, 32, 10–20. [Google Scholar] [CrossRef]
- Rondet, E.; Delalonde, M.; Chuetor, S.; Ruiz, T. Modeling of granular material’s packing: Equivalence between vibrated solicitations and consolidation. Powder Technol. 2017, 310, 287–294. [Google Scholar] [CrossRef]
- Cares-Pacheco, M.G.; Falk, V. A phenomenological law for complex granular materials from Mohr-Coulomb theory. Adv. Powder Technol. 2023, 34, 103888. [Google Scholar] [CrossRef]
- Roberts, R.J.; Rowe, R.C.; York, P. The Poisson’s ratio of microcrystalline cellulose. Int. J. Pharm. 1994, 105, 177–180. [Google Scholar] [CrossRef]
- David, S.E.; Ramirez, M.; Timmins, P.; Conway, B.R. Comparative physical, mechanical and crystallographic properties of a series of gemfibrozil salts. J. Pharm. Pharmacol. 2010, 62, 1519–1525. [Google Scholar] [CrossRef]
- Diarra, H.; Mazel, V.; Boillon, A.; Rehault, L.; Busignies, V.; Bureau, S.; Tchoreloff, P. Finite Element Method (FEM) modeling of the powder compaction of cosmetic products: Comparison between simulated and experimental results. Powder Technol. 2012, 224, 233–240. [Google Scholar] [CrossRef]
- Wang, C.; Sun, C.C. A critical examination of three-point bending for determining Young’s modulus. Int. J. Pharm. 2022, 629, 122409. [Google Scholar] [CrossRef] [PubMed]
- Bassam, F.; York, P.; Rowe, R.C.; Roberts, R.J. Young’s modulus of powders used as pharmaceutical excipients. Int. J. Pharm. 1990, 64, 55–60. [Google Scholar] [CrossRef]
- Eichhorn, Y.R. The young’s modulus of a microcrystalline cellulose. Cellulose 2001, 8, 197–207. [Google Scholar] [CrossRef]
- Yap, S.F.; Adams, M.J.; Seville, J.P.; Zhang, Z. Single and bulk compression of pharmaceutical excipients: Evaluation of mechanical properties. Powder Technol. 2008, 185, 1–10. [Google Scholar] [CrossRef]
- Portnikov, D.; Kalman, H. Determination of elastic properties of particles using single particle compression test. Powder Technol. 2014, 268, 244–252. [Google Scholar] [CrossRef]
- Aruffo, G.A.; Michrafy, M.; Oulahna, D.; Michrafy, A. Modelling powder compaction with consideration of a deep grooved punch. Powder Technol. 2022, 395, 681–694. [Google Scholar] [CrossRef]
- Desbois, L.; Tchoreloff, P.; Mazel, V. Characterization and modeling of the viscoelasticity of pharmaceutical tablets. Int. J. Pharm. 2020, 587, 119695. [Google Scholar] [CrossRef] [PubMed]
- Diarra, H.; Mazel, V.; Busignies, V.; Tchoreloff, P. Sensitivity of elastic parameters during the numerical simulation of pharmaceutical die compaction process with Drucker-Prager/Cap model. Powder Technol. 2018, 332, 150–157. [Google Scholar] [CrossRef]
- Han, L.H.; Elliott, J.A.; Bentham, A.C.; Mills, A.; Amidon, G.E.; Hancock, B.C. A modified Drucker-Prager Cap model for die compaction simulation of pharmaceutical powders. Int. J. Solids Struct. 2008, 45, 3088–3106. [Google Scholar] [CrossRef]
- Kachrimanis, K.; Malamataris, S. “Apparent” Young’s elastic modulus and radial recovery for some tableted pharmaceutical excipients. Eur. J. Pharm. Sci. 2004, 21, 197–207. [Google Scholar] [CrossRef] [PubMed]
- Mazel, V.; Busignies, V.; Diarra, H.; Tchoreloff, P. Measurements of elastic moduli of pharmaceutical compacts: A new methodology using double compaction on a compaction simulator. J. Pharm. Sci. 2012, 101, 23122. [Google Scholar] [CrossRef] [PubMed]
- Mazel, V.; Busignies, V.; Diarra, H.; Tchoreloff, P. On the Links Between Elastic Constants and Effective Elastic Behavior of Pharmaceutical Compacts: Importance of Poisson’s Ratio and Use of Bulk Modulus. J. Pharm. Sci. 2013, 102, 4009–4014. [Google Scholar] [CrossRef] [PubMed]
- Michrafy, A.; Ringenbacher, D.; Tchoreloff, P. Modelling the compaction behaviour of powders: Application to pharmaceutical powders. Powder Technol. 2002, 127, 257–266. [Google Scholar] [CrossRef]
- Nysaeter, T.O.; Enstad, G.G. On the elastic modulus of powders. Part. Part. Syst. Charact. 2012, 29, 53–63. [Google Scholar] [CrossRef]
- Aydin, I.; Briscoe, B.J.; Şanlitürk, K.Y. The internal form of compacted ceramic components: A comparison of a finite element modelling with experiment. Powder Technol. 1996, 89, 239–254. [Google Scholar] [CrossRef]
- Barona, D.; Shamsaddini, A.; Aisenstat, M.; Thalberg, K.; Lechuga-Ballesteros, D.; Damadzadeh, B.; Vehring, R. Modulated uniaxial compression analysis of respirable pharmaceutical powders. KONA Powder Part. J. 2021, 38, 209–225. [Google Scholar] [CrossRef]
- Ergen, S.; Yılmaz, F.; Gul, S.; Kolemen, U.; Kilicaslan, M.F.; Uzun, O. Structural and mechanical properties of hypereutectic AlSiFe powders and a new method for determination of sintering temperature. Adv. Powder Technol. 2018, 29, 563–572. [Google Scholar] [CrossRef]
- Taylor, L.J.; Papadopoulos, D.G.; Dunn, P.J.; Bentham, A.C.; Mitchell, J.C.; Snowden, M.J. Mechanical characterisation of powders using nanoindentation. Powder Technol. 2004, 143, 179–185. [Google Scholar] [CrossRef]
- Govedarica, B.; Ilić, I.; Šibanc, R.; Dreu, R.; Srčič, S. The use of single particle mechanical properties for predicting the compressibility of pharmaceutical materials. Powder Technol. 2012, 225, 43–51. [Google Scholar] [CrossRef]
- Sun, W.J.; Kothari, S.; Sun, C.C. The relationship among tensile strength, Young’s modulus, and indentation hardness of pharmaceutical compacts. Powder Technol. 2018, 331, 1–6. [Google Scholar] [CrossRef]
- Majumder, S.; Sun, C.C.; Mara, N.A. Nanomechanical testing in drug delivery: Theory, applications, and emerging trends. Adv. Drug Deliv. Rev. 2022, 183. [Google Scholar] [CrossRef] [PubMed]
- Mishra, M.K.; Mahur, P.; Manimunda, P.; Mishra, K. Recent Advances in Nanomechanical Measurements and Their Application for Pharmaceutical Crystals. Mol. Pharm. 2023, 20, 4848–4867. [Google Scholar] [CrossRef]
- Ramírez, A.; Moya, M.; Ayuga, F. Determination of the Mechanical Properties of Powdered Agricultural Products and Sugar. Part. Part. Syst. Charact. 2009, 26, 220–230. [Google Scholar] [CrossRef]
- Yost, E.; Mazel, V.; Sluga, K.K.; Nagapudi, K.; Muliadi, A.R. Beyond Brittle/Ductile Classification: Applying Proper Constitutive Mechanical Metrics to Understand the Compression Characteristics of Pharmaceutical Materials. J. Pharm. Sci. 2022, 111, 1984–1991. [Google Scholar] [CrossRef] [PubMed]
- Wünsch, I.; Michel, S.; Finke, J.H.; John, E.; Juhnke, M.; Kwade, A. How can single particle compression and nanoindentation contribute to the understanding of pharmaceutical powder compression? Eur. J. Pharm. Biopharm. 2021, 165, 203–218. [Google Scholar] [CrossRef]
- Okudaira, Y.; Ando, H.; Satoh, M.; Miyanami, K. Dynamic measurements for the stiffness constant of a powder bed. Powder Technol. 1994, 81, 139–147. [Google Scholar] [CrossRef]
- Yanagida, T.; Matchett, A.J.; Coulthard, J.M. Dissipation energy of powder beds subject to vibration. Chem. Eng. Res. Des. 2001, 79, 655–662. [Google Scholar] [CrossRef]
- Yanagida, T.; Matchett, A.J.; Coulthard, J.M. Damping and elastic properties of binary powder mixtures. Powder Technol. 2002, 127, 107–115. [Google Scholar] [CrossRef]
- Yanagida, T.; Matchett, A.J.; Coulthard, J.M.; Asmar, B.N.; Langston, P.A.; Walters, J.K. Dynamic measurement for the stiffness of loosely packed powder beds. AIChE J. 2002, 48, 2510–2517. [Google Scholar] [CrossRef]
- Kuo, H.P.; Cheng, C.H. The comparison of the elastic properties of the particle assembly in a vibrator determined by the top cap method, the apparent mass method and the energy dissipation method. J. Taiwan Inst. Chem. Eng. 2010, 41, 239–243. [Google Scholar] [CrossRef]
- Mazel, V.; Tchoreloff, P. Applicability of impulse excitation technique as a tool to characterize the elastic properties of pharmaceutical tablets: Experimental and numerical study. Int. J. Pharm. 2020, 590, 119892. [Google Scholar] [CrossRef] [PubMed]
- Lapčík, L.; Lapčíkova, B.; Gautam, S.; Vašina, M.; Valenta, T.; Řepka, D.; Čépe, K.; Rudolf, O. Acoustic and mechanical testing of commercial cocoa powders. Int. J. Food Prop. 2022, 25, 2127760. [Google Scholar] [CrossRef]
- Masmoudi, M.; Job, S.; Abbes, M.S.; Tawfiq, I.; Haddar, M. Experimental and numerical investigations of dissipation mechanisms in particle dampers. Granular Matter 2016, 18, 71. [Google Scholar] [CrossRef]
- Meynard, J.; Amado-Becker, F.; Tchoreloff, P.; Mazel, V. Use of impulse excitation technique for the characterization of the elastic anisotropy of pharmaceutical tablets. Int. J. Pharm. 2021, 605, 120797. [Google Scholar] [CrossRef] [PubMed]
- Meynard, J.; Amado-Becker, F.; Tchoreloff, P.; Mazel, V. Characterization of the viscoelasticity of pharmaceutical tablets using impulse excitation technique. Int. J. Pharm. 2022, 613, 121410. [Google Scholar] [CrossRef]
- Riera, M.D.; Prado, J.M.; Doremus, P. Model Input Data—Elastic Properties; Springer: London, UK, 2008; pp. 65–76. [Google Scholar] [CrossRef]
- Es-Saheb, M.H. Uniaxial strain rate effects in pharmaceutical powders during cold compaction. J. Mater. Sci. 1992, 27, 4151–4159. [Google Scholar] [CrossRef]
- Yanagida, T.; Matchett, A.; Asmar, B.; Langston, P.; Walters, K.; Coulthard, M. Damping characterisation of particulate materials using low intensity vibrations: Methodology for determining damping properties from acceleration transmissibility data and comparison with existing direct experimental techniques. J. Chem. Eng. Jpn. 2003, 36, 1327–1338. [Google Scholar] [CrossRef]
- Imole, O.I.; Paulick, M.; Magnanimo, V.; Morgeneyer, M.; Montes, B.E.C.; Ramaioli, M.; Kwade, A.; Luding, S. Slow stress relaxation behavior of cohesive powders. Powder Technol. 2016, 293, 82–93. [Google Scholar] [CrossRef]
- Saker, A.; Cares-Pacheco, M.G.; Marchal, P.; Falk, V. Powders flowability assessment in granular compaction: What about the consistency of Hausner ratio? Powder Technol. 2019, 354, 52–63. [Google Scholar] [CrossRef]
- Cares-Pacheco, M.G.; Garavito, M.C.J.; Ober, A.; Gerardin, F.; Silvente, E.; Falk, V. Effects of humidity and glidants on the flowability of pharmaceutical excipients. An experimental energetical approach during granular compaction. Int. J. Pharm. 2021, 604, 120747. [Google Scholar] [CrossRef] [PubMed]
- Hazzar, L.; Nuth, M.; Chekired, M. DEM simulation of drained triaxial tests for glass-beads. Powder Technol. 2020, 364, 123–134. [Google Scholar] [CrossRef]
- Mandal, S.; Nicolas, M.; Pouliquen, O. Insights into the rheology of cohesive granular media. Proc. Natl. Acad. Sci. USA 2020, 117, 8366–8373. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; LaMarche, C.Q.; Kellogg, K.M.; Hrenya, C.M. Fine-particle defluidization: Interaction between cohesion, Young’s modulus and static bed height. Chem. Eng. Sci. 2016, 145. [Google Scholar] [CrossRef]
- Wilson, R.; Dini, D.; van Wachem, B. A numerical study exploring the effect of particle properties on the fluidization of adhesive particles. AIChE J. 2016, 62, 1467–1477. [Google Scholar] [CrossRef]
- MacKenzie, J.K. The elastic constants of a solid containing spherical holes. Proc. Phys. Soc. Sect. B 1950, 63. [Google Scholar] [CrossRef]
- Spriggs, R.M. Expression for Effect of Porosity on Elastic Modulus of Polycrystalline Refractory Materials, Particularly Aluminum Oxide. J. Am. Ceram. Soc. 1961, 44, 628–629. [Google Scholar] [CrossRef]
- Phani, K.K.; Niyogi, S.K. Young’s modulus of porous brittle solids. J. Mater. Sci. 1987, 22, 257–263. [Google Scholar] [CrossRef]
- Munro, R.G. Effective Medium Theory of the Porosity Dependence of Bulk Moduli. J. Am. Ceram. Soc. 2001, 84, 1190–1192. [Google Scholar] [CrossRef]



| Material | d [m] | E [MPa] | Methodology and Comments |
|---|---|---|---|
| White carbon | 83.2 | 0.15/0.16 | Elastic coefficient through vibration Top Cap Method (TCM) (first row) and through sound absorption (second row); acrylic test cell (84 mm inner diameter, 20 mm height, bottom 20 mm thick); top cap: 76 mm diameter iron disc (71 g); pre-packing of powders by tapping and compacting under a 0.618 kg iron disc; acceleration from 0.01 to 3.16 m/s2; RH between 50 and 60% [41]. |
| Nylon powder | 85.5 | 0.80/0.99 | |
| Fused spherical silica | 19.3 | 0.25/0.28 | |
| Lycopodium | 32.3 | 0.61/0.74 | |
| Mica | 37.5 | 0.55/0.68 | |
| Vermiculite | 93.1 | 0.16/0.25 | |
| Glass beads | 232 | 20–35 | Elastic coefficient through vibration (TCM); Acrylic test cell (75 mm inner diameter, 50 mm height, bottom 10 mm thick); Top cap: 50 mm diameter iron disc (generating axial stresses from 150–1400 Pa); peak acceleration of 0.1 g [45]. |
| Glass beads | 463 | 13–26 | |
| Glass beads | 1060 | 33–64 | |
| Polyethylene powder | 395 | 0.8–1.4 | |
| Glass beads | 4417 | 15–28 | Elastic coefficient through vibration (TCM); acrylic test cell (78 mm inner diameter, 20 mm height, bottom 10 mm thick); top cap: 70 mm diameter disc (generating axial stresses from 150–1400 Pa); peak acceleration of 0.02 g [43]. |
| Glass beads | 1049 | 15–28 | |
| Glass beads | 459 | 8–15 | |
| Polyethylene powder | 462 | 0.5–1.0 | |
| Polyethylene powder | 320 | 0.3–0.9 | |
| Black resin powder | 219 | 0.5–1.0 | |
| Grey crumb powder | 382 | 0.15–0.31 | |
| Sand | 169 | 8–11 | |
| Polyethylene powder | 459 | 0.15 | Elastic coefficient through sound absorption; acrylic test cell (inner diameter from 34.5 to 149 mm, height from 10 to 80 mm); acceleration peak from 0.02 to 0.75 g [44]. |
| Glass beads | 462 | 5.76 | |
| Sand | 169 | 3.66 | |
| Grey crumb powder | 382 | 0.01 | |
| China clay-kaolin | 10.5 | 0.25 | |
| Glass beads | 335 | 0.12, TCM 0.21 | Elastic coefficient through vibration (TCM as [41]) and through sound absorption as [43]; acrylic test cell (74 mm inner diameter, 38 mm height); top cap of 13.9 g; RH = 68 ± 5% [45]. |
| Polyethylene powder | 400 | 0.18, TCM 0.29 | |
| 125 | 2.2–37.8 | Elastic coefficient through transmission of acoustic waves; freely poured samples; elastic modulus increases with the height of the powder bed (from 15 to 100 mm); frequency range 200–6400 Hz; RH = 40% [47]. | |
| Cocoa powder | 238 | 1.1–12.8 | |
| 303 | 1.8–19.3 |
| Powder | Particle Size Distribution [m] | True Density * | ||||
|---|---|---|---|---|---|---|
| [g/mL] | ||||||
| Avicel® PH-102 | 35 | 111 | 225 | 122 | 69 | 1.55 |
| Avicel® PH-105 | 7 | 21 | 45 | 24 | 13 | 1.58 |
| Glass beads | 4 | 24 | 60 | 29 | 8 | 2.66 |
| Wheat flour | 17 | 83 | 177 | 91 | 25 | 1.46 |
| Joint filler | 2 | 18 | 72 | 29 | 6 | 2.81 |
| Sericite | 3 | 9 | 27 | 17 | 6 | 2.88 |
| Wheat starch | 8 | 18 | 30 | 19 | 11 | 1.50 |
| Gluten | 18 | 74 | 124 | 74 | 13 | 1.30 |
| Powder | Porosity, | |||
|---|---|---|---|---|
| 80 MPa | 100 MPa | 200 MPa | 250 MPa | |
| Avicel® PH-102 | 0.33 ± 0.01 | 0.31 ± 0.01 | 0.22 ± 0.02 | 0.15 ± 0.02 |
| Avicel® PH-102 (60% RH) | 0.26 ± 0.02 | 0.20 ± 0.01 | 0.19 ± 0.01 | 0.18 ± 0.01 |
| Avicel® PH-105 | 0.33 ± 0.01 | 0.29 ± 0.01 | 0.21 ± 0.01 | 0.19 ± 0.01 |
| Wheat flour | 0.25 ± 0.01 | 0.22 ± 0.01 | 0.18 ± 0.01 | 0.17 ± 0.00 |
| Wheat flour (60% RH) | 0.23 ± 0.01 | 0.22 ± 0.01 | 0.20 ± 0.01 | 0.21 ± 0.01 |
| Sericite | 0.46 ± 0.01 | 0.45 ± 0.01 | 0.40 ± 0.01 | 0.38 ± 0.02 |
| Joint filler | 0.37 ± 0.00 | 0.35 ± 0.01 | 0.32 ± 0.00 | 0.31 ± 0.00 |
| Wheat starch | 0.37 ± 0.02 | 0.34 ± 0.01 | 0.23 ± 0.01 | 0.18 ± 0.01 |
| Gluten | 0.26 ± 0.00 | 0.23 ± 0.00 | 0.17 ± 0.01 | 0.16 ± 0.00 |
| Glass beads | 0.35 ± 0.00 | 0.33 ± 0.00 | 0.30 ± 0.00 | 0.28 ± 0.00 |
| Powder | [GPa] | ||
|---|---|---|---|
| Avicel® PH-105 | 0.19 ± 0.01 | 0.35 | 4.54 ± 0.14 |
| Avicel® PH-102 | 0.15 ± 0.02 | 0.35 [39] | 5.07 ± 0.14 |
| Sericite | 0.38 ± 0.02 | 0.30 | 5.53 ± 0.10 |
| Wheat flour | 0.17 ± 0.00 | 0.2 [38] | 7.12 ± 0.57 |
| Powder | [GPa] | |||
|---|---|---|---|---|
| 80 MPa | 100 MPa | 200 MPa | ||
| Sericite | 0.30 | 1.55 ± 0.02 | 2.03 ± 0.09 | 3.62 ± 0.33 |
| Wheat flour | 0.20 [38] | 2.05 ± 0.05 | 2.90 ± 0.10 | 4.77 ± 0.17 |
| Wheat flour (60%RH) | 0.20 [38] | 2.35 ± 0.05 | 3.45 ± 0.10 | 6.24 ± 0.17 |
| Avicel® PH-105 | 0.22/0.32/0.35 * | 2.44 ± 0.11 | 2.64 ± 0.42 | 4.25 ± 0.40 |
| Avicel® PH-102 | 0.22/0.32/0.35 * | 2.69 ± 0.01 | 2.52 ± 0.15 | 4.10 ± 0.25 |
| Avicel® PH-102 (60%RH) | 0.22/0.32/0.35 * | 2.84 ± 0.26 | 2.90 ± 0.12 | 3.47± 0.26 |
| Gluten | 0.30 | 2.53 ± 0.37 | 3.28 ± 0.33 | 4.85 ± 0.11 |
| Joint filler | 0.30 | 6.19 ± 0.12 | 7.61 ± 0.63 | 11.23 ± 0.37 |
| Glass beads | 0.21 | 2.25 ± 0.09 | 3.12 ± 0.12 | 4.62 ± 0.37 |
| Powder | [Hz] | [g] | [MPa] | |
|---|---|---|---|---|
| Avicel® PH-102 | 0.79 | 587 | 24.4 | 0.53 |
| Joint filler | 0.71 | 378 | 59.9 | 0.54 |
| Wheat flour | 0.67 | 581 | 35.5 | 0.76 |
| Glass beads | 0.50 | 792 | 96.7 | 3.84 |
| Sericite | 0.88 | 318 | 25.7 | 0.16 |
| Avicel® PH-105 | 0.81 | 396 | 22.5 | 0.22 |
| Gluten | 0.62 | 500 | 35.8 | 0.57 |
| Wheat starch | 0.67 | 410 | 36.4 | 0.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cares-Pacheco, M.-G.; Cordeiro-Silva, E.; Gerardin, F.; Falk, V. Consistency in Young’s Modulus of Powders: A Review with Experiments. Powders 2024, 3, 280-304. https://doi.org/10.3390/powders3020017
Cares-Pacheco M-G, Cordeiro-Silva E, Gerardin F, Falk V. Consistency in Young’s Modulus of Powders: A Review with Experiments. Powders. 2024; 3(2):280-304. https://doi.org/10.3390/powders3020017
Chicago/Turabian StyleCares-Pacheco, Maria-Graciela, Ellen Cordeiro-Silva, Fabien Gerardin, and Veronique Falk. 2024. "Consistency in Young’s Modulus of Powders: A Review with Experiments" Powders 3, no. 2: 280-304. https://doi.org/10.3390/powders3020017
APA StyleCares-Pacheco, M.-G., Cordeiro-Silva, E., Gerardin, F., & Falk, V. (2024). Consistency in Young’s Modulus of Powders: A Review with Experiments. Powders, 3(2), 280-304. https://doi.org/10.3390/powders3020017







