How Much Rationality Is Needed for Decision Making? ^†

Abstract

The Braess paradox (discovered in 1968 by the German mathematician Dietrich Braess) describes how a possible relief of a system, by introducing new possibilities to distribute load or local density in flows inside the system, can actually increase stress on the system. It is most often researched in a world of rational decision-makers, who are assumed to cause the worsening situation due to rational optimization of individual interests. In strongly complex networks, the exploitation of new possibilities most probably needs rational decision-makers who can see the use of new possibilities for them. Interestingly, a mechanical analogy of the situation also exists, where new possibilities—in this case for forces in a system to attack—lead to a loss of stability inside the system. In this example, a string that was introduced to relieve the load on two springs leads to counter-intuitive overloading. With the perspective that the evolution of information processing systems is already beginning in a physical and chemical pre-biotic world, this is an interesting case that might give further insight into how and when choices between many possibilities could threaten the function of a system rather than making it more durable and adaptable. The example is discussed based on a review of literature from the humanities as well as the natural sciences.

1. Introduction

It already occurs in real systems, as Braess has calculated with a theoretical model of changes in traffic-volume distribution when additional couplings between roads are added: Contraintuitively, the time needed to travel from A to B can increase, and congestion can worsen. In general, what has been learned from this “Braess’s paradox” [1,2] is this: The addition of seemingly beneficial elements to a network of paths can actually have adverse effects due to the interconnectedness and interdependencies of the components. New equilibrium points inside steady-state dynamics can be reached, which comprise nonlinearity and are called “unexpected” inside the respective systems. There exist at least two well-studied examples from road networks in Germany and the United States where closing a connecting road relieved traffic congestion [3,4]. The latter reference also quotes The New Yorker, saying that “(…) in the twenty-three American cities that added the most new roads per person during the 1990s, traffic congestion rose by more than 70%.” Braess’s paradox seems to be common in complex traffic networks. This result seems surprising, but why is it interesting outside the discipline of traffic planning? Because of the wide distribution of the phenomenon and its occurrence in various contexts, as will be discussed in the following. There are examples where Braess’s paradox’s occurrence can be attributed to rational decision-makers and their individual-centered (selfish) decision-making, but as we will show, there are other examples as well.

2. Discovery and Proposed Explanations for the Counterintuitive (Paradoxical) Behavior

In 1968, German mathematician Dietrich Braess, working at the institute for numerical and instrumental mathematics in Münster, showed for a simple network of four nodes and connecting edges with a sense of direction that a connection between two streets can counterintuitively increase travel time for all participants [1,2]. Likewise, a global solution for distributing the travel volume around the two streets can assign path decisions to each single one of the travelers, which results in shorter traveling times than path decisions that individuals would take for themselves. In the model, two similar narrow or congested parts of roads are connected with each other in series. A congested network or a congested part of paths inside a network is one where the cost of traveling along the path or arc (in parallel setups) depends on the number of participants in the network who are using that arc/the traffic volume. The connection counteracts the equal distribution of traffic volume between the two streets if the streets in total consist of narrow, congested, and broad, non-congested parts. This leads to saturation and bottleneck structures, increasing travel times for the whole system compared with the system without the connecting path.

Interestingly, when an electrical engineer sees the topology of the traffic two-terminal network that Braess used in his description and mathematical derivation of the cost function for participants inside the network in [1,2] they might be reminded of a Wheatstone network with a Wheatstone bridge (Figure 1). In such an electrical network, four nodes are connected by four corresponding edges. A fifth edge—the Wheatstone bridge—connects two of the nodes (C and B in Figure 1), splitting the network into two subsystems. In this topology, the presence or absence of the bridging edge makes a huge difference in the equilibrium states that can be reached. Braess observed this as the fact that an additional road inside an existing road network that is congested can worsen the cost for each participating driver in the form of increased travel time in his network. Shannon described the Wheatstone bridge as an example of a two-terminal circuit that is non-series-parallel [5], and it has been shown that Braess’s paradox “(…) occurs in an (undirected) two-terminal network if and only if it is not series-parallel.” [6]. This is interesting in the sense that the Wheatstone bridge circuit comprises a series as well as a parallel setup of resistances as a potentiality, but as long as there is flow over the bridge, it is neither and in an unbalanced state. In [7], Braess’s original road network topology (Figure 1b) was used as the basis for an imbalanced Wheatstone bridge topology network by modeling the congested, volume-dependent conducting parts of the edges with resistances and the broad, volume-independent parts with Zener diodes with fixed voltage. The imbalanced Wheatstone network, imbalanced due to R2/R1 ≠ Rx/R3 since R1 and R2 were replaced by Zener diodes, generates a voltage drop over each of the two arcs when current is applied, following Kirchhoff’s Laws. This voltage drop generates a potential difference between the arcs as soon as the bridge is added and a current flows through the connecting path, i.e., the connecting path is “used”.

Since Braess’s paradox was first described in the context of traffic planning, a reasonable assumption for its cause has been the selfish decision-making of rational participants in the traffic system [1,4]. It makes sense—there are two paths available for traveling from A to B, and each one has a part where travel time depends on traffic volume plus one part with a fixed travel time. If there is now a connecting road built to connect the two traffic-volume-dependent paths, as shown in Figure 1b, there are going to be individuals who use this apparent abbreviation. The problem of the connecting road is that the advantage for individuals viewed systemically is nullified since, by it, the two paths that are extensive in time (congested) are connected in series and can thereby no longer share their respective traffic loads. The advantage of one or a few individual road users grows to the disadvantage of all road users traveling from A to B, increasing the duration of travel compared with the situation when the connection road was absent. It seems the selfish—or more neutral—individual-borne rational thinking capacity of humans in decision-making causes Braess’s paradox. This explanation can also be formulated in a game-theoretic framework: The different paths are modeled as strategies between which participants in a non-cooperative game can choose. A global equilibrium between chosen strategies, i.e., a state where no player would change the chosen strategy while all other players stick to their chosen strategies, is called a Nash equilibrium in game theory. The Nash equilibrium that is being reached in the above-described Braess’s paradox situation is one of unequal distribution of load and gain. In game theory, one would additionally call it a Pareto-inefficient equilibrium [10] in that an alternative choice of routes would reduce the costs for all users, but the alternative choice is not taken by any player due to cost considerations. The Pareto optimum of a system is an equilibrium state where the positive outcome for all participants in the game cannot be improved without worsening the situation for at least one of the players. This cannot be reached on the basis of individually deciding non-cooperative players. It could only be reached with the help of a global organization and a cooperative agreement between strategies [11]. Since there are so many different network systems in which the paradox occurs, it soon became clear that rational agent-based decision-making cannot be a general explanation.

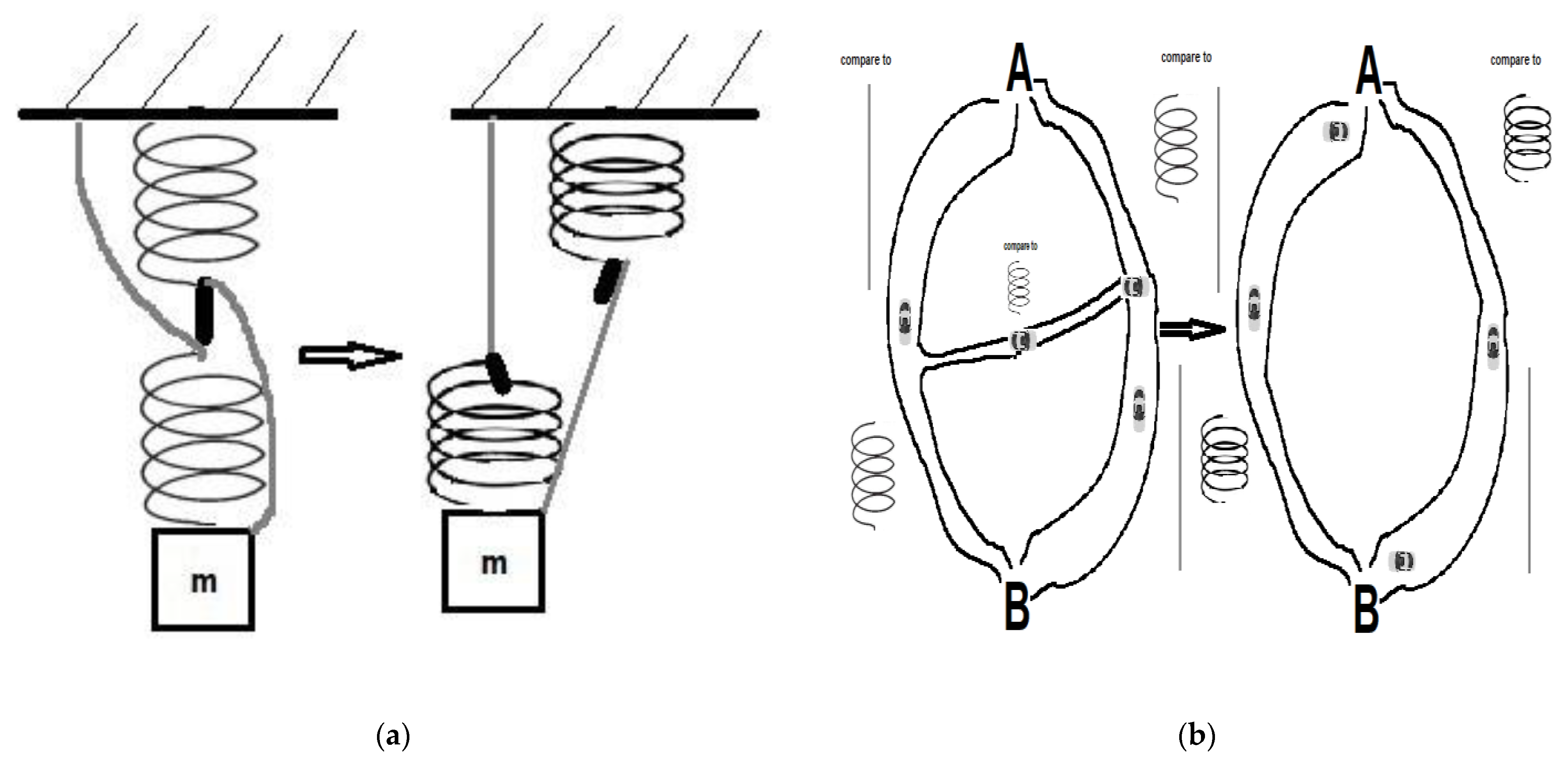
3. The Diversity of Network Systems in Which Braess’s Paradox Behavior Can Be Observed and the Search for More General Explanations

Before coming to more complex topologies and non-classical physical contexts where Braess’s paradox occurs, let us stay with the Wheatstone network setup. There exists a mechanical analogy for Braess’s paradox in exactly this setup: Initially, two springs with the same spring constant are coupled by an inelastic string (bold black in Figure 2a), thereby carrying the mass m in series (Figure 2a left). Two inelastic strings of equal length connect each spring to the ceiling, corresponding to the mass m, and are limp (grey in Figure 2a). When the strings are taut and the connection between strings is cut, a seemingly paradoxical behavior lets the springs contract and lift the mass m a bit (Figure 2a, right). But the apparent paradox is easily solved: In the new equilibrium state, the two inelastic strings share the mass m in a parallel setup [7,12]. To observe this inverse of Braess’s paradox—the reduction of force acting on each of the springs after removing an unfortunate coupling—the contracted springs reduction in length must exceed the extended strings additional length.

In this mechanical system, the string, which can be introduced with intuition to relieve the load on two springs, leads to counter-intuitive overloading because the new equilibrium state no longer allows an equal share of load between springs. The Wheatstone topological setup has been described for static (DC) electrical networks [7,13], connected springs and traffic networks, queuing [14], hydrodynamic as well as thermodynamic networks, which show the paradox. The unbalanced Wheatstone bridge appears to be a good model to understand Braess’s paradox in both purely physical (classical) network systems as well as in rational agent decision-making-based network systems. The connecting element seems to be that the bridging path between two arcs, which include dormant potential for becoming congested and then represent an imbalance for the distribution of flow on one side, and the imbalance between parallel arcs, which causes a dormant connecting bridge in-between them to conduct a differential flow and “become used” on the other side, are logically dual. Many of the more complex networks—at least valid for electrical networks—can actually be decomposed into embedded Wheatstone plus series-parallel sub-networks [6,13,15]. It has been found for complex electrical power networks that embedded Wheatstone bridge structures can cause congestion non-locally in other parts of the network without becoming congested [13]. The question about nonlocal failures in complex supply networks due to Braess’s paradox [16] might be related to Wheatstone sub-networks, too.

In electrical (AC) power networks, the effectiveness of the Wheatstone network as a model to explain the Braess paradox is at least questionable, since due to collective dynamics and the mentioned non-locality of effects, one would not be able to differentiate the Wheatstone sub-network that caused the paradox from those that are balanced. Braess’s paradox, or more generally, the “existence of non-intuitive equilibrium points (…) [17],” occurs over many scales of network complexity. Some more complex network topologies where the Wheatstone network model cannot be applied include AC power grids [16,18,19,20], or even teams of basketball players modeled as networks of ball transmission flow [21]. In large, complex networks, Braess’s paradox seems to be the rule rather than the exception [16]. Even in quantum transport systems where a two-dimensional electron gas is moving through a simple network (but different from the Wheatstone network topology in that there is an additional parallel arc instead of the orthogonal connection between arcs) of semiconductors [22,23,24], Braess’s paradox has been observed. The question of how congestion can play a role in quantum transport is not yet solved [25]. Linear as well as nonlinear effects are being discussed.

4. Conclusions

Braess’s paradox leads to an unexpected stable state (equilibrium) after additional paths or options for action have been added. The new equilibrium in cases of Braess’s paradox is worse than before in terms of equality of load distribution. As has been discussed here, there are many different cases where Braess’s paradox has been reported, and the conclusion that it is generated by the individual-centered decision-making of rational agents has since been refuted as being too specific. From an evolutionary perspective, the realm of intentional decision-making is a rather recently developed way of making decisions. It has to be assumed that the activation of new possibilities and the introduction of excess energy for work processes into systems can lead to Braess’s paradoxical developments long before rational decision-making evolved. What can be said from the described examples is that in electrical physical systems, to generate a current flow, there needs to be an imbalance between resistances or similar quantities to drive it first. In the Wheatstone network used to measure resistance, the bridge can be present, but within a balanced setup of the network, there will be no current flow over it.

There is no global driver like a potential difference. Contrary to that, in agent-based decentralized decision making, new paths are going to be explored as soon as they occur; the driver is the agents themselves. The newly introduced flux and redistribution of agents and congestion externalities are then possibly leading to or activating dormant imbalances. There appears to be a dual character in this, and the bridging between series-parallel arcs of networks and imbalances occurring nonlinearly along the arcs to drive flows is a good model to analyze this. Braess’s paradox is a reminder that not all of the possible new equilibrium states that are triggered unexpectedly in this way represent improvements to the stable state that existed before.