How Much Rationality Is Needed for Decision Making? †
Abstract
:1. Introduction
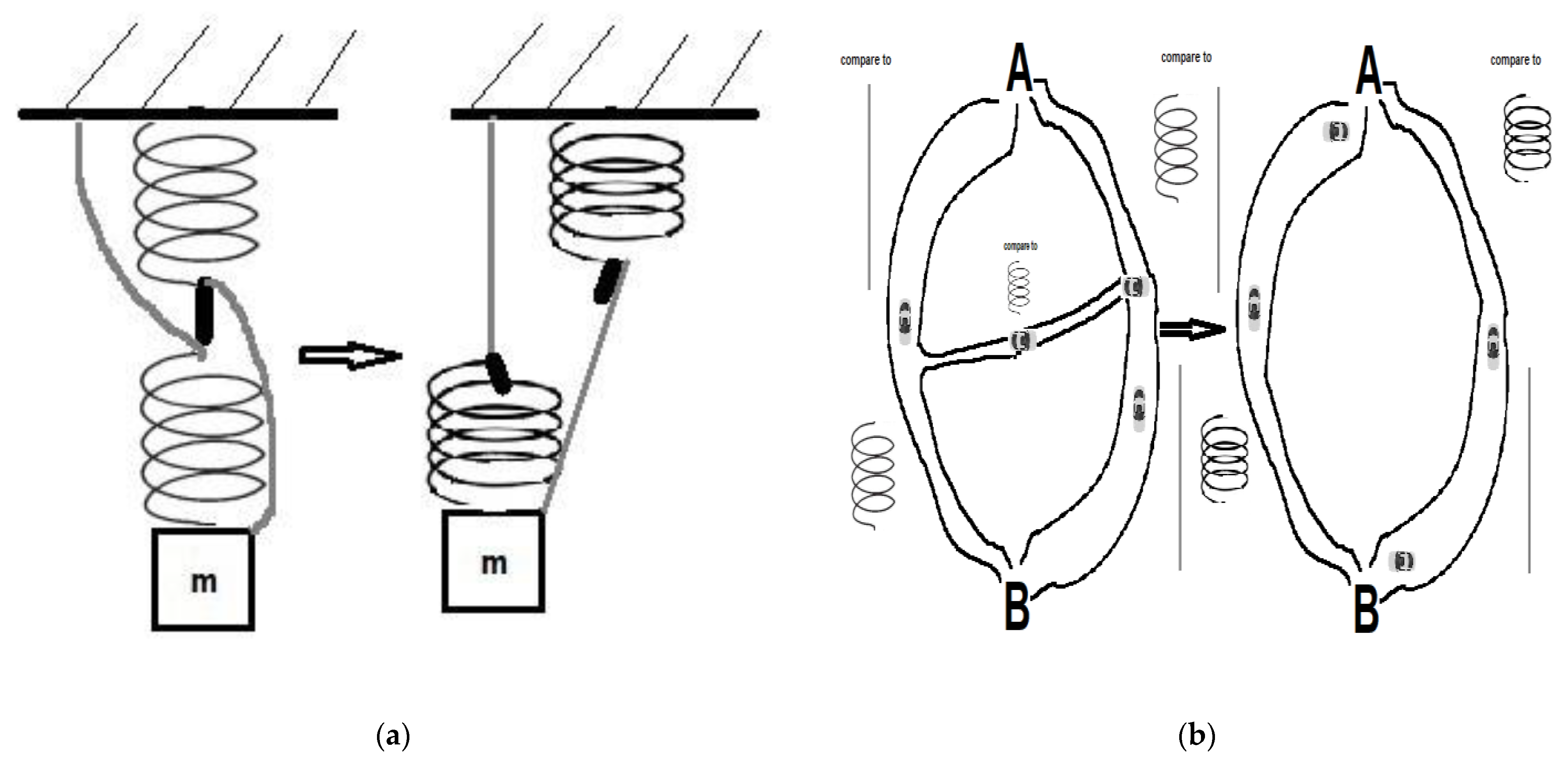
2. Discovery and Proposed Explanations for the Counterintuitive (Paradoxical) Behavior
3. The Diversity of Network Systems in Which Braess’s Paradox Behavior Can Be Observed and the Search for More General Explanations
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Braess, D. Über ein Paradoxon aus der Verkehrsplanung: Original German publication. Unternehm. Oper. Res. 1968, 12, 258–268. [Google Scholar] [CrossRef]
- Braess, D.; Nagurney, A.; Wakolbinger, T. On a Paradox of Traffic Planning. Transp. Sci. 2005, 39, 446–450. [Google Scholar] [CrossRef] [Green Version]
- Knödel, W. Graphentheoretische Methoden und ihre Anwendungen; Springer: Berlin, Germany, 1969. [Google Scholar]
- Havil, J. Impossible?: Surprising Solutions to Counterintuitive Conundrums; Chapter IV: Braess’s Paradox; Princeton University Press: Princeton, NJ, USA, 2011; ISBN 9781400829675. [Google Scholar]
- Shannon, C.E. A symbolic analysis of relay and switching circuits. Trans. Am. Inst. Electr. Eng. 1938, 57, 713–723. [Google Scholar] [CrossRef] [Green Version]
- Milchtaich, I. Network topology and the efficiency of equilibrium. Games Econ. Behav. 2006, 57, 321–346. [Google Scholar] [CrossRef] [Green Version]
- Cohen, J.E.; Horowitz, P. Paradoxical behaviour of mechanical and electrical networks. Nature 1991, 352, 699–701. [Google Scholar] [CrossRef]
- jjbeard. Wheatstone Bridge. Available online: https://commons.wikimedia.org/wiki/File:Wheatstone_Bridge.svg (accessed on 21 June 2023).
- Drawing Gallery. Rotes Auto, Wagen. Kostenlose Nutzung. Available online: https://pixabay.com/de/illustrations/linie-zeichnen-rotes-auto-wagen-4678636/ (accessed on 21 June 2023).
- Dubey, P. Inefficiency of Nash Equilibria. Math. Oper. Res. 1986, 11, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Youn, H.; Gastner, M.T.; Jeong, H. Price of anarchy in transportation networks: Efficiency and optimality control. Phys. Rev. Lett. 2008, 101, 128701. [Google Scholar] [CrossRef] [Green Version]
- Penchina, C.M.; Penchina, L.J. The Braess paradox in mechanical, traffic, and other networks. Am. J. Phys. 2003, 71, 479–482. [Google Scholar] [CrossRef]
- Blumsack, S.; Lave, L.B.; Ilić, M. A Quantitative Analysis of the Relationship Between Congestion and Reliability in Electric Power Networks. Energy J. 2007, 28, 73–100. [Google Scholar] [CrossRef] [Green Version]
- Cohen, J.E.; Kelly, F.P. A paradox of congestion in a queuing network. J. Appl. Probab. 1990, 27, 730–734. [Google Scholar] [CrossRef] [Green Version]
- Duffin, R.J. Topology of series-parallel networks. J. Math. Anal. Appl. 1965, 10, 303–318. [Google Scholar] [CrossRef] [Green Version]
- Witthaut, D.; Timme, M. Nonlocal failures in complex supply networks by single link additions. Eur. Phys. J. B 2013, 86, 48704. [Google Scholar] [CrossRef] [Green Version]
- Korilis, Y.A.; Lazar, A.A.; Orda, A. Avoiding the Braess paradox in non-cooperative networks. J. Appl. Probab. 1999, 36, 211–222. [Google Scholar] [CrossRef]
- Witthaut, D.; Timme, M. Braess’s paradox in oscillator networks, desynchronization and power outage. New J. Phys. 2012, 14, 83036. [Google Scholar] [CrossRef]
- Dörfler, F.; Chertkov, M.; Bullo, F. Synchronization in complex oscillator networks and smart grids. Proc. Natl. Acad. Sci. USA 2013, 110, 2005–2010. [Google Scholar] [CrossRef] [PubMed]
- Rohden, M.; Sorge, A.; Timme, M.; Witthaut, D. Self-organized synchronization in decentralized power grids. Phys. Rev. Lett. 2012, 109, 64101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Skinner, B. The Price of Anarchy in Basketball. J. Quant. Anal. Sports 2010, 6. [Google Scholar] [CrossRef] [Green Version]
- Pala, M.; Sellier, H.; Hackens, B.; Martins, F.; Bayot, V.; Huant, S. A new transport phenomenon in nanostructures: A mesoscopic analog of the Braess paradox encountered in road networks. Nanoscale Res. Lett. 2012, 7, 472. [Google Scholar] [CrossRef] [Green Version]
- Toussaint, S.; Martins, F.; Faniel, S.; Pala, M.G.; Desplanque, L.; Wallart, X.; Sellier, H.; Huant, S.; Bayot, V.; Hackens, B. On the origins of transport inefficiencies in mesoscopic networks. Sci. Rep. 2018, 8, 3017. [Google Scholar] [CrossRef] [Green Version]
- Pala, M.G.; Baltazar, S.; Liu, P.; Sellier, H.; Hackens, B.; Martins, F.; Bayot, V.; Wallart, X.; Desplanque, L.; Huant, S. Transport inefficiency in branched-out mesoscopic networks: An analog of the Braess paradox. Phys. Rev. Lett. 2012, 108, 76802. [Google Scholar] [CrossRef]
- Lobanova, A.D.; Lobanov, A.D.; Pupasov-Maksimov, A.M. Controversy of Quantum Congestion in Two-Particle Quantum Walks. arXiv 2021, arXiv:2112.13947. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grathoff, A. How Much Rationality Is Needed for Decision Making? Comput. Sci. Math. Forum 2023, 8, 12. https://doi.org/10.3390/cmsf2023008012
Grathoff A. How Much Rationality Is Needed for Decision Making? Computer Sciences & Mathematics Forum. 2023; 8(1):12. https://doi.org/10.3390/cmsf2023008012
Chicago/Turabian StyleGrathoff, Annette. 2023. "How Much Rationality Is Needed for Decision Making?" Computer Sciences & Mathematics Forum 8, no. 1: 12. https://doi.org/10.3390/cmsf2023008012
APA StyleGrathoff, A. (2023). How Much Rationality Is Needed for Decision Making? Computer Sciences & Mathematics Forum, 8(1), 12. https://doi.org/10.3390/cmsf2023008012




