1. Introduction
In the past, discussions were held about the existence of mathematics that followed a traditional research path. However, this approach had some limitations, so we are now attempting to use the philosophy of information to re-evaluate this topic.
2. Discussions on the Existence of Mathematics
In Plato’s famous “Allegory of the divided line”, he placed mathematics in the realm of ideas, and he believed that ideas are realities in the world, resulting in an early mathematical realism. Kantianism holds that mathematics is a product of human reason, intuition, and thinking. It is characterized by denying or belittling the empirical nature of mathematics and emphasizing it’s a priori nature [
1]. This form is innate and constant for each of us. Therefore, the Kantian view of the existence of mathematics may be ambiguous, but it is closer to Platonism.
Psychologism, which emerged in the late 19th and early 20th centuries, held that mathematics and logic should be regarded as parts of psychological activities for study. This perspective of regarding mathematics and logic as psychological activities with variability tends to categorize them as phenomena rather than entities in philosophy and in fact regards mathematics as a kind of non-reality.
In opposition to psychologism are the supporters of mathematical realism such as Husserl and Frege. Husserl argues that “when someone speaks of logical laws or mentions mathematical truths … what they refer to is not subjective experiences extended over time, but rather something non-temporal, objective, and permanently valid [
2] (p. 3).” Frege takes a similar approach but also refutes the physicalist stance of mathematical realism, which it includes two meanings: one being that numbers themselves are seen as objects possessing physical properties, and the other being that numbers are regarded as properties of some physical objects [
3]. Husserl and Frege define mathematics as having a non-temporal, objective, and conceptual existence to assert its reality, with Frege emphasizing the conceptual aspect through his critique of the physicalist stance. Both philosophers’ viewpoints reflect strong Platonism.
Russell’s paradox challenged the objectivity of mathematics. Mathematicians such as Brouwer and Weyl turned to intuition rather than language or logic as the basis for mathematics, endowing it with a priori existence in order to use the clarity brought by intuition to solve the crisis of objectivity, approaching Kantianism. However, such an approach resulted in the rejection of mathematical treasures such as irrational numbers and the law of the excluded middle. Hilbert could not accept this “broken mathematics”, so in order to balance the integrity and objectivity of mathematics, he proposed the formalization of mathematics as a system in which the objects (mathematical theorems and their proofs) of this formal system are expressed as statements in the language of symbolic logic, with these statements having only logical structure without actual content [
4] (p. 167). Thus, instead of seeking to restore the objectivity of mathematics through the clarity of intuition, Hilbert’s approach dissolves mathematical meaning, allowing mathematics to preserve its traditional treasures while restoring its objectivity.
Later, another group of mathematical philosophers emerged with the aim of restoring mathematical realism. One noteworthy form of mathematical realism is “the New Platonism”, which has two tendencies represented by Quine and Putnam and Gödel, respectively [
1]. Although these two approaches are more sophisticated in form, they are essentially the same as Platonism.
In conclusion, the traditional discussion on the existence of mathematics tends to lean toward Platonistic ontological views. However, when the objectivity of mathematics is challenged, if one resorts to intuitionism, which defines existence based on clarity, it poses a challenge to the integrity of mathematics. On the other hand, if one aims to balance both the integrity and objectivity of mathematics, it inevitably means that the meaning of mathematics must be dissolved.
3. The Existence of Mathematics under Information Ontology
The philosophy of information holds that conventional ontological attitudes can be broadly summarized into the following two types:
The ontological attitude of pre-naturalism, which holds that human beings can gradually understand the world only through the process of interacting with the external world and learning the differences between themselves and the external world [
5]. However, this ontological attitude, which begins from the subject of cognition, often tends to slide toward the attitude of idealism, because it deeply binds the existence of objects with the existence of subjects. Therefore, once the existence of the subject is dissolved, it means that the object no longer exists.
The ontological attitude of naturalism, which holds that objective things exist independently of the cognitive subject and dissolves the implicit proposition in pre-naturalism that the existence of the subject is higher than the existence of the object, giving them equal status. However, the challenge posed by this approach, beginning from the object, is that the ontological commitment made to objective things is difficult to accept due to the gap between the “thing-in-itself” and experience. Pre-naturalism does not face such a problem because the criterion for judging existence based on the subject’s perception is clarity.
The opposition between the two ontological attitudes directly affects the uncertainty of the ontological status of mathematics itself.
The philosophy of information first distinguishes between subjective existence and objective existence because clarity mainly comes from the uniqueness of the subjective perspective. Confusing subjective existence with objective existence and dividing ontology based on clarity is bound to be one-sided. Subjective existence is the category of “idea” and “spirit” under the ontological attitude of pre-naturalism.
Regarding the ontological issue of reality, the philosophy of information first inherits the doctrine of the primacy of matter in naturalistic ontology. That is, ontological assertions in the philosophy of information are not in conflict with materialism but even represent continued development. Abandoning the ontological assertion of materialism regarding the reality of the world would undoubtedly make the domain of reality a field that we cannot accept, just as Hilbert described broken mathematics. As the concept of “matter” originates from naïve extensional induction, we can adopt the view of Plekhanov that the term “matter” is identical to the thing-in-itself and use “information” to express our experience, as defined by the philosophy of information. “Information” is a philosophical category that signifies indirect existence; it is the self-revelation of the mode and state of existence of “matter” (which exists directly) [
6] (p. 109). What sets this claim apart from the agnostic gap caused by the traditional dichotomy between the thing-in-itself and experience is that although the conservation of “matter” and “energy” seems to limit the boundaries of human knowledge, the lack of conservation of “information” means that human knowledge can continue to deepen and develop. This opens a window for knowledge to continue developing after the doors of the traditional agnostic perspective of the thing-in-itself are closed.
As for the issue of unifying and clarifying the ambiguous ontology and making the domain of existence orderly, the main approach is to distinguish between subjective and objective existence and introduce “information” to describe non-real existence.
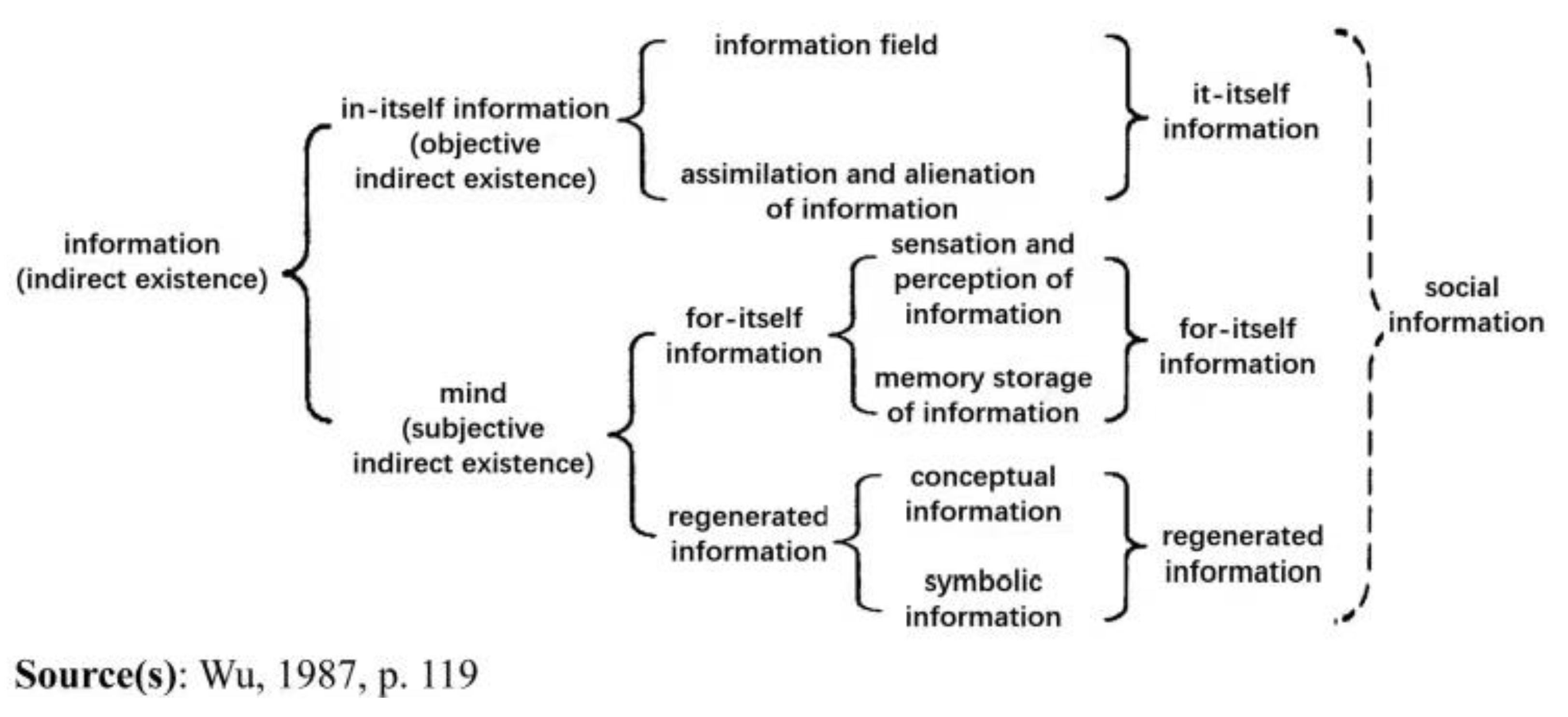
We know that traditional views of the existence of mathematics are mainly the Platonic and Kantian assertions of an existence of information. Therefore, whether mathematics can be ultimately proven to have objectivity or clarity cannot be a sufficient reason to regard mathematics as real. From the perspective of the philosophy of information, mathematics should be regarded as a kind of objective but unreal information. However, this does not mean that the task is complete. In the philosophy of information, the existence of information also falls into different categories, as shown in
Figure 1:
The figure distinguishes between it-itself, for-itself, and regenerated information. It-itself information is the sign of objective indirect existence in its primitive form, before being recognized by the subject. For-itself information is the primary form of subjective indirect existence, which is the subject’s direct intuition of it-itself information. Regenerated information is the advanced form of subjective indirect existence, which is created by the subject [
6] (p. 111).
How does mathematics exist both objectively and subjectively? If we admit the subjectivity of mathematics, it seems to imply the recognition of individual differences, which is clearly inconsistent with objectivity. However, the problem with this questioning is that it narrows the meaning of the term “subjective” to individual differences while disregarding species differences. Just as the difference between the world seen by a color-blind person and the world seen by a non-color-blind person is a subjective difference at the individual level, Thomas Nagel believes that the difference in the world seen by humans and the world seen by bats is a subjective difference at the level of class concepts [
8]. Therefore, mathematics exists both as subjective and objective, which also means that mathematics is simultaneously it-itself information, for-itself information, and regenerated information. So, how should we define mathematics?
As shown in
Figure 1, there is also an organic unity of social information as a combination of the three states of information: social information is not an independent form of information but a comprehensive form of information that emerges from the relationship between the three basic forms of it-itself, for-itself, and regenerated information [
6] (p. 112). Mathematics may be a form of indirect existence of a social information system that integrates the three states of it-itself, for-itself, and regenerated information.
4. The Existence of Mathematics in the Epistemology of Information
The epistemology of information posits that “Human cognition is a form of for-itself and regenerated information, which is a high-level information activity process … The level of human information activities and the ability to process information are constructed and developed episodically in the process of biological evolution … Specifically, human information activities can be divided into five basic levels … [
9] (pp. 53–54).” That is to say, human information activity, from a historical perspective, has developed from a low level to a high level, and the five basic levels of information activities basically cover the process of human information activities from simplicity to complexity, and the three forms of it-itself, for-itself, and regenerated information are included among them.
The first level is the spontaneous activity of information, which is the activity of information related to a “quantity” that humans do not grasp and is carried by a material body external to humans that can enrich mathematical forms. The second level is the subjective recognition of information in which a human can grasp and understand the information about “quantity” and their own mathematical abilities. The third level is the memory storage of information, including concrete “quantities” and symbolic form systems and other conceptual information. The fourth level is the creation of subject information, including processing and extracting information about “quantity” from representational information of perceptual memory and creating corresponding symbolic conceptual information. The fifth level is the social implementation of subject information, which includes capturing the information about the relationships between quantities and correcting plans through practice and promoting mathematical symbolic form systems. Together, these levels constitute the process of the formation and development of modern complex mathematical abilities.
In addition, understanding the evolution of mathematical movements and developments must be further integrated into the development of human civilization.
Engels proposed the attitude of historical materialism, which legitimizes abstract conclusions based on the foundation of reality.
Adhering to this method, Raphael once summarized: “Humans and many nonhuman species do have biologically endowed abilities for perceiving and discriminating quantities, at least in an imprecise manner and in particular formats (e.g., food items). Although robust, these observations do not support claims that there is an evolved capacity specific for number and arithmetic [
10].” Raphael disagreed with Kant that the degree of human evolution in terms of physiological evolution had reached a perfect level of mathematical ability. In fact, according to the content of Raphael’s article, among human populations still maintaining their primitive lifestyles, the symbol systems of these groups do not include the sophisticated mathematical formal systems and corresponding symbol concepts that we are familiar with. Their mathematical abilities are only limited to a level similar to those of certain advanced animals, that is, they can only perceive a small amount of numerical information (about four), and there are no corresponding concepts and symbols for numbers greater than this, let alone mathematical operations [
10]. In other words, for humans whose mathematical abilities are limited to this level, their mathematical information activities are only limited to the first three levels, and the fourth level and above are in nascent or undeveloped states. This is also the “natural mathematical ability” that we should distinguish from the “complex mathematical ability” of modern humans.
Engels also mentioned: “(In the advanced stage of human barbarism) it starts from the smelting of iron ore and transitions to the civilized era due to the invention of phonetic writing and its application in document recording [
11] (p. 25).” Until now, humans who maintained a primitive way of life had never encountered a complex enough practical activity to force the evolution of conceptual information and symbol information systems [
10]. Therefore, regarding the development of the second stage of mathematics, we can say that in the process of entering the history of civilization, human mathematical ability has been continuously improved in practice. Specifically, this can be manifested as the separation of quantitative information from the object of cognition and its combination with symbol information; the emergence of the concept of numbers and the laws governing the relationship between complex quantities in practice have shaped complex human mathematical systems. These three manifestations, respectively, represent the beginning of mathematical information activities at the fourth and fifth levels and are evolving toward maturity and humans’ gradually attainment of “complex mathematical abilities”. This demonstrates the dynamic development of mathematics.
Author Contributions
Conceptualization, Y.Q. and T.W.; methodology, Y.Q. and T.W.; writing—original draft preparation, Y.Q.; writing—review and editing, T.W.; supervision, T.W.; project administration, T.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The article does not have any newly created data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huang, Q. The Evolution and Review of Mathematical Realism in the Perspective of Ontology. Stud. Sci. Technol. Philos. 2013, 30, 7–12. [Google Scholar]
- Zahavi, D. Husserl’s Phenomenology; Li, Z., Translator; Shanghai Translation Publishing House: Shanghai, China, 2007; p. 8. [Google Scholar]
- Dai, M. On What Is Number: An Analysis of Frege’s Mathematical Ontology. Hebei Acad. 2018, 38, 200–204. [Google Scholar]
- Reid, C.H.; Li, W. Translator; Shanghai Scientific & Technical Publishers: Shanghai, China, 2018; p. 8. [Google Scholar]
- Wu, T. Reflection on the Basic Issues of Philosophy from the Perspective of the Epistemology of Information. J. Syst. Sci. Complex. 2019, 27, 11–16. [Google Scholar]
- Wu, K. (Ed.) Theoretical Foundations of Complex Information Systems; Xi’an Jiaotong University Press: Xi’an, China, 2010; p. 9. [Google Scholar]
- Wu, T.; Da, K. The Chinese philosophy of information by Kun Wu. J. Doc. 2021, 77, 4. [Google Scholar] [CrossRef]
- Nagel, T. What is it like to be a bat? Philos. Rev. 1974, 83, 435–450. [Google Scholar] [CrossRef]
- Wu, K. Epistemology of Information; China Social Sciences Press: Beijing, China, 2002; p. 9. [Google Scholar]
- Núñez, R.E. Is there really an evolved capacity for number? Trends Cogn. Sci. 2017, 21, 409–424. [Google Scholar] [CrossRef] [PubMed]
- Engels, F. The Origin of the Family, Private Property and the State; Compiled and translated by the Compilation and Translation Bureau of the Works of Marx, Engels, Lenin and Stalin of the CPC Central Committee; People’s Publishing House: Beijing, China, 2018; p. 3. [Google Scholar]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).