The Proof and Decryption of Goldbach Conjecture ^†

Abstract

In this paper, a few mathematical bases are given firstly. Then, the step thinness τp of primes is given as τp = Lo1 = P1ΠP/(P−1) for the inner character, having an lnX logarithmic outer character. The “best estimation and mutual exchange equivalent” are easily obtained as Lo1 = P1Π P/(P−1)~τp~lnX(ε). This is the principal contradiction, and P is the main aspect. Then, the sparsity τt of twin primes is defined as Lo2 = τt = P2 Π P/(P−2) = C2Lo1² = C2ln²X(C2 = 0.75739006). Then, the sparsity τg of the Goldbach pair and τb of both the twin and Goldbach pairs are obtained as Lo3 = τg = {2Lo1, Lo1², 2C2Lo1²} and Lo4 = τb =4.7Lo1³ (or they are omitted). Lastly, all conjectures can be proved with the same frame formula, N = X/LOK. The twin prime conjecture and Goldbach conjecture low bound are clearly and accurately proved with T = X/(C2Lo1²) = 1.32032X/ln²X and Gd = X/(2C2Lo1²) = 0.66016X/ln²X. Using Lo1 + C2 to decrypt the Selberg formula C(ω) = 2C(N) obtains the totally same results.

1. Introduction

Goldbach’s conjecture is a worldwide problem, which has caused many mathematicians to study it. This paper studies the top design and technical route to solve pure primes, twin prime pairs, and Goldbach prime pairs, i.e., all PPP, or prime property problems (Figure 1).

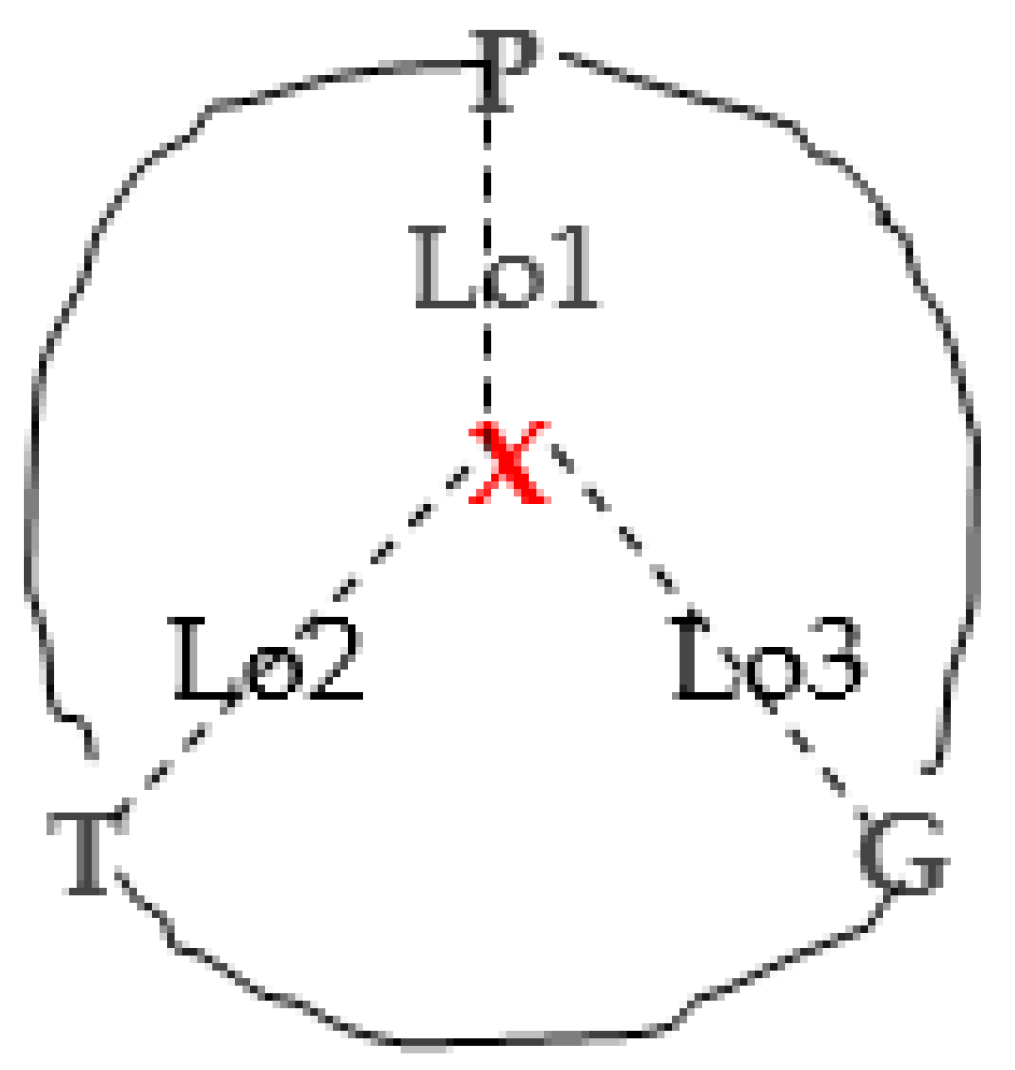
Figure 1. Top design figure of solving Goldbach’s conjecture.

Frame formula expression: {P,T,G} = X/Lok [1].

G: Goldbach conjecture (being wavy).

In this top design diagram, using Lo1, Lo2, and Lo3, all {P,T,G} = X/Lok expressions can be obtained.

(Z = PR ≤ √X is the necessary or critical point, and X/2 is the sufficient point for the sieve principle).

2. Pure Primes (P)

According to filter-sifter (sieve) principle, Lo1 = P1 Π P/(P−1) is defined for pure prime numbers.

P1 = 1, P2 = 2, P3 = 3, P4 = 5, and P5 = 7…; Z = PR ≤ √X is the necessary or critical point for the sieve principle.

The function Π P/(P−1) is called the Euler function or Riemann function, which previous mathematicians proved before. Here is a newer and more primary proof as follows:

X’s factorial: ΠX = 1*2*3*4*5*6…*X = X!

Prime’s factorial: ΠP = 2*3*5*7…*P = P!

Composition’s factorial: ΠC = 4*6*8*9…*C =C!

Ratio product: ΠX/(X−1) = 2/1 * 3/2 * 4/3 * 5/4…X/(X−1) = X

=(X/(X−1))! = Π(P/(P−1)) * (C/(C−1)) = (P/(P−1))! * (C/(C−1))! = X.

The geometric average must be √X.

Let Lo1 = Π(P/(P−1)) and Loc = Π(C/(C−1)):

X = 6 15/4 = 3.75 24/15 = 1.6.

10 4.375 2.2857

47 7.209592623 > 6.519092349

52 < 7.212612812

53 7.348238615 >

54 < 7.348699846; the later Loc is greater.

Geometric average √X must not be changed.

Hence, Lo1 << √X << Loc; √X is the watershed, and Lo1 is the sparsity function of the sieve principle.

∵ √X is the watershed.

∴ Np = X/Lo1 >> √X; this means prime numbers must be infinite ∞.

Lo1 = ΠP/(P−1) ≈ τp ≈ lnX, i.e., the inner character and outer character are equivalent. The authors of paper [2], with results of (10.16)~(10.24), proved this equation, but the inner character was not used.

The double-face prime number theorem is proved.

QED.

3. Twin Pairs (T)

And similarly [3],

Lo2 = P2 Π P/(P−2) = C2Lo1² = C2ln²X(C2 = 0.75739006) identifies twin prime pairs.

The step constant C2 (twin bridge) is obtained from Lo2 = P2 Π P/(P−2) = C2Lo1².

C2 = 1/2 Π(P−1)²/(P(P−2)) = 0.75739006…

4. Gold Pairs (G)

Also similarly [4],

Lo3 = {2Lo1, Lo1², 2C2Lo1²} for the Goldbach conjecture pairs of up, average, and down.

So, {Gu, Ga, Gd} = X/Lo3 can be obtained.

5. All {PP, TP, GP} Formal Proofs

Frame formula expression: {P,T,G}= X/Lok; Lo1 = P1 Π P/(P−1)~τp~lnX(ε).

Independent proofs:

5.1. ∵ Lo1= ΠP/(P−1) ≈ τp ≈ lnX(ε).

∴ Np = X/Lo1 (X is out bound, Z = PR ≤ √X is the necessary point, and P is the filter variable.)

5.2. ∵ Lo2 = 2ΠP/(P−2) = C2Lo1².

∴ T =X/Lo2 = X/C2 Lo1² = 1.32032X/Lo1².

5.3. ∵ Lo3 = 2*2ΠP/(P−(1 + X%P! = 0)) = {2Lo1, Lo1², 2C2Lo1²} wavy.

∴ G = {Gu, Ga, Gd} = {Np/2, X/Lo1², 0.66016 X/Lo1²} wavy.

5.4. ∵ Lo4 = 4.7Lo1³.

∴ B = X/Lo4 = X/(4.7ln³X), (reasoning process omitted).

QED.

Decryption proofs: (using Lo1 + C2 to decrypt the Selberg formula C(ω) = 2C(N) as follows:)

∵ C(K) = LOK is for the denominator in the GES method, ∴ N = X/LOK, while

∵ C(ω) = 2C(N) is for the numerator in the SES method, ∴ N = C(ω)|2C(N) · X/ln²X. Therefore,

here Lo1~τp~lnX; (equivalent mutual exchange).

∴ Lo1 = lnX ∴ decrypt: C(ω) = 2C(N) = (|)Lo1/(!)C2.

Np = X/Lo1 Np = (|)C(ω) = Lo1*X/Lo1² = X/Lo1.

T = X/Lo2 = X/C2Lo1² = 1.32032X/Lo1² T = (!)C(ω) = X/C2Lo1² = X/C2Lo1² = 1.32032X/Lo1².

G = X/Lo3 = X/{2Lo1, Lo1², 2C2 Lo1²} = {Gu = Np/2, Ga = X/Lo1², and Gd = 0.66016 X/Lo1²}

while 3E: E1 = {P!}, E2 = {others}, and E3 = {2^n} to meet.

Lo4 = 4.7Lo1³ (reasoning process omitted).

Horizontal compression ratio Np/T equals vertical wavy ratio Gu/Gd = C2Lo1.

Decrypt QED.

6. Conclusions

Due to all the above, all {PP, TP, GP} can be obtained using {P,T,G} = X/Lok, and in using Lo1 + C2, all PPP{PP,TP,GP}, i.e., {P,T,G} i.e., pure primes, twin pairs, and Goldbach pairs, are totally proved and decrypted. So, all of the prime problems, including the Goldbach conjecture, are totally solved with Gd = 0.66016 X/Lo1². This is the fundamental conclusion of this paper [4].