Unveiling the Impact of Socioeconomic and Demographic Factors on Graduate Salaries: A Machine Learning Explanatory Analytical Approach Using Higher Education Statistical Agency Data
Abstract
1. Introduction
1.1. Global Higher Education (HE) Growth
1.2. Paper Organisation
2. Literature Review
2.1. Factors Affecting Graduate Salaries
2.1.1. Employability
2.1.2. Discipline and Gender
2.1.3. Socioeconomic Background
3. Methodology
3.1. Study Design, Data Collection, and Selection Criteria
3.2. Machine Learning Model Selection
3.2.1. Logistic Regression (LR)
3.2.2. K-Nearest Neighbours (KNN)
3.2.3. Linear Discriminant Analysis (LDA)
3.2.4. Decision Tree
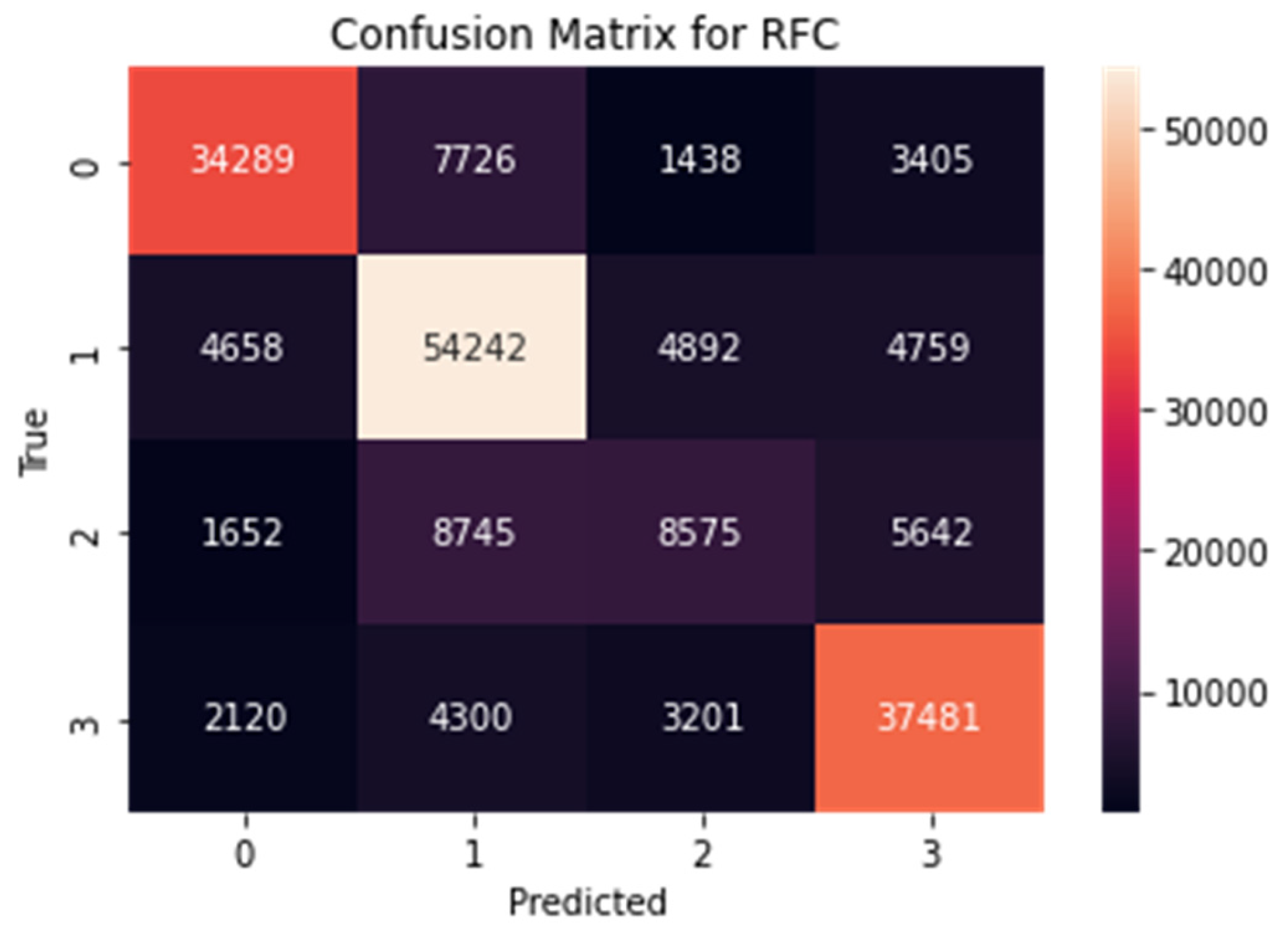
3.2.5. Random Forest (RF) Algorithm
3.2.6. Gaussian Naïve Bayes (GNB)
3.2.7. Gradient Boosting Algorithm
3.2.8. Support Vector Machine (SVM) Algorithm
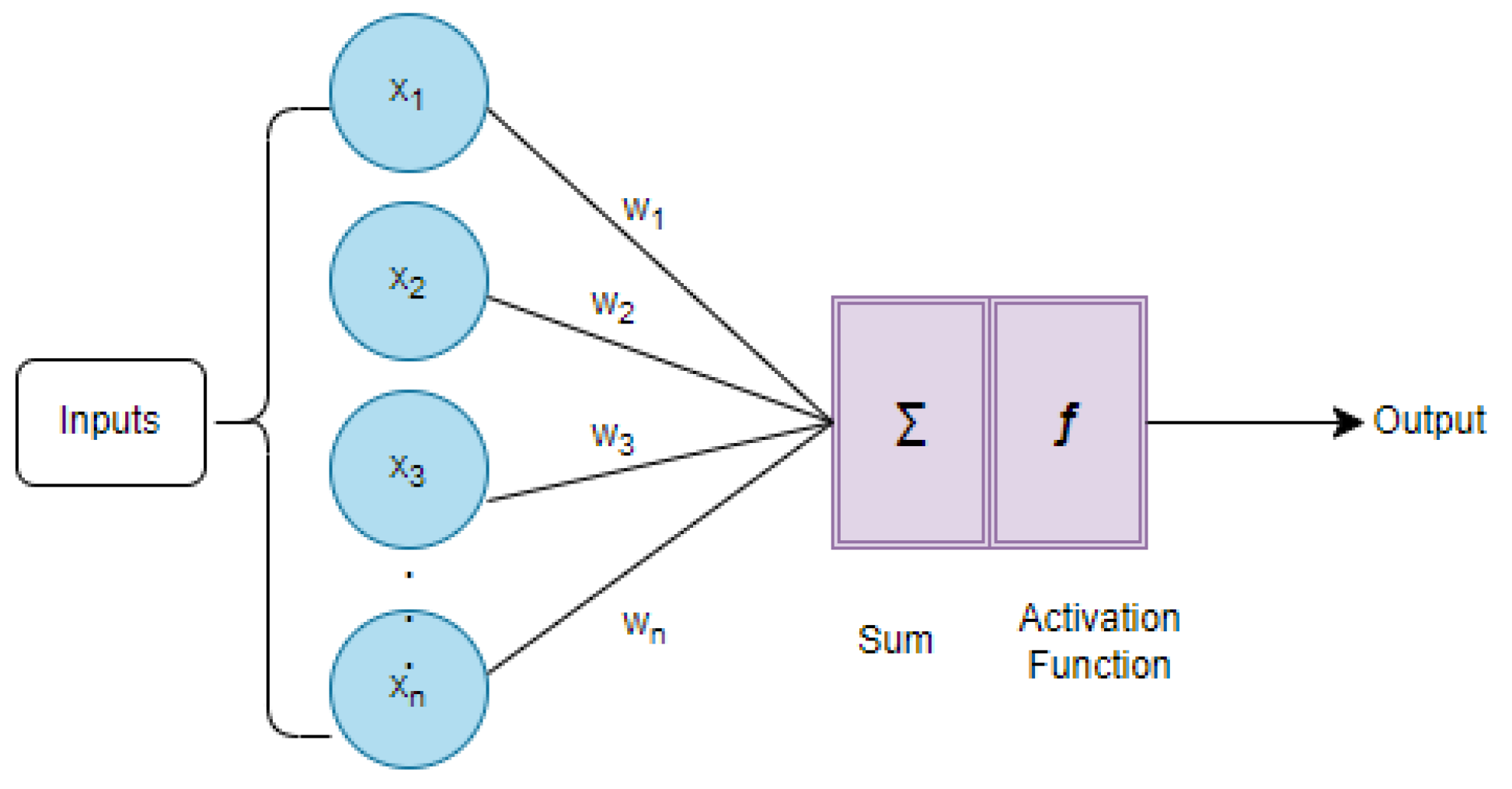
3.2.9. Neural Networks
3.2.10. Adaptive Boosting Classifier Algorithm (AdaBoost)
3.3. Analysis of Variance (ANOVA)
3.4. The Data Science Pipeline
3.4.1. Data Overview
3.4.2. Data Types and Outcome Variables
3.4.3. Limitations and Constraints of Secondary Data
3.4.4. Missing Data and Outliers
4. Results Analysis
4.1. Model Training Results
4.2. Feature Importance Analysis Using Shapley Additive Explanations (SHAP)
4.3. Interaction of Significant Factors: An Analysis of Variance (ANOVA) Approach
5. Discussion
5.1. The Variable Impacts
5.2. Challenges and Limitations of This Study
5.3. Statistical Significant Interactions Between Contributors and Graduate Salaries
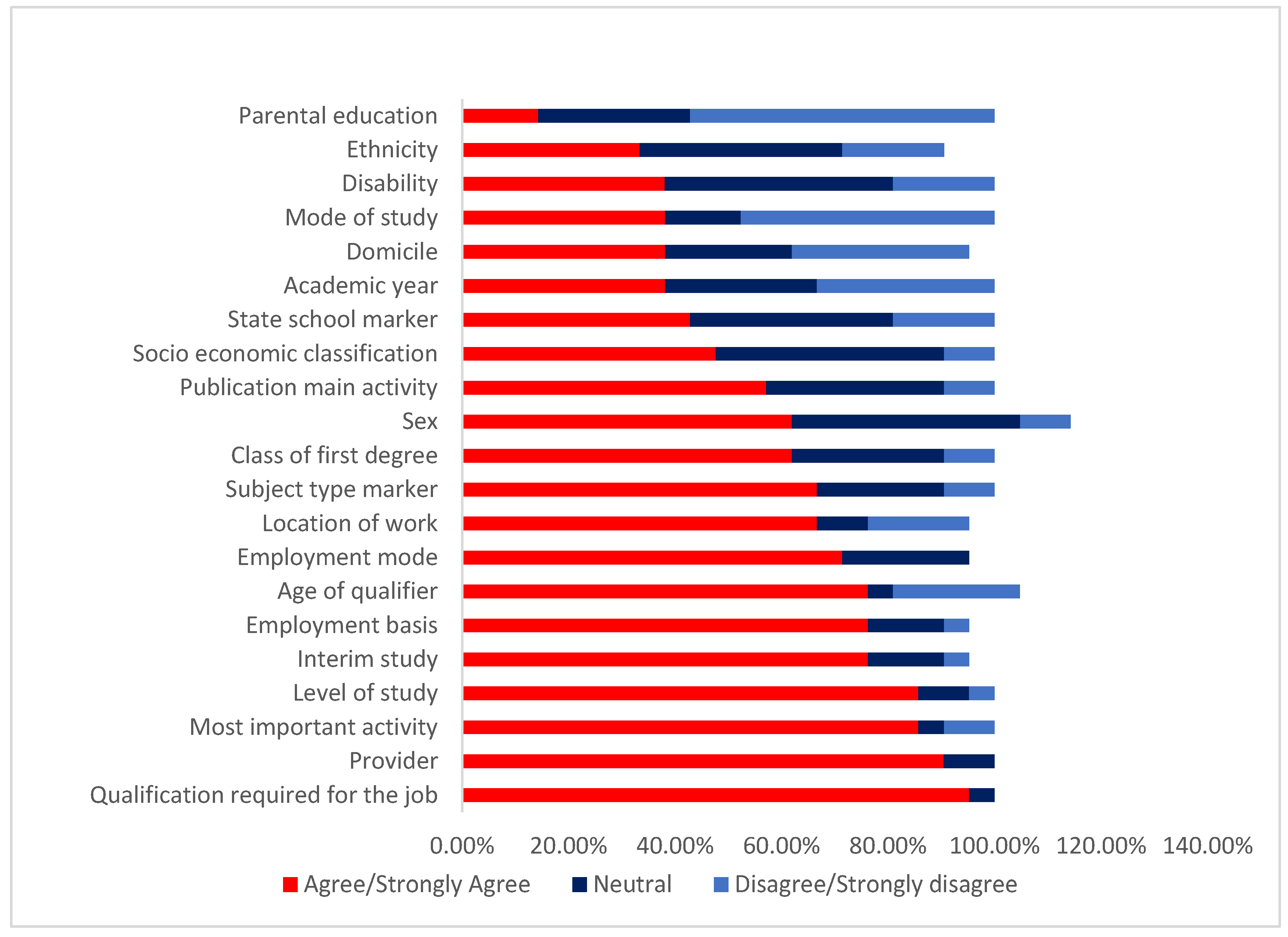
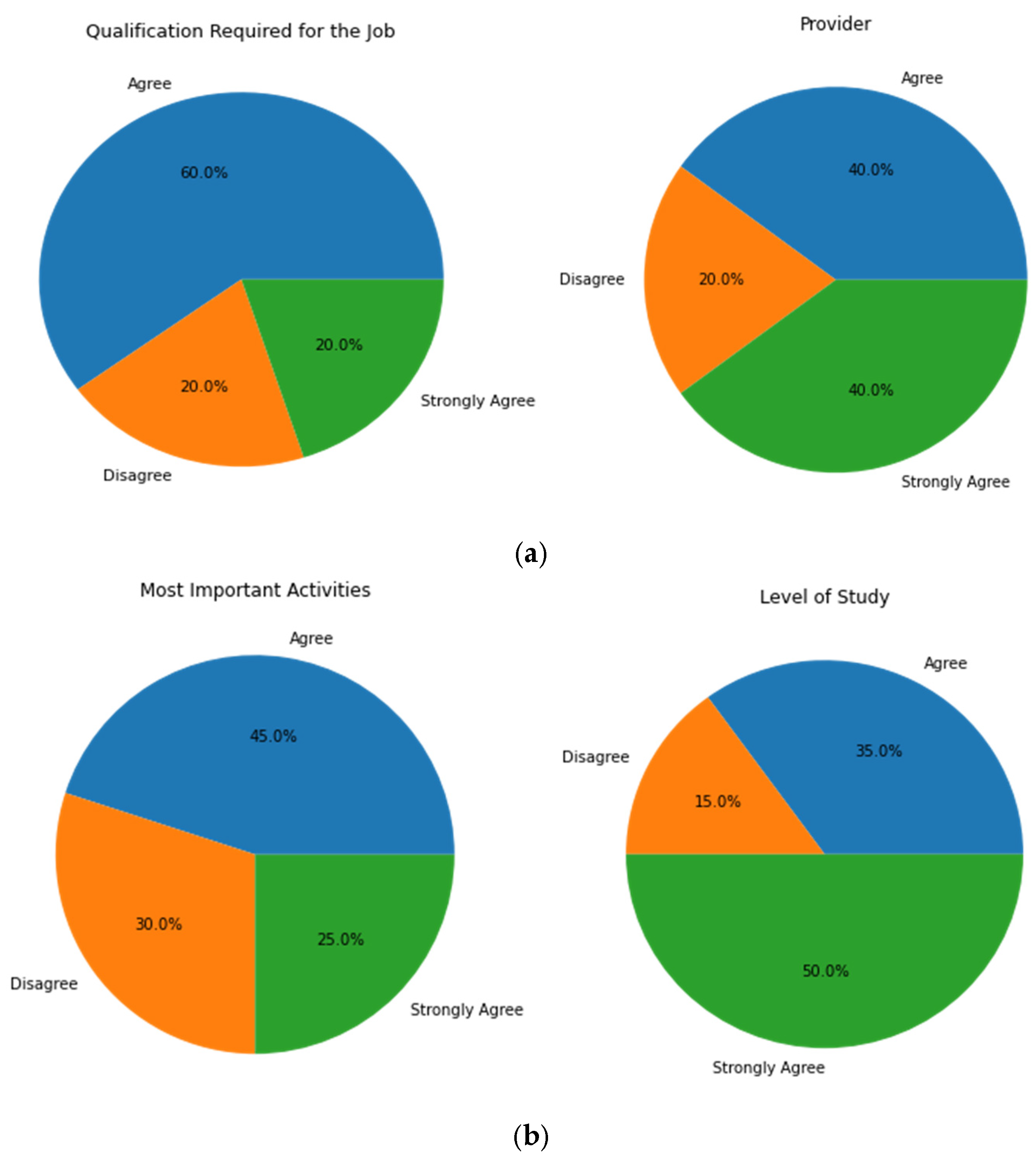
5.4. Validation of Results by Industry Experts
6. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chankseliani, M. International Development Higher Education: Looking from the Past, Looking to the Future. Oxf. Rev. Educ. 2022, 48, 457–473. [Google Scholar] [CrossRef]
- Green, F.; Henseke, G. Europe’s Evolving Graduate Labour Markets: Supply, Demand, Underemployment and Pay. J. Labour Mark. Res. 2021, 55, 1–13. [Google Scholar] [CrossRef]
- Sabiote, C. Use of Binomial Logistic Regression Models for the Study of Determining Variables in the Labour Insertion of University Graduates. Res. Postgrad. 2022, 22, 109–144. [Google Scholar]
- Maquera-Luque, P.J.; Morales-Rocha, J.L.; Apaza-Panca, C.M. Socio-Economic and Cultural Factors That Influence the Labour Insertion of University Graduates, Peru. Heliyon 2021, 7, e07420. [Google Scholar] [CrossRef] [PubMed]
- Walker, I.; Zhu, Y. Impact of University Degrees on the Lifecycle of Earnings: Some Further Analysis. 2013. Available online: https://assets.publishing.service.gov.uk/media/5a7b8cc5e5274a7202e17e36/bis-13-899-the-impact-of-university-degrees-on-the-lifecycle-of-earnings-further-analysis.pdf (accessed on 22 November 2024).
- Holmes, C.; Mayhew, K. The economics of higher education. Oxf. Rev. Econ. Policy 2016, 32, 475–496. [Google Scholar] [CrossRef]
- Duta, A.; Wielgoszewska, B.; Iannelli, C. Different Degrees of Career Success: Social Origin and Graduates’ Education and Labour Market Trajectories. Adv. Life Course Res. 2021, 47, 100376. [Google Scholar] [CrossRef]
- Anders, J. Does Socioeconomic Background Affect Pay Growth among Early Entrants to High-Status Jobs? National Institute of Economic and Social Research (NIESR) Discussion Papers; National Institute of Economic and Social Research: London, UK, 2015. [Google Scholar]
- Guri-Rosenblit, S.; Šebková, H.; Teichler, U. Massification and Diversity of Higher Education Systems: Interplay of Complex Dimensions. High. Educ. Policy 2007, 20, 373–389. [Google Scholar] [CrossRef]
- Webb, S.; Bathmaker, A.-M.; Gale, T.; Hodge, S.; Parker, S.; Rawolle, S. Higher Vocational Education and Social Mobility: Educational Participation in Australia and England. J. Vocat. Educ. Train. 2017, 69, 147–167. [Google Scholar] [CrossRef][Green Version]
- Đonlagić, S.; Kurtić, A. The Role of Higher Education in a Knowledge Economy. In Economic Development and Entrepreneurship in Transition Economies; Ateljević, J., Trivić, J., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 91–106. ISBN 978-3-319-28855-0. [Google Scholar]
- Anderson, R. University Fees in Historical Perspective. History & Policy. 2016. Available online: https://historyandpolicy.org/policy-papers/papers/university-fees-in-historical-perspective (accessed on 22 November 2024).
- Daly, A.; Lewis, P.; Corliss, M.; Heaslip, T. The Private Rate of Return to a University Degree in Australia. Aust. J. Educ. 2015, 59, 97–112. [Google Scholar] [CrossRef]
- Dietrichson, J.; Bøg, M.; Filges, T.; Klint Jørgensen, A.-M. Academic Interventions for Elementary and Middle School Students with Low Socioeconomic Status: A Systematic Review and Meta-Analysis. Rev. Educ. Res. 2017, 87, 243–282. [Google Scholar] [CrossRef]
- Cooper, D.; Mokhiber, Z.; Zipperer, B. Raising the Federal Minimum Wage to $15 by 2025 Would Lift the Pay of 32 Million Workers; Economic Policy Institute (EPI): Washington, DC, USA, 2021; Available online: https://www.epi.org/publication/raising-the-federal-minimum-wage-to-15-by-2025-would-lift-the-pay-of-32-million-workers/ (accessed on 25 November 2024).
- Bertrand, M.; Duflo, E. Field Experiments on Discriminationa. In Handbook of Economic Field Experiments; Elsevier: Amsterdam, The Netherlands, 2017; Volume 1, pp. 309–393. Available online: https://www.sciencedirect.com/science/article/pii/S2214658X1630006X (accessed on 22 November 2024).
- Blau, F.D.; Kahn, L.M. The Gender Wage Gap: Extent, Trends, and Explanations. J. Econ. Lit. 2017, 55, 789–865. [Google Scholar] [CrossRef]
- Smith, A.E.; Hassan, S.; Hatmaker, D.M.; DeHart-Davis, L.; Humphrey, N. Gender, Race, and Experiences of Workplace Incivility in Public Organizations. Rev. Public. Pers. Adm. 2021, 41, 674–699. [Google Scholar] [CrossRef]
- Chetty, R.; Friedman, J.N.; Saez, E.; Turner, N.; Yagan, D. Mobility Report Cards: The Role of Colleges in Intergenerational Mobility; National Bureau of Economic Research: Cambridge, MA, USA, 2017. [Google Scholar] [CrossRef]
- Meara, K.; Pastore, F.; Webster, A. The Gender Pay Gap in the USA: A Matching Study. J. Popul. Econ. 2020, 33, 271–305. [Google Scholar] [CrossRef]
- Hogan, R.; Chamorro-Premuzic, T.; Kaiser, R.B. Employability and Career Success: Bridging the Gap Between Theory and Reality. Ind. Organ. Psychol. 2013, 6, 3–16. [Google Scholar] [CrossRef]
- Fugate, M.; Kinicki, A.J. A Dispositional Approach to Employability: Development of a Measure and Test of Implications for Employee Reactions to Organizational Change. J. Occup. Organ. Psychol. 2024, 81, 503–527. [Google Scholar] [CrossRef]
- Rosenberg, S.; Heimler, R.; Morote, E. Basic Employability Skills: A Triangular Design Approach. Educ. + Train. 2012, 54, 7–20. [Google Scholar] [CrossRef]
- Jackson, D.; Sibson, R.; Riebe, L. Delivering Work-Ready Business Graduates—Keeping Our Promises and Evaluating Our Performance. J. Teach. Learn. Grad. Employab. 2013, 4, 2–22. [Google Scholar] [CrossRef]
- Cai, Y. Graduate Employability: A Conceptual Framework for Understanding Employers’ Perceptions. High. Educ. 2013, 65, 457–469. [Google Scholar] [CrossRef]
- Light, A.; Strayer, W. Who receives the college wage premium?: Assessing the labor market returns to degrees and college transfer patterns. J. Hum. Resour. 2004, 39, 746–773. [Google Scholar] [CrossRef]
- Zhang, L. Gender and racial gaps in earnings among recent college graduates. Rev. High. Educ. 2008, 32, 51–72. [Google Scholar] [CrossRef]
- Taniguchi, H. The influence of age at degree completion on college wage premiums. Res. High. Educ. 2005, 46, 861–881. [Google Scholar] [CrossRef]
- Quadlin, N.; VanHeuvelen, T.; Ahearn, C.E. Higher Education and High-Wage Gender Inequality. Soc. Sci. Res. 2023, 112, 102873. [Google Scholar] [CrossRef] [PubMed]
- Davidovitch, N. Discipline and Gender: Factors Affecting Graduates’ Salaries. US-China Foreign Lang. 2013, 11, 770–778. [Google Scholar] [CrossRef][Green Version]
- Macmillan, L.; Tyler, C.; Vignoles, A. Who Gets the Top Jobs? The Role of Family Background and Networks in Recent Graduates’ Access to High-Status Professions. J. Soc. Pol. 2015, 44, 487–515. [Google Scholar] [CrossRef]
- Charizanos, G.; Demirhan, H.; İçen, D. Binary Classification with Fuzzy Logistic Regression under Class Imbalance and Complete Separation in Clinical Studies. BMC Med. Res. Methodol. 2024, 24, 145. [Google Scholar] [CrossRef]
- Cunningham, P.; Delany, S.J. K-Nearest Neighbour Classifiers—A Tutorial. ACM Comput. Surv. 2022, 54, 1–25. [Google Scholar] [CrossRef]
- Alizadeh, E.; Maleki, A. A Novel K-NN Algorithm for Imbalanced Datasets Using Euclidean-Smote. Eng. Appl. Artif. Intell. 2021, 100, 104163. [Google Scholar] [CrossRef]
- López-Meneses, E.; López-Catalán, L.; Pelícano-Piris, N.; Mellado-Moreno, P.C. Artificial Intelligence in Educational Data Mining and Human-in-the-Loop Machine Learning and Machine Teaching: Analysis of Scientific Knowledge. Appl. Sci. 2025, 15, 772. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Zou, B.; Lui, H.; Wei, X. An Improved Linear Discriminant Analysis Based on Pseudo Inverse for Small Sample Size Problem. Neural Comput. Appl. 2021, 33, 3931–3939. [Google Scholar]
- Ma, S.; Huang, H.; Luo, Y.; Gao, Y. Feature Selection Based on Improved Fisher’s Linear Discriminant Analysis for Fault Diagnosis of Rotating Machinery. Mech. Syst. Signal Process 2021, 157, 107752. [Google Scholar]
- Safi, S.K.; Gul, S. An Enhanced Tree Ensemble for Classification in the Presence of Extreme Class Imbalance. Mathematics 2024, 12, 3243. [Google Scholar] [CrossRef]
- Lu, J.; Wu, H.; Wu, Y.; Wang, J.; Zhou, Y. An Improved Decision Tree Algorithm Based on Information Gain Ratio. J. Intell. Fuzzy Syst. 2021, 40, 41–50. [Google Scholar]
- Atzmueller, M.; Fürnkranz, J.; Kliegr, T.; Schmid, U. Explainable and Interpretable Machine Learning and Data Mining. Data Min. Knowl. Disc 2024, 38, 2571–2595. [Google Scholar] [CrossRef]
- Mohri, M.; Rostamizadeh, A.; Talwalkar, A. Foundations of Machine Learning, 2nd ed.; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2018; ISBN 978-0-262-03940-6. [Google Scholar]
- Lee, H.; Jang, Y.; Lee, J.; Kim, J. Robust Decision Tree Pruning via Rule-Based Regularization. Neural Netw. 2021, 144, 12–23. [Google Scholar] [CrossRef]
- Fuseini, I.; Missah, Y.M. A Critical Review of Data Mining in Education on the Levels and Aspects of Education. Qual. Educ. All 2024, 1, 41–59. [Google Scholar] [CrossRef]
- Han, S.; Kim, H.; Lee, Y.-S. Double Random Forest. Mach. Learn. 2020, 109, 1569–1586. [Google Scholar] [CrossRef]
- Shashaani, S.; Sürer, Ö.; Plumlee, M.; Guikema, S. Building Trees for Probabilistic Prediction via Scoring Rules. Technometrics 2024, 66, 625–637. [Google Scholar] [CrossRef]
- Hue, C.; Boullé, M.; Lemaire, V. Online Learning of a Weighted Selective Naive Bayes Classifier with Non-Convex Optimization. In Advances in Knowledge Discovery and Management; Guillet, F., Pinaud, B., Venturini, G., Eds.; Studies in Computational Intelligence; Springer International Publishing: Cham, Switzerland, 2017; Volume 665, pp. 3–17. ISBN 978-3-319-45762-8. [Google Scholar]
- Khan, A.A.; Chaudhari, O.; Chandra, R. A Review of Ensemble Learning and Data Augmentation Models for Class Imbalanced Problems: Combination, Implementation and Evaluation. Expert. Syst. Appl. 2024, 244, 122778. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. arXiv 2016, arXiv:1603.02754. [Google Scholar] [CrossRef]
- Sohil, F.; Sohali, M.U.; Shabbir, J. An Introduction to Statistical Learning with Applications in R. Stat. Theory Relat. Fields 2022, 6, 87. [Google Scholar] [CrossRef]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A Comprehensive Survey on Support Vector Machine Classification: Applications, Challenges and Trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Seo, Y.; Shin, K. Hierarchical Convolutional Neural Networks for Fashion Image Classification. Expert. Syst. Appl. 2019, 116, 328–339. [Google Scholar] [CrossRef]
- García-Blanco, M.; Cárdenas Sempértegui, E.B. Labour Insertion in Higher Education: The Latin American Perspective. Educ. XX1 2018, 21, 323–347. [Google Scholar] [CrossRef]
- Delaney, B.; Tansey, K.; Whelan, M. Satellite Remote Sensing Techniques and Limitations for Identifying Bare Soil. Remote Sens. 2025, 17, 630. [Google Scholar] [CrossRef]
- Ren, Y.; Xie, Z.; Zhai, S. Urban Land Use Classification Model Fusing Multimodal Deep Features. ISPRS Int. J. Geo-Inf. 2024, 13, 378. [Google Scholar] [CrossRef]
- Bengio, S.; Deng, L.; Larochelle, H.; Lee, H.; Salakhutdinov, R. Guest Editors’ Introduction: Special Section on Learning Deep Architectures. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1795–1797. [Google Scholar] [CrossRef]
- Kiran, R.J.; Sanil, J.; Asharaf, S. A Novel Approach for Model Interpretability and Domain Aware Fine-Tuning in AdaBoost. Hum-Cent. Intell. Syst. 2024, 4, 610–632. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R, 2nd ed.; Springer Texts in Statistics; Springer: New York, NY, USA, 2021; ISBN 978-1-07-161418-1. [Google Scholar]
- Curley, C.; Krause, R.M.; Feiock, R.; Hawkins, C.V. Dealing with Missing Data: A Comparative Exploration of Approaches Using the Integrated City Sustainability Database. Urban. Aff. Rev. 2019, 55, 591–615. [Google Scholar] [CrossRef]
- Chen, W.; Yang, K.; Yu, Z.; Shi, Y.; Chen, C.L.P. A Survey on Imbalanced Learning: Latest Research, Applications and Future Directions. Artif. Intell. Rev. 2024, 57, 137. [Google Scholar] [CrossRef]
- Rudin, C.; Chen, C.; Chen, Z.; Huang, H.; Semenova, L.; Zhong, C. Interpretable Machine Learning: Fundamental Principles and 10 Grand Challenges. Statist. Surv. 2022, 16, 1–85. [Google Scholar] [CrossRef]
- Salih, A.M.; Raisi-Estabragh, Z.; Galazzo, I.B.; Radeva, P.; Petersen, S.E.; Lekadir, K.; Menegaz, G. A Perspective on Explainable Artificial Intelligence Methods: SHAP and LIME. Adv. Intell. Syst. 2025, 7, 2400304. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, Q.; Yao, C.; Liu, Z. The Signaling Paradox: Revisiting the Impacts of Overeducation in the Chinese Labour Market. Educ. Sci. 2024, 14, 900. [Google Scholar] [CrossRef]
- Asfaw, A. Racial and Ethnic Disparities in Teleworking Due to the COVID-19 Pandemic in the United States: A Mediation Analysis. Int. J. Environ. Res. Public Health 2022, 19, 4680. [Google Scholar] [CrossRef] [PubMed]
- McKnight, A.; Naylor, R. Going to University: The Influence of Schools, Information and Parental Expectations. Oxf. Rev. Educ. 2015, 41, 231–248. [Google Scholar]
- Sutton, T. Mobility Manifesto: A Lifetime of Opportunities. Mobil. Manif. 2020. Available online: https://www.suttontrust.com/wp-content/uploads/2019/12/Mobility-Manifesto-2019-1.pdf (accessed on 24 November 2024).
- Institute for Fiscal Studies. The Impact of Higher Education on Regional Economies and Lifetime Earnings. IFS. 2020. Available online: https://ifs.org.uk/publications/impact-undergraduate-degrees-lifetime-earnings (accessed on 25 November 2024).
- Pérez-Rivas, F.J.; Jiménez-González, J.; Bayón Cabeza, M.; Belmonte Cortés, S.; De Diego Díaz-Plaza, M.; Domínguez-Bidagor, J.; García-García, D.; Gómez Puente, J.; Gómez-Gascón, T. Design and Content Validation Using Expert Opinions of an Instrument Assessing the Lifestyle of Adults: The ‘PONTE A 100’ Questionnaire. Healthcare 2023, 11, 2038. [Google Scholar] [CrossRef]





| Source of Variation | Sum of Squares | df | Mean Square | F |
|---|---|---|---|---|
| Between groups | SSB | (p-1) | ||
| Error (within groups) | SSW | (N-p) | ||
| Total | SST | (N-1) |
| Model | Type | Key Characteristics | Strengths in Graduate Salary Prediction | Limitations | Reason for Selection in This Study |
|---|---|---|---|---|---|
| Logistic Regression (LR) | Classification | Assumes a linear relationship between independent variables (demographic/socioeconomic factors) and salary groups. | Simple and interpretable; useful for understanding relationships between predictors and salary categories. | Assumes linearity; may not capture complex relationships between factors like institutional prestige and salaries. | Used as a baseline model to compare performance with more complex ML methods. |
| K-Nearest Neighbours (KNN) | Classification | Classifies salaries based on the most similar historical cases; uses distance metrics. | Effective for detecting local salary patterns (e.g., institution-based salary clusters). | Computationally expensive for large datasets (1.87 M+ records); sensitive to irrelevant features. | Tested for its ability to capture salary variations based on demographic similarities. |
| Linear Discriminant Analysis (LDA) | Classification | Reduces dimensionality while maintaining class separability; assumes normal distribution. | Useful for analysing how multiple socioeconomic factors interact to classify salaries. | Assumes normality; may not perform well with non-Gaussian salary distributions. | Applied for dimensionality reduction and exploratory analysis of salary classifications. |
| Decision Tree (DT) | Classification | Recursive partitioning method; identifies key decision rules (e.g., “Did graduate attend a top-tier university?”). | Highly interpretable; detects hierarchical salary determinants (institution > job qualification > parental education). | Prone to overfitting without pruning; splits may be biased towards dominant features. | Identified as the best-performing model due to its ability to classify salary groups with high accuracy. |
| Random Forest (RF) | Classification | Ensemble of decision trees; aggregates multiple models to improve accuracy and reduce overfitting. | Handles large datasets effectively; identifies the most influential salary determinants across multiple trees. | Less interpretable than a single decision tree; computationally intensive. | Provided the highest accuracy and robust feature importance ranking (validated by SHAP analysis). |
| Gaussian Naïve Bayes (GNB) | Classification | Probabilistic model assuming feature independence; calculates salary probabilities per demographic group. | Works well on high-dimensional categorical data (e.g., ethnicity, institution type). | Assumes feature independence, which may not hold (e.g., parental education and socioeconomic status are correlated). | Included as a benchmark for probabilistic classification of graduate salary categories. |
| Gradient Boosting (GB) | Classification | Boosting technique that sequentially improves salary classification by correcting previous errors. | Strong predictive performance; handles interactions between features like “field of study × institution reputation”. | Prone to overfitting; requires extensive tuning. | Applied to test boosting-based performance improvement techniques. |
| Support Vector Machine (SVM) | Classification | Maximises margin between salary classes; effective in high-dimensional spaces. | Can model non-linear salary patterns using kernel trick (e.g., interaction of job qualification and domicile). | Computationally expensive on large datasets; sensitive to hyperparameter tuning. | Evaluated for its ability to classify salaries in complex feature spaces. |
| Neural Network (NN) | Classification | Learns hierarchical patterns in salary determinants; captures non-linear relationships. | Can detect deep salary trends (e.g., how combinations of ethnicity, institution, and job type influence pay). | Requires extensive data; hard to interpret; high computational cost. | Included to compare deep learning techniques with traditional ML models. |
| AdaBoost (ADA) | Classification | Assigns more weight to misclassified salary instances; iteratively improves model accuracy. | Improves weak learners; enhances salary predictions for minority groups. | Sensitive to noisy data; requires many iterations. | Used to assess the performance of boosting-based classifiers in handling salary disparities. |
| ANOVA (Analysis of Variance) | Statistical Analysis | Tests whether salary differences across demographic groups (e.g., gender, ethnicity) are statistically significant. | Validates machine learning findings; confirms whether socioeconomic factors significantly impact salaries. | Assumes homogeneity of variance; outliers can impact results. | Used to confirm statistical significance of identified salary determinants before ML modeling. |
| Category | Specific Variables | Pre-Processed |
|---|---|---|
| Personal Characteristics | Sex Disability | Male = 1, Female = 0, Others = 2 No known disability = 1, Known disability = 0 |
| Socioeconomic | Socio economic classification Parental education | Higher managerial and professional occupations = 0, Not classified = 5, Intermediate occupations = 1, Lower managerial and professional occupations = 2, Routine occupations = 6, Lower supervisory and technical occupations = 3, Semi-routine occupations = 7, Small employers and own account workers = 8, Never worked and long-term unemployed = 4 Yes = 4, No = 2, Information refused = 1, No response given = 3, Do not know = 0 |
| Demographic | Domicile Ethnicity | England = 0, Non-European Union = 1, Other European Union = 4, Scotland = 6, Wales = 7, Northern Ireland = 2, Other UK = 5, Not known = 3 White = 6, non-UK = 3, Asian = 0, Black = 1, Mixed = 2, Other = 5, Not known = 4 |
| Academic level/Qualification | Level of study Class of first-degree Mode of study Academic Year Interim study | First degree = 0, Postgraduate (taught) = 1, Other undergraduate = 2, Postgraduate (research) = 3 Classification not applicable = 0, Upper second-class honours = 6, First class honours = 2, Lower second class honours = 3, Unclassified third class honours/Pass = 4, FE level qualification = 1 Full time = 0, Part time = 1 2017/18 = 0, 2018/19 = 1, 2019/20 = 2 No significant interim study = 0, Unknown interim study = 2, Significant interim study = 1 |
| Employment type/location | Location of work Employment basis Employment mode Most important activity Publication main activity Salary groups | England = 0, Northern Ireland = 1, Overseas = 4, Wales = 6, Scotland = 5, Not known = 2, Other UK = 6 On a permanent/open-ended contract = 3, On a fixed-term contract lasting 12 months or longer = 1, On a fixed-term contract lasting less than 12 months = 2, On a zero-hour contract = 4, On an internship = 5, Temping (including supply teaching) = 7, Other = 6, Volunteering = 8, Not known = 0 Full time = 0, Part time = 1 Paid work for an employer = 4, Engaged in a course of study, training or research = 3, Running my own business = 6, Self-employment/freelancing = 7, Developing a creative, artistic, or professional portfolio = 1, Unemployed and looking for work = 9, Retired = 5, Doing something else = 2, Caring for someone (unpaid) = 0, Voluntary/unpaid work for an employer = 10, Taking time out to travel—this does not include short-term holidays = 8 Full-time employment = 1, Part-time employment = 4, Employment and further study = 0, Full-time further study = 2, Part-time further study = 5, Unemployed = 6, Other including travel, caring for someone, or retired = 3, Voluntary or unpaid work = 11, Unemployed and due to start work = 8, Unknown pattern of employment = 9, Unemployed and due to start further study = 7, Unknown pattern of further study = 10 Minimum wage = 2, Living wage = 0, Median wage = 1, Top wage = 3 |
| Markers | Subject type marker State school marker | Non-science = 1, Science = 0 State-funded school or college = 1, Unknown or not applicable school type = 2, Privately funded school = 0 |
| Original Classification Data | ||||
|---|---|---|---|---|
| Model Evaluation Index | ||||
| Model | Precision | F1-Score | Recall | Accuracy |
| Logistic Regression | 0.49 | 0.45 | 0.46 | 0.54 |
| K-Nearest Neighbours | 0.62 | 0.61 | 0.61 | 0.66 |
| Linear Discriminant Analysis | 0.49 | 0.46 | 0.46 | 0.54 |
| Decision Tree | 0.66 | 0.61 | 0.62 | 0.69 |
| Gaussian Naïve Bayes | 0.48 | 0.47 | 0.47 | 0.52 |
| Gradient Boosting | 0.64 | 0.59 | 0.59 | 0.67 |
| Support Vector Machine | 0.47 | 0.45 | 0.45 | 0.54 |
| Neural Network | 0.09 | 0.13 | 0.25 | 0.37 |
| AdaBoost | 0.56 | 0.51 | 0.52 | 0.6 |
| Random Forest | 0.68 | 0.67 | 0.67 | 0.72 |
| Model Evaluation Index | |||||
|---|---|---|---|---|---|
| Model | Precision | Recall | F1-Score | Accuracy | |
| Oversampling | Logistic Regression | 0.5 | 0.5 | 0.49 | 0.5 |
| K-Nearest Neighbours | 0.61 | 0.61 | 0.6 | 0.62 | |
| Linear Discriminant Ana. | 0.51 | 0.5 | 0.48 | 0.5 | |
| Decision Tree | 0.86 | 0.85 | 0.85 | 0.85 | |
| Gaussian Naïve Bayes | 0.48 | 0.48 | 0.46 | 0.47 | |
| Gradient Boosting | 0.64 | 0.63 | 0.62 | 0.63 | |
| Support Vector Machine | 0.64 | 0.65 | 0.64 | 0.65 | |
| Neural Network | 0.25 | 0.27 | 0.18 | 0.39 | |
| AdaBoost | 0.54 | 0.55 | 0.54 | 0.56 | |
| Random Forest | 0.67 | 0.67 | 0.67 | 0.71 | |
| Undersampling | Logistic Regression | 0.5 | 0.5 | 0.49 | 0.5 |
| K-Nearest Neighbours | 0.61 | 0.62 | 0.61 | 0.63 | |
| Linear Discriminant. | 0.52 | 0.5 | 0.47 | 0.47 | |
| Decision Tree | 1 | 1 | 1 | 0.99 | |
| Gaussian Naïve Bayes | 0.48 | 0.47 | 0.46 | 0.47 | |
| Gradient Boosting | 0.65 | 0.63 | 0.6 | 0.6 | |
| Support Vector Machine | 0.63 | 0.63 | 0.65 | 0.64 | |
| Neural Network | 0.27 | 0.3 | 0.23 | 0.42 | |
| AdaBoost | 0.54 | 0.55 | 0.54 | 0.56 | |
| Random Forest | 0.68 | 0.67 | 0.67 | 0.72 | |
| Features | Importance |
|---|---|
| Provider | 0.1450 (14.50%) |
| Age of qualifier | 0.0941 (9.41%) |
| Academic year | 0.0805 (8.05%) |
| Most important activity | 0.0765 (7.65%) |
| Interim study | 0.0677 (6.77%) |
| Employment basis | 0.0665 (6.65%) |
| Socio economic classification | 0.0634 (6.34%) |
| Domicile | 0.0596 (5.96%) |
| Location of work | 0.0437 (4.37%) |
| Publication main activity | 0.0409 (4.09%) |
| Parental education | 0.0363 (3.63%) |
| Qualification required for the job | 0.0362 (3.62%) |
| Class of first degree | 0.0343 (3.43%) |
| Ethnicity | 0.0319 (3.19%) |
| Subject type marker | 0.0214 (2.14%) |
| Sex | 0.0204 (2.04%) |
| Level of study | 0.0180 (1.80%) |
| Employment mode | 0.0174 (1.74%) |
| State school marker | 0.0170 (1.70%) |
| Disability | 0.0162 (1.62%) |
| Mode of study | 0.0099 (0.99%) |
| sum_sq | df | F | PR (>F) | |
|---|---|---|---|---|
| Provider | 5.78 × 1010 | 1 | 30.095345 | 4.11 × 10−8 |
| Academic_year | 1.43 × 1013 | 1 | 7427.0483 | 0.00 × 100 |
| Age_of_qualifier | 9.65 × 1012 | 1 | 5023.6164 | 0.00 × 100 |
| Socio_economic_classification | 4.81 × 1011 | 1 | 250.31424 | 2.24 × 10−56 |
| Most_important_activity | 5.85 × 1012 | 1 | 3048.1864 | 0.00 × 100 |
| Location_of_work | 2.71 × 1013 | 1 | 14,116.678 | 0.00 × 100 |
| Employment_basis | 6.06 × 1011 | 1 | 315.54089 | 1.37 × 10−70 |
| Publication_main_activity | 3.00 × 1013 | 1 | 15,602.032 | 0.00 × 100 |
| Domicile | 9.05 × 1013 | 1 | 47,135.846 | 0.00 × 100 |
| Interim_study | 3.94 × 1013 | 1 | 20,514.903 | 0.00 × 100 |
| Qualification_required_for_the_job | 6.10 × 1012 | 1 | 3173.9941 | 0.00 × 100 |
| Parental_education | 1.55 × 1012 | 1 | 809.56141 | 4.91 × 10−178 |
| Input Variables |
|---|
| Academic_year |
| Publication_main_activity |
| Most_important_activity |
| Employment_mode |
| Interim_study |
| Sex |
| Domicile |
| Parental_education |
| State_school_marker |
| Socio_economic_classification |
| Age_of_qualifier |
| Disability |
| Ethnicity |
| Subject_type_marker |
| Level_of_study |
| Class_of_first_degree |
| Provider |
| Mode_of_study |
| Employment_basis |
| Location_of_work |
| Qualification_required_for_the_job |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Henshaw, B.; Mishra, B.K.; Sayers, W.; Pervez, Z. Unveiling the Impact of Socioeconomic and Demographic Factors on Graduate Salaries: A Machine Learning Explanatory Analytical Approach Using Higher Education Statistical Agency Data. Analytics 2025, 4, 10. https://doi.org/10.3390/analytics4010010
Henshaw B, Mishra BK, Sayers W, Pervez Z. Unveiling the Impact of Socioeconomic and Demographic Factors on Graduate Salaries: A Machine Learning Explanatory Analytical Approach Using Higher Education Statistical Agency Data. Analytics. 2025; 4(1):10. https://doi.org/10.3390/analytics4010010
Chicago/Turabian StyleHenshaw, Bassey, Bhupesh Kumar Mishra, William Sayers, and Zeeshan Pervez. 2025. "Unveiling the Impact of Socioeconomic and Demographic Factors on Graduate Salaries: A Machine Learning Explanatory Analytical Approach Using Higher Education Statistical Agency Data" Analytics 4, no. 1: 10. https://doi.org/10.3390/analytics4010010
APA StyleHenshaw, B., Mishra, B. K., Sayers, W., & Pervez, Z. (2025). Unveiling the Impact of Socioeconomic and Demographic Factors on Graduate Salaries: A Machine Learning Explanatory Analytical Approach Using Higher Education Statistical Agency Data. Analytics, 4(1), 10. https://doi.org/10.3390/analytics4010010







