Barrier to Methyl Internal Rotation and Equilibrium Structure of 2-Methylthiophene Determined by Microwave Spectroscopy
Abstract
1. Introduction
2. Quantum Chemical Calculations
2.1. Geometry Optimizations
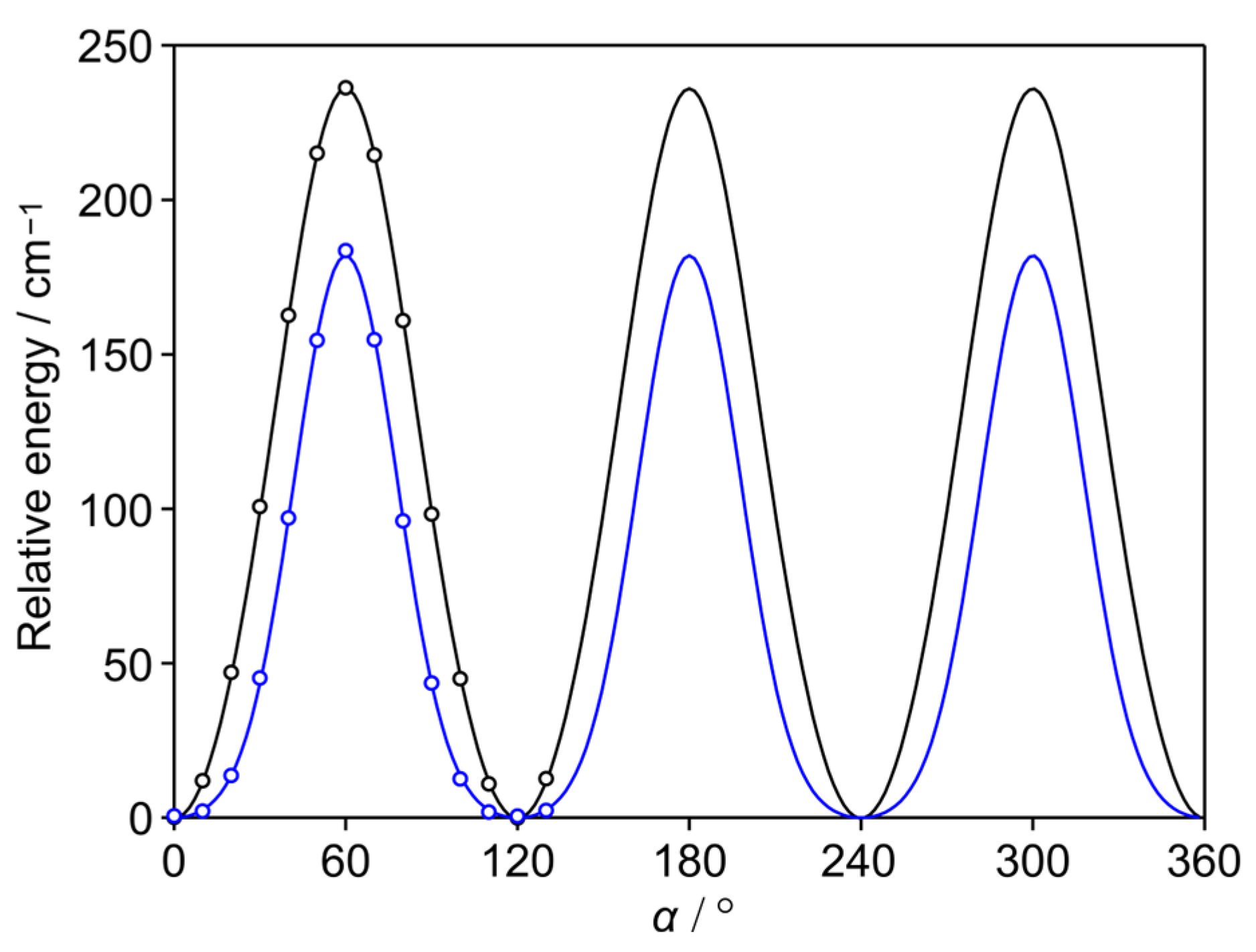
2.2. Methyl Internal Rotation
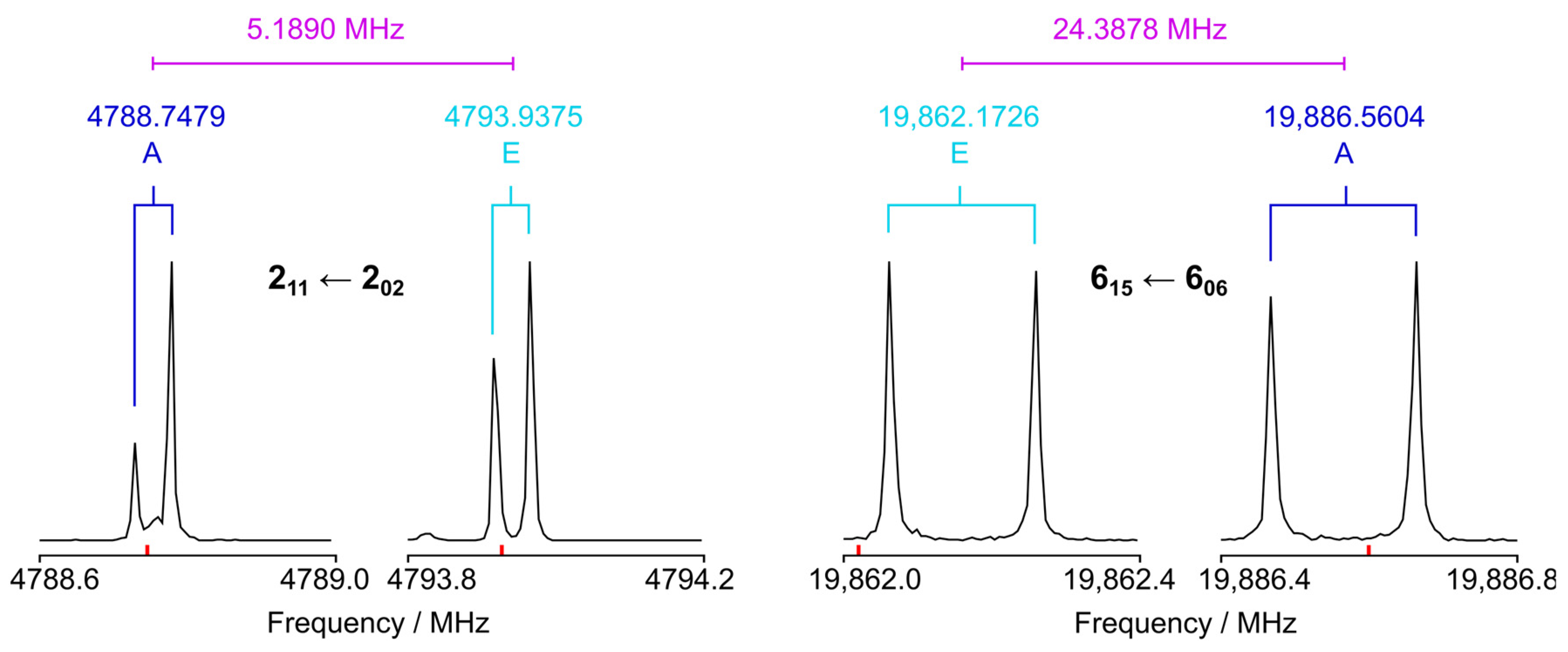
3. Microwave Spectroscopy
4. Semiexperimental Equilibrium Structure
5. Discussion
5.1. Molecular Parameters
5.2. Methyl Internal Rotation
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cameron, M.D. Victor Meyer and the Thiophene Compounds. J. Chem. Educ. 1949, 26, 521–524. [Google Scholar] [CrossRef]
- Ware, D.N.; Pillai, S. Thiophene: Versatile Medicine. J. Biol. Chem. Chron. 2019, 5, 150–162. [Google Scholar]
- Banerjee, R.; Banerjee, M. Medicinal Significance of Furan Derivates: A Review. Int. J. Rev. Life. Sci. 2012, 2, 7–16. [Google Scholar]
- Gholap, S.S. Pyrrole: An Emerging Scaffold for Construction of Valuable Therapeutic Agents. Eur. J. Med. Chem. 2016, 110, 13–31. [Google Scholar] [CrossRef] [PubMed]
- Katritzky, A.R.; Balasubramanian, M.; Siskin, M. Aqueous High-Temperature Chemistry of Carbo- and Heterocycles. 17. Thiophene, Tetrahydrothiophene, 2-Methylthiophene, 2,5-Dimethilthiophene, Benzo[b]thiophene, and Dibenzothiophene. Energy Fuels 1992, 6, 431–438. [Google Scholar]
- Chen, J.; Young, V.G.; Angelici, R.J. Reactions of the Iridathiabenzene Complex Cp*Ir(2,5-dimethylthiophene) with Co2(CO)8, Co4(CO)12, and (η6-C6H3Me3)Co4(CO)9. Organometallics 1996, 15, 1414–1421. [Google Scholar] [CrossRef]
- Sokmen, M.; Allen, D.; Hewson, A.; Clench, M. Photocatalytic Oxidative Degradation of 2-Methylthiophene in Suspensions of TiO2: Identification of Intermediates and Degradation Pathways. J. Photochem. Photobiol. A 2001, 141, 63–67. [Google Scholar] [CrossRef]
- Pozdeev, N.M.; Latypova, R.G.; Shapkin, A.A. Microwave Spectrum, Internal Rotation, and Dipole Moment of 2-Methyl Thiophene. Opt. Spektrosk. 1970, 28, 254. [Google Scholar]
- Pozdeev, N.M.; Latypova, R.G.; Gunderova, L.N. Microwave Spectrum of 2-Methylthiophene in an Excited Torsional State and the Form of the Potential Barrier. J. Struc. Chem. 1976, 17, 313–314. [Google Scholar] [CrossRef]
- Tanabe, M.; Kuze, N.; Fujiwara, H.; Takeuchi, H.; Konaka, S. Molecular Structure of 2-Methylthiophene Studied by Gas Electron Diffraction Combined with Microwave Spectroscopic Data. J. Mol. Struct. 1995, 372, 173–180. [Google Scholar]
- Bermudez, C.; Motiyenko, R.A.; Cabezas, C.; Ilyushin, V.V.; Margulès, L.; Endo, Y.; Guillemin, J.-C. Internal Rotation Analysis of the Microwave and Millimeter Wave Spectra of Fluoral (CF3CHO). Spectrochim. Acta A 2022, 274, 121071. [Google Scholar] [CrossRef]
- Rodríguez, C.; Macario, A.; López, J.C.; Blanco, S. The Conformational Landscape of α-Aminoglycine. J. Mol. Spectrosc. 2022, 387, 111667. [Google Scholar] [CrossRef]
- Ma, J.; Insausti, A.; Mort, A.N.; Xu, Y. Rotation-Tunneling Spectra and Barriers of Isotopologues of 2,2,2-Trifluoroethanol and 2,2,3,3,3-Pentafluoropropanol. J. Mol. Spectrosc. 2022, 388, 111687. [Google Scholar] [CrossRef]
- Melli, A.; Melosso, M.; Lengsfeld, K.G.; Bizzocchi, L.; Rivilla, V.M.; Dore, L.; Barone, V.; Grabow, J.-U.; Puzzarini, C. Spectroscopic Characterization of 3-Aminosoxazole, a Prebiotic Precursor of Ribonucleotides. Molecules 2022, 27, 3278. [Google Scholar] [CrossRef] [PubMed]
- Gougoula, E.; Medcraft, C.; Heitkämper, J.; Walker, N.R. Barriers to Internal Rotation in Methylimidazole Isomers Determined by Rotational Spectroscopy. J. Chem. Phys. 2019, 151, 144301. [Google Scholar] [CrossRef] [PubMed]
- Demaison, J.; Vogt, N.; Nguyen, H.V.L. Determination of Rotational Constants in the Presence of Methyl Internal Rotation: 2-Acetylfuran and 2-Acetylthiophene as Examples. Chem. Phys. Lett. 2022, 794, 139488. [Google Scholar] [CrossRef]
- Dindić, C.; Lüchow, A.; Vogt, N.; Demaison, J.; Nguyen, H.V.L. Equilibrium Structure in the Presence of Methyl Internal Rotation: Microwave Spectroscopy and Quantum Chemistry Study of the Two Conformers of 2-Acetylfuran. J. Phys. Chem. A 2021, 125, 4986–4997. [Google Scholar] [CrossRef] [PubMed]
- Dindić, C.; Ludovicy, J.; Terzi, V.; Lüchow, A.; Vogt, N.; Demaison, J.; Nguyen, H.V.L. Determination of the Semiexperimental Equilibrium Structure of 2-Acetylthiophene in the Presence of Methyl Internal Rotation and Substituent Effects Compared to Thiophene. Phys. Chem. Chem. Phys. 2022, 24, 3804–3815. [Google Scholar] [CrossRef]
- Nguyen, H.V.L.; Caminati, W.; Grabow, J.-U. The LAM of the Rings: Large Amplitude Motions in Aromatic Molecules Studied by Microwave Spectroscopy. Molecules 2022, 27, 3948. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Møller, C.; Plesset, M.S. Note on an Approximation Treatment on Many-Electron Systems. Phys. Rev. 1934, 46, 618. [Google Scholar] [CrossRef]
- Purvis, G.D., III; Bartlett, R.J. A Full Coupled-Cluster Singles and Doubles Model: The Inclusion of Disconnected Triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
- Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Head-Gordon, M. A Fifth-Orders Perturbation Comparison of Electron Correlation Theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
- Becke, A.D. A New Mixing of Hartree-Fock and Local Density-Functional Theories. J. Chem. Phys. 1993, 98, 1372. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Wang, Y. Erratum: Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Phys. Rev. B 1992, 45, 13244. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 Suite for Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of for M06-Class Functionals and 12 Other Functionals. Theor. Chem. Acc. 2008, 120, 215. [Google Scholar]
- Chai, J.-D.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615. [Google Scholar] [CrossRef]
- Yu, H.S.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn-Sham Global-Hybrid Exchange-Correlation Density Functional with Broad Accuracy for Multi-Reference and Single-Reference Systems and Noncovalent Interactions. Chem. Sci. 2016, 7, 5032–5051. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew-Burke-Ernzerhof Exchange-Correlation Functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Georigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density functional Dispersion Correction (DFT-D) for the 94 Elements, H.-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Yanai, T.; Tew, D.; Handy, N.C. A New Hybrid Exchange-Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Frisch, M.J.; Pople, J.A.; Binkley, J.S. Self-Consistent Molecular Orbital Methods 25. Supplementary Functions for Gaussian Basis Sets. J. Chem. Phys. 1984, 80, 3265. [Google Scholar]
- Dunning, T.H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron Through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007. [Google Scholar]
- Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron Affinities of the First-Row Atoms Revisited. Systematic Basis Sets and Wave Functions. J. Chem. Phys. 1992, 96, 6796. [Google Scholar]
- Peterson, K.A.; Dunning, T.H. Accurate Correlation Consistent Basis Sets for Molecular Core-Valence Correlation Effects: The Second Row Atoms Al-Ar, and the First Row Atoms B-Ne Revisited. J. Chem. Phys 2002, 117, 10548–10560. [Google Scholar] [CrossRef]
- Werner, H.-J.; Knowles, P.J.; Knizia, G.; Manby, V.; Schütz, M.; Celani, P.; Györffy, W.; Kats, D.; Korona, T.; Lindh, R.; et al. MOLPRO, Version 2020.1, a Package of ab Initio Programs. Available online: https://www.molpro.net (accessed on 29 March 2023).
- Werner, H.-J.; Knowles, P.J.; Manby, F.R.; Black, J.A.; Doll, K.; Heßelmann, A.; Kats, D.; Köhn, A.; Korona, T.; Kreplin, D.A.; et al. The Molpro Quantum Chemistry Package. J. Chem. Phys. 2020, 152, 144107. [Google Scholar] [CrossRef]
- Kraitchman, J. Determination of Molecular Structure from Microwave Spectroscopic Data. Am. J. Phys. 1953, 21, 17–24. [Google Scholar] [CrossRef]
- Costain, C.C. Further Comments on the Accuracy of rs Substitution Structures. Trans. Am. Crystallogr. Assoc. 1966, 2, 157. [Google Scholar]
- Demaison, J.; Vogt, N. Accurate Structure Determination of Free Molecules; Springer Nature Switzerland AG: Cham, Switzerland, 2020. [Google Scholar]
- Grabow, J.-U.; Stahl, W.; Dreizler, H. A Multioctave Coaxially Oriented Beam-Resonator Arrangement Fourier-Transform Microwave Spectrometer. Rev. Sci. Instrum. 1996, 67, 4072. [Google Scholar] [CrossRef]
- Hartwig, H.; Dreizler, H. The Microwave Spectrum of Trans-2,3-Dimethyloxirane in Torsional Excited States. Z. Naturforsch. 1996, 51a, 923–932. [Google Scholar] [CrossRef]
- Watson, J.K.G. Aspects of Quartic and Sextic Centrifugal Effects on Rotational Energy Levels. In Vibrational Spectra and Structure; Durig, J.R., Ed.; Elsevier: New York, NY, USA, 1977; Volume 6, pp. 1–89. [Google Scholar]
- Vázquez, J.; Stanton, J.F. Semiexperimental Equilibrium Structures: Computational Aspects. In Equilibrium Molecular Structures: From Spectroscopy to Quantum Chemistry; Demaison, J., Boggs, J.E., Császár, A.G., Eds.; CRC Press: Boca Raton, FL, USA, 2011; pp. 53–87. [Google Scholar]
- Dindić, C.; Stahl, W.; Nguyen, H.V.L. 2-Propionylthiophene: Planar, or Not Planar, That is the Question. Phys. Chem. Chem. Phys. 2020, 22, 19704. [Google Scholar] [CrossRef]
- Hakiri, R.; Derbel, N.; Bailey, W.C.; Nguyen, H.V.L.; Mouhib, H. The Heavy Atom Structures and 33S Quadrupole Coupling Constants of 2-Thiophenecarboxaldehyde: Insights from Microwave Spectroscopy. Mol. Phys. 2020, 118, e1728406. [Google Scholar] [CrossRef]
- Demaison, J.; Boggs, J.E.; Császár, A.G. The Method of Least Squares. In Equilibrium Molecular Structures; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Belsey, D.A. Conditioning Diagnostics; Wiley: New York, NY, USA, 1991; pp. 298–299. [Google Scholar]
- Bartell, L.S.; Romanesko, D.J.; Wong, T.C. Chemical Society Specialist Periodical Report No. 20; Sim, G.A., Sutton, L.E., Eds.; The Chemical Society: London, UK, 1975; Volume 3, pp. 72–79. [Google Scholar]
- Hamilton, L. Regression with Graphics: A Second Course in Applied Statistics; Duxbury Press, Wadsworth: Belmont, CA, USA, 1992. [Google Scholar]
- Kummli, D.S.; Frey, H.M.; Leutwyler, S. Femtosecond Degenerate Four-Wave Mixing of Carbon Disulfide: High-Accuracy Rotational Constants. J. Chem. Phys. 2006, 124, 144307. [Google Scholar] [CrossRef] [PubMed]
- Kummli, D.S.; Lobsiger, S.; Frey, H.-M.; Leutwyler, S.; Stanton, J.F. Accurate Determination of the Structure of Cyclooctatetraene by Femtosecond Rotational Coherence Spectroscopy and Ab Initio Calculations. J. Phys. Chem. A 2008, 112, 9134–9143. [Google Scholar] [CrossRef] [PubMed]
- Kyker, G.C. The Range of a Data Set: A Quick Estimator of the Standard Deviation. Am. J. Phys. 1983, 51, 852. [Google Scholar] [CrossRef]
- Orr, V.L.; Ichikawa, Y.; Patel, A.R.; Kougias, A.M.; Kobayashi, K.; Stanton, J.F.; Esselman, B.J.; Woods, R.C.; McMahon, R.J. Precise Equilibrium Structure Determination of Thiophene (c-C4H4S) by Rotational Spectroscopy-Structure of a Five-Membered Heterocycle Containing a Third-Row Atom. J. Chem. Phys. 2021, 154, 244310. [Google Scholar] [CrossRef]
- Kisiel, Z. Prospe—Programs for Rotational Spectroscopy. Available online: http://info.ifpan.edu.pl/~kisiel/prospe.htm (accessed on 29 March 2023).
- Esselman, B.J.; Kougias, S.M.; Fellows, M.D.; Woods, R.C.; McMahon, R.J. The 130-360 GHz Rotational Spectrum of Isocyanocyclobutane (C4H7NC) and Cyanocyclobutane (C4H7CN). J. Mol. Spectrosc. 2022, 388, 111684. [Google Scholar] [CrossRef]
- Esselman, B.J.; Zdanovskaia, M.A.; Smith, H.H.; Woods, R.C.; McMahon, R.J. The 130–500 GHz Rotational Spectroscopy of Cyanopyrazine (C4H3N2-CN). J. Mol. Spectrosc. 2022, 389, 111703. [Google Scholar] [CrossRef]
- Owen, A.N.; Zdanovskaia, M.A.; Esselman, B.J.; Stanton, J.F.; Woods, R.C.; McMahon, R.J. Semi-Experimental Equilibrium (reSE) and Theoretical Structures of Pyradizine (o-C4H4N2). J. Phys. Chem. A 2021, 125, 7976–7987. [Google Scholar]
- Esselman, B.J.; Zdanovskaia, M.A.; Owen, A.N.; Stanton, J.F.; Woods, R.C.; McMahon, R.J. Precise Equilibrium Structure of Thiazole (c-C3H3NS) from Twenty-Four Isotopologues. J. Chem. Phys. 2021, 155, 054302. [Google Scholar] [CrossRef]
- Gillespie, R.J.; Popelier, P.L.A. Chemical Bonding and Molecular Geometry; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Marenich, A.V.; Jerome, S.V.; Cramer, C.J.; Truhlar, D.G. Charge Model 5: An Extension of Hirshfeld Population Analysis for the Accurate Description of Molecular Interactions in Gaseous and Condensed Phases. J. Chem. Theory Comput. 2012, 8, 527. [Google Scholar] [CrossRef]
- Demaison, J.; Craig, N.C.; Gurusinghe, R.; Tubergen, M.J.; Rudolph, H.D.; Coudert, L.H.; Szálay, P.G.; Császár, A.G. Fourier Transform Microwave Spectrum of Propene-3-d1 (CH2=CHCH2D), Quadrupole Coupling Constants of Deuterium, and a Semiexperimental Equilibrium Structure of Propene. J. Phys. Chem. A 2017, 121, 3155–3166. [Google Scholar] [CrossRef]
- Stoicheff, B. The Variation of Carbon-Carbon Bond Lengths with Environment as Determined by Spectroscopic Studies of Simple Polyatomic Molecules. Tetrahedron 1962, 17, 135–145. [Google Scholar] [CrossRef]
- Kuchitsu, K. Gas Electron Diffraction. In Molecular Structure and Properties; Allen, G., Ed.; Butterworth: Baltimore, MD, USA, 1972; pp. 203–240. [Google Scholar]
- Van, V.; Stahl, W.; Nguyen, H.V.L. Two Equivalent Methyl Internal Rotations in 2,5-Dimethylthiophene Investigated by Microwave Spectroscopy. Phys. Chem. Chem. Phys. 2015, 17, 32111–32114. [Google Scholar] [CrossRef]
- Dindić, C.; Nguyen, H.V.L. Benchmarking Acetylthiophene Derivates: Methyl Internal Rotations in the Microwave Spectrum of 2-Acetyl-5-Methylthiophene. Phys. Chem. Chem. Phys. 2023, 25, 509–519. [Google Scholar] [CrossRef]
- Finneran, I.A.; Shipman, S.T.; Weaver, S.L.W. Rotational Spectroscopy of 2-Methylfuran from 8.7 to 960 GHz. J. Mol. Spectrosc. 2012, 280, 27–33. [Google Scholar] [CrossRef]
- Van, V.; Bruckhuisen, J.; Stahl, W.; Ilyushin, V.; Nguyen, H.V.L. The Torsional Barriers of Two Equivalent Methyl Internal Rotations in 2,5-Dimethylfuran Investigated by Microwave Spectroscopy. J. Mol. Spectrosc. 2018, 343, 121–125. [Google Scholar] [CrossRef]
- Van, V.; Stahl, W.; Nguyen, H.V.L. The Structure and Torsional Dynamics of Two Methyl Groups in 2-Acetyl-5-Methylfuran as Observed by Microwave Spectroscopy. Chem. Phys. Chem. 2016, 17, 3223–3228. [Google Scholar] [CrossRef] [PubMed]
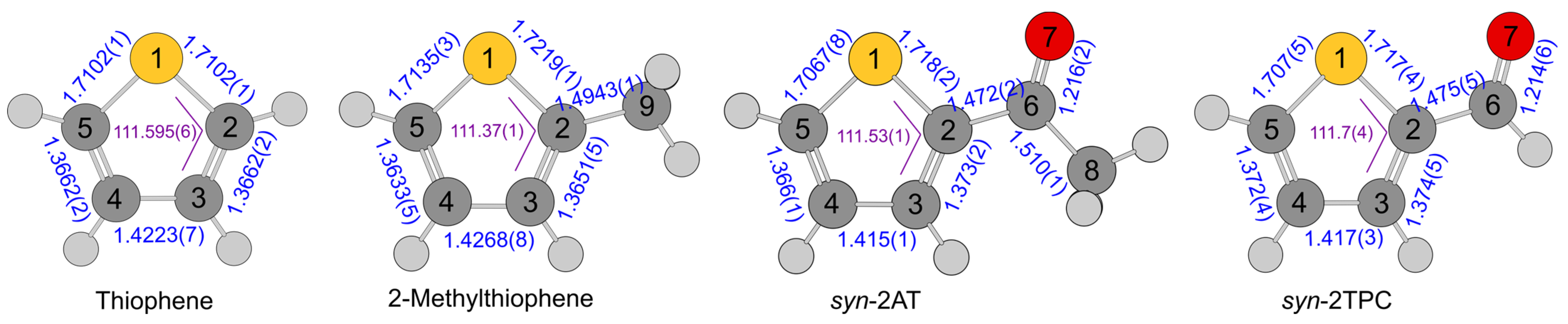
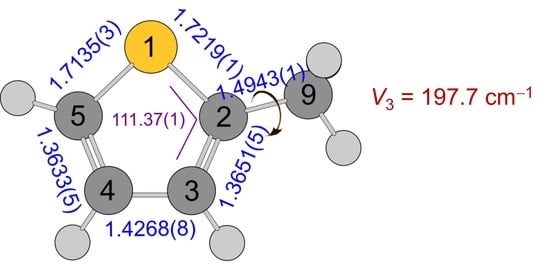
| a | b | c | d | e | f | ||
|---|---|---|---|---|---|---|---|
| cc-pwCVTZ | cc-pwCVQZ | I | II | III | IV | ||
| C5–S | 1.7189 | 1.7146 | 1.7135(3) | 1.7137(4) | 1.7139(4) | 1.721(77) | 1.7314(79) |
| C4–C5 | 1.3653 | 1.3640 | 1.3633(5) | 1.3637(1) | 1.3628(6) | 1.3676(75) | 1.3654(75) |
| C3–C4 | 1.4264 | 1.4246 | 1.4268(7) | 1.4242(2) | 1.4267(7) | 1.428(30) | 1.428(35) |
| C2–C3 | 1.3677 | 1.3666 | 1.3651(5) | 1.3654(75) | 1.3676(75) | ||
| C2–S | 1.7272 | 1.7225 | 1.7219(1) | 1.7215(5) | 1.7221(2) | 1.7253(67) | 1.7158(70) |
| C2–C9 | 1.4969 | 1.4953 | 1.49434(6) | 1.4950(1) | 1.49434(6) | 1.5083(22) | 1.5108(22) |
| C9–Ha | 1.0904 | 1.0896 | 1.090(1) | 1.08942(8) | 1.089(1) | ||
| C9–Hs | 1.0891 | 1.0883 | 1.089(2) | 1.08817(7) | 1.089(2) | ||
| C5–H6 | 1.0770 | 1.0765 | 1.078(2) | 1.07634(5) | 1.077(2) | ||
| C4–H7 | 1.0796 | 1.0790 | 1.081(2) | 1.07882(6) | 1.081(2) | ||
| C3–H8 | 1.0807 | 1.0801 | 1.081(2) | 1.07992(6) | 1.081(2) | ||
| S–C5–C4 | 111.449 | 111.377 | 111.37(1) | 111.362(7) | 111.39(2) | 111.32(22) | 111.24(22) |
| C3–C4–C5 | 112.349 | 112.348 | 112.354(7) | 112.34788(5) | 112.359(8) | 112.36(25) | 112.57(30) |
| C2–S–C3 | 92.364 | 92.516 | 92.55(1) | 92.55(1) | 92.52(3) | 92.66(27) | 91.64(27) |
| S–C2–C9 | 121.316 | 121.358 | 121.303(8) | 121.367(4) | 121.298(8) | 121.63(67) | 121.75(57) |
| Ha–C9–C2 | 111.593 | 111.574 | 111.6(1) | 111.570(2) | 111.6(1) | ||
| Hs–C9–C2 | 109.498 | 109.490 | 109.4(3) | 109.4883(8) | 109.42(2) | ||
| H6–C5–S | 120.361 | 120.346 | 120.6(3) | 120.343(1) | 120.6(3) | ||
| H7–C4–C5 | 123.468 | 123.444 | 123.5(2) | 123.439(2) | 123.5(2) | ||
| H8–C3–C4 | 124.087 | 124.122 | 123.5(2) | 124.129(3) | 123.6(3) | ||
| Ha–C9–C2–S | 60.353 | 60.350 | 60.1(1) | 60.3495(2) | 60.2(1) | ||
| Par a | Unit | Parent | 34S | 13C(2) | 13C(3) | 13C(4) | 13C(5) | 13C(9) |
|---|---|---|---|---|---|---|---|---|
| A0 | MHz | 5299.85002(45) | 5161.33031(63) | 5296.47565(86) | 5194.52016(96) | 5232.18924(71) | 5297.71936(65) | 5298.8233(15) |
| B0 | MHz | 3114.09632(30) | 3112.72380(44) | 3101.70161(38) | 3114.13512(38) | 3078.91352(30) | 3064.14021(29) | 3015.87188(63) |
| C0 | MHz | 1985.26582(21) | 1964.94486(32) | 1979.75497(20) | 1970.31198(19) | 1961.46901(20) | 1964.55468(18) | 1944.73180(31) |
| DJ | kHz | 0.1659(41) | 0.1625(75) | 0.1461(76) | 0.1397(73) | 0.1471(64) | 0.1584(60) | 0.126(11) |
| DJK | kHz | 1.1631(57) | 1.135(11) | 1.330(74) | 1.100(79) | 1.170(50) | 1.245(45) | 1.39(12) |
| DK | kHz | 0.252(15) | 0.214(31) | 0.252 b | 0.252 b | 0.252 b | 0.252 b | 0.252 b |
| d1 | kHz | −0.06917(83) | −0.0703(13) | −0.0633(41) | −0.0522(41) | −0.0588(28) | −0.0633(28) | −0.0526(68) |
| d2 | kHz | −0.02293(29) | −0.02415(50) | −0.02293 b | −0.02293 b | −0.02293 b | −0.02293 b | −0.02293 b |
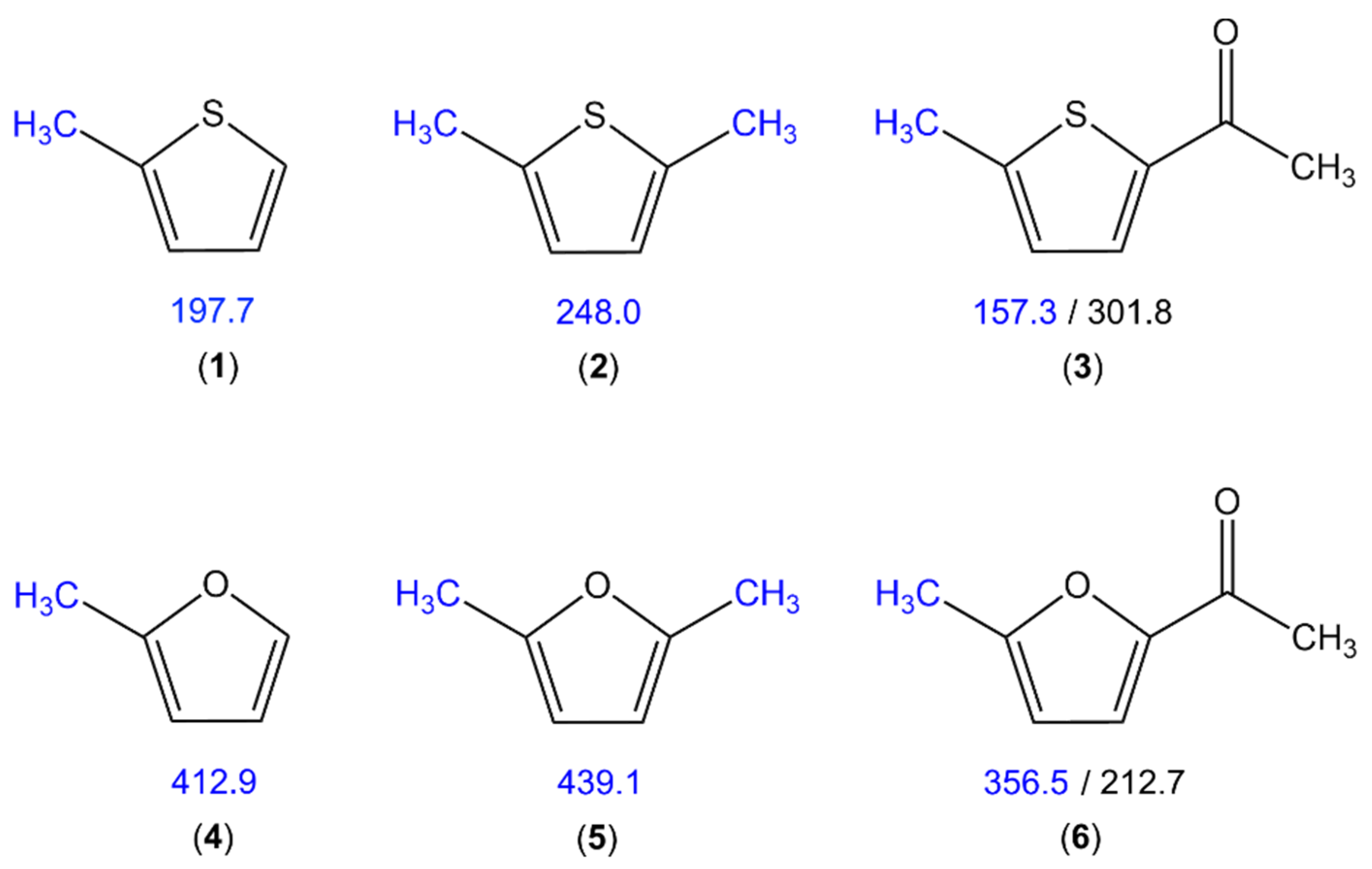
| V3 | cm−1 | 197.7324(18) | 197.5735(27) | 197.8327(16) | 197.8717(15) | 197.6937(15) | 197.7704(14) | 197.8801(24) |
| kHz | −14.93(65) | −18.25(97) | −14.31(44) | −14.09(39) | −14.24(44) | −14.310(40) | −12.61(62) | |
| kHz | −296.9(19) | −286.49(28) | −298.2(35) | −278.0(32) | −288.1(31) | −294.9(26) | −347.7(55) | |
| kHz | 8.22(46) | 7.36(71) | 8.22 b | 8.22 b | 8.22 b | 8.22 b | 8.22 b | |
| ∠(i,a) | deg | 3.678(23) | 4.013(32) | 3.871(18) | 3.712(17) | 2.313(27) | 3.976(16) | 3.898(27) |
| ∠(i,b) c | deg | 86.322(23) | 85.987(32) | 86.129(18) | 86.288(17) | 87.687(27) | 86.024(16) | 86.102(27) |
| ∆c d | uÅ2 | −3.079855(50) | −3.077964(76) | −3.080517(60) | −3.079360(62) | −3.079026(54) | −3.080329(50) | −3.07801(11) |
| N e | 148 | 127 | 51 | 47 | 55 | 54 | 42 | |
| σ f | kHz | 4.4 | 5.6 | 2.8 | 2.5 | 2.9 | 2.6 | 3.8 |
| Isotopologue | ξ | Exp−calc a | |||
|---|---|---|---|---|---|
| Parent | a | 5331.4578 | −0.0004 | 31.435 | 0.1728 |
| b | 3134.1632 | 0.0047 | 19.965 | 0.1019 | |
| c | 1998.1047 | 0.0009 | 12.855 | −0.0161 | |
| 34S(1) | a | 5191.7574 | −0.0244 | 30.263 | 0.1639 |
| b | 3132.6954 | 0.0042 | 19.87 | 0.1018 | |
| c | 1977.5740 | 0.0001 | 12.645 | −0.0158 | |
| 13C(2) | a | 5225.5364 | 0.0004 | 30.847 | 0.1693 |
| b | 3134.0950 | −0.0067 | 19.858 | 0.1019 | |
| c | 1983.0151 | −0.0013 | 12.719 | −0.0159 | |
| 13C(3) | a | 5329.1650 | −0.0241 | 31.275 | 0.1706 |
| b | 3083.8288 | 0.0019 | 19.590 | 0.0987 | |
| c | 1977.2129 | −0.0022 | 12.674 | −0.0158 | |
| 13C(4) | a | 5263.0555 | −0.0001 | 30.699 | 0.1672 |
| b | 3098.7631 | −0.0036 | 19.750 | 0.0996 | |
| c | 1974.1143 | 0.0003 | 12.661 | −0.0157 | |
| 13C(5) | a | 5327.8373 | 0.0001 | 31.189 | 0.1727 |
| b | 3121.4697 | −0.0005 | 19.667 | 0.1011 | |
| c | 1992.4330 | 0.0000 | 12.694 | −0.0160 | |
| 13C(9) | a | 5330.4216 | 0.0000 | 31.429 | 0.1683 |
| b | 3035.0735 | 0.0000 | 19.107 | 0.0956 | |
| c | 1957.2253 | 0.0000 | 12.509 | −0.0155 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koziol, K.J.; El Hadki, H.; Lüchow, A.; Vogt, N.; Demaison, J.; Nguyen, H.V.L. Barrier to Methyl Internal Rotation and Equilibrium Structure of 2-Methylthiophene Determined by Microwave Spectroscopy. Spectrosc. J. 2023, 1, 49-64. https://doi.org/10.3390/spectroscj1010005
Koziol KJ, El Hadki H, Lüchow A, Vogt N, Demaison J, Nguyen HVL. Barrier to Methyl Internal Rotation and Equilibrium Structure of 2-Methylthiophene Determined by Microwave Spectroscopy. Spectroscopy Journal. 2023; 1(1):49-64. https://doi.org/10.3390/spectroscj1010005
Chicago/Turabian StyleKoziol, Kenneth J., Hamza El Hadki, Arne Lüchow, Natalja Vogt, Jean Demaison, and Ha Vinh Lam Nguyen. 2023. "Barrier to Methyl Internal Rotation and Equilibrium Structure of 2-Methylthiophene Determined by Microwave Spectroscopy" Spectroscopy Journal 1, no. 1: 49-64. https://doi.org/10.3390/spectroscj1010005
APA StyleKoziol, K. J., El Hadki, H., Lüchow, A., Vogt, N., Demaison, J., & Nguyen, H. V. L. (2023). Barrier to Methyl Internal Rotation and Equilibrium Structure of 2-Methylthiophene Determined by Microwave Spectroscopy. Spectroscopy Journal, 1(1), 49-64. https://doi.org/10.3390/spectroscj1010005