Embedding Ordinal Optimization into Tree–Seed Algorithm for Solving the Probabilistic Constrained Simulation Optimization Problems
Abstract
:1. Introduction
2. Embedded Ordinal Optimization into Tree–Seed Algorithm
2.1. Mathematical Formulation
2.2. RMTS Surrogate Model
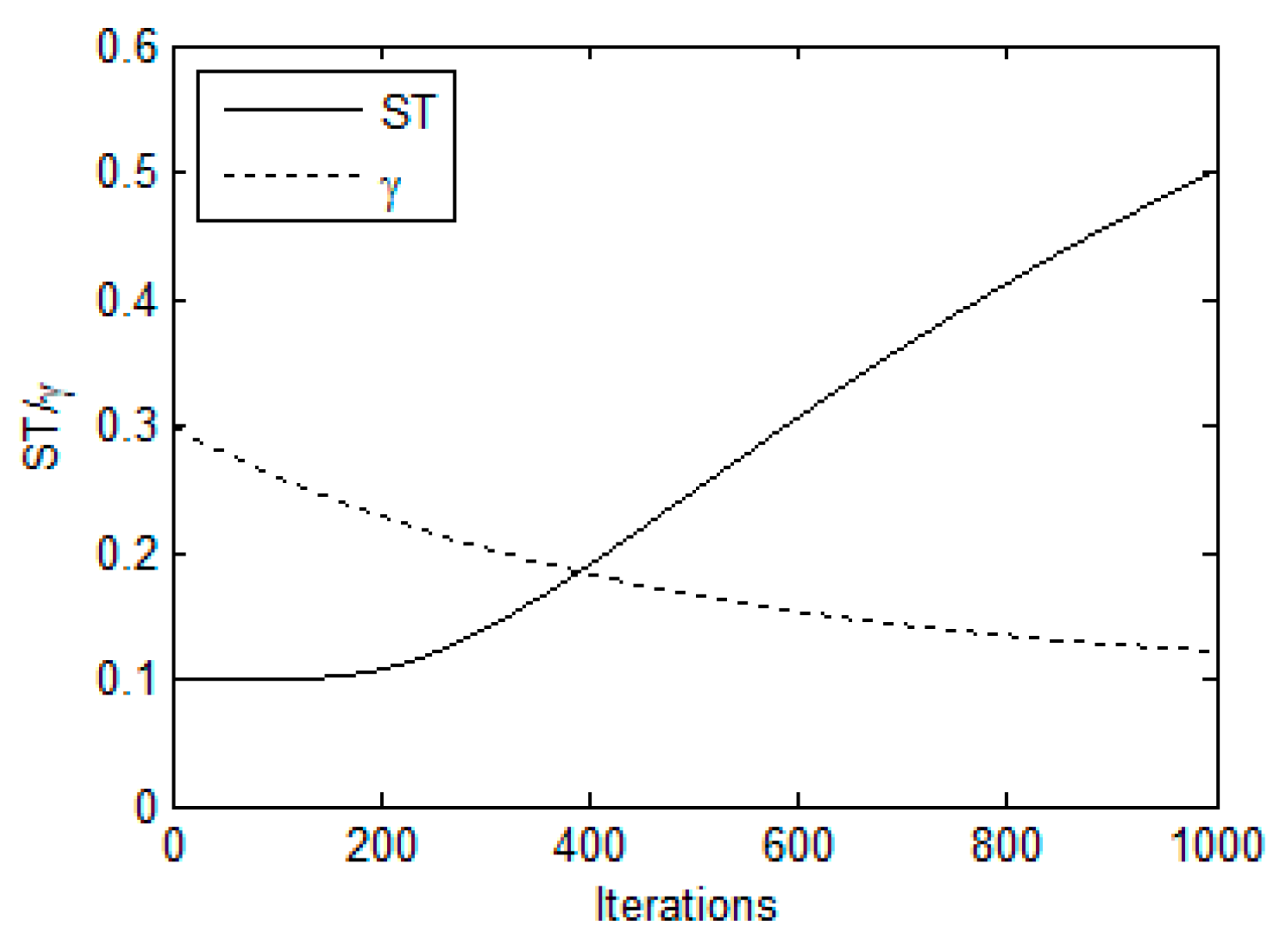
2.3. Improved Tree–Seed Algorithm
| Algorithm 1: The ITSA |
| Step 1: Define parameters Define the values of , , , , , , and set , , , where denotes the iteration index. Step 2: Initialization (a) Initialize the first population of trees with positions as follows. (b) Evaluate the approximate fitness of each tree assisted by the RMTS, . (c) Rank these trees based on their fitness from lowest to highest, then determine the best-so-far tree . Step 3: Generate the number of seeds for each tree Step 4: Spreading seeds (a) Generate positions of all seeds For , do For , do For , do If (b) Evaluate the approximate fitness for each seed produced from the ith tree assisted by the RMTS, . (c) Rank these seeds based on their fitness from lowest to highest, then select the best seed . Apply the greedy choice among and . If , then set ; else, set . Step 5: Update control parameters Apply the greedy choice among and , . If , then set . Step 7: Termination If , stop; otherwise, set and go to Step 3. |
2.4. Incremental Optimal Computing Budget Allocation
| Algorithm 2: The IOCBA |
| Step 1. Define the value of and set , ,…, . Determine the value of . Step 2. If , terminate and select the best solution with minimum objective value; else, go to Step 3. Step 3. Increase a pre-specified computing budget to , and calculate the new number of simulation runs by Step 4. Carry out additional number of simulation runs, i.e., , on the th promising solution, then compute the means and standard deviations of those additional number of simulation runs by Step 5. Compute the means and standard deviations of cumulative amount of simulation runs for the th promising solution by |
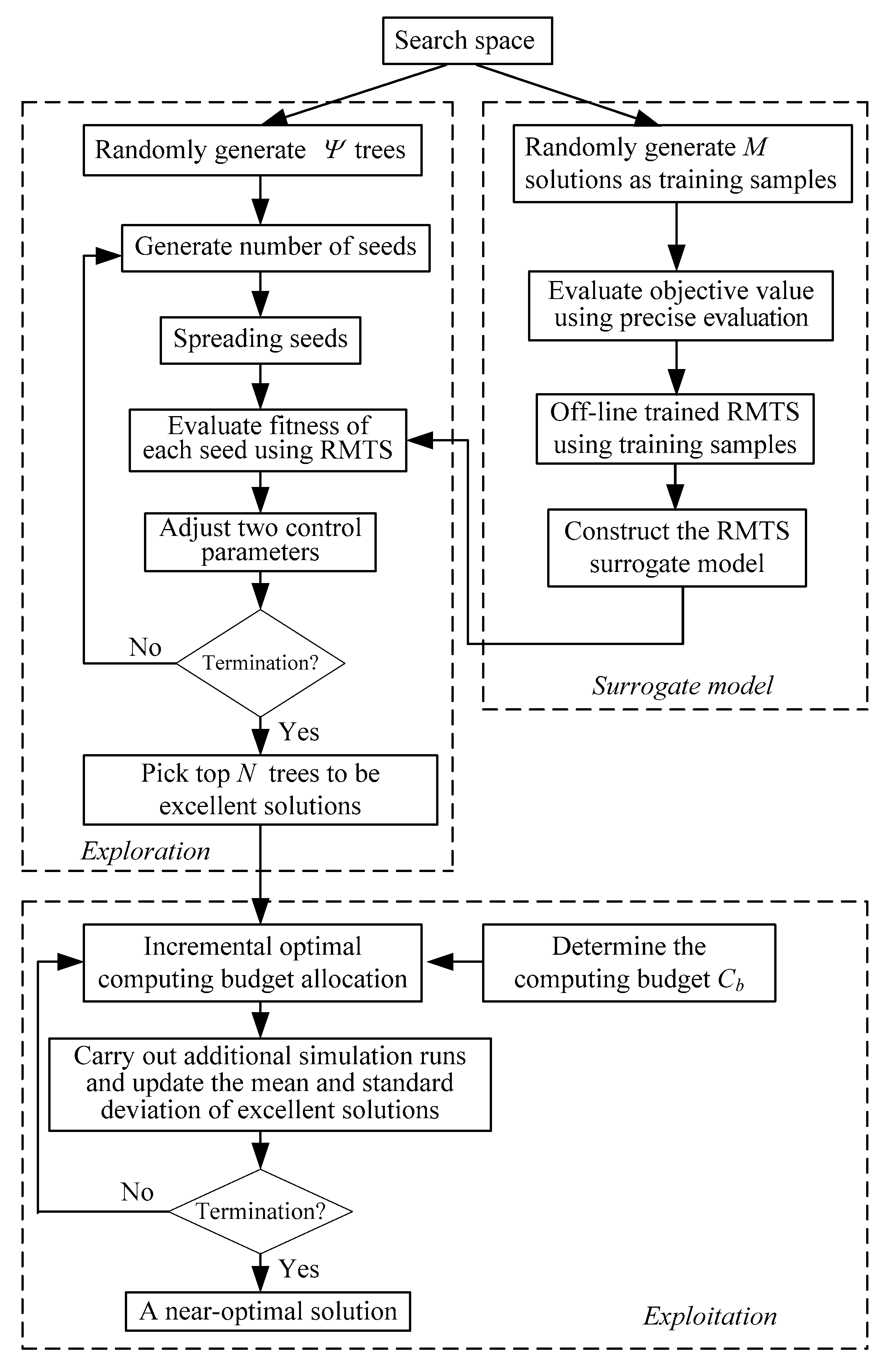
2.5. The Proposed OOTSA Approach
| Algorithm 3: The OOTSA |
|
3. Application to Pull-Type Production System
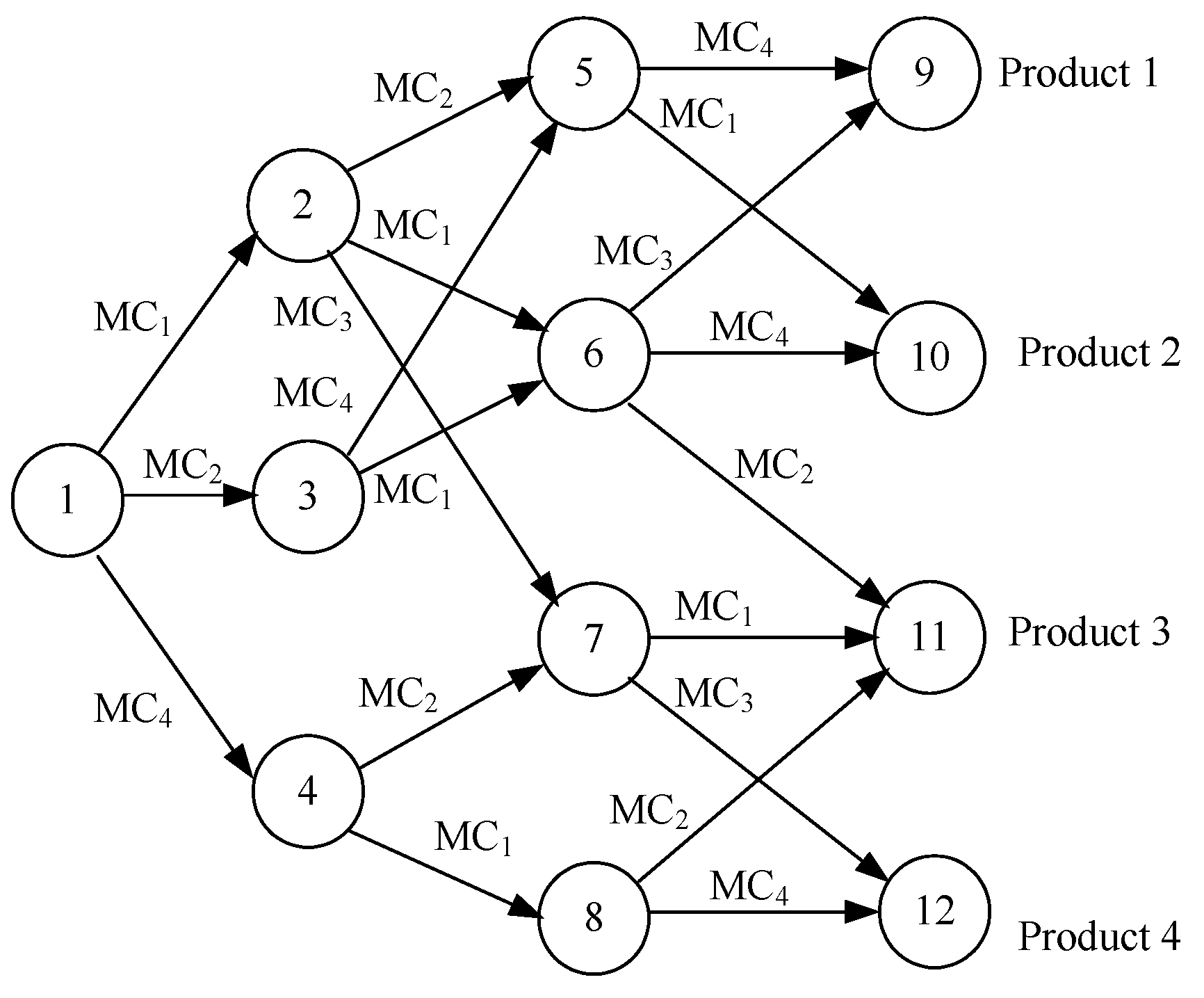
3.1. Pull-Type Production System
3.2. Mathematical Formulation
3.3. Employ the OOTSA Approach
3.3.1. Construct the Surrogate Model
3.3.2. Employ the ITSA to choose outstanding solutions
3.3.3. Search for the Excellent Solution
4. Simulation Results and Comparisons
4.1. Test Example and Results
4.2. Comparisons of Large Problem
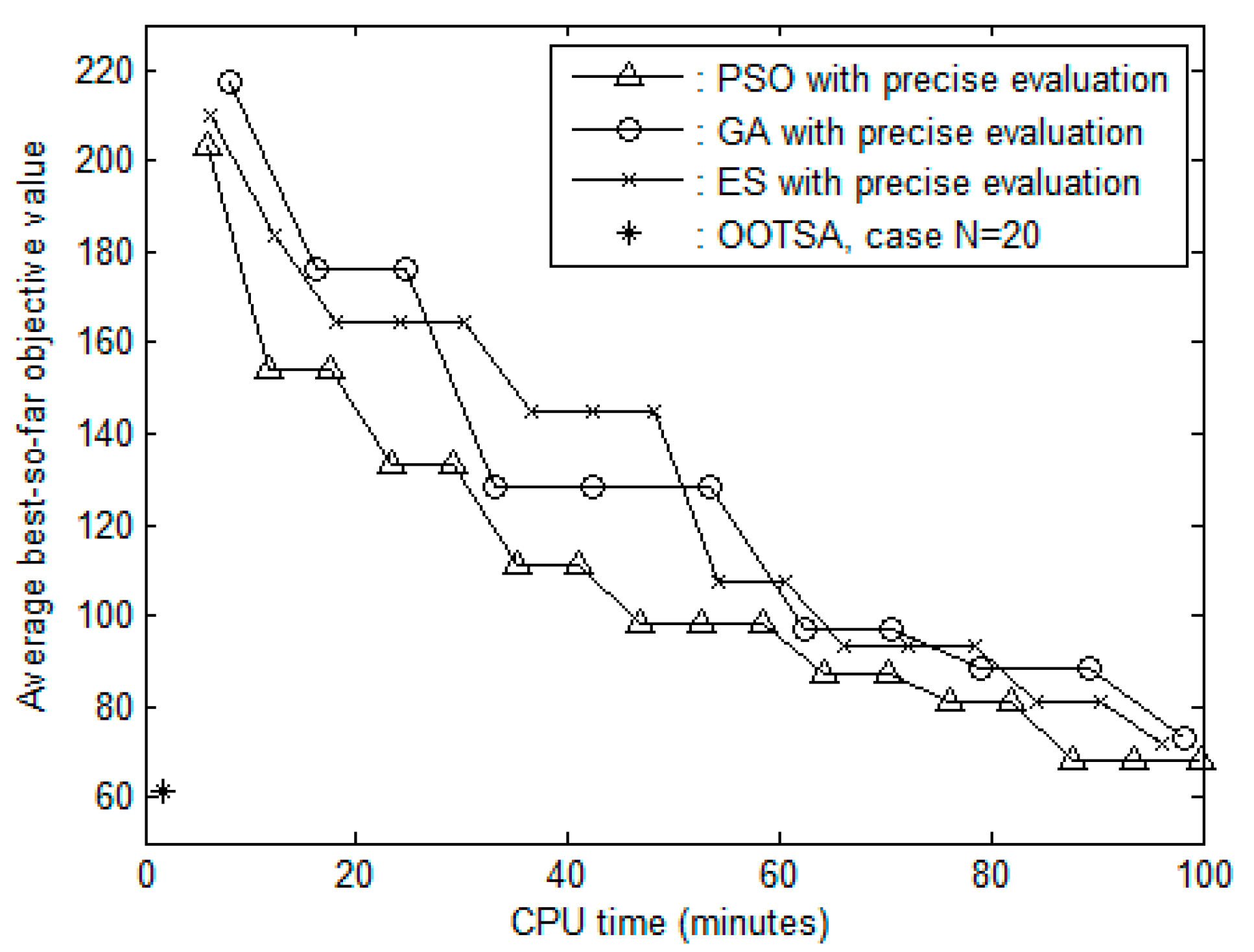
 ”, solid line with open circles “
”, solid line with open circles “  ”, and solid line with crosses “
”, and solid line with crosses “  ”, respectively. Table 3 demonstrates that the average best-so-far objective values that were obtained by PSO, GA and ES were 10.74%, 18.47% and 16.21% larger than that obtained by OOTSA. The average best-so-far objective values obtained by the three heuristic methods were worse than not only that determined by the OOTSA with = 20, but also those obtained using the three other values of . Test results reveal that the OOTSA approach frequently determines an excellent solution in a limited amount of time and significantly outperforms three heuristic methods with precise evaluation.
”, respectively. Table 3 demonstrates that the average best-so-far objective values that were obtained by PSO, GA and ES were 10.74%, 18.47% and 16.21% larger than that obtained by OOTSA. The average best-so-far objective values obtained by the three heuristic methods were worse than not only that determined by the OOTSA with = 20, but also those obtained using the three other values of . Test results reveal that the OOTSA approach frequently determines an excellent solution in a limited amount of time and significantly outperforms three heuristic methods with precise evaluation.5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ghanem, R.; Soize, C. Probabilistic nonconvex constrained optimization with fixed number of function evaluations. Int. J. Numer. Methods Eng. 2018, 113, 719–741. [Google Scholar] [CrossRef]
- Lejeune, M.A.; Shen, S.Q. Multi-objective probabilistically constrained programs with variable risk: Models for multi-portfolio financial optimization. Eur. J. Oper. Res. 2016, 252, 522–539. [Google Scholar] [CrossRef]
- Chen, J.F.; Nair, V.; Menzies, T. Beyond evolutionary algorithms for search-based software engineering. Inf. Softw. Technol. 2018, 95, 281–294. [Google Scholar] [CrossRef] [Green Version]
- Chang, M.X.; Chang, W.Y. Efficient detection for MIMO systems based on gradient search. IEEE Trans. Veh. Technol. 2016, 65, 10057–10063. [Google Scholar] [CrossRef]
- Triki, C.; Mirmohammadsadeghi, S.; Piya, S. Heuristic methods for the periodic shipper lane selection problem in transportation auctions. Comput. Ind. Eng. 2017, 106, 182–191. [Google Scholar] [CrossRef]
- Ertenlice, O.; Kalayci, C.B. A survey of swarm intelligence for portfolio optimization: Algorithms and applications. Swarm Evolut. Comput. 2018, 39, 36–52. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.; Li, C.H.; Yang, S.X. A survey of swarm intelligence for dynamic optimization: Algorithms and applications. Swarm Evolut. Comput. 2017, 33, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Piotrowski, A.P.; Napiorkowski, M.J.; Napiorkowski, J.J.; Rowinski, P.M. Swarm intelligence and evolutionary algorithms: Performance versus speed. Inf. Sci. 2017, 384, 34–85. [Google Scholar] [CrossRef]
- Ho, Y.C.; Zhao, Q.C.; Jia, Q.S. Ordinal Optimization: Soft Optimization for Hard Problems; Springer: New York, NY, USA, 2007. [Google Scholar]
- Horng, S.C.; Lin, S.S. Embedding advanced harmony search in ordinal optimization to maximize throughput rate of flow line. Arab. J. Sci. Eng. 2018, 43, 1015–1031. [Google Scholar] [CrossRef]
- Horng, S.C.; Lin, S.S. Ordinal optimization based metaheuristic algorithm for optimal inventory policy of assemble-to-order systems. Appl. Math. Modell. 2017, 42, 43–57. [Google Scholar] [CrossRef]
- Horng, S.C.; Lin, S.S. Merging crow search into ordinal optimization for solving equality constrained simulation optimization problems. J. Comput. Sci. 2017, 23, 44–57. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; Hasanien, H.M. Tree-seed algorithm for solving optimal power flow problem in large-scale power systems incorporating validations and comparisons. Appl. Soft Comput. 2018, 64, 307–316. [Google Scholar] [CrossRef]
- Babalik, A.; Cinar, A.C.; Kiran, M.S. A modification of tree-seed algorithm using Deb’s rules for constrained optimization. Appl. Soft Comput. 2018, 63, 289–305. [Google Scholar] [CrossRef]
- Cinar, A.C.; Kiran, M.S. Similarity and logic gate-based tree-seed algorithms for binary optimization. Comput. Ind. Eng. 2018, 115, 631–646. [Google Scholar] [CrossRef]
- Kiran, M.S. TSA: Tree-seed algorithm for continuous optimization. Expert Syst. Appl. 2015, 42, 6686–6698. [Google Scholar] [CrossRef]
- Hwang, J.T.; Martins, J.R.R.A. A fast-prediction surrogate model for large datasets. Aerosp. Sci. Technol. 2018, 75, 74–87. [Google Scholar] [CrossRef]
- Igarashi, Y.; Yabe, H. A primal-dual exterior point method with a primal-dual quadratic penalty function for nonlinear optimization. Pac. J. Optim. 2015, 11, 721–736. [Google Scholar]
- Smith, R.C. Uncertainty Quantification: Theory, Implementation, and Applications; SIAM: Philadelphia, PA, USA, 2014. [Google Scholar]
- Niutta, C.B.; Wehrle, E.J.; Duddeck, F.; Belingardi, G. Surrogate modeling in design optimization of structures with discontinuous responses. Struct. Multi. Optim. 2018, 57, 1857–1869. [Google Scholar] [CrossRef]
- Kang, L.L.; Joseph, V.R. Kernel approximation: From regression to interpolation. SIAM-ASA J. Uncertain Quantif. 2016, 4, 112–129. [Google Scholar] [CrossRef]
- Chen, C.H.; Lee, L.H. Stochastic Simulation Optimization: An Optimal Computing Budget Allocation; World Scientific: New Jersey, NJ, USA, 2010. [Google Scholar]
- Karakul, P.M.; Dasci, A. An approximation method to analyse polling models of pull-type production systems. Eur. J. Ind. Eng. 2007, 1, 200–222. [Google Scholar] [CrossRef]
- Ulewicz, R.; Nowakowska-Grunt, J.; Jelonek, D. Performance evaluation of the production control systems of push and pull type. Appl. Mech. Mater. 2015, 795, 235–242. [Google Scholar] [CrossRef]
- Tseng, T.; Gung, R.R.; Huang, C. Performance evaluation for pull-type supply chains using an agent-based approach. Am. J. Ind. Bus. Manag. 2013, 3, 91–100. [Google Scholar] [CrossRef]
- SimOpt.org. Strategic Location of Semi-Finished Products. Available online: http://simopt.org/wiki/index.php?title=Strategic_Location_of_Semi-Finished_Prod, 2016 (accessed on 16 June 2016).
- Ryan, T.P. Sample Size Determination and Power; John Wiley and Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Qian, W.Y.; Li, M. Convergence analysis of standard particle swarm optimization algorithm and its improvement. Soft Comput. 2018, 22, 4047–4070. [Google Scholar] [CrossRef]
- Pathan, M.V.; Patsias, S.; Tagarielli, V.L. A real-coded genetic algorithm for optimizing the damping response of composite laminates. Comput. Struct. 2018, 198, 51–60. [Google Scholar] [CrossRef]
- Abad, A.; Elipe, A. Evolution strategies for computing periodic orbits. Math. Comput. Simul. 2018, 146, 251–261. [Google Scholar] [CrossRef]
- Facchini, F.; De Pascale, G.; Faccilongo, N. Pallet picking strategy in food collecting center. Appl. Sci. 2018, 8, 1503. [Google Scholar] [CrossRef]
- Boenzi, F.; Facchini, F.; Digiesi, S.; Mummolo, G. Ergonomic improvement through job rotations in repetitive manual tasks in case of limited specialization and differentiated ergonomic requirements. IFAC-PapersOnLine 2016, 49, 1667–1672. [Google Scholar] [CrossRef]
- Sakalli, U.S.; Atabas, I. Ant colony optimization and genetic algorithm for fuzzy stochastic production-distribution planning. Appl. Sci. 2018, 8, 2042. [Google Scholar] [CrossRef]
- Park, J.; Mei, Y.; Nguyen, S.; Chen, G.; Zhang, M.J. An investigation of ensemble combination schemes for genetic programming based hyper-heuristic approaches to dynamic job shop scheduling. Appl. Soft Comput. 2018, 63, 72–86. [Google Scholar] [CrossRef]
- Yao, B.Z.; Chen, G. Stochastic simulation and optimization in supply chain management. Simulation 2018, 94, 561–562. [Google Scholar] [CrossRef] [Green Version]



| CPU Times (s) | ||||
|---|---|---|---|---|
| [19,28,28,42,42,41]T | 10.72 | 0.9009 | 9.648 | 24.67 |
| N | CPU Times (s) | ||||
|---|---|---|---|---|---|
| 20 | [51,49,48,47,48,30,29,20,20,20,19,19]T | 68.39 | 0.9002 | 61.56 | 96.35 |
| 15 | [52,47,48,49,49,29,29,20,20,19,19,19]T | 69.75 | 0.9013 | 62.77 | 93.41 |
| 10 | [53,48,49,48,47,29,30,20,20,19,19,18]T | 70.94 | 0.9024 | 63.84 | 90.94 |
| 5 | [54,49,47,48,48,30,29,20,19,18,20,18]T | 71.39 | 0.9019 | 64.25 | 89.17 |
| Methods | ABOV † | |
|---|---|---|
| OOTSA, case = 20 | 61.55 | 0 |
| PSO with precise evaluation | 68.16 | 10.74% |
| GA with precise evaluation | 72.92 | 18.47% |
| ES with precise evaluation | 71.53 | 16.21% |
| Approaches | Minimum | Maximum | Mean | Standard Deviation | Standard Error of the Mean | Average Ranking Ate |
|---|---|---|---|---|---|---|
| OOTSA, case = 20 | 60.37 | 62.97 | 61.55 | 0.52 | 0.0949 | 0.002% |
| PSO with precise evaluation | 66.56 | 70.42 | 68.16 | 0.76 | 0.1388 | 0.562% |
| GA with precise evaluation | 70.38 | 75.81 | 72.92 | 1.03 | 0.1881 | 0.821% |
| ES with precise evaluation | 69.91 | 73.68 | 71.53 | 0.87 | 0.1588 | 0.658% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horng, S.-C.; Lin, S.-S. Embedding Ordinal Optimization into Tree–Seed Algorithm for Solving the Probabilistic Constrained Simulation Optimization Problems. Appl. Sci. 2018, 8, 2153. https://doi.org/10.3390/app8112153
Horng S-C, Lin S-S. Embedding Ordinal Optimization into Tree–Seed Algorithm for Solving the Probabilistic Constrained Simulation Optimization Problems. Applied Sciences. 2018; 8(11):2153. https://doi.org/10.3390/app8112153
Chicago/Turabian StyleHorng, Shih-Cheng, and Shieh-Shing Lin. 2018. "Embedding Ordinal Optimization into Tree–Seed Algorithm for Solving the Probabilistic Constrained Simulation Optimization Problems" Applied Sciences 8, no. 11: 2153. https://doi.org/10.3390/app8112153
APA StyleHorng, S. -C., & Lin, S. -S. (2018). Embedding Ordinal Optimization into Tree–Seed Algorithm for Solving the Probabilistic Constrained Simulation Optimization Problems. Applied Sciences, 8(11), 2153. https://doi.org/10.3390/app8112153






