Acquisition of Dynamic Material Properties in the Electrohydraulic Forming Process Using Artificial Neural Network
Abstract
:1. Introduction
2. Finite Element Method for the Electrohydraulic Forming Process
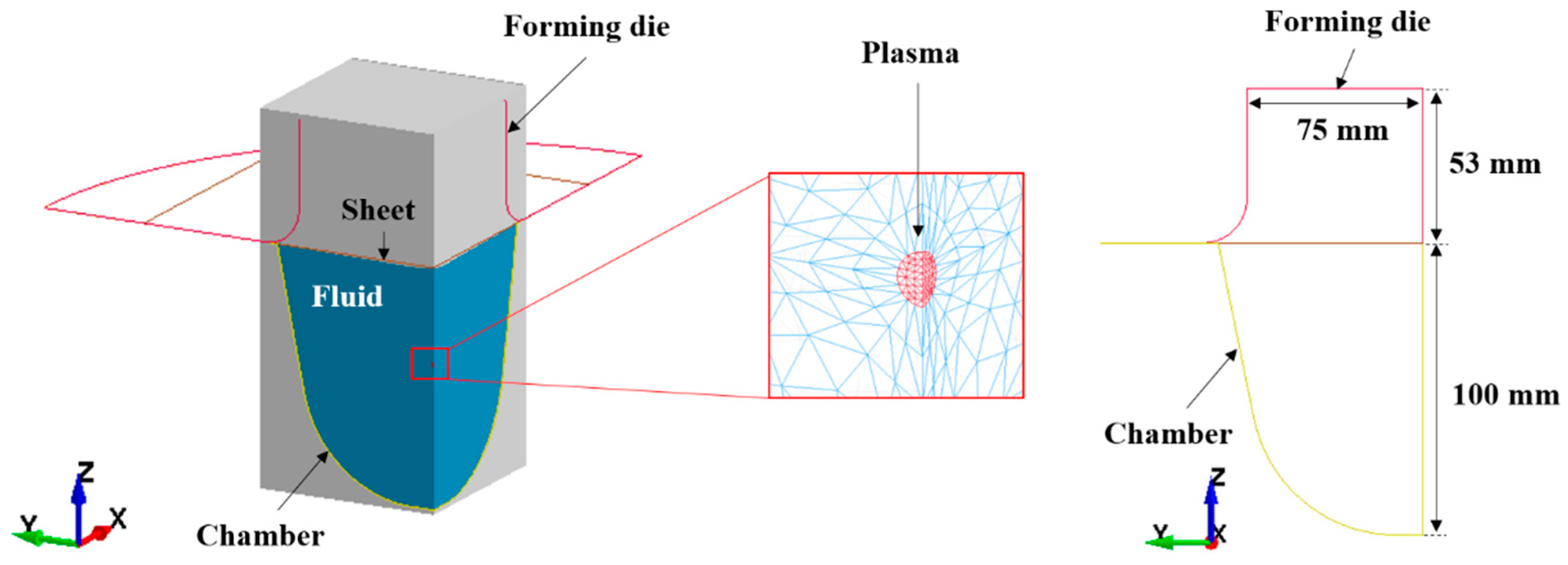
2.1. Numerical Modeling
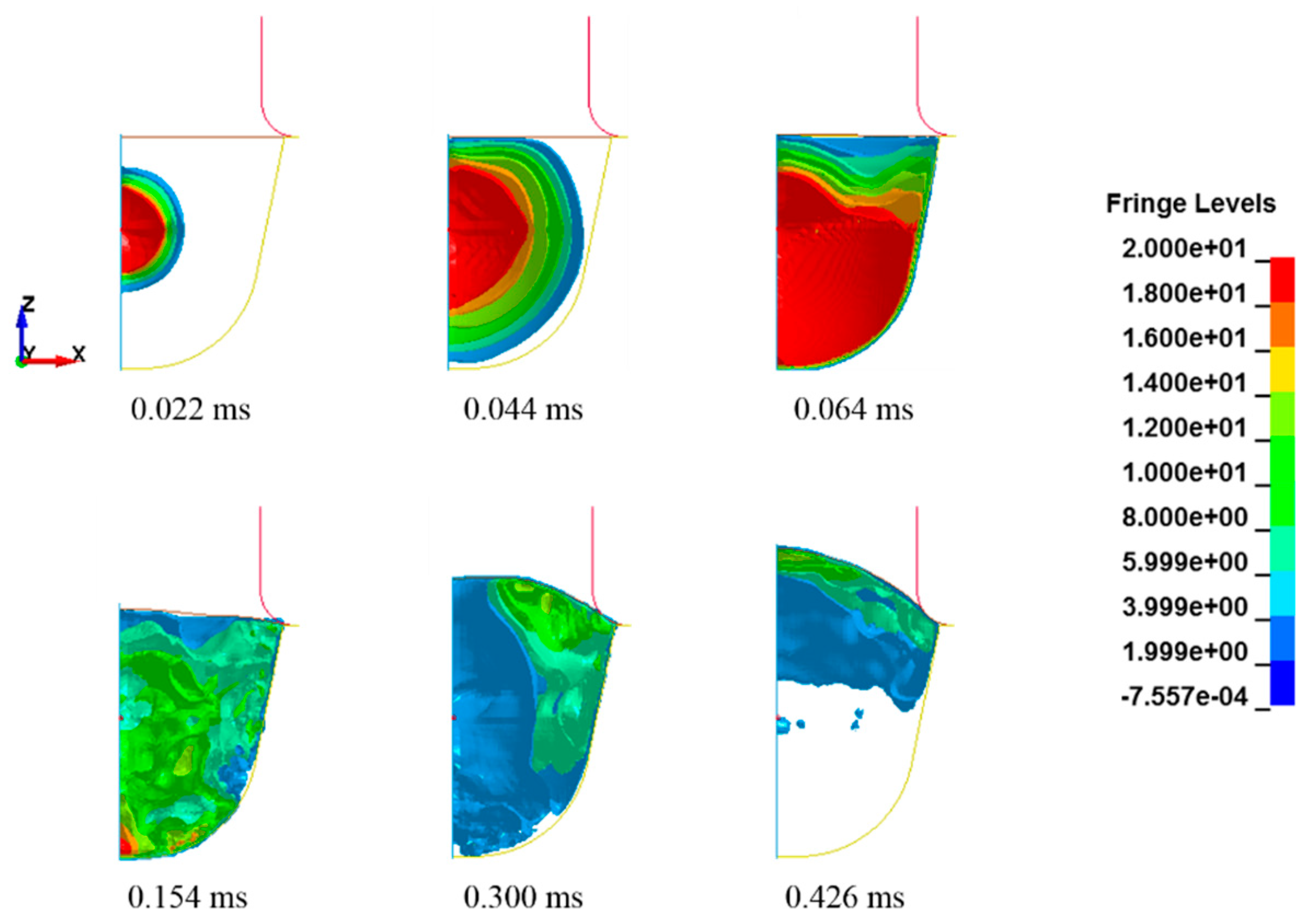
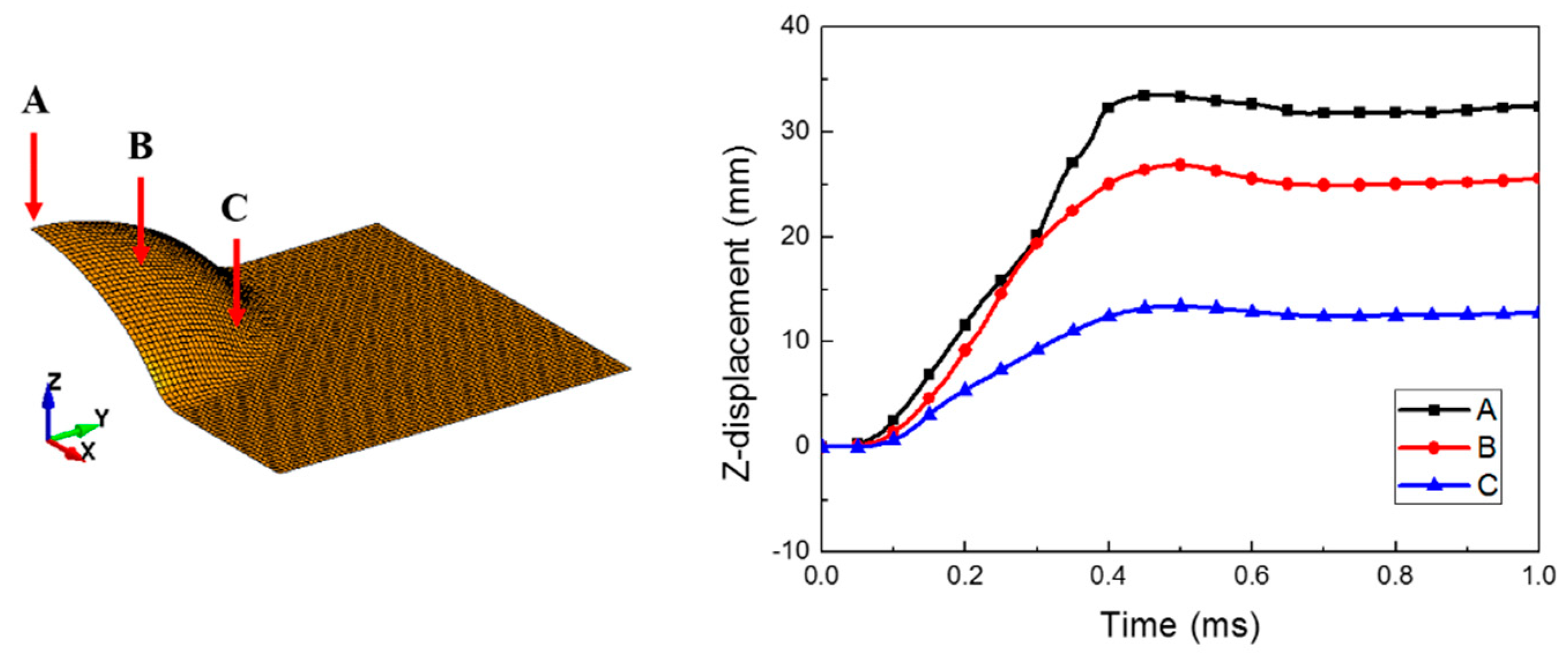
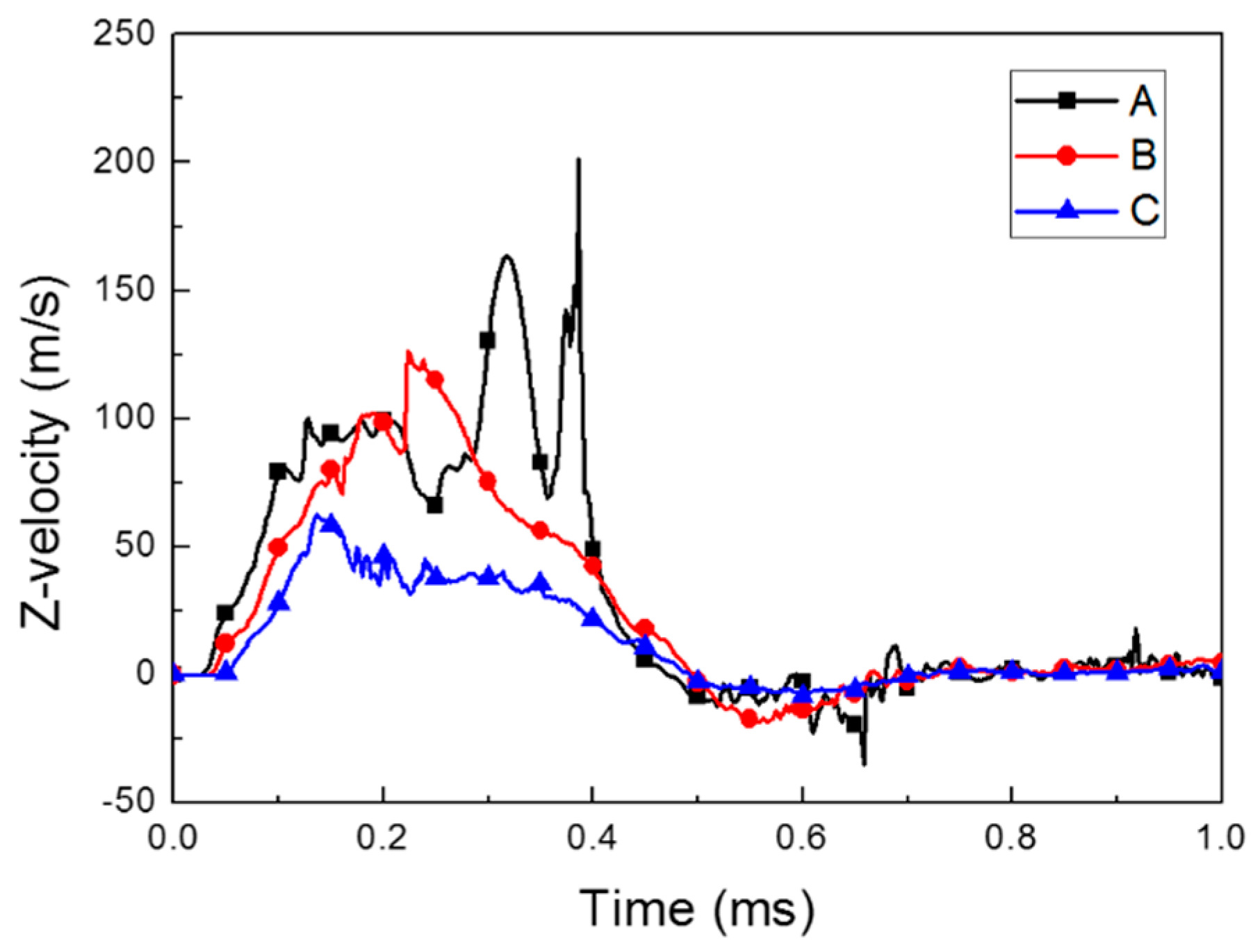
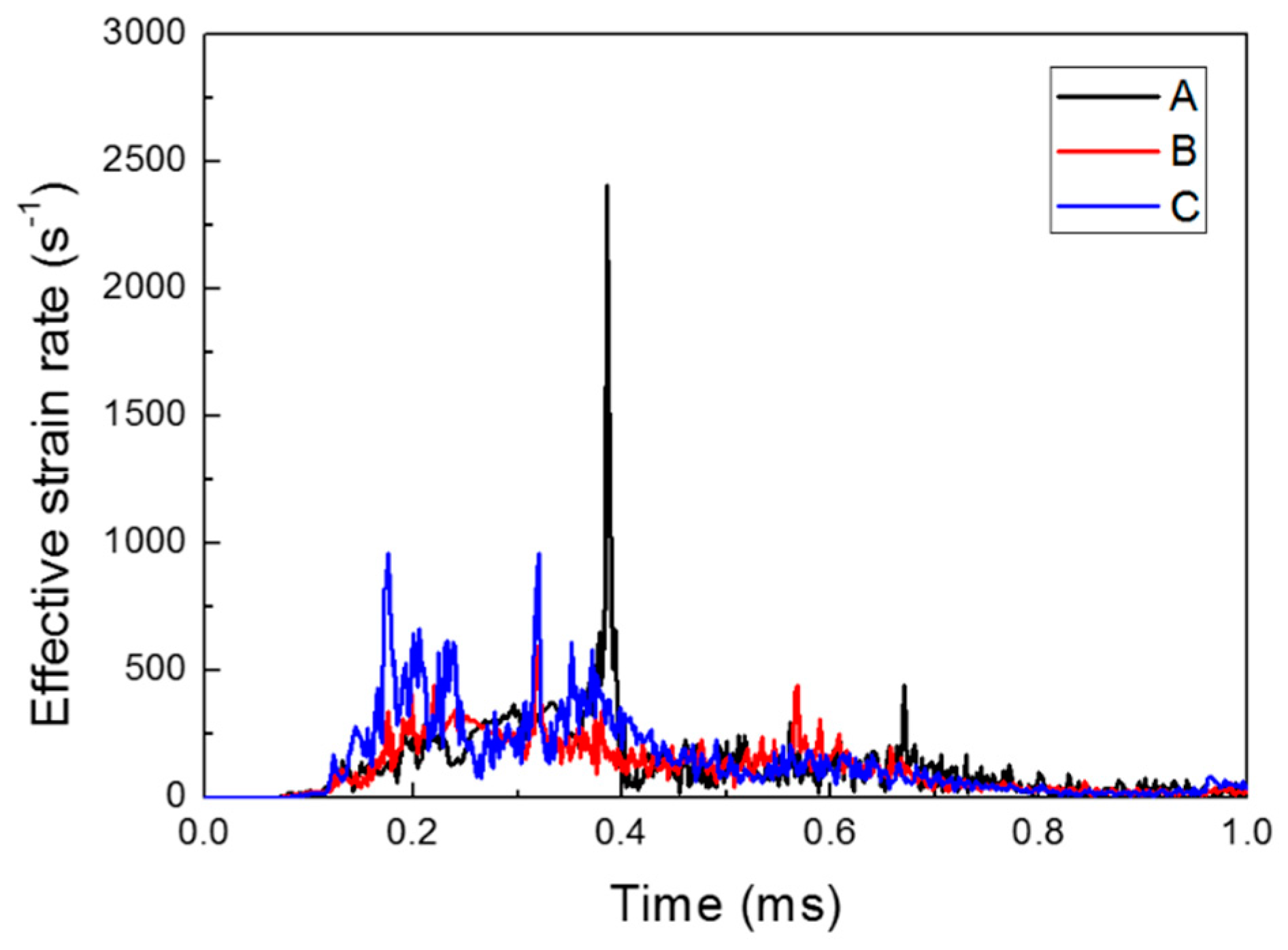
2.2. Numerical Results
3. Surrogate Model Using Order Reduction and ANN
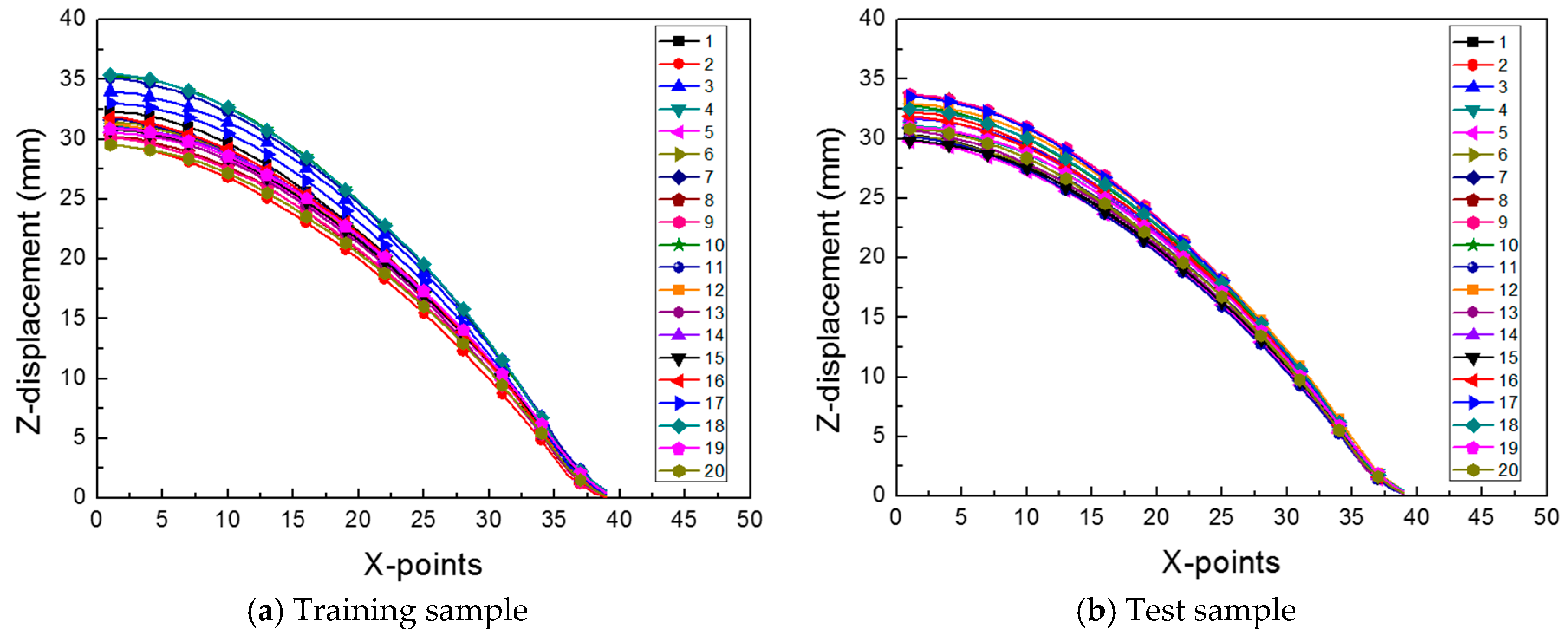
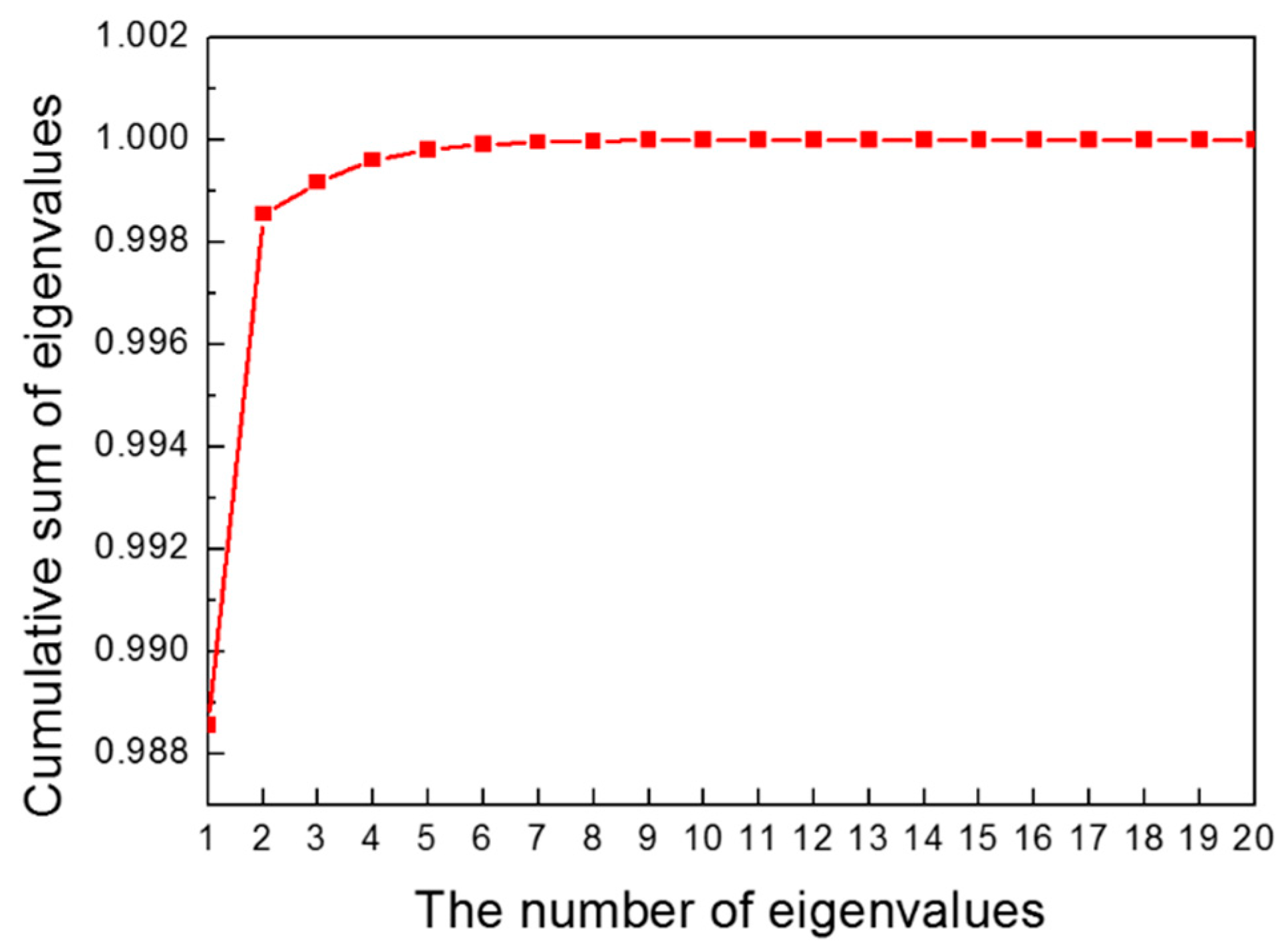
3.1. Reduced Order Model
3.2. Prediction of the Weighting Coefficients by Using ANN
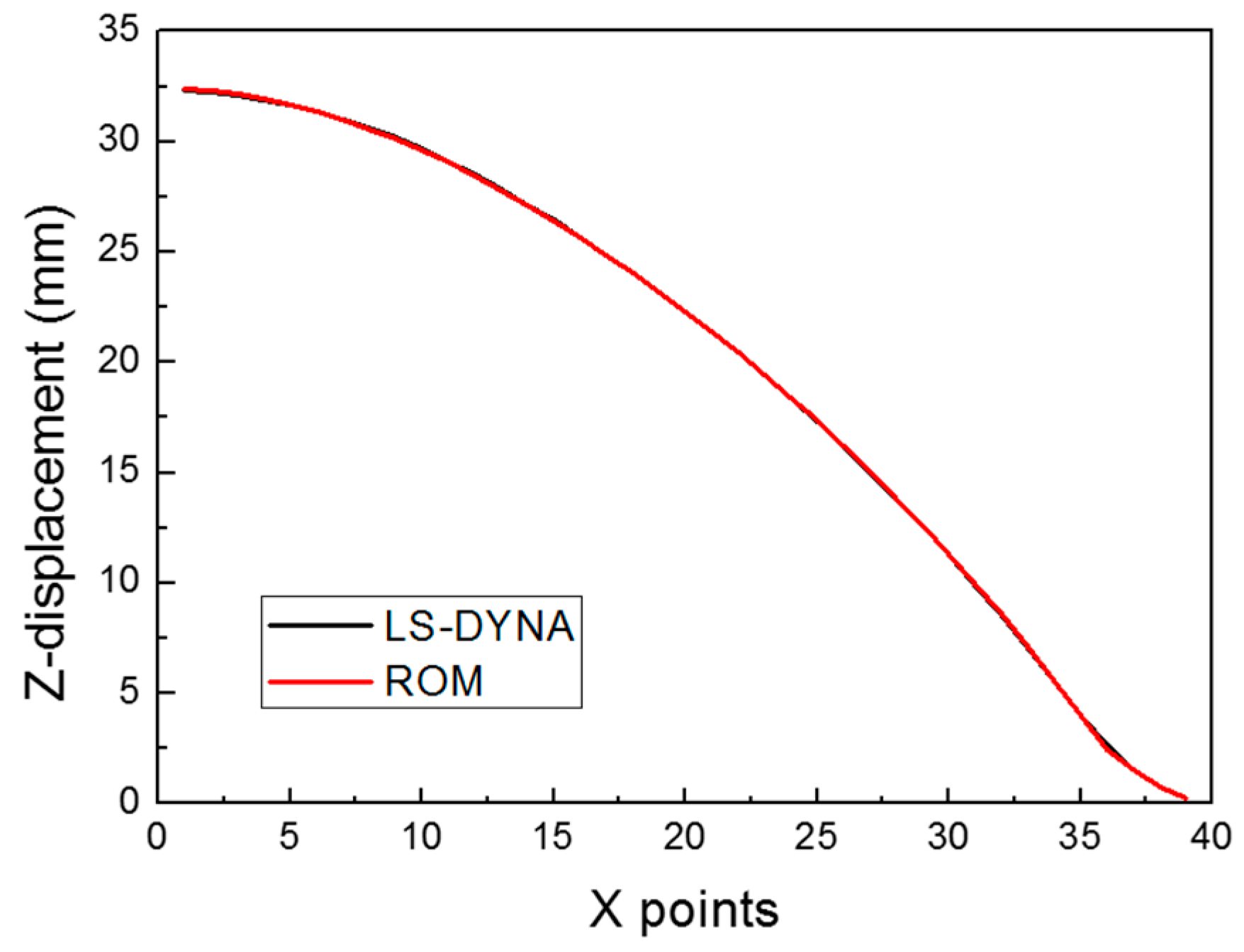
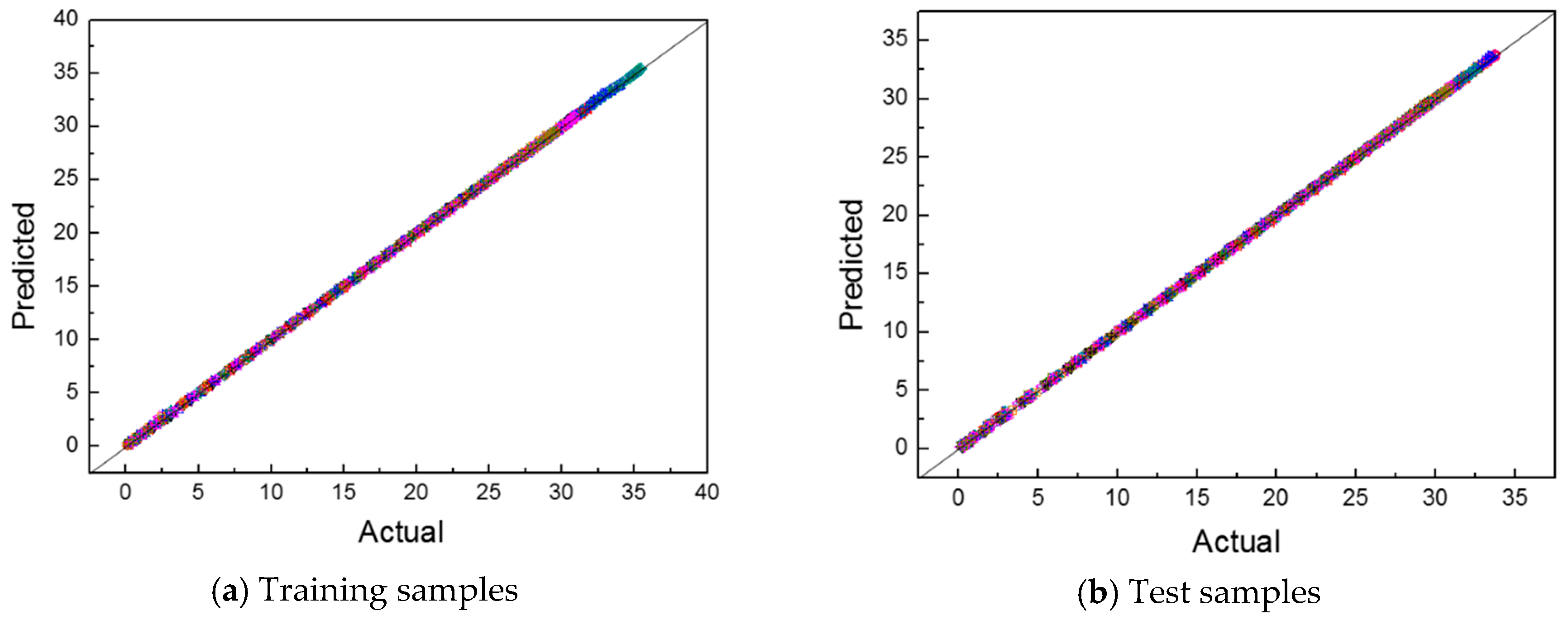
4. Validation of the Surrogate Model
5. Optimal Material Parameters for Al 6061-T6
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Altan, T.A.; Tekkaya, E. Sheet Metal Forming: Processes and Applications; ASM International: Almere, The Netherlands, 2012. [Google Scholar]
- Shim, J.Y.; Kang, B.Y. Development of electrohydraulic forming process for aluminum sheet with sharp edge. Adv. Mater. Sci. Eng. 2017, 11, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Gillard, A.J.; Golovashchenko, S.F.; Mamutov, A.V. Effect of quasi-static prestrain on the formability of dual phase steels in electrohydraulic forming. J. Manuf. Processes 2013, 15, 201–218. [Google Scholar] [CrossRef]
- Golovaschenko, S.F. Electrohydraulic Forming of Near-Net Shape Automotive Panels; Ford Motor Company: Dearborn, MI, USA, 2013. [Google Scholar]
- Golovashchenko, S.F.; Gillard, A.J.; Mamutov, A.V. Formability of dual phase steels in electrohydraulic forming. J. Mater. Process Technol. 2013, 213, 1191–1212. [Google Scholar] [CrossRef]
- Imbert, B.J. Increased Formability and the Effects of the Tool/Sheet Interaction in Electromagnetic Forming of Aluminum Alloy Sheet. Master’s Thesis, University of Waterloo, Waterloo, Belgium, 2005. [Google Scholar]
- Imbert, J.M.; Worswick, M.J.; Golovashchenko, S. Contributing Factors to the Increased Formability Observed in Electromagnetically Formed Aluminum Alloy Sheet. In Proceedings of the 2nd International Conference on High Speed Forming, Dortmund, Germany, 20–21 March 2006. [Google Scholar]
- Shin, C.; Jin, H.H.; Lee, J.G.; Lee, D.J.; Rhee, C.K.; Hong, J.H. Expansion of a low conductive metal tube by an electromagnetic forming process: Finite element modeling. Met. Mater. Int. 2008, 14, 91–97. [Google Scholar] [CrossRef]
- Noh, H.G.; Song, W.J.; Kang, B.S.; Kim, J. Numerical and experimental approach to reduce bouncing effect in electromagnetic forming process using cushion plate. J. Mech. Sci. Technol. 2014, 28, 3263–3271. [Google Scholar] [CrossRef]
- Woo, M.A.; Noh, H.G.; An, W.J.; Song, W.J.; Kang, B.S.; Kim, J. Numerical study on electrohydraulic forming process to reduce the bouncing effect in electromagnetic forming. Int. J. Adv. Manuf. Technol. 2017, 89, 1813–1825. [Google Scholar] [CrossRef]
- American Society for Testing and Materials (ASTM). Standard Test Methods for Tension Testing of Metallic Materials. Annual Book of ASTM Standards; ASTM: West Conshohocken, PA, USA, 2001. [Google Scholar]
- Kolsky, H. Stress Waves in Solids; Courier Corporation: New Chelmsford, MA, USA, 1963; 1098p. [Google Scholar]
- Siemann, M.H.; Langrand, B. Coupled fluid-structure computational methods for aircraft ditching simulations: Comparison of ALE-FE and SPH-FE approaches. Comput. Struct. 2017, 188, 95–108. [Google Scholar] [CrossRef] [Green Version]
- Slavik, T.P. A coupling of empirical explosive blast loads to ALE air domains in LS-DYNA®. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2010. [Google Scholar]
- Baranowski, P.; Malachowski, J.; Mazurkiewicz, L. Numerical and experimental testing of vehicle tyre under impulse loading conditions. Int. J. Mech. Sci. 2016, 106, 346–356. [Google Scholar] [CrossRef]
- Hallquist, J.O. LS-DYNA Keyword User’s Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2007; pp. 299–800. [Google Scholar]
- Cowper, G.R.; Symonds, P.S. Strain-Hardening and Strain-Rate Effects in the Impact Loading of Cantilever Beams; (No. TR-C11-28); Brown University: Providence, RI, USA, 1957. [Google Scholar]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Lieu, T.; Farhat, C.; Lesoinne, M. Reduced-Order fluid/structure modeling of a complete aircraft configuration. Comput. Meth. Appl. Mech. Eng. 2006, 195, 5730–5742. [Google Scholar] [CrossRef]
- Lucia, D.J.; Pachter, M.; Beran, P.S. Rocket nozzle flow control using a reduced-order computational fluid dynamics model. J. Guid. Control. Dyn. 2002, 25, 449–454. [Google Scholar] [CrossRef]
- Wang, Q.; Hesthaven, J.S.; Ray, D. Non-Intrusive reduced order modeling of unsteady flows using artificial neural networks with application to a combustion problem. J. Comput. Phys. 2019, 384, 289–307. [Google Scholar] [CrossRef]
- Principal Component Analysis. Available online: https://ratsgo.github.io/machine%20learning/2017/04/24/PCA/ (accessed on 10 September 2019).
- Friedberg, S.; Insel, A.; Spence, L. Linear Algebra: Pearson New, 4th ed.; Pearson: London, UK, 2013. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. [Google Scholar] [CrossRef] [Green Version]
- Woo, M.A.; Noh, H.G.; Song, W.J.; Kang, B.S.; Kim, J. Experimental validation of numerical modeling of electrohydraulic forming using an Al 5052-H34 sheet. Int. J. Adv. Manuf. Technol. 2017, 93, 1819–1828. [Google Scholar] [CrossRef]









| LS-DYNA Keywords | Description |
|---|---|
| *MAT_PIECWISE_LINEAR_PLASTICITY | Material keyword for Al 6061-T6 |
| *CONTACT_SURFACE_TO_SURFACE | Contact keyword for structural parts |
| *CONSTRAINED_LAGRANGE_IN_SOLID | Contact keyword for coupling between structure and fluid parts |
| *INITIAL_VOLUME_FRACTION_GEOMETRY | Volume fraction keyword for generating water part |
| *EOS_LINEAR_POLYNOMIAL_WITH_ENERGY_LEAK | Equation of state keyword for electric power in plasma part |
| *ALE_MULTI-MATERIAL_GROUP | Keyword for defining ALE materials group (plasma, water and air) |
| Training Sample | Test Smple | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| No. | R2 | RMSE | MARE | Max. ARE | No. | R2 | RMSE | MARE | Max. ARE |
| 1 | 9.999E-01 | 4.835E-02 | 6.048E-03 | 8.119E-02 | 1 | 9.995E-01 | 1.983E-01 | 2.268E-02 | 2.334E-01 |
| 2 | 9.999E-01 | 5.312E-02 | 3.036E-02 | 7.184E-01 | 2 | 9.995E-01 | 2.189E-01 | 2.474E-02 | 2.094E-01 |
| 3 | 9.999E-01 | 4.087E-02 | 3.354E-03 | 3.864E-02 | 3 | 9.995E-01 | 2.082E-01 | 1.669E-02 | 1.840E-02 |
| 4 | 9.999E-01 | 3.374E-02 | 2.729E-03 | 2.571E-02 | 4 | 9.996E-01 | 1.987E-01 | 1.264E-02 | 5.855E-02 |
| 5 | 9.999E-01 | 9.558E-02 | 1.529E-02 | 3.233E-03 | 5 | 9.996E-01 | 1.992E-01 | 1.987E-02 | 2.034E-01 |
| 6 | 9.999E-01 | 5.749E-02 | 6.005E-03 | 1.349E-02 | 6 | 9.995E-01 | 2.122E-01 | 1.059E-02 | 1.666E-02 |
| 7 | 9.999E-01 | 3.348E-02 | 6.363E-03 | 2.655E-03 | 7 | 9.996E-01 | 1.974E-01 | 1.581E-02 | 1.006E-01 |
| 8 | 9.999E-01 | 4.260E-02 | 3.520E-03 | 2.054E-02 | 8 | 9.997E-01 | 1.981E-01 | 1.395E-02 | 6.089E-02 |
| 9 | 9.999E-01 | 4.228E-02 | 8.438E-03 | 1.070E-02 | 9 | 9.994E-01 | 2.033E-01 | 1.356E-02 | 1.059E-01 |
| 10 | 9.999E-01 | 4.052E-02 | 2.298E-03 | 6.936E-03 | 10 | 9.996E-01 | 1.977E-01 | 1.091E-02 | 3.819E-02 |
| 11 | 9.999E-01 | 5.653E-02 | 5.126E-03 | 5.224E-02 | 11 | 9.995E-01 | 2.092E-01 | 3.432E-02 | 4.571E-01 |
| 12 | 9.999E-01 | 7.672E-02 | 1.217E-02 | 7.476E-03 | 12 | 9.996E-01 | 2.007E-01 | 1.397E-02 | 6.695E-02 |
| 13 | 9.999E-01 | 4.057E-02 | 6.139E-03 | 3.676E-02 | 13 | 9.996E-01 | 2.059E-01 | 2.265E-02 | 1.911E-01 |
| 14 | 9.999E-01 | 7.306E-02 | 9.832E-03 | 9.419E-02 | 14 | 9.996E-01 | 1.999E-01 | 1.855E-02 | 1.504E-01 |
| 15 | 9.999E-01 | 5.273E-02 | 7.811E-03 | 7.290E-02 | 15 | 9.996E-01 | 1.986E-01 | 1.684E-02 | 1.033E-01 |
| 16 | 9.999E-01 | 4.708E-02 | 7.075E-03 | 6.479E-03 | 16 | 9.996E-01 | 2.152E-01 | 1.381E-02 | 3.668E-02 |
| 17 | 9.999E-01 | 4.191E-02 | 4.357E-03 | 2.803E-03 | 17 | 9.993E-01 | 2.045E-01 | 1.475E-02 | 8.087E-02 |
| 18 | 9.999E-01 | 3.483E-02 | 3.333E-03 | 2.347E-02 | 18 | 9.996E-01 | 2.012E-01 | 1.257E-02 | 5.468E-02 |
| 19 | 9.999E-01 | 3.159E-02 | 3.926E-03 | 3.929E-02 | 19 | 9.996E-01 | 2.019E-01 | 1.409E-02 | 8.220E-02 |
| 20 | 9.999E-01 | 2.188E-02 | 3.200E-03 | 5.797E-03 | 20 | 9.996E-01 | 1.976E-01 | 1.594E-02 | 9.812E-02 |
| Error | Experiment–Surrogate Model | Experiment–Numerical Simulation | Numerical Simulation–Surrogate Model |
|---|---|---|---|
| R2 | 9.977E-01 | 9.964E-01 | 9.985E-01 |
| RMSE | 4.608E-01 | 5.793E-01 | 3.701E-01 |
| MARE | 6.390E-02 | 9.620E-02 | 3.640E-02 |
| Max. ARE | 3.417E-01 | 7.980E-01 | 2.552E-01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woo, M.-A.; Moon, Y.-H.; Song, W.-J.; Kang, B.-S.; Kim, J. Acquisition of Dynamic Material Properties in the Electrohydraulic Forming Process Using Artificial Neural Network. Materials 2019, 12, 3544. https://doi.org/10.3390/ma12213544
Woo M-A, Moon Y-H, Song W-J, Kang B-S, Kim J. Acquisition of Dynamic Material Properties in the Electrohydraulic Forming Process Using Artificial Neural Network. Materials. 2019; 12(21):3544. https://doi.org/10.3390/ma12213544
Chicago/Turabian StyleWoo, Min-A, Young-Hoon Moon, Woo-Jin Song, Beom-Soo Kang, and Jeong Kim. 2019. "Acquisition of Dynamic Material Properties in the Electrohydraulic Forming Process Using Artificial Neural Network" Materials 12, no. 21: 3544. https://doi.org/10.3390/ma12213544
APA StyleWoo, M.-A., Moon, Y.-H., Song, W.-J., Kang, B.-S., & Kim, J. (2019). Acquisition of Dynamic Material Properties in the Electrohydraulic Forming Process Using Artificial Neural Network. Materials, 12(21), 3544. https://doi.org/10.3390/ma12213544






