Sliding Mode Switch Control of Adjustable Hydro-Pneumatic Suspension based on Parallel Adaptive Clonal Selection Algorithm
Abstract
:1. Introduction
- (1)
- The 6-DOF model of the adjustable hydro-pneumatic suspension based on the rescue vehicle is established, and the sliding mode controller is applied on the rescue vehicle because of its robust and easy realization.
- (2)
- A Switched SMC is proposed and built for the control of the adjustable hydro-pneumatic suspension system, which can address concerns on both ride comfort and handling stability under different road surfaces and driving conditions through switch actions, and the optimization ability of the proposed control strategy is proven compared with the conventional SMC based on MATLAB/Simulink.
- (3)
- PACSA is used to optimize the parameters of the Switched SMC, which is verified as more suitable for tuning the parameters of the SMC controller.
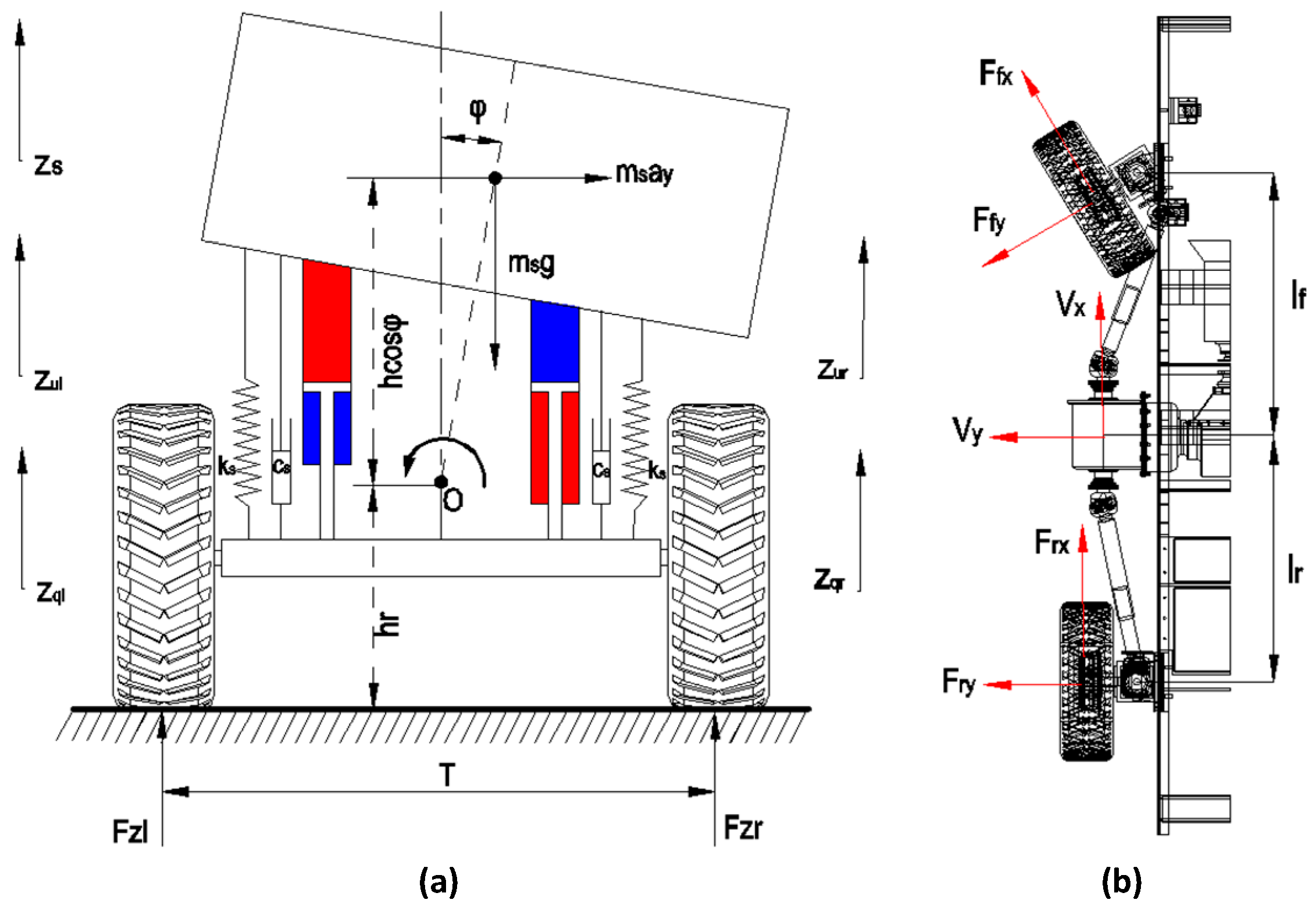
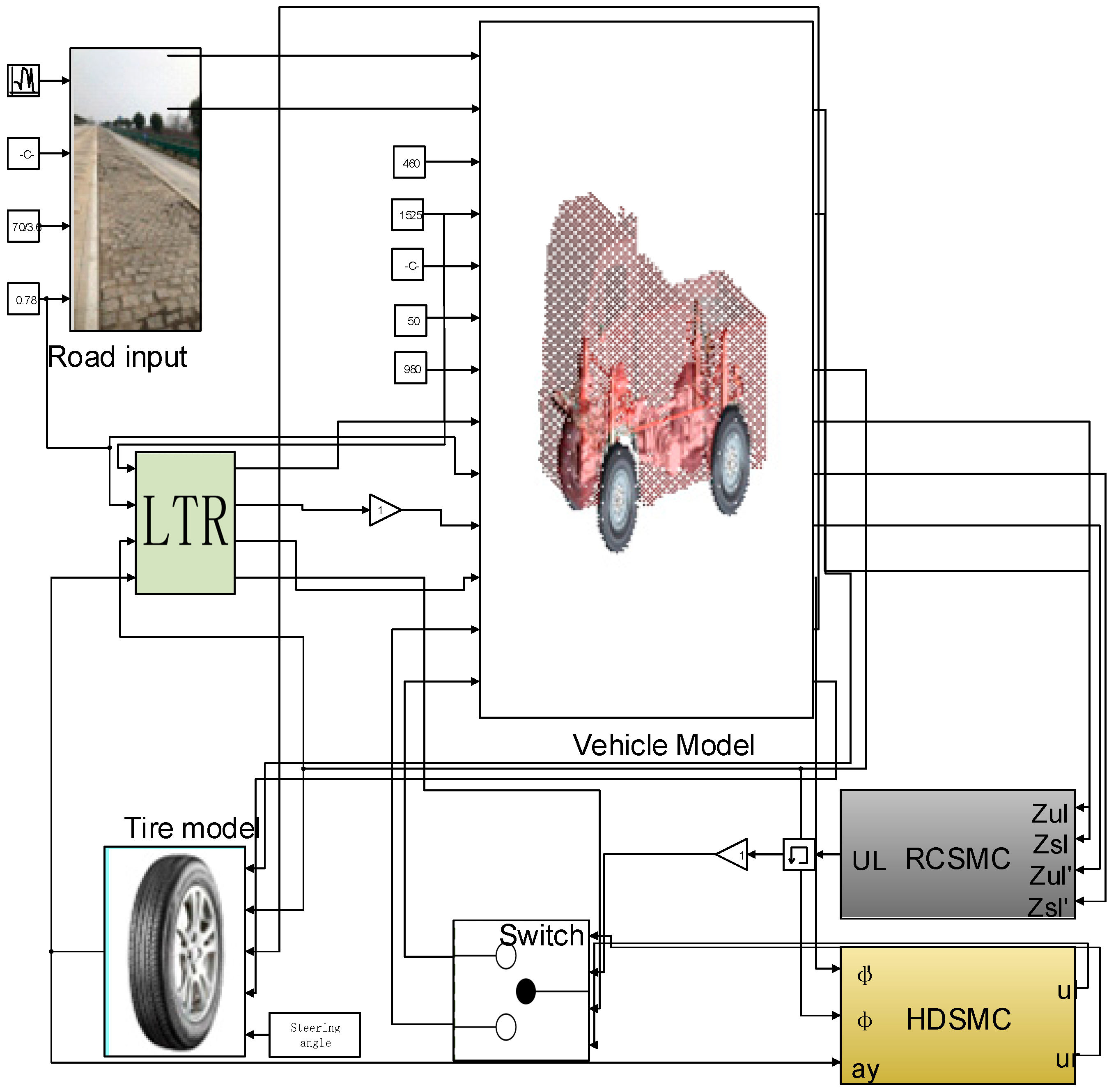
2. System Modelling
2.1. Modelling of the Hydro-Pneumatic Suspension System
2.2. Tire Model
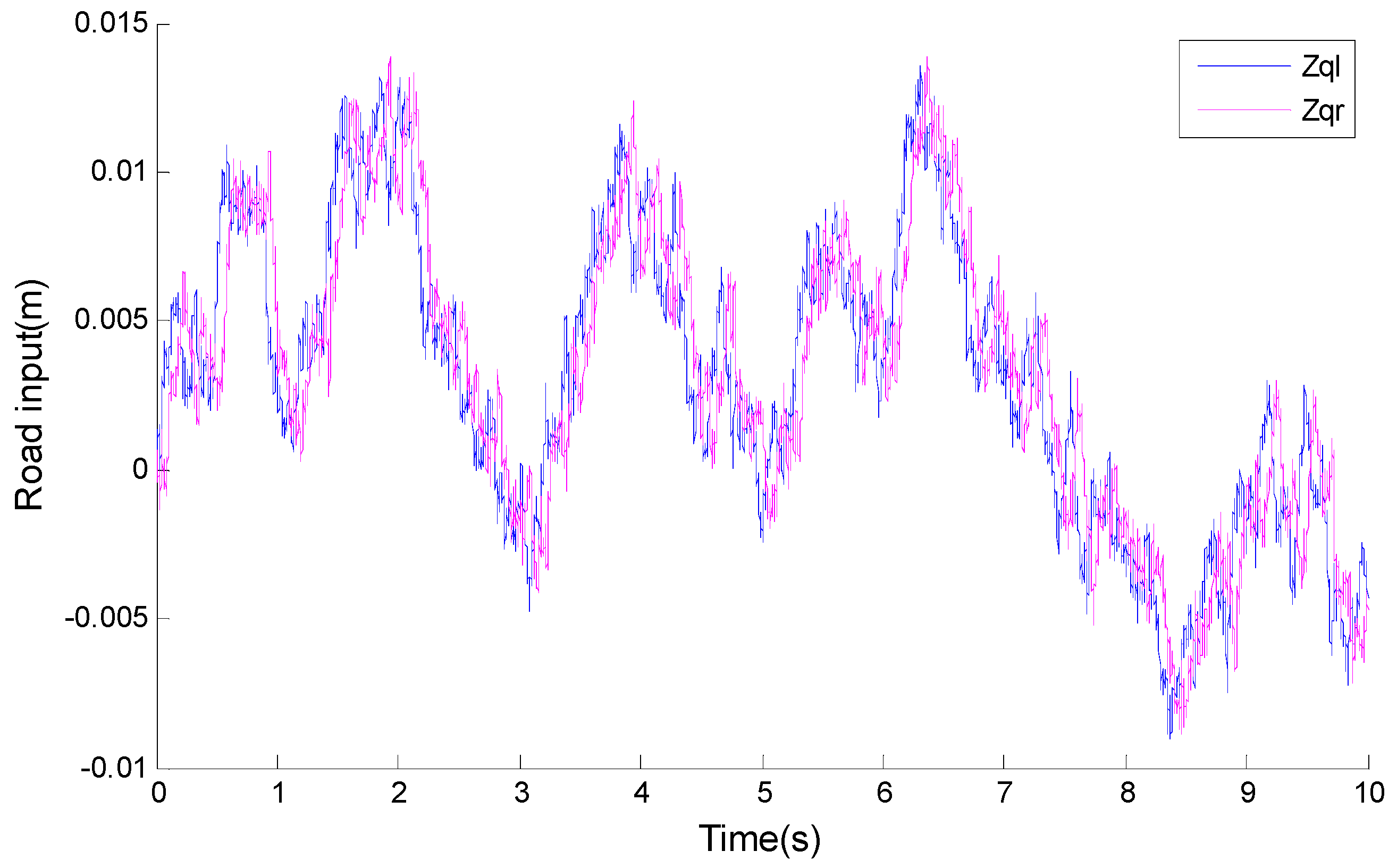
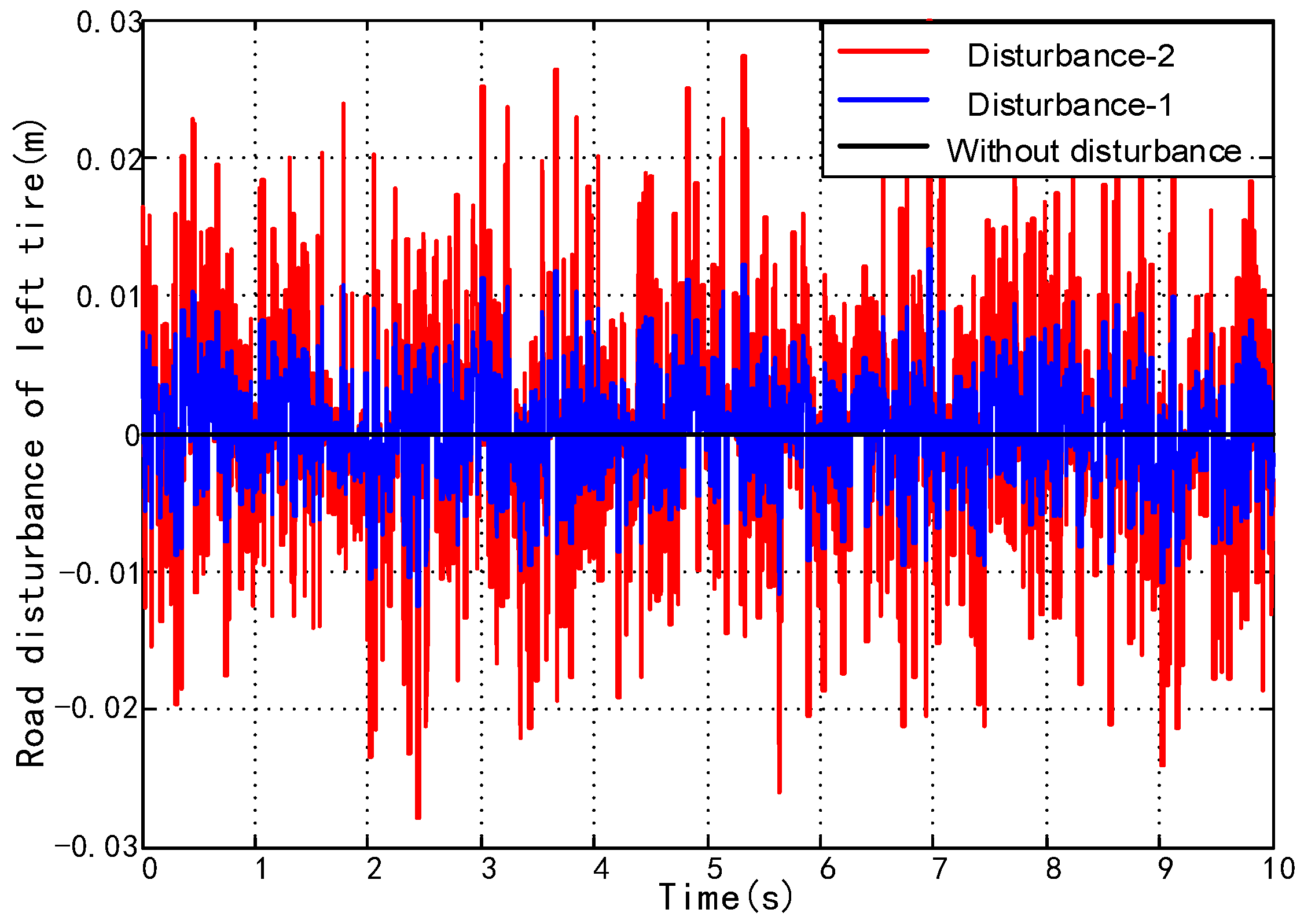
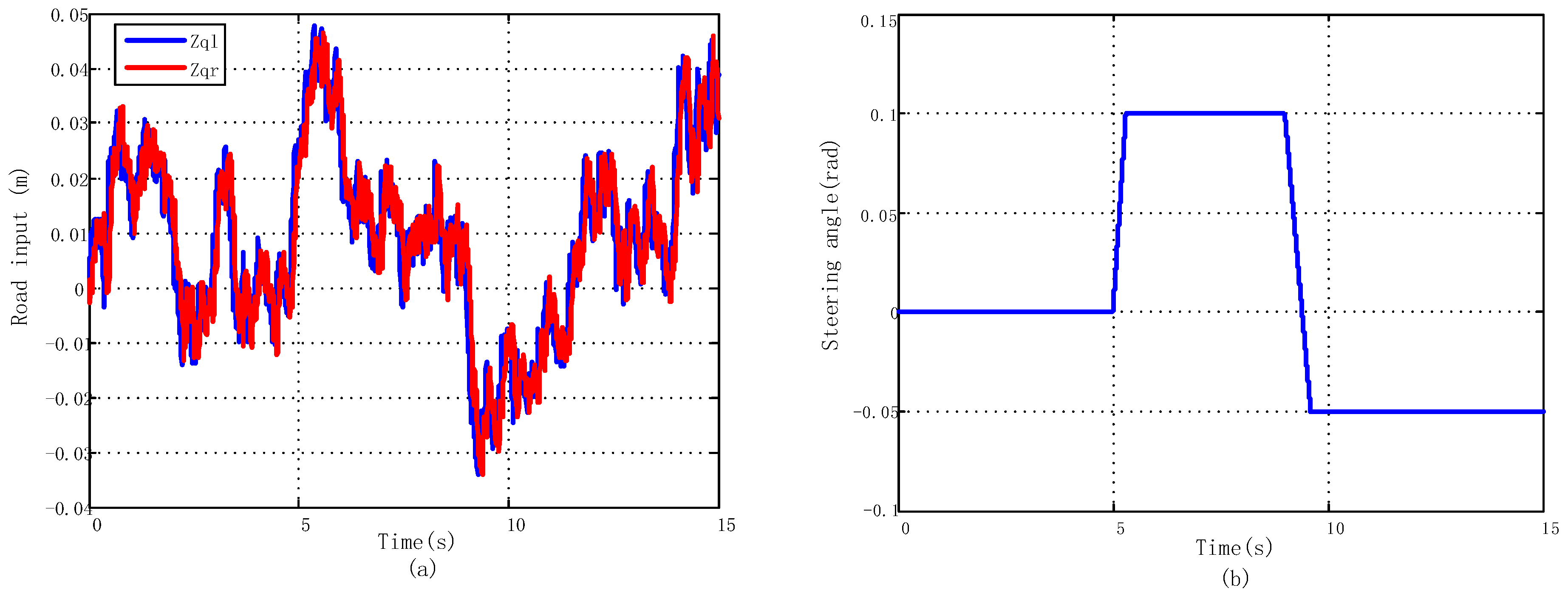
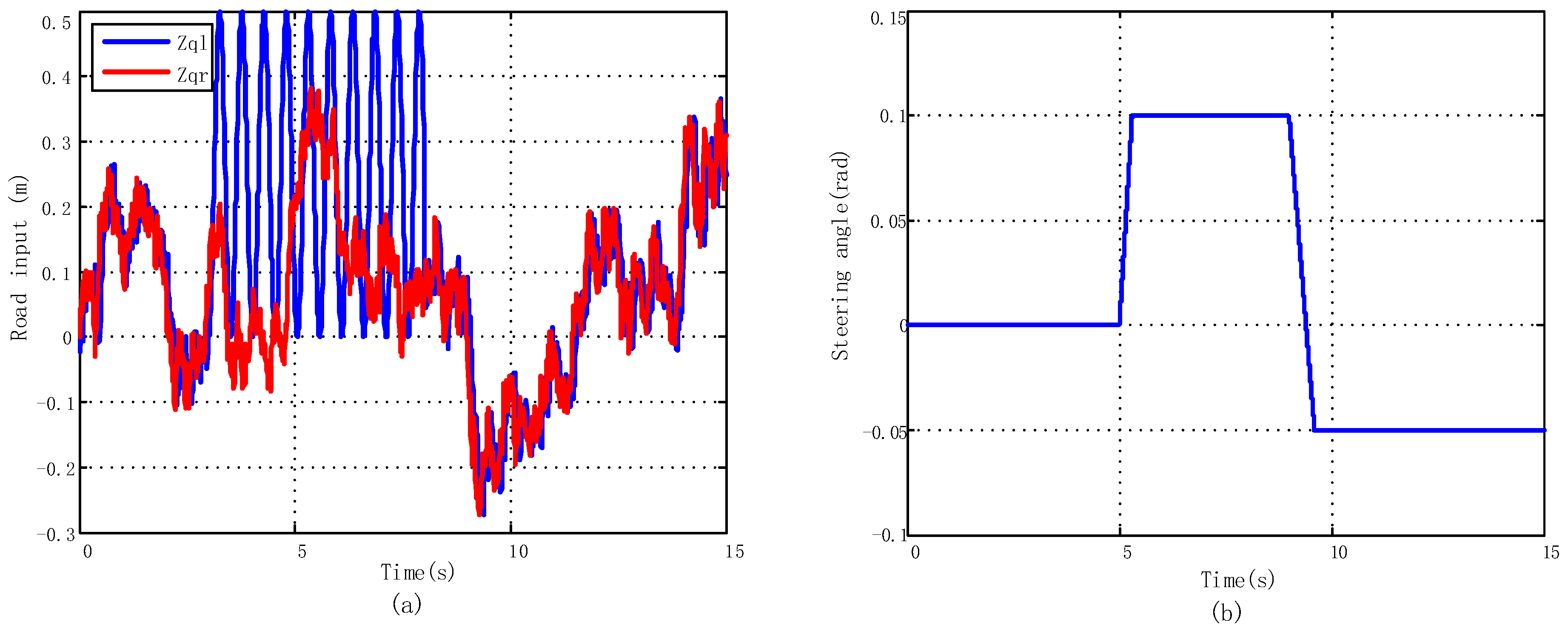
2.3. Road Input Modelling
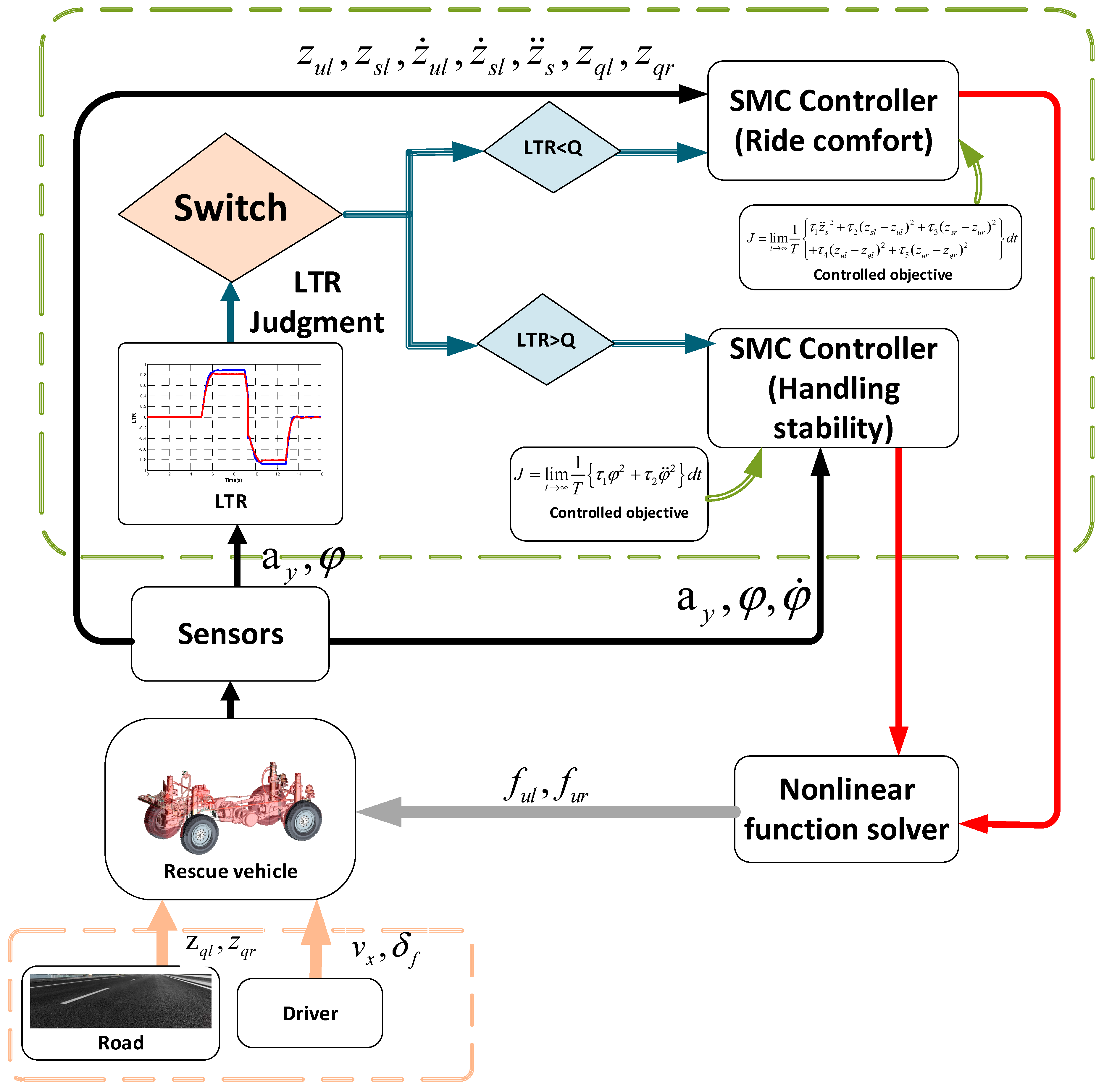
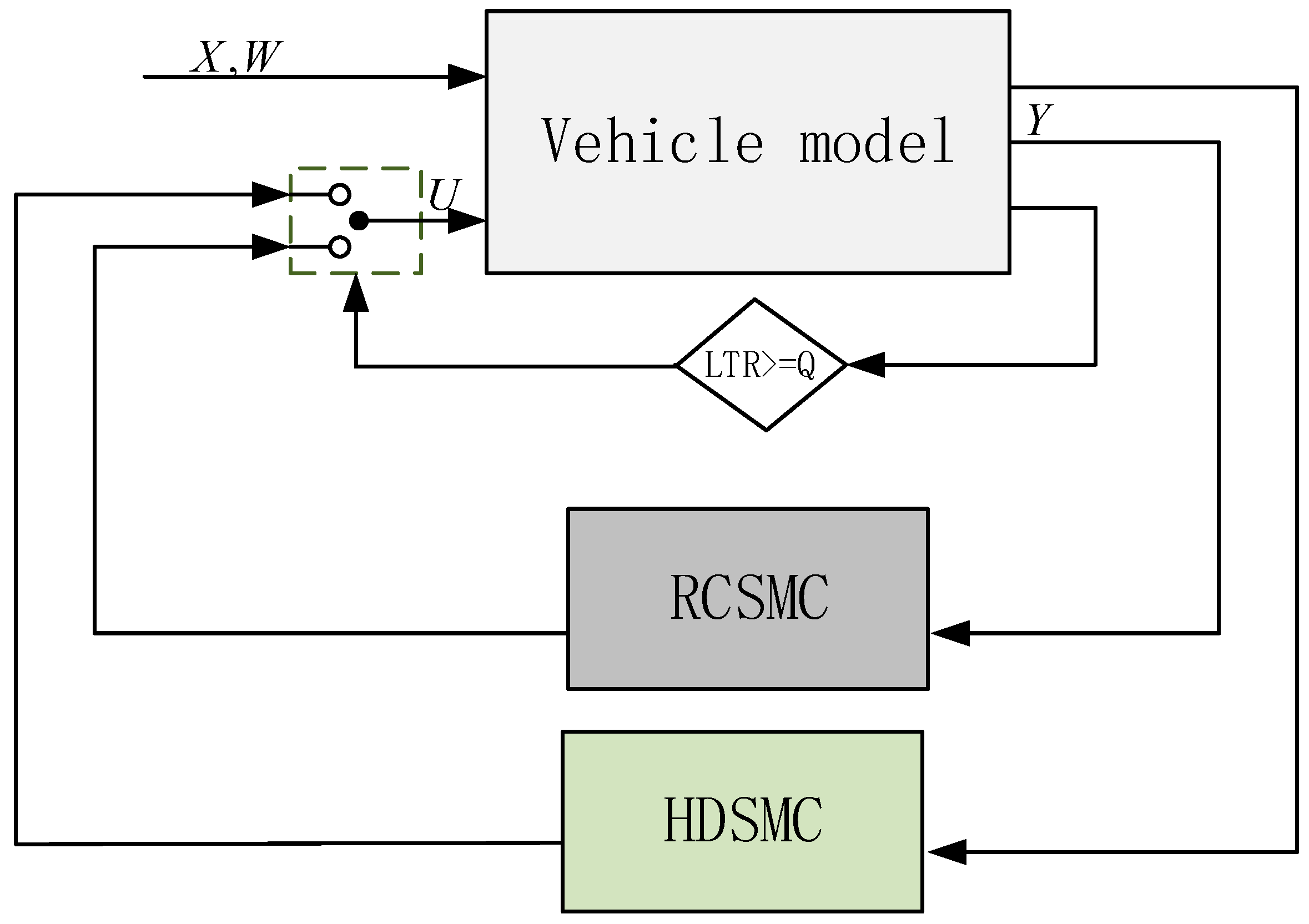
3. The Switch Control Strategy of the Hydro-Pneumatic Suspension
3.1. Switch Control Strategy
3.2. Handling Stability Control
3.3. Ride Comfort Control
4. SMC Parameters Tuning Based on PACSA
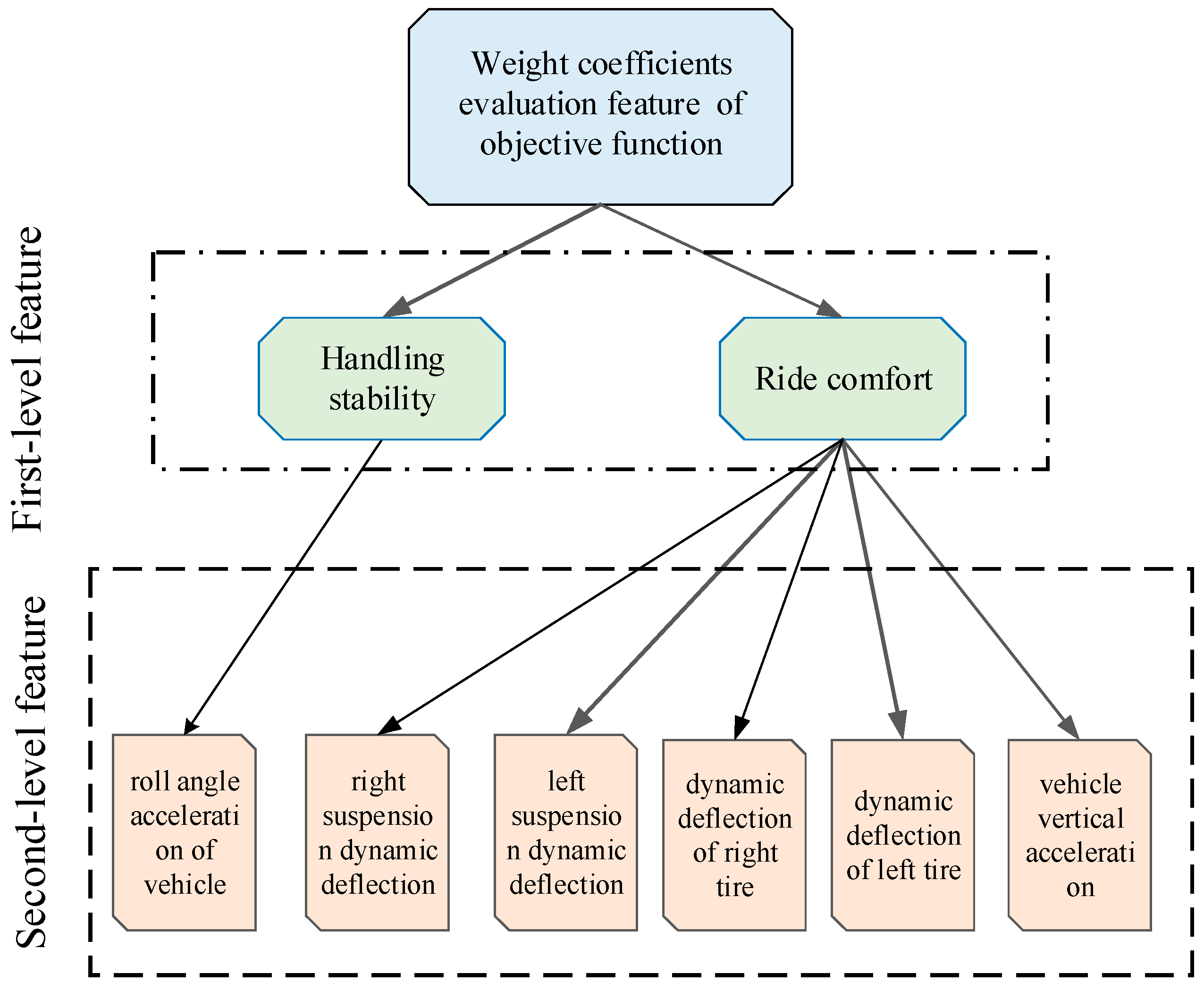
4.1. Design of Objective Function based on AHP
4.1.1. Objective Function
4.1.2. Weighting Coefficient Optimization of the Objective Function based on AHP
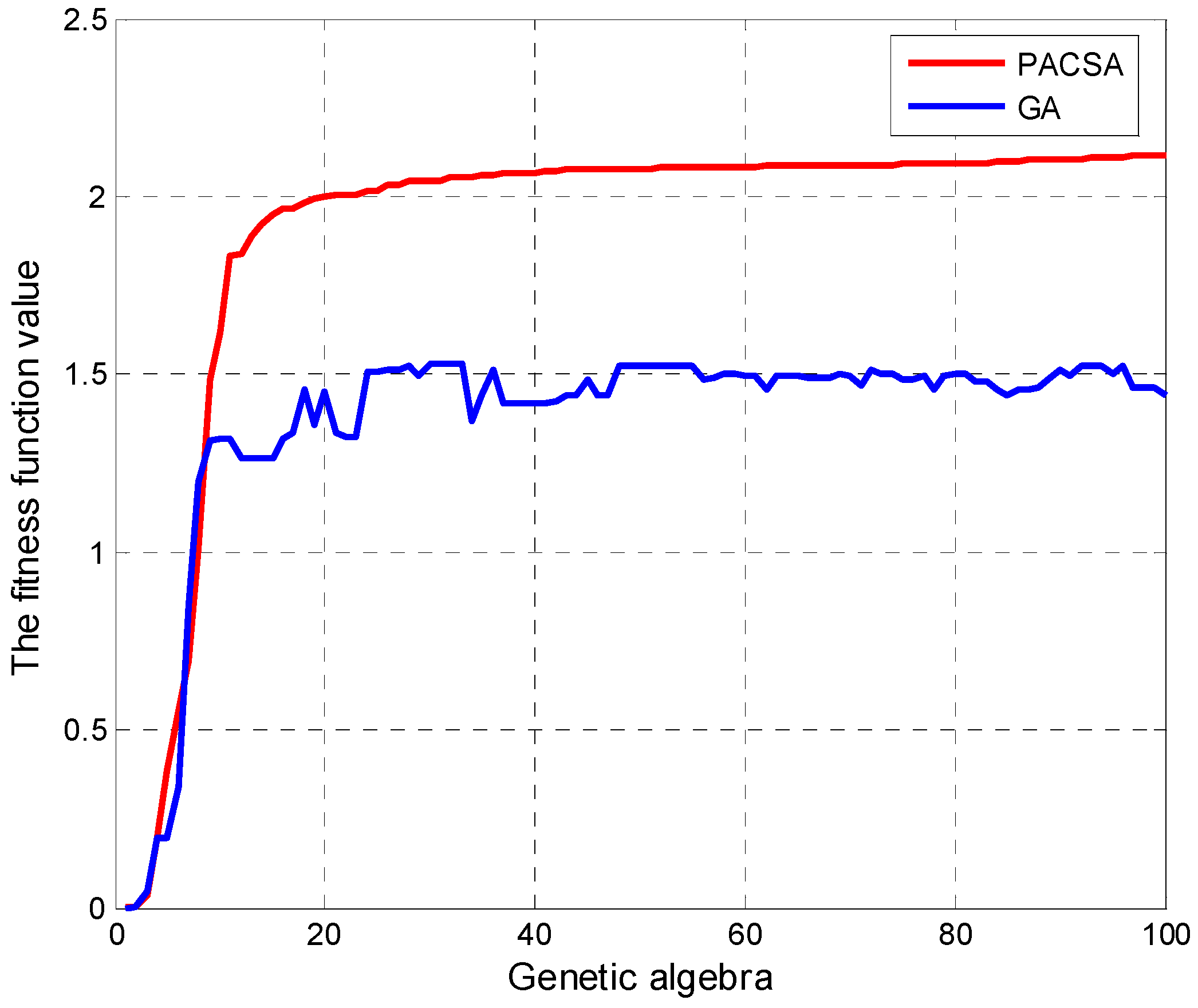
4.2. Optimal Tuning Process of SMC based on PACSA
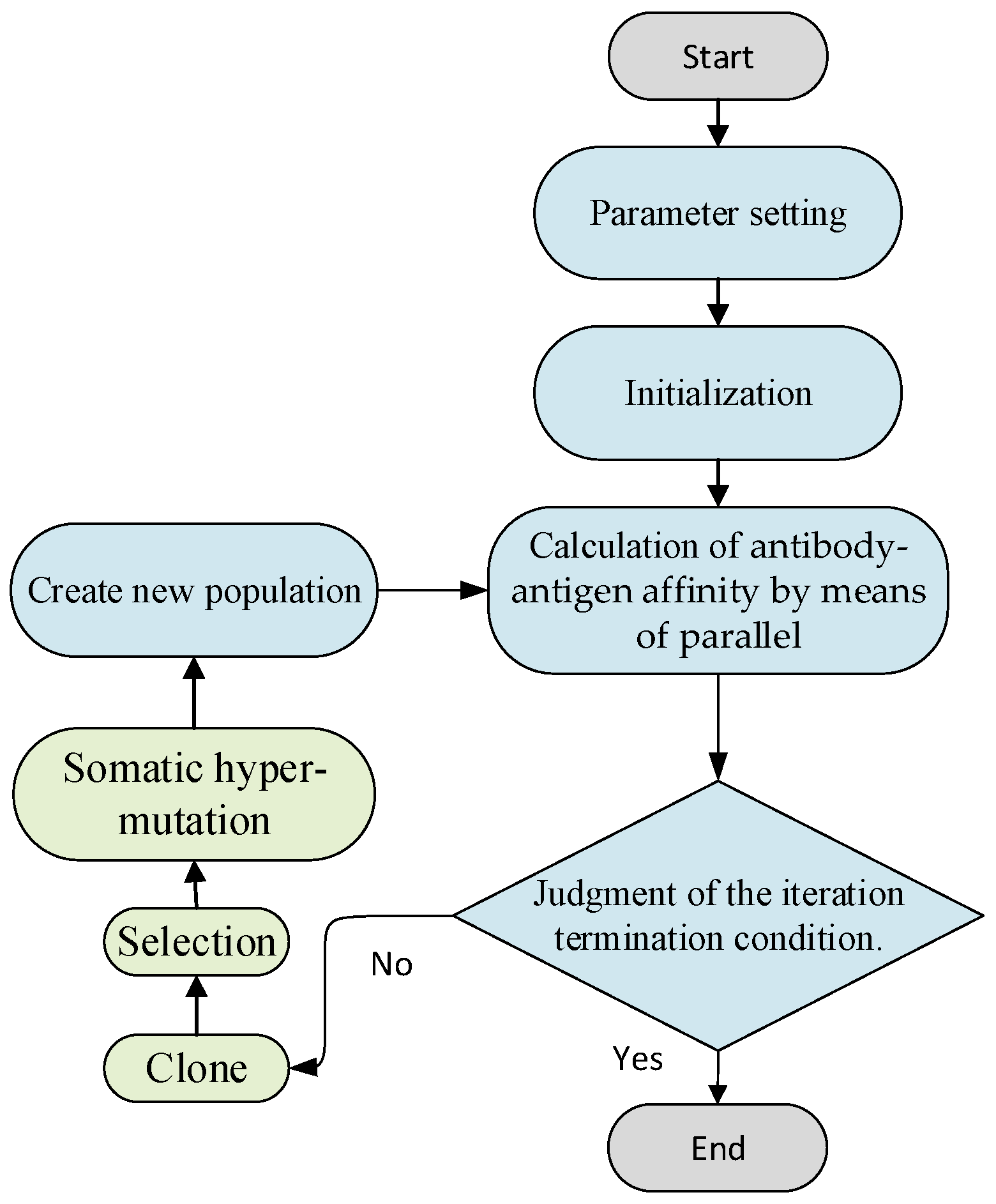
4.2.1. Brief Introduction of PACSA
4.2.2. Optimization Process of PACSA
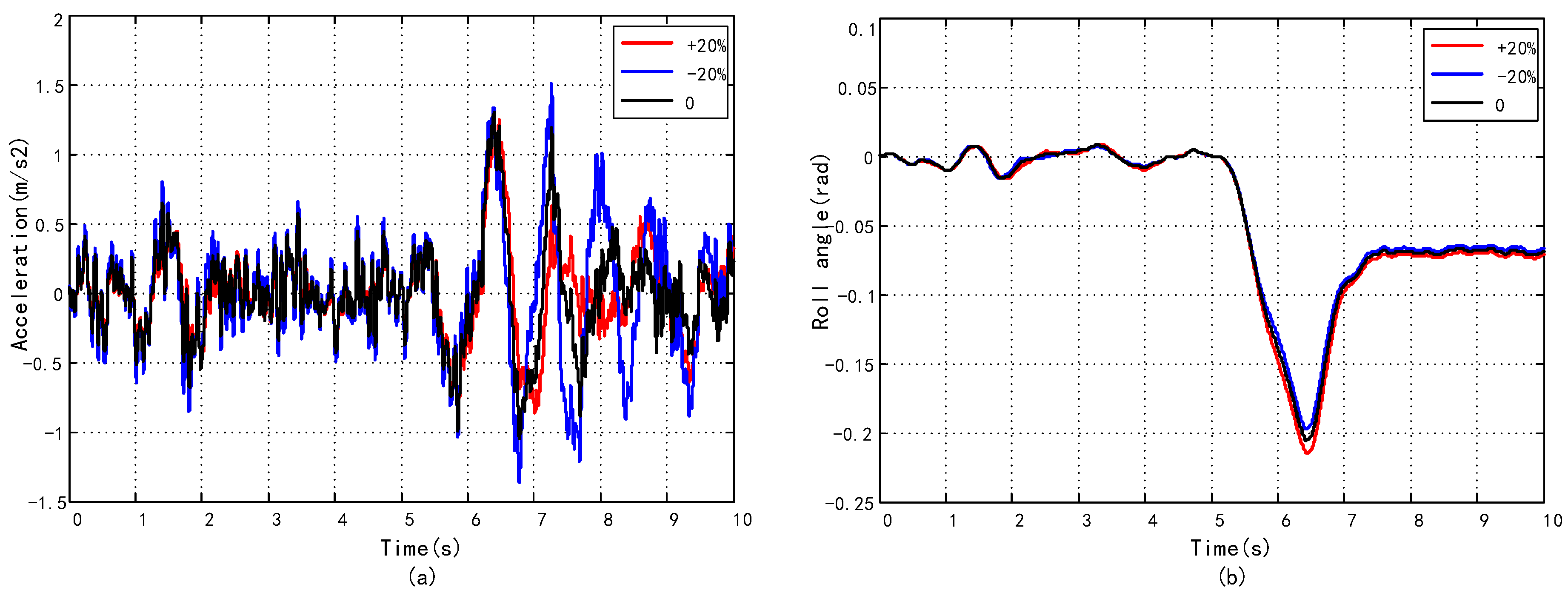
5. Simulations Results and Analysis
5.1. SMC Controller Tuning Results of PACSA
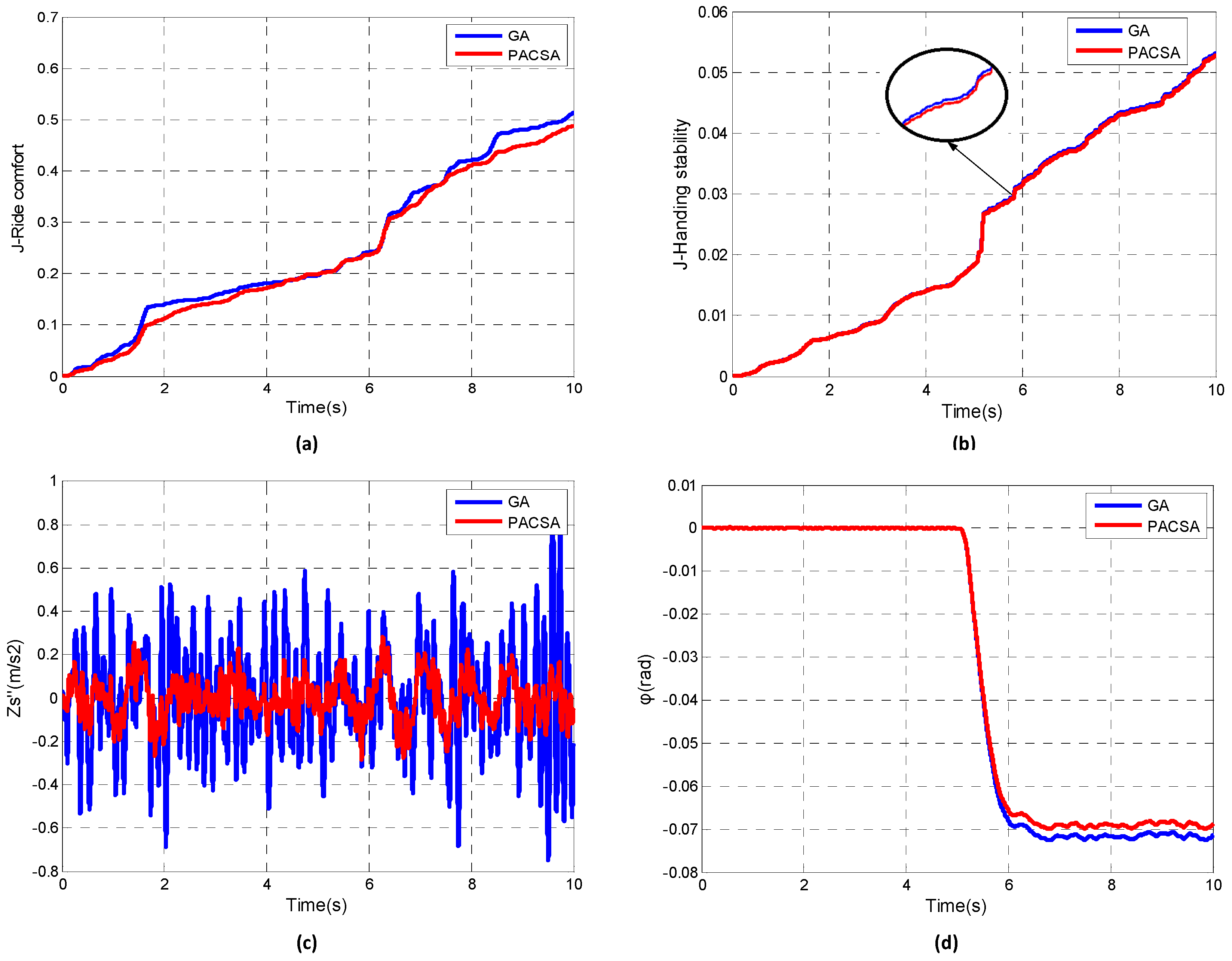
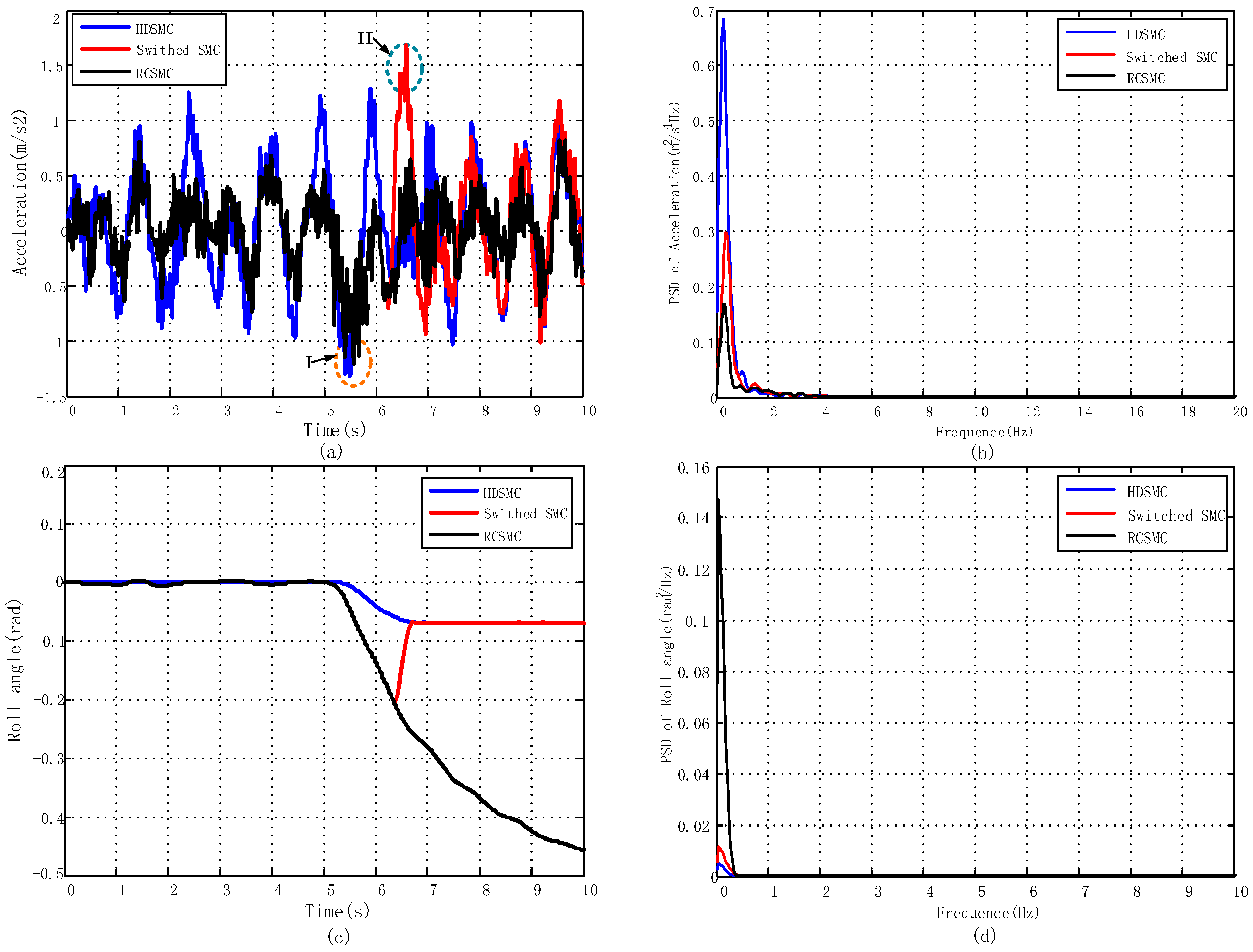
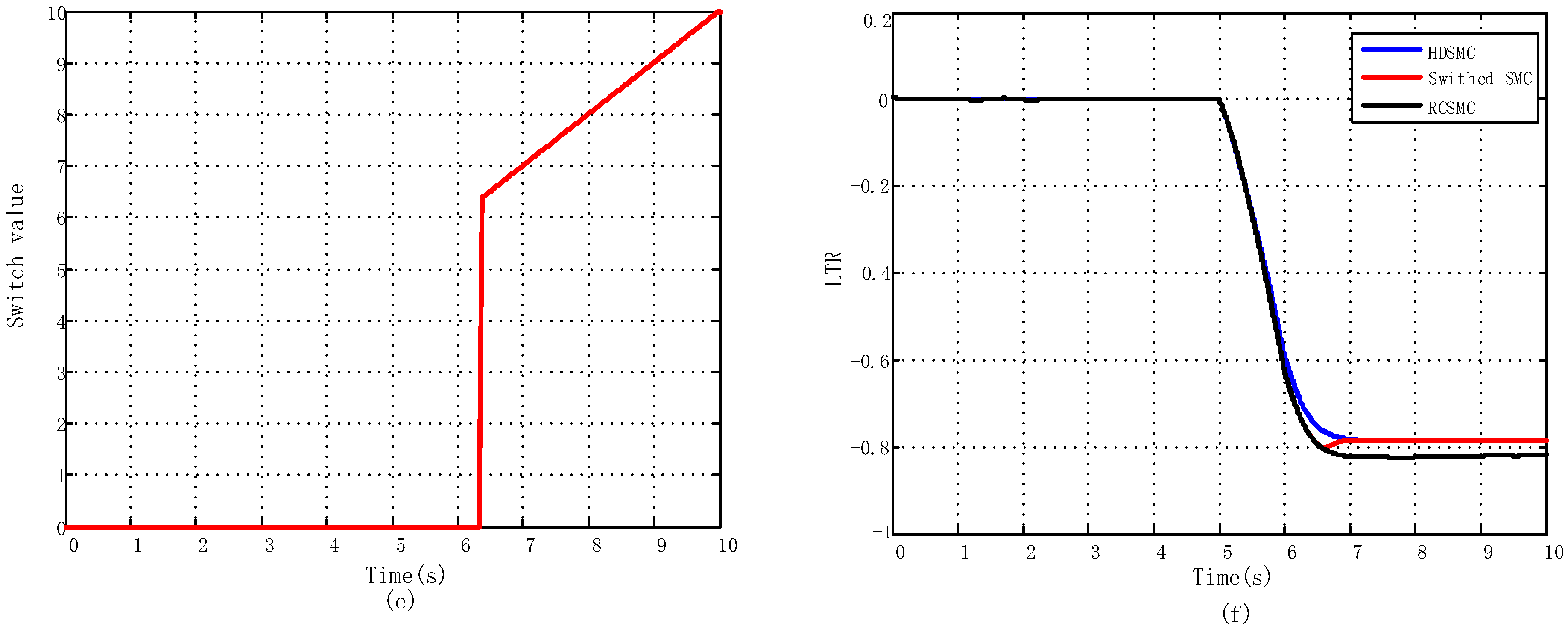
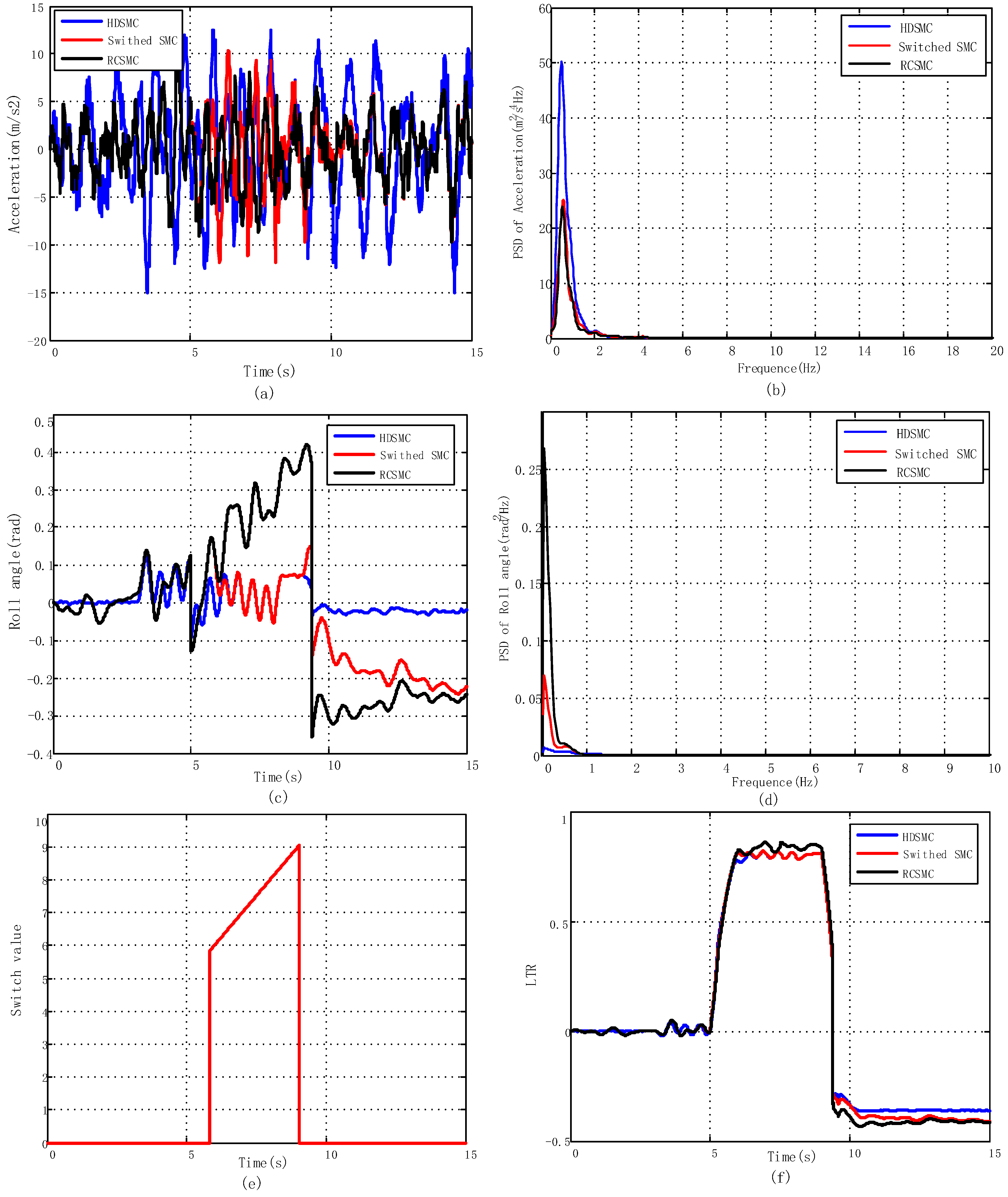
5.2. Results of Switch Control Strategy
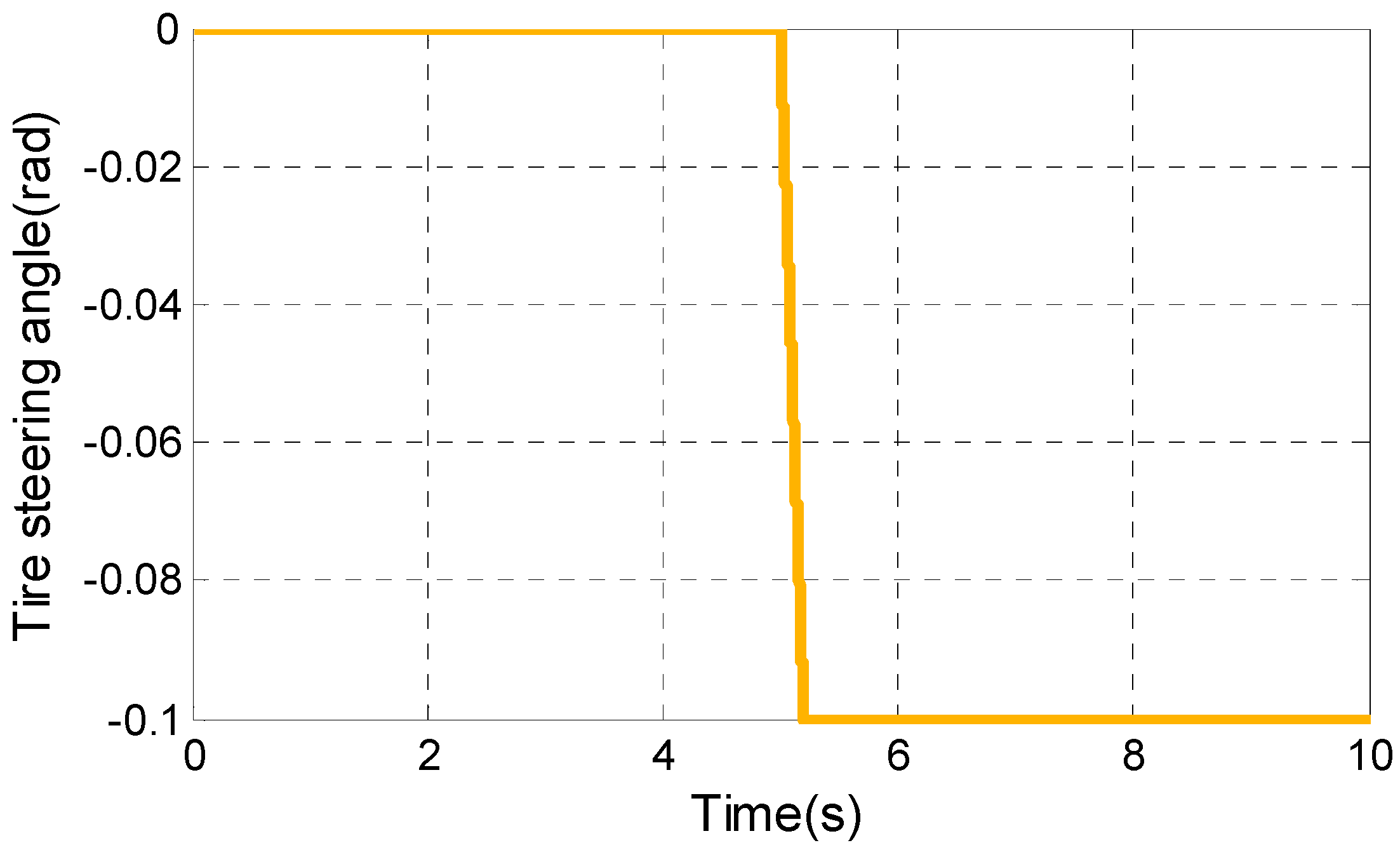
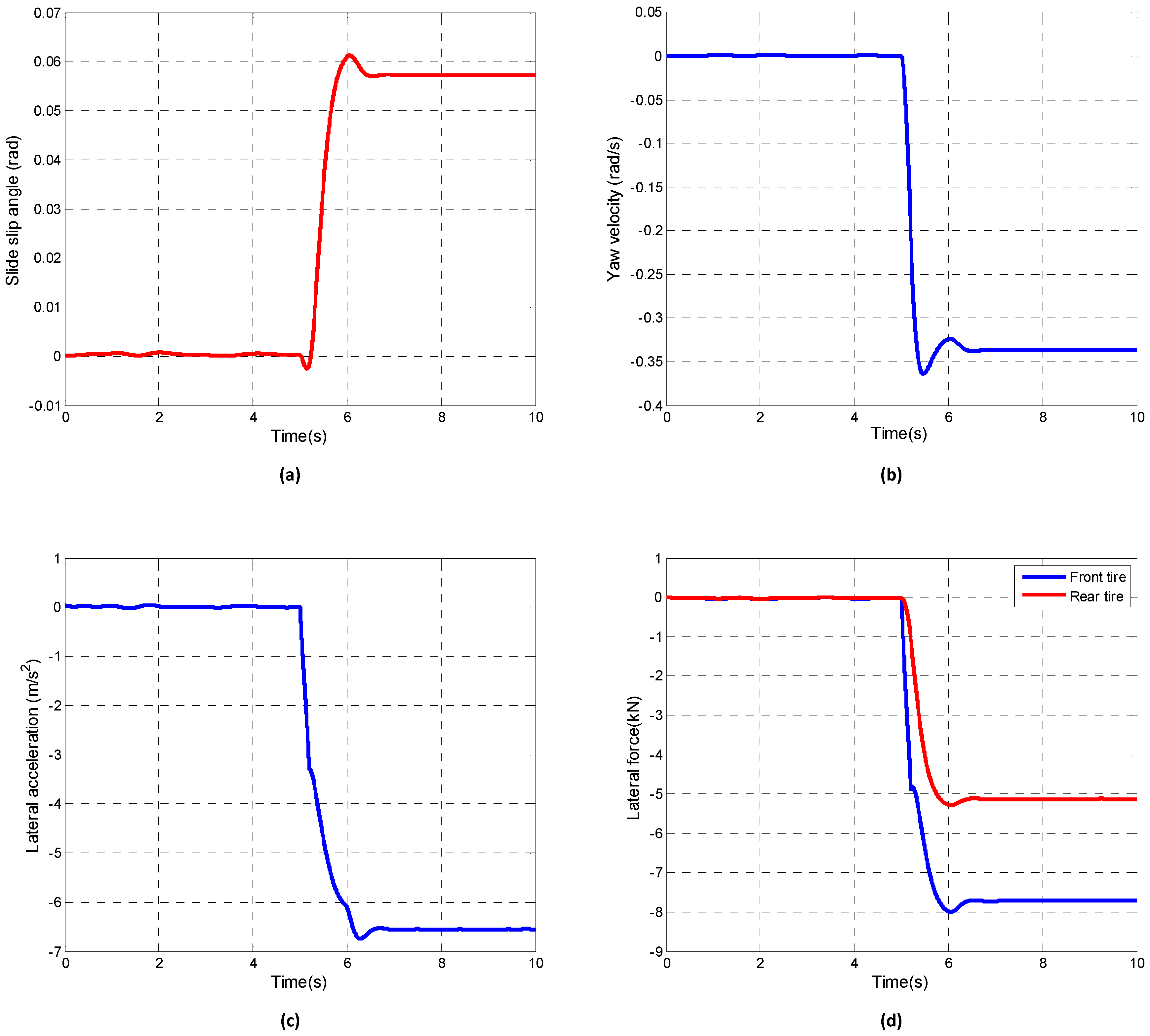
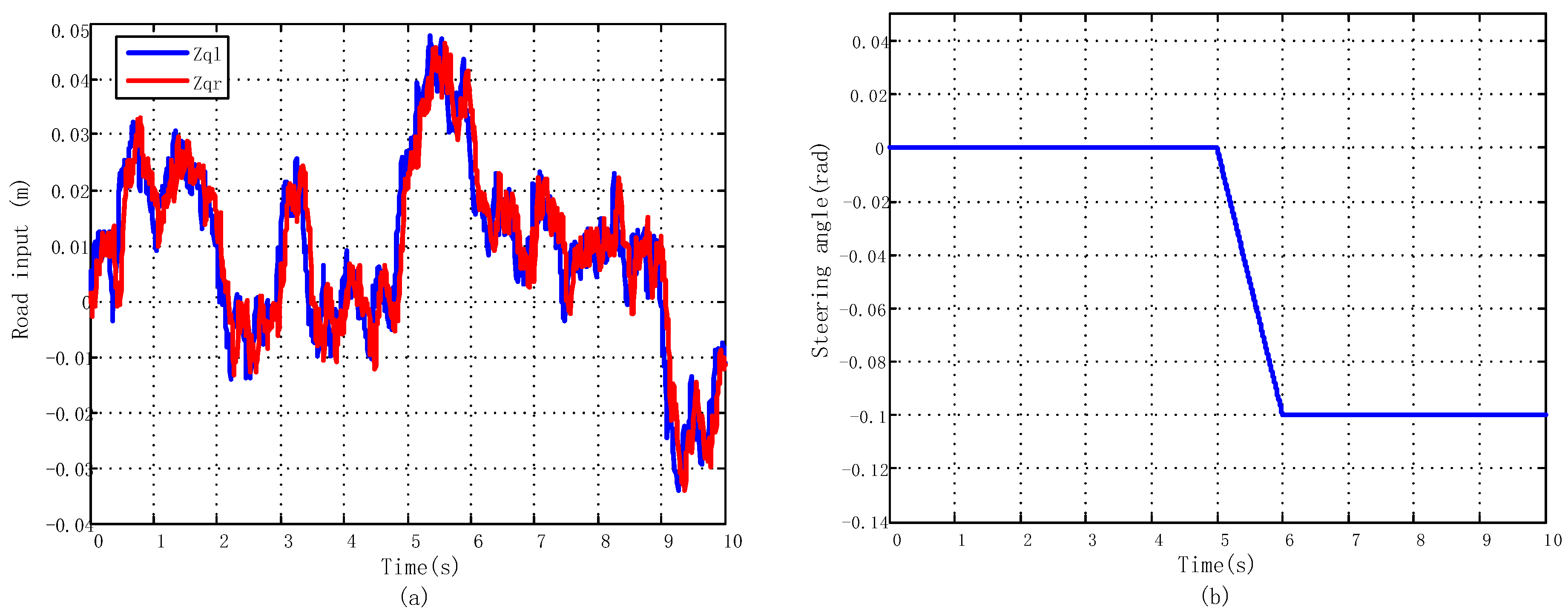
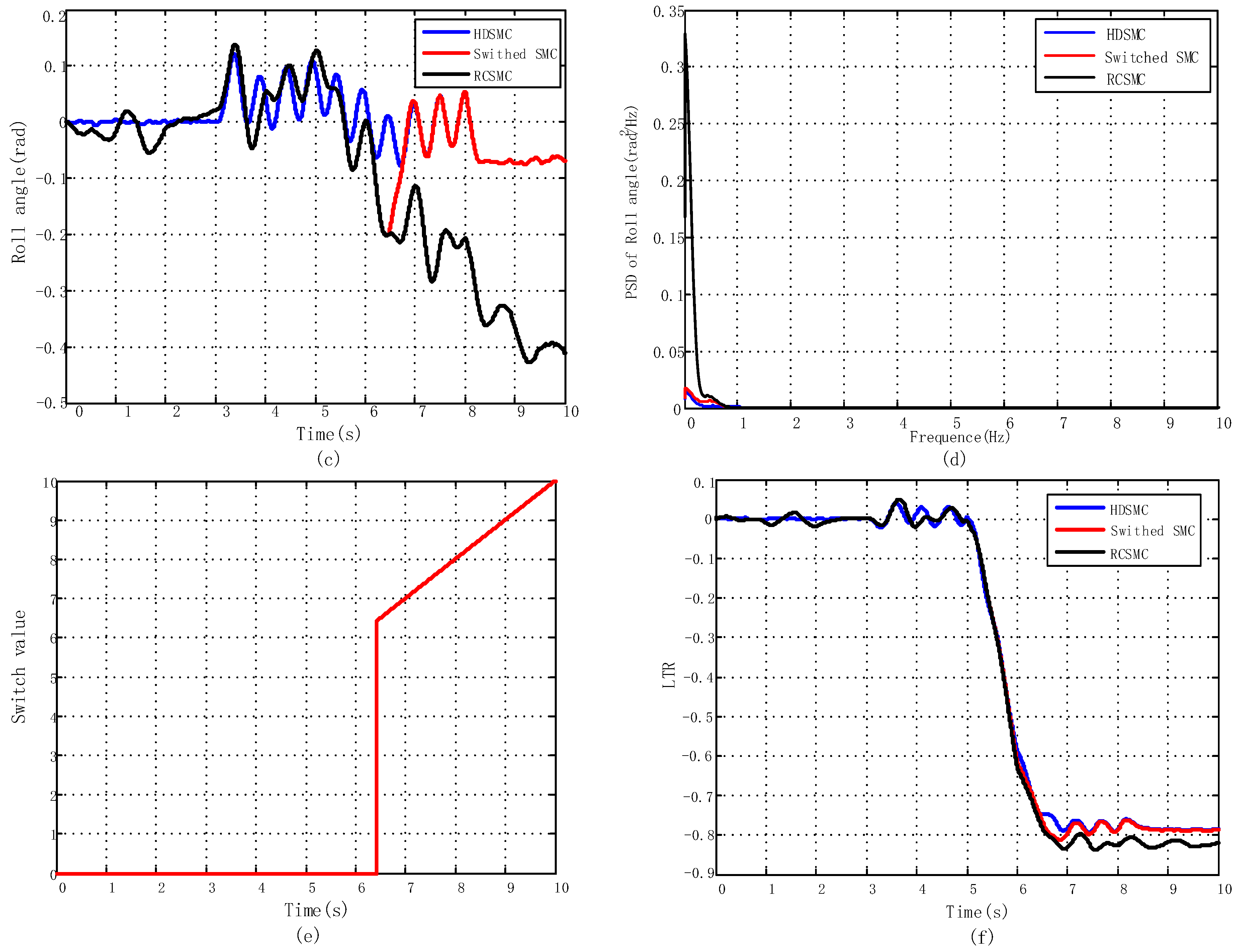
5.2.1. J-Turn Maneuver
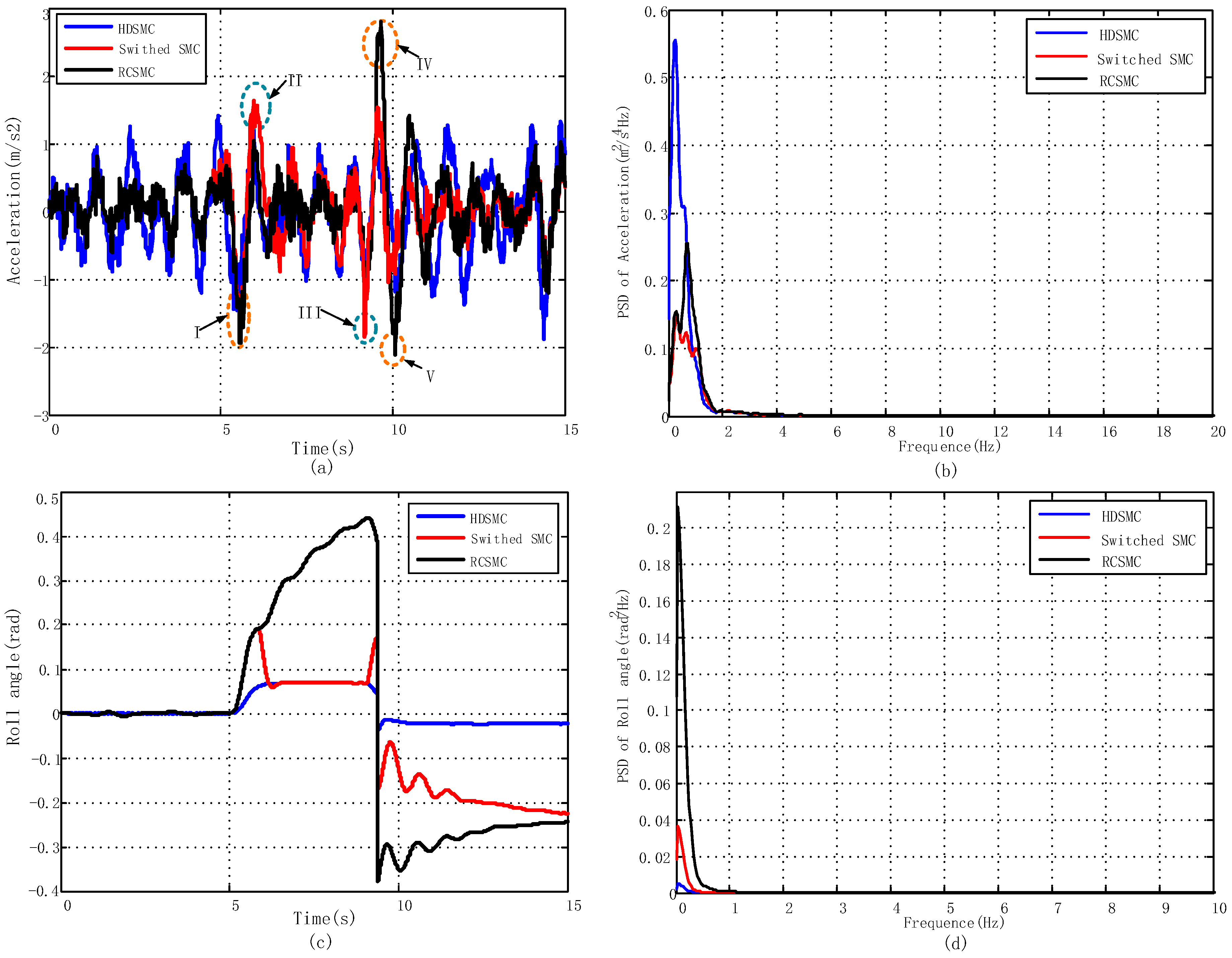
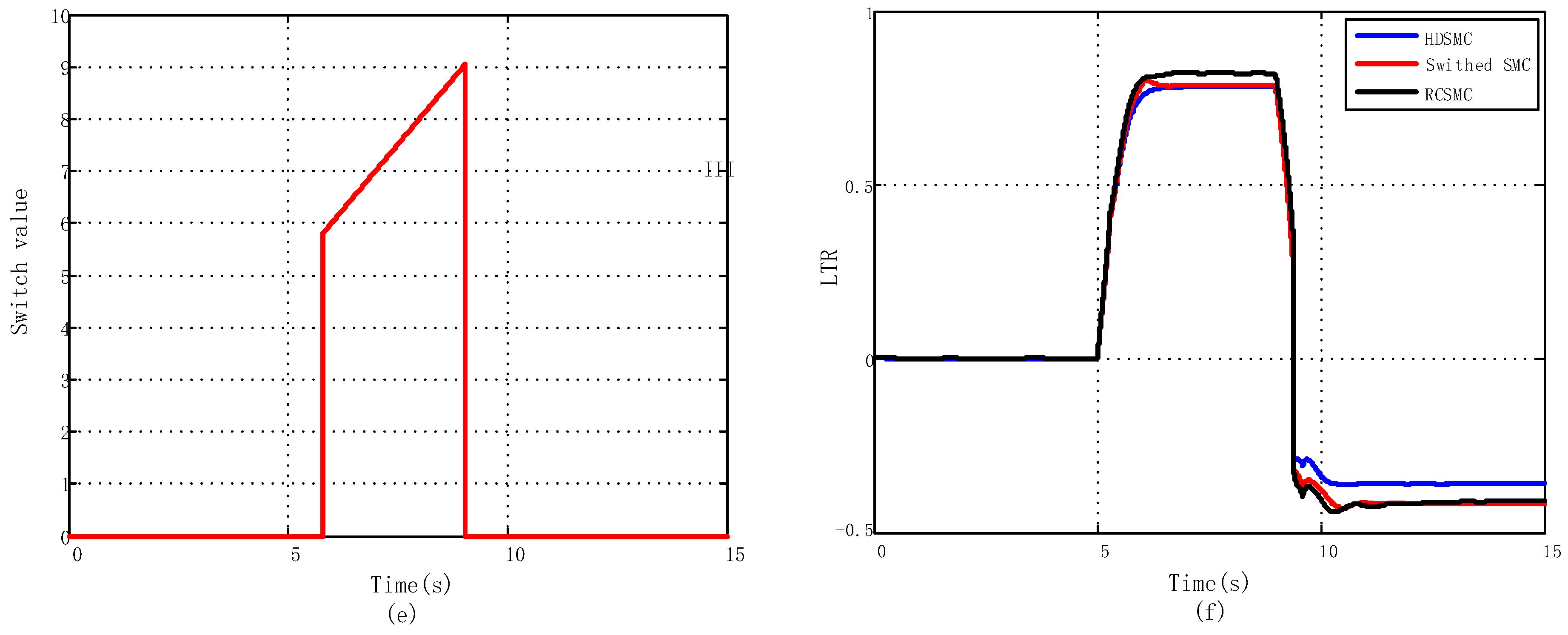
5.2.2. Fishhook Maneuver
6. Conclusions
- (1)
- The PACSA performs better than a genetic algorithm in terms of parameter optimization of the SMC.
- (2)
- The proposed switch control strategy can simultaneously address concerns on both ride comfort and handling stability under different road surfaces and driving conditions through switch actions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hongbin, R.; Lin, Y. Sliding mode control based on improved virtual reference model for damping adjustable hydro-pneumatic suspension systems. J. Vibroeng. 2015, 17, 3196–3210. [Google Scholar]
- Chen, Z.; Liu, X. Optimal Sliding Mode Control for an Active Suspension System Based on a Genetic Algorithm. Algorithms 2018, 11, 205. [Google Scholar]
- Riofrio, A.; Sanz, S.; Boada, M.J.L. A LQR-Based Controller with Estimation of Road Bank for Improving Vehicle Lateral and Rollover Stability via Active Suspension. Sensors 2017, 17, 2318. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, S.; Lu, Z.; Liu, X. Active control of hydro pneumatic suspension parameters of wheel loaders based on road condition identification. Int. J. Adv. Robot. Syst. 2018, 15. [Google Scholar] [CrossRef]
- Awad, M.N.; Sokar, M.I. Hydro-Pneumatic Energy Harvesting Suspension System Using a PSO Based PID Controller. SAE Int. J. Commer. Veh. 2018, 11, 1–11. [Google Scholar] [CrossRef]
- Pradhan, S.; Singh, B. A Composite Sliding Mode Controller for Wind Power Extraction in Remotely Located Solar PV-Wind Hybrid System. IEEE Trans. Ind. Electron. 2019, 66, 5321–5331. [Google Scholar] [CrossRef]
- Biricik, S.; Komurcugil, H. Protection of Sensitive Loads Using Sliding Mode Controlled Three-Phase DVR with Adaptive Notch Filter. IEEE Trans. Ind. Electron. 2019, 66, 5465–5475. [Google Scholar] [CrossRef]
- Farahmandrad, M.; Ganjefar, S. Fuzzy Sliding Mode Controller Design for a Cooperative Robotic System with Uncertainty for Handling an Object. J. Dyn. Syst. Meas. Control Trans. ASME 2019, 141. [Google Scholar] [CrossRef]
- Abtahi, S.M. Suppression of chaotic vibrations in suspension system of vehicle dynamics using chattering-free optimal sliding mode control. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 210. [Google Scholar] [CrossRef]
- Soltanpour, M.R.; Khooban, M.H. A particle swarm optimization approach for fuzzy sliding mode control for tracking the robot manipulator. Nonlinear Dyn. 2013, 74, 467–478. [Google Scholar] [CrossRef]
- Long, Y.; Du, Z.-j. Robust Sliding Mode Control Based on GA Optimization and CMAC Compensation for Lower Limb Exoskeleton. Appl. Bionics Biomech. 2016, 2016, 5017381. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.; Xia, Y.; Sahli, H. CSA-DE/EDA: A Clonal Selection Algorithm Using Differential Evolution and Estimation of Distribution Algorithm. In Proceedings of the Advances in Brain Inspired Cognitive Systems, 9th International Conference, Xi’an, China, 7–8 July 2018. [Google Scholar]
- Hashemipour, M.S.; Soleimani, S.A. Artificial immune system based on adaptive clonal selection for feature selection and parameters optimization of support vector machines. Connect. Sci. 2016, 28, 47–62. [Google Scholar] [CrossRef]
- Liang, H.; Kang, F. Adaptive chaos parallel clonal selection algorithm for objective optimization in WTA application. OPTIK 2016, 127, 3459–3465. [Google Scholar]
- Srinivasa Rao, B.; Vaisakh, K. Multi-objective adaptive Clonal selection algorithm for solving environmental/economic dispatch and OPF problems with load uncertainty. Int. J. Electr. Power Energy Syst. 2013, 53, 390–408. [Google Scholar] [CrossRef]
- Tan, D.; Wang, H. Fully Homomorphic Encryption Based On the Parallel Computing. Ksii Trans. Internet Inf. Syst. 2018, 12, 497–522. [Google Scholar]
- Liang, B.; Zheng, S. The attribute reduction algorithm based on parallel computing. J. Intell. Fuzzy Syst. 2017, 32, 1867–1875. [Google Scholar] [CrossRef]
- Yuan, Z. Research on the Steady-State Model of Tire; Jilin University: Changchun, China, 2006. [Google Scholar]
- Kasprzak, E.M. Extension of the Nondimensional Tire Theory to General Operating Conditions; State University of New York at Buffalo: Buffalo, NY, USA, 2007. [Google Scholar]
- Wei, Y.; Feng, X.; Zhang, F.Q. State of the art for tire dynamical model research. J. Automot. Saf. Energy 2014, 5, 311–323. [Google Scholar]
- Yasheen, B. Large Tyre Testing and Modelling for Handling; University of Pretoria: Pretoria, South Africa, 2015. [Google Scholar]
- Iraj, D.; Ali, A.R. Identification of tire forces using Dual Unscented Kalman Filter algorithm. Nonlinear Dyn. 2014, 78, 1907–1919. [Google Scholar]
- Zhang, L. Analysis and Control of Non-stationary Ride Comfort of Vehicles with Random Excitation; Northeastern University: ShenYang, China, 2012. [Google Scholar]
- Cheng, L.; Wei, L. Neutral network-PID control algorithm for semi-active suspensions with magneto-rheological damper. IEEE Sens. J. 2015, 18, 4432–4444. [Google Scholar]
- Li, H.; Zhao, Y. Design of an improved predictive LTR for rollover warning systems. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 3779–3791. [Google Scholar] [CrossRef]
- Huangfu, Y.; Zhuo, S. Robust Voltage Control of Floating Interleaved Boost Converter for Fuel Cell Systems. IEEE Trans. Ind. Appl. 2018, 54, 665–674. [Google Scholar] [CrossRef]
- Nagarkar, M.P.; Patil, G.; Vikhe, J. Optimization of nonlinear quarter car suspension-seat-driver model. J. Adv. Res. 2016, 7, 991–1007. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, J. Simulation of Sliding Mode Control Based on MATLAB; Tsinghua University press: Beijing, China, 2015; pp. 4–25. [Google Scholar]
- Susatio, Y.; Oktaviana, L. Design of half-car active suspension system for passenger riding comfort. J. Phys. Conf. Ser. 2018, 1075, 012030. [Google Scholar] [CrossRef]
- Faried, H.; Waleed, F.F. Ride comfort performance of a vehicle using active suspension system with active disturbance rejection control. Int. J. Veh. Noise Vib. 2015, 11, 78–101. [Google Scholar]
- Zhang, L.; Li, L. Rollover prevention control for a four in-wheel motors drive electric vehicle on an uneven road. Sci. China Technol. Sci. 2018, 61, 934–948. [Google Scholar] [CrossRef]
- Liao, C.; Wu, X. Semi-active Suspension Anti Rollover Control for Bus Using Fuzzy Sliding Mode Theory. J. Xiamen Univ. 2014, 3, 373–377. [Google Scholar]
- Dnyandeo, D.S.; Ramjee, P. Application of AHP for Ranking of Total Productive Maintenance Pillars. Wirel. Pers. Commun. 2018, 100, 449–462. [Google Scholar]
- De Castro, L.N.; Von Zuben, F.J. Learning and optimization using the clonal selection principle. Ieee Trans. Evol. Comput. 2002, 6, 239–251. [Google Scholar] [CrossRef]


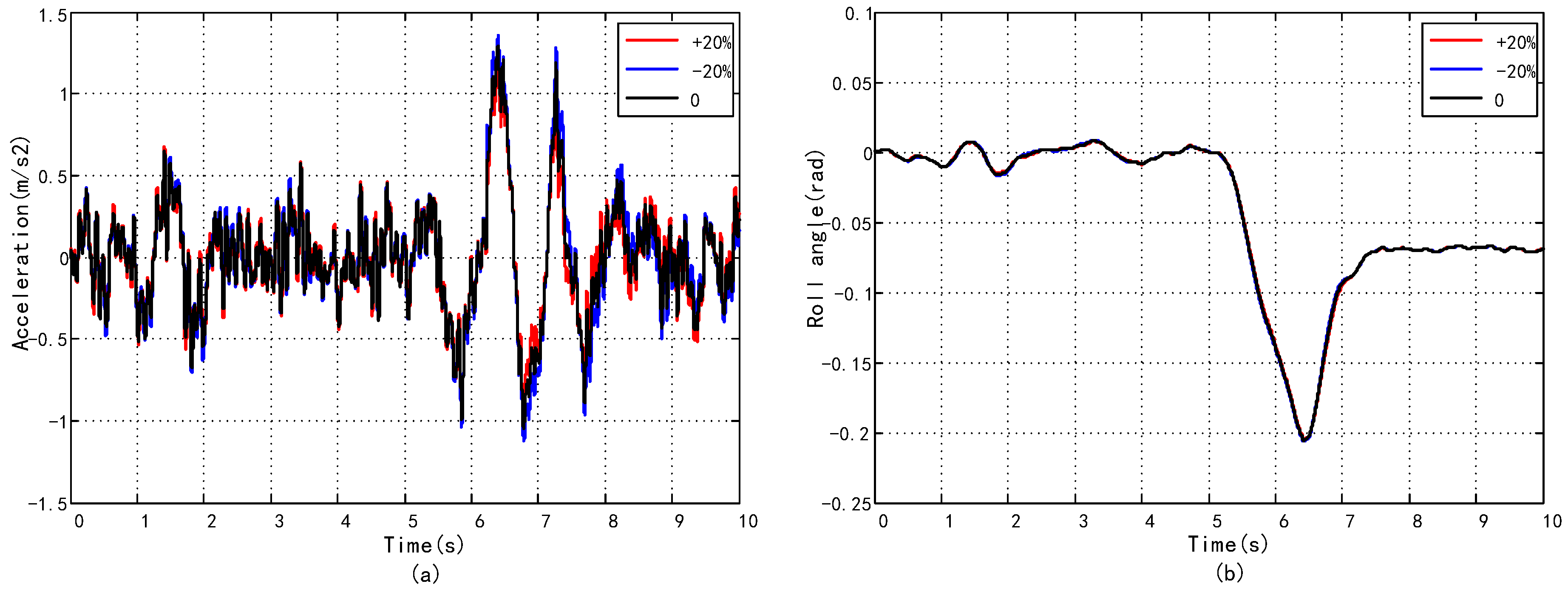
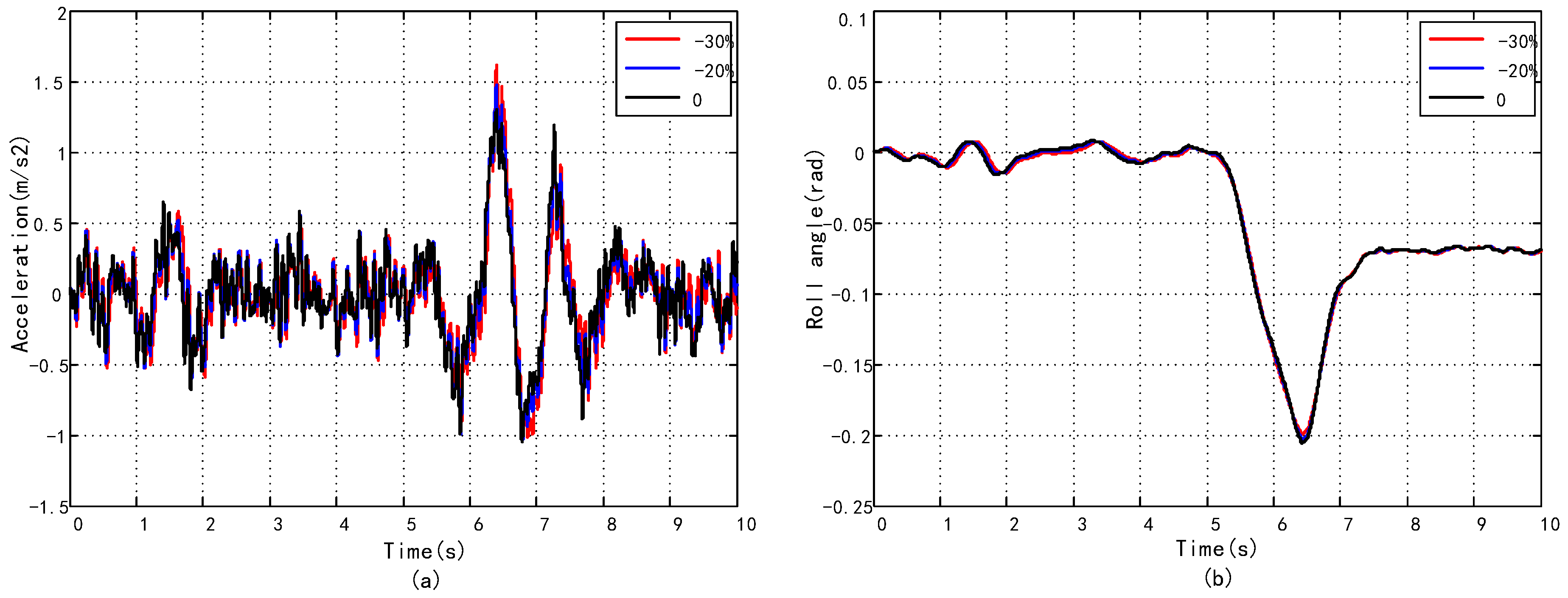
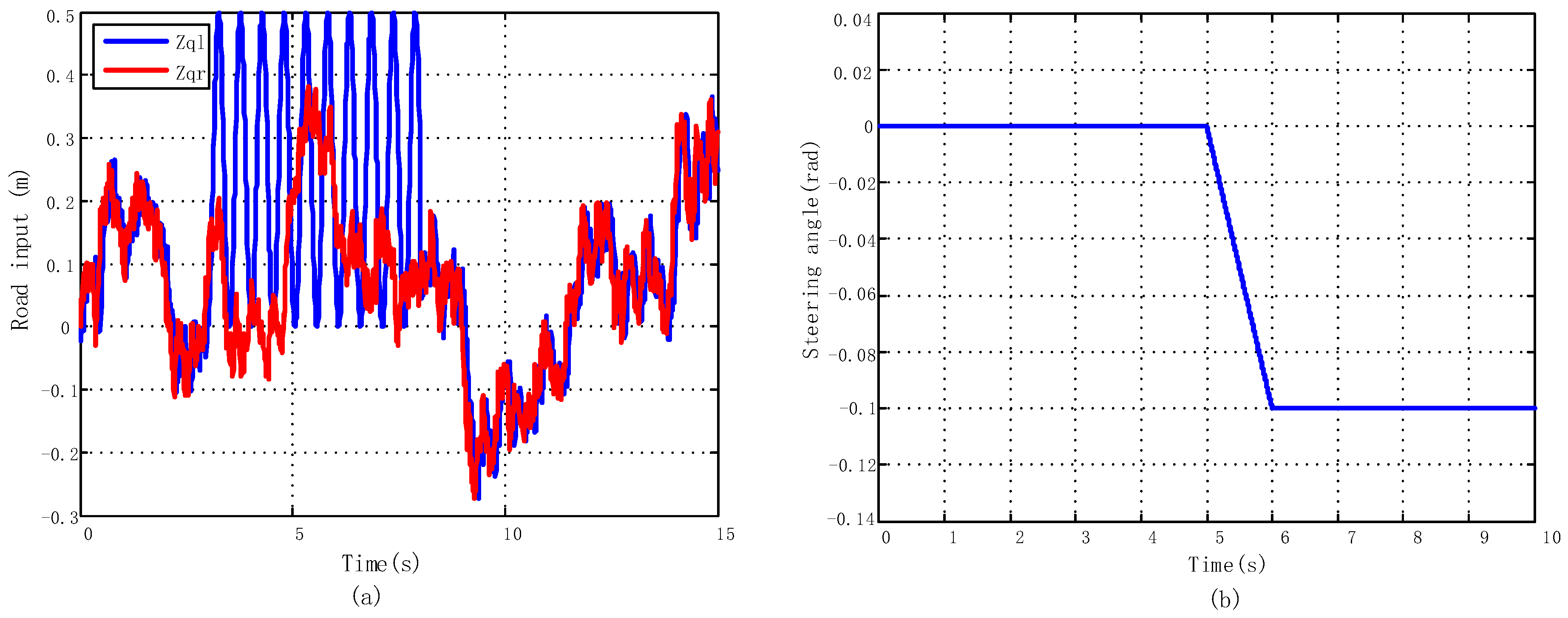
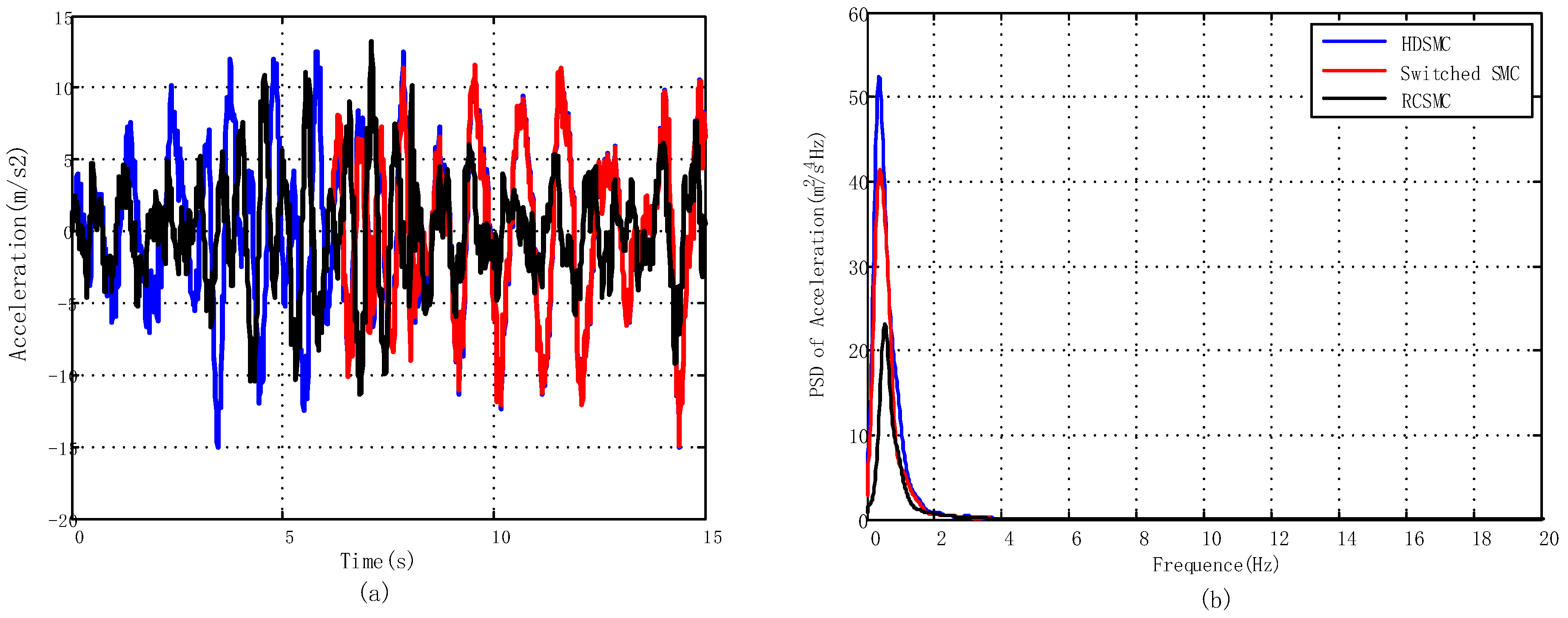
| Parameters | Symbol | Value | Unit |
|---|---|---|---|
| Spring mass | 1525 | ||
| Unspring mass | 50 | ||
| Tread | 1.56 | ||
| Suspension spring fitting stiffness | 35,000 | ||
| Suspension spring fitting damping | 980 | ||
| Tire vertical elastic stiffness | 190,000 | ||
| Yaw moment of inertia | 2500 | ||
| Roll moment of inertia | 460 | ||
| Distance from the center of gravity to the center of the roll | 0.45 | ||
| Distance from the center of gravity to the ground | 0.5 | ||
| Distance between the center of gravity and the front axle | 1.27 | ||
| Distance between the center of gravity and the rear axle | 1.94 |
| RMS | 0.92 | 1.18 | 0.032 | 0.0008 | 0.00214 | 0.0096 |
| Quantized ScaleFactor | 1 | 0.6 | 826.56 | 13,225 | 184,819.64 | 9184.03 |
| r | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| RI | 0 | 0 | 0.58 | 0.9 | 1.12 | 1.24 | 1.32 | 1.41 |
| Weight Coefficients | ||||||
| Handling Stability Control | 0.053 | 0.8623 | 0.2362 | 0.1764 | 2.142 | 1.661 |
| Ride Comfort Control | 0.48 | 0.06 | 131.3 | 210000 | 9777 | 485.8 |
| RCSMC | HDSMC | ||||
|---|---|---|---|---|---|
| PACSA | GA | PACSA | GA | ||
| −0.575 | −2.55 | 5 | 4.73 | ||
| 0.6559 | 9.7 | 3 | 2.99 | ||
| 0 | −0.063 | 25 | 24.92 | ||
| 11 | 14.939 | 0.0012 | 0.73 | ||
| 0.0005 | 0.15 | 0.0014 | 0.0025 | ||
| 0.444 | 0.39 | ||||
| J-turn/Fishhook | ||
|---|---|---|
| Road Condition | Random Road | Bump Road |
| Vehicle speed | 70 km/h | 60 km/h |
| Road level (ISO/DIS8608) | C | F |
| Steering angle | / | / |
| 0.1 | 0.1 | |
| 0.1 | 0.1 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, C.; Liu, X.; Xu, F.; Chen, W. Sliding Mode Switch Control of Adjustable Hydro-Pneumatic Suspension based on Parallel Adaptive Clonal Selection Algorithm. Appl. Sci. 2020, 10, 1852. https://doi.org/10.3390/app10051852
Zhou C, Liu X, Xu F, Chen W. Sliding Mode Switch Control of Adjustable Hydro-Pneumatic Suspension based on Parallel Adaptive Clonal Selection Algorithm. Applied Sciences. 2020; 10(5):1852. https://doi.org/10.3390/app10051852
Chicago/Turabian StyleZhou, Chen, Xinhui Liu, Feixiang Xu, and Wei Chen. 2020. "Sliding Mode Switch Control of Adjustable Hydro-Pneumatic Suspension based on Parallel Adaptive Clonal Selection Algorithm" Applied Sciences 10, no. 5: 1852. https://doi.org/10.3390/app10051852
APA StyleZhou, C., Liu, X., Xu, F., & Chen, W. (2020). Sliding Mode Switch Control of Adjustable Hydro-Pneumatic Suspension based on Parallel Adaptive Clonal Selection Algorithm. Applied Sciences, 10(5), 1852. https://doi.org/10.3390/app10051852





