Volt-Var Curve Reactive Power Control Requirements and Risks for Feeders with Distributed Roof-Top Photovoltaic Systems
Abstract
:1. Introduction
- Define feeder’s voltage response at different load and PV generation amounts to review each control approaches impact.
- Assess sample voltage profiles from the substation to a PV system, which highlights the difference in voltage on the primary and secondary lines under different operating conditions (i.e., no PV systems, with PV systems, and PV systems with the VVC turned on).
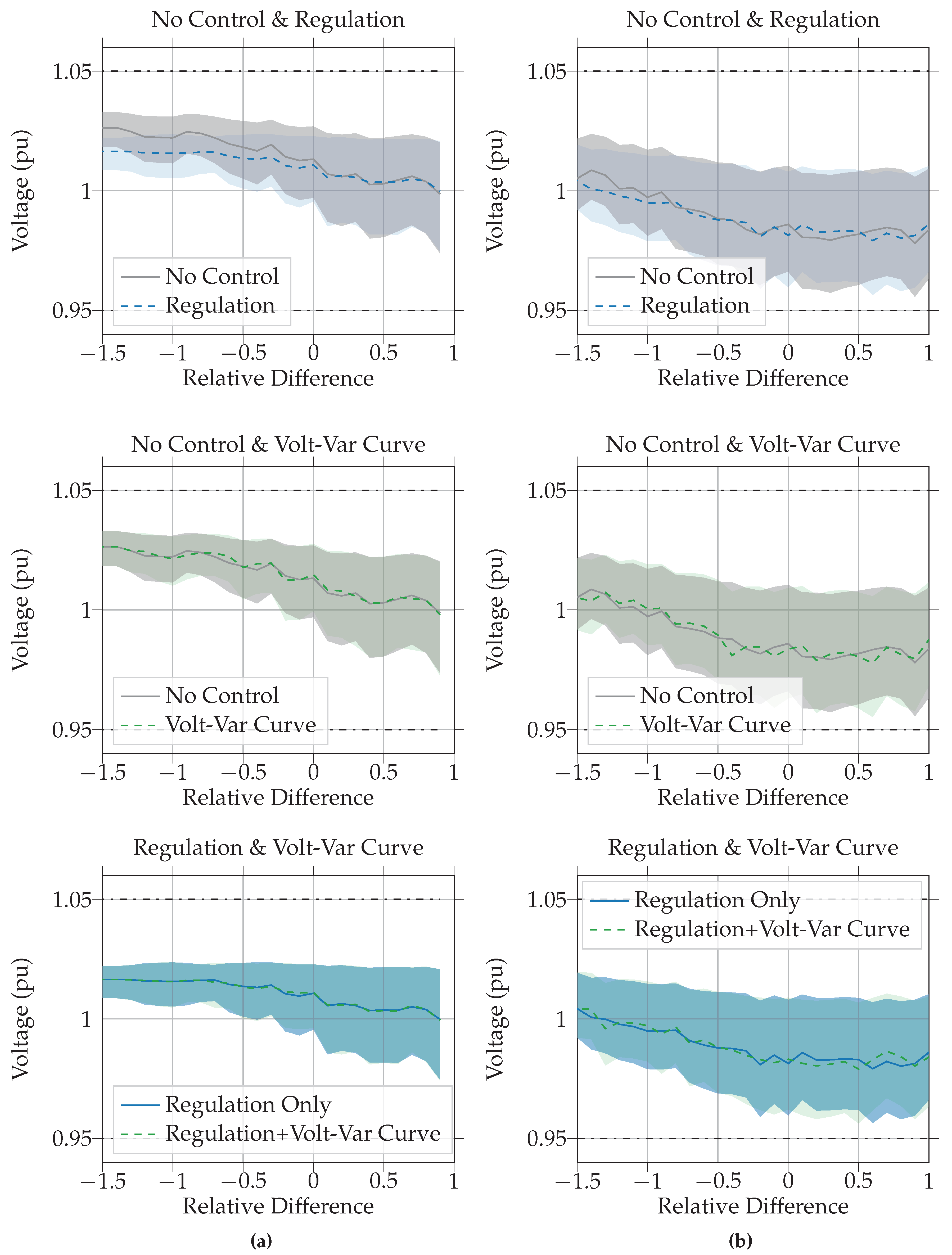
- Perform a statistical evaluation, using boxplots, of the feeder voltages when subjected to potential daily operations using different voltage management methods.
- Compare the distributed, roof-top PV integration strategy with a different strategy (i.e., large scale systems installed at a single point) to review the potential differences.
2. Methodology
2.1. Voltage Controls
2.1.1. Voltage Control Strategies
- No Control—Simulations with the LTCs, SCBs, and PV inverter VVC functions disabled.
- Regulators Only—Simulations that had none of the PV inverters VVCs providing reactive power support, but the LTCs and SCB could operate and potentially alter the feeder’s voltage.
- PV Inverter VVC Only—Simulations where each of the PV inverters absorbed or injected reactive power and none of the LTCs or SCB provided support.
- Regulators plus PV Inverter VVC—Simulations that enabled all of the control functions (LTCs, SCBs, and PV inverter VVCs).
2.1.2. Volt-Var Curve Control Parameter Settings
2.2. PV Integration Strategy
2.3. Grid Simulations
2.3.1. Feeder Model
2.3.2. Stochastic Hosting Capacity
3. Results
3.1. Photovoltaic Integration Impact and Control Need
3.1.1. Stochastic Hosting Capacity
3.1.2. Voltage Profile Example
3.1.3. Statistical Assessment for Realistic Operations
3.2. Cyber-Attack Consequences
4. Discussion
5. Conclusions
- The maximum voltage on the two feeders rose only slightly as the relative difference decreased.
- VVC control did not play a role in managing the voltage for the two feeders.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Available online: https://webstore.ansi.org/standards/nema/ansic842016 (accessed on 18 August 2020).
- Padullaparti, H.V.; Nguyen, Q.; Santoso, S. Advances in volt-var control approaches in utility distribution systems. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Basso, T.; Chakraborty, S.; Hoke, A.; Coddington, M. IEEE 1547 Standards advancing grid modernization. In Proceedings of the 2015 IEEE 42nd Photovoltaic Specialist Conference (PVSC), New Orleans, LA, USA, 14–19 June 2015; pp. 1–5. [Google Scholar] [CrossRef]
- 1547-2018-IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces; IEEE: Piscataway, NJ, USA, 2018.
- Smith, J.W.; Sunderman, W.; Dugan, R.; Seal, B. Smart inverter volt/var control functions for high penetration of PV on distribution systems. In Proceedings of the 2011 IEEE/PES Power Systems Conference and Exposition, Phoenix, AZ, USA, 20–23 March 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Tang, N.C.; Chang, G.W. A stochastic approach for determining PV hosting capacity of a distribution feeder considering voltage quality constraints. In Proceedings of the 2018 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13–16 May 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Rossi, M.; Viganò, G.; Moneta, D.; Clerici, D. Stochastic evaluation of distribution network hosting capacity: Evaluation of the benefits introduced by smart grid technology. In Proceedings of the 2017 AEIT International Annual Conference, Cagliari, Italy, 20–22 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Vukojevic, A.; Frey, P.; Smith, M.; Picarelli, J. Integrated volt/var control using single-phase capacitor bank switching. In Proceedings of the 2013 IEEE PES Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 24–27 February 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Juamperez, M.; Yang, G.; Kjær, S.B. Voltage regulation in LV grids by coordinated volt-var control strategies. J. Mod. Power Syst. Clean Energy 2014, 2, 319–328. [Google Scholar] [CrossRef] [Green Version]
- O’Connell, A.; Keane, A. Volt–var curves for photovoltaic inverters in distribution systems. IET Gener. Transm. Distrib. 2017, 11, 730–739. [Google Scholar] [CrossRef]
- Johnson, J. PV Cybersecurity Final Report; Technical Report SAND2019-0494R; Sandia National Laboratories: Albuquerque, NM, USA, 2019.
- Carter, C.; Onunkwo, I.; Cordeiro, P.; Johnson, J. Cyber Security Assessment of Distributed Energy Resources. In Proceedings of the 2017 IEEE 44th Photovoltaic Specialist Conference (PVSC), Washington, DC, USA, 25–30 June 2017; pp. 2135–2140. [Google Scholar] [CrossRef]
- Chavez, A.; Lai, C.; Jacobs, N.; Hossain-McKenzie, S.; Jones, C.B.; Johnson, J.; Summers, A. Hybrid Intrusion Detection System Design for Distributed Energy Resource Systems. In Proceedings of the 2019 IEEE CyberPELS (CyberPELS), Knoxville, TN, USA, 29 April–1 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Johnson, J.; Quiroz, J.; Concepcion, R.; Wilches-Bernal, F.; Reno, M.J. Power system effects and mitigation recommendations for DER cyberattacks. IET Cyber Phys. Syst. Theory Appl. 2019, 4, 240–249. [Google Scholar] [CrossRef]
- Dubey, A.; Santoso, S.; Maitra, A. Understanding photovoltaic hosting capacity of distribution circuits. In Proceedings of the 2015 IEEE Power Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Coogan, K.; Reno, M.J.; Grijalva, S.; Broderick, R.J. Locational dependence of PV hosting capacity correlated with feeder load. In Proceedings of the 2014 IEEE PES T D Conference and Exposition, Chicago, IL, USA, 14–17 April 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Stanfield, S.; Stephanie, S. Optimizing the Grid: Regulator’s Guide to Hosting Capacity Analyses for Distributed Energy Resources; Technical Report; Interstate Renewable Energy Council: Latham, NY, USA, 2017. [Google Scholar]
- Reno, M.J.; Coogan, K.; Seuss, J.; Broderick, R.J. Novel Methods to Determine Feeder Locational PV Hosting Capacity and PV Impact Signatures; Technical Report SAND2017-4954; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2017. [Google Scholar] [CrossRef]
- Seuss, J.; Reno, M.J.; Broderick, R.J.; Grijalva, S. Improving distribution network PV hosting capacity via smart inverter reactive power support. In Proceedings of the 2015 IEEE Power Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Smith, J.W.; Dugan, R.; Rylander, M.; Key, T. Advanced distribution planning tools for high penetration PV deployment. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–7. [Google Scholar] [CrossRef]
- Rylander, M.; Smith, J.; Lewis, D.; Steffel, S. Voltage impacts from distributed photovoltaics on two distribution feeders. In Proceedings of the 2013 IEEE Power Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Smith, J. Stochastic Analysis to Determine Feeder Hosting Capacity for Distributed Solar PV; Technical Report 1026640; Electric Power Research Institute: Palo Alto, CA, USA, 2012. [Google Scholar]
- Rylander, M.; Smith, J.; Sunderman, W. Streamlined Method for Determining Distribution System Hosting Capacity. IEEE Trans. Ind. Appl. 2016, 52, 105–111. [Google Scholar] [CrossRef]
- Rylander, M.; Smith, J.; Sunderman, W.; Smith, D.; Glass, J. Application of new method for distribution-wide assessment of Distributed Energy Resources. In Proceedings of the 2016 IEEE/PES Transmission and Distribution Conference and Exposition (T D), Dallas, TX, USA, 3–5 May 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Ismael, S.M.; Abdel Aleem, S.H.E.; Abdelaziz, A.Y.; Zobaa, A.F. State-of-the-art of hosting capacity in modern power systems with distributed generation. Renew. Energy 2019, 130, 1002–1020. [Google Scholar] [CrossRef]
- Rylander, M.; Smith, J.; Rogers, L. Impact Factors, Methods, and Considerations for Calculating and Applying Hosting Capacity; Technical Report 3002011009; Electric Power Research Institute: Palo Alto, CA, USA, 2018. [Google Scholar]
- Commercial and Residential Hourly Load Profiles for All TMY3 Locations in the United States-OpenEI DOE Open Data. Library Catalog: openei.org. Available online: https://openei.org/doe-opendata/dataset/commercial-and-residential-hourly-load-profiles-for-all-tmy3-locations-in-the-united-states (accessed on 30 April 2020).
- Dobos, A.P. PVWatts Version 5 Manual; Technical Report NREL/TP-6A20-62641; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2014. [CrossRef] [Green Version]
- Holmgren, W.; Hansen, C.; Mikofski, M. pvlib python: A python package for modeling solar energy systems. J. Open Source Softw. 2018, 3, 884. [Google Scholar] [CrossRef] [Green Version]
- Quiroz, J.E.; Reno, M.J.; Lavrova, O.; Byrne, R.H. Communication requirements for hierarchical control of volt-VAr function for steady-state voltage. In Proceedings of the 2017 IEEE Power Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 23–26 April 2017; pp. 1–5. [Google Scholar] [CrossRef]









| Feeder | Voltage Rating (kV) | Length (km) | Max. Load Demand (MW) | Number of Loads | Voltage Regulation Device |
|---|---|---|---|---|---|
| EPRI K1 | 12 | 7 | 4.8 | 321 | Capcitor |
| Unnamed | 12 | 4.6 | 7.9 | 39 | Load Tap Changer, Capacitor |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jones, C.B.; Lave, M.; Reno, M.J.; Darbali-Zamora, R.; Summers, A.; Hossain-McKenzie, S. Volt-Var Curve Reactive Power Control Requirements and Risks for Feeders with Distributed Roof-Top Photovoltaic Systems. Energies 2020, 13, 4303. https://doi.org/10.3390/en13174303
Jones CB, Lave M, Reno MJ, Darbali-Zamora R, Summers A, Hossain-McKenzie S. Volt-Var Curve Reactive Power Control Requirements and Risks for Feeders with Distributed Roof-Top Photovoltaic Systems. Energies. 2020; 13(17):4303. https://doi.org/10.3390/en13174303
Chicago/Turabian StyleJones, C. Birk, Matthew Lave, Matthew J. Reno, Rachid Darbali-Zamora, Adam Summers, and Shamina Hossain-McKenzie. 2020. "Volt-Var Curve Reactive Power Control Requirements and Risks for Feeders with Distributed Roof-Top Photovoltaic Systems" Energies 13, no. 17: 4303. https://doi.org/10.3390/en13174303
APA StyleJones, C. B., Lave, M., Reno, M. J., Darbali-Zamora, R., Summers, A., & Hossain-McKenzie, S. (2020). Volt-Var Curve Reactive Power Control Requirements and Risks for Feeders with Distributed Roof-Top Photovoltaic Systems. Energies, 13(17), 4303. https://doi.org/10.3390/en13174303






