Active Reinforcing Fiber of Cementitious Materials Using Crimped NiTi SMA Fiber for Crack-Bridging and Pullout Resistance
Abstract
:1. Introduction
2. Characteristics of Crimped SMA Fibers
2.1. Properties of NiTi SMA Fibers
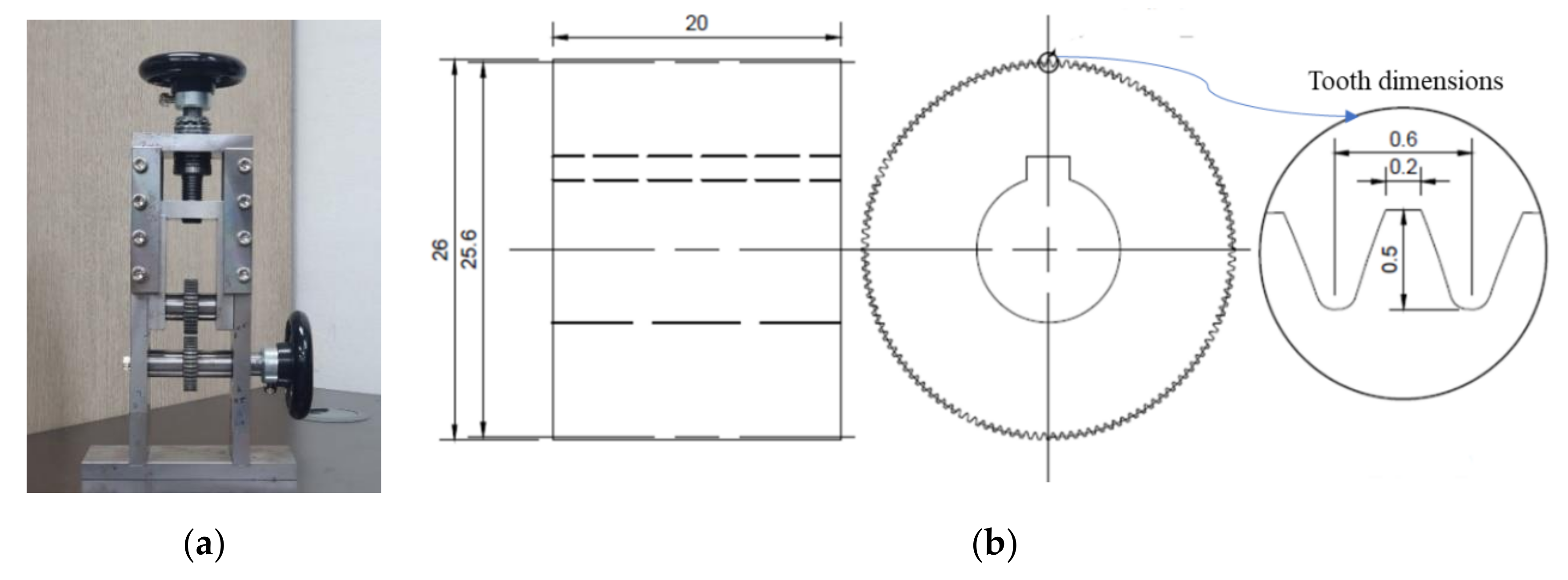
2.2. Production of Crimped Fibers
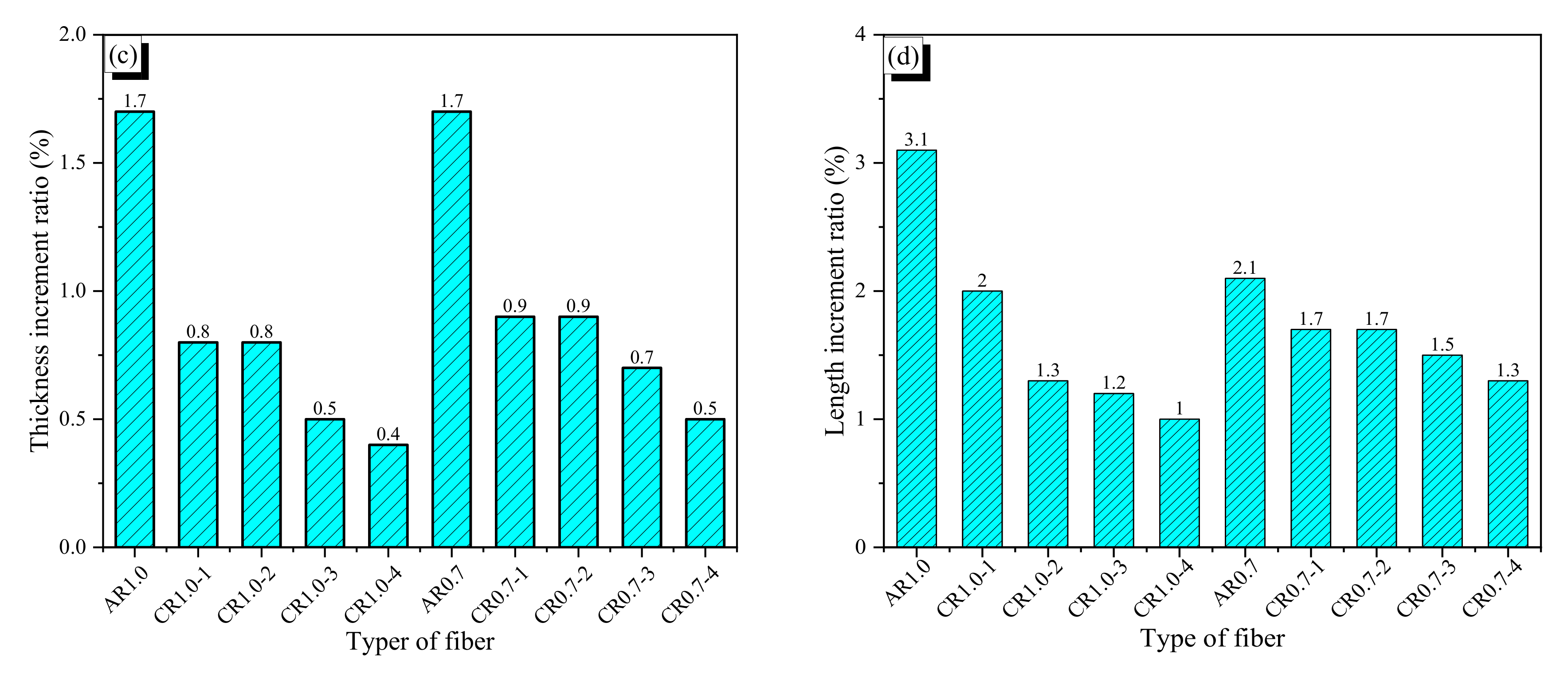
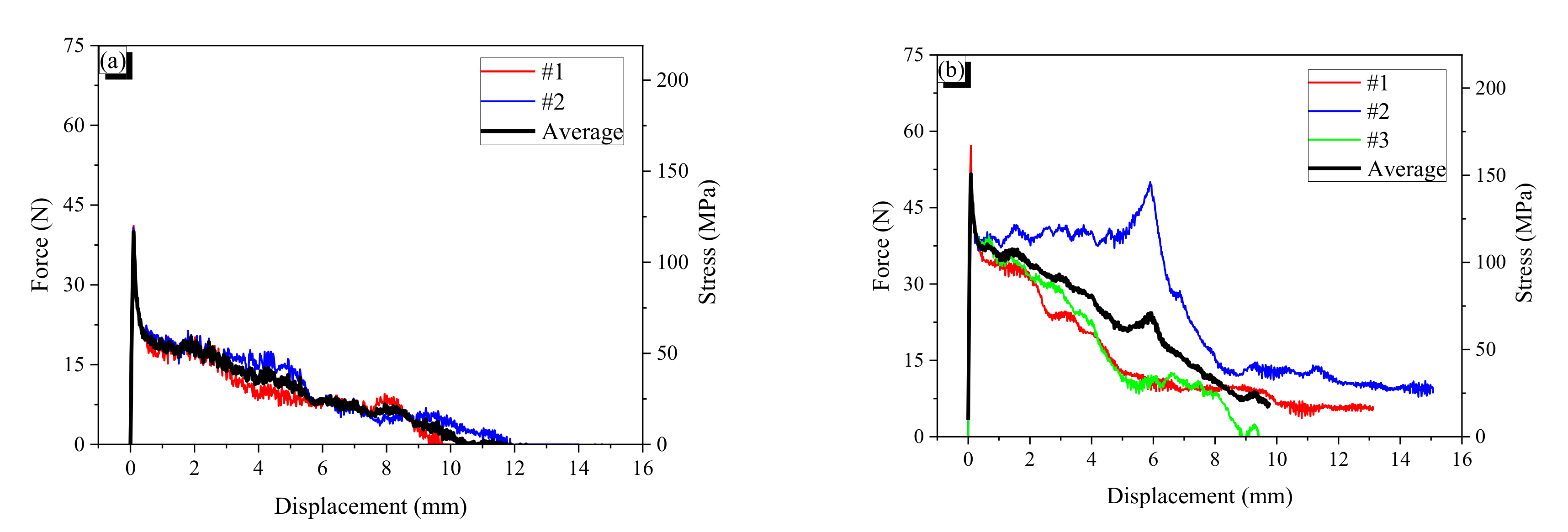
2.3. Tensile Behavior of the Fibers
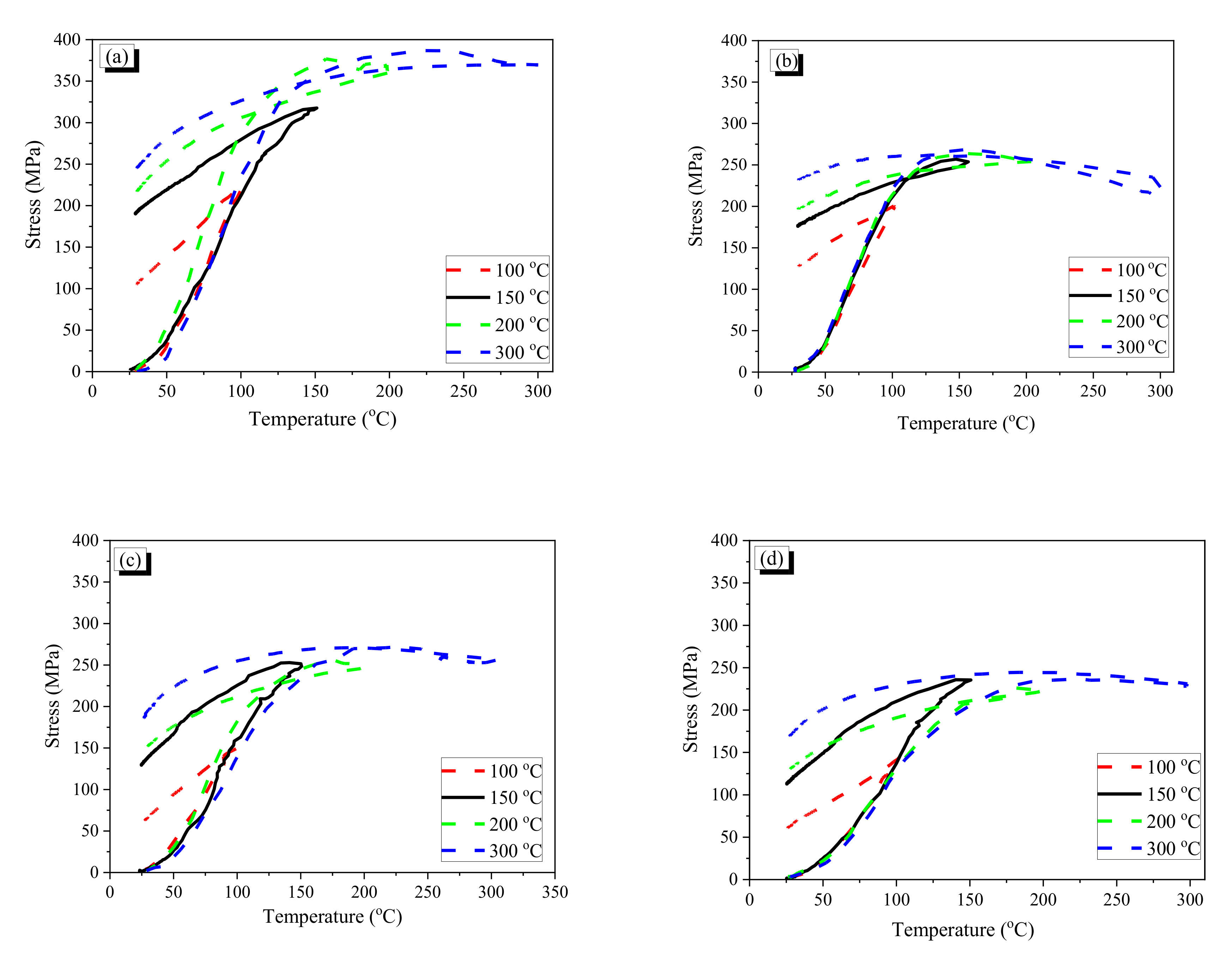
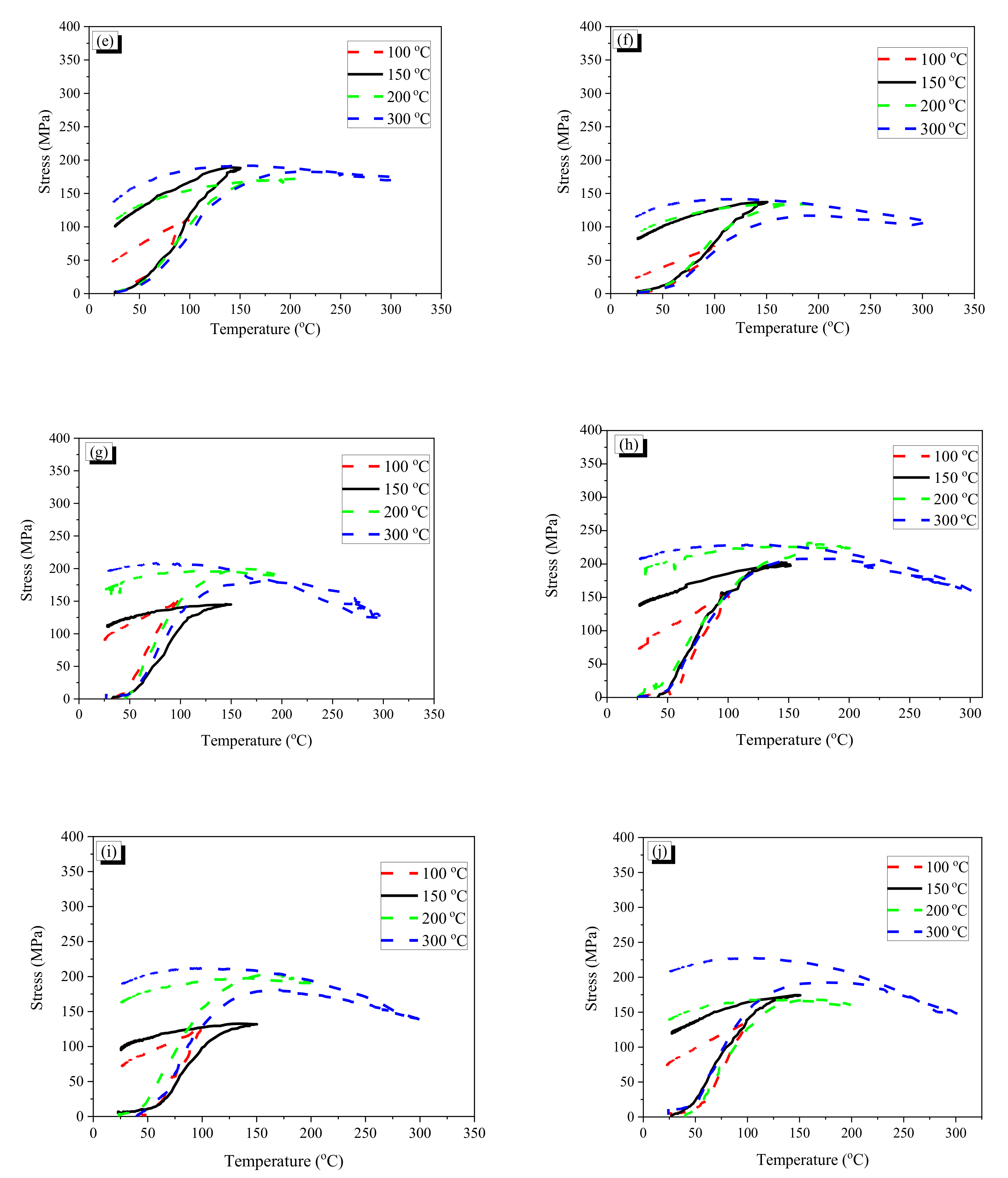
2.4. Recovery Stress of the Crimped Fiber
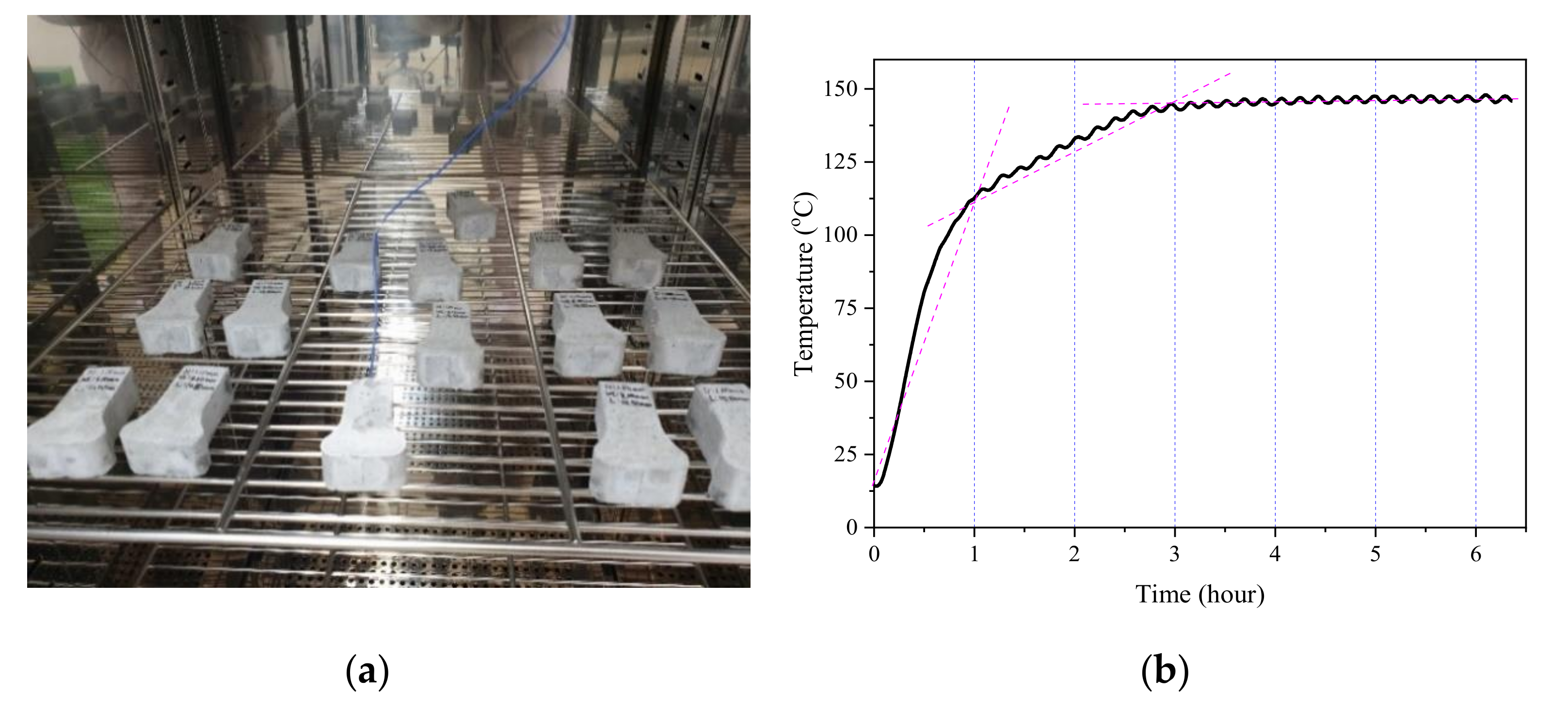
2.4.1. Test Set-Up
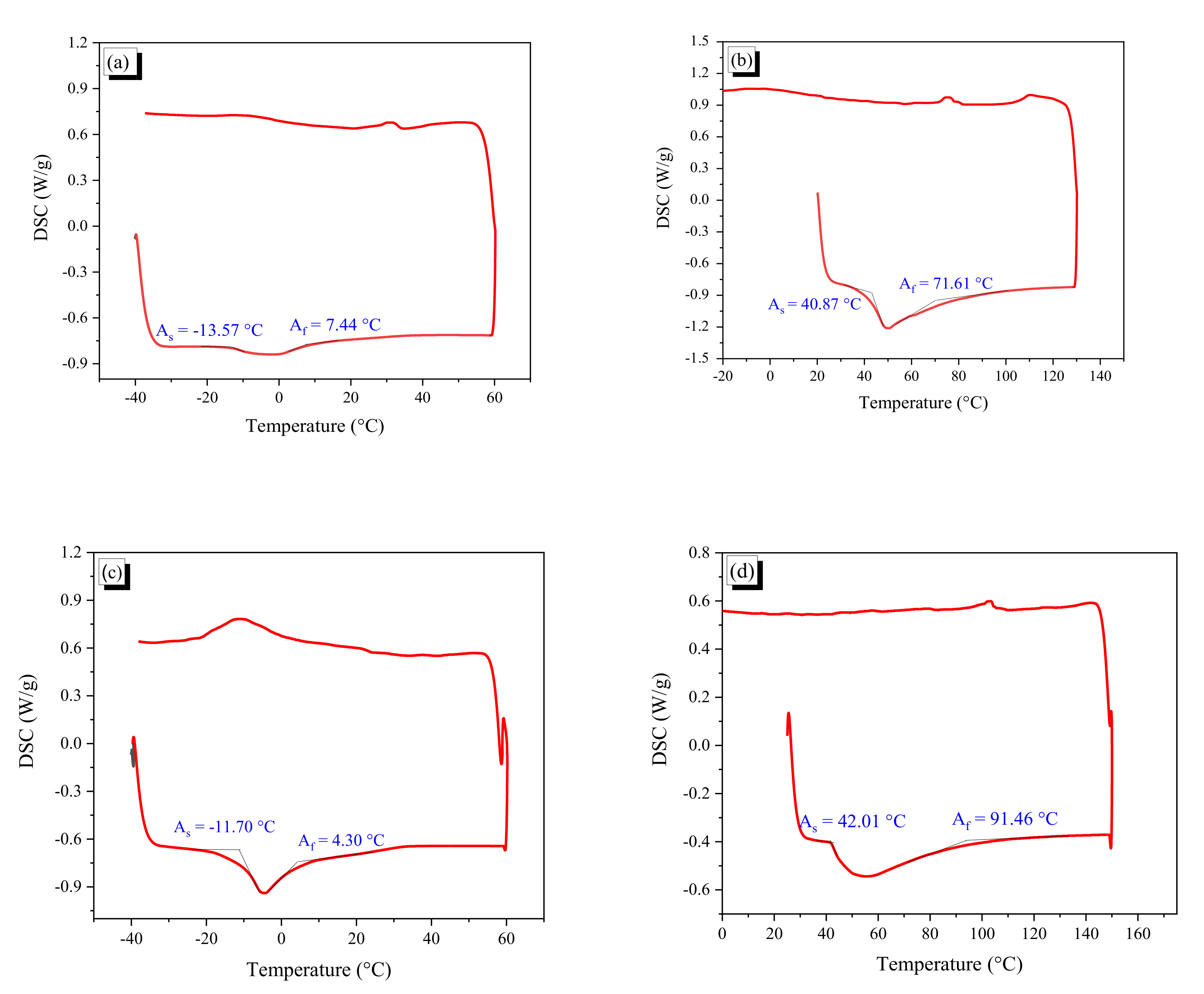
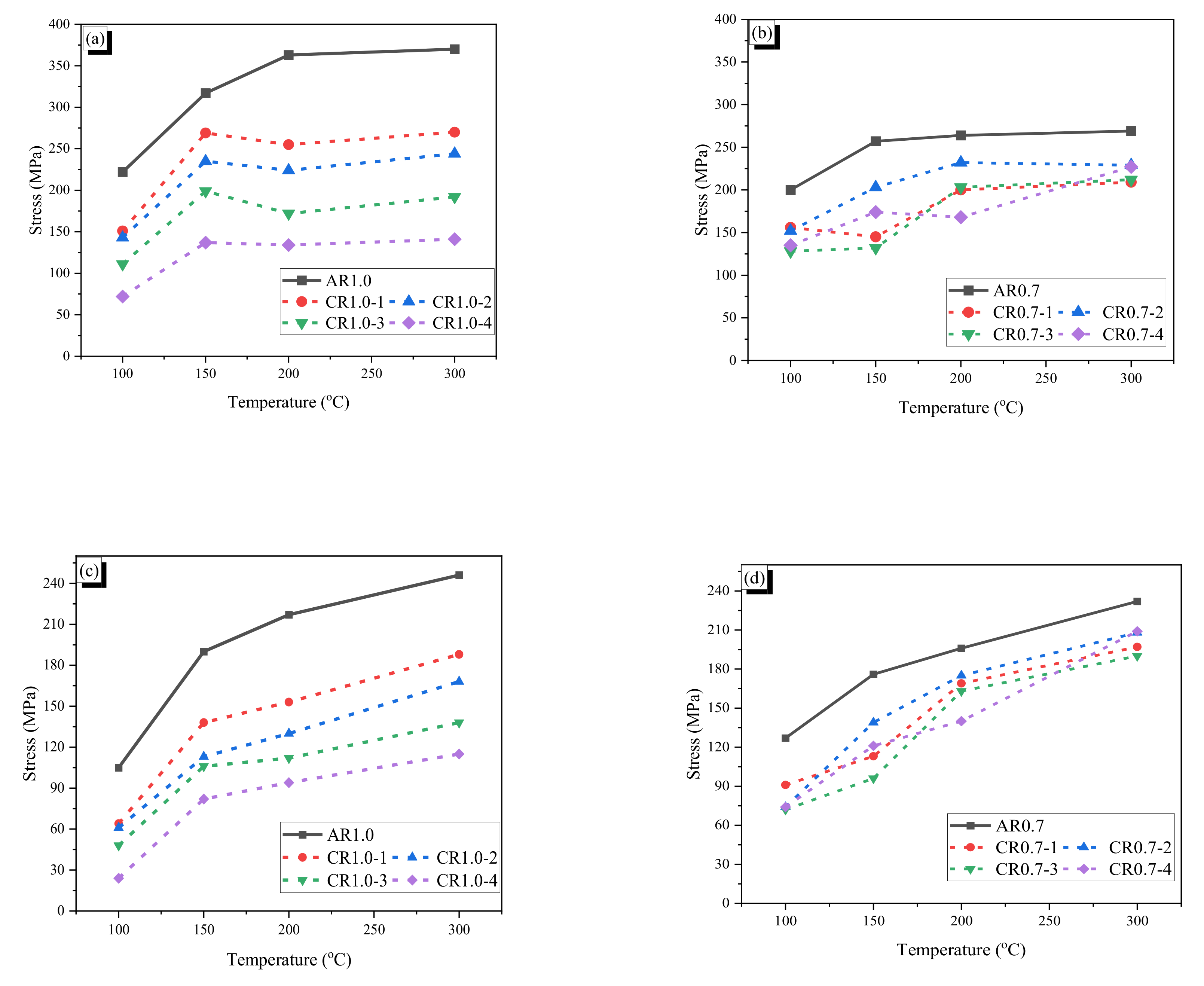
2.4.2. Recovery and Residual Stress
3. Pullout Test and Results
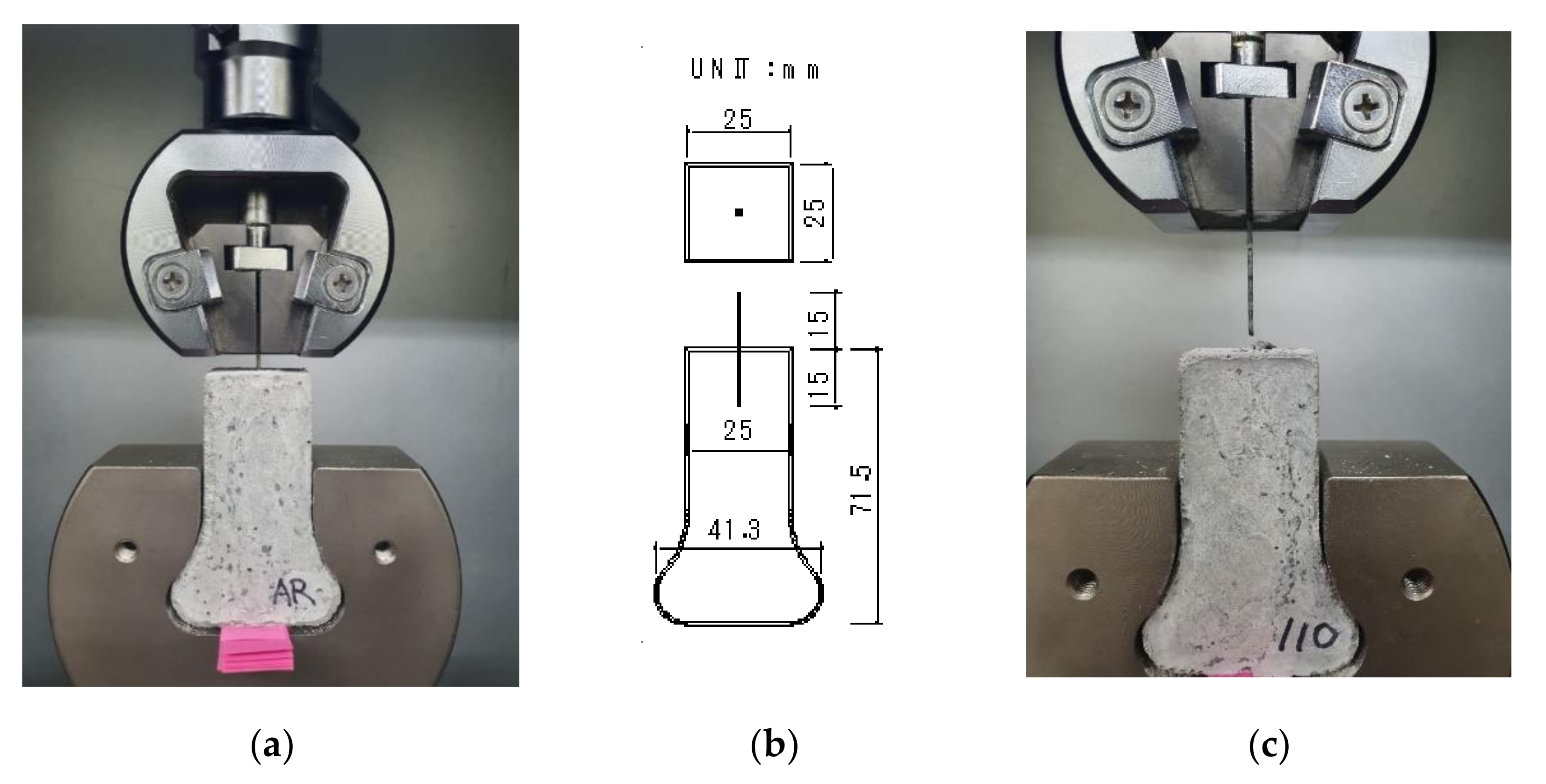
3.1. Specimens and Test Set-Up
3.2. Pullout Behavior
3.2.1. General
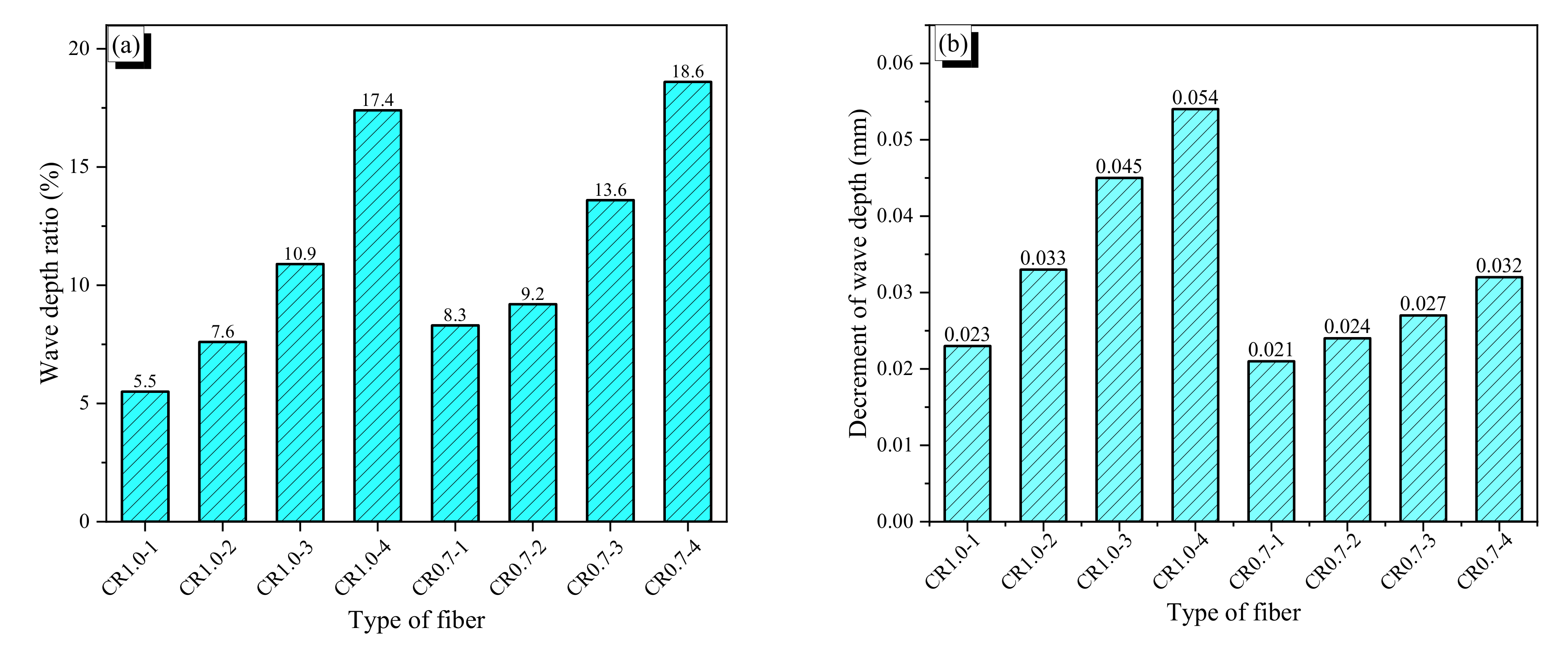
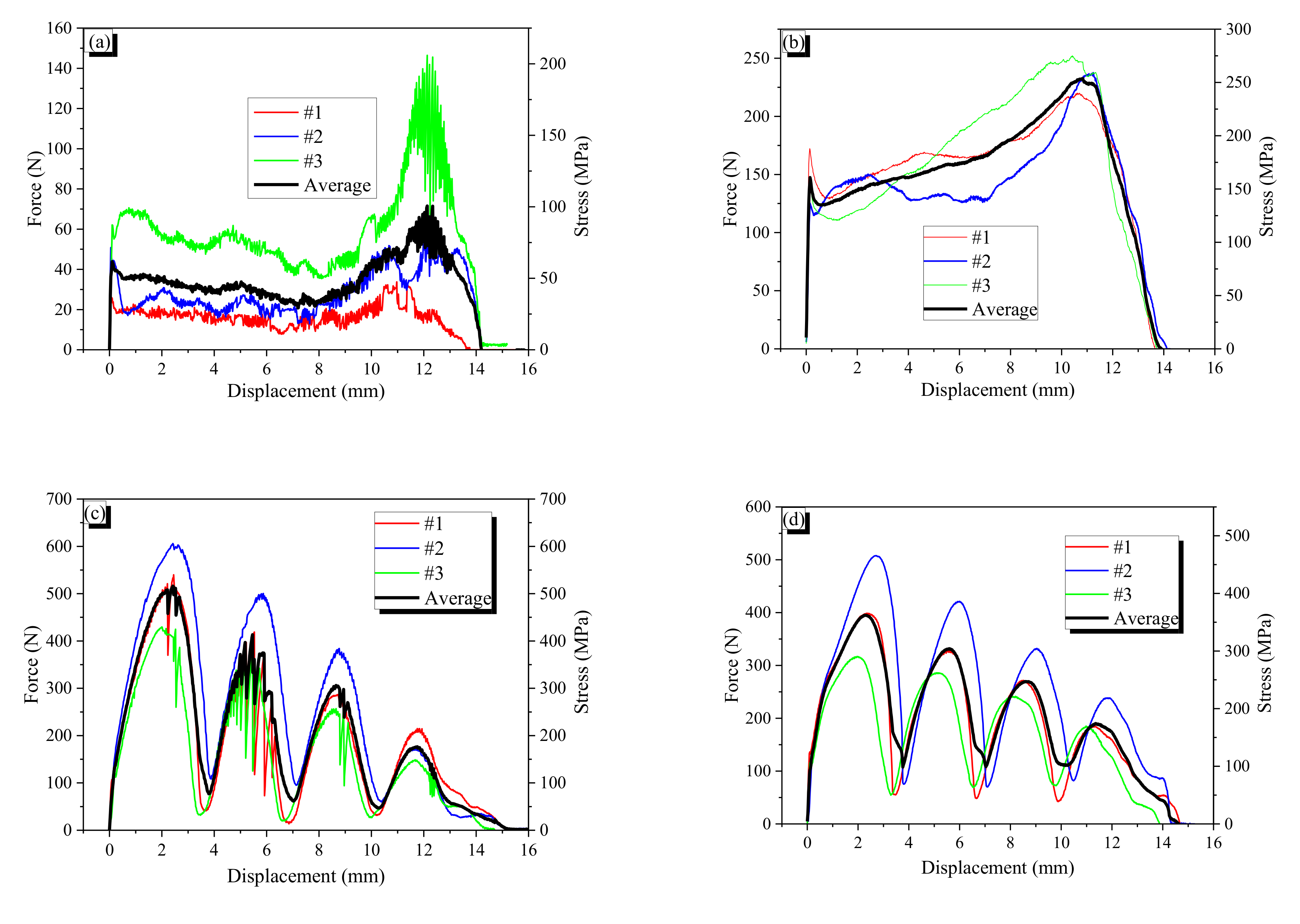
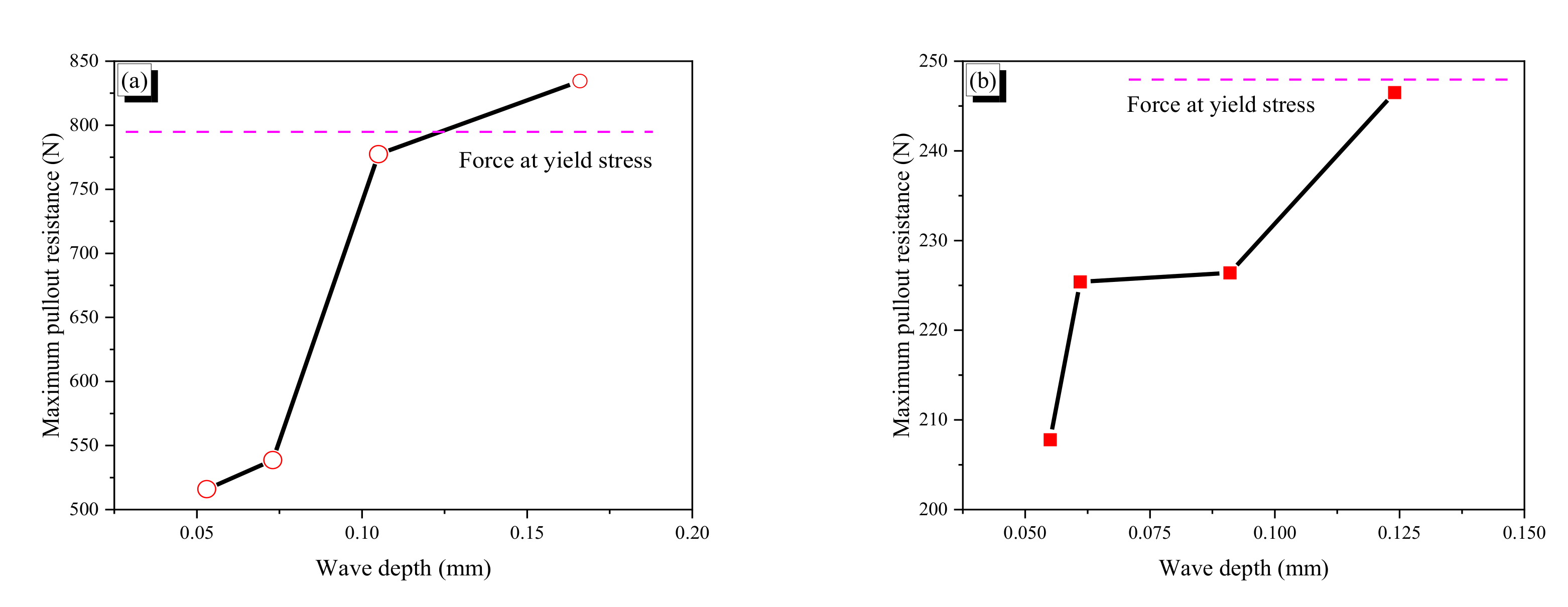
3.2.2. Wave Depth Effect on Pullout Resistance
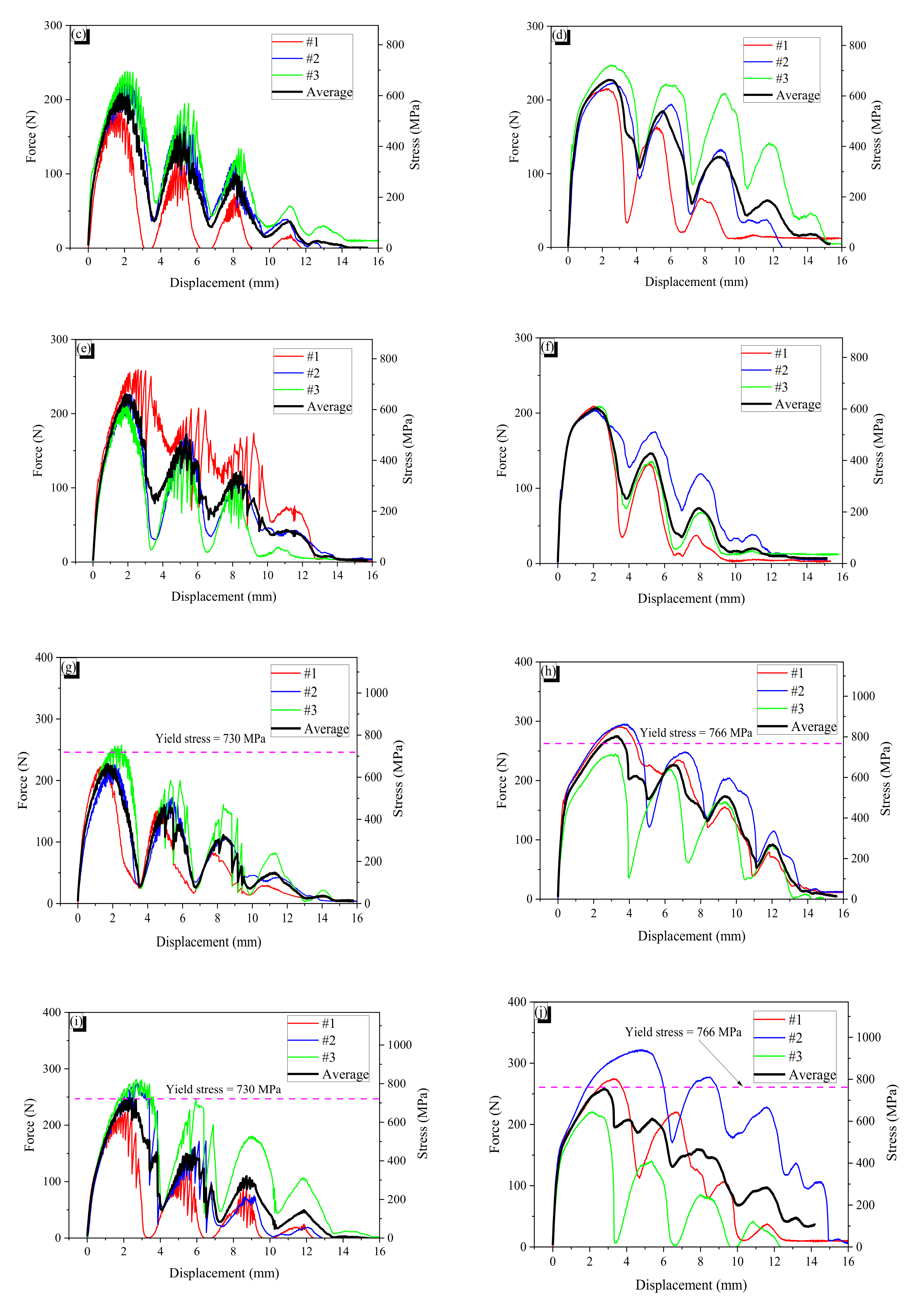
3.2.3. Pullout Resistance of Each Wave of Indentation
3.2.4. Heating Effect on Pullout Resistance
4. Conclusions
- CR fibers show more softening behavior in tension in comparison with AR fibers. However, after heating to induce phase transformation, the CR and AR fibers show almost the same tensile behavior.
- Crimped fibers by heating show lower recovery stress and residual stress in comparison with AR fiber having the same initial diameter because of the stretching effect. For CR1.0, the fibers with lower wave height showed higher values of recovery and residual stresses; however, the stresses of CR0.7 fibers were disturbed with increasing temperature.
- For both CR1.0-N and CR0.7-N, a larger wave depth induced a greater pullout resistance until they yielded. The critical wave depths of the CR1.0-N and CR0.7-N fibers for yielding were around 0.105 and 0.124 mm. If the pullout resistance exceeded the yield stress of a fiber, the wave pattern in pullout behavior was disturbed or eliminated.
- The maximum pullout resistance is a function of wave height (or wave depth) as well as the flexural rigidity of the fiber under the same fiber length; the wave depth and flexural rigidity consist of the flexural stiffness at the bent part in crimped fiber. The flexural rigidity (EI) of CR0.7-N was four times lower than that of CR1.0-N. Therefore, CR0.7-N was easily stretched during the pullout process and provide relatively lower pullout resistance.
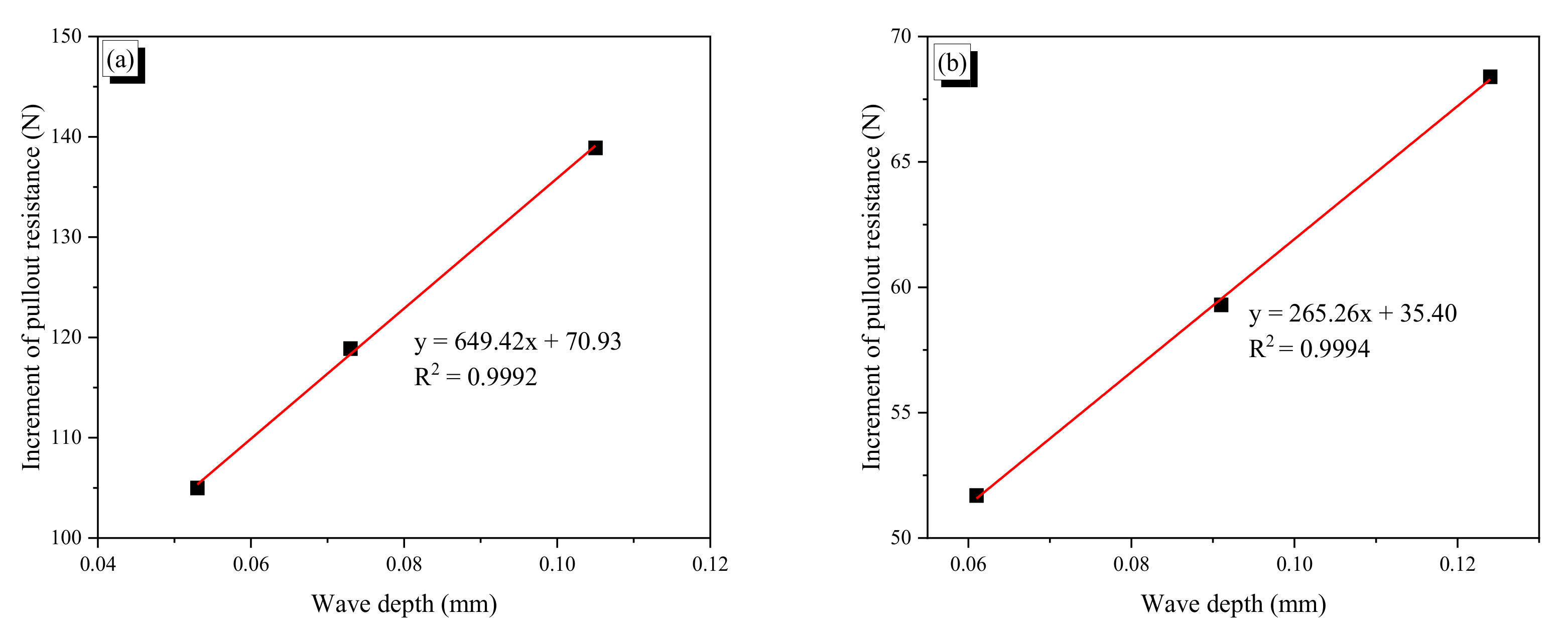
- For the non-heated fibers, the peak pullout resistance decreased linearly with decreasing number of waves; this indicates that each wave produces constant pullout resistance. Moreover, the increment of pullout resistance due to increasing wave depth is also linear until yielding. Thus, for the CR1.0-N fiber, in the wave depth range from 0.053 to 0.105 mm, the maximum pullout resistance could be estimated for a fiber with specific wave depth and fiber length. The same assessment was possible for the CR0.7-N fiber with wave depth ranging from 0.061 to 0.124 mm.
Author Contributions
Funding
Conflicts of Interest
References
- Abdallah, S.; Fan, M.; Rees, D.W.A. Effect of elevated temperature on pull-out behaviour of 4DH/5DH hooked end steel fibres. Compos. Struct. 2017, 165, 180–191. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Won, J. Flexural behavior of precast reinforced concrete composite members reinforced with structural nano-synthetic and steel fibers. Compos. Struct. 2014, 118, 571–579. [Google Scholar] [CrossRef]
- Beglarigale, A.; Yazıcı, H. Pull-out behavior of steel fiber embedded in flowable RPC and ordinary mortar. Constr. Build. Mater. 2015, 75, 255–265. [Google Scholar] [CrossRef]
- Villar, V.P.; Medina, N.F. Alignment of hooked-end fibres in matrices with similar rheological behavior to cementitious composites through homogeneous magnetic fields. Constr. Build. Mater. 2018, 163, 256–266. [Google Scholar] [CrossRef]
- Arisoy, B. Development and Fracture Evaluation of High Performance Fiber Reinforced Lightweight Concrete. Phd. Thesis, Wayne State University, Detroit, MI, USA, 2002. [Google Scholar]
- Noushini, A.; Samali, B.; Vessalas, K. Flexural toughness and ductility characteristics of polyvinyl-alcohol fibre reinforced concrete (PVA-FRC). In Proceedings of the 8th International Conference on Fracture Mechanics of Concrete and Concrete Structures, FraMCoS-8, Toledo, Spain, 11–14 March 2013; pp. 1110–1121. [Google Scholar]
- Noushini, A.; Vessalas, K.; Ghosni, N.; Samali, B. Effect of polyvinyl alcohol fibre and fly ash on flexural tensile properties of concrete. In Proceedings of the 22nd Australasian Conference on the Mechanics of Structures and Materials, ACMSM, Sydney, NSW, Australia, 11–14 December 2012; pp. 1165–1170. [Google Scholar]
- Banthia, N.; Trottier, J.F. Concrete reinforced with deformed steel fibres, Part II: Toughness characterization. ACI Mater. J. 1995, 2, 146–154. [Google Scholar]
- Kurihara, N.; Kunieda, M.; Kamada, T.; Uchida, Y.; Rokugo, K. Tension softening diagrams and evaluation of properties of steel fibre reinforced concrete. Eng. Fract. Mech. 2000, 65, 235–245. [Google Scholar] [CrossRef]
- Choi, E.; Mohammadzadeh, B.; Hwang, J.H.; Kim, J.W. Pullout behavior of superelastic SMA fibers with various end-shapes embedded in cement mortar. Constr. Build. Mater. 2018, 167, 605–616. [Google Scholar] [CrossRef]
- Abdallah, S.; Fan, M.; Zhou, X. Pull-out behaviour of hooked end steel fibres embedded in ultra-high performance mortar with various W/B ratios. Int. J. Concr. Struct. Mater. 2017, 11, 1–13. [Google Scholar] [CrossRef]
- Naaman, A.E.; Najm, H. Bond-Slip Mechanisms of Steel Fibers in Concrete. ACI Mater. J. 1991, 2, 135–145. [Google Scholar]
- Abdallah, S.; Fan, M.; Cashell, K.A. Bond-slip behaviour of steel fibres in concrete after exposure to elevated temperatures. Constr. Build. Mater. 2007, 140, 542–551. [Google Scholar] [CrossRef]
- Venkateshwaran, A.; Tan, K.H.; Li, Y. Residual flexural strengths of steel fiber reinforced concrete with multiple hooked-end fibers. Struct. Concr. 2018, 2, 352–365. [Google Scholar] [CrossRef]
- Gündüz, Y.; Taşkan, E.; Şahin, Y. Using hooked-end fibres on high performance steel fibre reinforced concrete. High Perform. Optim. Des. Struct. Mater. II 2016, 1, 265–276. [Google Scholar]
- Reinhardt, H.W.; Naaman, A.E. (Eds.) Fibers with Slip-Hardening Bond. In High-Performance Fiber Reinforced Cement Composites (HPFRCC-3); RILEM Proceedings: Paris, France, 1999; Volume 6, pp. 371–385. [Google Scholar]
- Naaman, A.E. Engineered Steel Fibers with Optimal Properties for Reinforcement of Cement Composites. J. Adv. Concr. Tech. 2003, 3, 241–252. [Google Scholar] [CrossRef] [Green Version]
- Zile, E.; Zile, O. Effect of the fiber geometry on the pullout response of mechanically deformed steel fibers. Cement Concr. Res. 2013, 44, 18–24. [Google Scholar] [CrossRef]
- Zheng, Z.; Feldman, D. Synthetic fibre-reinforced concrete. Prog. Polym. Sci. 1995, 2, 185–210. [Google Scholar] [CrossRef]
- Densai, T.; Shah, R.; Peled, A.; Mobasher, B. Mechanical Properties of Concrete Reinforced with AR-Glass Fibers. In Brittle Matrix Composites 7; Institute of Fundamental Technological Research; Woodhead Publishing: Cambridge, UK, 2003; pp. 223–232. [Google Scholar]
- Maji, A.K.; Negret, I. Smart prestressing with shape memory alloy. J. Eng. Mech. 1998, 124, 1121–1128. [Google Scholar] [CrossRef]
- Moser, K.; Bergamini, A.; Christen, R.; Czaderski, C. Feasibility of concrete prestressed by shape memory alloy short fibers. Mater. Struct. 2005, 28, 593–600. [Google Scholar] [CrossRef] [Green Version]
- Choi, E.; Kim, D.J.; Hwang, J.H.; Kim, W.J. Prestressing effect of cold-drawn short NiTi SMA fibres in Steel reinforced mortar beams. Smart Mater. Struct. 2016, 25, 085041. [Google Scholar] [CrossRef]
- Choi, E.; Hong, H.K.; Kim, H.S.; Chung, Y.S. Hysteretic behavior of NiTi and NiTiNb SMA wires under recovery or prestressing stress. J. Alloy. Compd. 2013, 577, S444–S447. [Google Scholar] [CrossRef]
- Lee, W.J.; Weber, B.; Feltrin, G.; Czaderski, C.; Motavalli, M.; Leinenbach, C. Stress recovery behavior of an Fe-Mn-Si-Cr-Ni-VC shape memory alloy used for prestressing. Smart Mater. Struct. 2013, 22, 125037. [Google Scholar] [CrossRef]
- Rojob, H.; El-Hacha, R. Self-prestressing using iron-based shape memory alloy for flexural strengthening of reinforced concrete beams. ACI Struct. J. 2017, 114, 523–532. [Google Scholar] [CrossRef]
- Choi, E.; Kim, D.J.; Chung, Y.S.; Kim, H.S.; Jung, C. Crack-closing of cement mortar beams using NiTi clod-drawn SMA short fibers. Smart Mater. Struct. 2015, 24, 015018. [Google Scholar] [CrossRef]
- Lee, K.J.; Lee, J.H.; Jung, C.Y.; Choi, E. Crack-closing performance of NiTi and NiTiNb fibers in cement mortar beams using shape memory effects. Compos. Struct. 2018, 202, 710–718. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, K.J.; Choi, E. Flexural capacity and crack-closing performance of NiTi and NiTiNb shape memory alloys fibers randomly distributed in mortar beams. Compos. Part B 2018, 153, 264–276. [Google Scholar] [CrossRef]
- Choi, E.; Kim, D.; Chung, Y.S.; Nam, T.H. Bond-slip characteristics of SMA reinforcing fibers obtained by pull-out tests. Mater. Res. Bull. 2014, 58, 28–31. [Google Scholar] [CrossRef]
- Choi, E.; Kim, D.J.; Nam, T.H.; Kim, D.; Kang, J.W. Bond resistance of L-shaped shape memory alloy fibers in mortar. J. Nanosci. Nanotech. 2016, 16, 11500–11504. [Google Scholar] [CrossRef]
- Choi, E.; Chae, S.W.; Park, H.; Nam, T.H.; Mohammadzadeh, B.; Hwang, J.H. Investigating self-centering capacity of superelastic shape memory alloy fibers with different anchorages through pullout tests. J. Nanosci. Nanotech. 2018, 18, 6228–6232. [Google Scholar] [CrossRef]
- Kim, D.J.; Kim, H.A.; Chung, Y.S.; Choi, E. Pullout resistance of deformed shape memory alloy fibers embedded in cement mortar. J. Intell. Mater. Syst. Struct. 2016, 27, 249–260. [Google Scholar] [CrossRef]
- Farmani, M.A.; Ghassemieh, M. Shape memory alloy-based moment connections with superior self-centering properties. Smart Mater. Struct. 2016, 25, 1–17. [Google Scholar] [CrossRef]
- Kim, M.K.; Kim, D.J.; Chung, Y.S.; Choi, E. Direct tensile behavior of shape-memory-alloy fiber-reinforced cement composites. Constr. Build. Mater. 2016, 102, 462–470. [Google Scholar] [CrossRef]
- Kim, M.K.; Kim, D.J.; Chung, Y.S.; Choi, E. Effects of a short heat treatment period on the pullout resistance of shape memory alloy fibers in mortar. Materials 2019, 12, 2278. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Choi, E.; Kim, H.S.; Nam, T. Effect of crimped SMA fiber geometry on recovery stress and pullout resistance. Compos. Struct. 2020, 247, 112466. [Google Scholar] [CrossRef]
- Choi, E.; Ostadrahimi, A.; Park, J. On mechanical properties of NiTi SMA wires prestrained by cold rolling. Smart Mater. Struct. 2020, 29, 065009. [Google Scholar] [CrossRef]
- Li, L.; Zhang, R.; Jin, L.; Du, X.; Duan, W. Experimental study on dynamic compressive behavior of steel fiber reinforced concrete at elevated temperatures. Constr. Build. Mater. 2019, 210, 673–684. [Google Scholar] [CrossRef]






| Fiber Types | AR1.0 | AR0.7 |
|---|---|---|
| Diameter (mm) | 1.020 | 0.702 |
| Reduction of diameter (mm) | 0.065 | 0.042 |
| ARR (%) | 12.3 | 11.6 |
| Name | Before Heating | After Heating | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Thick- Ness | Height | Depth | WDR (%) | Length | Thick- Ness | Height | Depth | Length | ∆L/L (%) | |
| AR1.0 | 0.955 | - | - | 50.44 | 0.971 | - | - | 48.86 | 3.13 | |
| CR1.0-1 | 0.965 | 1.018 | 0.053 | 5.5 | 50.36 | 0.973 | 1.003 | 0.030 | 49.38 | 1.95 |
| CR1.0-2 | 0.966 | 1.039 | 0.073 | 7.6 | 50.22 | 0.974 | 1.014 | 0.040 | 49.55 | 1.33 |
| CR1.0-3 | 0.972 | 1.077 | 0.105 | 10.9 | 50.54 | 0.977 | 1.037 | 0.060 | 49.93 | 1.21 |
| CR1.0-4 | 0.972 | 1.138 | 0.166 | 17.4 | 50.39 | 0.976 | 1.088 | 0.112 | 49.88 | 1.01 |
| AR0.7 | 0.660 | - | - | 50.45 | 0.671 | - | - | 49.39 | 2.10 | |
| CR0.7-1 | 0.665 | 0.720 | 0.055 | 8.3 | 50.51 | 0.671 | 0.705 | 0.034 | 49.65 | 1.70 |
| CR0.7-2 | 0.666 | 0.727 | 0.061 | 9.2 | 50.49 | 0.672 | 0.709 | 0.037 | 49.62 | 1.72 |
| CR0.7-3 | 0.667 | 0.758 | 0.091 | 13.6 | 49.32 | 0.672 | 0.736 | 0.064 | 48.59 | 1.48 |
| CR0.7-4 | 0.667 | 0.791 | 0.124 | 18.6 | 49.92 | 0.670 | 0.762 | 0.092 | 49.26 | 1.32 |
| AR1.0 | CR1.0-1 | CR1.0-2 | CR1.0-3 | CR1.0-4 | AR0.7 | CR0.7-1 | CR0.7-2 | CR0.7-3 | CR0.7-4 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Non-heating | Stress (MPa) | 950 | 863 | 840 | 800 | 775 | 730 | 685 | 650 | 615 | 602 |
| Strain (%) | 8.7 | 8.7 | 8.7 | 8.7 | 8.7 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | |
| Heating | Stress (MPa) | 979 | 1006 | 990 | 966 | 966 | 766 | 786 | 833 | 833 | 833 |
| Strain (%) | 12.3 | 12.3 | 12.3 | 12.3 | 12.3 | 17.2 | 17.2 | 17.2 | 17.2 | 17.2 |
| Type | Maximum Recovery Stress (MPa) | Residual Stress (MPa) | ||||||
|---|---|---|---|---|---|---|---|---|
| 100 °C | 150 °C | 200 °C | 300 °C | 100 °C | 150 °C | 200 °C | 300 °C | |
| AR1.0 | 222 | 317 | 363 | 370 | 105 | 190 | 217 | 246 |
| CR1.0-1 | 151 | 269 | 255 | 270 | 64 | 138 | 153 | 188 |
| CR1.0-2 | 143 | 235 | 224 | 244 | 61 | 113 | 130 | 168 |
| CR1.0-3 | 111 | 199 | 172 | 192 | 48 | 106 | 112 | 138 |
| CR1.0-4 | 72 | 137 | 134 | 141 | 24 | 82 | 94 | 115 |
| AR0.7 | 200 | 257 | 264 | 269 | 127 | 176 | 196 | 232 |
| CR0.7-1 | 156 | 145 | 200 | 209 | 91 | 113 | 169 | 197 |
| CR0.7-2 | 152 | 203 | 232 | 229 | 74 | 139 | 175 | 208 |
| CR0.7-3 | 128 | 132 | 203 | 212 | 72 | 96 | 163 | 190 |
| CR0.7-4 | 135 | 174 | 168 | 227 | 74 | 121 | 140 | 209 |
| Cement (Type III) | Fly Ash | Silica Sand | High-Range Water, Reducing Admixture | Water |
|---|---|---|---|---|
| 1.00 | 0.15 | 1.00 | 0.009 | 0.35 |
| Type/ Peak Points | 1st Peak | 2nd Peak | 3rd Peak | 4th Peak | (N) | (N) | Average (N) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Force (N) | Slip (mm) | Force (N) | Slip (mm) | Force (N) | Slip (mm) | Force (N) | Slip (mm) | ||||
| CR1.0-1N | 515.9 | 2.4 | 413.3 | 5.5 | 306.0 | 8.7 | 176.5 | 11.8 | 102.6 | 107.3 | 105.0 |
| CR1.0-2N | 538.6 | 2.3 | 376.1 | 5.5 | 300.8 | 8.8 | 190.4 | 11.6 | 162.5 | 75.3 | 118.9 |
| CR1.0-3N | 777.4 | 4.2 | 666.6 | 7.5 | 499.6 | 10.5 | 239.2 | 13.1 | 110.8 | 167.0 | 138.9 |
| CR1.0-4N | 834.5 | 5.7 | - | - | - | - | - | - | - | - | - |
| CR1.0-1H | 394.9 | 2.3 | 331.5 | 5.6 | 269.5 | 8.7 | 190.2 | 11.4 | 63.4 | 62.0 | 62.7 |
| CR1.0-2H | 517.1 | 2.6 | 435.0 | 5.9 | 365.1 | 9.1 | 270.7 | 12.1 | 82.1 | 69.9 | 76.0 |
| CR1.0-3H | 752.3 | 3.9 | 573.8 | 7.6 | 442.6 | 10.8 | 216.4 | 13.4 | 178.5 | 131.2 | 154.9 |
| CR1.0-4H | 823.2 | 4.8 | - | - | - | - | - | - | - | - | - |
| CR0.7-1N | 207.8 | 1.9 | 152.9 | 5.3 | 98.5 | 8.2 | 36.0 | 11.0 | 54.9 | 54.4 | 54.7 |
| CR0.7-2N | 225.4 | 2.1 | 171.4 | 5.3 | 122.0 | 8.4 | 43.4 | 11.1 | 54.0 | 49.4 | 51.7 |
| CR0.7-3N | 226.4 | 1.7 | 157.7 | 5.3 | 107.9 | 8.3 | 49.0 | 11.0 | 68.7 | 49.8 | 59.3 |
| CR0.7-4N | 246.5 | 2.5 | 149.4 | 5.9 | 109.7 | 8.7 | 46.8 | 11.7 | 97.1 | 39.7 | 68.4 |
| CR0.7-1H | 227.0 | 2.5 | 184.9 | 5.5 | 122.5 | 8.9 | 63.9 | 11.6 | 42.1 | 62.4 | 52.3 |
| CR0.7-2H | 206.4 | 2.2 | 146.5 | 5.2 | 73.3 | 7.9 | 20.0 | 11.0 | 59.9 | 73.2 | 66.6 |
| CR0.7-3H | 274.5 | 3.2 | 225.7 | 6.4 | 173.5 | 9.4 | 91.9 | 12.1 | 48.8 | 52.2 | 50.5 |
| CR0.7-4H | 257.9 | 2.8 | 209.5 | 5.4 | 159.5 | 7.8 | 97.2 | 11.6 | 48.4 | 50.0 | 49.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, E.; Ho, H.V.; Jeon, J.-S. Active Reinforcing Fiber of Cementitious Materials Using Crimped NiTi SMA Fiber for Crack-Bridging and Pullout Resistance. Materials 2020, 13, 3845. https://doi.org/10.3390/ma13173845
Choi E, Ho HV, Jeon J-S. Active Reinforcing Fiber of Cementitious Materials Using Crimped NiTi SMA Fiber for Crack-Bridging and Pullout Resistance. Materials. 2020; 13(17):3845. https://doi.org/10.3390/ma13173845
Chicago/Turabian StyleChoi, Eunsoo, Ha Vinh Ho, and Jong-Su Jeon. 2020. "Active Reinforcing Fiber of Cementitious Materials Using Crimped NiTi SMA Fiber for Crack-Bridging and Pullout Resistance" Materials 13, no. 17: 3845. https://doi.org/10.3390/ma13173845
APA StyleChoi, E., Ho, H. V., & Jeon, J.-S. (2020). Active Reinforcing Fiber of Cementitious Materials Using Crimped NiTi SMA Fiber for Crack-Bridging and Pullout Resistance. Materials, 13(17), 3845. https://doi.org/10.3390/ma13173845






