Single Image Super-Resolution Method Using CNN-Based Lightweight Neural Networks
Abstract
:1. Introduction
2. Related Works
3. Proposed Method
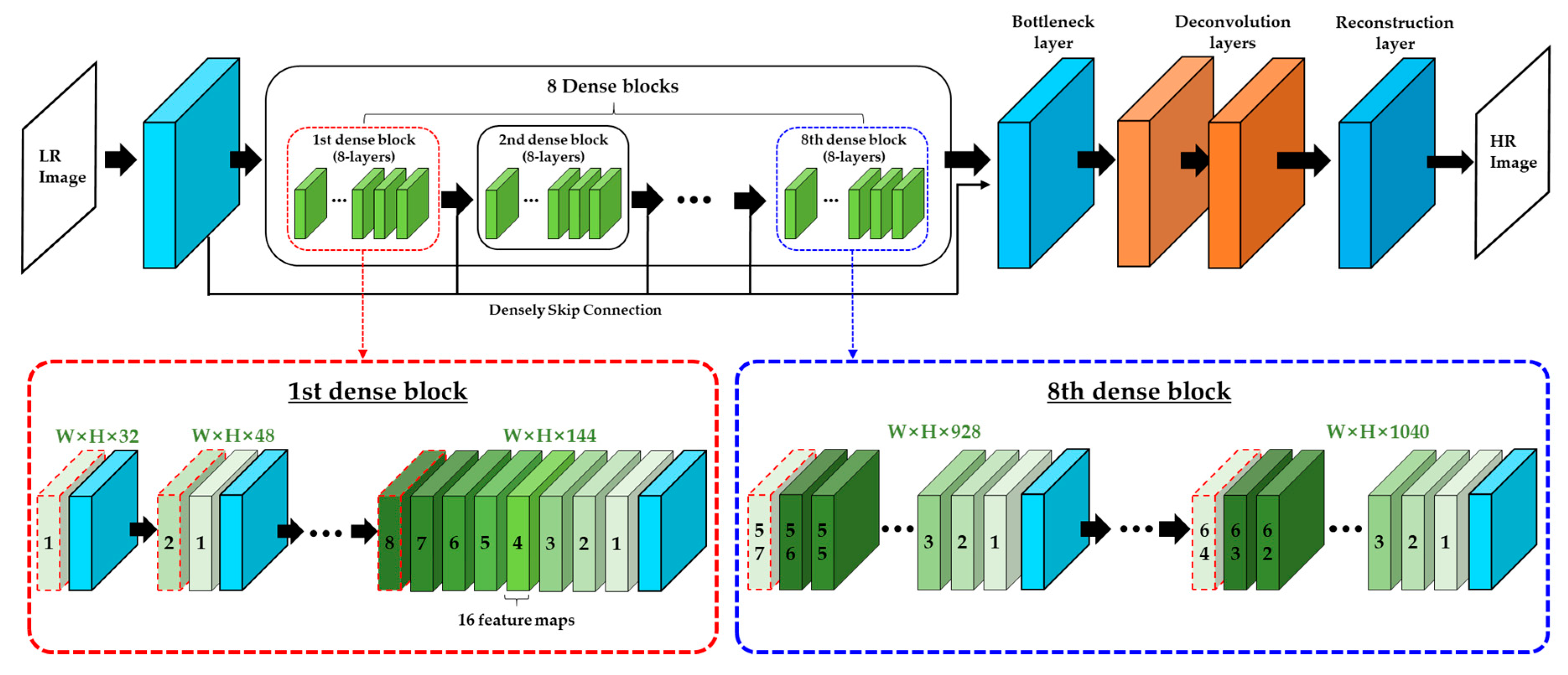
3.1. Architecture of SR-ILLNN
3.2. Architecture of SR-SLNN
3.3. Loss Function and Hyper-Parameters
4. Experimental Results
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, W.; Zhang, X.; Tian, Y.; Wang, W.; Xue, J.; Liao, Q. Deep Learning for Single Image Super-Resolution: A Brief Review. IEEE Trans. Multimed. 2019, 21, 3106–3121. [Google Scholar] [CrossRef] [Green Version]
- Anwar, S.; Khan, S.; Barnes, N. A deep journey into super-resolution: A survey. arXiv 2019, arXiv:1904.07523. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Hoi, S.C.H. Deep Learning for Image Super-resolution: A Survey. IEEE Trans. Pattern. Anal. Mach. Intell. 2020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keys, R. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. 1981, 29, 1153–1160. [Google Scholar] [CrossRef] [Green Version]
- Freeman, T.; Jones, R.; Pasztor, C. Example-based super-resolution. IEEE Comput. Graph. Appl. 2002, 22, 56–65. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Kim, B.; Roy, P.; Partha, P.; Jeong, D. Efficient facial expression recognition algorithm based on hierarchical deep neural network structure. IEEE Access 2019, 7, 41273–41285. [Google Scholar] [CrossRef]
- Kim, J.; Hong, G.; Kim, B.; Dogra, D. deepGesture: Deep learning-based gesture recognition scheme using motion sensors. Displays 2018, 55, 38–45. [Google Scholar] [CrossRef]
- Jeong, D.; Kim, B.; Dong, S. Deep Joint Spatiotemporal Network (DJSTN) for Efficient Facial Expression Recognition. Sensors 2020, 20, 1936. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern. Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Simonyan, K.; Zisserman, A. Very deep convolution networks for large -scale image recognition. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Las Vegas, NY, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the Machine Learning Research, Lille, France, 7–9 July 2015; pp. 448–456. [Google Scholar]
- Dong, C.; Deng, Y.; Change Loy, C.; Tang, X. Compression artifacts reduction by a deep convolutional network. In Proceedings of the International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 576–584. [Google Scholar]
- Kim, J.; Lee, J.; Lee, K. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Las Vegas, NY, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K. Enhanced deep residual networks for single image super-resolution. In Proceedings of the Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar]
- Tong, T.; Li, G.; Liu, X.; Gao, Q. Image super-resolution using dense skip connections. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4799–4807. [Google Scholar]
- Ye, Y.; Alshina, E.; Chen, J.; Liu, S.; Pfaff, J.; Wang, S. [DNNVC] AhG on Deep neural networks based video coding, Joint Video Experts Team (JVET) of ITU-T SG 16 WP 3 and ISO/IEC JTC 1/SC29, Document JVET-T0121, Input Document to JVET Teleconference. 2020.
- Cho, S.; Lee, J.; Kim, J.; Kim, Y.; Kim, D.; Chung, J.; Jung, S. Low Bit-rate Image Compression based on Post-processing with Grouped Residual Dense Network. In Proceedings of the Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Yang, R.; Xu, M.; Liu, T.; Wang, Z.; Guan, Z. Enhancing quality for HEVC compressed videos. IEEE Trans. Circuits Syst. Video Technol. 2018, 29, 2039–2054. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Fan, Z.; Ling, N.; Jiang, M. Recursive Residual Convolutional Neural Network-Based In-Loop Filtering for Intra Frames. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 1888–1900. [Google Scholar] [CrossRef]
- Lui, G.; Shih, K.; Wang, T.; Reda, F.; Sapra, K.; Yu, Z.; Tao, A.; Catanzaro, B. Partial convolution based padding. arXiv 2018, arXiv:1811.11718. [Google Scholar]
- Agustsson, E.; Timofte, R. NTIRE 2017 Challenge on Single Image Super-Resolution: Dataset and Study. In Proceedings of the Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Processing 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, C.; Ma, C.; Yang, M. Single-image super-resolution: A benchmark. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 372–386. [Google Scholar]







| Layer Name | Kernel Size | Num. of Kernels | Padding Size | Output Feature Map (W × H × C) | Num. of Parameters |
|---|---|---|---|---|---|
| Conv1 | 3 × 3 × 1 | 64 | 1 | N × M × 64 | 640 |
| Conv2 | 3 × 3 × 64 | 64 | 1 | N × M × 64 | 36,928 |
| Conv3 | 3 × 3 × 128 | 64 | 1 | N × M × 64 | 73,792 |
| Conv4 | 3 × 3 × 192 | 64 | 1 | N × M × 64 | 110,656 |
| Conv5 | 1 × 1 × 64 | 32 | 0 | N × M × 32 | 2080 |
| Deconv1 | 4 × 4 × 32 | 32 | 1 | 2N × 2M × 32 | 16,416 |
| Conv6, 7 | 3 × 3 × 32 | 32 | 1 | 2N × 2M × 32 | 9248 |
| Deconv2 | 4 × 4 × 32 | 32 | 1 | 4N × 4M × 32 | 16,416 |
| Conv8 | 3 × 3 × 32 | 16 | 1 | 4N × 4M × 16 | 4624 |
| Conv9 | 5 × 5 × 1 | 64 | 2 | 4N × 4M × 64 | 1664 |
| Conv10 | 3 × 3 × 64 | 64 | 1 | 4N × 4M × 64 | 36,928 |
| Conv11 | 3 × 3 × 128 | 64 | 1 | 4N × 4M × 64 | 73,792 |
| Conv12 | 3 × 3 × 192 | 16 | 1 | 4N × 4M × 16 | 27,664 |
| Conv13, 14 | 3 × 3 × 32 | 32 | 1 | 4N × 4M × 32 | 9248 |
| Conv15 | 5 × 5 × 32 | 1 | 2 | 4N × 4M × 1 | 801 |
| Layer Name | Kernel Size | Num. of Kernels | Padding Size | Output Feature Map (W × H × C) | Num. of Parameters |
|---|---|---|---|---|---|
| Conv1 | 5 × 5 × 1 | 64 | 2 | N × M × 64 | 1664 |
| Conv2 | 3 × 3 × 64 | 64 | 1 | N × M × 64 | 36,928 |
| Conv3 | 3 × 3 × 128 | 64 | 1 | N × M × 64 | 73,792 |
| Conv4 | 3 × 3 × 192 | 64 | 1 | N × M × 64 | 110,656 |
| Conv5 | 1 × 1 × 64 | 32 | 0 | N × M × 32 | 2080 |
| Deconv1 | 4 × 4 × 32 | 32 | 1 | 2N × 2M × 32 | 16,416 |
| Deconv2 | 4 × 4 × 32 | 32 | 1 | 4N × 4M × 32 | 16,416 |
| Conv6 | 3 × 3 × 32 | 16 | 1 | 4N × 4M × 16 | 4624 |
| Conv7 | 5 × 5 × 16 | 1 | 2 | 4N × 4M × 1 | 401 |
| Optimizer | Adam |
|---|---|
| Learning Rate | 10−3 to 10−5 |
| Activation function | ReLU |
| Padding Mode | Partial convolutional based padding [23] |
| Num. of epochs | 50 |
| Batch size | 128 |
| Initial weight | Xavier |
| Networks | Filter Size (Width × Height) | Num. of Parameters | PSNR (dB) |
|---|---|---|---|
| SR-ILLNN | 3 × 3 | 439,393 | 31.41 |
| 5 × 5 | 1,153,121 | 31.38 | |
| 7 × 7 | 2,223,713 | 31.29 | |
| 9 × 9 | 3,651,169 | 28.44 | |
| SR-SLNN | 3 × 3 | 262,977 | 31.29 |
| 5 × 5 | 664,385 | 31.19 | |
| 7 × 7 | 1,266,497 | 31.16 | |
| 9 × 9 | 2,069,313 | 31.15 |
| Num. of Training Samples | 210,048 |
| Input size (XLR) | 25 × 25 × 1 |
| Interpolated input size (XILR) | 100 × 100 × 1 |
| Label size (YHR) | 100 × 100 × 1 |
| Linux version | Ubuntu 16.04 |
| CUDA version | 10.1 |
| Deep learning frameworks | Pytorch 1.4.0 |
| Dataset | Bicubic | SR-CNN [9] | AR-CNN [14] | SR-DenseNet [18] | SR-ILLNN | SR-SLNN |
|---|---|---|---|---|---|---|
| Set5 | 28.44 | 30.30 | 30.35 | 31.43 | 31.41 | 31.29 |
| Set14 | 25.80 | 27.09 | 27.10 | 27.84 | 27.83 | 27.73 |
| BSD100 | 25.99 | 26.86 | 26.86 | 27.34 | 27.33 | 27.28 |
| Urban100 | 23.14 | 24.33 | 24.34 | 25.30 | 25.32 | 25.18 |
| Average | 24.73 | 25.80 | 25.81 | 26.53 | 26.54 | 26.44 |
| Dataset | Bicubic | SR-CNN [9] | AR-CNN [14] | SR-DenseNet [18] | SR-ILLNN | SR-SLNN |
|---|---|---|---|---|---|---|
| Set5 | 0.8112 | 0.8599 | 0.8614 | 0.8844 | 0.8848 | 0.8827 |
| Set14 | 0.7033 | 0.7495 | 0.7511 | 0.7708 | 0.7709 | 0.7689 |
| BSD100 | 0.6699 | 0.7112 | 0.7126 | 0.7279 | 0.7275 | 0.7260 |
| Urban100 | 0.6589 | 0.7158 | 0.7177 | 0.7584 | 0.7583 | 0.7532 |
| Average | 0.6702 | 0.7192 | 0.7208 | 0.7481 | 0.7479 | 0.7447 |
| Skip Connections | Dense Connections | Set5 (PSNR) | Set14 (PSNR) | BSD100 (PSNR) | Urban100 (PSNR) | ||||
|---|---|---|---|---|---|---|---|---|---|
| SR-ILLNN | SR-SLNN | SR-ILLNN | SR-SLNN | SR-ILLNN | SR-SLNN | SR-ILLNN | SR-SLNN | ||
| Disable | Disable | 31.34 | 31.15 | 27.80 | 27.62 | 27.31 | 27.20 | 25.27 | 25.01 |
| Enable | Disable | 31.35 | 31.21 | 27.81 | 27.68 | 27.33 | 27.26 | 25.31 | 25.13 |
| Disable | Enable | 31.40 | 31.18 | 27.81 | 27.65 | 27.32 | 27.23 | 25.29 | 25.07 |
| Enable | Enable | 31.41 | 31.29 | 27.83 | 27.73 | 27.33 | 27.28 | 25.32 | 25.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Jun, D.; Kim, B.-G.; Lee, H.; Rhee, E. Single Image Super-Resolution Method Using CNN-Based Lightweight Neural Networks. Appl. Sci. 2021, 11, 1092. https://doi.org/10.3390/app11031092
Kim S, Jun D, Kim B-G, Lee H, Rhee E. Single Image Super-Resolution Method Using CNN-Based Lightweight Neural Networks. Applied Sciences. 2021; 11(3):1092. https://doi.org/10.3390/app11031092
Chicago/Turabian StyleKim, Seonjae, Dongsan Jun, Byung-Gyu Kim, Hunjoo Lee, and Eunjun Rhee. 2021. "Single Image Super-Resolution Method Using CNN-Based Lightweight Neural Networks" Applied Sciences 11, no. 3: 1092. https://doi.org/10.3390/app11031092
APA StyleKim, S., Jun, D., Kim, B.-G., Lee, H., & Rhee, E. (2021). Single Image Super-Resolution Method Using CNN-Based Lightweight Neural Networks. Applied Sciences, 11(3), 1092. https://doi.org/10.3390/app11031092







