Wind Tunnel Tests of 3D-Printed Variable Camber Morphing Wing
Abstract
:1. Introduction
2. Variable Camber Morphing Wing
2.1. Design Methodology
- A proper airfoil shape parametrization method, class–shape transformation (CST) , is used to describe the airfoil profile. As a combination of class and shape functions, class–shape transformation (CST) is a popular method of creating analytical representations of the surface coordinates of aerospace vehicles [41];
- A hybrid mesh deformation strategy consists of the deformation of the surface mesh by a radial basis function (RBF) tool, and the deformation of the surrounding volume mesh by the formulation of linear elasticity. The radial basis function is a real-valued function whose value depends only on the distance to the origin. It was first used to deal with the surface fitting problem of aircraft shape design by Hardy in 1971 [42];
- SU2 is an open-source suite for multiphysics simulation and design. It is a collection of software tools written in C++ and Python for the analysis of partial differential equations (PDEs) and PDE-constrained optimization problems on unstructured meshes with state-of-the-art numerical methods [43]. This was used as an aerodynamic and adjoint solver. Our analyses were carried out using fully turbulent fields that do not account for boundary layer transition.
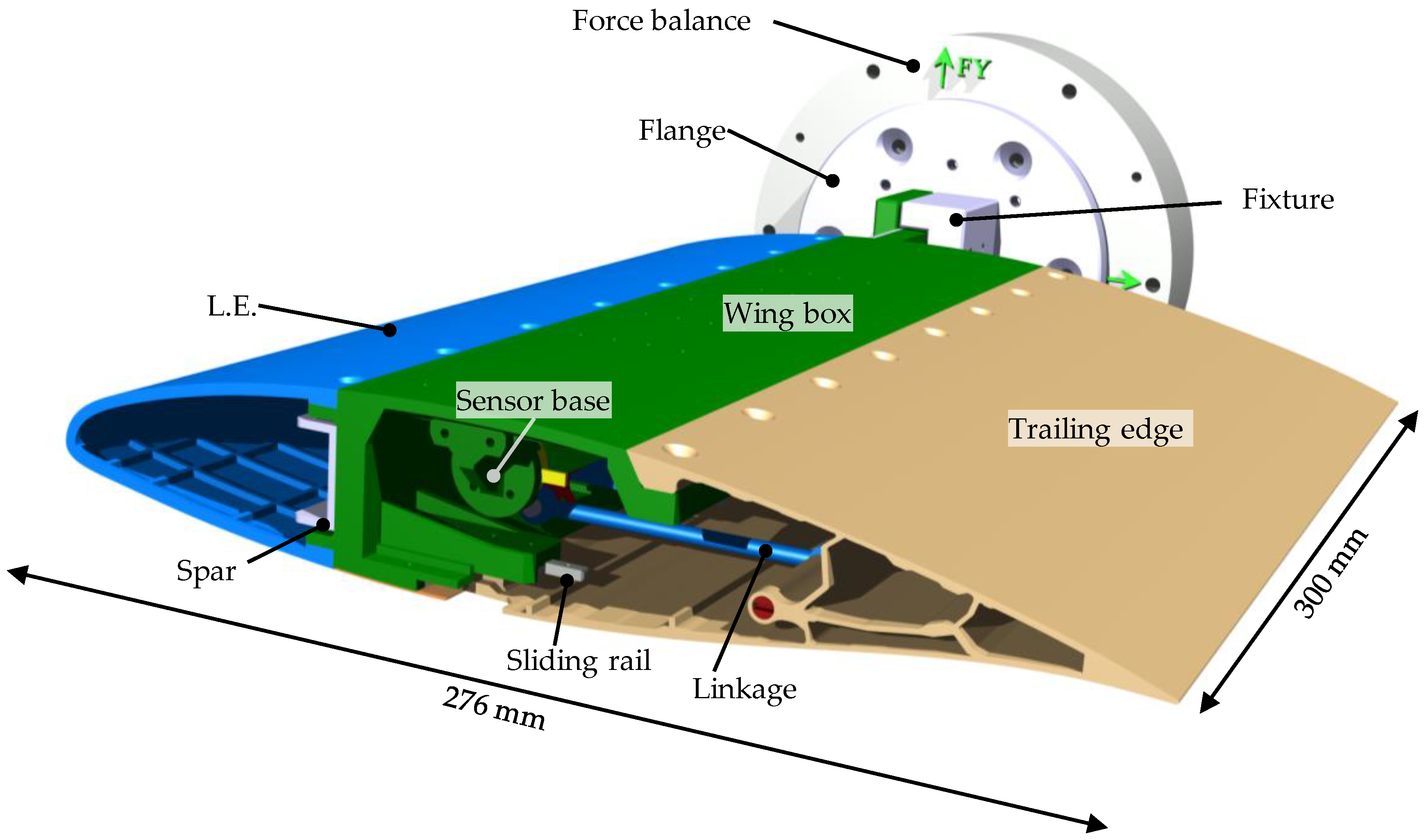
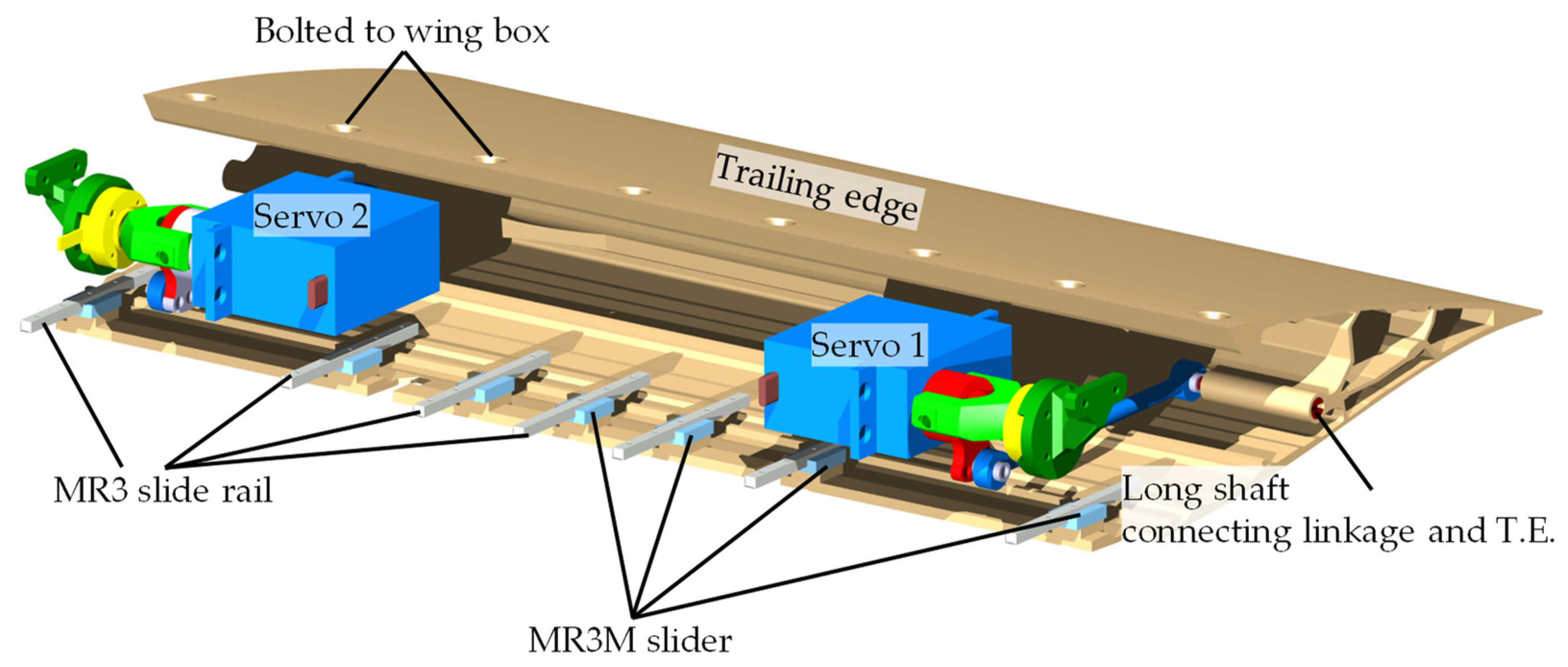
2.2. Wind Tunnel Model
2.3. Structural Properties
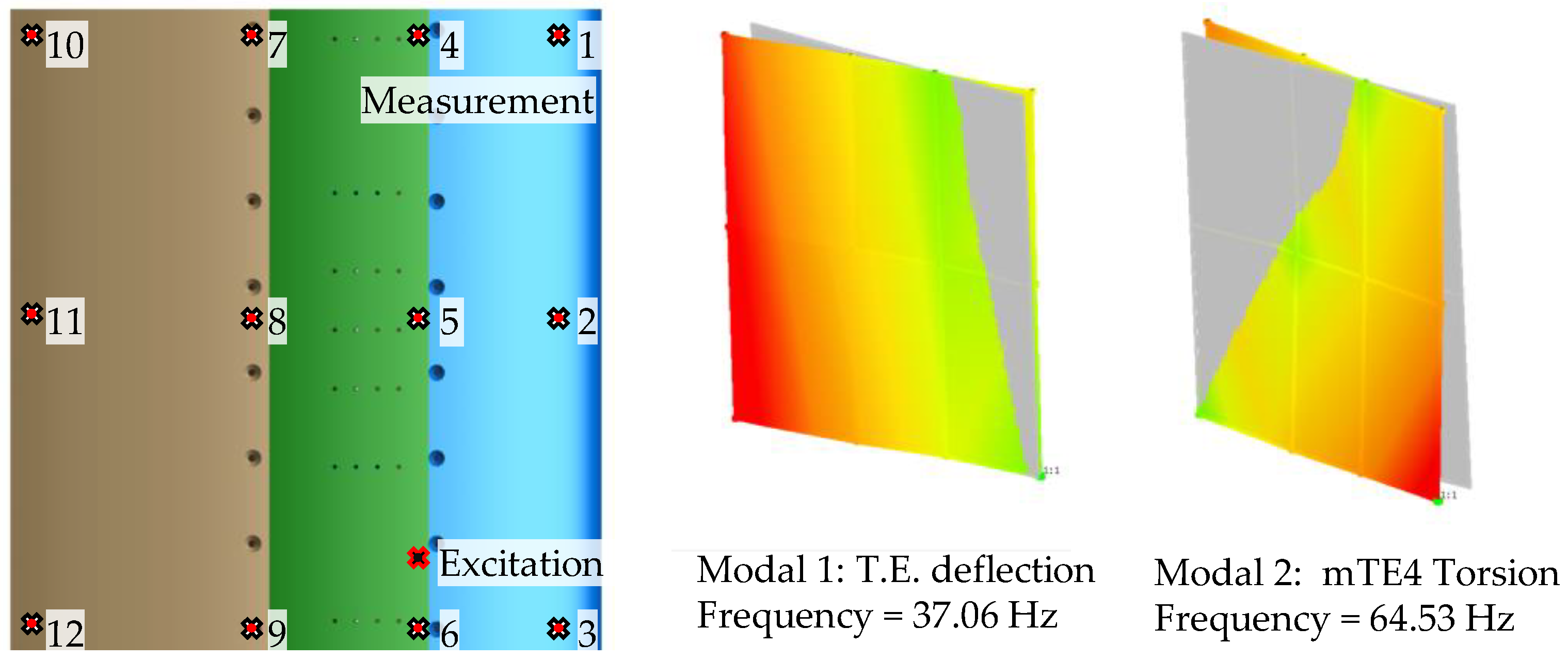
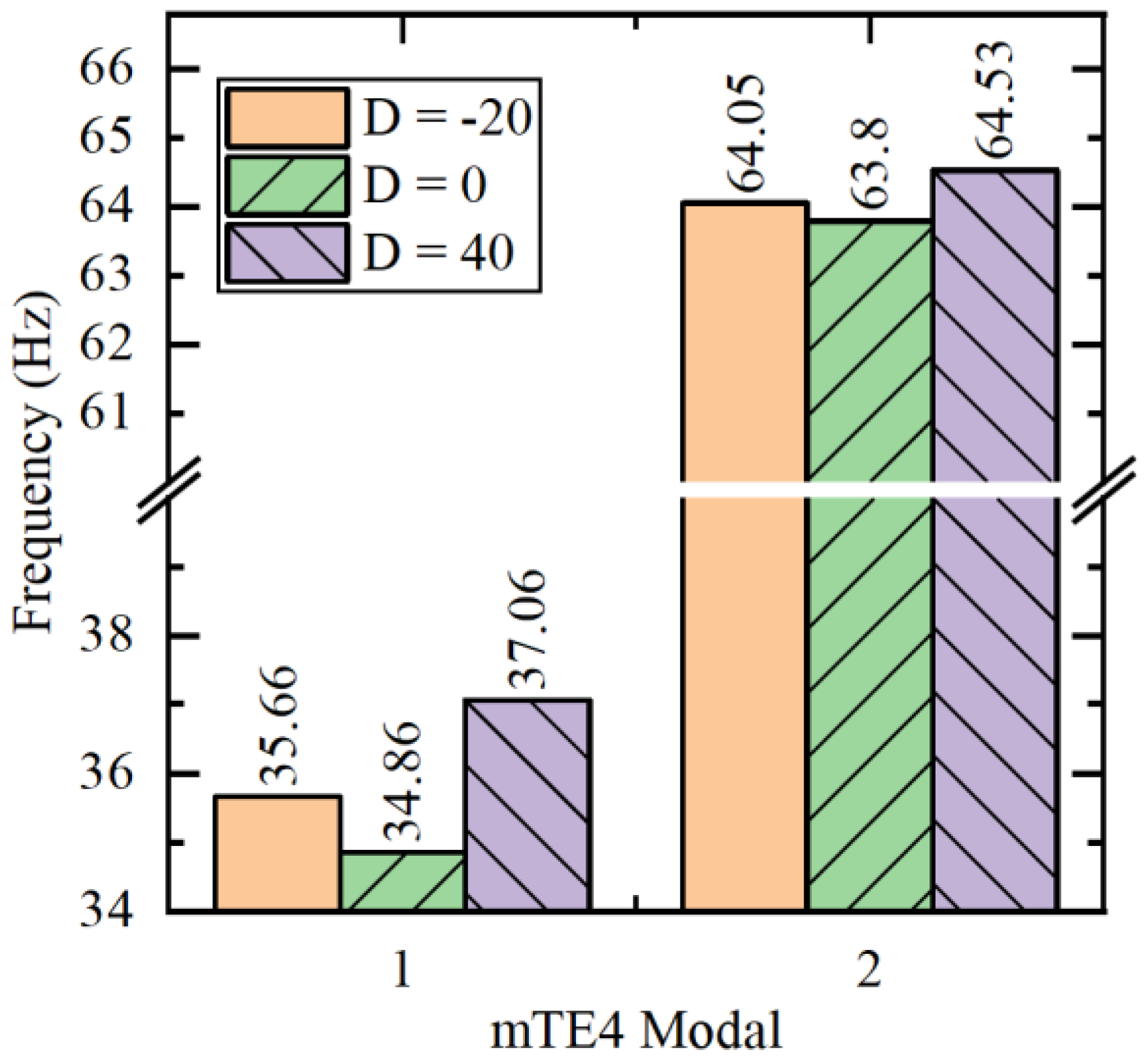
2.3.1. Modal Analysis
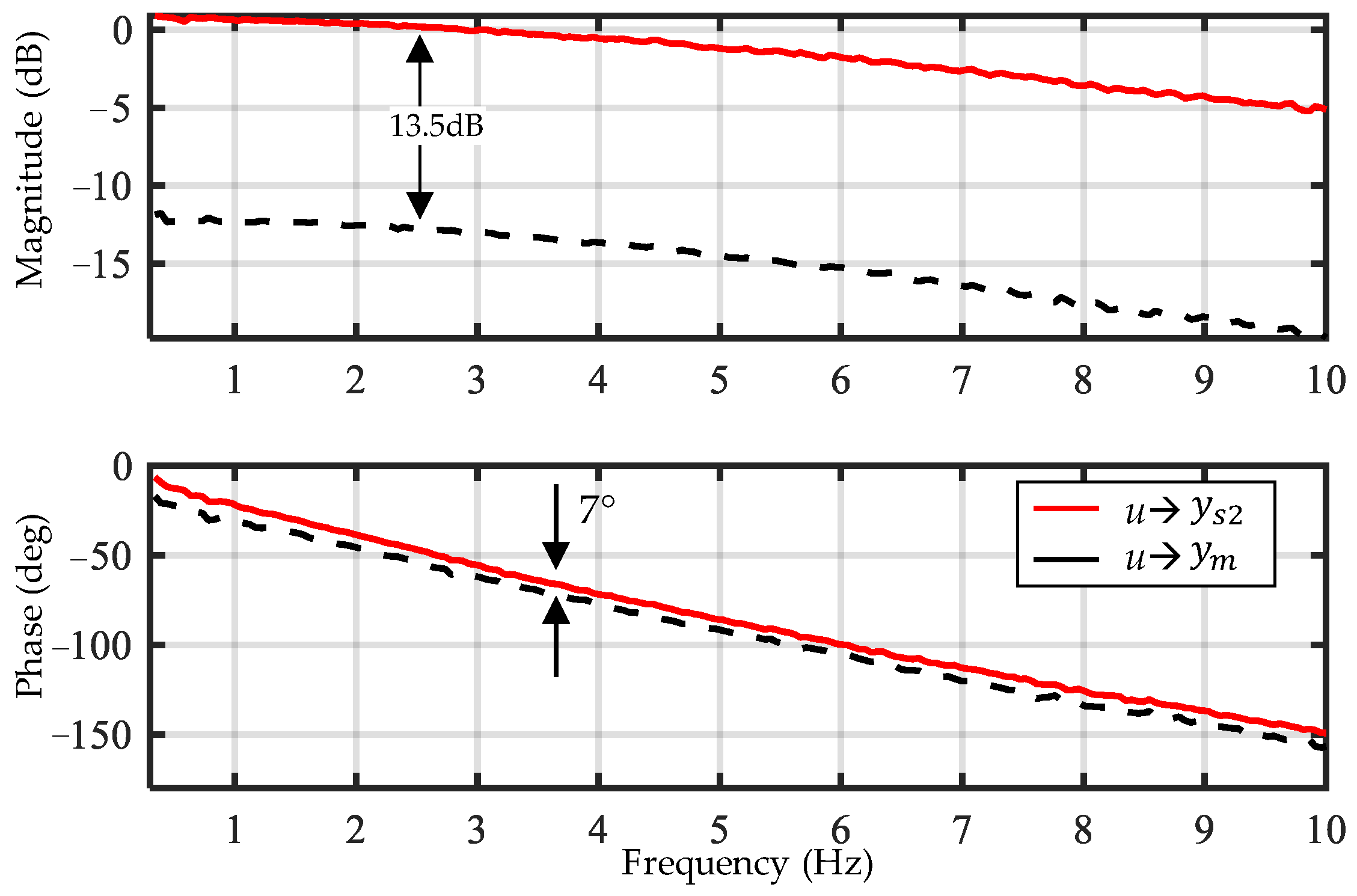
2.3.2. Dynamic Characteristics
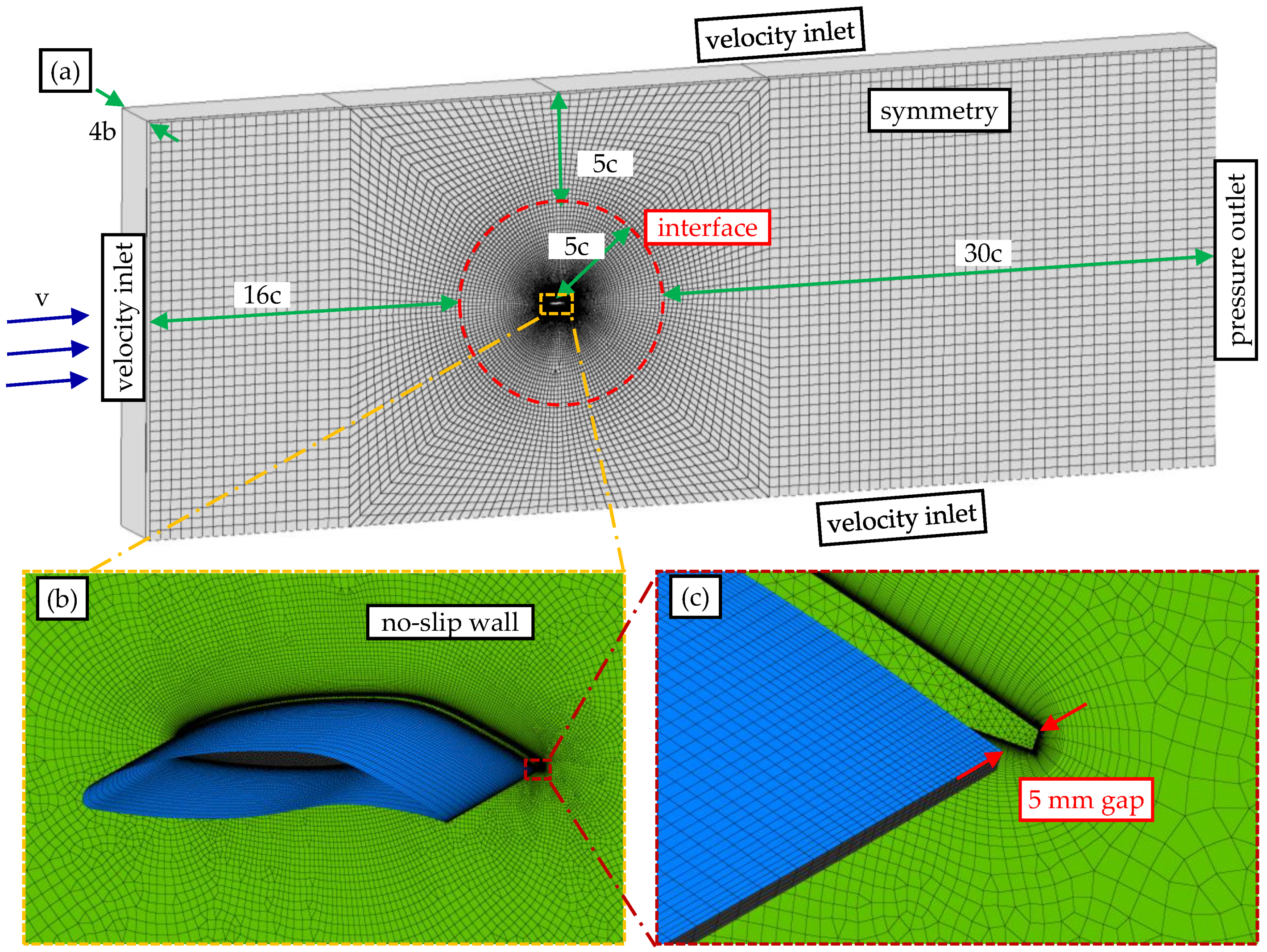
2.4. Numerical Aerodynamic Simulation
2.4.1. Numerical Methodologies
2.4.2. Results
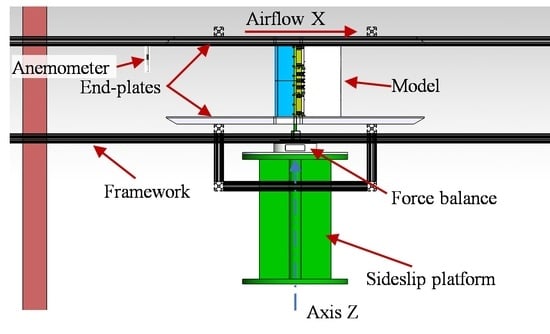
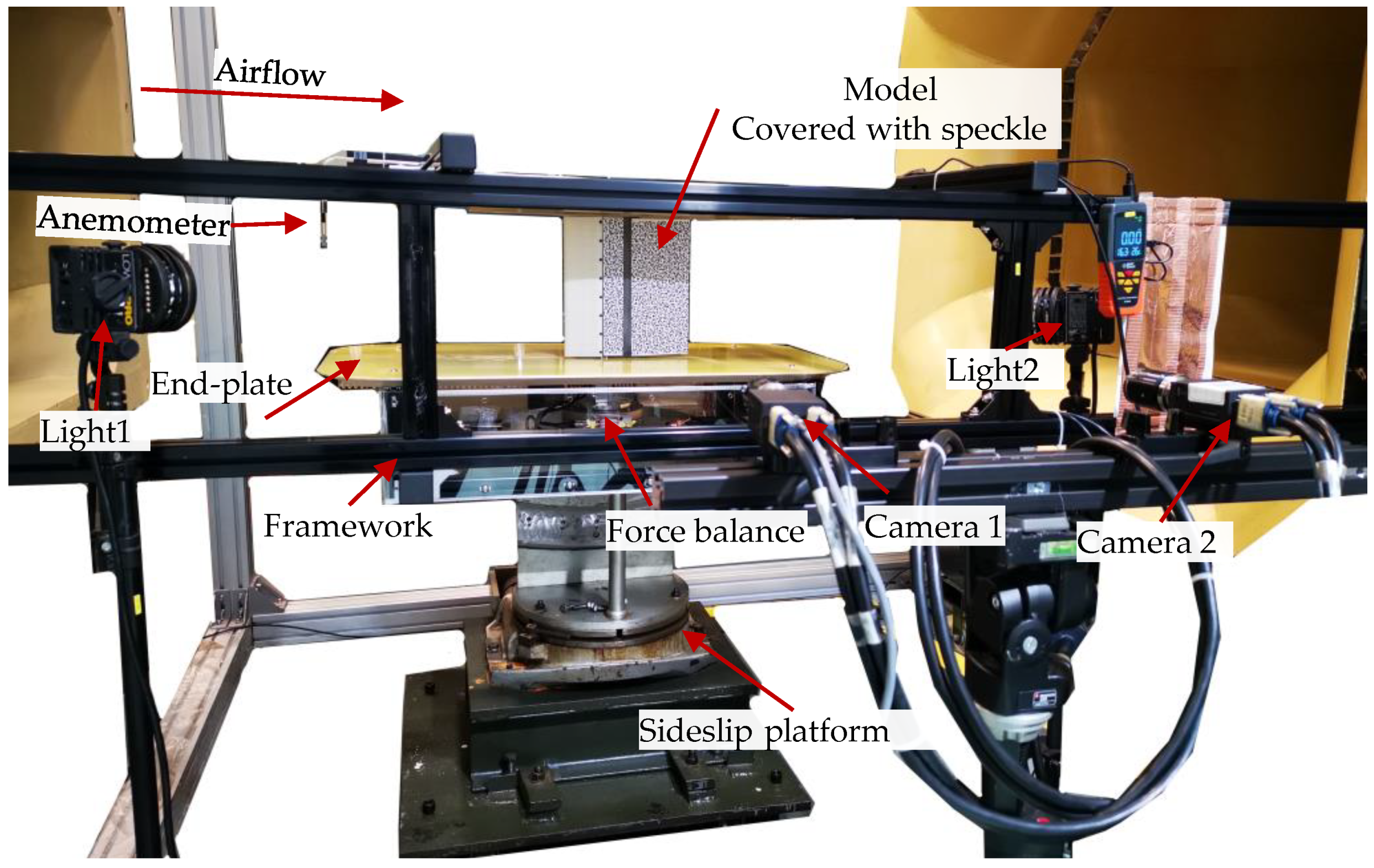
3. Wind Tunnel Setup
- Aerodynamic characteristics of mTE4 with different actuation inputs, airspeeds and angles of attack;
- Aeroelastic characteristics with different actuation inputs;
- Stall mitigation by trailing edge vibration with different frequencies and amplitudes.
4. Aerodynamic Results
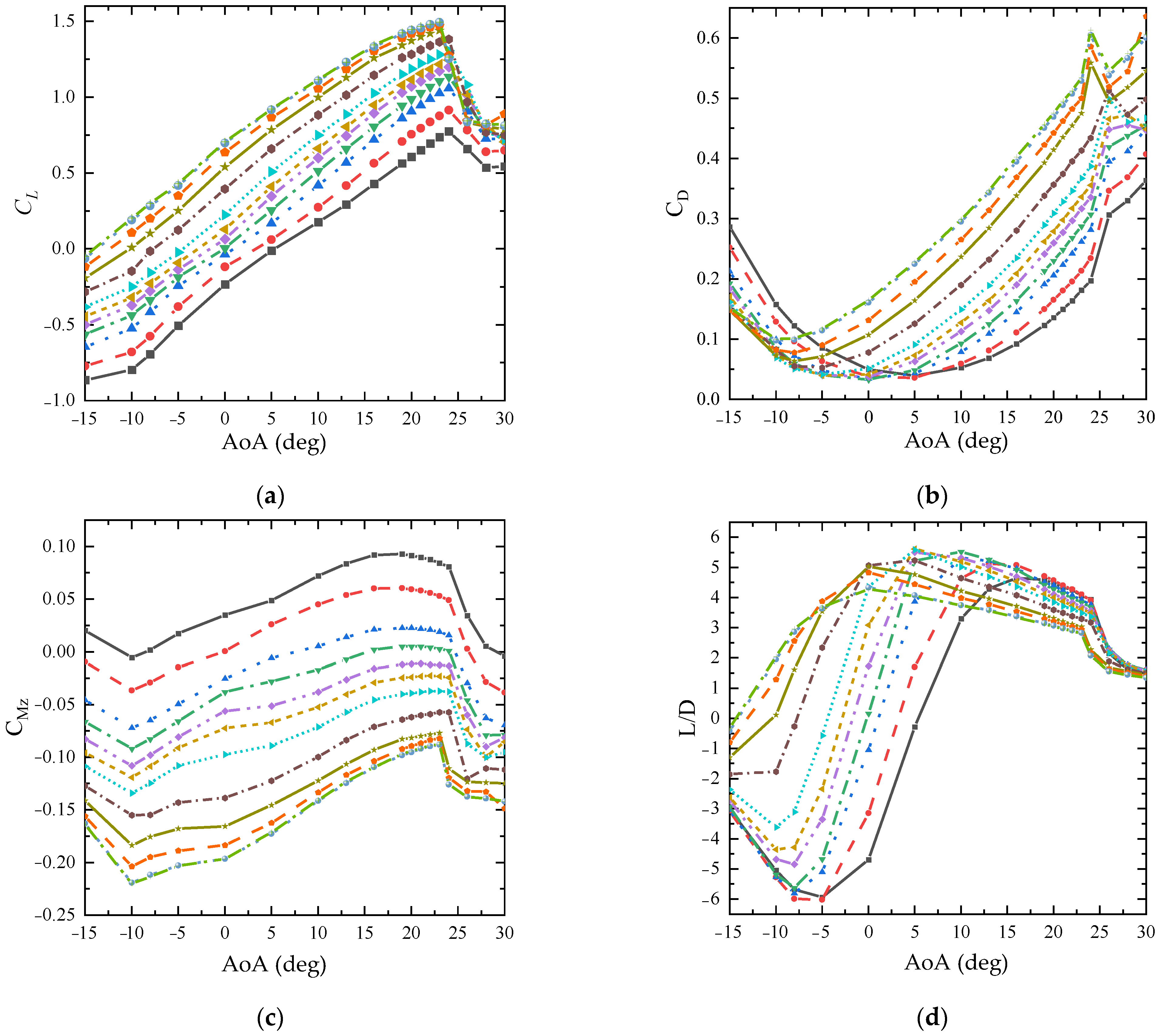
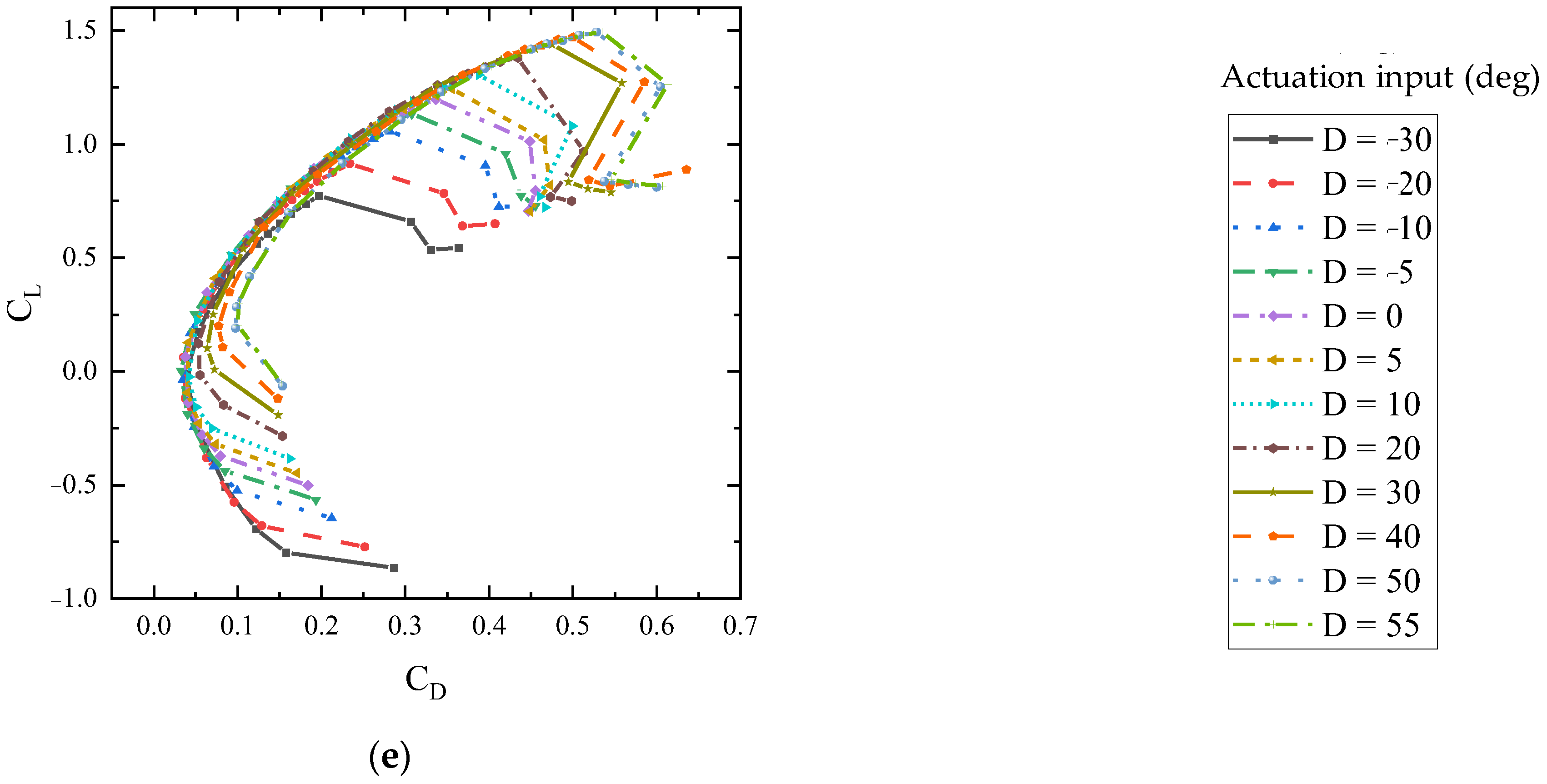
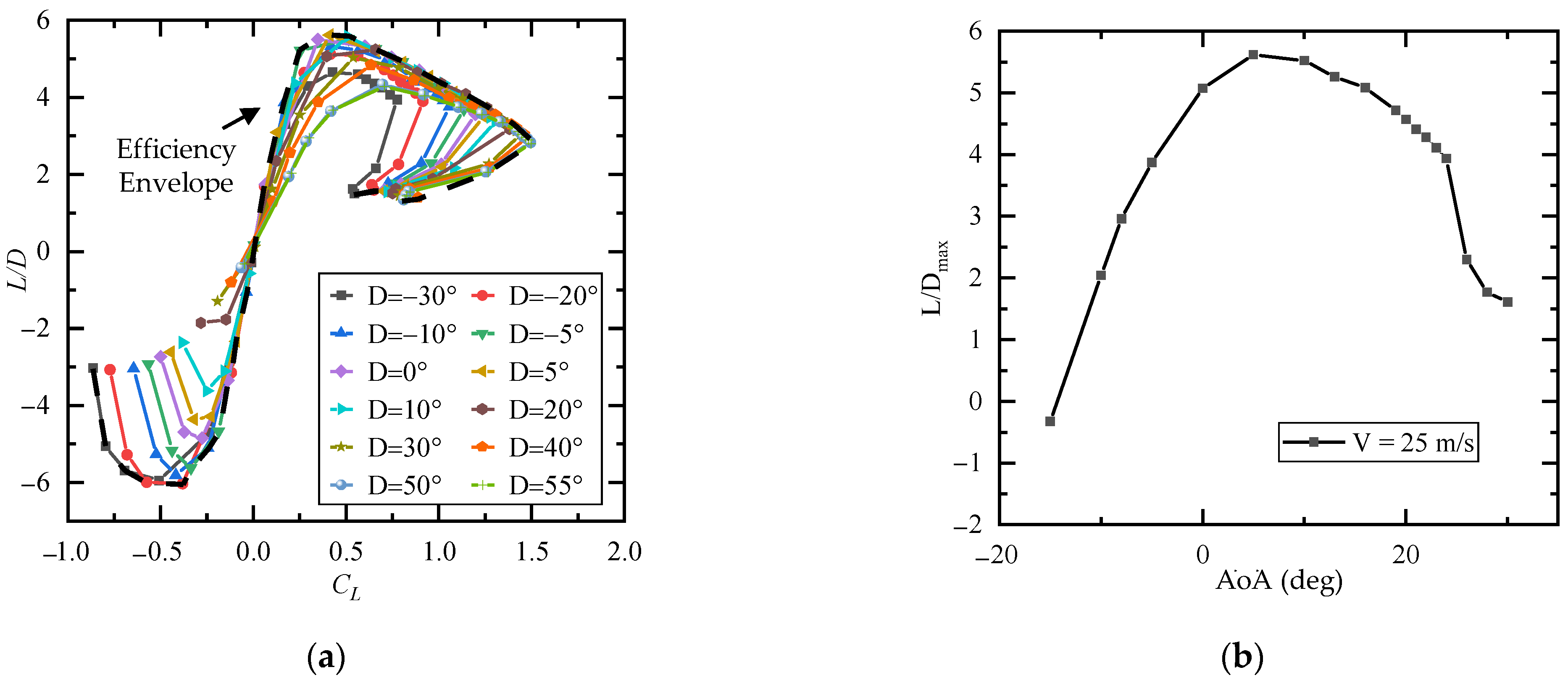
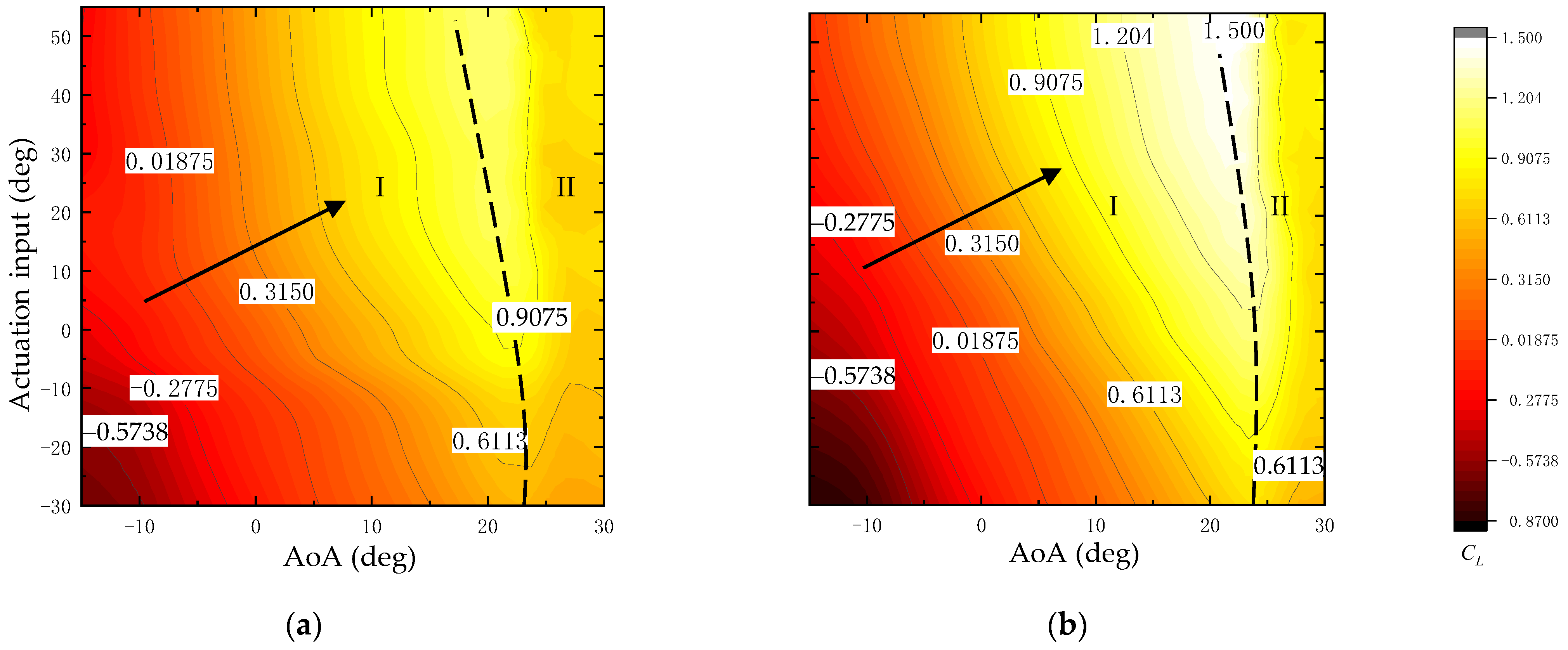
4.1. Aerodynamic Characteristics at Fixed Airspeed
4.2. Aerodynamic Characteristics at Various Airspeeds
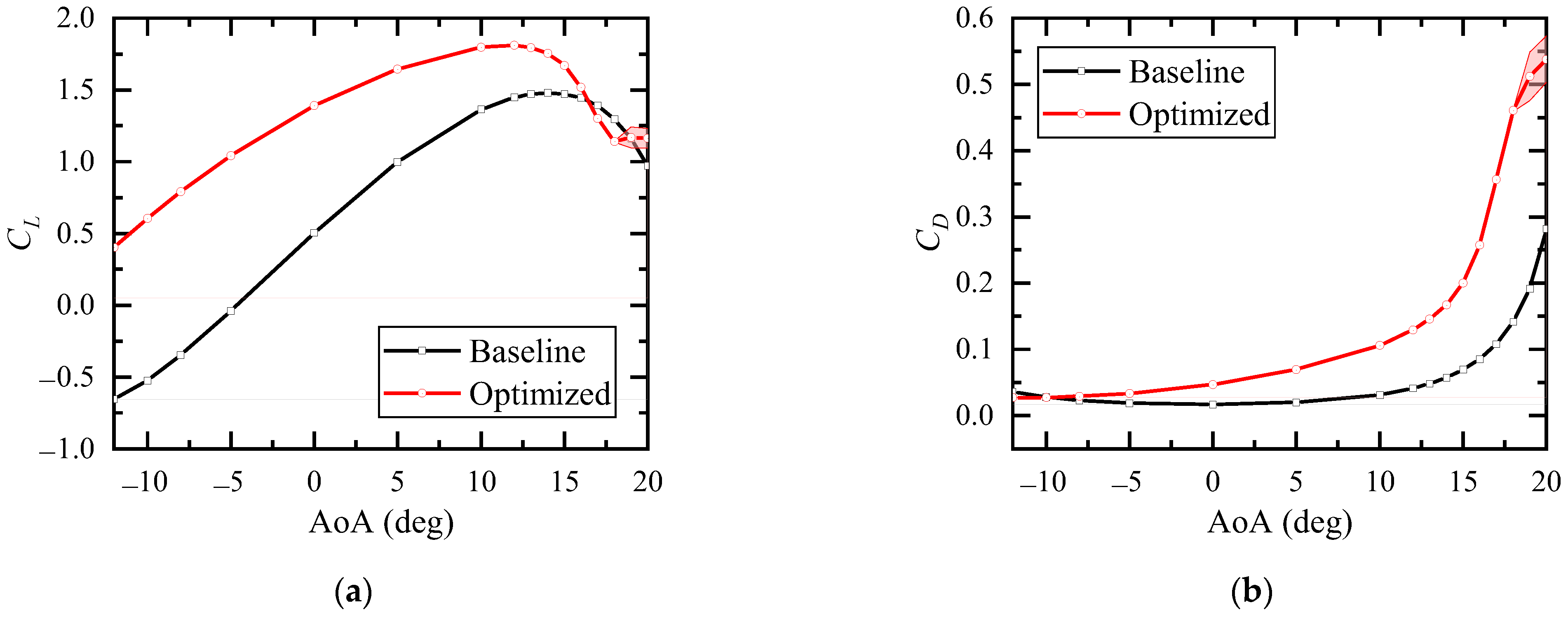
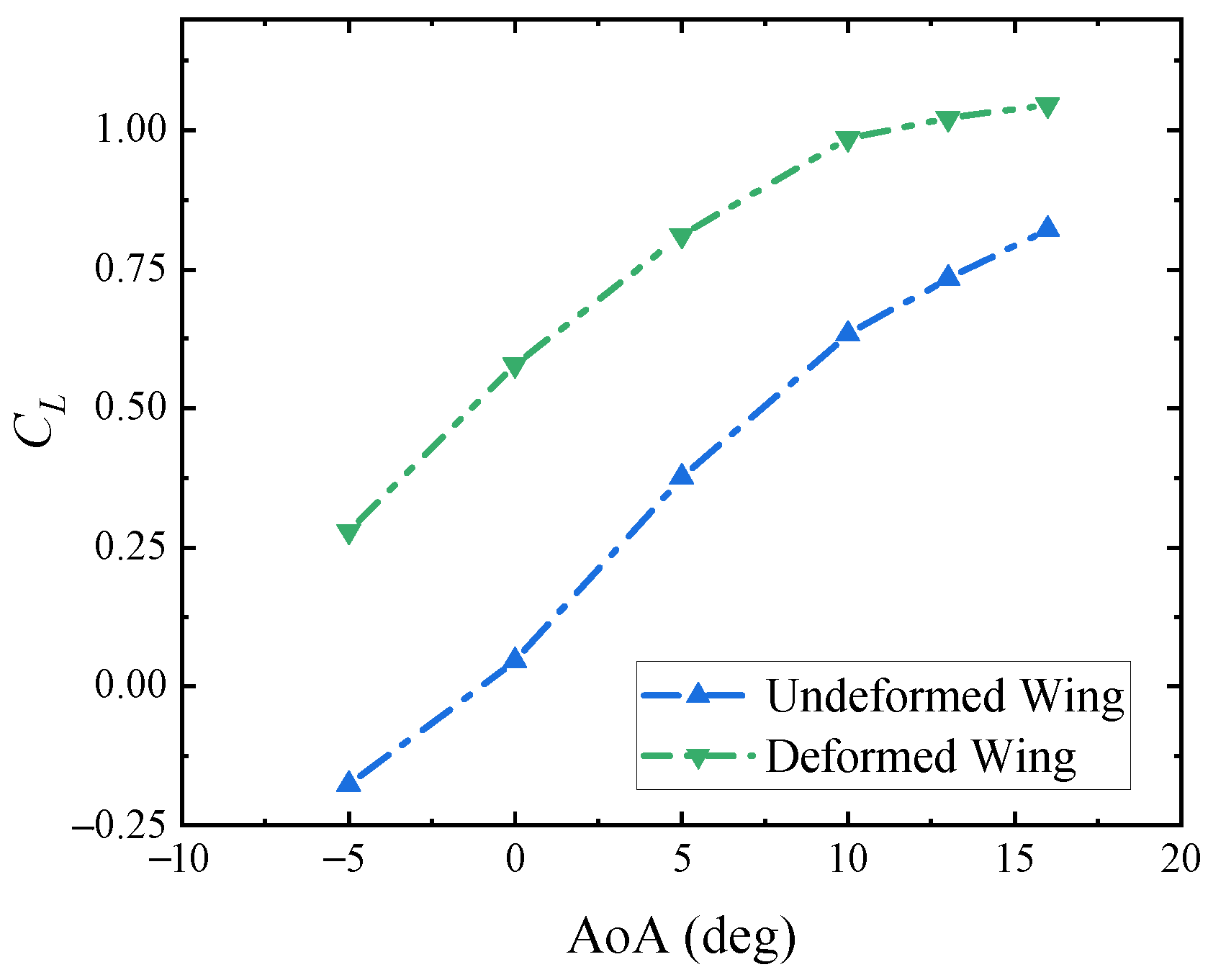
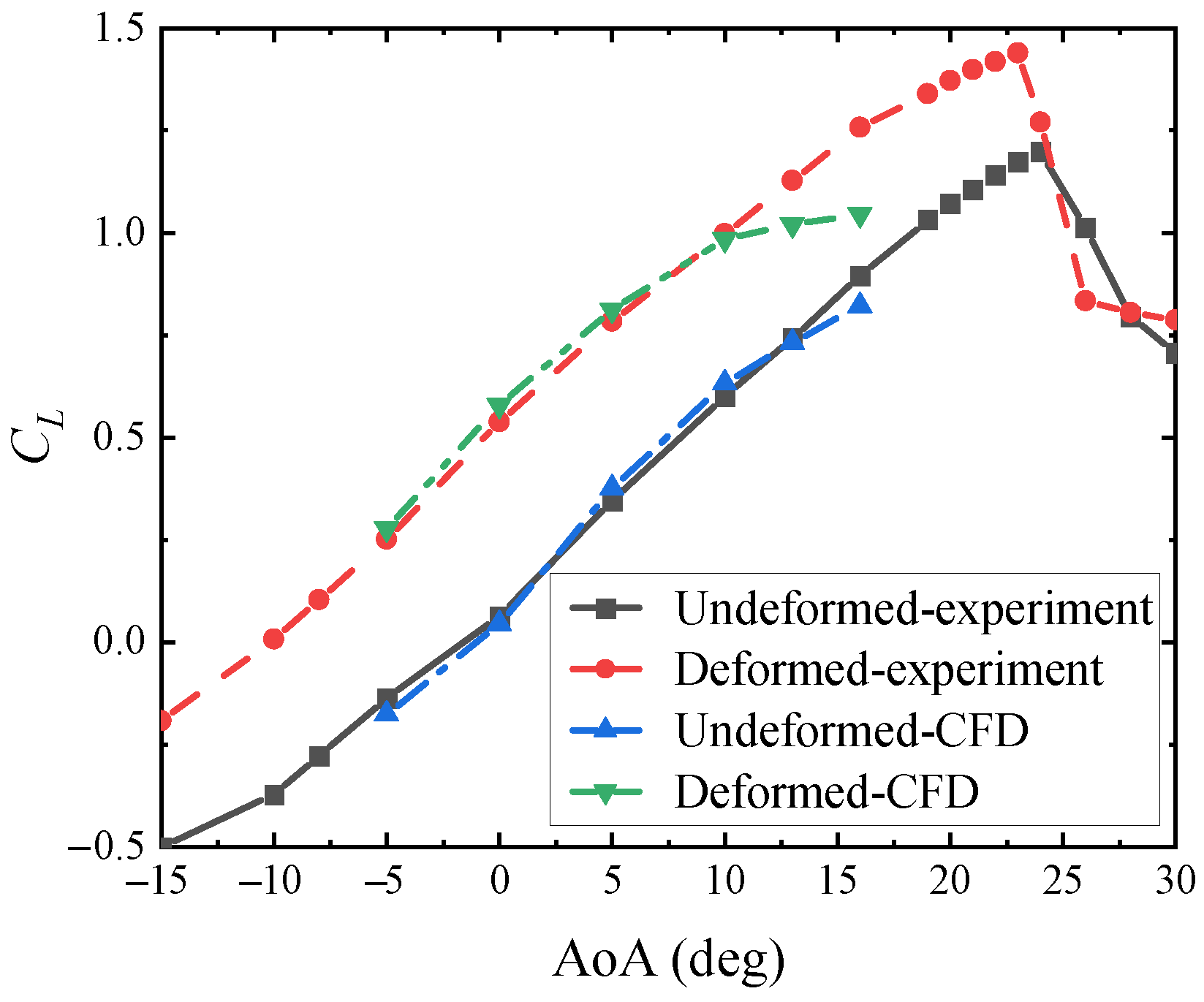
4.3. Comparison and Validation
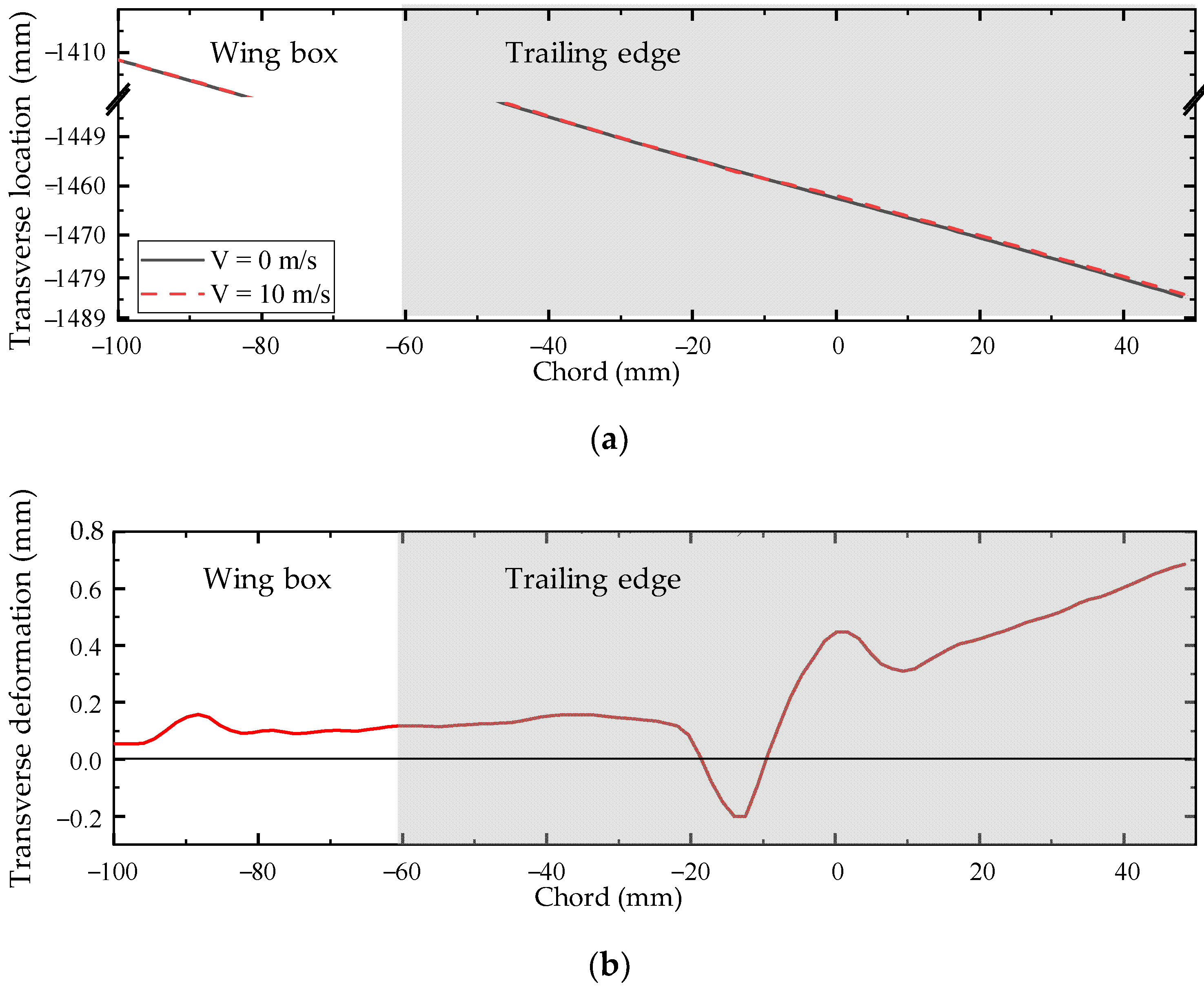
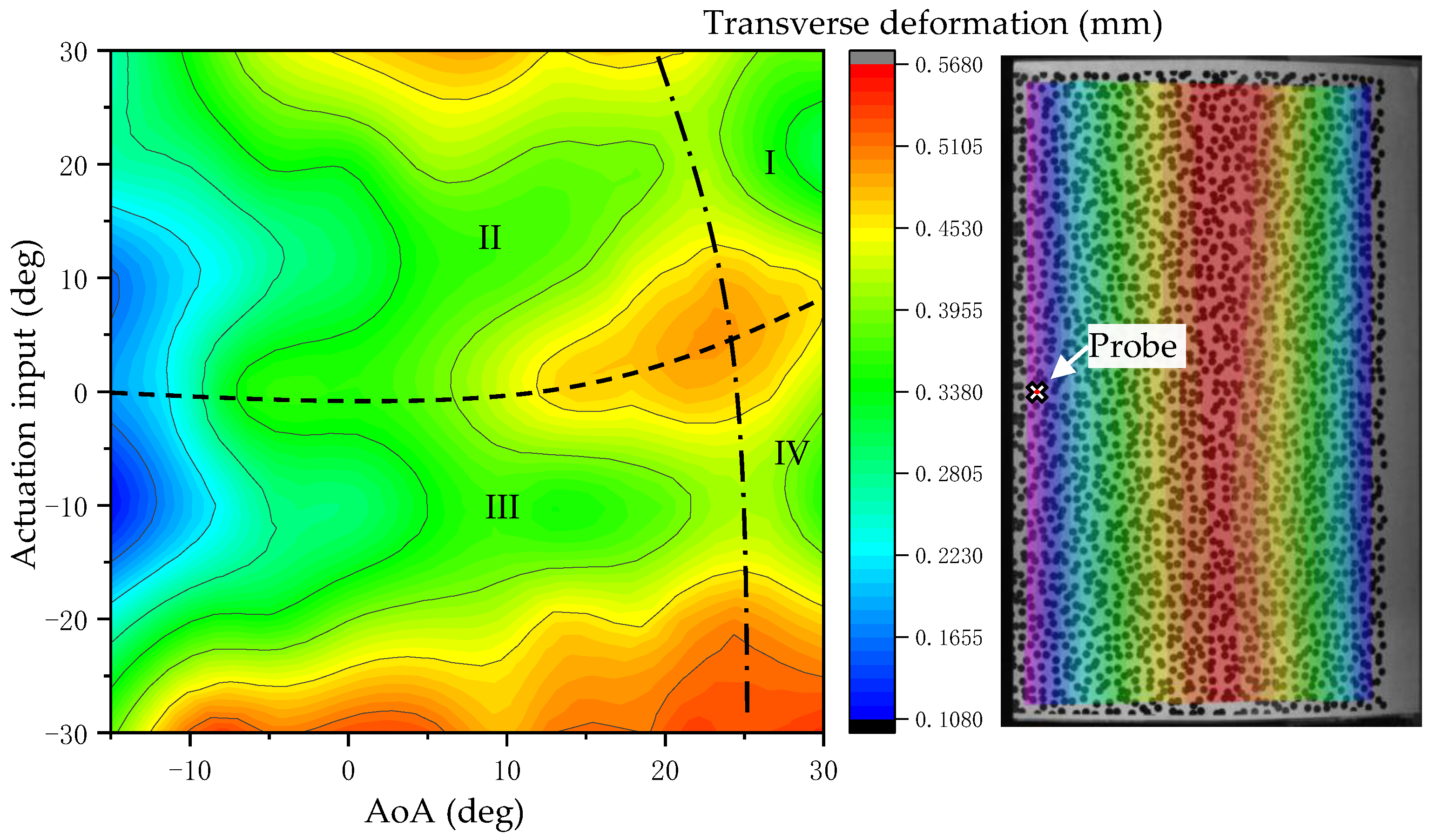
5. Aeroelastic Results
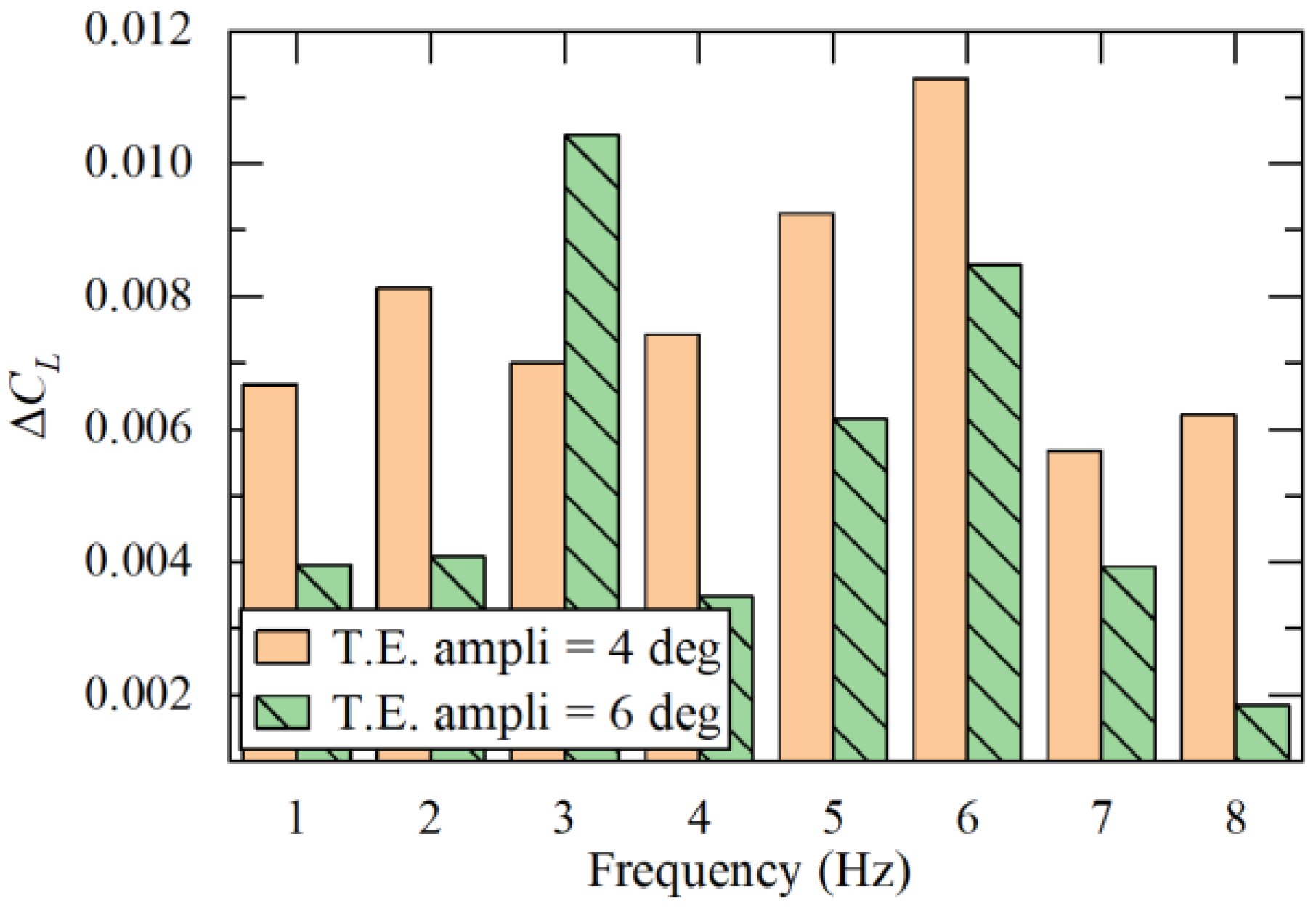
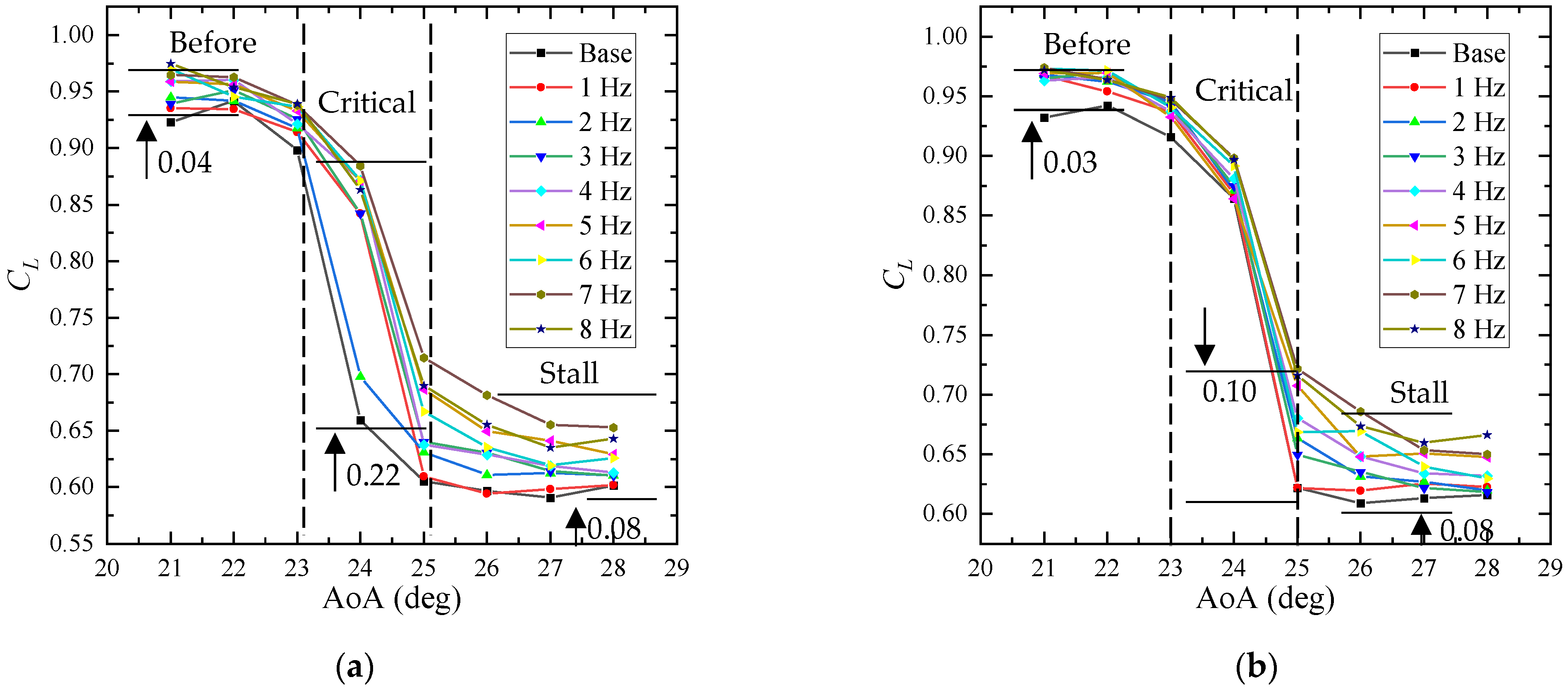
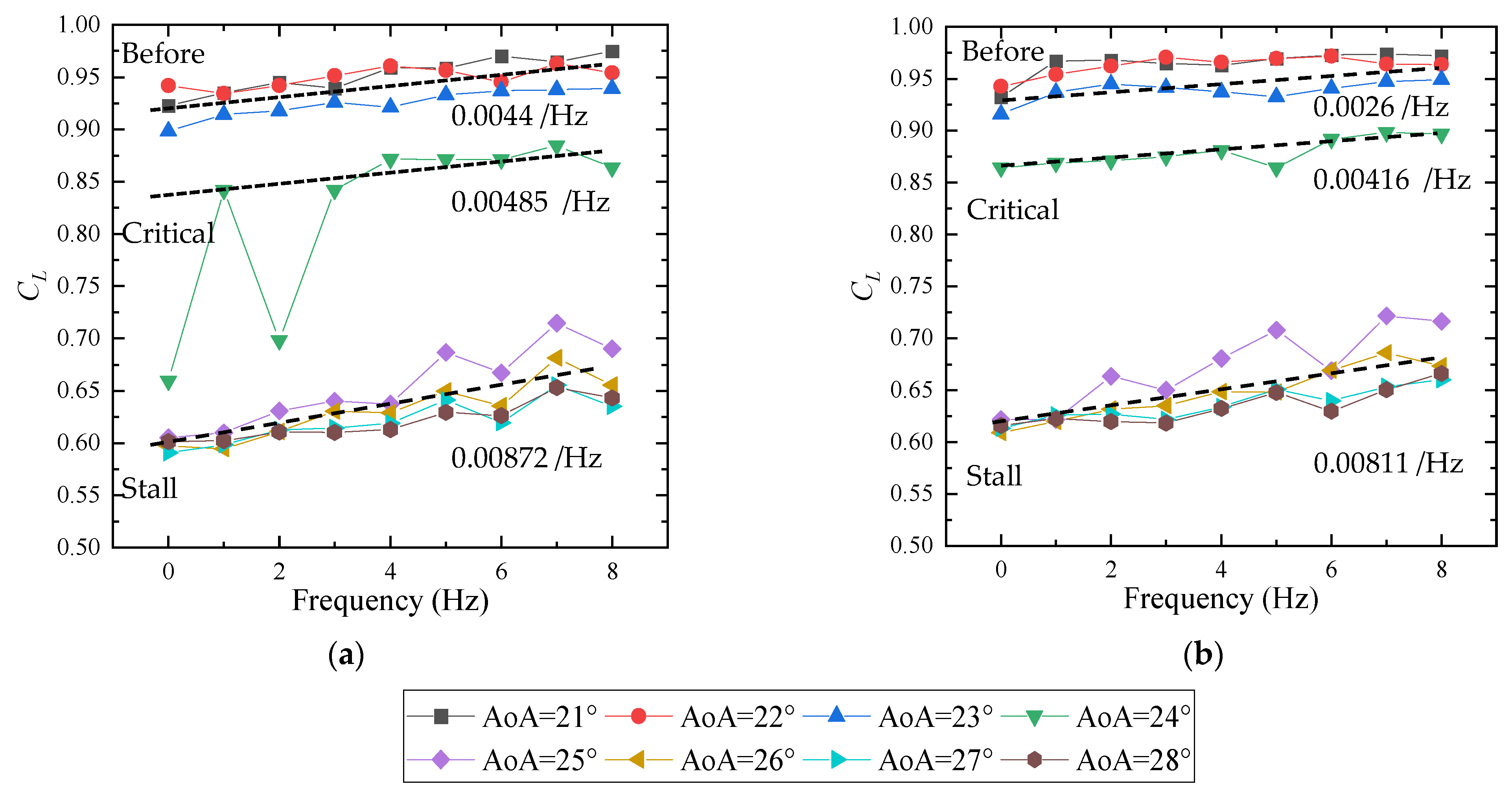
6. Application in Stall Mitigation
7. Conclusions
- The proposed morphing wing concept is manufacturable. Under actuation, the skin length of the trailing edge upper surface remains constant, and the lower surface is allowed to slide into the wing box, solving the challenge of skin continuity during the deformation process;
- The novel wing concept is actuated by a traditional servo system, while the aim of smoothing deformation is achieved by compliant mechanisms. The manufactured morphing wing can achieve a maximum deflection range of 37.9° continuously, proving its morphing capacity. The model operates as expected, demonstrating robustness and load-bearing ability;
- By activating the actuators, variations in lift coefficient ∆CL ≈ 0.23 and pitch moment coefficient ∆CMz ≈ 0.22 in various angles of attack at 25 m/s can be achieved;
- Different wind speeds lead to different Reynolds numbers, which affect the test results. As the airspeed increases, the airflow is less likely to separate from the upper surface of the wing, resulting in increments in the maximum lift coefficient, the stall angle, and the lift curve slope;
- Stall mitigation is achieved by periodically deflecting the morphing trailing edge, enabling a stall angle delay of approximately 1° and 13% increase in post-stall lift coefficient;
- Good correspondence between the CFD and the experimental lift coefficients validates the effectiveness of the development procedure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, B.; Yang, Y.; Qian, Z.; Wang, Z.; Lyu, S.; Sun, X. Technical development of variable camber wing: Review. Acta Aeronaut. Astronaut. Sin. 2022, 43, 024943. [Google Scholar] [CrossRef]
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswell, M.I.; Inman, D.J. A Review of Morphing Aircraft. J. Intell. Mater. Syst. Struct. 2011, 22, 823–877. [Google Scholar] [CrossRef]
- Chu, L.; Li, Q.; Gu, F.; Du, X.; He, Y.; Deng, Y. Design, Modeling, and Control of Morphing Aircraft: A Review. Chin. J. Aeronaut. 2021, 35, 220–246. [Google Scholar] [CrossRef]
- Ajaj, R.M.; Parancheerivilakkathil, M.S.; Amoozgar, M.; Friswell, M.I.; Cantwell, W.J. Recent Developments in the Aeroelasticity of Morphing Aircraft. Prog. Aerosp. Sci. 2021, 120, 100682. [Google Scholar] [CrossRef]
- Monner, H.P. Realization of an Optimized Wing Camber by Using Formvariable Flap Structures. Aerosp. Sci. Technol. 2001, 5, 445–455. [Google Scholar] [CrossRef]
- Wang, A.D.P.; Bartley-Cho, J.D.; Martin, C.A.; Hallam, B.J. Development of High-Rate Large-Deflection Hingeless Trailing-Edge Control Surface for the Smart Wing Wind Tunnel Model. In Proceedings of the SPIE’s International Symposium on Smart Structures and Materials, Newport Beach, CA, USA, 4–8 March 2001; pp. 407–418. [Google Scholar]
- Campanile, L.F.; Sachau, D. Belt-Rib Concept: A Structronic Approach to Variable Camber. J. Intell. Mater. Syst. Struct. 2000, 11, 215–224. [Google Scholar] [CrossRef]
- Woods, B.K.S.; Friswell, M.I. Preliminary Investigation of a Fishbone Active Camber Concept. In Proceedings of the ASME 2012 Conference on Smart Materials, Adaptive Structures and Intelligent System, Stone Mountain, GA, USA, 19–21 September 2012; Volume 2, pp. 555–563. [Google Scholar] [CrossRef]
- Hetrick, J.; Osborn, R.; Kota, S.; Flick, P.; Paul, D. Flight Testing of Mission Adaptive Compliant Wing. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2007; pp. 1–17. [Google Scholar]
- Wild, J. Recent Research Topics in High-Lift Aerodynamics. CEAS Aeronaut. J. 2016, 7, 345–355. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Guo, S.; Xiang, J. Modeling and Nonlinear Aeroelastic Analysis of a Wing with Morphing Trailing Edge. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2013, 227, 619–631. [Google Scholar] [CrossRef]
- Steenhuizen, D.; Van Tooren, M. The Implementation of a Knowledge-Based Framework for the Aerodynamic Optimization of a Morphing Wing Device. Adv. Eng. Inform. 2012, 26, 207–218. [Google Scholar] [CrossRef]
- Guo, S.; Li, D.; Liu, Y. Multi-Objective Optimization of a Composite Wing Subject to Strength and Aeroelastic Constraints. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2012, 226, 1095–1106. [Google Scholar] [CrossRef]
- Barbarino, M.; Dimino, I.; Carozza, A.; Nae, C.; Stoica, C.; Pricop, V.; Peng, S.H.; Eliasson, P.; Grundestam, O.; Tysell, L.; et al. Airframe Noise Reduction Technologies Applied to High-Lift Devices of Future Green Regional Aircraft. In Proceedings of the 3AF/CEAS Conference “Greener Aviation: Clean Sky Breakthroughs and Worldwide Status”, Brussel, Belgium, 12–14 March 2014; HAL: Brussel, Belgium, 2014; Volume hal-010821, pp. 1–11. [Google Scholar]
- Hellstrom, T. The Clean Sky “Smart Fixed Wing Aircraft Integrated Technology Demonstrator”: Technology Targets and Project Status. In Proceedings of the 27th Congress of the International Council of the Aeronautical Sciences 2010, ICAS 2010, Nice, France, 19–24 September 2010; Volume 6, pp. 5101–5110. [Google Scholar]
- Broughton-Venner, J.J.; Wynn, A.; Palacios, R. Aeroservoelastic Optimisation of an Aerofoil with Active Compliant Flap via Reparametrisation and Variable Selection. In Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Grapevine, TX, USA, 9–13 January 2017; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2017; pp. 1–20. [Google Scholar]
- Nickol, C.L.; Haller, W.J. Assessment of the Performance Potential of Advanced Subsonic Transport Concepts for NASA’s Environmentally Responsible Aviation Project. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; Volume F, pp. 1–21. [Google Scholar]
- Miller, E.J.; Cruz, J.; Lung, S.; Kota, S.; Ervin, G.; Lu, K.-J.; Flick, P. Evaluation of the Hinge Moment and Normal Force Aerodynamic Loads from a Seamless Adaptive Compliant Trailing Edge Flap in Flight. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Woods, B.K.S.; Parsons, L.; Coles, A.B.; Fincham, J.H.S.; Friswell, M.I. Morphing Elastically Lofted Transition for Active Camber Control Surfaces. Aerosp. Sci. Technol. 2016, 55, 439–448. [Google Scholar] [CrossRef] [Green Version]
- Woods, B.K.S.; Dayyani, I.; Friswell, M.I. Fluid/Structure-Interaction Analysis of the Fish-Bone-Active-Camber Morphing Concept. J. Aircr. 2015, 52, 307–319. [Google Scholar] [CrossRef] [Green Version]
- Ting, E.; Chaparro, D.; Nguyen, N.; Fujiwara, G.E.C. Optimization of Variable-Camber Continuous Trailing-Edge Flap Configuration for Drag Reduction. J. Aircr. 2018, 55, 2217–2239. [Google Scholar] [CrossRef]
- Vasista, S.; Riemenschneider, J.; van de Kamp, B.; Monner, H.P.; Cheung, R.C.M.; Wales, C.; Cooper, J.E. Evaluation of a Compliant Droop-Nose Morphing Wing Tip via Experimental Tests. J. Aircr. 2017, 54, 519–534. [Google Scholar] [CrossRef] [Green Version]
- Rudenko, A.; Hannig, A.; Monner, H.P.; Horst, P. Extremely Deformable Morphing Leading Edge: Optimization, Design and Structural Testing. J. Intell. Mater. Syst. Struct. 2018, 29, 764–773. [Google Scholar] [CrossRef]
- Wölcken, P.C.; Papadopoulos, M. Smart Intelligent Aircraft Structures (SARISTU); Wölcken, P.C., Papadopoulos, M., Eds.; Springer International Publishing: Hamburg, Germany, 2016; pp. 1–1025. [Google Scholar]
- Henry, A.C.; Molinari, G.; Rivas-Padilla, J.R.; Arrieta, A.F. Smart Morphing Wing: Optimization of Distributed Piezoelectric Actuation. AIAA J. 2019, 57, 2384–2393. [Google Scholar] [CrossRef]
- Keidel, D.; Molinari, G.; Ermanni, P. Aero-Structural Optimization and Analysis of a Camber-Morphing Flying Wing: Structural and Wind Tunnel Testing. J. Intell. Mater. Syst. Struct. 2019, 30, 908–923. [Google Scholar] [CrossRef]
- Radestock, M.; Riemenschneider, J.; Monner, H.P.; Huxdorf, O.; Werter, N.P.M.; De Breuker, R. Deformation Measurement in the Wind Tunnel for an UAV Leading Edge with a Morphing Mechanism. In Proceedings of the 30th Congress of the International Council of the Aeronautical Sciences, Daejeon, Korea, 25–30 September 2016; pp. 1–9. [Google Scholar]
- Riemenschneider, J.; Radestock, M.; Vasista, S.; Huxdorf, O.; Monner, H.P. Droop Nose with Elastic Skin. In Proceedings of the ASME 2016 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Stowe, VT, USA, 28–30 September 2016; ASME: Stowe, VT, USA, 2016; pp. 1–8. [Google Scholar]
- Dimino, I.; Moens, F.; Pecora, R.; Ricci, S.; Ameduri, S.; Concilio, A.; Mercurio, U.; Carossa, G.M. Morphing Wing Technologies within the Airgreen 2 Project. AIAA Sci. Technol. Forum Expo. AIAA SciTech Forum 2022, 2022, 0718. [Google Scholar] [CrossRef]
- Pecora, R. Morphing Wing Flaps for Large Civil Aircraft: Evolution of a Smart Technology across the Clean Sky Program. Chin. J. Aeronaut. 2021, 34, 13–28. [Google Scholar] [CrossRef]
- Mkhoyan, T.; Thakrar, N.R.; De Breuker, R.; Sodja, J. Design and Development of a Seamless Smart Morphing Wing Using Distributed Trailing Edge Camber Morphing for Active Control. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–15 & 19–21 January 2021; pp. 1–16. [Google Scholar]
- Simiriotis, N.; Jodin, G.; Marouf, A.; Elyakime, P.; Hoarau, Y.; Hunt, J.C.R.; Rouchon, J.F.; Braza, M. Morphing of a Supercritical Wing by Means of Trailing Edge Deformation and Vibration at High Reynolds Numbers: Experimental and Numerical Investigation. J. Fluids Struct. 2019, 91, 102676. [Google Scholar] [CrossRef] [Green Version]
- Howell, L.L. Compliant Mechanisms; John Wiley: New York, NY, USA, 2001; ISBN 0-471-38478-X. [Google Scholar]
- Herrera, C.; Spivey, N.; Lung, S.; Ervin, G.; Flick, P. Aeroelastic Response of the ACTE Transition Section. In Proceedings of the 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, San Diego, CA, USA, 4–8 January 2016; pp. 1–19. [Google Scholar]
- Saggere, L.; Kota, S. Static Shape Control of Smart Structures Using Compliant Mechanisms. AIAA J. 1999, 37, 572–578. [Google Scholar] [CrossRef]
- Kota, S.; Flick, P.; Collier, F.S. Flight Testing of FlexFloil TM Adaptive Compliant Trailing Edge. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- De Gaspari, A.; Ricci, S. A Two-Level Approach for the Optimal Design of Morphing Wings Based On Compliant Structures. J. Intell. Mater. Syst. Struct. 2011, 22, 1091–1111. [Google Scholar] [CrossRef]
- De Gaspari, A.; Riccobene, L.; Ricci, S. Design, Manufacturing and Wind Tunnel Validation of a Morphing Compliant Wing. J. Aircr. 2018, 55, 2313–2326. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Ge, W.; Zhang, Z.; Mo, X.; Zhang, Y. Design of Compliant Mechanism-Based Variable Camber Morphing Wing with Nonlinear Large Deformation. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419886740. [Google Scholar] [CrossRef]
- Zhang, Z.; De Gaspari, A.; Ricci, S.; Song, C.; Yang, C. Gradient-Based Aerodynamic Optimization of an Airfoil with Morphing Leading and Trailing Edges. Appl. Sci. 2021, 11, 1929. [Google Scholar] [CrossRef]
- Olson, E.D. Three-Dimensional Piecewise-Continuous Class-Shape Transformation of Wings. In Proceedings of the Multidisciplinary Analysis and Optimization Conference, Dallas, TX, USA, 22–26 June 2015; pp. 1–16. [Google Scholar]
- Hardy, R.L. Theory and Applications of the Multiquadric-Biharmonic Method 20 Years of Discovery 1968-1988. Comput. Math. Appl. 1990, 19, 163–208. [Google Scholar] [CrossRef] [Green Version]
- SU2 v7.4.0 Blackbird. Available online: https://su2code.github.io/ (accessed on 10 August 2022).
- Eiter, T.; Mannila, H. Computing Discrete Fréchet Distance; Citeseer: Princeton, NJ, USA, 1994. [Google Scholar]
- Molinari, G. Multidisciplinary Optimization of Morphing Wings with Distributed Compliance and Smart Actuation. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2016. [Google Scholar]
- Zhang, Z.; Jia, S.; Song, C.; Yang, C. Optimum design of wind tunnel test model for compliant morphing trailing edge. Acta Aeronaut. Astronaut. Sin. 2021, 43, 026071. [Google Scholar] [CrossRef]
- Shenzhen Wenext Technology Co., Ltd. Material Manual. 2021. Available online: https://www.wenext.cn/index.php?route=product/material/view&material_id=27 (accessed on 8 August 2022).
- Schreier, H.; Orteu, J.J.; Sutton, M.A. Image Correlation for Shape, Motion and Deformation Measurements: Basic Concepts, Theory and Applications; Springer: New York, NY, USA, 2009; ISBN 9780387787466. [Google Scholar]
- Bigger, R.; Blaysat, B.; Boo, C.; Grewer, M.; Hu, J.; Jones, A.; Klein, M.; Raghavan, K.; Reu, P.; Schmidt, T.; et al. A Good Practices Guide for Digital Image Correlation; Jones, E., Iadicola, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Tank, J.D.; Klose, B.F.; Jacobs, G.B.; Spedding, G.R. Flow Transitions on a Cambered Airfoil at Moderate Reynolds Number. Phys. Fluids 2021, 33, 093105. [Google Scholar] [CrossRef]
- Woods, B.K.; Bilgen, O.; Friswell, M.I. Wind Tunnel Testing of the Fish Bone Active Camber Morphing Concept. J. Intell. Mater. Syst. Struct. 2014, 25, 772–785. [Google Scholar] [CrossRef]
- Rivero, A.E.; Fournier, S.; Manolesos, M.; Cooper, J.E.; Woods, B.K.S.S. Experimental Aerodynamic Comparison of Active Camber Morphing and Trailing-Edge Flaps. AIAA J. 2021, 59, 2627–2640. [Google Scholar] [CrossRef]
- Rogers, S.E.; Roth, K.; Cao, H.V.; Slotnick, J.P.; Whitlock, M.; Nash, S.M.; David Baker, M. Computation of Viscous Flow for a Boeing 777 Aircraft in Landing Configuration. In Proceedings of the 18th Applied Aerodynamics Conference, Denver, CO, USA, 14–17 August 2000; pp. 1–11. [Google Scholar] [CrossRef]
- Kan, Z.; Li, D.; Xiang, J.; Cheng, C. Delaying Stall of Morphing Wing by Periodic Trailing-Edge Deflection. Chin. J. Aeronaut. 2020, 33, 493–500. [Google Scholar] [CrossRef]
- Jodin, G.; Motta, V.; Scheller, J.; Duhayon, E.; Döll, C.; Rouchon, J.F.; Braza, M. Dynamics of a Hybrid Morphing Wing with Active Open Loop Vibrating Trailing Edge by Time-Resolved PIV and Force Measures. J. Fluids Struct. 2017, 74, 263–290. [Google Scholar] [CrossRef]











| Project | Abbreviation | Period |
|---|---|---|
| Smart High Lift Devices for Next Generation Wings [10,11,12,13] | SADE | 2008–2012 |
| Smart Fixed Wing Aircraft [14,15] | SFWA | 2008–2017 |
| Mission Adaptive Compliant Wing [16,17,18] | MACW | 1998–2020 |
| Optimization of Multiscale Structures with Applications to Morphing Aircraft [19,20] | OMSASA | 2010–2015 |
| Variable Camber Continuous Trailing Edge Flap [21] | VCCTEF | 2010 |
| Novel Air Vehicle Configurations: From Fluttering Wings to Morphing Flight [22,23] | NOVEMOR | 2011–2015 |
| Smart Intelligent Aircraft Structures [24] | SARISTU | 2011–2015 |
| Smart Morphing Wing [25,26] | ETH–SMW | 2011–2019 |
| Combined morphing assessment software using flight envelope data and mission-based morphing prototype wing development [27,28] | CHANGE | 2012–2015 |
| AIRGREEN2 [29,30] | AG2 | 2014–2021 |
| Smart-X [31] | Smart–X | 2016–2022 |
| Smart Morphing and Sensing [32] | SMS | 2017–2020 |
| Part | Material Name | Serial | Manufacturing Technique | Tensile Modulus (MPa) | Tensile Strength (MPa) |
|---|---|---|---|---|---|
| Leading edge | Photosensitive resin | 8200 Pro Resin | Stereolithographic (SLA) | 2589~2695 | 38~56 |
| Wing box | Glass fiber-reinforced polyamide 12 | 7200 Nylon | Selective laser sintering (SLS) | 3500 | 44 |
| Compliant morphing trailing edge | HP 3D polyamide 12 | 7500 Nylon | Multi Jet Fusion (MJF) | 1700 | 48 |
| Frequency (Hz) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Reduced Frequency | 0.1759 | 0.3519 | 0.5278 | 0.7037 | 0.8796 | 1.0556 | 1.2315 | 1.4074 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, S.; Zhang, Z.; Zhang, H.; Song, C.; Yang, C. Wind Tunnel Tests of 3D-Printed Variable Camber Morphing Wing. Aerospace 2022, 9, 699. https://doi.org/10.3390/aerospace9110699
Jia S, Zhang Z, Zhang H, Song C, Yang C. Wind Tunnel Tests of 3D-Printed Variable Camber Morphing Wing. Aerospace. 2022; 9(11):699. https://doi.org/10.3390/aerospace9110699
Chicago/Turabian StyleJia, Sijia, Zhenkai Zhang, Haibo Zhang, Chen Song, and Chao Yang. 2022. "Wind Tunnel Tests of 3D-Printed Variable Camber Morphing Wing" Aerospace 9, no. 11: 699. https://doi.org/10.3390/aerospace9110699
APA StyleJia, S., Zhang, Z., Zhang, H., Song, C., & Yang, C. (2022). Wind Tunnel Tests of 3D-Printed Variable Camber Morphing Wing. Aerospace, 9(11), 699. https://doi.org/10.3390/aerospace9110699