Optimization of Apron Support Vehicle Operation Scheduling Based on Multi-Layer Coding Genetic Algorithm
Abstract
:1. Introduction
2. Operation Analysis of Apron Support Vehicles
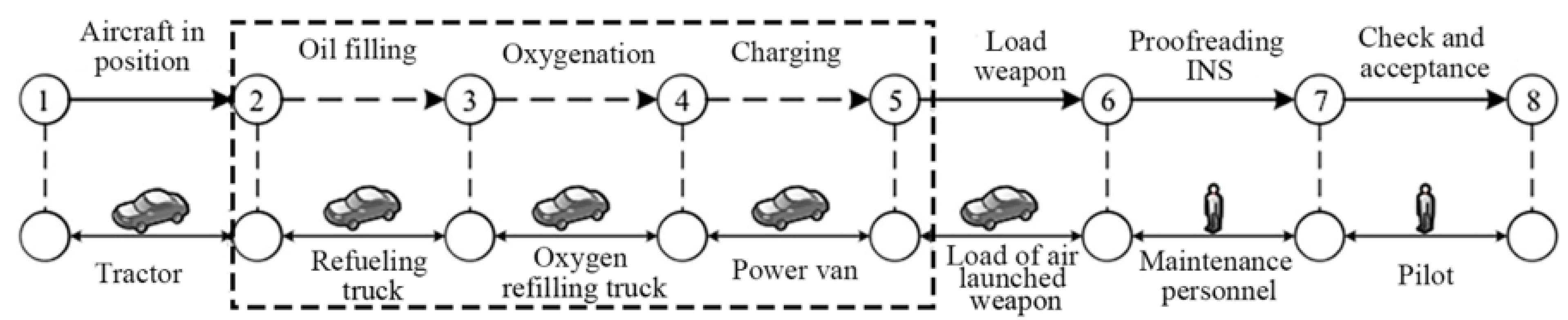
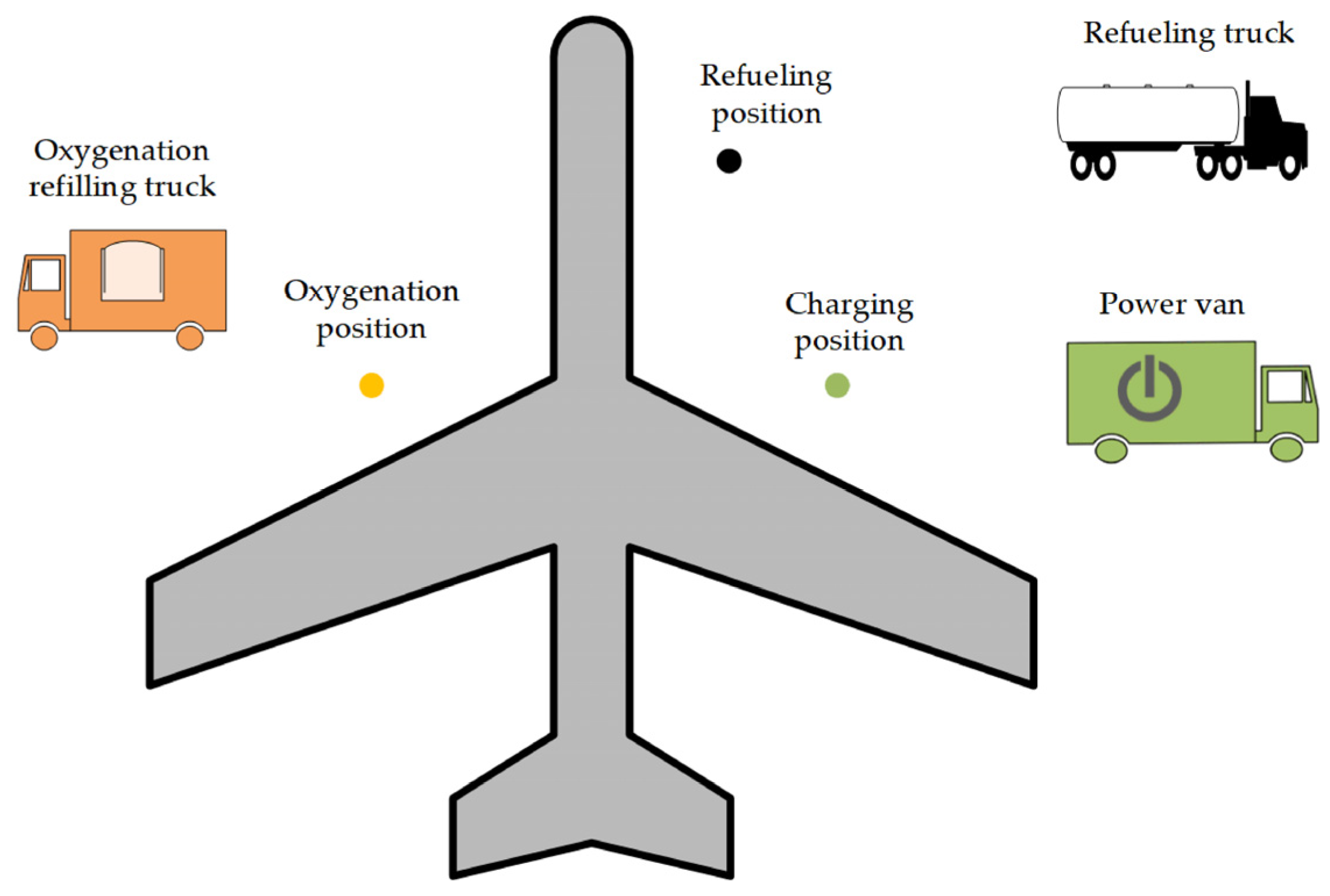
2.1. Operation Process of Apron Support Vehicles
2.2. Contents of Apron Support Operations
3. Modeling of Apron Support Vehicle Operation Scheduling Problem
3.1. Problem Description
- (1)
- The travel time of the support vehicle is ignored, and only the support operation time is calculated;
- (2)
- The problems of aircraft towing, bomb hanging, calibration of inertial navigation, and inspection and acceptance are free from resource constraints;
- (3)
- Each support operation of the aircraft requires only one type of support vehicle for one service;
- (4)
- For a certain type of aircraft, the operating hours of the guaranteed vehicles are the same;
- (5)
- The contents of support operations for all aircraft are independent of each other, and there is no mutual restraint between aircraft;
- (6)
- A guaranteed vehicle can only serve one aircraft at the same time;
- (7)
- Each aircraft must complete all support operations;
- (8)
- The support vehicle is allowed to be idle and the aircraft to wait for the support vehicle;
- (9)
- Once the vehicle starts, the support operation to a certain aircraft starts, and there is no interruption until the service support operation is completed;
- (10)
- The resources carried by each support vehicle are sufficient or can be replenished in time, without affecting the aircraft support mission.
3.2. Construct Mathematical Model
3.3. Empirical Method of Apron Support Vehicle Operation Scheduling
- (1)
- Sort ti, t1 < t2 < t3.
- (2)
- Use the sequential sorting method for optimal sorting:The support vehicle P3 performs support operations on J1, J2, …, J6 in sequence;The support vehicle P2 performs support operations on J1, J2, …, J6 in sequence;The support vehicle P1 performs support operations on J1, J2, …, J6 in sequence.
- (3)
- Implement support operations.
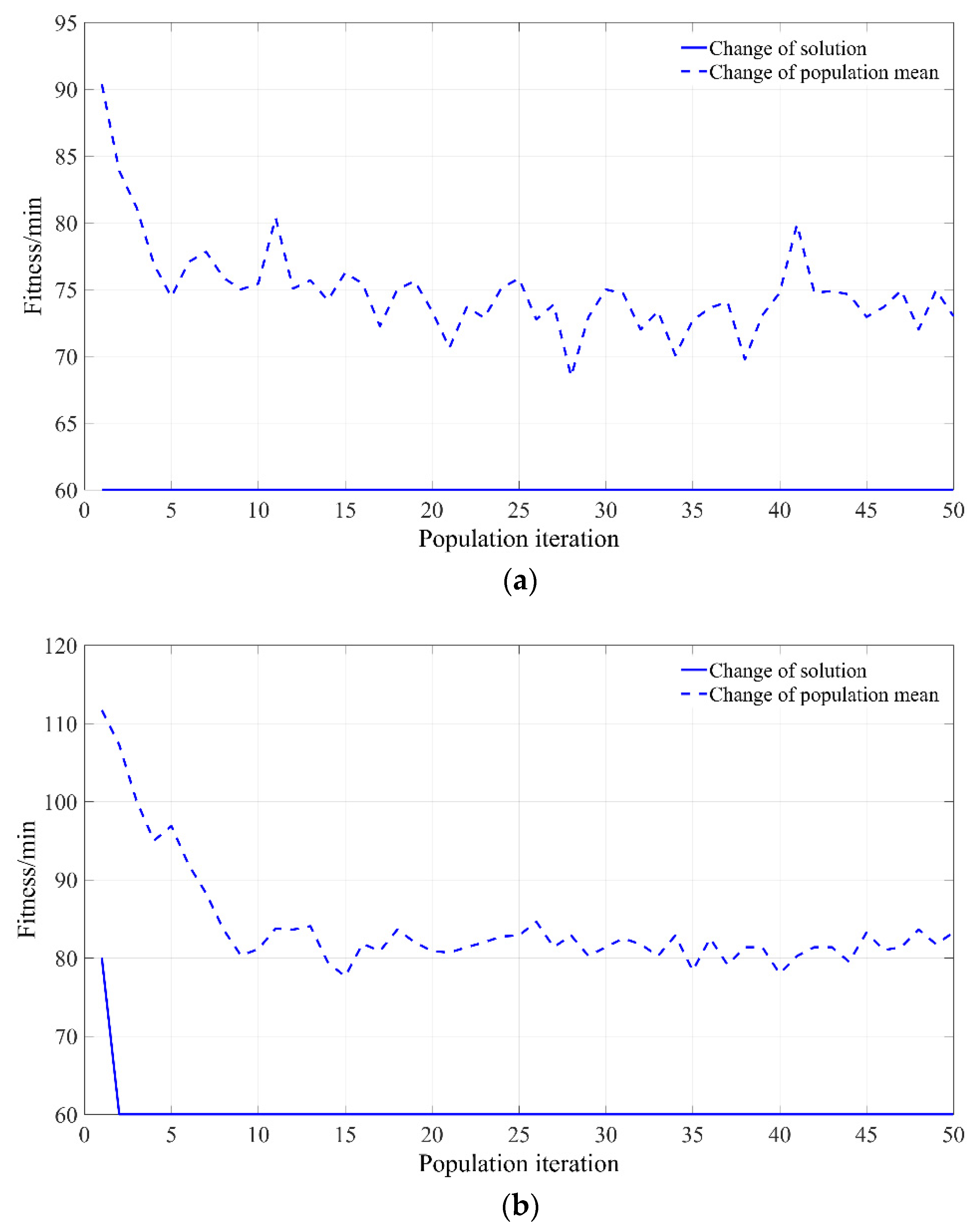
4. Design of Multi-Layer Coding Genetic Algorithm
| Algorithm 1 Overview of GA | |
| 1: | Initialize the population m |
| 2: | for i = 0→max do |
| 3: | (a) Two parent P1 and P2 are selected from the population m |
| 4: | (b) Use the crossover algorithm to get an offspring C |
| 5: | (c) Educate the offspring C with the mutation algorithm to obtain the new solution S |
| 6: | (d) Update the population M with S |
| 7: | end for |
| 8: | Return the solution S with minimum C in the population m |
4.1. Individual Coding
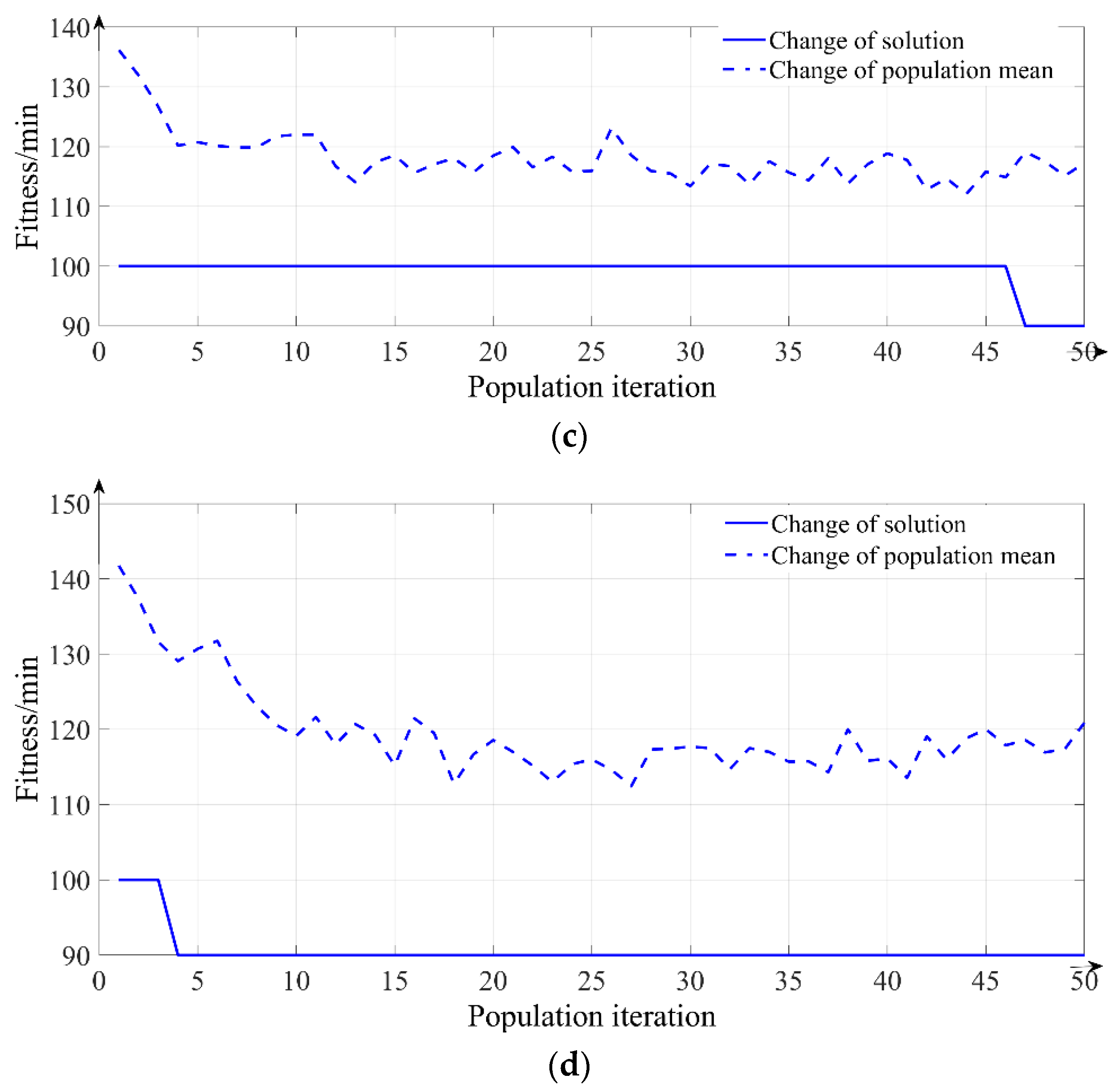
4.2. Fitness Value
4.3. Selection
4.4. Crossover Operation
4.5. Mutation Operation
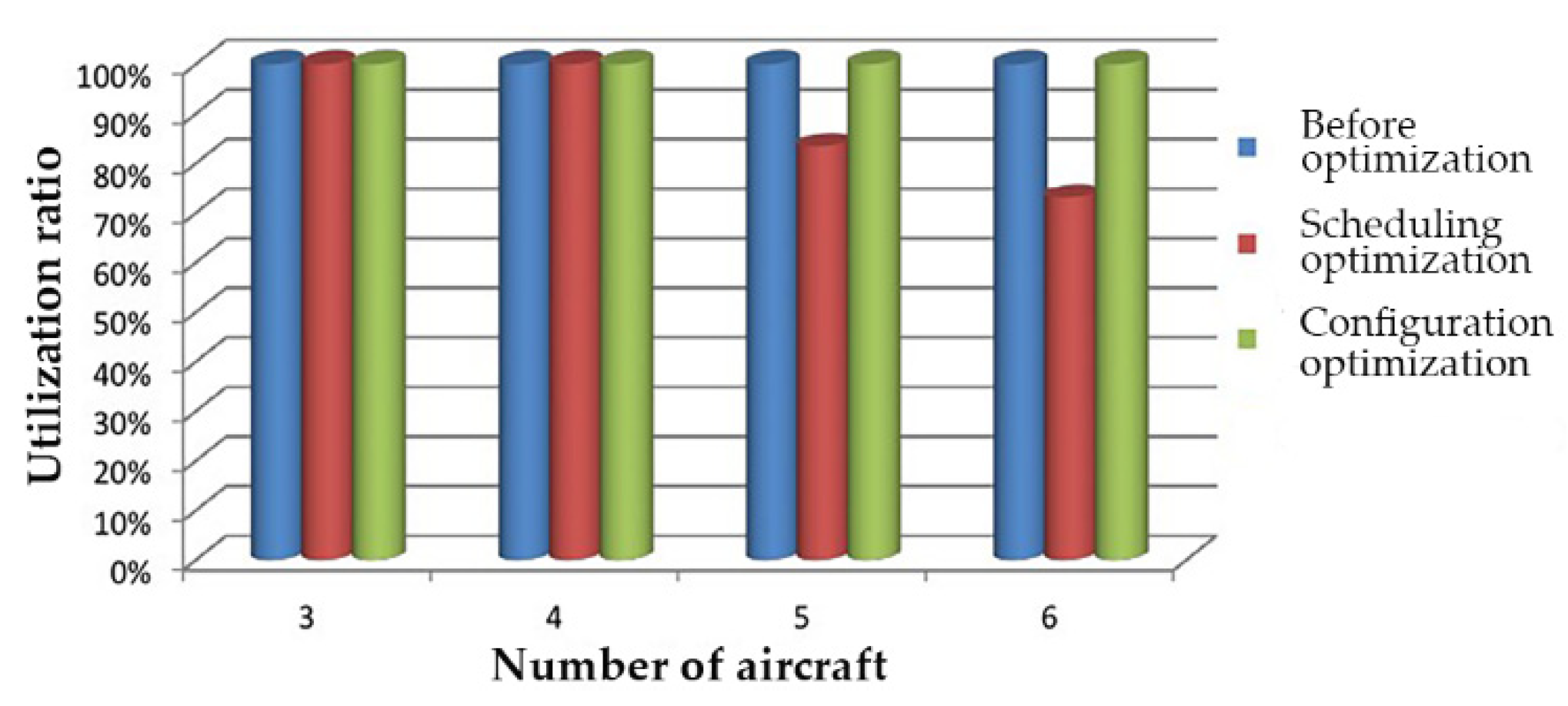
5. Examples of Scheduling Optimization of Apron Support Vehicles
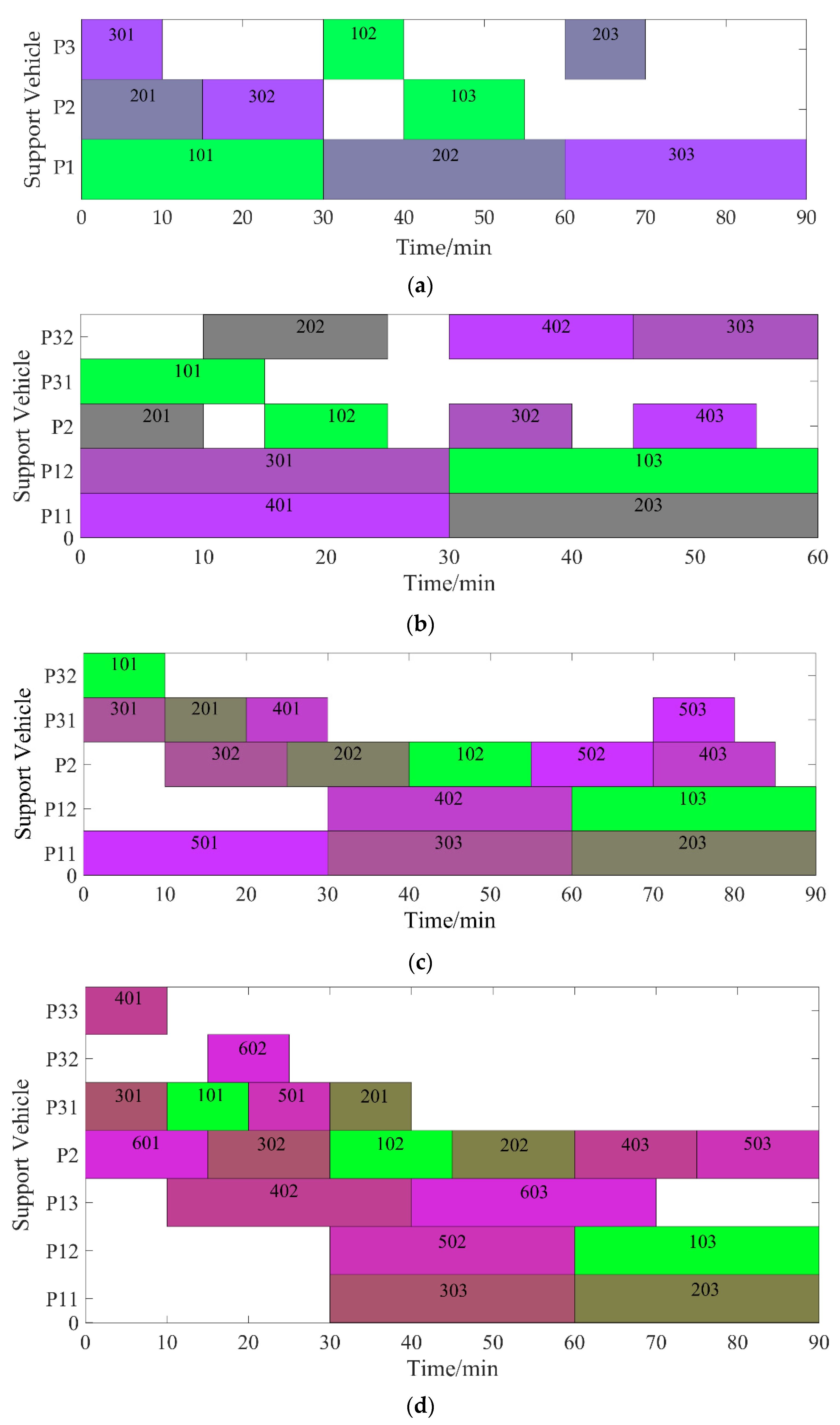
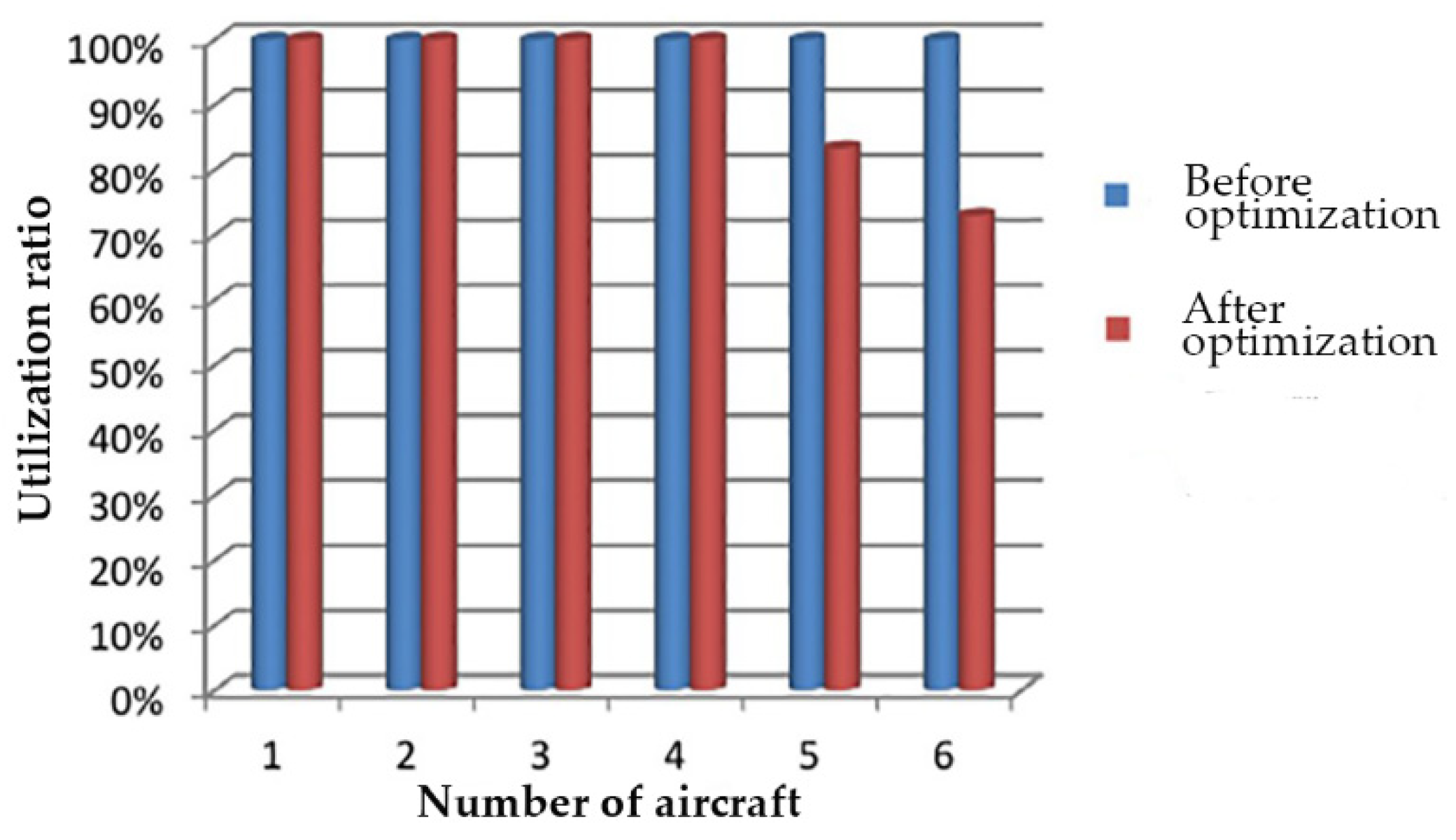
5.1. Simulation 1: Traditional Assurance Model
- (1)
- Optimization of vehicle operation scheduling guaranteed by 3 aircraft
- (2)
- Optimization of vehicle operation scheduling supported by 4 aircraft
- (3)
- Optimization of vehicle operation scheduling supported by 5 aircraft
- (4)
- Optimization of vehicle operation scheduling guaranteed by 6 aircraft
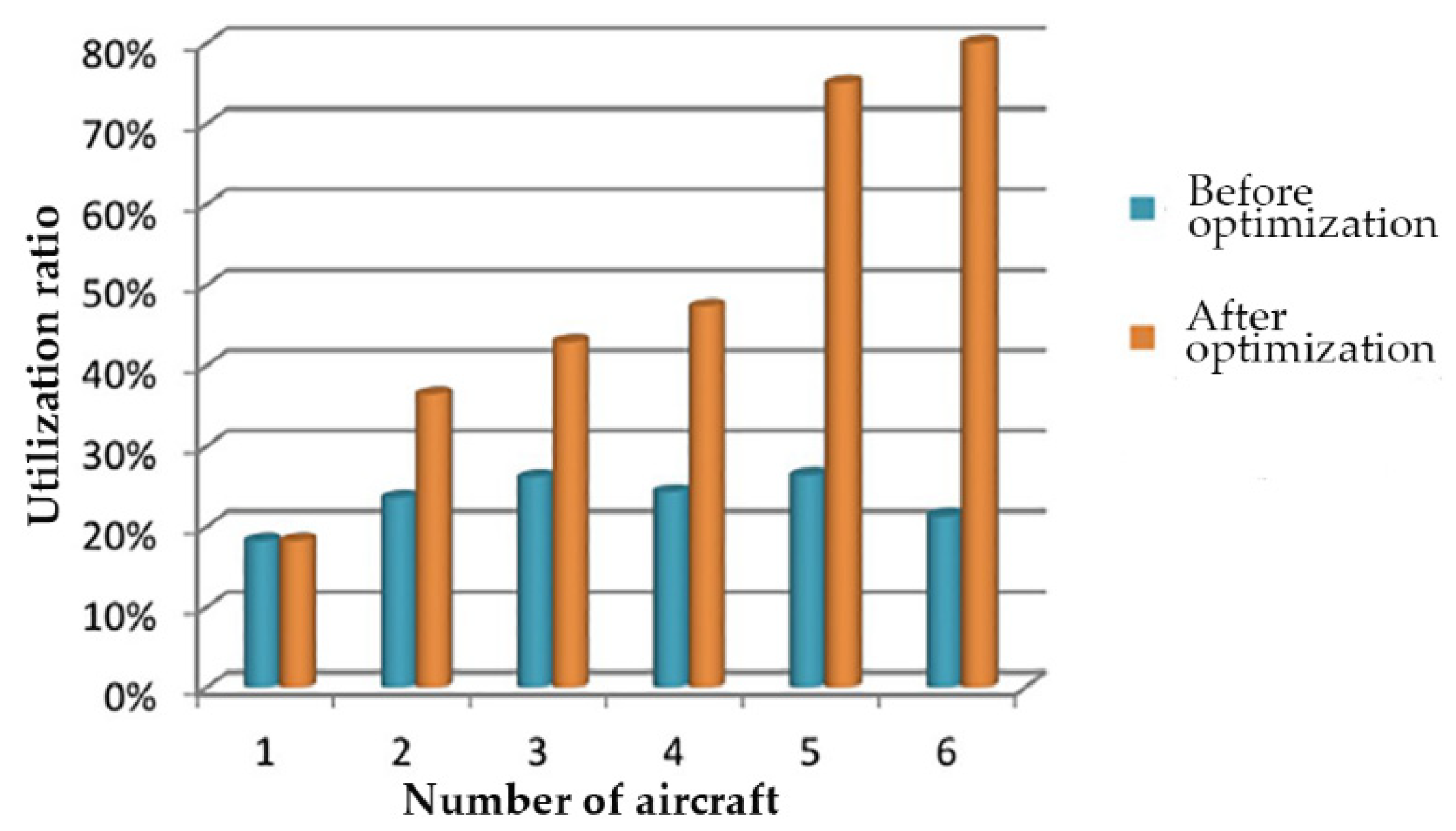
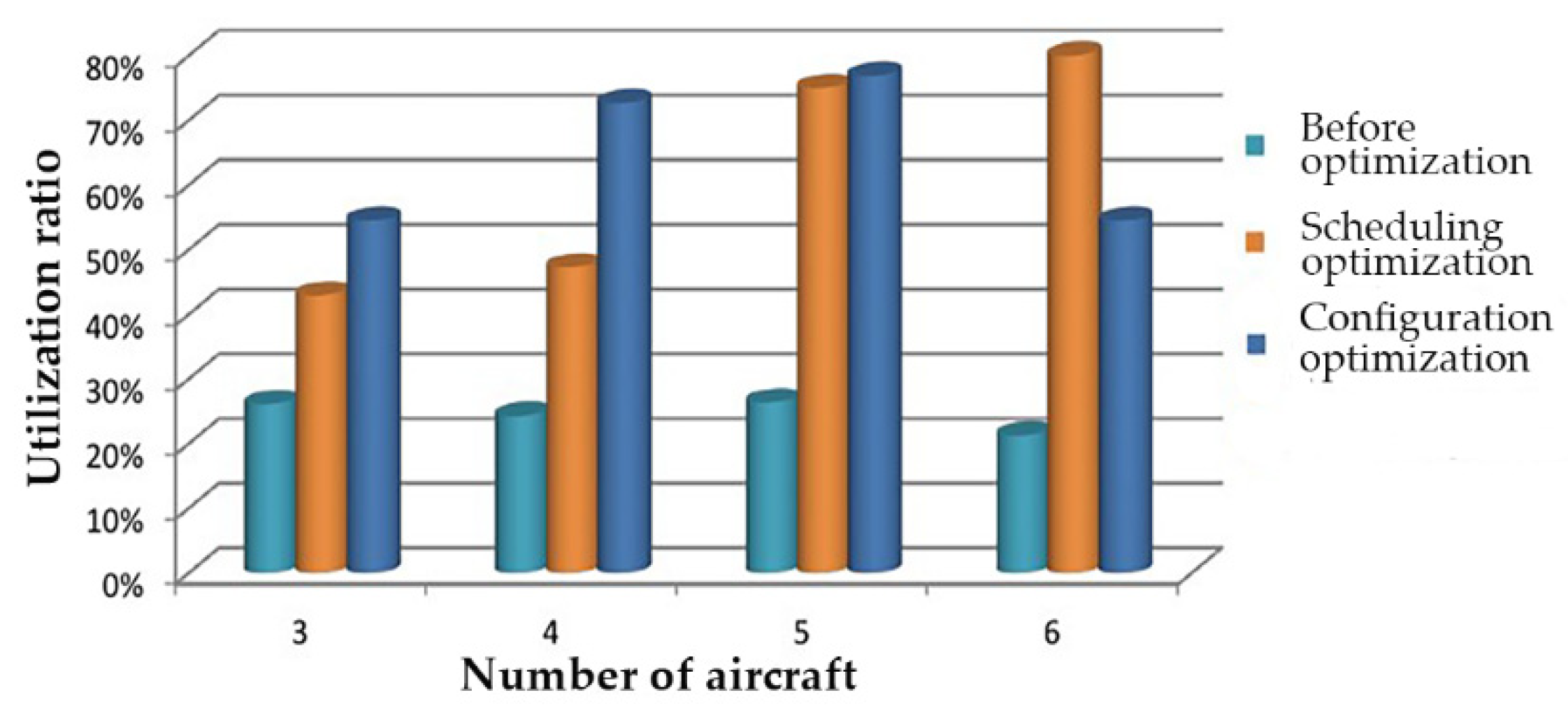
5.2. Simulation 2: Configuration Optimization of Support Vehicle Quantity
- (1)
- Optimization of vehicle configuration with 3-aircraft support
- (2)
- Optimization of vehicle configuration with 4-aircraft support
- (3)
- Optimization of vehicle configuration with 5-aircraft support
- (4)
- Optimization of vehicle configuration with 6-aircraft support
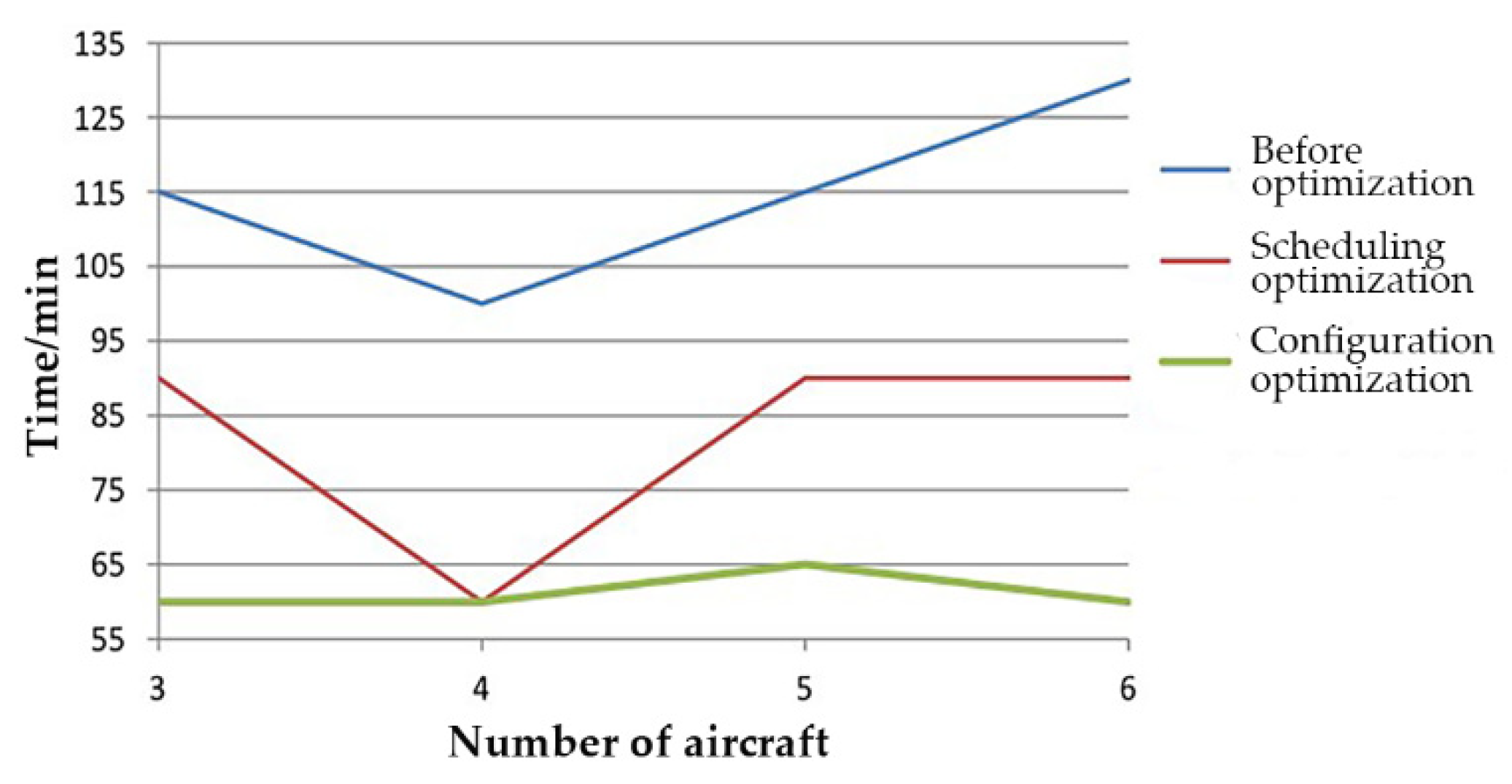
5.3. Operation Scheduling Optimization Scheme of Apron Support Vehicles
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schmidt, M. A review of aircraft turnaround operations and simulations. Prog. Aerosp. Sci. 2017, 92, 25–38. [Google Scholar] [CrossRef]
- Tabares, D.A.; Mora-Camino, F.; Drouin, A. A multi-time scale management structure for airport ground handling automation. J. Air Transp. Manag. 2021, 90, 101959. [Google Scholar] [CrossRef]
- Alomar, I.; Tolujevs, J. Optimization of ground vehicles movement on the aerodrome. Transp. Res. Procedia 2017, 24, 58–64. [Google Scholar] [CrossRef]
- Gok, Y.S.; Padron, S.; Tomasella, M.; Guimarans, D.; Ozturk, C. Constraint-based robust planning and scheduling of airport apron operations through simheuristics. Ann. Oper. Res. 2022, 1–36. [Google Scholar] [CrossRef]
- Andreatta, G.; Capanna, L.; De Giovanni, L.; Monaci, M.; Righi, L. Efficiency and Robustness in a Support Platform for Intelligent Airport Ground Handling. J. Intell. Transport. Syst. 2014, 18, 121–130. [Google Scholar] [CrossRef]
- Padrón Astorga, S. A Multi-Objective Optimization Approach to the Ground Handling Scheduling Problem; Universitat Autònoma de Barcelona: Bellaterra, Spain, 2014. [Google Scholar]
- Perez-Rodriguez, R.; Hernandez-Aguirre, A. A hybrid estimation of distribution algorithm for the vehicle routing problem with time windows. Comput. Ind. Eng. 2019, 130, 75–96. [Google Scholar] [CrossRef]
- Du, Y.Q.; Zhang, Q.; Chen, Q.S. ACO-IH: An Improved Ant Colony Optimization Algorithm for Airport Ground Service Scheduling. In Proceedings of the 2008 IEEE International Conference on Industrial Technology, Chengdu, China, 21–24 April 2008; IEEE: Piscataway, NJ, USA; Volumes 1–5, pp. 1926–1931. [Google Scholar]
- Schyns, M. An ant colony system for responsive dynamic vehicle routing. Eur. J. Oper. Res. 2015, 245, 704–718. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.H.; Wu, J.J.; Tang, J.; Wang, W.P.; Wang, X.F. Scheduling optimisation of multi-type special vehicles in an airport. Transp. B 2022, 10, 954–970. [Google Scholar] [CrossRef]
- Kuhn, K.; Loth, S. Airport service vehicle scheduling. In Proceedings of the ATM Seminar 2009, Napa, CA, USA, 29 June–2 July 2009. [Google Scholar]
- Wang, Z.; Li, Y.; Hei, X.; Meng, H. Research on Airport Refueling Vehicle Scheduling Problem Based on Greedy Algorithm. In Intelligent Computing Theories and Application; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Qin, W.J.; Shi, Z.C.; Li, W.H.; Li, K.W.; Zhang, T.; Wang, R. Multiobjective routing optimization of mobile charging vehicles for UAV power supply guarantees. Comput. Ind. Eng. 2021, 162, 107714. [Google Scholar] [CrossRef]
- Evler, J.; Asadi, E.; Preis, H.; Fricke, H. Airline ground operations: Schedule recovery optimization approach with constrained resources. Transport. Res. C-Emer. 2021, 128, 103129. [Google Scholar] [CrossRef]
- Padron, S.; Guimarans, D.; Ramos, J.J.; Fitouri-Trabelsi, S. A bi-objective approach for scheduling ground-handling vehicles in airports. Comput. Oper. Res. 2016, 71, 34–53. [Google Scholar] [CrossRef] [Green Version]
- Tang, F.; Liu, S. Research of Aircraft Ground Service Scheduling Problems. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016. [Google Scholar]
- Li, Q.; Bi, J.; Li, Z. Research on Ferry Vehicle Scheduling Problem within Airport Operations. In Proceedings of the 2017 10th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 9–10 December 2017. [Google Scholar]
- Mota, M.M.; Boosten, G.; De Bock, N.; Jimenez, E.; de Sousa, J.P. Simulation-based turnaround evaluation for Lelystad Airport. J. Air Transp. Manag. 2017, 64, 21–32. [Google Scholar] [CrossRef]
- Li, K.; Huang, Z.; Zhu, Q. Research on Modeling and Simulation of Support ability of Aerial Air-Conditioning Vehicle. Comput. Simul. 2017, 34, 443–449. [Google Scholar]
- Sheng, J.; Wang, Q.; Hou, L.; Zhu, H. Simulation optimization for equipment support plan of aviation fourth station based on orthogonal design method. Logist. Technol. 2013, 32, 296–299. [Google Scholar]
- Wang, S.X.; Che, Y.X.; Zhao, H.J.; Lim, A. Accurate Tracking, Collision Detection, and Optimal Scheduling of Airport Ground Support Equipment. IEEE Internet Things J. 2021, 8, 572–584. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, T.; Chen, W.; Chen, Y.; Li, Z. Study on optimization allocation methods of equipment support personnel. Fire Control Command Control 2016, 41, 192–196. [Google Scholar]
- Wang, W.; Zhu, H.; Sun, L.; Wu, S.; Jia, X. Optimization configuration of equipment in maintenance. Sci. Technol. Eng. 2009, 9, 6601–6602. [Google Scholar]
- Liu, Y.; Zhang, J.; Ding, C.; Bi, J. Modeling and heuristic algorithm of ground ferry vehicle scheduling in large airports. In Proceedings of the 19th COTA International Conference of Transportation, Nanjing, China, 6–8 July 2019; pp. 159–170. [Google Scholar]
- Heng, H.; Yan, X.; Wang, F.; Li, H. Research on dynamic scheduling of airport fuel filling vehicles. Comput. Eng. Des. 2017, 38, 1382–1388. [Google Scholar]
- Han, X.; Zhao, P.X.; Meng, Q.C.; Yin, S.N.; Wan, D. Optimal scheduling of airport ferry vehicles based on capacity network. Ann. Oper. Res. 2020, 295, 163–182. [Google Scholar] [CrossRef]
- Widemann, M.; Farschtschi, Y.; Wittmann, J.; Möller, D.P. Work flow management of the ground handling at the airport through modular system optimizing. In Proceedings of the Eurosim 2010, Prague, Czech Republic, 6–10 September 2010. [Google Scholar]
- Zhao, P.X.; Gao, W.Q.; Han, X.; Luo, W.H. Bi-Objective Collaborative Scheduling Optimization of Airport Ferry Vehicle and Tractor. Int. J. Simul. Model. 2019, 18, 355–365. [Google Scholar] [CrossRef]
- Zhao, G.H.; Du, Y.P. Research on Airport Apron Service Based on Particle Swarm Optimization. In Proceedings of the 2013 International Conference on Management Science and Engineering 20th Annual Conference, Harbin, China, 17–19 July 2013; Hua, L., Ed.; IEEE: Piscataway, NJ, USA, 2013; pp. 484–488. [Google Scholar]
- Alcaraz, J.; Maroto, C.; Ruiz, R. Solving the multi-mode resource-constrained project scheduling problem with genetic algorithms. J. Oper. Res. Soc. 2003, 54, 614–626. [Google Scholar] [CrossRef]
- Tareghian, H.R.; Farahi, M.H.; Moarab, M. Solving resource constrained scheduling problem by genetic algorithm. Shahid Chamran Univ. J. Sci. 2007, 16, 24–34. [Google Scholar]
- Nonobe, K.; Ibaraki, T. Formulation and Tabu Search Algorithm for the Resource Constrained Project Scheduling Problem. In Essays and Surveys in Metaheuristics; Springer: Boston, MA, USA, 2002; pp. 557–588. [Google Scholar]
- Merkle, D.; Middendorf, M.; Schmeck, H. Ant colony optimization for resource-constrained project scheduling. IEEE Trans. Evolut. Comput. 2002, 6, 333–346. [Google Scholar] [CrossRef] [Green Version]
- Fleszar, K.; Hindi, K.S. Solving the resource-constrained project scheduling problem by a variable neighbourhood search. Eur. J. Oper. Res. 2004, 155, 402–413. [Google Scholar] [CrossRef]
- Chen, R.; Yang, B.; Li, S.; Wang, S. A self-learning genetic algorithm based on reinforcement learning for flexible job-shop scheduling problem. Comput. Ind. Eng. 2020, 149, 106778. [Google Scholar] [CrossRef]
- Kacem, I. Genetic Algorithm for the Flexible Job-Shop Scheduling Problem. In Proceedings of the SMC’03 IEEE International Conference on Systems, Man and Cybernetics, Conference Theme—System Security and Assurance (Cat. No.03CH37483). Washington, DC, USA, 8 October 2003. [Google Scholar]
- Chiang, T.; Lin, H. A simple and effective evolutionary algorithm for multiobjective flexible job shop scheduling. Int. J. Prod. Econ. 2013, 141, 87–98. [Google Scholar] [CrossRef]
- Brucker, P.; Drexl, A.; Möhring, R.; Neumann, K.; Pesch, E. Resource-constrained project scheduling: Notation, classification, models, and methods. Eur. J. Oper. Res. 1999, 112, 3–41. [Google Scholar] [CrossRef]
- Xu, L.; Cao, Y.; Huang, B. Research on Multi-Distribution Center Vehicle Routing Optimization Method Based on Improved Multi-Layer Coding Genetic Algorithm. Open J. Transp. Technol. 2019, 8, 222–232. [Google Scholar]








| Specialty | Main Work |
|---|---|
| Mechanical specialty | Responsible for aircraft structure, engine, operating system, and so on. Complete the filling of oil, hydraulic oil and lubricating oil, nitrogen, etc. with the assistance of the refueling truck, air conditioner, and other supporting vehicles. |
| Avionics specialty | Responsible for the aircraft control system, fire control system, communication and navigation equipment, etc. Complete the inspection and collation with the assistance of power vehicles. |
| Ordnance specialty | Responsible for aircraft’s seats, pylons, aircraft guns, etc. Complete the loading and unloading of weapons with the assistance of the loader of air-launched weapons. |
| Ad hoc specialty | Responsible for cockpit electronics, instruments, special equipment, and so on with the assistance of power vans and oxygen filling vehicles. |
| Notation | Definition |
|---|---|
| Om | m processors |
| Cmax | the time objective function |
| Cmax = max{Cj} | equal to the end time of the last completed task |
| P | job time matrix, representing the time when j task completes the corresponding job on the i processor. |
| Tmin | the minimum time for ground support operations |
| Mij | the j support operation of the i aircraft |
| Pij | the support vehicle for the support operation Mij |
| Tij | the operation time of the guaranteed operation Mij |
| Sij | the start operation time of the guarantee operation Mij |
| Fij | the end operation time of the guarantee operation Mij |
| MaxF | the longest guarantee operation end time |
| Ω | the set of feasible solutions |
| P | the parent solution which is selected from the population |
| C | the child solution after crossover |
| M | the population which has several initial solutions |
| pi(i) | the probability which the chromosome is selected |
| Re | refueling truck |
| Ox | oxygen refilling truck |
| Po | power van |
| To | operation time, min |
| Tw | waiting time, min |
| Tt | total time, min |
| Vehicle | Tractor | Refueling Truck | Oxygenation Refilling Truck | Power Van | Loader of Air-Launched Weapon |
|---|---|---|---|---|---|
| Time/min | 10 | 30 | 15 | 10 | 2 |
| Vehicle | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| Aircraft | |||||||
| Re | 1 | 1 | 1 | 2 | 2 | 3 | |
| Ox | 1 | 1 | 1 | 1 | 1 | 1 | |
| Po | 1 | 1 | 1 | 2 | 2 | 3 | |
| Aircraft | Before | After | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Vehicle | To | Tw | Utilization Ratio | Tt | Vehicle | To | Tw | Utilization Ratio | Tt | |
| 3 | Re | 90 | 0 | 100% | 115 | Re | 90 | 0 | 100% | 90 |
| Ox | 45 | 60 | 42.9% | Ox | 45 | 10 | 81.8% | |||
| Po | 30 | 85 | 26.1% | Po | 30 | 40 | 42.9% | |||
| 4 | Re1 | 60 | 0 | 100% | 100 | Re1 | 60 | 0 | 100% | 60 |
| Re2 | 60 | 0 | 100% | Re2 | 60 | 0 | 100% | |||
| Ox | 60 | 30 | 66.7% | Ox | 60 | 0 | 100% | |||
| Po1 | 20 | 50 | 28.6% | Po1 | 10 | 15 | 40% | |||
| Po2 | 20 | 80 | 20% | Po2 | 30 | 25 | 54.5% | |||
| 5 | Re1 | 90 | 0 | 100% | 115 | Re1 | 90 | 0 | 100% | 90 |
| Re2 | 60 | 0 | 100% | Re2 | 60 | 30 | 66.7% | |||
| Ox | 75 | 30 | 71.4% | Ox | 75 | 10 | 88.23% | |||
| Po1 | 30 | 55 | 35.3% | Po1 | 40 | 40 | 50% | |||
| Po2 | 20 | 95 | 17.4% | Po2 | 10 | 0 | 100% | |||
| 6 | Re1 | 60 | 0 | 100% | 130 | Re1 | 60 | 30 | 66.7% | 90 |
| Re2 | 60 | 0 | 100% | Re2 | 60 | 30 | 66.7% | |||
| Re3 | 60 | 0 | 100% | Re3 | 60 | 10 | 85.7% | |||
| Ox | 90 | 30 | 75% | Ox | 90 | 0 | 100% | |||
| Po1 | 20 | 50 | 28.6% | Po1 | 40 | 0 | 100% | |||
| Po2 | 20 | 80 | 20% | Po2 | 10 | 15 | 40% | |||
| Po3 | 20 | 110 | 15.4% | Po3 | 10 | 0 | 100% | |||
| Vehicle | Single-Aircraft before | Single-Aircraft after | Two-Aircraft before | Two-Aircraft after | ||||
|---|---|---|---|---|---|---|---|---|
| Utilization Ratio | Tt | Utilization Ratio | Tt | Utilization Ratio | Tt | Utilization Ratio | Tt | |
| Re | 100% | 55 | 100% | 55 | 100% | 85 | 100% | 60 |
| Ox | 33.3% | 33.3% | 40% | 66.7% | ||||
| Po | 18.2% | 18.2% | 23.5% | 36.4% | ||||
| Aircraft | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|
| Vehicle | |||||
| Re | 2 | 2 | 3 | 3 | |
| Ox | 1 | 1 | 2 | 2 | |
| Po | 1 | 1 | 1 | 2 | |
| Aircraft | Vehicle | To | Tw | Utilization Ratio | Tt |
|---|---|---|---|---|---|
| 3 | Re1 | 30 | 0 | 100% | 60 |
| Re2 | 60 | 0 | 100% | ||
| Ox | 45 | 15 | 75% | ||
| Po | 30 | 25 | 54.5% | ||
| 4 | Re1 | 60 | 0 | 100% | 60 |
| Re2 | 60 | 0 | 100% | ||
| Ox | 60 | 0 | 100% | ||
| Po | 40 | 15 | 72.7% | ||
| 5 | Re1 | 30 | 0 | 100% | 65 |
| Re2 | 60 | 0 | 100% | ||
| Re3 | 60 | 0 | 100% | ||
| Ox1 | 30 | 15 | 66.7% | ||
| Ox2 | 45 | 15 | 75% | ||
| Po | 50 | 15 | 76.9% | ||
| 6 | Re1 | 60 | 0 | 100% | 60 |
| Re2 | 60 | 0 | 100% | ||
| Re3 | 60 | 0 | 100% | ||
| Ox1 | 45 | 15 | 75% | ||
| Ox2 | 45 | 0 | 100% | ||
| Po1 | 30 | 25 | 54.5% | ||
| Po2 | 30 | 25 | 54.5% |
| Aircraft | Vehicle Configuration (Re:Ox:Po) | Vehicle Scheduling | Least Time/Min |
|---|---|---|---|
| 1 | 1:1:1 | Re: A1 Ox: A1 Po: A1 | 55 |
| 2 | 1:1:1 | Re: A1 → A2 Ox: A2 → A1 Po: A2 → A1 | 60 |
| 3 | 2:1:1 | Re1: A2 Re2: A3 → A1 Ox: A1 → A3 → A2 Po: A1 → A2 → A3 | 60 |
| 4 | 2:1:1 | Re1: A3 → A2 Re2: A4 → A1 Ox: A2 → A1 → A3 → A4 Po: A1 → A2 → A4 → A3 | 60 |
| 5 | 3:2:1 | Re1: A5 Re2: A2 → A1 Re3: A4 → A3 Ox1: A2 → A1 → A3 → A4 Ox2: A2 → A1 → A3 → A4 Po: A1 → A3 → A2 → A5 → A4 | 65 |
| 6 | 3:2:2 | Re1: A5 → A2 Re2: A4 → A3 Re3: A6 → A1 Ox1: A2 → A4 → A6 Ox2: A3 → A1 → A5 Po1: A1 → A3 → A5 Po2: A2 → A6 → A4 | 60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Chong, X.; Wei, Y.; Bi, Z.; Yu, Q. Optimization of Apron Support Vehicle Operation Scheduling Based on Multi-Layer Coding Genetic Algorithm. Appl. Sci. 2022, 12, 5279. https://doi.org/10.3390/app12105279
Zhang J, Chong X, Wei Y, Bi Z, Yu Q. Optimization of Apron Support Vehicle Operation Scheduling Based on Multi-Layer Coding Genetic Algorithm. Applied Sciences. 2022; 12(10):5279. https://doi.org/10.3390/app12105279
Chicago/Turabian StyleZhang, Jichao, Xiaolei Chong, Yazhi Wei, Zheng Bi, and Qingkun Yu. 2022. "Optimization of Apron Support Vehicle Operation Scheduling Based on Multi-Layer Coding Genetic Algorithm" Applied Sciences 12, no. 10: 5279. https://doi.org/10.3390/app12105279
APA StyleZhang, J., Chong, X., Wei, Y., Bi, Z., & Yu, Q. (2022). Optimization of Apron Support Vehicle Operation Scheduling Based on Multi-Layer Coding Genetic Algorithm. Applied Sciences, 12(10), 5279. https://doi.org/10.3390/app12105279






