Next Article in Journal
DRL-FVRestore: An Adaptive Selection and Restoration Method for Finger Vein Images Based on Deep Reinforcement
Previous Article in Journal
A Mixed Integer Linear Programming Model with Heuristic Improvements for Single-Track Railway Rescheduling Problem
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 13
Issue 2
10.3390/app13020700
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Evaluating the Drainage Density Characteristics on Climate and Drainage Area Using LiDAR Data

by
Seoyoung Kim
1,
Sun-Kwon Yoon
2,* and
Namjeong Choi
3
1
Stantec Inc., San Antonio, TX 78216, USA
2
Department of Living Environment Research, Seoul Institute of Technology, Seoul 03909, Republic of Korea
3
Department of Civil and Environmental Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
*
Author to whom correspondence should be addressed.
Appl. Sci. 2023, 13(2), 700; https://doi.org/10.3390/app13020700
Submission received: 1 December 2022 / Revised: 21 December 2022 / Accepted: 29 December 2022 / Published: 4 January 2023
(This article belongs to the Section Earth Sciences)
Browse Figures
Versions Notes

Abstract

:
The purpose of this study is to identify the relationship between drainage density and climate, as represented by the climate aridity index, and to understand the relationship between drainage density and drainage area. A total of 121 study sites with low human impact, and a wide range of climate aridity index 0.3 (humid)–10.4 (arid), were selected based on the availability of light detection and ranging (LiDAR) data, producing a digital elevation model (DEM) with a spatial resolution of 1 m. A curvature-based method, incorporating both positive and negative curvature information, was used to extract the valley (drainage) network from the LiDAR-based DEMs. Drainage density and climate aridity index exhibited a monotonically increasing trend, contrary to the previous results that have shown a U-shaped relationship. This discrepancy was caused by the selection of watersheds with extensive human activity in the previous study. One-meter resolution DEM produced greater drainage density than the previous studies with a coarse spatial resolution of 30 m as small valleys are not detectable in low-resolution topography datasets. The discrepancy between the previous study and the current study results encouraged further investigation of the impact of the drainage area (watershed size). A negative correlation between drainage density and drainage area was reconfirmed, while a stronger decreasing trend was observed in arid regions than in humid regions.

1. Introduction

The drainage network of a watershed controls surface runoff, which makes it an important geomorphological and hydrological feature. A drainage network comprises unchannelized valleys and channels [1]. At a valley head, unconfined sheet flow on the hillslope enters the valley and turns into a confined flow [2,3]. The convergent topography with positive contour curvature of the valley causes localized confined flow [4,5]. Traditionally, a drainage network can be identified using three possible methods: (1) the contour crenulation method based on V-shaped contours on topographic maps [6], (2) a contributing area threshold [7,8,9], and (3) a slope-area relationship [10,11,12,13,14]. Recently developed technology, such as airborne light detection and ranging (LiDAR), is able to obtain high spatial resolution topographic data and allows the extraction of accurate topographic features [15,16,17,18]. Based on the high-resolution digital resolution model (DEM) derived from LiDAR data, curvature thresholds have been used to extract the channel and valley networks [19,20,21,22].
One of the important parameters to describe a drainage network is drainage density ( D d ), which is defined as the ratio of the total valley length to the drainage area of the watershed [23,24]. Drainage density is an indicator of drainage efficiency and is closely related to runoff responses [25,26,27,28,29,30]. Usually, watersheds with higher drainage densities produce a higher peak flow and sediment load [31]. Spatial heterogeneity of drainage density also affects surface and subsurface runoff [32].
Various factors control drainage density, including climate, lithology, vegetation, and topography [10,33,34,35]. The most crucial factor that controls the watershed topography is considered to be climate [36]. Arid regions show a large variability of drainage density compared to humid regions because of the seasonal variation of climate [37]. Melton [33] identified a negative correlation between drainage density and precipitation effectiveness (PE) index, which is defined as the product of 10 and the summation of ratios between monthly average precipitation and evaporation in watersheds in arid regions in the southwestern United States [38]. In contrast, Madduma Bandara [39] discovered a positive correlation between drainage density and PE index for humid watersheds in Sri Lanka. The contrasting relationships between D d and PE index found in an arid region [33] and in a humid region [39] were explained as a U-shaped relationship by combining the data from both studies [40,41,42]. The U-shaped relationship has been explained as the trade-off between the resistance force of vegetation and the erosion force of runoff [40,41,42].
Not only the climate but also the size of a drainage area (A) affects the drainage density [43]. The drainage area is a proxy of watershed properties [44]. The hydrologic phenomenon is correlated with physiographic properties, which include the size of the drainage area [45]. Pethick [46] utilized a power law relationship, D d   ∝ A − 0.337 , to describe the relationship between drainage area and drainage density, which indicates that drainage density decreases with a drainage area. The value of the exponent in the power law relationship depends on environmental characteristics such as climate, vegetation, and geology [47,48]. Since both watershed properties and climate control drainage density, the relationship between drainage area and drainage density may vary from humid to arid regions.
Therefore, it is necessary to investigate the impact of long-term climate and drainage area on drainage density simultaneously. For an accurate assessment, this study utilizes high-resolution DEMs to extract drainage networks. The extracted drainage networks were used to examine the relationship between drainage density, climate, and drainage area. The objectives of this paper are 1) the introduction of a method for extraction of valley network maps using high-resolution LiDAR-based DEMs, 2) the re-examination of the U-shaped relationship between drainage density and climate aridity index, which was established in previous studies, and 3) the investigation of the relationships of drainage density and drainage area (watershed size). The current study results are compared to the established understanding of drainage density characteristics.

2. Data and Methodology

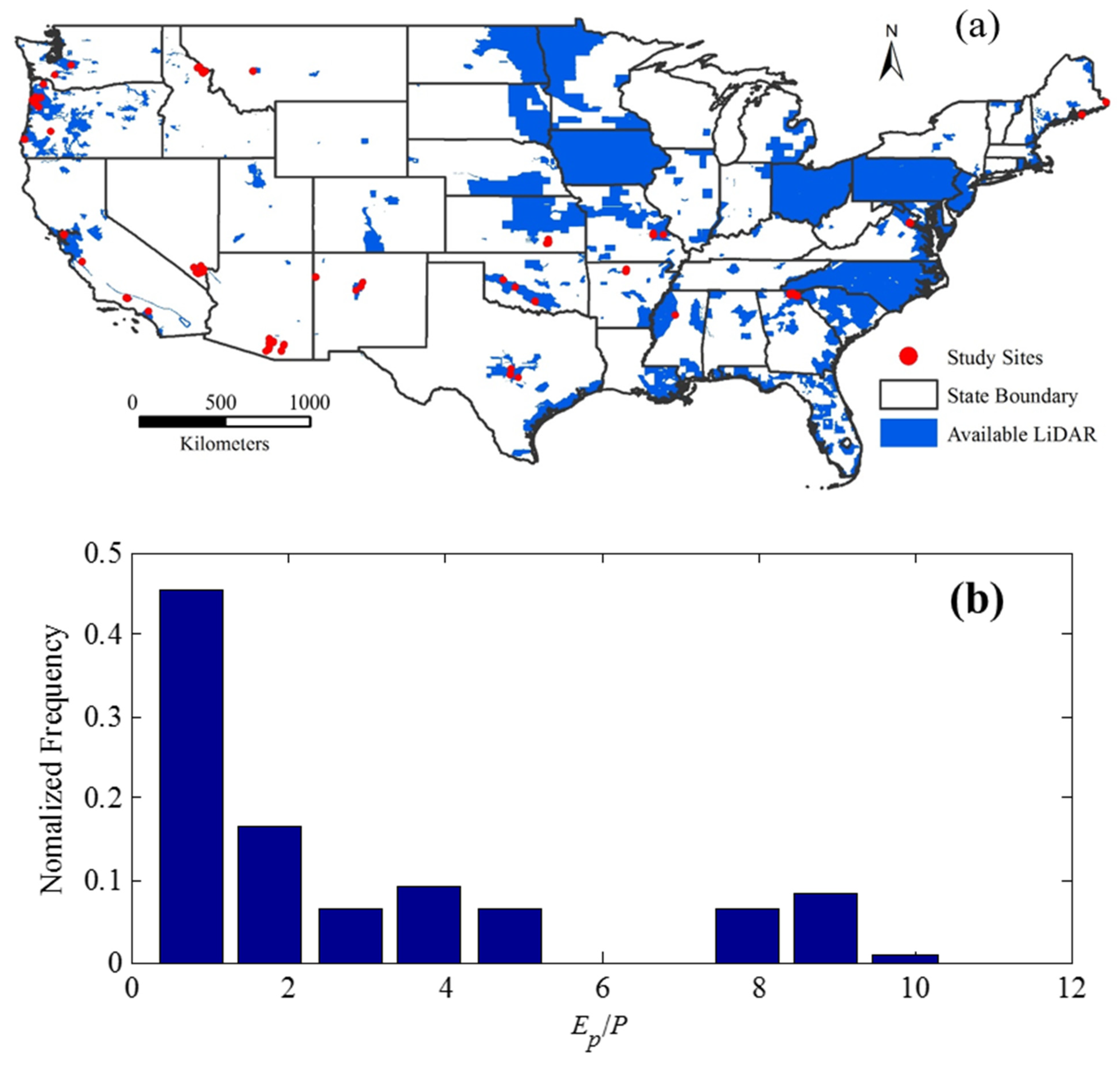
2.1. Study Sites and Data Sources

The study sites were selected based on the availability of LiDAR data. The data were chosen from regions with minimal land use change and artificial structures including buildings, dams, and roads. The high-resolution LiDAR data were obtained from the Center for LiDAR Information, Coordination and Knowledge (CLICK, http://lidar.cr.usgs.gov, accessed on 20 August 2015). The CLICK website offers data tiled by USGS Quarter Quadrangles in LAS and ASCII formats [48]. The spatial availability of LiDAR data from the CLICK website is presented in Figure 1a in blue. The red dots are 121 study sites that were selected for this study. The study sites are located in 17 states with various climate conditions. The ground returns of LiDAR data, in which vegetation and buildings are cleaned out by the data providers, are used in this study. The point cloud data are processed to derive 1 m DEMs and land surface topography using QCoherent software LP360 for ArcGIS (https://www.lp360.com/, accessed on 20 August 2015).
The climate aridity index, defined as the ratio of potential evaporation to precipitation ( E P / P ), is used as an indicator of the climate [49,50]. This index provides a useful tool to differentiate energy-limited or humid regions, ( E P / P < 1 ) and water-limited or arid regions ( E P / P > 1 ). Monthly potential evaporation data at 8 km spatial resolution from Zhang et al. [51] is aggregated into mean annual values. The parameter-elevation regressions on independent slopes model (PRISM) provides the gridded annual, monthly, and event-based precipitation data [52]. Mean annual precipitation data from PRISM with a 4 km spatial resolution are used for the period of 1981–2010. Mean annual potential evaporation and precipitation data are averaged to the watershed scale values for computing   E P / P . Figure 1b shows the distribution of E P / P for the 121 study watersheds. The distribution is represented by normalized frequency, which is defined as the ratio of the number of watersheds in each bin to the total number of watersheds. The values of E P / P for the selected study watersheds ranges from 0.3 to 10.4.
For comparison, the PE index, precipitation effectiveness index, for the watersheds from Melton [33] and Madduma Bandara [39] are converted to E P / P . The relationship between PE index and E P / P is derived after removing the outliers from the data by Wang and Wu [53] as shown in Figure 2a. Lower E P / P corresponds to higher PE index. The U-shaped trend for data points from Melton [33] and Madduma Bandara [39] is still visible after converting PE to E P / P , and the transition occurs at E P / P ≈ 2 (Figure 2b).

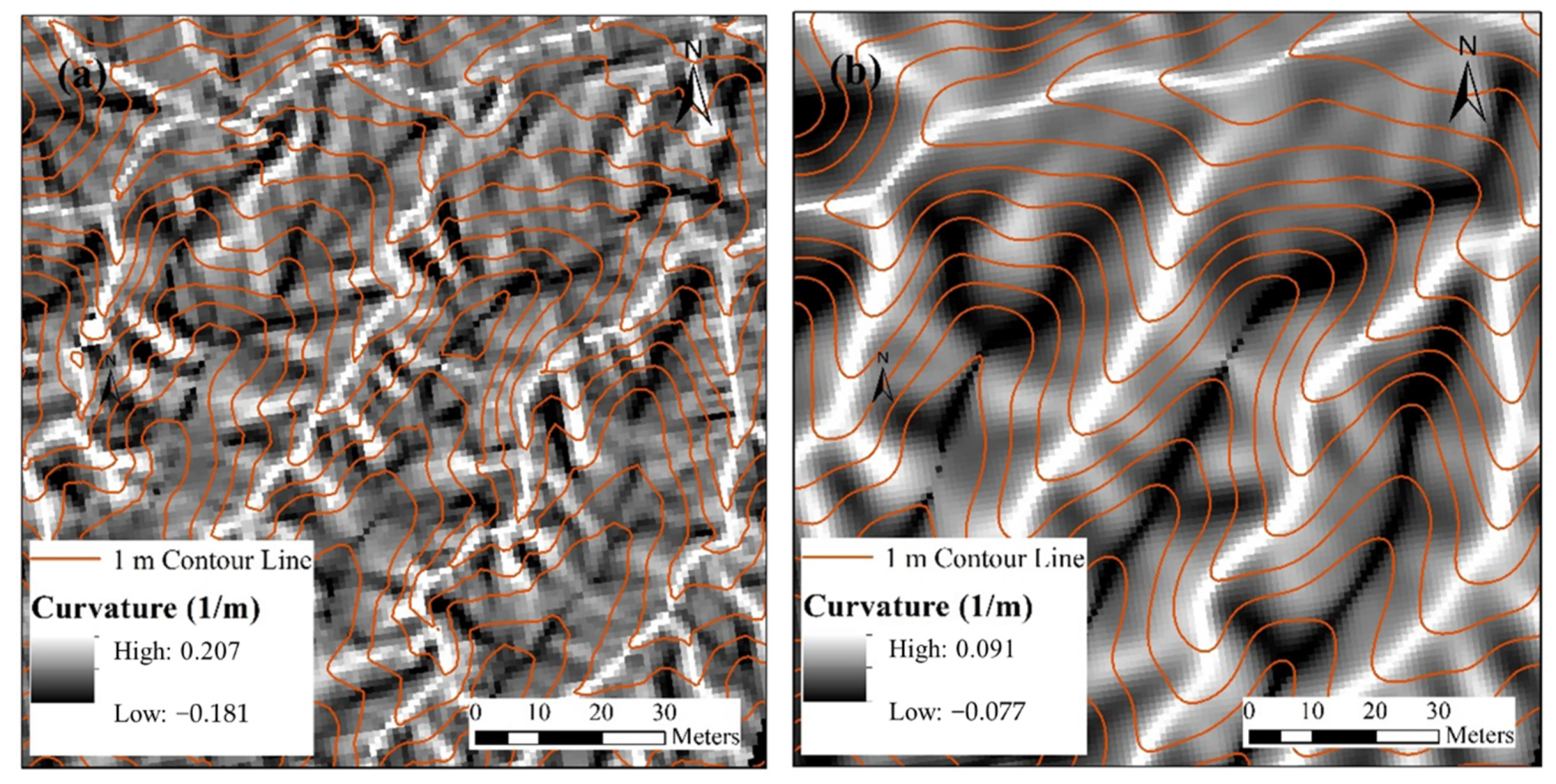
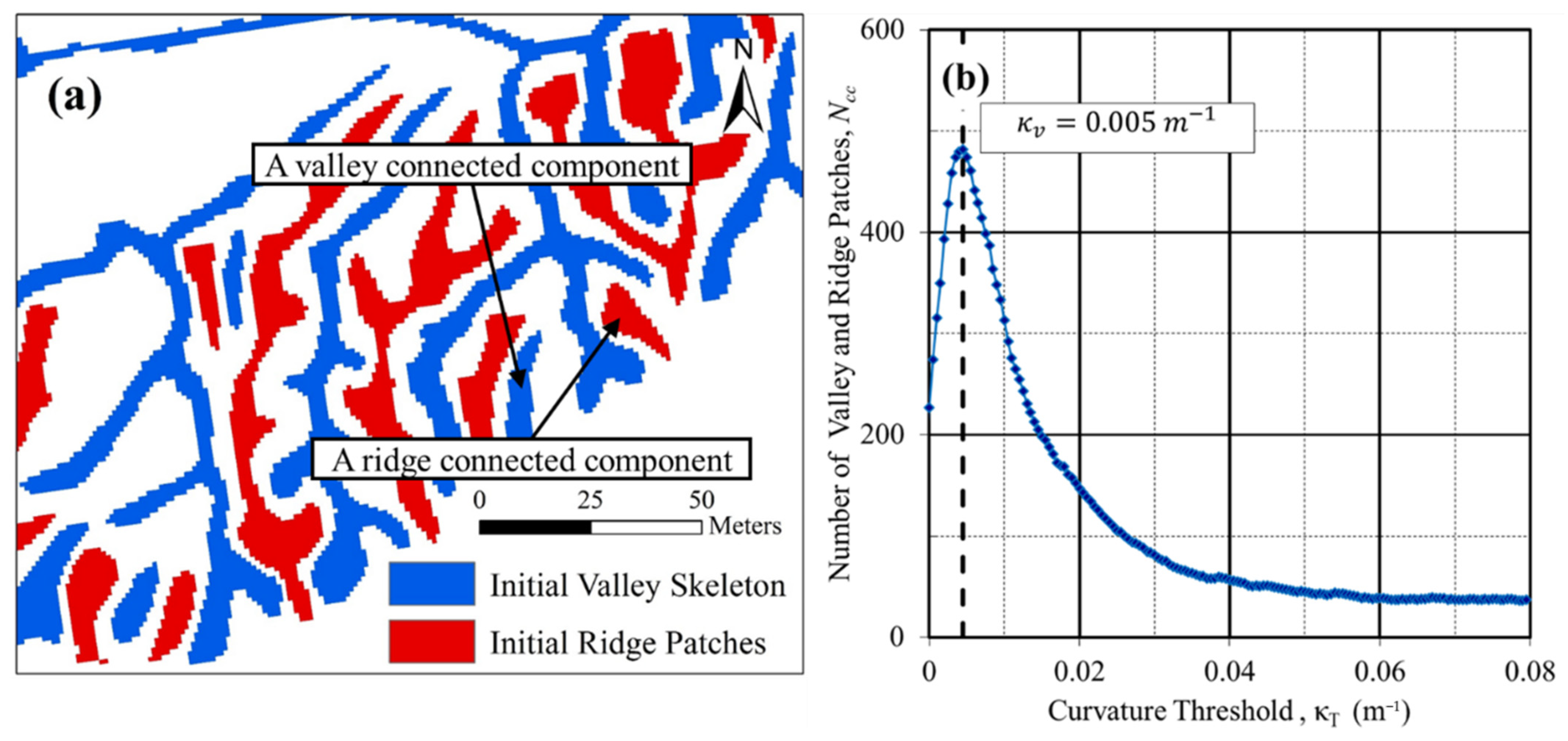
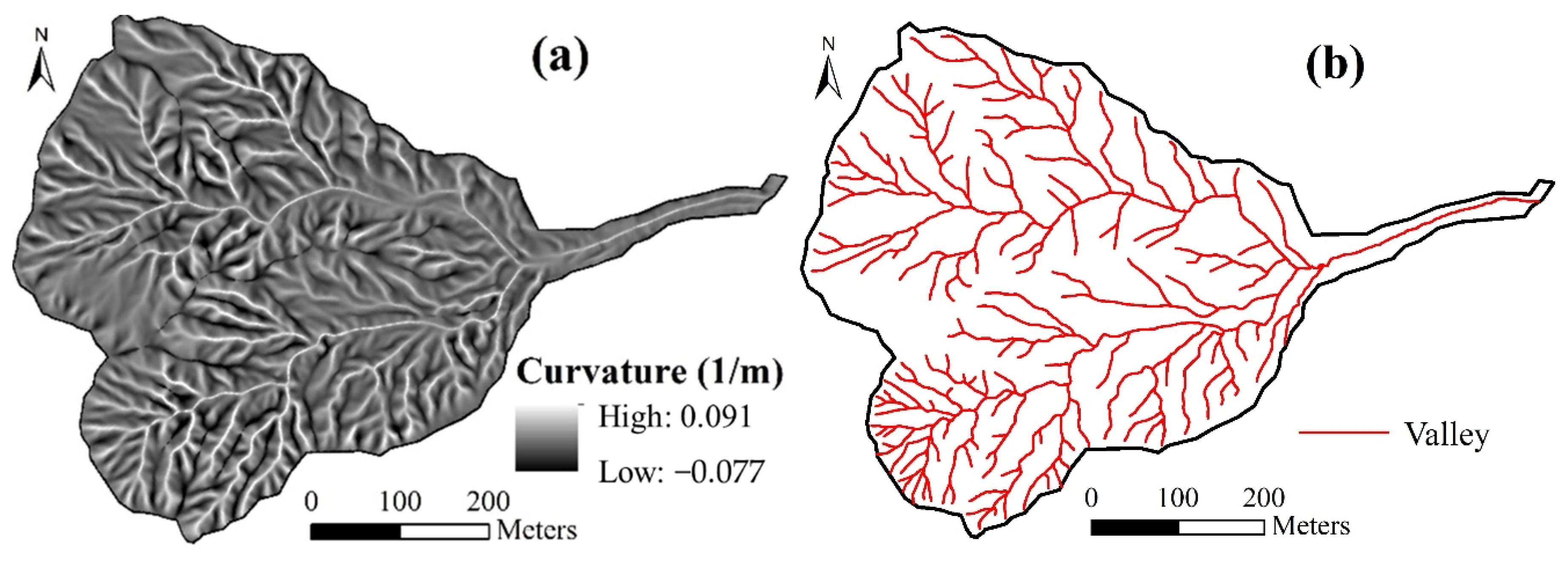
2.2. Valley Network Extraction

In this study, the valley network is extracted using a curvature-based method that was proposed and explained in the previous study conducted by Hooshyar et al. (2015, 2016) [17,21]. Curvature-based methods for valley or channel network delineation usually require filtering the noise and insignificant features to obtain a robust curvature grid. The Perona-Malik filter used in this study is a nonlinear diffusive filter that efficiently smooths DEMs while preserving significant features such as valleys [19]. This filter has one parameter called “time of forward diffusion,” which indicates the number of iterations for filtering the DEM as a numerical representation of derivatives for smoothing [21]. The time of forward diffusion denoted by T F is set to 50 in the study. From the filtered DEM, the curvature is calculated using Equation (1) [54]:
κ = z x x z y 2 − 2 z x y z x z y + z y y z x 2 ( z x 2 + z y 2 ) 1 + z x 2 + z y 2
where κ is the curvature, and z x and   z x x ( z y and   z y y ) denote the first and second derivatives of elevation ( z ) with respect to x ( y ). z x y is the first derivative of z x with respect to y . Figure 3 shows the curvature extracted from the original and filtered DEMs overlaid with contour lines in the Isleta Drain watershed located in New Mexico.
Valley or drainage network extraction is based on the curvature analysis using positive and negative curvature as indicators of the significance of convergence or divergence. Valleys are defined as convergent surfaces which are associated with positive curvature. Ridges are the segments with negative curvature (i.e., divergent surface), which are typically located between the valleys as the signature of flow separation lines between tributaries.
In order to differentiate valleys, a positive curvature threshold ( κ v ) is automatically derived which is used to cluster the landscape into convergent ( κ > κ v ), divergent ( κ < − κ v ), and insignificant ( | κ | ≤ κ v ) pixels. κ v is calculated through connected component analysis on the curvature grid. Figure 4 shows the number of connected components ( N c c ) for any given curvature threshold, denoted by κ T in the Isleta Drain watershed. A connected component is a set of connected pixels which are all either convergent or divergent (Figure 4a). In order to compute N c c for each value of κ T , the territory is clustered into convergent (curvature greater than κ T ) and divergent (curvature less than − κ T ) pixels, and then the connected component is counted using a binary labeling algorithm [55]. As shown in Figure 4b, decreasing κ T initially leads to more connected components since there are more pixels labeled as convergent or divergent. However, at a certain point, the number of connected components drops due to the merging process. In other words, the existing components start to merge together resulting in less N c c . The peak of the connected component curve is considered as the curvature threshold for valley extraction since it produces the most separated clusters in the landscape and efficiently identifies the local optimums in the curvature grid.
Given the obtained κ v , the initial valley skeleton is generated by imposing κ > κ v to the curvature grid. The skeleton is thinned to form a 1-pixel-wide valley line. Afterwards, any two neighboring valleys are checked for the existence of at least one ridge (patches with κ < − κ v ) between them. Following this step, only valleys with well-defined ridges (reflected as negative curvature patches in the curvature grid), at least in some part of their length, are kept and the rest are eliminated.
The resulting valley network is further processed to connect isolated valleys when the length of the gap is less than 0.25 l v , where l v is the total length of the upstream isolated segment. Additionally, the valley network is manually edited based on 1 m contours to get the best possible accuracy and minimize the effects of missing data and man-made structures such as roads. An example of the resulting valley network in the Isleta Drain watershed is presented in Figure 5. Figure 5a shows the contour curvature image computed from the filtered DEM, and Figure 5b shows the corresponding valley network delineated using the developed valley extraction method. More details regarding the methodology can be found in Hooshyar et al. (2015, 2016) [17,21].

3. Results and Discussion

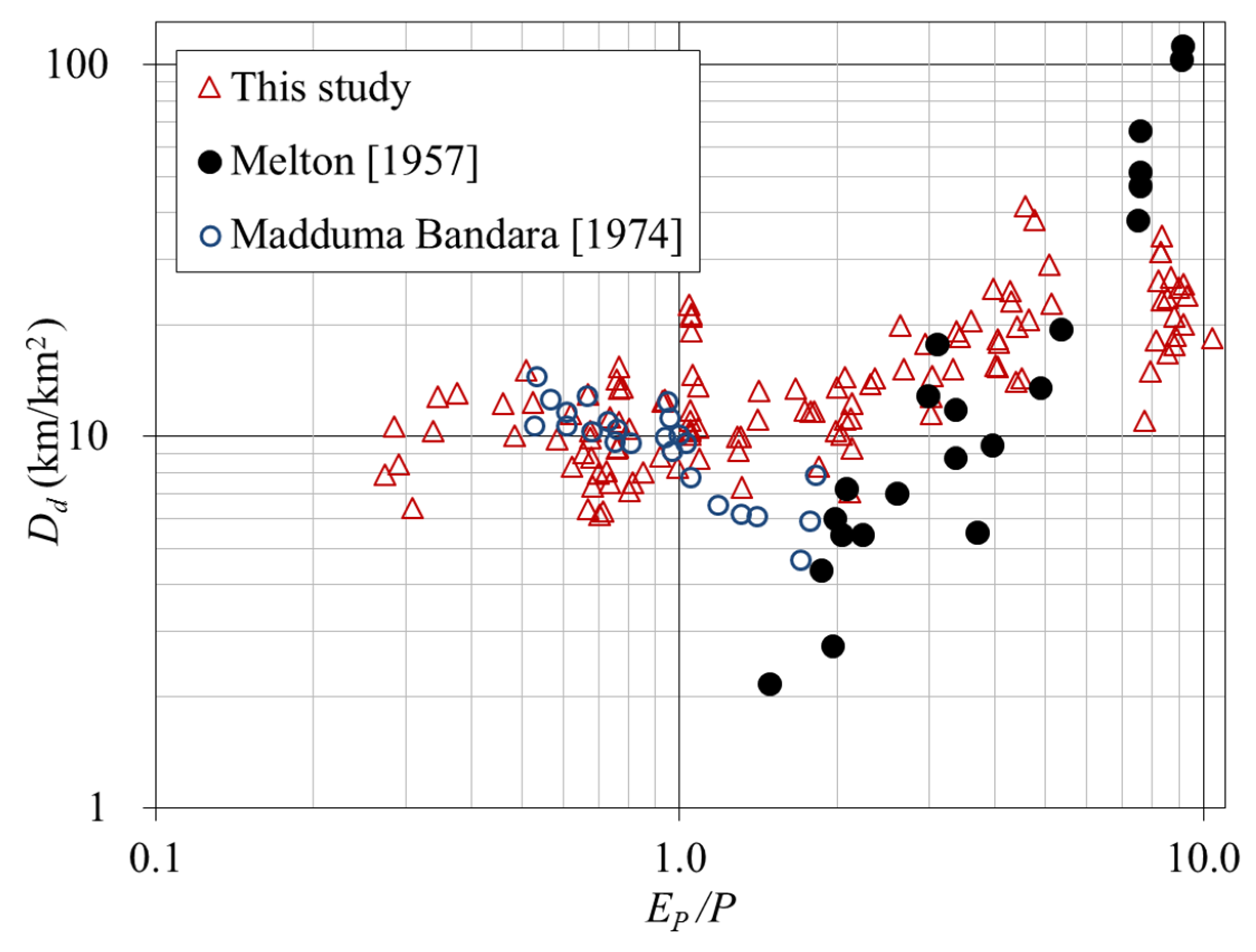
3.1. Relationship between Drainage Density and Climate Aridity Index

A total of 121 study watersheds in arid and humid regions were selected, then the valley networks were extracted using 1 m resolution LiDAR-based DEMs. The drainage area of most watersheds is less than 3 km2, and the average drainage area is 1.31 km2, with a minimum of 0.04 km2 and a maximum of 8.19 km2. The range of D d is from 6.2 km/km2 to 41.5 km/km2. Figure 6 shows the obtained results from this study overlaid with the reported data by Melton [31] and Madduma Bandara [39]. For the climate aridity index, E P / P ≤ 1 , the data points by Madduma Bandara [36] follow a decreasing trend, whereas such a declining trend does not exist for the watersheds in this study (Figure 6). The decreasing trend by Madduma Bandara [39] continues until E P / P approaches ~1.8. This discrepancy can be explained by the land use in Madduma Bandara’s watersheds, in which the natural land cover has been consistently removed due to a tea plantation over a 100 year period. In Madduma Bandara’s watersheds, the same vegetation cover exists in a different climates leading to the same resistance force against erosion enforced by rainfall. Given this circumstance, when E P / P increases (i.e., less rainfall), the erosion force drops while the resistance force is constant. This condition results in decreasing D d as E P / P increases. Thus, those data points are affected by human interferences to drainage density.
For 1 ≤ E P / P ≤ 6 , the drainage densities from both Melton [33] and this study show increasing trends (Figure 7). However, the magnitude of Dd is higher than those of Melton [33]. This difference can be explained by the spatial resolution of topographic maps. The topographic maps with a scale of 1:24,000 were used for extracting drainage networks by Melton [33] for watersheds with E P / P less than 6. These topographic maps with bare-earth contours are approximately equivalent to DEMs with a cell size of 30 m [56], from which small valleys are not detectable. Therefore, the drainage density is underestimated. However, the spatial resolution of LiDAR-based DEMs is 1 m in this study. The extracted drainage network from coarse topographic maps deviates significantly from the correspondingly observed one in the field [6,57]. In order to demonstrate the effect of DEM resolution on drainage density, 1 m DEMs for the study watersheds were resampled to 30 m DEMs for generating a drainage network. Twenty watersheds with E P / P less than six and drainage areas larger than 0.2 km2 were randomly selected. As shown in Figure 7, drainage densities from 1 m DEMs are higher than those from 30 m DEMs. As a demonstration, Figure 8 shows the extracted valley lines from 1 m and 30 m DEMs for the Isleta Drain watershed in New Mexico.
As indicated in Figure 6, the drainage densities from Melton [33] are higher than those in this study when E P / P ≥ 7 . The difference may be a result of the watersheds’ size between the two studies. The six watersheds used in Melton [33] are located in Arizona, southwestern United States. The method that was used to map the valley networks in these six watersheds were field survey. The range of the watershed sizes is from 0.001 to 0.006 km2, which was smaller than the current study. The study watersheds selected for the current study have an average watershed size of 0.40 km2 when E P / P ≥ 7 . The difference in watershed sizes between Melton’s [33] study and the current study may contribute to the difference in drainage density. Thus, the impact of drainage area on drainage density is investigated in the next section.

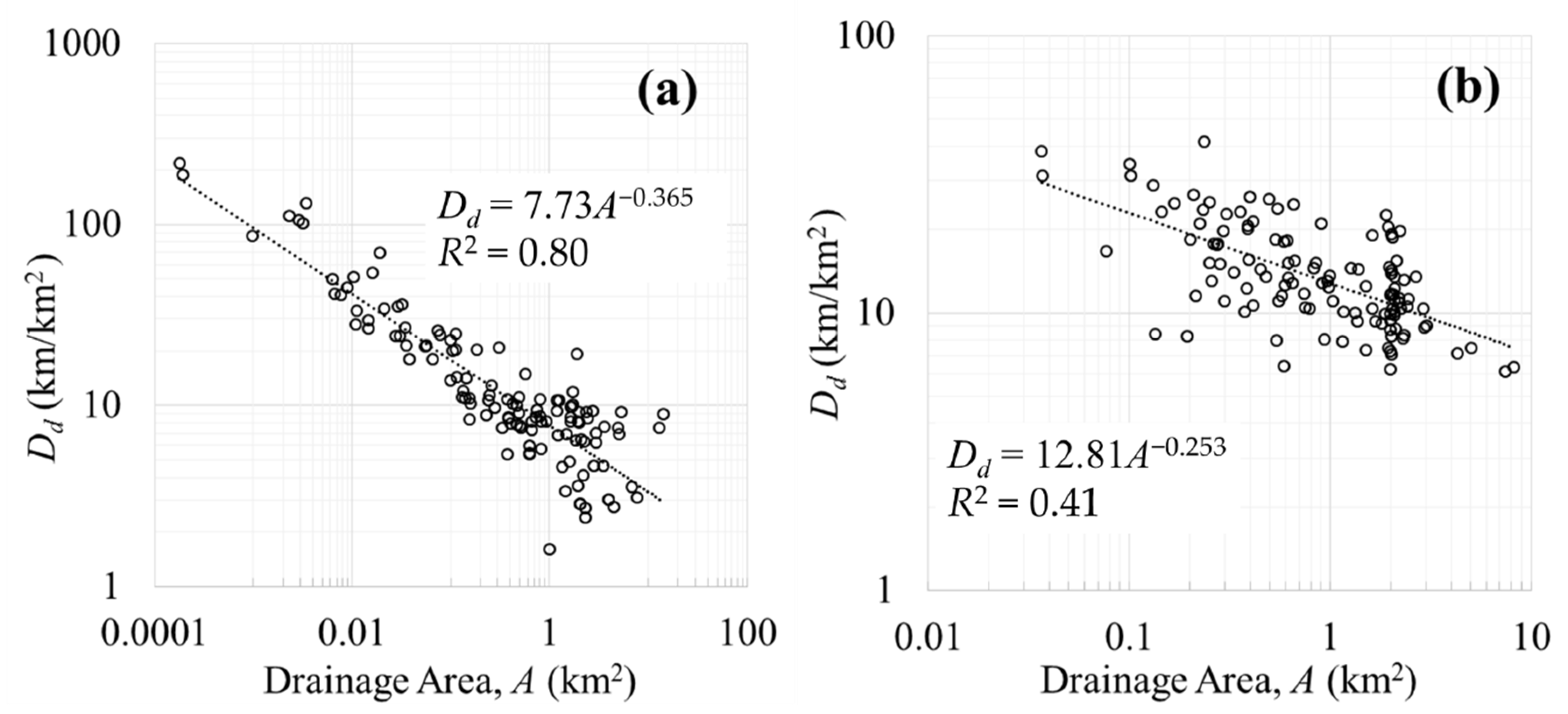
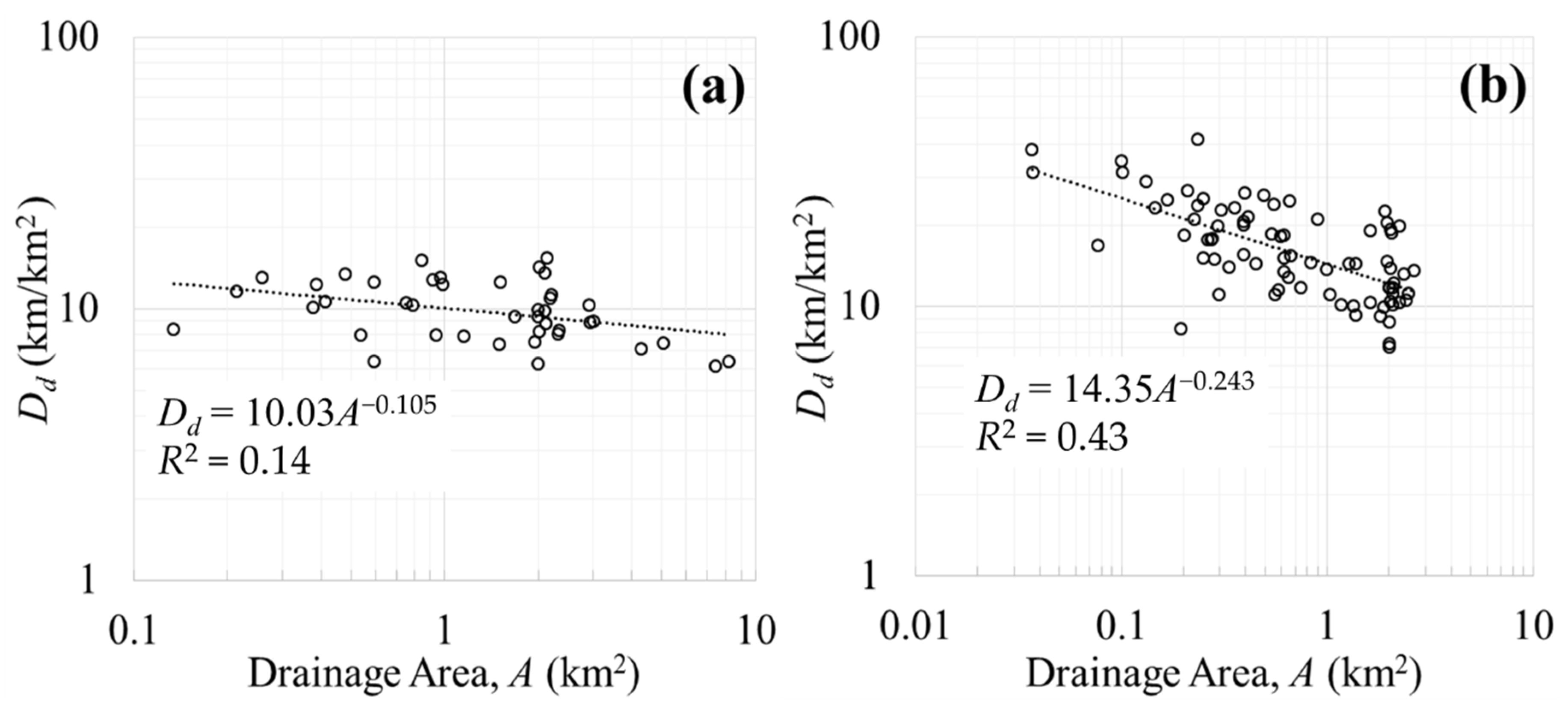
3.2. Impact of Drainage Area on Drainage Density

In addition to climate, a relationship between drainage area ( A ) and drainage density ( D d ) have been investigated in the literature. Gregory and Walling [43] showed an inverse relationship between D d and A . Pethick [46] presented a relationship of D d = 6.6 A − 0.337 based on 228 watersheds over different climates even though the general consensus is that D d is independent of A .
Figure 9 shows the relationship between D d and A for: (a) 124 watersheds in the arid climate from Melton [33] and (b) 121 watersheds from both humid and arid climates in this study. There is a strong negative correlation between drainage density and drainage area for both datasets. The data points in Figure 9b are more scattered due to the broader range of climate aridity index.
To investigate the climate effect on the relationship between Dd and A , the study watersheds were categorized into two groups: 1) humid ( E P / P < 1 ) and 2) arid ( E P / P ≥ 1 ). Figure 10 shows the relationship between Dd and A for humid (Figure 10a) and arid watersheds (Figure 10b). Although the relationship in the humid region is not as prominent, a clear negative correlation was observed in the arid region.
The results indicate that the conventional U-shaped relationship between drainage density and climate aridity index could be reevaluated, especially in the humid region (low climate aridity index). The negative correlation found in the data from Madduma Bandara [39], which were from agricultural watersheds, was not prominent in the study sites, which were natural watersheds. The negative correlation between drainage density and drainage area was still valid in the data from this study. However, high-resolution DEM tended to produce greater drainage density while arid area displayed a strong negative correlation than the humid area did. The results of this study added a new perspective to understanding drainage density data, which are affected by land use practices, climate, and input topography data resolution.

4. Summary and Conclusions

The aim of this study was to re-examine the dependence of drainage density on climate and the size of the drainage area. A total of 121 watersheds with pristine natural conditions were selected based on LiDAR data availability. The climate aridity index was used as an indicator of long-term climate. The range of climate aridity index for the study watersheds was from 0.3 to 10.4. Valley networks were extracted from the 1-m LiDAR-based DEMs using the topographic curvature threshold derived from connected component analysis, and the drainage density of each watershed was calculated.
When the climate aridity index is smaller than 1, the negative correlation between drainage density and climate aridity index presented in Madduma Bandara [39] was not observed in the data from this study; there was no strong positive or negative correlation. The decreasing trend in the data from Madduma Bandara [38] is thought to be caused by the elevated human interference over a 100 year period that affected the drainage characteristics of the watersheds.
When the climate aridity index is within the range 1–6, both the dataset from Melton [33] and the current study showed a positive correlation between drainage density and climate aridity index. Overall, drainage density was greater than that of the data from Melton. The reason for the positive shift was caused by the use of high-resolution DEM in this study; coarse DEM produced smaller drainage density as small valleys were not detectable.
When the climate aridity index is greater than 7, the drainage density of the dataset from Melton was greater than that of the current study. The difference might have been caused by the difference in watershed size; Melton’s watersheds (0.001–0.006 km2) were smaller than the watersheds in the current study (0.40 km2).
A negative correlation between drainage density and drainage area was presented in the datasets from Melton and reconfirmed in the current study. The decreasing trend of drainage density as drainage area increases was more prominent when the climate aridity index was greater than 1, which means a stronger decreasing trend was observed between drainage density and drainage area in arid regions than in humid regions. This study revisited previous studies on the drainage density characteristics related to climate aridity index and drainage area. The results of this study added a new perspective to understanding drainage density data. Land use change, climate, and input topography data resolution have significant impact on the relationship between drainage density and climate aridity index.
The valley networks used in this study were extracted from LiDAR data, which represent the hydrological conditions of the LiDAR acquisition periods only. Thus, the results may contain an unexpected seasonality effect. It can be improved by introducing other contemporaneous climate data, i.e., soil moisture conditions, in future research. The application of the methodology could be expanded to broader climate conditions as well as urban watersheds to understand the general characteristics of a drainage network. Additionally, more study watersheds with a broader range of drainage areas can be selected and included in future analysis.

Author Contributions

Conceptualization, S.K.; Formal analysis, S.K.; Methodology, S.K. and S.-K.Y.; Resources, S.-K.Y.; Writing—original draft preparation, S.K., S.-K.Y., and N.C.; Writing—review and editing, S.K., S.-K.Y., and N.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

The first author, Kim, acknowledges that this work is a part of his dissertation at the University of Central Florida (UCF), Orlando, Florida. The corresponding author Yoon acknowledges that this work was supported by the Seoul Institute of Technology (Project number: 2021-AB-007). The authors appreciate the United States Geological Survey (USGS) for providing the LiDAR datasets employed in the current study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Montgomery, D.R.; Foufoula-Georgiou, E. Channel network source representation using digital elevation models. Water Resour. Res. 1993, 29, 3925–3934. [Google Scholar] [CrossRef]
  2. Montgomery, D.R.; Dietrich, W.E. Source areas, drainage density, and channel initiation. Water Resour. Res. 1989, 25, 1907–1918. [Google Scholar] [CrossRef] [Green Version]
  3. Moglen, G.E.; Eltahir, E.A.; Bras, R.L. On the sensitivity of drainage density to climate change. Water Resour. Res. 1998, 34, 855–862. [Google Scholar] [CrossRef] [Green Version]
  4. Peucker, T.K.; Douglas, D.H. Detection of surface-specific points by local parallel processing of discrete terrain elevation data. Comput. Graph. Image Process. 1975, 4, 375–387. [Google Scholar] [CrossRef]
  5. Howard, A.D. A detachment-limited model of drainage basin evolution. Water Resour. Res. 1994, 30, 2261–2285. [Google Scholar] [CrossRef] [Green Version]
  6. Morisawa, M. Accuracy of determination of stream lengths from topographic maps. Eos Trans. Am. Geophys. Union 1957, 38, 86–88. [Google Scholar] [CrossRef]
  7. O’Callaghan, J.F.; Mark, D.M. The extraction of drainage networks from digital elevation data. Comput. Vis. Graph. Image Process. 1984, 28, 323–344. [Google Scholar] [CrossRef]
  8. Band, L.E. Topographic Partition of Watersheds with Digital Elevation Models. Water Resour. Res. 1986, 22, 15–24. [Google Scholar] [CrossRef]
  9. Tarboton, D.G.; Bras, R.L.; Rodriguez-Iturbe, I. On the extraction of channel networks from digital elevation data. Hydrol. Process. 1991, 5, 81–100. [Google Scholar] [CrossRef]
  10. Montgomery, D.R.; Dietrich, W.E. Where do channels begin? Nature 1988, 336, 232–234. [Google Scholar] [CrossRef]
  11. Willgoose, G.; Bras, R.L.; Rodriguez-Iturbe, I. A coupled channel network growth and hillslope evolution model: 1. Theory. Water Resour. Res. 1991, 27, 1671–1684. [Google Scholar] [CrossRef] [Green Version]
  12. Dietrich, W.E.; Wilson, C.J.; Montgomery, D.R.; McKean, J.; Bauer, R. Erosion thresholds and land surface morphology. Geology 1992, 20, 675–679. [Google Scholar] [CrossRef]
  13. Dietrich, W.E.; Wilson, C.J.; Montgomery, D.R.; McKean, J. Analysis of erosion thresholds, channel networks, and landscape morphology using a digital terrain model. J. Geol. 1993, 101, 259–278. [Google Scholar] [CrossRef] [Green Version]
  14. Ijjasz-Vasquez, E.J.; Bras, R.L. Scaling regimes of local slope versus contributing area in digital elevation models. Geomorphology 1995, 12, 299–311. [Google Scholar] [CrossRef]
  15. Yokoyama, R.; Shirasawa, M.; Pike, R.J. Visualizing topography by openness: A new application of image processing to digital elevation models. Photogramm. Eng. Remote Sens. 2002, 68, 257–266. [Google Scholar]
  16. Le, P.V.; Kumar, P. Power law scaling of topographic depressions and their hydrologic connectivity. Geophys. Res. Lett. 2014, 41, 1553–1559. [Google Scholar] [CrossRef]
  17. Hooshyar, M.; Kim, S.; Wang, D.; Medeiros, S.C. Wet channel network extraction by integrating LiDAR intensity and elevation data. Water Resour. Res. 2015, 51, 10029–10046. [Google Scholar] [CrossRef]
  18. Cao, H.; Pan, Z.; Chang, Q.; Zhou, A.; Wang, X.; Sun, Z. Stream network modeling using remote sensing data in an alpine cold catchment. Water 2021, 13, 1585. [Google Scholar] [CrossRef]
  19. Pelletier, J.D. A robust, two-parameter method for the extraction of drainage networks from high-resolution digital elevation models (DEMs): Evaluation using synthetic and real-world DEMs. Water Resour. Res. 2013, 49, 75–89. [Google Scholar] [CrossRef] [Green Version]
  20. Clubb, F.J.; Mudd, S.M.; Milodowski, D.T.; Hurst, M.D.; Slater, L.J. Objective extraction of channel heads from high-resolution topographic data. Water Resour. Res. 2014, 50, 4283–4304. [Google Scholar] [CrossRef] [Green Version]
  21. Hooshyar, M.; Wang, D.; Kim, S.; Medeiros, S.C.; Hagen, S.C. Valley and channel network extraction based on local topographic curvature and K-means. Water Resour. Res. 2016, 52, 8081–8102. [Google Scholar] [CrossRef]
  22. Metes, M.; Jones, D.K.; Baker, M.E.; Miller, A.J.; Hogan, D.M.; Loperfido, J.V.; Hopkins, K.G. Ephemeral stream network extraction from lidar-derived elevation and topographic attributes in urban and forested landscapes. J. Am. Water Resour. Assoc. 2022, 58, 547–565. [Google Scholar] [CrossRef]
  23. Horton, R.E. Drainage-basin characteristics. Eos Trans. Am. Geophys. Union 1932, 13, 350–361. [Google Scholar] [CrossRef]
  24. Horton, R.E. Erosional development of streams and their drainage basins; hydrophysical approach to quantitative morphology. Geol. Soc. Am. Bull. 1945, 56, 275–370. [Google Scholar] [CrossRef] [Green Version]
  25. Rinaldo, A.; Marani, A.; Rigon, R. Geomorphological dispersion. Water Resour. Res. 1991, 27, 513–525. [Google Scholar] [CrossRef]
  26. Rodriguez-Iturbe, I.; Muneepeerakul, R.; Bertuzzo, E.; Levin, S.A.; Rinaldo, A. River networks as ecological corridors: A complex systems perspective for integrating hydrologic, geomorphologic, and ecologic dynamics. Water Resour. Res. 2009, 45, 1–22. [Google Scholar] [CrossRef]
  27. Biswal, B.; Marani, M. Geomorphological origin of recession curves. Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef]
  28. Mutzner, R.; Bertuzzo, E.; Tarolli, P.; Weijs, S.V.; Nicotina, L.; Ceola, S.; Tomasic, N.; Rodriguez-Iturbe, I.; Parlange, M.B.; Rinaldo, A. Geomorphic signatures on Brutsaert base flow recession analysis. Water Resour. Res. 2013, 49, 5462–5472. [Google Scholar] [CrossRef] [Green Version]
  29. Godsey, S.; Kirchner, J. Dynamic, discontinuous stream networks: Hydrologically driven variations in active drainage density, flowing channels and stream order. Hydrol. Process. 2014, 28, 5791–5803. [Google Scholar] [CrossRef]
  30. Ghosh, D.K.; Wang, D.; Zhu, T. On the transition of base flow recession from early stage to late stage. Adv. Water Resour. 2016, 88, 8–13. [Google Scholar] [CrossRef]
  31. Dunne, T.; Leopold, L. Water in Environment Planning; Freeman: San Francisco, CA, USA, 1978. [Google Scholar]
  32. Di Lazzaro, M.; Zarlenga, A.; Volpi, E. Hydrological effects of within-catchment heterogeneity of drainage density. Adv. Water Resour. 2015, 76, 157–167. [Google Scholar] [CrossRef]
  33. Melton, M.A. An Analysis of the Relations among Elements of Climate, Surface Properties, and Geomorphology; DTIC Document; Columbia University: New York, NY, USA, 1957. [Google Scholar]
  34. Carlston, C.W. Drainage Density and Streamflow; US Government Printing Office: Washington, DC, USA, 1963. [Google Scholar]
  35. Sangireddy, H.; Carothers, R.A.; Stark, C.P.; Passalacqua, P. Controls of climate, topography, vegetation, and lithology on drainage density extracted from high resolution topography data. J. Hydrol. 2016, 537, 271–282. [Google Scholar] [CrossRef] [Green Version]
  36. Chen, S.A.; Michaelides, K.; Grieve, S.W.D.; Singer, M.B. Aridity is expressed in river topography globally. Nature 2019, 573, 573–577. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  37. Gregory, K.; Gardiner, V. Drainage density and climate. Z. Geomorphol. 1975, 19, 287–298. [Google Scholar]
  38. Thornthwaite, C.W. The climates of North America: According to a new classification. Geogr. Rev. 1931, 21, 633–655. [Google Scholar] [CrossRef]
  39. Madduma Bandara, C.M. Drainage density and effective precipitation. J. Hydrol. 1974, 21, 187–190. [Google Scholar] [CrossRef]
  40. Abrahams, A.D. Channel networks: A geomorphological perspective. Water Resour. Res. 1984, 20, 161–188. [Google Scholar] [CrossRef]
  41. Istanbulluoglu, E.; Bras, R.L. Vegetation-modulated landscape evolution: Effects of vegetation on landscape processes, drainage density, and topography. J. Geophys. Res. Earth Surf. 2005, 110, 1–19. [Google Scholar] [CrossRef] [Green Version]
  42. Collins, D.B.G.; Bras, R.L. Climatic and ecological controls of equilibrium drainage density, relief, and channel concavity in dry lands. Water Resour. Res. 2010, 46, 1–18. [Google Scholar] [CrossRef] [Green Version]
  43. Gregory, K.J.; Walling, D.E. Drainage Basin Form and Process: A Geomorphological Approach; Edward Arnold: London, UK, 1973. [Google Scholar]
  44. Strahler, A.N. Quantitative analysis of watershed geomorphology. Eos Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar] [CrossRef] [Green Version]
  45. Rastogi, R.A.; Sharma, T. Quantitative analysis of drainage basin characteristics. J. Soil Water Conserv. 2022, 26, 18–25. [Google Scholar]
  46. Pethick, J. A note on the drainage density-basin area relationship. Area 1975, 7, 217–222. [Google Scholar]
  47. Richards, K.S. Yet more notes on the drainage density-basin area relationship. Area 1978, 10, 344–348. [Google Scholar]
  48. Stoker, J.M.; Greenlee, S.K.; Gesch, D.B.; Menig, J.C. CLICK: The new USGS center for lidar information coordination and knowledge. Photogramm. Eng. Remote Sens. 2006, 72, 613–616. [Google Scholar]
  49. Budyko, M.I. The Heat Balance of the Earth’s Surface; US Department of Commerce: Washington, DC, USA, 1958. [Google Scholar]
  50. Budyko, M.I. Climate and Life; Academic Press: New York, NY, USA, 1974; 508 p. [Google Scholar]
  51. Zhang, K.; Kimball, J.S.; Nemani, R.R.; Running, S.W. A continuous satellite-derived global record of land surface evapotranspiration from 1983 to 2006. Water Resour. Res. 2010, 46, 1–21. [Google Scholar] [CrossRef] [Green Version]
  52. Daly, C.; Neilson, R.P.; Phillips, D.L. A statistical-topographic model for mapping climatological precipitation over mountainous terrain. J. Appl. Meteorol. 1994, 33, 140–158. [Google Scholar] [CrossRef]
  53. Wang, D.; Wu, L. Similarity of climate control on base flow and perennial stream density in the Budyko framework. Hydrol. Earth Syst. Sci. 2013, 17, 315–324. [Google Scholar] [CrossRef] [Green Version]
  54. Mitášová, H.; Hofierka, J. Interpolation by regularized spline with tension: II. Application to terrain modeling and surface geometry analysis. Math. Geol. 1993, 25, 657–669. [Google Scholar] [CrossRef]
  55. Suzuki, K.; Horiba, I.; Sugie, N. Linear-time connected-component labeling based on sequential local operations. Computer Vision and Image Understanding 2003, 89, 1–23. [Google Scholar] [CrossRef]
  56. Kosovich, J.J. State of Florida 1:24,000-and 1:100,000-Scale Quadrangle Index Map, Highlighting Low-lying Areas Derived from USGS Digital Elevation Models; US Department of the Interior, US Geological Survey: Washington, DC, USA, 2008. [Google Scholar]
  57. Schneider, W.J. A note on the accuracy of drainage densities computed from topographic maps. J. Geophys. Res. 1961, 66, 3617–3618. [Google Scholar] [CrossRef]
Applsci 13 00700 g001 550
Figure 1. Study sites (a) Location of study sites and LiDAR data availability as of 2015 and (b) normalized frequency distribution of E p / P for the study sites.
Figure 1. Study sites (a) Location of study sites and LiDAR data availability as of 2015 and (b) normalized frequency distribution of E p / P for the study sites.
Applsci 13 00700 g001
Applsci 13 00700 g002 550
Figure 2. (a) The relationship (PE = 176 E P / P −1.22) between PE index and climate aridity index ( E P / P ) and (b) drainage density ( D d ) versus E P / P from Melton [32] and Madduma Bandara [38].
Figure 2. (a) The relationship (PE = 176 E P / P −1.22) between PE index and climate aridity index ( E P / P ) and (b) drainage density ( D d ) versus E P / P from Melton [32] and Madduma Bandara [38].
Applsci 13 00700 g002
Applsci 13 00700 g003 550
Figure 3. One-meter contour lines and the curvature grid for (a) the original DEM and (b) the smoothed DEM after applying Perona-Malik filter with the time of forward diffusion set to 50 ( T F = 50 ) on the Isleta Drain watershed located in New Mexico.
Figure 3. One-meter contour lines and the curvature grid for (a) the original DEM and (b) the smoothed DEM after applying Perona-Malik filter with the time of forward diffusion set to 50 ( T F = 50 ) on the Isleta Drain watershed located in New Mexico.
Applsci 13 00700 g003
Applsci 13 00700 g004 550
Figure 4. Valley differentiation: (a) Examples of connected components for valley and ridge and (b) the number of valley and ridge connected components ( N c c ) vs. curvature threshold ( κ T ) in the Isleta Drain watershed located in New Mexico. The peak value represents the transition from insignificant to significant convergence/divergence features ( κ v = 0.005   m − 1 ).
Figure 4. Valley differentiation: (a) Examples of connected components for valley and ridge and (b) the number of valley and ridge connected components ( N c c ) vs. curvature threshold ( κ T ) in the Isleta Drain watershed located in New Mexico. The peak value represents the transition from insignificant to significant convergence/divergence features ( κ v = 0.005   m − 1 ).
Applsci 13 00700 g004
Applsci 13 00700 g005 550
Figure 5. Curvature-based valley network extraction: (a) Contour curvature computed from the filtered DEM and (b) extracted valley network based on the curvature threshold in the Isleta Drain watershed located in New Mexico.
Figure 5. Curvature-based valley network extraction: (a) Contour curvature computed from the filtered DEM and (b) extracted valley network based on the curvature threshold in the Isleta Drain watershed located in New Mexico.
Applsci 13 00700 g005
Applsci 13 00700 g006 550
Figure 6. Drainage density (Dd) versus climate aridity index ( E P / P ) from Melton [33], Madduma Bandara [39], and this study.
Figure 6. Drainage density (Dd) versus climate aridity index ( E P / P ) from Melton [33], Madduma Bandara [39], and this study.
Applsci 13 00700 g006
Applsci 13 00700 g007 550
Figure 7. Drainage densities (Dd) derived from LiDAR-based 1 m DEM and its resampled 30 m DEM.
Figure 7. Drainage densities (Dd) derived from LiDAR-based 1 m DEM and its resampled 30 m DEM.
Applsci 13 00700 g007
Applsci 13 00700 g008 550
Figure 8. The derived valley lines from 1 m DEM and 30 m DEM in the Isleta Drain watershed located in New Mexico.
Figure 8. The derived valley lines from 1 m DEM and 30 m DEM in the Isleta Drain watershed located in New Mexico.
Applsci 13 00700 g008
Applsci 13 00700 g009 550
Figure 9. The relationship between drainage density ( D d ) and drainage area: (a) 124 watersheds in arid regions from Melton [33] and (b) 121 watersheds in humid to arid regions from this study.
Figure 9. The relationship between drainage density ( D d ) and drainage area: (a) 124 watersheds in arid regions from Melton [33] and (b) 121 watersheds in humid to arid regions from this study.
Applsci 13 00700 g009
Applsci 13 00700 g010 550
Figure 10. The relationship between drainage density ( D d ) and drainage area from the watersheds in this study: (a) 42 watersheds from the humid region ( E P / P < 1) and (b) 79 watersheds from the arid region ( E P / P > 1).
Figure 10. The relationship between drainage density ( D d ) and drainage area from the watersheds in this study: (a) 42 watersheds from the humid region ( E P / P < 1) and (b) 79 watersheds from the arid region ( E P / P > 1).
Applsci 13 00700 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Kim, S.; Yoon, S.-K.; Choi, N. Evaluating the Drainage Density Characteristics on Climate and Drainage Area Using LiDAR Data. Appl. Sci. 2023, 13, 700. https://doi.org/10.3390/app13020700

AMA Style

Kim S, Yoon S-K, Choi N. Evaluating the Drainage Density Characteristics on Climate and Drainage Area Using LiDAR Data. Applied Sciences. 2023; 13(2):700. https://doi.org/10.3390/app13020700

Chicago/Turabian Style

Kim, Seoyoung, Sun-Kwon Yoon, and Namjeong Choi. 2023. "Evaluating the Drainage Density Characteristics on Climate and Drainage Area Using LiDAR Data" Applied Sciences 13, no. 2: 700. https://doi.org/10.3390/app13020700

APA Style

Kim, S., Yoon, S. -K., & Choi, N. (2023). Evaluating the Drainage Density Characteristics on Climate and Drainage Area Using LiDAR Data. Applied Sciences, 13(2), 700. https://doi.org/10.3390/app13020700

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop