Optimal Complex Morlet Wavelet Parameters for Quantitative Time-Frequency Analysis of Molecular Vibration
Abstract
:1. Introduction
2. Selection Method of Wavelet Parameters
2.1. The Essence of CMOR Wavelet Transform
2.2. Time-Frequency Resolution and Edge Effect
2.3. CMOR Wavelet Parameters of Target Frequency
3. Simulation Results and Discussions
3.1. CMOR Wavelet Parameters for Water Molecule Vibration
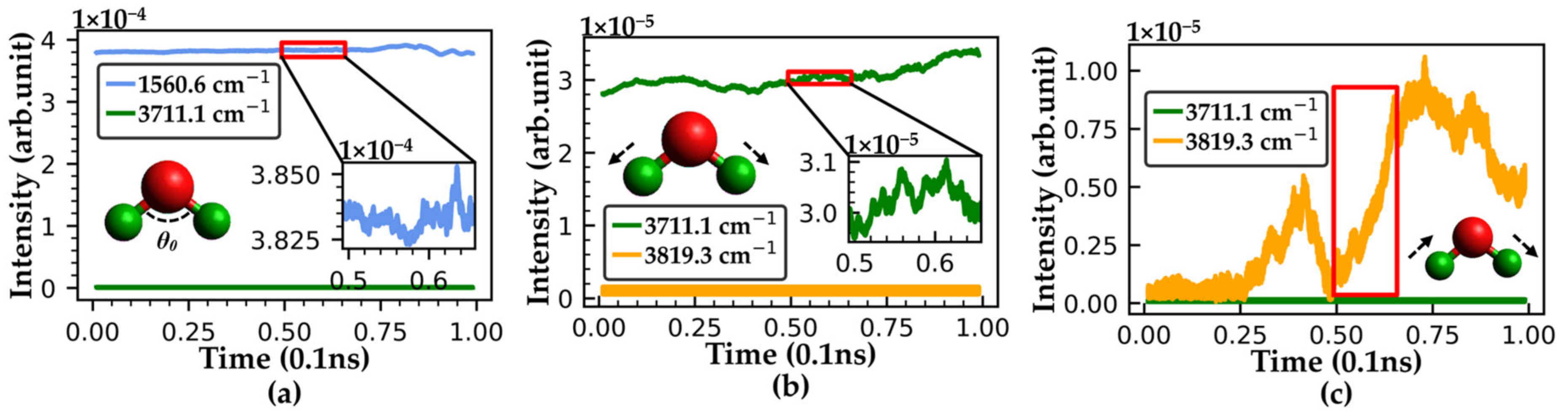
3.2. Quantitative Time-Frequency Analysis of Water Molecule
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Varanis, M.; Silva, A.L.; Balthazar, J.M.; Pederiva, R. A tutorial review on time-frequency analysis of non-stationary vibration signals with nonlinear dynamics applications. Braz. J. Phys. 2021, 51, 859–877. [Google Scholar] [CrossRef]
- Li, H.; Lv, H.; Gu, J.; Xiong, J.; Han, Q.; Liu, J.; Qin, Z. Nonlinear vibration characteristics of fibre reinforced composite cylindrical shells in thermal environment. Mech. Syst. Signal Process. 2021, 156, 107665. [Google Scholar] [CrossRef]
- Gao, J.; Song, Q.; Liu, Z. Chatter detection and stability region acquisition in thin-walled workpiece milling based on CMWT. Int. J. Adv. Manuf. Technol. 2018, 98, 699–713. [Google Scholar] [CrossRef]
- Wei, D.; Hu, M. Theory and applications of short-time linear canonical transform. Digit. Signal Process. 2021, 118, 103239. [Google Scholar] [CrossRef]
- Feng, Z.; Liang, M.; Chu, F. Recent advances in time–frequency analysis methods for Machinery Fault Diagnosis: A review with application examples. Mech. Syst. Signal Process. 2013, 38, 165–205. [Google Scholar] [CrossRef]
- Cohen, L. Time-frequency distributions-A Review. Proc. IEEE 1989, 77, 941–981. [Google Scholar] [CrossRef] [Green Version]
- Rioul, O.; Flandrin, P. Time-scale energy distributions: A general class extending wavelet transforms. IEEE Trans. Signal Process. 1992, 40, 1746–1757. [Google Scholar] [CrossRef]
- Baraniuk, R.G.; Jones, D.L. A signal-dependent time-frequency representation: Optimal Kernel Design. IEEE Trans. Signal Process. 1993, 41, 1589–1602. [Google Scholar] [CrossRef]
- Rodríguez Fonollosa, J.; Nikias, C.L. Analysis of finite-energy signals higher-order moments- and spectra-based time-frequency distributions. Signal Process. 1994, 36, 315–328. [Google Scholar] [CrossRef]
- Stankovic, L.J. L-class of time-frequency distributions. IEEE Signal Process. Lett. 1996, 3, 22–25. [Google Scholar] [CrossRef]
- Stankovic, L.J. S-class of time–frequency distributions. IEEE Proc. Vis. Image Signal Process. 1997, 144, 57. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z. A review on Hilbert-Huang Transform: Method and its Applications to Geophysical Studies. Rev. Geophys. 2008, 46, 2. [Google Scholar] [CrossRef] [Green Version]
- Ramasesha, K.; De Marco, L.; Mandal, A.; Tokmakoff, A. Water vibrations have strongly mixed intra- and intermolecular character. Nat. Chem. 2013, 5, 935–940. [Google Scholar] [CrossRef] [PubMed]
- De Marco, L.; Fournier, J.A.; Thämer, M.; Carpenter, W.; Tokmakoff, A. Anharmonic exciton dynamics and energy dissipation in liquid water from two-dimensional infrared spectroscopy. J. Chem. Phys. 2016, 145, 094501. [Google Scholar] [CrossRef] [PubMed]
- Matt, S.M.; Ben-Amotz, D. Influence of intermolecular coupling on the vibrational spectrum of water. J. Phys. Chem. B 2018, 122, 5375–5380. [Google Scholar] [CrossRef] [PubMed]
- Rhif, M.; Ben Abbes, A.; Farah, I.; Martínez, B.; Sang, Y. Wavelet transform application for/in Non-Stationary Time-Series Analysis: A Review. Appl. Sci. 2019, 9, 1345. [Google Scholar] [CrossRef] [Green Version]
- Cohen, M.X. A better way to define and describe Morlet wavelets for time-frequency analysis. NeuroImage 2019, 199, 81–86. [Google Scholar] [CrossRef]
- Dinç, E.; Baleanu, D. A review on the wavelet transform applications in analytical chemistry. Math. Methods Eng. 2007, 265–284. [Google Scholar]
- Yan, B.F.; Miyamoto, A.; Brühwiler, E. Wavelet transform-based modal parameter identification considering uncertainty. J. Sound Vib. 2006, 291, 285–301. [Google Scholar] [CrossRef]
- Gaviria, C.A.; Montejo, L.A. Optimal wavelet parameters for system identification of civil engineering structures. Earthq. Spectra 2018, 34, 197–216. [Google Scholar] [CrossRef]
- Deák, D.K.; Kocsis, K.I. Complex morlet wavelet design with global parameter optimization for diagnosis of industrial manufacturing faults of tapered roller bearing in noisycondition. Diagnostyka 2019, 20, 77–86. [Google Scholar] [CrossRef]
- Li, W.; Huang, Q.-A.; Yang, C.; Chen, J.; Tang, Z.; Zhang, F.; Li, A.; Zhang, L.; Zhang, J. A fast measurement of Warburg-like impedance spectra with Morlet wavelet transform for electrochemical energy devices. Electrochim. Acta 2019, 322, 134760. [Google Scholar] [CrossRef]
- Năstac, S.; Debeleac, C.; Simionescu, C. Dynamic diagnosis of elastic coupling transmissions of technological equipments based on joint time-frequency evaluations. Appl. Mech. Mater. 2014, 657, 465–469. [Google Scholar] [CrossRef]
- Blair, G.M. A review of the discrete Fourier transform. part 1: Manipulating the powers of two. Electron. Commun. Eng. J. 1995, 7, 169–177. [Google Scholar] [CrossRef]
- DasGupta, A.; Casella, G.; Fienberg, S.; Olkin, I. Normal Distribution. In Fundamentals of Probability a First Course; Springer: New York, NY, USA, 2010; pp. 195–212. [Google Scholar]
- Goh, T.N. Some common measurement limits used in quality control. Int. J. Qual. Reliab. Manag. 1986, 3, 21–30. [Google Scholar] [CrossRef]
- Rosaiah, K.; Rao, B.S.; Reddy, J.P.; Chinnamamba, C. Variable control charts for Gumbel Distribution based on percentiles. J. Comput. Math. Sci. 2018, 9, 1890–1897. [Google Scholar] [CrossRef]
- Brian, R.; Jiajun, H. Jean Morlet and the continuous wavelet transform. CREWES Res. Rep. 2016, 28, 115. Available online: https://www.crewes.org/Documents/ResearchReports/2016/CRR201668.pdf (accessed on 16 October 2022).
- Pal, M.P.; Panigrahi, P.K. A multi scale time–frequency analysis on electroencephalogram signals. Phys. A Stat. Mech. Its Appl. 2022, 586, 126516. [Google Scholar] [CrossRef]
- Lee, G.; Gommers, R.; Waselewski, F.; Wohlfahrt, K.; O’Leary, A. PyWavelets: A python package for Wavelet Analysis. J. Open Source Softw. 2019, 4, 1237. [Google Scholar] [CrossRef]
- Hutter, J.; Iannuzzi, M.; Schiffmann, F.; Vondele, J.V. Cp2k: Atomistic simulations of condensed matter systems. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef] [Green Version]
- Vondele, J.V.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005, 167, 103–128. [Google Scholar] [CrossRef] [Green Version]
- Goedecker, S.; Teter, M.; Hutter, J. Separable dual-space gaussian pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, S. Efficiently calculating anharmonic frequencies of molecular vibration by molecular dynamics trajectory analysis. ACS Omega 2019, 4, 9271–9283. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carpenter, W.B.; Fournier, J.A.; Biswas, R.; Voth, G.A.; Tokmakoff, A. Delocalization and stretch-bend mixing of the Hoh Bend in Liquid Water. J. Chem. Phys. 2017, 147, 84503. [Google Scholar] [CrossRef]
- Yu, C.-C.; Chiang, K.-Y.; Okuno, M.; Seki, T.; Ohto, T.; Yu, X.; Korepanov, V.; Hamaguchi, H.-O.; Bonn, M.; Hunger, J.; et al. Vibrational couplings and energy transfer pathways of water’s bending mode. Nat. Commun. 2020, 11, 5977. [Google Scholar] [CrossRef]

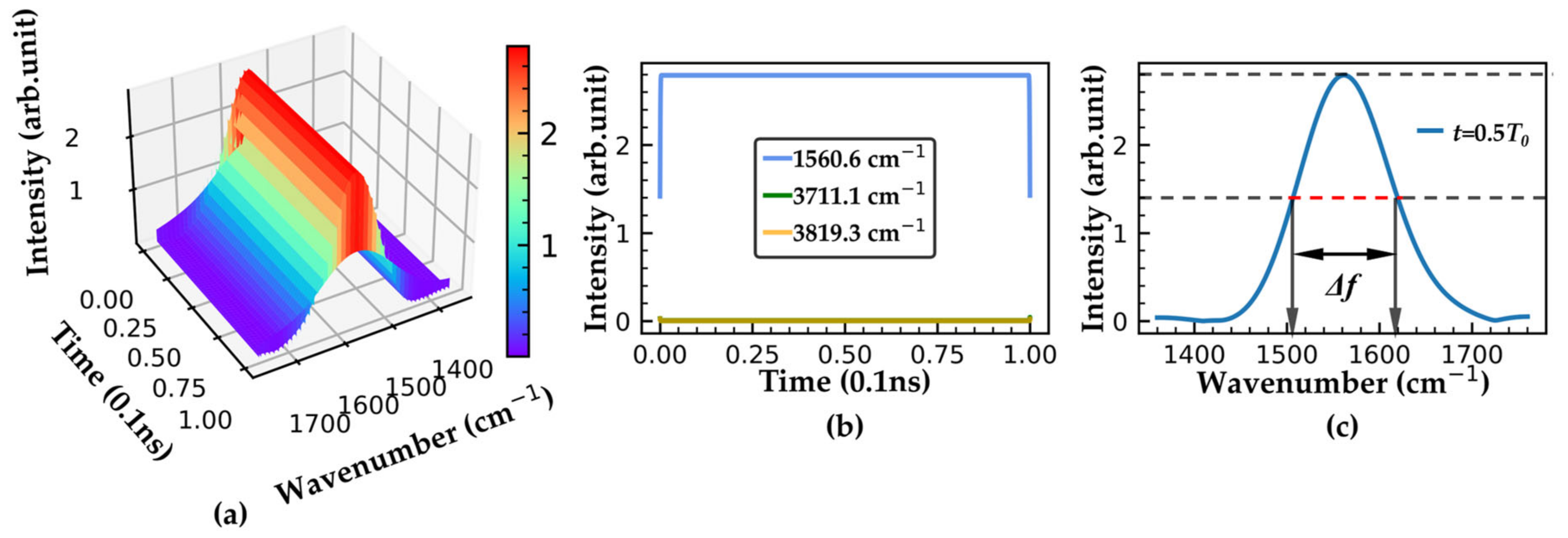
| Wavenumber (cm −1) | δf (cm −1) | δf′ (cm −1) | fb | fc | Δf (cm −1) | δt (10 −10 s) |
|---|---|---|---|---|---|---|
| 1560.6 | 2150.5 | 100.0 | 6.0 | 3.0 | 113 | 0.00667 |
| 3711.1 | 108.2 | 70.0 | 20.0 | 6.0 | 74 | 0.01024 |
| 3819.3 | 108.2 | 60.0 | 24.0 | 7.0 | 59 | 0.01271 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Ma, S.; Wang, S. Optimal Complex Morlet Wavelet Parameters for Quantitative Time-Frequency Analysis of Molecular Vibration. Appl. Sci. 2023, 13, 2734. https://doi.org/10.3390/app13042734
Li S, Ma S, Wang S. Optimal Complex Morlet Wavelet Parameters for Quantitative Time-Frequency Analysis of Molecular Vibration. Applied Sciences. 2023; 13(4):2734. https://doi.org/10.3390/app13042734
Chicago/Turabian StyleLi, Shuangquan, Shangyi Ma, and Shaoqing Wang. 2023. "Optimal Complex Morlet Wavelet Parameters for Quantitative Time-Frequency Analysis of Molecular Vibration" Applied Sciences 13, no. 4: 2734. https://doi.org/10.3390/app13042734
APA StyleLi, S., Ma, S., & Wang, S. (2023). Optimal Complex Morlet Wavelet Parameters for Quantitative Time-Frequency Analysis of Molecular Vibration. Applied Sciences, 13(4), 2734. https://doi.org/10.3390/app13042734







