Abstract
The past decade has witnessed the great success of deep neural networks in various domains. However, deep neural networks are very resource-intensive in terms of energy consumption, data requirements, and high computational costs. With the recent increasing need for the autonomy of machines in the real world, e.g., self-driving vehicles, drones, and collaborative robots, exploitation of deep neural networks in those applications has been actively investigated. In those applications, energy and computational efficiencies are especially important because of the need for real-time responses and the limited energy supply. A promising solution to these previously infeasible applications has recently been given by biologically plausible spiking neural networks. Spiking neural networks aim to bridge the gap between neuroscience and machine learning, using biologically realistic models of neurons to carry out the computation. Due to their functional similarity to the biological neural network, spiking neural networks can embrace the sparsity found in biology and are highly compatible with temporal code. Our contributions in this work are: (i) we give a comprehensive review of theories of biological neurons; (ii) we present various existing spike-based neuron models, which have been studied in neuroscience; (iii) we detail synapse models; (iv) we provide a review of artificial neural networks; (v) we provide detailed guidance on how to train spike-based neuron models; (vi) we revise available spike-based neuron frameworks that have been developed to support implementing spiking neural networks; (vii) finally, we cover existing spiking neural network applications in computer vision and robotics domains. The paper concludes with discussions of future perspectives.
1. Introduction
The last decade has witnessed the growing abilities of artificial neural networks (ANNs) from the first generation multi-layer perceptron (MLP) to the many state-of-the-art techniques in the second generation deep neural networks (DNNs). This achievement strongly depends on a large amount of annotated data and the widespread availability of high-performance computing devices as well as the general-purpose Graphics Processing Units (GPUs). Despite this great advancement, ANNs still lag behind the biological neural networks in terms of energy efficiency and abilities for online learning. Many attempts have been made to reduce the power consumption of traditional deep learning models. In order to find more compact networks that can achieve similar performance with much less complexity and a smaller number of parameters compared to the original network, many techniques have been developed such as quantization [1], pruning [2], and knowledge distillation [3]. Quantization converts the weights and inputs of the network into integer types, which makes the overall operations lighter than the floating-point operations. In pruning, the connections of a network are iteratively removed during or after the training. To compress a neural network without dropping performance, knowledge distillation transfers complex knowledge learned by a heavy network called a teacher to a lightweight network called a student.
Although ANNs/DNNs are historically brain-inspired, they are fundamentally different in structure, neural computations, and learning rules compared to the biological neural network. This observation leads to the spiking neural networks (SNNs), which are often referred to as the third generation of neural networks that could be a breakthrough of bottlenecks of ANNs. Using SNNs on neuromorphic hardware, such as TrueNorth [4], Loihi [5], SpiNNaker [6], NeuroGrid [7], etc., is worth mentioning and a promising approach to the energy consumption problem. In SNNs, such as in biological neural networks, neurons communicate with each other with discrete electrical signals called spikes and work in continuous time.
Due to their functional similarity to the biological neural networks, SNNs can embrace the sparsity found in biology and are highly compatible with temporal code [8]. Although SNNs still lag behind DNNs in terms of their performance, the gap is vanishing on some tasks, while SNNs typically require much lower energy for the operation. However, SNNs are still difficult to train in general, mainly owing to their complex dynamics of neurons and the non-differentiable nature of spike operations. A comparison between biological neural networks, ANNs, and SNNs is given in Table 1. BP is backpropagation.

Table 1.
A comparison of properties between biological neural networks, ANNs, and SNNs.
2. Biological Neurons
Neurons are the basic working units of the nervous system that process information by propagating electrochemical signals through action potentials. Neurons are not electrically neutral nor extracellular fluid because of the presence of ions within them. Ions are constantly moving in and out of the cell through a membrane that can dynamically modify its electric permeability with external electrochemical signals. The flux of ions entering and exiting the cell causes a virtual current flow through the membrane, mostly ascribed to Na, K, and Cl ions.
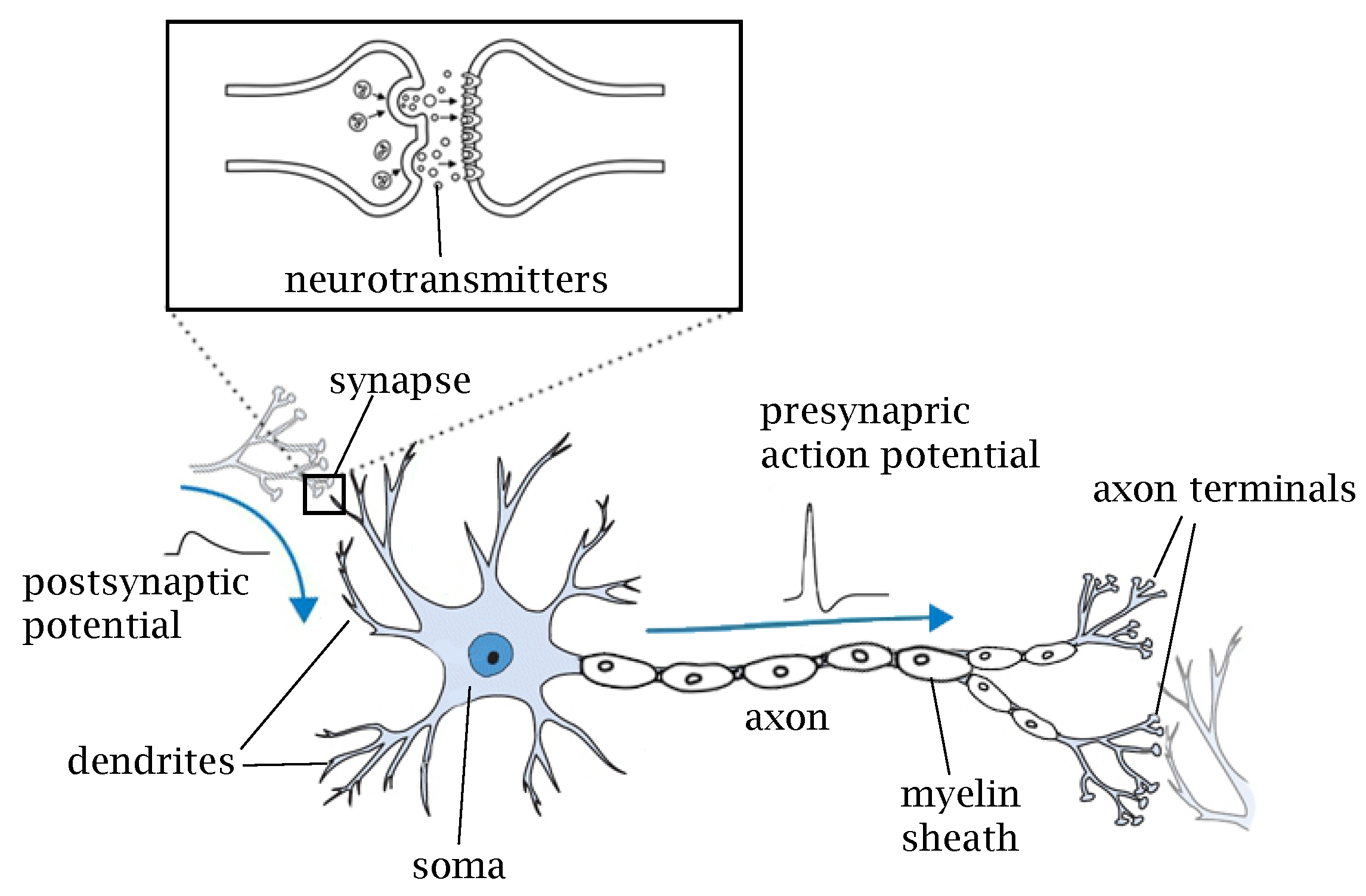
Figure 1 shows a typical structure of a neuron with four main components: dendrites, soma, axon, and synapse. Dendrites are the short nervous termination that can be considered as the input of the neuron. They translate the chemical signals carried by neurotransmitters released from the pre-synaptic neuron into electric signals. Soma is the cell body where membrane potentials propagated from synaptic inputs are integrated, which ultimately determines whether the post-synaptic cell fires action potentials before being transmitted to the axon. This interaction of influences is called neural integration. Axon carries the action potential towards other nerve cells. In order to rapidly carry the action potential at long distances without attenuation, some axons are coated with a myelin sheath. Synapses are the contact structure for information transfer that interconnect neurons in a neural network. Synapses can be broadly divided into chemical and electrical synapses. In chemical synapses, there is no direct contact between the pre- and post-synaptic neurons. The signal from the pre-synaptic neuron is transmitted via neurotransmitters contained in the synaptic granules released into the synaptic cleft. Neurotransmitters bind to receptors in the post-synaptic cell, directly altering membrane potential or activating intracellular secondary messengers to transmit the information. This type of transmission is slow but amplifies the signal and can make the effects of the incoming spike last longer. Chemical synapses can be subdivided into excitatory and inhibitory synapses. Excitatory synapses are synaptic connections that depolarize post-synaptic cells through synaptic transmission and promote the firing of action potentials. Inhibitory synapses are synaptic connections that hyperpolarize post-synaptic cells by synaptic transmission and inhibit the development of action potentials. Glutamate and GABA are the most common excitatory and inhibitory neurotransmitters, respectively; ionotropic receptors for glutamate are AMPA and NMDA and that of GABA are and [9]. Electrical synapses, on the other hand, are structures that transmit membrane potential charges directly to the next neuron via gap junctions on the contact membrane. This kind of communication is very rapid since there are no chemical reactions within the transmission; however, there is no gain in signal amplitude as in the chemical synapses.
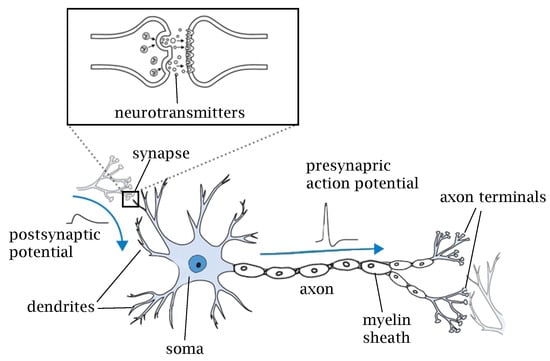
Figure 1.
A typical structure of a biological neuron and synapse.
2.1. Membrane Potential
The electric potential inside a cell with respect to the outside of the cell is called the membrane potential. The membrane potential can be derived using the Goldman–Hodgkin–Katz equation, which takes into consideration the relative permeability of the plasma membrane to each ion in question.
where R is the universal gas constant, T is the absolute temperature (K) at human body temperature (37 [°C]), F is the Faraday constant (= (C· mol)), is the extracellular concentration of ion A, and is the intracellular concentration of ion A, and is the membrane permeability for ion A, and for a typical neuron at rest, it is known that ::::. In contrast, approximate relative permeability at the peak of a typical neuronal action potential are :::12: [10].
2.1.1. Resting Membrane Potential
Due to the action of a number of proteins, ions are constantly moving in and out of the cell. Although the influx of ions does not stop, charge transfer becomes apparently immobile when the total charge of the outflowing ions and the total charge of the inflowing ions per unit time becomes the same. The resting membrane potential of a cell is determined by the net flow of ions through the “leak” channels that are open in the resting state. Based on the relative membrane permeability for a typical neuron at rest, we can calculate the resting membrane potential as follows:
Since the reversal potential for Cl ion is typically close to the resting membrane potential, the Cl ion is usually ignored when discussing a neuron’s resting membrane potential.
2.1.2. Action Potential
When an action potential occurs, sodium channels on the axon are opened and Na ions are free to move in and out of the cell membrane. The membrane potential fluctuates accordingly toward the reversal potential of the Na ion. The sodium channel is then inactivated and closed, and now the potassium channel, which is potential-dependent, is opened. Now, the membrane potential descends back toward the reversal potential of the K ion and undershoots beyond the resting membrane potential .
3. ANN Models
A rate-based neuron models the activity of a neuron only by the macroscopic feature, firing rate r, regardless of the change in membrane potential or spike timing. The first rate-coded artificial neuron, which is known as formal neuron or threshold logic unit, was proposed by [11]. Based on the formal neuron, reference [12] introduced perceptron, using the Heaviside step function as the activation function. These first-generation neurons fire binary signals when the sum of incoming signals reaches a threshold of a neuron. This concept is later extended to utilize continuous activation functions, including the sigmoid [13] or hyperbolic tangent function, to deal with analog inputs and outputs; consequently, this enabled the training of the neural network through a powerful backpropagation algorithm that exploits gradient-descent. Because of the proven ability of a sufficiently large neural network of artificial neurons to approximate any analog function arbitrarily well (universal approximation theorem states that a feed-forward network with a single hidden layer with a finite number of neurons can approximate continuous functions, under assumptions on the non-polynomial activation function [14,15]; Sigmoidal activation function and the ReLU are also proved to follow the universal approximation theorem [16]), artificial neural networks have been widely used as a powerful information-processing tool in machine learning. In general, the discrete-time firing rate model can be formulated as and usually grouped together for computational efficiency:
where is the firing rate of pre-synaptic neurons, is the firing rate of post-synaptic neurons, is the weight matrix that represents the synaptic strength between the pre- and post-synaptic neurons, is the bias term, and is the non-linear activation function.
Nowadays, Rectified Linear Unit (ReLU) [17] and its variants are commonly employed as the non-linearity because they tend to show better convergence performance than the sigmoidal activation function [18]. This formulation of the group of rate-based neurons is often referred to as a fully-connected layer. The modern architecture of neural networks stacks a variant of this layer to create very deep networks of neurons, which is often referred to as deep neural networks (DNNs). Neural networks are typically called deep when they have at least two hidden layers computing non-linear transformations of the input. One of the commonly used building blocks of DNNs is a convolutional layer. A convolutional layer is a special case of the fully connected layer that implements weight sharing for processing data that has a known grid-like topology, e.g., images. Because of this inductive bias, convolutional neural networks (CNNs) [19,20] can utilize the spatial correlation of the signal in a more sensible way. The representational properties of early layers in the CNNs are similar to the response properties of neurons in the primary visual cortex (V1), which is the first cortical area in the visual hierarchy of the primate’s brain. CNNs possess two key properties that make them extremely useful for image applications: spatially shared weights and spatial pooling. This kind of network learns features that are shift-invariant, i.e., filters that are useful across the entire image (due to the fact that image statistics are stationary). The pooling layers are responsible for reducing the sensitivity of the output to slight input-shift and distortions and increasing the reception field for later layers. Since 2012, one of the most notable results in deep learning is the use of CNNs to obtain a remarkable improvement in the ImageNet classification challenge [21,22]. Based on this technological breakthrough in image classification, various improvements have been proposed for the network architectures in vision models [23,24,25]. Although ANNs have been remarkably successful in many applications, including object detection [26,27], image segmentation [28,29,30], and action recognition [31,32], they are still limited in the way they deal with temporal information.
4. SNN Models
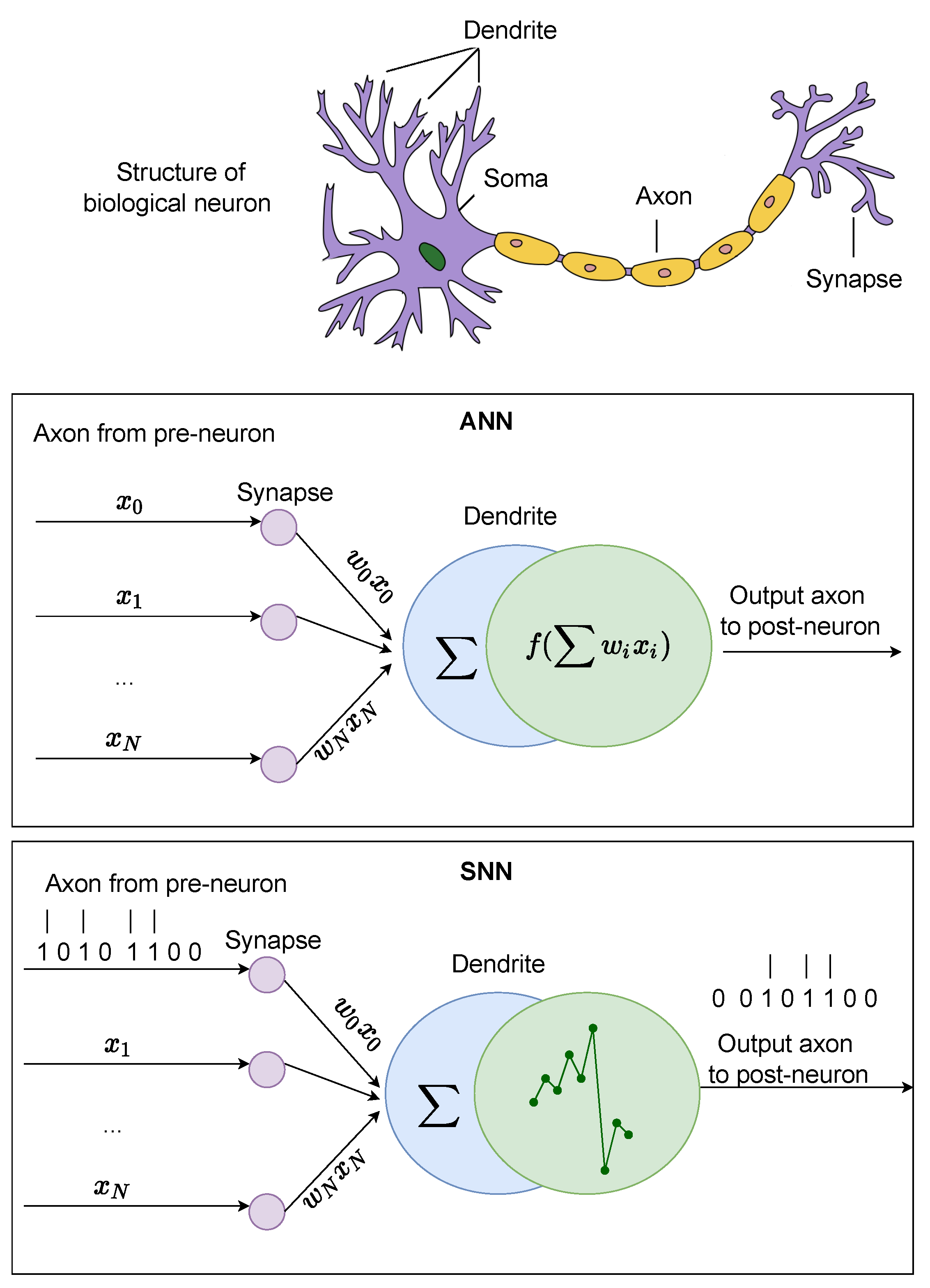
The ability to simultaneously record the activity of multiple cells has led to the idea that the time difference between spikes in different neurons and the spike timing itself can have functional significance. Since the firing rate model cannot handle the problem of this perspective, a model describing the timing of spikes and the variation of the sub-threshold membrane potential has been investigated. A model that handles the generation of such spikes is distinguished from the firing rate model and called the spiking model. Such neuron models are generally expressed in the form of ordinary differential equations. Figure 2 depicts the differences between the biological neuron, artificial neuron, and spiking neuron.
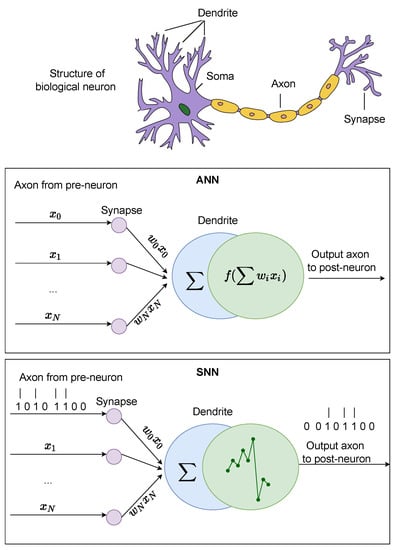
Figure 2.
A comparison between the biological neuron, artificial neuron, and spiking neuron.
4.1. Spiking Neuron Models
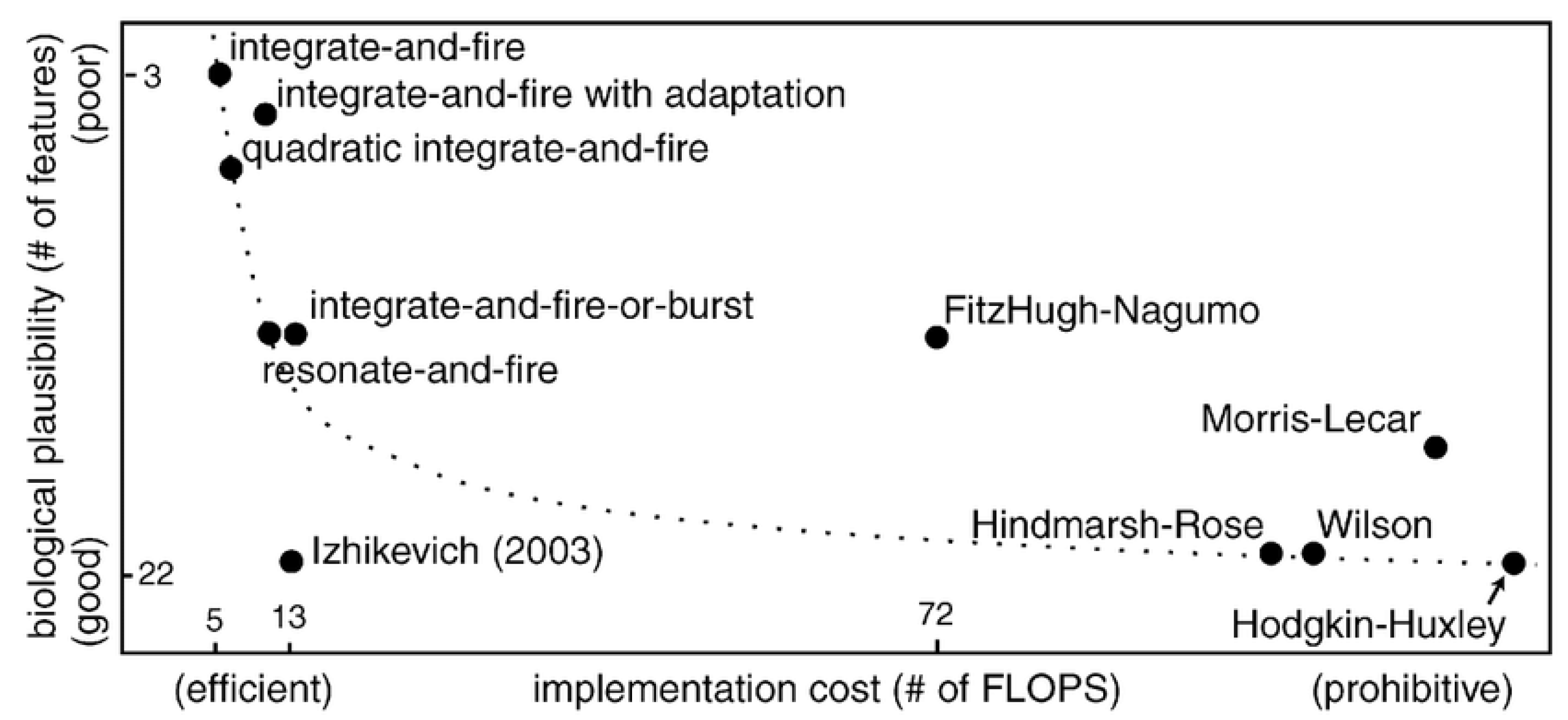
A variety of spiking neuron models have been proposed, and they display trade-offs between biological accuracy and computational feasibility (Figure 3). Choosing an appropriate model depends on the user requirements. Spike-based neuron models are reviewed regarding the computational efficiency and biological plausibility in [33]. In this section, several models of spiking neurons are presented.
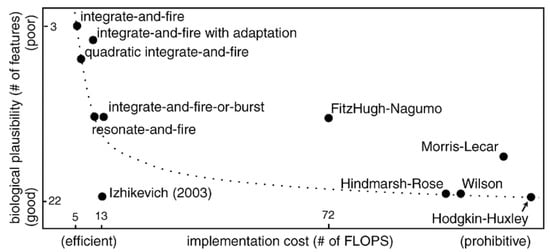
Figure 3.
A comparison of spiking neuron models in terms of implementation cost and biological plausibility (adopted from [33]).
4.1.1. Hodgkin–Huxley (HH) Model
Hodgkin and Huxley conducted the experiment on the giant axon of a squid and concluded that two types of ion channels, K channel and Na channel, are involved in the generation of the action potential [34]. This model can be expressed by adding two terms that take care of the behavior of those two ion channels to Equation (9). Although the change in permeability of the ion channel is actually due to the structural change of the protein, it can be described phenomenologically by the analogy of opening and closing the gates.
where is membrane capacitance (), is the membrane potential (), is synaptic input current (), represents conductance of K ion, represents reversal potential of K ion, represents conductance of Na ion, represents reversal potential of Na ion, represents leak conductance, and represents leak reversal potential, which is now thought to be a Cl ion’s reversal potential. n, m, and h are dimensionless quantities between zero and one that are associated with potassium channel activation, sodium channel activation, and sodium channel inactivation, respectively.
The three gates, n, m, and h, are described by the following differential equation, where g represents the gating variables n, m, and h, and the transition rate (where is the transition rate from non-permissive to permissive states, whereas is the transition rate from permissive to non-permissive states) for each gate and are defined in Equation (8) (in neural simulation software packages, the rate constants in Hodgkin–Huxley models are often parameterized using a generic functional form [35]: ).
By solving these equations, the Hodgkin–Huxley model can simulate the membrane potential behavior during spike generation without introducing spike generation procedures presented in the LIF model (Equation (10)). Although the Hodgkin–Huxley model is biologically accurate (the model is limited in the way that it only describes the channels and flow of ions in the neuron when generating spikes; several drawbacks have been pointed out [36,37]), it demands large computational resources and is infeasible in large-scale simulations.
4.1.2. Leaky Integrate and Fire (LIF) Model
The model in which the input current is integrated over time until the membrane potential reaches a threshold without taking into account the biological ion channel behavior is called the integrate-and-fire (IF) model. The leaky integrate-and-fire (LIF) model reflects the diffusion of ions that occurs through the membrane when some equilibrium is not reached in the cell by introducing a “leak” term to the IF model. Because of its simplicity and low computational cost, the LIF model and its variants are one of the widely used instances of the spiking neuron model. The model dynamics are represented by the following equation:
where is the threshold voltage, is the action potential, and is the resetting membrane potential. When the voltage reaches the threshold , usually one is used for simplicity, the neuron fires the spike, and then the voltage is reset to zero for a refractory period that limits the firing frequency of a neuron.
When the synaptic input current is constant () and , we can solve for the membrane potential as follows:
where is the membrane resistance (), is the membrane time constant. Since the neuron fires the spike when the membrane potential reaches the threshold, the first spike time can be found by setting :
Therefore, steady-state firing rate can be found as:
Theoretically, it is possible to train a deep neural network using Equation (12) as the static non-linearity and make a reasonable approximation of the network in spiking neurons [38]. Intuitively, especially when and , the firing rate of the neuron corresponding to the input current behaves similar to the ReLU activation function in ANNs. This feature is often utilized for ANN-to-SNN conversion.
4.1.3. Izhikevich Model
Izhikevich proposed a model that combines the biological plausibility of the HH model’s dynamics and the computational efficiency of the LIF neurons [39]. The model is represented by the two-dimensional (2D) system of ordinary differential equations, and the Izhikevich model [40] can be expressed in the following form:
with the auxiliary after-spike resetting
where u represents the activation of K ionic currents and inactivation of Na ionic currents (), and is the instantaneous threshold potential ().
The Izhikevich model can exhibit the firing patterns of all known types of cortical neurons with the choice of parameters based on [40].
4.1.4. Adaptive Exponential Integrate-and-Fire (AdEx) Model
The aforementioned Izhikevich neuron can be considered to be an adaptive quadratic integrate-and-fire model, whereas the adaptive exponential integrate-and-fire (AdEx) model [41] has an exponential voltage dependence, coupled with a slow variable, which models threshold adaptation as follows:
with reset conditions
where w is the slow variable taking into account adaptation, is the rheobase current, models the sharpness of the Na channels’ activation function.
The LIF model can be obtained from the AdEx model by taking the limit and removing the adaptation current w. The AdEx model shares the ability to reproduce firing patterns at a low computational cost such as the Izhikevich neuron.
4.2. Synaptic Models
A synaptic interaction can be modeled as a process of binding a neurotransmitter to a closed receptor, which consequently opens it, and unbinding the transmitter from the receptor closing it. These can be modeled as a rate of ion channel opening or a variation of the conductance, as in the Hodgkin–Huxley model. Synaptic kinetics is defined by the number of neurotransmitters released from the pre-synaptic cell, the number of neurotransmitters bonded to the post-synaptic cell, or the opening rate of the ion channel of the post-synaptic cell. The following models are used to model the post-synaptic current (PSC) as well as the post-synaptic potential (PSP).
4.2.1. Single Exponential Model
Assuming the binding of neurotransmitters is instantaneous, the behavior of PSC can be modeled as an exponential decay with a time constant. This can be modeled as:
where is synaptic kinetics, is the kth spike occurrence timing, and is synaptic decay time constant.
The previous equation can be expressed in a differential equation form:
where is the Dirac delta function that represents the occurrence of a spike.
4.2.2. Double Exponential Model
While ignoring the physiological process, the double exponential model reproduces the behavior of the post-synaptic current (PSC) well, considering not only decay but the rise of the PSC.
where A is the normalizing constant and is the synaptic rising time constant.
The double exponential model can be expressed in a form of differential equations as follows:
where h is the helping variable. When , Equation (21) is called the alpha function With these synaptic models, the input current to the cell can be expressed as follows if we consider as the pre-synaptic kinetics:
where , is synaptic input of post-synaptic neurons, and is the weight matrix that represents the synaptic strength between the pre- and post-synaptic neurons.
5. SNN Learning Mechanisms
Learning in neural networks involves the modification of the connectivity of neurons. Unlike the ANNs, which can be successfully trained by stochastic gradient descent and backpropagation, SNNs still do not have solid training methods. The native training methods of SNNs can be classified into: supervised learning with gradient descent and spike backpropagation, unsupervised learning with local learning rule at the synapse (e.g., spike-time-dependent plasticity), and reinforcement learning with reward/error signal using reward modulated plasticity. Synaptic plasticity is the biological process by which specific patterns of synaptic activity result in changes in synaptic strength. Synaptic plasticity was first proposed as a mechanism for learning and memory on the basis of theoretical analysis by [42]. Although the local learning rule at the synapse is said to be biologically more plausible, the learning performance is usually lower than that of supervised learning. An alternative approach to indirectly train the SNNs is the conversion of ANNs to SNNs [43]. Among those methods, state-of-the-art results are mostly obtained from the model conversion from ANNs.
5.1. Spike-Based Backpropagation
Similar to the backpropagation algorithm for ANNs, SpikeProp [44] is designed to determine a set of the desired firing timings of all output neurons at the post-synaptic neurons for a given set of the input pattern. Event-based methods, including SpikeProp, have the derivative term defined only around the firing time, whereas [45,46,47] ignore the temporal effect of the spike signal. Reference [48] proposed an improved method of SpikeProp called SuperSpike that utilizes the derivative of the membrane potential instead of the spike, which allows training a model with an absence of spike occurrence. SuperSpike uses the van Rossum distance [49] between the output and desired spike trains as the loss function, while SpikeProp uses the sum-squared error. The following shows the loss function for the network in time interval .
where is a normalized smooth temporal convolution kernel, is the output spike train, and is a target spike train. Here, spike train is represented as .
When calculating the derivative of Equation (24) with respect to the synaptic weights, the problematic term that contains the Dirac delta function appears. In order to avoid this term, the spike train is approximated with a continuous auxiliary function of the membrane potential of the LIF model.
where represents a fast sigmoid. Here we further approximate with a normalized smooth temporal convolution kernel .
where the is an error signal and is a synaptic eligibility trace.
SLAYER [50] distributes the credit of error back in time in order to solve the drawback of event-based methods. SLAYER assumes a stochastic spiking neuron approximation for the IF model with a refractory response and can simultaneously learn both synaptic weights and axonal delays.
where is the probability density function that could be formulated with the spike escape rate function [51], ⊙ represents the element-wise correlation in time, and e is the backpropagation estimate of error.
5.2. Spike-Time-Dependent Plasticity (STDP)
Spike-time-dependent plasticity (STDP) is an unsupervised Hebbian learning mechanism, which adjusts synaptic weight based on the temporal order of the pre- and post-synaptic spikes [52,53]. When the pre-synaptic spike arrives before a post-synaptic spike, the synaptic weight is increased, which is known as long-term potential (LTP). If the arrival timing of the synaptic spike is reversed, the synaptic weight is decreased, which is known as long-term depression (LTD).
Equation (28) suggests that the synaptic strength can be increased or decreased infinitely, which is biologically unrealistic and makes learning unstable. Biological neurons have a capacity to regulate their own excitability relative to network activity by decreasing the strength of each synapse so that the relative synaptic weighting of each synapse is preserved [54]. This phenomenon is called homeostatic scaling and can be implemented by making weight dependent. With the following exponential rule, the magnitude of the weight modification is regularized according to the current synaptic weight.
Here, are learning rates that take small positive values, and refers to the initial weight of the synapse (sometimes this term is dropped).
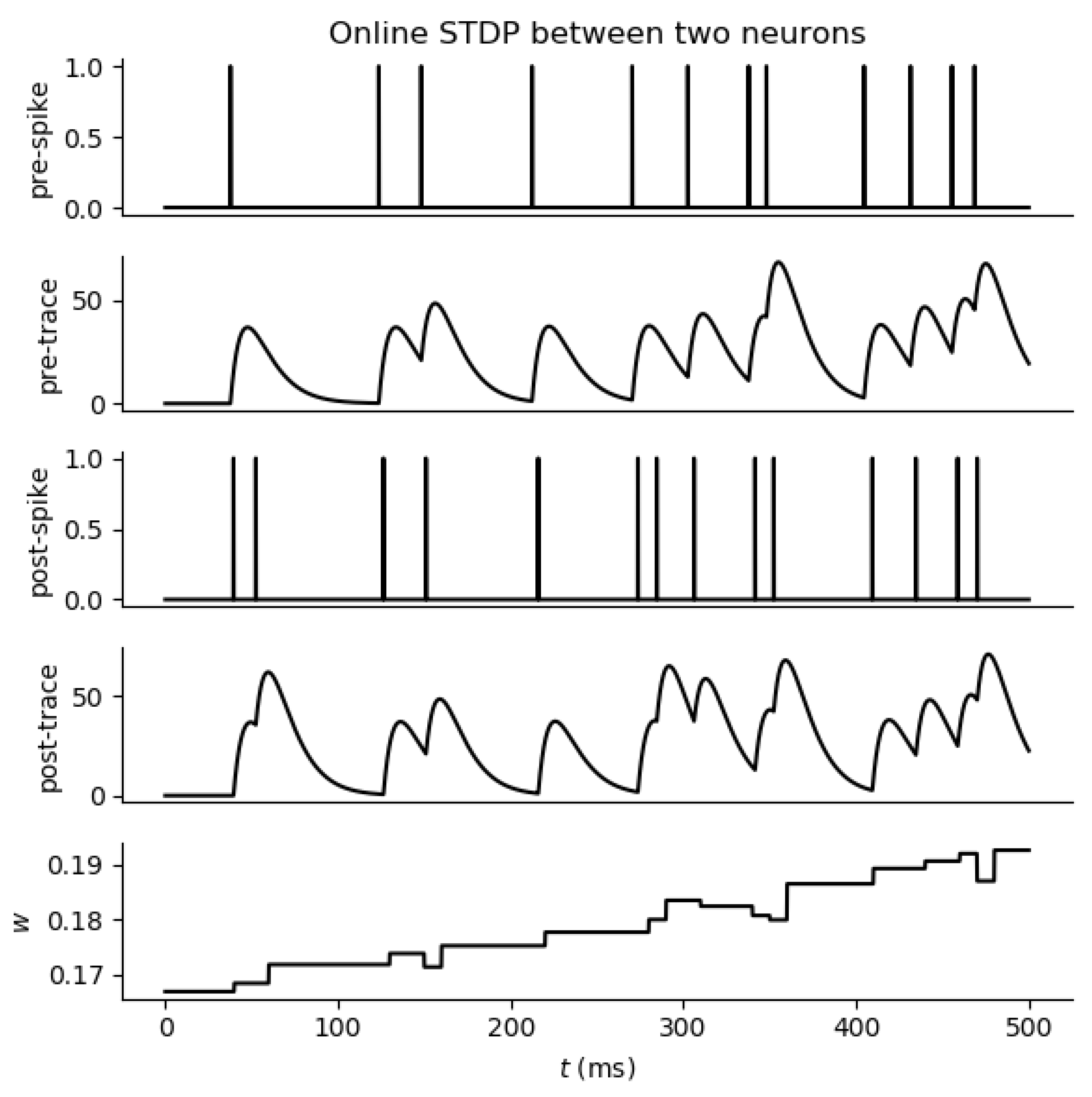
In terms of biology as well as the implementation, it is infeasible to remember all the times of spike occurrence, as seen in Equation (28). This is where the spike trace x is introduced:
where and are the time constants. Figure 4 shows the response of a spike trace and corresponding weight modifications based on STDP. The spike trace can be interpreted as an opening rate of N-methyl-D-aspartate (NMDA) receptor and as influx through voltage-gated channels activated by a backpropagating action potential (bAP). This multiplicative STDP implementation that is inherently stable by combining the weight-dependent exponential rule with spike trace information is often referred to as stable STDP (S-STDP) [55].
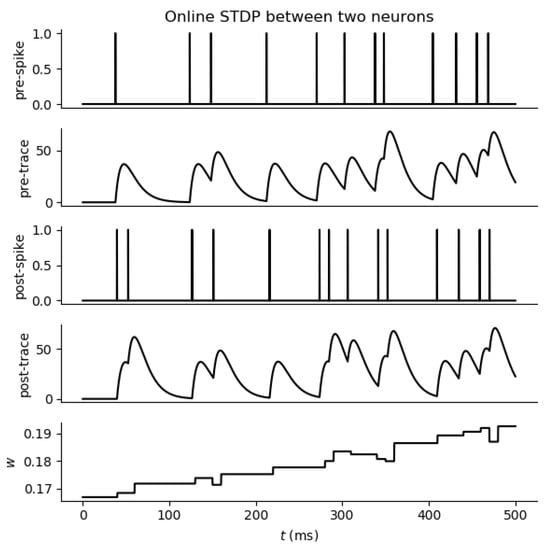
Figure 4.
Weight change in two neurons based on STDP learning rule.
In the following subsections, we will review various STDP variants.
5.2.1. Anti-Hebbian STDP (aSTDP)
Although STDP-like synaptic weight modifications have been found in various neuronal systems, all the systems do not follow the STDP rule. Synapses between parallel fibers and Purkinje-cells in the cerebellum-like structure, for example, follow an anti-Hebbian temporal order [56]. The anti-Hebbian STDP (aSTDP) shows the opposite dependence on the relative timing of pre-synaptic input and the post-synaptic spike compared to STDP. With aSTDP, pre-synaptic activity occurring before post-synaptic activity leads to depression, and vice versa. The aSTDP rule is given:
Compared to the standard STDP, the directions of the greater than/less than signs is opposite, and the magnitude of the learning rate could be different from that for STDP.
5.2.2. Mirrored STDP (mSTDP)
Mirrored STDP was introduced as an effort to implement autoencoders in a biologically realistic fashion [57]. mSTDP combines STDP and aSTDP for feedforward and feedback connections of a two-layer autoencoder such that feedforward and feedback learning is symmetric. This learning rule accounts for high LTP correlation with no causality. However, the biological plausibility is limited because it neglects the causality underlined by Hebb [42].
5.2.3. Probabilistic STDP
A probabilistic variant of simplified STDP [58] that adjusts the synaptic weight for LTP according to an exponential function of the current weight magnitude was introduced by [59]. Probabilistic STDP shows the robustness in performance regardless of a complexity in the spiking neuron model, i.e., non-leaky IF neurons and Izhikevich-like neurons.
5.2.4. Reward Modulated STDP (R-STDP)
While STDP operates based upon the correlation between the spike timings of the pre- and post-synaptic neurons, a reward signal is introduced to modulate STDP in order to implement a reinforcement learning mechanism. If the reward is positive, the corresponding synapse is potentiated; otherwise, the corresponding synapse is depressed. According to [60], dopaminergic neurons are characterized as having two different firing patterns. In the absence of any stimulus, they exhibit a slow (1–8 Hz) firing rate, known as background firing. When stimulated, the dopaminergic neurons exhibit burst firing. Burst firing is where neurons fire in very rapid bursts, followed by a period of inactivity. The modulation is conducted by introducing an eligibility trace z for pre- and post-synaptic spike occurrence as follows:
where is the reward given at time t, z is the eligibility trace.
5.3. Prescribed Error Sensitivity (PES)
Prescribed error sensitivity (PES) is a supervised learning rule suited for online learning for adaptive control that learns a function by minimizing an external error signal frequently used with the neural engineering framework (NEF) [61]. This rule has been used for many works, including a biologically detailed neural model of hierarchical reinforcement learning [62] and adoptive control of quadcopter flight [63]. The weight update for this rule is defined as follows:
where is an error signal at time t, and a is the rate activity of each neuron.
5.4. Intrinsic Plasticity
The intensity of an average synaptic input in the brain may change dramatically. Neurons maintain responsiveness to both small and large synaptic inputs by regulating intrinsic excitability to promote stable firing. This way, neuronal activity can keep from falling silent or saturating when the average synaptic input falls extremely low or rises significantly high. Intrinsic plasticity (IP) regulates the firing rate of a neuron within an appropriate range [64,65]. The firing rate entropy can be influenced by the neuron’s intrinsic properties. By changing these intrinsic properties, the neuron can achieve the optimal firing rate distribution.
where is a learning rate, and are thresholds that determine the desired range of inter-spike interval (ISI) represented as .
During the training, the most recent ISI is examined and neuronal excitability is adjusted. When ISI is larger than the threshold , the neuronal excitability is strengthened to make the neuron more sensitive to input stimuli, and if ISI is less than the threshold , the neuronal excitability is weakened to make the neuron less sensitive to input stimuli.
5.5. ANN-to-SNN Conversion
Most ANN-to-SNN conversion methods have focused on converting ReLU to IF neurons. Reference [43] proposed an ANN-to-SNN conversion method that neglects bias and max-pooling. In subsequent work, reference [66] proposed data-based normalization to improve the performance in deep SNNs. Reference [67] presented conversion methods of batch normalization and spike max-pooling. Reference [68] expanded conversion methods to VGG and residual architectures. One core hypothesis of several ANN-to-SNN conversion designs is that the heavy computational cost of existing ANNs results from the continual transmission of real-valued activities between connected nodes in the network, as well as the subsequent matrix multiplication or convolution [69]. As a result, implementing ANN-to-SNN conversion may enable the same information transmission and function but decrease the costs of signal transmission and computation. Binary-valued spikes both reduce the number of bits per transmission by turning real-valued signals into binary ones, and they make signals sparse in time by not transmitting information for each connection every timestep. These ANN-to-SNN conversion methods are based on the idea of importing pre-trained parameters (e.g., weights and biases) from an ANN to an SNN. ANN-to-SNN conversion methods have achieved comparable results in deep SNNs to those of original ANNs (e.g., VGG and ResNet) and can be considered as a solution to the energy-efficiency problem of ANNs in the deployment time.
6. Spike Encoding
Since SNNs utilize the spike and spike sequences to convey the information, encoding real data into spikes is a substantial step in creating SNNs. Although the way information is encoded into spikes in biology is one of the biggest unresolved challenges in neuroscience. Two main encoding schemes, rate encoding and temporal (pulse) encoding, can be found in many kinds of literature. In addition, it is noteworthy that some sensors, such as Dynamic Vision Sensor (DVS), can produce raw spike sequences.
6.1. Rate Encoding
The rate encoding scheme is based on the average number of spikes over time; information is encoded with a number of spikes generated over a time window. Depending on the different averaging schemes, there are several ways to define the firing rate, such as an average over time or an average over several repetitions.
where T is the time window, and is the time of spike occurrence. Then, the firing rate r can be expressed as:
This firing rate can be used as an input for rate-base neuron models, i.e., ANNs, where the activation function represents the frequency–current (FI) curve.
The firing rate can also be utilized to model the discrete spikes with the point process. In the Poisson process, which is one of the point processes, the probability of the random variable being equal to n, i.e., when the probability of a point occurring follows a Poisson distribution with intensity , the probability of a spike occurring n times by time t, is given by: . Then, the single spike occurrence during a short time step is:
where the term is approximated with the McLaughlin expansion.
When encoding an image into spike sequence, we can assume each pixel value corresponds to the firing rate r, and following Equation (41), spike occurrence for each time step t can be obtained as:
6.2. Temporal Encoding
The temporal encoding scheme is based on the exact timing of spikes, where the more salient information is encoded as earlier spike times. Compared to the rate encoding scheme, temporal encoding produces much sparser spikes since the spike-timing rather than the spike-frequency represents information. Although the temporal code allows representing the features of the input with small groups of neurons, it contains a vulnerability to input noise or temporal jitter.
When encoding an image, each individual pixel value ranging from 0 to 255 can be simply used to produce the spike time that is proportional to the brightness of the pixel. For instance, a pixel with normalized brightness of 0.1 corresponds to a spike time at . In a grayscale image, white pixels (brightness equals 1 or 255) do not cause spikes, as it can be considered that they do not carry any information.
7. SNNs in Computer Vision
SNNs have been a driving factor in the development of many modern computer vision and other signal processing techniques. The application of SNNs is gradually being considered in computer vision where data consisting of temporal information is handled or where the saving of computational resources is aimed. The former case often involves the use of an event camera or LiDAR sensor whose data has importance in the temporal dimension. The latter case often focuses on the conversion of ANNs into SNNs so that deep neural network models can embrace the energy-efficient operations of neuromorphic hardware.
Although some studies have shown SNNs can be used for image classification on large datasets such as ImageNet [38,67,68], most applications of SNNs are still limited to less complex datasets such as MNIST [70], N-MNIST [71], and N-Caltech101 [71]. One of the primary reasons for the limited application scope is the complex dynamics and non-differentiable operations of spiking neurons. Recently, some remarkable studies have applied SNNs for object detection tasks [72,73,74], showing comparative results with DNNs while requiring much less energy for the computations. Following the successes of the ANNs to SNNs conversion methods on image classification and object detection tasks, reference [75] leveraged SiamFC [76] and introduced SiamSNN, a spike-based Siamese network for object tracking. Recently, UNet-based SNN in [69] leveraged the Nengo framework to translate a simplified U-Net into a spiking network to deploy on the Intel Loihi neuromorphic chip. The UNet-based SNN model is implemented with two frameworks: TensorFlow and NengoDL [77]. Furthermore, a partitioning algorithm, which minimizes inter-chip communication resulting in a faster and more energy-efficient network, is proposed in [69] to deploy SNN on Loihi.
Unlike frame-based cameras, event-based cameras are often referred to as bio-inspired silicon retinas. However, event-based cameras require a high temporal resolution (in the order of microseconds) and a fraction of power consumption. The combination of spiking neural networks and event-based vision sensors holds the potential of highly efficient and high-bandwidth optical flow estimation [55]. Reference [78] proposed Spike-FlowNet, a deep hybrid neural network architecture integrating SNNs and ANNs for efficiently estimating optical flow from sparse event camera outputs without sacrificing performance.
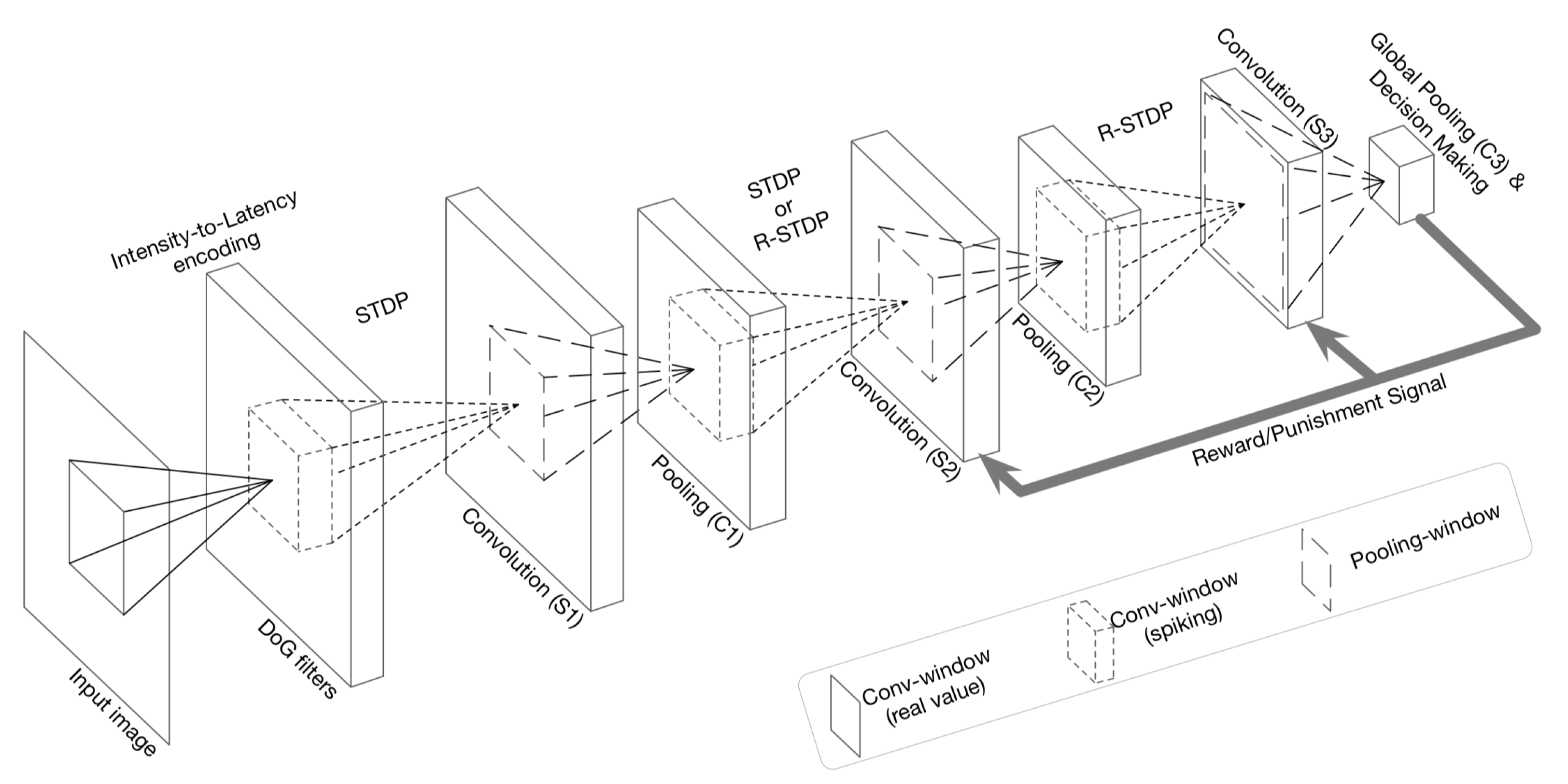
To illustrate how to implement an SNN framework for computer vision, we choose the task of image classification with the DCSNN network [79]. The overall structure of DCSNN for digit recognition is shown in Figure 5. The input image is convolved with six different Gaussian (DoG) filters at various scales with zero padding. Window sizes are set to 3 × 3, 7 × 7, and 13 × 13, where their standard deviations (1, 2) are (3/9, 6/9), (7/9, 14/9), and (13/9, 26/9), respectively. Then, a spike is generated and propagated to the next layer by an intensity-to-latency encoding [80]. From the output of the DoG filters, all the values below 50 are ignored and the remaining values are descendingly sorted, denoting the order of spike propagation. Generated spikes are processed through three spiking convolution-then-pooling layers (S1–C1, S2–C2, and S3–C3). The convolutional layer (S-layer) contains several 2-dimensional grids of IF neurons, which constitute the feature maps. All S-layers are trainable, employing either STDP or R-STDP learning rules. The C-layer has the same number of feature maps as its previous S-layer, and there is a one-to-one association between maps of the two layers. There are two types of C-layers: spike-based and potential-based. The network makes its decision in C3, where neurons are pre-assigned to digits, and the decision is the digit assigned to the neuron with either the maximum internal potential or the earliest spike time. When the decision of the network has been made, it will be compared with the original label of the input image. By using the R-STDP rule for synaptic plasticity, a reward or punishment will be generated depending on if the decision and ground truth label match or mismatch [67].
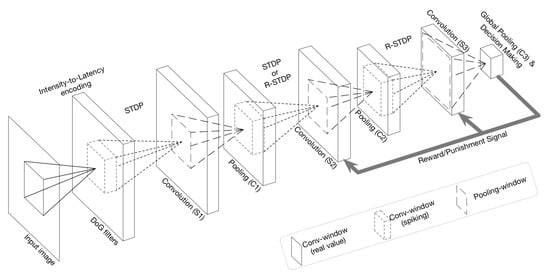
Figure 5.
The overall structure of DCSNN for digit recognition. Courtesy of [79].
Table 2 summarizes the use of SNNs in the field of computer vision.
8. SNNs in Robotic Control
Mobile robots with continuous high-dimensional observation and action spaces are increasingly being deployed to solve complex real-world tasks. Given their limited onboard energy resources, there is an unmet need to design energy-efficient solutions for the continuous control of these autonomous robots.
Biology shows that the event-based paradigm is applicable not just to perception and inference but also to control. Spiking neural networks have been utilized as a “brain” of robots that provides robotic perception and action to mimic the behaviors captured in nature. Most commonly, the utilization of SNNs in robotic applications involves hand-crafting and tuning for the task of interest. Many fields of robotics, e.g., locomotor systems, have been inspired by biological systems. Nowadays, several methods have been proposed to achieve locomotion in a variety of robots, which is known as a central pattern generator (CPG). CPG is a neural network in which interconnected excitatory and inhibitory neurons produce an oscillatory, rhythmic output without some rhythmic inputs. Most of the current research explores ANNs based on non-spiking neurons, but there is a growing body of research on SNNs. Reference [81] presented the first implementation of a real-time neuromorphic spiking CPG (sCPG) that runs on the SpiNNaker to command a hexapod robot to perform a walk, trot, or run motion. Reference [82] implemented sCPG with an AdEx neuron model that exhibits a tripod-like gait. Their model can manipulate the amplitude, frequency, and phase while the network is running, indicating that these characteristics can be updated in an online manner to further explore the role of sensory feedback in shaping locomotion.
In robotics, the lamprey has often been used as a model for understanding the role of CPG in locomotion. The lamprey swims by propagating a mechanical wave, transmitted along the body. Reference [83] proposed to implement a sCPG using an analog/digital VLSI device interfaced with an FPGA board, which can be directly interfaced to the actuators of a bio-mimetic robotic lamprey. Reference [84] used the sCPG model implemented in Nengo to produce the swimming gaits modulated by the high-level brainstem control of a simulated lamprey robot model in various scenarios. They showed that the robot can be controlled dynamically in direction and pace by modifying the input to the network.
Inspired by the success of SNNs on event-based cameras, reference [85] proposed, for the very first time, a fully embedded application of the Loihi neuromorphic chip prototype in a flying robot to bridge the gap between simulation and the real world. In this work, the SNN architecture is evolved in a highly randomized and abstracted vertical simulation and takes the ventral optic flow divergence as its input to determine the thrust setpoint to achieve a smooth landing. Focusing on proportional, integral, derivative (PID) controller in neuromorphic hardware, reference [86] improved the work in [87] and proposed an event-based PID controller to improve the PID controller on Loihi. In [86], they re-designed the integral path of the controller to cope with a limited resolution of value representation, which led to fast saturation of the I-path. Then, they simplified the network, removing the inner control loop and simplified the network, removing the inner control loop.
In addition to a pattern generator and motor control, navigation is an important task in robotics. With the requirement of energy efficiency in simultaneous localization and mapping (SLAM), which is crucial for mobile robots exploring unknown environments, SNN is an appropriate solution. Reference [88] proposed a biologically constrained SNN architecture to solve the unidimensional SLAM problem on Loihi. In [88], the robot’s heading is determined via spike-based recursive Bayesian inference of multisensory cues (i.e., visual and odometry information). Reference [89] demonstrated a model of rat hippocampus place, grid, and border cells implemented with the SpiNNaker. The implemented place cells were used to represent the location of landmarks for “home” and “cheese”, whereas the grid cells provide displacement information to the robot. They showed that the robot can detect these landmarks correctly. Reference [90] presented a brain-like navigation system with LIF neurons trained by STDP. In this work, reference [90] shows that SNN may robustly control an autonomous robot in mapping and exploring an unknown environment, while compensating for its own intrinsic hardware imperfections, such as partial or total loss of visual input. Reference [91] proposed a variant of deep deterministic policy gradient (DDPG), called spiking deep deterministic policy gradient (SDDPG), which consists of a spiking actor network and a deep critic network that were trained jointly using gradient descent for energy-efficient mapless navigation. This work explored an indirect SNN training approach based on the reward-modulated spike-timing-dependent plasticity (R-STDP) learning rule and supervised learning framework. The model was validated with Turtlebot2 platform and Intel’s Kapoho-Bay USB chipset. The authors claimed that the proposed method performed slightly better than the state-of-the-art thanks to the generalization introduced by the Poisson spike encoding of the state input.
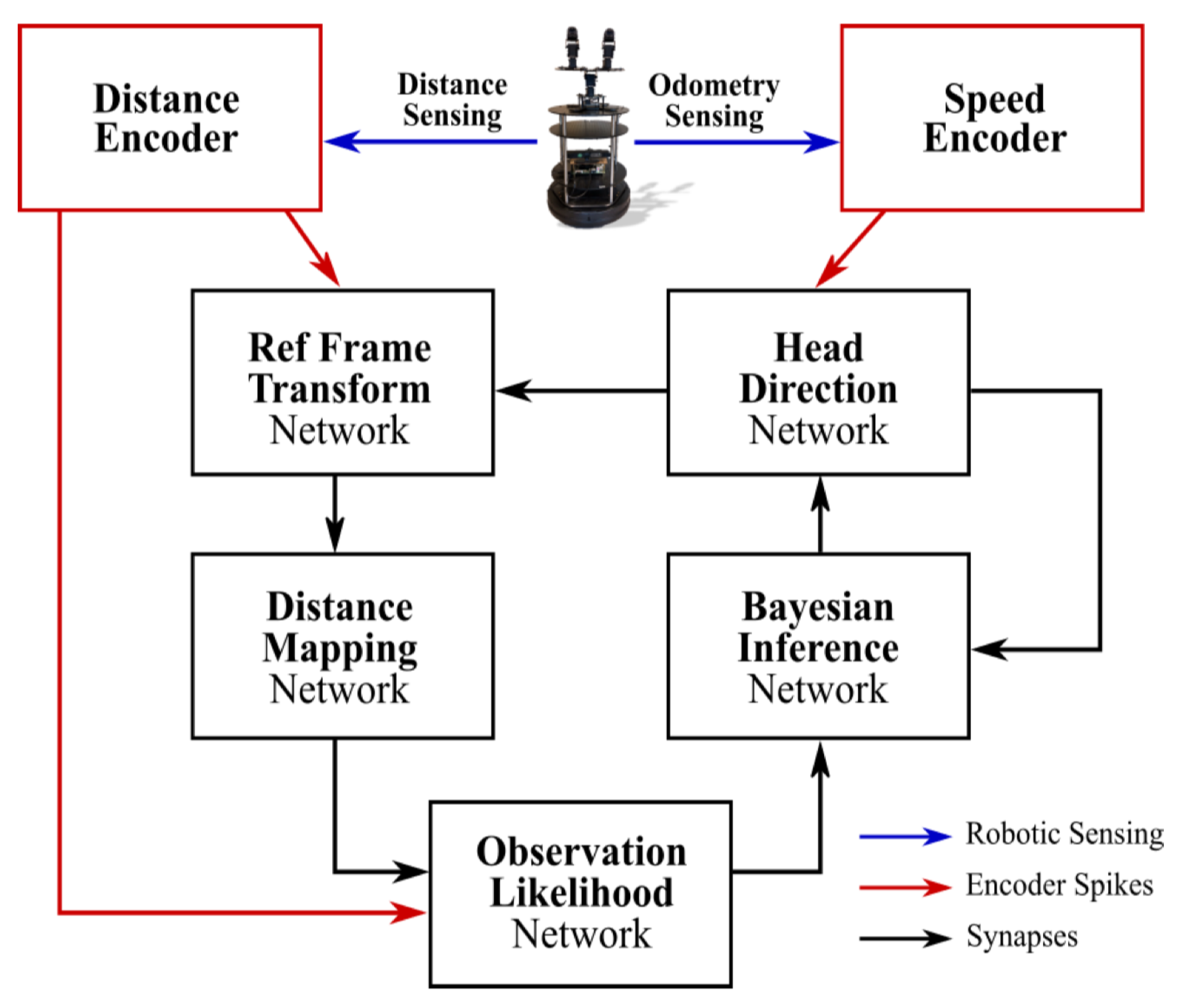
In this category, we will introduce [88] as an instance to show how SNNs are used in robotics. The model has two sensory spike rate-encoders and five sub-networks, as shown in Figure 6. The odometry sensor and the RGB-depth camera signals drive the neural activity of speed cells and sensory neurons encoding the angular speed and the distance to the nearest object, respectively. With five sub-networks, Head Direction (HD) receives the input from the speed cells and plays the role of the heading of the robot; Reference Frame Transformation (RFT) receives the egocentric input from sensory neurons and generates the allocentric distance representation in the world reference frame (defined by the HD network); Distance Mapping (DM) learns the allocentric observations from the RFT and forms a map of the robot’s surrounding environment; Observation Likelihood (OL) uses the map from the DM to compute the observation likelihood distribution of the robot’s heading based on the egocentric observation from sensory neurons; Bayesian Inference (BI) produces a near-optimal posterior of the robot’s heading and corrects the heading representation within the HD.
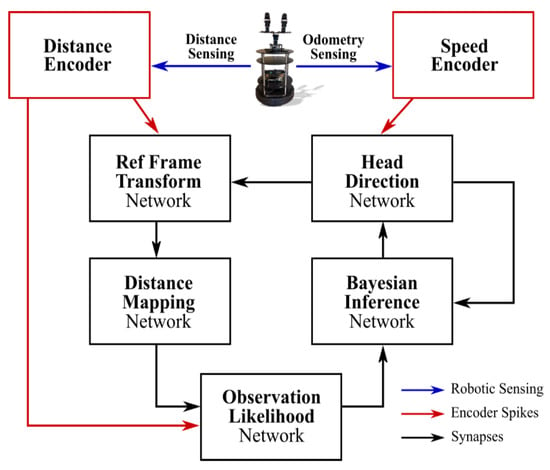
Figure 6.
The overall structure of SNN architecture for SLAM. Courtesy of [88].
Table 3 summarizes the use of SNNs in the field of robotics.
9. Available Software Frameworks
The steadily increasing interest in SNN has led to many attempts to develop SNN libraries for Python. Unlike ANNs, the objectives in SNNs are time consumption and energy efficiency. To provide functional systems for researchers to execute applications that are designed with SNNs, several software frameworks have been proposed to provide SNN platforms. We provide a list of open-source software frameworks for the SNN simulation with some emphasis on the relation with deep learning frameworks in Table 4.
10. Conclusions and Future Perspectives
In this paper, we present a review of the fundamentals of spiking neural networks (SNNs) and provide a survey of the literature on the use of SNNs in computer vision and robotics applications, which demonstrates the great potential of SNNs in the research community. Over the past decade, SNNs have gained huge attention and shown they are promising in temporal information processing capability, low power consumption, and high biological plausibility. However, realizing the full potential of SNNs requires solving several challenges ahead of us.
- Training of SNNs: There are two main approaches to train SNNs: (i) training SNNs directly based on either supervised learning with gradient descent or unsupervised learning with STDP (ii) convert a pre-trained ANN to an SNN model. The first approach has the problem of gradient vanishing or explosion because of a non-differentiable spiking signal. Furthermore, an SNN trained by gradient descent is restricted to shallow architectures and produces low performance on large-scale datasets such as ImageNet. The second approach increases the computational complexity because of the large number of timesteps, even though these SNNs achieve comparable accuracy to ANNs, due to the similarity between SNNs and recurrent neural networks (RNNs), and results in backpropagation through time (BPTT). Recently, reference [92] showed that RTRL, an online algorithm to compute gradients in RNNs, can be combined with an LIP neuron to provide good performance with a low memory footprint.
- SNNs Architecture: While the majority of existing works on SNNs have focused on the image classification problem and utilize available ANN architectures such as VGG or Resnet, having an appropriate SNN architecture is critical. Recently, meta-learning such as neural architecture search (NAS) has been utilized to find the best SNN architecture [93].
- SNNs Performance on Large-scale Data: While SNNs have shown an impressive advantage with regard to energy efficiency, their accuracy performances are still low compared to ANNs on large-scale datasets such as ImageNet. Recently, references [94,95,96] utilized the huge success of ResNet in ANNs to train deep SNNs with residual learning on ImageNet.

Table 2.
Summary of recent applications of SNNs in computer vision.
Table 2.
Summary of recent applications of SNNs in computer vision.
| Method Year | Training Paradigm | Description | Performance |
|---|---|---|---|
| Image Classification | |||
| DCSNN [79] (2018) | STDP and RSTDP | A convolutional SNN was trained by a combination of STDP for the lower layers and reward-modulated STDP for the higher ones, which allows training the entire network in a biologically plausible way in an end-to-end fashion. | They have achieved 97.2% accuracy on the MNIST dataset. https://github.com/miladmozafari/SpykeTorch (accessed on 5 September 2021) |
| LM-SNNs [97] 2020 | STDP | Lattice map spiking neural network (LM-SNN) model with modified STDP learning rule and biological inspired decision-making mechanism was introduced. Learning algorithm in LM-SNN manifests an unsupervised learning scheme. | Dataset: MNIST handwritten digits and a collection of snapshots of Atari Breakout. |
| Zhou et al. [98] (2020) | STDP | First work to apply SNNs to a medical image classification task. Utilized an STDP-based convolutional SNN to distinguish melanoma from melanocytic nevi. | Dataset: ISIC 2018 [74] includes 1113 images of MEL and 6705 images of NV. Performance: Without feature selection: 83.8% With feature selection: 87.7% |
| Zhou et al. [99] (2020) | R-STDP | An imbalanced reward coefficient was introduced for the R-STDP learning rule to set the reward from the minority class to be higher than that of the majority class and to set the class-dependent rewards according to the data statistic of the training dataset. | Dataset: ISIC 2018. Performance: classification rate of the minority class from 0.774 to 0.966, and the classification rate of the majority class is also improved from 0.984 to 0.993. |
| Lou et al. [100] (2020) | STDP | Both temporal and spatial characteristics of SNN are employed for recognizing EEG signals and classifying emotion states. Both spatial and temporal neuroinformatic data to be encoded with synapse and neuron locations as well as timing of the spiking activities. | 74%, 78%, 80% and 86.27% for the DEAP dataset, and the overall accuracy is 96.67% for the SEED dataset |
| Object Detection | |||
| Spiking YOLO [73] (2019) | ANN-to-SNN Conversion | Spiking-YOLO was presented for the first kind to perform energy-efficient object detection. They proposed channel-wise normalization and signed neuron with imbalanced threshold to convert leaky-ReLU in a biologically plausible way. | They have achieved mAP% 51.83 on PASCAL VOC and mAP% 25.66 on MS COCO |
| Deep SCNN [74] (2020) | Backpropagation | SNN based on the Complex-YOLO was applied on 3D point-cloud data acquired from a LiDAR sensor by converting them into spike time data. The SNN model proposed in the article utilized the IF neuron in spike time form (such as the one presented in Equation (11)) trained with ordinary backpropagation. | They obtained comparative results on the KITTI dataset with bird’s-eye view compared to Complex-YOLO with fewer energy requirements. Mean sparsity of 56.24% and extremely low total energy consumption of 0.247 mJ only. |
| Image Classification | |||
| FSHNN [101] (2021) | STDP & SGD | Monte Carlo dropout methodology is adopted to quantify uncertainty for FSHNN and used to discriminate true positives from false positives. | FSHNN provides better accuracy compared to ANN-based object detectors (on MSCOCO dataset) while being more energy-efficient. Features from both unsupervised STDP-based learning and supervised backpropagation-based learning are fused. It also outperforms ANN, when subjected to noisy input data and less labeled training data with a lower uncertainty error. |
| Object Tracking | |||
| SiamSNN [75] (2020) | ANN-to-SNN Conversion | SiamSNN, the first SNN for object tracking that achieves short latency and low precision loss of the original SiamFC was introduced along with an optimized hybrid similarity estimation method for SNN. | OTB-2013, OTB-2015, and VOT2016. SiamSNN achieves 50 FPS and extremely low energy consumption on TrueNorth. |
| Two multi-layered SNNs [102] (2020) | R-STDP | This addressed the issue of SNN-based moving-target tracking on a wheel-less snake robot. A Dynamic Vision Sensor (DVS) is utilized to perceive the target and encode it as spikes that are fed into the SNN to drive the locomotion controller of the snake robot. | The simulation experiments conducted in the NRP. Compared to SNN, the relative direction of the target to the robot is with less fluctuation when using the multi-layered SNN. |
| Object Segmentation | |||
| Unet-based SNN [69] (2021) | ANN-to-SNN Conversion | Instead of using a fixed firing rate target for all neurons on all examples, Unet-based SNN regularizes a rank-based statistic computed across a neuron’s firing rates on multiple examples to allow a range of firing rates. Unet-based SNN also proposes the percentile-based loss function to regularize the (almost) maximum firing rate of each neuron across all examples. During the forward pass, it uses a modification of the ReLU non-linearity | Even achieve lower accuracy performance (92.13%) compared to Unet baseline (94.98% on Tensorflow and 92.81% on NengoDL) on the ISBI 2D EM Segmentation dataset, Unet-based SNN runs on the Loihi neuromorphic hardware with greater energy efficiency. |
| SpikeMS [103] (2021) | Backpropagation | SpikeMS includes spike counts and classification labels to address the problem of motion segmentation using the event-based DVS camera as input | SpikeMS achieves performance comparable to an ANN method but with 50× less power consumption on EV-IMO, EED and MOD datasets. |
| Chen et al. [104] (2021) | ANN-to-SNN conversion | Temporal redundancy between adjacent frames is capitalized to propose an interval reset method where the network state is reset after a fixed number of frames. | It achieved a 35.7× increase in convergence speed with only 1.5% accuracy drop using an interval reset of 20 frame |
| Image Classification | |||
| SpikeSEG [105] (2021) | STDP & backpropagation | This is a spiking fully convolutional neural network used for semantic event-based image segmentation through the use of active pixel saliency mapping. Both spike-based imaging and spike-based processing are utilized to deliver fast and accurate class segmented spiking images. | The SpikeSEG network performs well on the synthetic dataset with accuracy values of 97% and mIoU of 74% |
| Optical-Flow Estimation | |||
| Hierarchical cuSNN [55] (2019) | Stable STDP | The selectivity of the local and global motion of the visual scene emerges through STDP from event-based stimuli. The input statistics of event-based sensors are handled by an adaptive spiking neuron model. The neuron is learnt by the proposed stable STDP. The neuron model and STDP rule are combined in a hierarchical SNN architecture to capture geometric features, identify the local motion of these features, and integrate this information into a global ego-motion estimate. | It is evaluated on synthetic and real event sequences with the Event Camera Dataset on DAVIS and SEES1 DVS sensors. Code available: https://github.com/tudelft/cuSNN (accessed on 4 September 2021) |
| Spike-FlowNet [78] (2020) | Backpropagation | Spike-FlowNet, a deep hybrid neural network, integrating SNNs and ANNs for efficiently estimating optical flow from sparse event camera outputs without sacrificing the performance was proposed. They trained the IF neuron with spike-base backpropagation. | On the MVSEC dataset, Spike-FlowNet accurately predicts the optical flow from discrete and asynchronous event streams along with substantial benefits in terms of computational efficiency compared to the corresponding ANN architecture. Code available: https://github.com/chan8972/Spike-FlowNet (accessed on 27 August 2021) |
| STaRFlow [106] (2021) | Backpropagation | STaRFlow is a lightweight CNN for multi-frame optical flow estimation with occlusion handling. Temporal information is exploited by temporal recurrence, where the same weights over a scale recurrence are repeatedly used. | STaRFlow obtains SOTA performances on MPI Sintel and Kitti2015 and involves significantly fewer parameters. Code available: https://github.com/pgodet/star_flow (accessed on 5 September 2021) |

Table 3.
Summary of recent applications of SNNs in robotics.
Table 3.
Summary of recent applications of SNNs in robotics.
| Method Year | Software/ Hardware | Description | Performance |
|---|---|---|---|
| Pattern Generation | |||
| Cuevas-Arteaga et al. [107] (2017) | PyNN/SpiNNaker | Spiking CPG (sCPG) to command a hexapod robot to perform walk, trot, or run. | |
| NeuroPod [81] (2019) | -/SpiNNaker | The first implementation of a real-time neuromorphic sCPG that runs on the SpiNNaker to command a hexapod robot to perform walk, trot, or run. | The robot was based on the design from https://www.thingiverse.com/thing:1021540 (accessed on 5 September 2021) |
| Strohmer et al. [82] (2020) | NEST/- | An sCPG with AdEx neuron model that exhibits a tripod-like gait. Their model can manipulate the amplitude, frequency, and phase while the network is running, indicating that these characteristics can be updated in an online manner to further explore the role of sensory feedback in shaping locomotion. | A validation test was performed on the Modular Robot Framework (MORF), and source code is available at: https://gitlab.com/esrl/scpg-network-simulation (accessed on 4 September 2021) |
| Donati et al. [83] (2014) | -/FPGA | Implement an sCPG using analog/digital VLSI device interfaced with an FPGA board, which can be directly interfaced to the actuators of a bio-mimetic robotic lamprey. CPG network is implemented using silicon neurons and synapses with biologically plausible time constants. | The neuromorphic chip can reproduce the behavior of the theoretical CPG model, offering the possibility of directly controling the actuators of an artificial bio-inspired lamprey robot. The neuron produces periodic bursting, lasting approximately 60 ms, with an inter-burst interval of about 1.5 s. The spiking frequency during the burst is about 35 Hz. |
| Angelidis et al. [84] (2021) | Nengo/SpiNNaker | Used the sCPG model implemented in Nengo to produce the swimming gaits modulated by the high-level brainstem control of a simulated lamprey robot model in various scenarios. They showed that the robot can be controlled dynamically in direction and pace by modifying the input to the network. | The experiments are conducted on an isolated CPG model and neuromechanical simulations. It provides a vast number of possible synchronized gaits, e.g., traveling and standing waves, and smoothly controls a lamprey robot that, with regulation of the high-level drive, adapts to various simulation scenarios. On neuromorphic hardware, it achieves real-time operation. |
| Motor Control | |||
| Dupeyroux et al. [85] (2020) | PySNN/Loihi | This is a fully embedded application of the Loihi neuromorphic chip prototype in a flying robot. It uses an evolutionary algorithm to optimize SNN controllers and an abstracted simulation environment for evaluation. | The resulting network architecture consists of only 35 neurons distributed among three layers. Quantitative analysis between simulation and Loihi reveals a root-mean-square error of the thrust setpoint as low as 0.005 g, along with a 99.8% matching of the spike sequences in the hidden layer and 99.7% in the output layer. Videos of the flight tests can be found at https://mavlab.tudelft.nl/loihi/ (accessed on 5 September 2021) |
| Stagsted et al. [86] (2020) | Nengo/Loihi | By modifying SNN architecture and improving the interface between neuromorphic cores and the host computer allowed, it improves the latency and frequency of the controller. The integral path of the controller was re-designed to cope with a limited resolution of value representation. The inner control loop was removed to simplify the network, and the time step duration of the control loop was decreased to improve the I/O interface. | SNN-based proportional, integral, derivative (PID) controller was tested on a drone constrained to rotate on a single axis. They achieved comparable performance for overshoot, rise and settling times. |
| Navigation | |||
| Spiking RatSLAM [89] (2012) | Spatial Envelope Synthesis (SES) | It demonstrates a model of rat hippocampus place, grid, and border cells implemented with the SpiNNaker. The implemented place cells were used to represent the location of landmarks for “home” and “cheese” whereas the grid cells provide displacement information to the robot. They showed that the robot can detect these landmarks correctly. | Place cells represent the location of landmarks for “home” and “cheese”, while Grid cells provide displacement information to the robot. The experiment shows that that robot is correctly able to detect these landmarks http://neuromorphs.net/nm/wiki/act12/results/Combined (accessed on 5 September 2021) |
| Gridbot [90] (2018) | ROS/- | Gridbot is an autonomously moving robot with 1321 spiking neurons and is able to map the environment by itself. Gridbot contains neurons that were modeled as LIF units; synapses that were either hardwired or underwent plastic changes through STDP, dendritic trees that integrated synaptic inputs. Gridbot encoded sensory information into distributed maps and generated motor commands to control the robot movement. | Three experiments: follow the walls of the environment for 30 min; explored the environment randomly; the robot walked through the learned environment for more than 2 h |
| Bing et al. [108] (2019) | -/Kapoho-Bay USB chipset | It is a fast method to build an SNN-based controller for performing robotic implementations by using a model-based control method to shape a desired behavior of the robot as a dataset and then use it to train an SNN based on supervised learning. | It performed slightly better than the state-of-the-art thanks to generalization introduced by Poisson spike encoding of the state input |
| Tang et al. [88] (2019) | Gazebo/- | The model has two sensory spike rate-encoders and five sub-networks (head direction, reference frame transformation, distance mapping, observation likelihood, Bayesian inference). All five sub-networks are integrated, and the model has intrinsic asynchronous parallelism by incorporating spiking neurons, multi-compartmental dendritic trees, and plastic synapses, all of which are supported by Loihi. | A mobile robot is equipped with an RGB-depth camera, in both the AprilTag real-world and Gazebo simulator, for validating our method. It is validated for accuracy and energy-efficiency in both real- world and simulated environments by comparing with the GMapping algorithm. It consumes 100 times less energy than GMapping run on a CPU while having comparable accuracy in the head direction localization and map-generation. |
| SDDPG [91] (2020) | PyTroch/- | Spiking deep deterministic policy gradient (SDDPG), which consists of a spiking actor network and a deep critic network that were trained jointly using gradient descent for energy-efficient mapless navigation. | The model was validated with Turtlebot2 platform and Intel’s Kapoho-Bay USB chipset. https://github.com/combra-lab/spiking-ddpg-mapless-navigation (accessed on 6 September 2021) |

Table 4.
List of available software frameworks for SNNs simulation.
Table 4.
List of available software frameworks for SNNs simulation.
| Framework | Training Paradigm | Description |
|---|---|---|
| SNN simulator | ||
| Brain2 [109] | STDP | Brian2 is a widely-used open-source simulator for spiking neural networks. https://opensourcelibs.com/lib/brian2 (accessed on 6 September 2021) |
| Nest [110] | STDP/RSTDP | Nest focuses on the dynamics and structure of neural systems, and it is used in medical/biological applications but maps poorly to large datasets and deep learning. |
| Nengo [111] | STDP PES | Neural simulator for large-scale neural networks based on the neural engineering framework (NEF), which is a large-scale modeling approach that can leverage single neuron models to build neural networks. |
| Nengo DL [77] | ANN conversion | NengoDL allows users to construct biologically detailed neural models, intermixed with deep-learning elements bucked by TensorFlow and Keras [112]. |
| SpykeTorch [113] | STDP/RSTDP | SpykeTorch is based on PyTorch [114] and simulates convolutional SNNs with at most one spike per neuron and the rank-order encoding scheme. |
| BindsNet [115] | STDP/RSTDP ANN conversion | BindsNet is also based on PyTorch targeting machine-learning tasks. Currently, synapses are implemented without their own dynamics. |
| Slayer PyTorch [116] | BP | Slayer PyTorch provides solutions for the temporal credit problem of spiking neurons that allows backpropagation of errors. |
| Norse | BPTT RSNN | Norse is an expansion of PyTorch to perform deep learning with spiking neural networks using sparse and event-driven hardware and data. Used in long short-term spiking neural networks (Bellec 2018). https://github.com/norse/norse (accessed on 7 September 2021) |
| snn_toolbox [67] | ANN conversion | SNN toolbox is used to transform rate-based ANNs defined in different deep-learning frameworks, such as TensorFlow, PyTorch, etc., into SNNs and provides an interface to several backends for simulation (pyNN, Brian2, etc.) or deployment (SpiNNaker, Loihi). https://github.com/NeuromorphicProcessorProject/snn_toolbox (accessed on 7 September 2021) |
| GeNN [117] | SNN | GeNN provides an interface for simulating SNNs on NVIDIA GPUs by generating model-driven and hardware-specific C/C++ CUDA code. https://genn-team.github.io/ (accessed on 7 September 2021) |
| PySNN | STDP | PySNN focuses on having an efficient simulation of SNN on both CPU and GPU. Written on top of PyTorch to achieve this. https://github.com/BasBuller/PySNN (accessed on 7 September 2021) |
| CARLsim [118,119] | STP STDP | CARLsim allows th euser to simulate large-scale SNNs using multiple GPUs and CPU cores concurrently. The simulator provides a PyNN-like programming interface in C/C++, which allows for details and parameters to be specified at the synapse, neuron, and network level. https://github.com/UCI-CARL/CARLsim5 (accessed on 4 September 2021) |
| Auryn [120] | STDP | Auyrn is a simulator for a recurrent spiking neural network with synaptic plasticity. https://github.com/fzenke/auryn (accessed on 5 September 2021) |
| SNN-based brain simulator | ||
| Neucube [121] | STDP | NeuCube is the development environment and a computational architecture for the creation of brain-like artificial intelligence. https://kedri.aut.ac.nz/R-and-D-Systems/neucube (accessed on 4 September 2021) |
| FNS [122] | STDP | FNS is an event-driven spiking neural network framework oriented to data-driven brain simulations. https://www.fnsneuralsimulator.org/ (accessed on 6 September 2021) |
Author Contributions
Conceptualization, K.Y., V.-K.V.-H., D.B. and N.L.; Review and editing, K.Y., V.-K.V.-H. and N.L.; Formal analysis, D.B. and N.L.; project Administration, N.L. All authors have read and agreed to the published version of the manuscript.
Funding
This material is based upon work supported in part by the Engineering Research and Innovation Seed Funding Program (ERISF), US National Science Foundation, under Award No. OIA-1946391, NSF 1920920.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, D.; Yang, J.; Ye, D.; Hua, G. Lq-nets: Learned quantization for highly accurate and compact deep neural networks. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 365–382. [Google Scholar]
- Li, G.; Qian, C.; Jiang, C.; Lu, X.; Tang, K. Optimization based Layer-wise Magnitude-based Pruning for DNN Compression. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 2383–2389. [Google Scholar]
- Jin, X.; Peng, B.; Wu, Y.; Liu, Y.; Liu, J.; Liang, D.; Yan, J.; Hu, X. Knowledge distillation via route constrained optimization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 1345–1354. [Google Scholar]
- Merolla, P.A.; Arthur, J.V.; Alvarez-Icaza, R.; Cassidy, A.S.; Sawada, J.; Akopyan, F.; Jackson, B.L.; Imam, N.; Guo, C.; Nakamura, Y.; et al. A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 2014, 345, 668–673. [Google Scholar] [CrossRef] [PubMed]
- Davies, M.; Srinivasa, N.; Lin, T.; Chinya, G.; Cao, Y.; Choday, S.H.; Dimou, G.; Joshi, P.; Imam, N.; Jain, S.; et al. Loihi: A Neuromorphic Manycore Processor with On-Chip Learning. IEEE Micro 2018, 38, 82–99. [Google Scholar] [CrossRef]
- Furber, S.B.; Galluppi, F.; Temple, S.; Plana, L.A. The SpiNNaker Project. Proc. IEEE 2014, 102, 652–665. [Google Scholar] [CrossRef]
- Benjamin, B.V.; Gao, P.; McQuinn, E.; Choudhary, S.; Chandrasekaran, A.R.; Bussat, J.; Alvarez-Icaza, R.; Arthur, J.V.; Merolla, P.A.; Boahen, K. Neurogrid: A Mixed-Analog-Digital Multichip System for Large-Scale Neural Simulations. Proc. IEEE 2014, 102, 699–716. [Google Scholar] [CrossRef]
- Kasabov, N.K. Time-Space, Spiking Neural Networks and Brain-Inspired Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Dayan, P.; Abbott, L.F. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Strickholm, A. Ionic permeability of K, Na, and Cl in potassium-depolarized nerve. Dependency on pH, cooperative effects, and action of tetrodotoxin. Biophys. J. 1981, 35, 677–697. [Google Scholar] [CrossRef] [Green Version]
- Mcculloch, W.; Pitts, W. A Logical Calculus of Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 1943, 5, 127–147. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [Green Version]
- Han, J.; Moraga, C. The influence of the sigmoid function parameters on the speed of backpropagation learning. In From Natural to Artificial Neural Computation; Mira, J., Sandoval, F., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; pp. 195–201. [Google Scholar]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signals, Syst. (MCSS) 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Leshno, M.; Lin, V.; Pinkus, A.; Schocken, S. Multilayer feedforward networks with a nonpolynomial activation function can approximate any function. Neural Netw. 1993, 6, 861–867. [Google Scholar] [CrossRef] [Green Version]
- Sonoda, S.; Murata, N. Neural Network with Unbounded Activation Functions is Universal Approximator. arXiv 2015, arXiv:1505.03654. [Google Scholar] [CrossRef] [Green Version]
- Nair, V.; Hinton, G. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- LeCun, Y.; Touresky, D.; Hinton, G.; Sejnowski, T. A theoretical framework for back-propagation. In Proceedings of the 1988 Connectionist Models Summer School, Pittsburgh, PA, USA, 17–26 June 1988; pp. 21–28. [Google Scholar]
- LeCun, Y.; Bottou, L.; Orr, G.B.; Müller, K.R. Efficient backprop. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 1998; pp. 9–50. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, AL, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. arXiv 2015, arXiv:1512.00567. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. arXiv 2015, arXiv:1506.02640. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. arXiv 2015, arXiv:1506.01497. [Google Scholar] [CrossRef] [Green Version]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. arXiv 2014, arXiv:1411.4038. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. arXiv 2017, arXiv:1703.06870. [Google Scholar]
- Feichtenhofer, C.; Fan, H.; Malik, J.; He, K. Slowfast networks for video recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 6202–6211. [Google Scholar]
- Fan, Y.; Lu, X.; Li, D.; Liu, Y. Video-based emotion recognition using CNN-RNN and C3D hybrid networks. In Proceedings of the 18th ACM International Conference on Multimodal Interaction, Tokyo, Japan, 12–16 November 2016; pp. 445–450. [Google Scholar]
- Izhikevich, E.M. Which model to use for cortical spiking neurons? IEEE Trans. Neural Netw. 2004, 15, 1063–1070. [Google Scholar] [CrossRef]
- Hodgkin, L.; Huxley, F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef]
- Nelson, M. Electrophysiological Models. In Databasing the Brain: From Data to Knowledge; Wiley: New York, NY, USA, 2005; pp. 285–301. [Google Scholar]
- Meunier, C.; Segev, I. Playing the Devil’s advocate: Is the Hodgkin–Huxley model useful? Trends Neurosci. 2002, 25, 558–563. [Google Scholar] [CrossRef]
- Strassberg, A.; DeFelice, L. Limitations of the Hodgkin-Huxley Formalism: Effects of Single Channel Kinetics on Transmembrane Voltage Dynamics. Neural Comput. 1993, 5, 843–855. [Google Scholar] [CrossRef]
- Hunsberger, E.; Eliasmith, C. Training Spiking Deep Networks for Neuromorphic Hardware. arXiv 2016, arXiv:1611.05141. [Google Scholar]
- Izhikevich, E. Simple model of Spiking Neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef] [Green Version]
- Izhikevich, E. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Brette, R.; Gerstner, W. Adaptive Exponential Integrate-and-Fire Model as an Effective Description of Neuronal Activity. J. Neurophysiol. 2005, 94, 3637–3642. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hebb, D.O. The Organization of Behavior: A Neuropsychological Theory; Wiley: New York, NY, USA, 1949. [Google Scholar]
- Cao, Y.; Chen, Y.; Khosla, D. Spiking Deep Convolutional Neural Networks for Energy-Efficient Object Recognition. Int. J. Comput. Vis. 2015, 113, 54–66. [Google Scholar] [CrossRef]
- Bohte, S.; Kok, J.; Poutré, J. SpikeProp: Backpropagation for Networks of Spiking Neurons. In Proceedings of the 8th European Symposium on Artificial Neural Networks, ESANN 2000, Bruges, Belgium, 26–28 April 2000; Volume 48, pp. 419–424. [Google Scholar]
- Sporea, I.; Grüning, A. Supervised Learning in Multilayer Spiking Neural Networks. arXiv 2012, arXiv:1202.2249. [Google Scholar] [CrossRef] [Green Version]
- Panda, P.; Roy, K. Unsupervised Regenerative Learning of Hierarchical Features in Spiking Deep Networks for Object Recognition. arXiv 2016, arXiv:1602.01510. [Google Scholar]
- Lee, J.H.; Delbruck, T.; Pfeiffer, M. Training Deep Spiking Neural Networks Using Backpropagation. Front. Neurosci. 2016, 10, 508. [Google Scholar] [CrossRef] [Green Version]
- Zenke, F.; Ganguli, S. SuperSpike: Supervised learning in multi-layer spiking neural networks. arXiv 2017, arXiv:1705.11146. [Google Scholar]
- van Rossum, M. A Novel Spike Distance. Neural Comput. 2001, 13, 751–763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bam Shrestha, S.; Orchard, G. SLAYER: Spike Layer Error Reassignment in Time. arXiv 2018, arXiv:1810.08646. [Google Scholar]
- Gerstner, W.; Kistler, W.M. Spiking Neuron Models: Single Neurons, Populations, Plasticity; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Bi, G.; Poo, M. Synaptic Modifications in Cultured Hippocampal Neurons: Dependence on Spike Timing, Synaptic Strength, and Postsynaptic Cell Type. J. Neurosci. 1998, 18, 10464–10472. [Google Scholar] [CrossRef] [PubMed]
- Song, S.; Miller, K.; Abbott, L. Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 2000, 3, 919–926. [Google Scholar] [CrossRef] [PubMed]
- Siddoway, B.; Hou, H.; Xia, H. Molecular mechanisms of homeostatic synaptic downscaling. Neuropharmacology 2014, 78, 38–44. [Google Scholar] [CrossRef]
- Paredes-Vallés, F.; Scheper, K.Y.W.; de Croon, G.C.H.E. Unsupervised Learning of a Hierarchical Spiking Neural Network for Optical Flow Estimation: From Events to Global Motion Perception. arXiv 2018, arXiv:1807.10936. [Google Scholar] [CrossRef] [Green Version]
- Bell, C.; Han, V.; Sugawara, Y.; Grant, K. Synaptic plasticity in a cerebellum-like structure depends on temporal order. Nature 1997, 387, 278–281. [Google Scholar] [CrossRef]
- Burbank, K.S. Mirrored STDP Implements Autoencoder Learning in a Network of Spiking Neurons. PLoS Comput. Biol. 2015, 11, e1004566. [Google Scholar] [CrossRef] [Green Version]
- Masquelier, T.; Thorpe, S.J. Unsupervised Learning of Visual Features through Spike Timing Dependent Plasticity. PLoS Comput. Biol. 2007, 3, e31. [Google Scholar] [CrossRef]
- Tavanaei, A.; Masquelier, T.; Maida, A.S. Acquisition of Visual Features Through Probabilistic Spike-Timing-Dependent Plasticity. arXiv 2016, arXiv:1606.01102. [Google Scholar]
- Izhikevich, E. Solving the Distal Reward Problem through Linkage of STDP and Dopamine Signaling. Cereb. Cortex 2007, 17, 2443–2452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bekolay, T.; Kolbeck, C.; Eliasmith, C. Simultaneous Unsupervised and Supervised Learning of Cognitive Functions in Biologically Plausible Spiking Neural Networks. In Proceedings of the 35th Annual Meeting of the Cognitive Science Society, Berlin, Germany, 31 July–3 August 2013; pp. 169–174. [Google Scholar]
- Rasmussen, D.; Eliasmith, C. A neural model of hierarchical reinforcement learning. PLoS ONE 2014, 12, e0180234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Komer, B. Biologically Inspired Adaptive Control of Quadcopter Flight. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2015. [Google Scholar]
- Stemmler, M.; Koch, C. How voltage-dependent conductances can adapt to maximize the information encoded by neuronal firing rate. Nat. Neurosci. 1999, 2, 521–527. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, W.; Xue, F.; Song, Y. Computational modeling of spiking neural network with learning rules from STDP and intrinsic plasticity. Phys. A Stat. Mech. Its Appl. 2018, 491, 716–728. [Google Scholar] [CrossRef]
- Diehl, P.; Neil, D.; Binas, J.; Cook, M.; Liu, S.C.; Pfeiffer, M. Fast-Classifying, High-Accuracy Spiking Deep Networks Through Weight and Threshold Balancing. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015. [Google Scholar] [CrossRef]
- Rueckauer, B.; Lungu, I.A.; Hu, Y.; Pfeiffer, M.; Liu, S.C. Conversion of Continuous-Valued Deep Networks to Efficient Event-Driven Networks for Image Classification. Front. Neurosci. 2017, 11, 682. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, A.; Ye, Y.; Wang, R.; Liu, C.; Roy, K. Going Deeper in Spiking Neural Networks: VGG and Residual Architectures. Front. Neurosci. 2019, 13, 95. [Google Scholar] [CrossRef]
- Patel, K.; Hunsberger, E.; Batir, S.; Eliasmith, C. A spiking neural network for image segmentation. arXiv 2021, arXiv:2106.08921. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Orchard, G.; Jayawant, A.; Cohen, G.K.; Thakor, N. Converting static image datasets to spiking neuromorphic datasets using saccades. Front. Neurosci. 2015, 9, 437. [Google Scholar] [CrossRef] [Green Version]
- Kheradpisheh, S.R.; Ganjtabesh, M.; Thorpe, S.J.; Masquelier, T. STDP-based spiking deep convolutional neural networks for object recognition. Neural Netw. 2018, 99, 56–67. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Park, S.; Na, B.; Yoon, S. Spiking-YOLO: Spiking Neural Network for Energy-Efficient Object Detection. arXiv 2019, arXiv:1903.06530. [Google Scholar] [CrossRef]
- Zhou, S.; Chen, Y.; Li, X.; Sanyal, A. Deep SCNN-Based Real-Time Object Detection for Self-Driving Vehicles Using LiDAR Temporal Data. IEEE Access 2020, 8, 76903–76912. [Google Scholar] [CrossRef]
- Luo, Y.; Xu, M.; Yuan, C.; Cao, X.; Xu, Y.; Wang, T.; Feng, Q. SiamSNN: Spike-based Siamese Network for Energy-Efficient and Real-time Object Tracking. arXiv 2020, arXiv:2003.07584. [Google Scholar]
- Bertinetto, L.; Valmadre, J.; Henriques, J.F.; Vedaldi, A.; Torr, P.H. Fully-convolutional siamese networks for object tracking. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 850–865. [Google Scholar]
- Rasmussen, D. NengoDL: Combining deep learning and neuromorphic modelling methods. arXiv 2018, arXiv:1805.11144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, C.; Kosta, A.K.; Zihao Zhu, A.; Chaney, K.; Daniilidis, K.; Roy, K. Spike-FlowNet: Event-based Optical Flow Estimation with Energy-Efficient Hybrid Neural Networks. arXiv 2020, arXiv:2003.06696. [Google Scholar]
- Mozafari, M.; Ganjtabesh, M.; Nowzari-Dalini, A.; Thorpe, S.J.; Masquelier, T. Bio-inspired digit recognition using reward-modulated spike-timing-dependent plasticity in deep convolutional networks. arXiv 2018, arXiv:1804.00227. [Google Scholar] [CrossRef] [Green Version]
- Gautrais, J.; Thorpe, S. Rate coding versus temporal order coding: A theoretical approach. Biosystems 1998, 48, 57–65. [Google Scholar] [CrossRef]
- Gutierrez-Galan, D.; Dominguez-Morales, J.P.; Perez-Pena, F.; Linares-Barranco, A. NeuroPod: A real-time neuromorphic spiking CPG applied to robotics. arXiv 2019, arXiv:1904.11243. [Google Scholar] [CrossRef] [Green Version]
- Strohmer, B.; Manoonpong, P.; Larsen, L.B. Flexible Spiking CPGs for Online Manipulation During Hexapod Walking. Front. Neurorobot. 2020, 14, 41. [Google Scholar] [CrossRef]
- Donati, E.; Corradi, F.; Stefanini, C.; Indiveri, G. A spiking implementation of the lamprey’s Central Pattern Generator in neuromorphic VLSI. In Proceedings of the 2014 IEEE Biomedical Circuits and Systems Conference (BioCAS), Lausanne, Switzerland, 22–24 October 2014; pp. 512–515. [Google Scholar]
- Angelidis, E.; Buchholz, E.; Arreguit O’Neil, J.P.; Rougè, A.; Stewart, T.; von Arnim, A.; Knoll, A.; Ijspeert, A. A Spiking Central Pattern Generator for the control of a simulated lamprey robot running on SpiNNaker and Loihi neuromorphic boards. arXiv 2021, arXiv:2101.07001. [Google Scholar] [CrossRef]
- Dupeyroux, J.; Hagenaars, J.; Paredes-Vallés, F.; de Croon, G. Neuromorphic control for optic-flow-based landings of MAVs using the Loihi processor. arXiv 2020, arXiv:2011.00534. [Google Scholar]
- Stagsted, R.K.; Vitale, A.; Renner, A.; Larsen, L.B.; Christensen, A.L.; Sandamirskaya, Y. Event-based PID controller fully realized in neuromorphic hardware: A one DoF study. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 10939–10944. [Google Scholar] [CrossRef]
- Stagsted, R.; Vitale, A.; Binz, J.; Bonde Larsen, L.; Sandamirskaya, Y. Towards neuromorphic control: A spiking neural network based PID controller for UAV. In Proceedings of the Robotics: Science and Systems 2020, Corvalis, OR, USA, 12–16 July 2020. [Google Scholar]
- Tang, G.; Shah, A.; Michmizos, K.P. Spiking Neural Network on Neuromorphic Hardware for Energy-Efficient Unidimensional SLAM. arXiv 2019, arXiv:1903.02504. [Google Scholar]
- Galluppi, F.; Conradt, J.; Stewart, T.; Eliasmith, C.; Horiuchi, T.; Tapson, J.; Tripp, B.; Furber, S.; Etienne-Cummings, R. Live Demo: Spiking ratSLAM: Rat hippocampus cells in spiking neural hardware. In Proceedings of the 2012 IEEE Biomedical Circuits and Systems Conference (BioCAS), Hsinchu, Taiwan, 28–30 November 2012; p. 91. [Google Scholar] [CrossRef]
- Tang, G.; Michmizos, K.P. Gridbot: An autonomous robot controlled by a Spiking Neural Network mimicking the brain’s navigational system. arXiv 2018, arXiv:1807.02155. [Google Scholar]
- Tang, G.; Kumar, N.; Michmizos, K.P. Reinforcement co-Learning of Deep and Spiking Neural Networks for Energy-Efficient Mapless Navigation with Neuromorphic Hardware. arXiv 2020, arXiv:2003.01157. [Google Scholar]
- He, W.; Wu, Y.; Deng, L.; Li, G.; Wang, H.; Tian, Y.; Ding, W.; Wang, W.; Xie, Y. Comparing SNNs and RNNs on neuromorphic vision datasets: Similarities and differences. Neural Netw. 2020, 132, 108–120. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Li, Y.; Park, H.; Venkatesha, Y.; Panda, P. Neural Architecture Search for Spiking Neural Networks. arXiv 2022, arXiv:2201.10355. [Google Scholar]
- Han, B.; Srinivasan, G.; Roy, K. Rmp-snn: Residual membrane potential neuron for enabling deeper high-accuracy and low-latency spiking neural network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 13558–13567. [Google Scholar]
- Li, Y.; Deng, S.; Dong, X.; Gong, R.; Gu, S. A free lunch from ANN: Towards efficient, accurate spiking neural networks calibration. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 6316–6325. [Google Scholar]
- Fang, W.; Yu, Z.; Chen, Y.; Huang, T.; Masquelier, T.; Tian, Y. Deep residual learning in spiking neural networks. In Proceedings of the 35th Conference on Neural Information Processing Systems (NeurIPS 2021), Virtual, 6–14 December 2021; Volume 34. [Google Scholar]
- Hazan, H.; Saunders, D.J.; Sanghavi, D.T.; Siegelmann, H.; Kozma, R. Lattice map spiking neural networks (LM-SNNs) for clustering and classifying image data. Ann. Math. Artif. Intell. 2020, 88, 1237–1260. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Q.; Shi, Y.; Xu, Z.; Qu, R.; Xu, G. Classifying Melanoma Skin Lesions Using Convolutional Spiking Neural Networks with Unsupervised STDP Learning Rule. IEEE Access 2020, 8, 101309–101319. [Google Scholar] [CrossRef]
- Zhou, Q.; Ren, C.; Qi, S. An Imbalanced R-STDP Learning Rule in Spiking Neural Networks for Medical Image Classification. IEEE Access 2020, 8, 224162–224177. [Google Scholar] [CrossRef]
- Luo, Y.; Fu, Q.; Xie, J.; Qin, Y.; Wu, G.; Liu, J.; Jiang, F.; Cao, Y.; Ding, X. EEG-Based Emotion Classification Using Spiking Neural Networks. IEEE Access 2020, 8, 46007–46016. [Google Scholar] [CrossRef]
- Chakraborty, B.; She, X.; Mukhopadhyay, S. A Fully Spiking Hybrid Neural Network for Energy-Efficient Object Detection. arXiv 2021, arXiv:2104.10719. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Otto, R.; Bing, Z.; Huang, K.; Knoll, A. Target Tracking Control of a Wheel-less Snake Robot Based on a Supervised Multi-layered SNN. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 7124–7130. [Google Scholar]
- Parameshwara, C.M.; Li, S.; Fermüller, C.; Sanket, N.J.; Evanusa, M.S.; Aloimonos, Y. SpikeMS: Deep Spiking Neural Network for Motion Segmentation. arXiv 2021, arXiv:2105.06562. [Google Scholar]
- Chen, Q.; Rueckauer, B.; Li, L.; Delbruck, T.; Liu, S.C. Reducing Latency in a Converted Spiking Video Segmentation Network. In Proceedings of the 2021 IEEE International Symposium on Circuits and Systems (ISCAS), Daegu, Korea, 22–28 May 2021; pp. 1–5. [Google Scholar]
- Kirkland, P.; Di Caterina, G.; Soraghan, J.; Matich, G. SpikeSEG: Spiking Segmentation via STDP Saliency Mapping. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Godet, P.; Boulch, A.; Plyer, A.; Le Besnerais, G. STaRFlow: A SpatioTemporal Recurrent Cell for Lightweight Multi-Frame Optical Flow Estimation. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 2462–2469. [Google Scholar]
- Cuevas-Arteaga, B.; Dominguez-Morales, J.P.; Rostro-Gonzalez, H.; Espinal, A.; Jiménez-Fernandez, A.; Gómez-Rodríguez, F.; Linares-Barranco, A. A SpiNNaker Application: Design, Implementation and Validation of SCPGs. In Proceedings of the 14th International Work-Conference on Artificial Neural Networks, IWANN 2017, Cadiz, Spain, 14–16 June 2017; Volume 10305. [Google Scholar]
- Bing, Z.; Baumann, I.; Jiang, Z.; Huang, K.; Cai, C.; Knoll, A. Supervised Learning in SNN via Reward-Modulated Spike-Timing-Dependent Plasticity for a Target Reaching Vehicle. Front. Neurorobot. 2019, 13, 18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stimberg, M.; Brette, R.; Goodman, D.F. Brian 2, an intuitive and efficient neural simulator. eLife 2019, 8, e47314. [Google Scholar] [CrossRef]
- Gewaltig, M.O.; Diesmann, M. NEST (NEural Simulation Tool). Scholarpedia 2007, 2, 1430. [Google Scholar] [CrossRef]
- Bekolay, T.; Bergstra, J.; Hunsberger, E.; DeWolf, T.; Stewart, T.; Rasmussen, D.; Choo, X.; Voelker, A.; Eliasmith, C. Nengo: A Python tool for building large-scale functional brain models. Front. Neuroinform. 2014, 7, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Keras. Available online: https://github.com/keras-team/keras (accessed on 5 September 2021).
- Mozafari, M.; Ganjtabesh, M.; Nowzari-Dalini, A.; Masquelier, T. SpykeTorch: Efficient Simulation of Convolutional Spiking Neural Networks With at Most One Spike per Neuron. Front. Neurosci. 2019, 13, 625. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
- Hazan, H.; Saunders, D.J.; Khan, H.; Sanghavi, D.T.; Siegelmann, H.T.; Kozma, R. BindsNET: A machine learning-oriented spiking neural networks library in Python. arXiv 2018, arXiv:1806.01423. [Google Scholar] [CrossRef]
- Shrestha, S.B.; Orchard, G. SLAYER: Spike Layer Error Reassignment in Time. In Advances in Neural Information Processing Systems 31; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018; pp. 1419–1428. [Google Scholar]
- Yavuz, E.; Turner, J.; Nowotny, T. GeNN: A code generation framework for accelerated brain simulations. Sci. Rep. 2016, 6, 18854. [Google Scholar] [CrossRef] [Green Version]
- Chou, T.S.; Kashyap, H.J.; Xing, J.; Listopad, S.; Rounds, E.L.; Beyeler, M.; Dutt, N.; Krichmar, J.L. CARLsim 4: An Open Source Library for Large Scale, Biologically Detailed Spiking Neural Network Simulation using Heterogeneous Clusters. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Balaji, A.; Adiraju, P.; Kashyap, H.J.; Das, A.; Krichmar, J.L.; Dutt, N.D.; Catthoor, F. PyCARL: A PyNN Interface for Hardware-Software Co-Simulation of Spiking Neural Network. arXiv 2020, arXiv:2003.09696. [Google Scholar]
- Zenke, F.; Gerstner, W. Limits to high-speed simulations of spiking neural networks using general-purpose computers. Front. Neuroinform. 2014, 8, 76. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kasabov, N.K. NeuCube: A spiking neural network architecture for mapping, learning and understanding of spatio-temporal brain data. Neural Netw. 2014, 52, 62–76. [Google Scholar] [CrossRef] [PubMed]
- Susi, G.; Garcés, P.; Paracone, E.; Cristini, A.; Salerno, M.; Maestú, F.; Pereda, E. FNS allows efficient event-driven spiking neural network simulations based on a neuron model supporting spike latency. Sci. Rep. 2021, 11, 12160. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).