Voltage Profile and Sensitivity Analysis for a Grid Connected Solar, Wind and Small Hydro Hybrid System

Abstract

Due to increase in integration of renewable energy into the grid and power quality issues arising from it, there is need for analysis and power improvement of such networks. This paper presents voltage profile, Q-V sensitivity analysis and Q-V curves analysis for a grid that is highly penetrated by renewable energy sources; solar PV, wind power and small hydro systems. Analysis is done on IEEE 39 bus test system with Wind power injection alone, PV power injection alone, with PV and wind power injection and with PV, wind and micro hydro power injection to the grid. The analysis is used to determine the buses where voltage stability improvement is needed. From the results, it was concluded that injection of the modeled wind power alone helped in stabilizing the voltage levels as determined from voltage profiles and reactive power margins. Replacing some of the conventional sources with PV power led to reduction of voltages for weak buses below the required standards. Injection of power from more than one renewable energy source helped in slightly improving the voltage levels. Distribution Static compensators (D-STATCOMs) were used to improve the voltage levels of the buses that were below the required standards.

1. Introduction

The demand for electric energy is rapidly increasing and putting pressure on utilities to expand their generation. This coupled with the need for clean energy has led to energy demand growth. Because of this, the researchers are envisaging the power generation technique from the renewable energy sources such as solar, hydro and wind. These energy sources are preferred for distributed generation because of their abundance, cleanliness and low cost [1,2]

Solar PV and Wind power systems are getting popular because of their availability and reducing cost. However, they are intermittent in nature [3,4,5,6] and cannot satisfy power requirements alone throughout the year. Small hydro systems are also getting interest to generate electrical power in remote areas. The limitation to small hydro power is its poor voltage and frequency regulation. Therefore, a reliable technique is required to maintain constant voltage and frequency irrespective of the load and load types [7].

Grid interconnection of these renewable energy sources come with many advantages such as [8,9,10]:

• Less environmental pollution because of increased use of non- polluting generation sources.
• Low cost because of non- consumption of fuel.
• The power capacity of connected grids increase to meet the increase in demand.
• Improved supply security.
• Cheaper power for consumers due to increase in power supply from cheaper sources.

Photovoltaic (PV) can generate electricity from readily available sunlight [11]. This power can either be utilized in stand-alone mode of connected to the grid. Significant increase in PV generation connected to the grid present technical challenges and major impacts on system stability due to its stochastic nature [12]. Literature [13] analyzes voltage stability of a power system using P-V curves. In [12,14] the effects of photovoltaic integration at different levels is analyzed. Literature [15] discusses the effects of high penetration of PV power on voltage stability of a network. It also analyzes the effects on voltage levels when the connected PV power is lost due to shading of PV panels by movement of clouds. It also proposes the use of D-STATCOM to compensate for instability.

There is a high growth of wind power generation which is estimated to reach 20% of the total generation by the year 2040 [16,17]. The mostly used generator in wind farms is the doubly fed induction generators [18]. Due to the intermittency of wind power and the reactive power consumption of DFIG, the effects of integration of wind farms into the grid cannot be neglected [19,20]. Integration of small amounts of wind power while maintaining the conventional sources can help in voltage support as found in [21]. Serious problems on voltage stability and power quality arise due to wind farm integration with the grid on large scales [22].

The majority of power used worldwide is from hydro power plants; up to 20% of the total power [8,23]. However this power comes from large hydro power plants that require huge amounts of land for water reservoirs and dams and usually cause environmental effects. This has led to increased research on small hydro power plants that operate on run-off rivers which do not require any reservoirs [24,25]. Small hydro power plants can handle peak load demand easily with less cost compared to their conventional generating plants due to the slow start-up and operational needs of the latter [26,27]. The increase in grid interconnection of micro-hydro power plants in the recent past is due to their excellent performance and benefits such as high efficiencies (70–90%), high capacity factors (greater than 50%) and low output power variations [8,28,29,30].

Voltage stability is one of the main challenges that come up with grid interconnection of intermittent renewable energy sources. Voltage stability can be divided into static or dynamic. Dynamic voltage stability is based on differential equations that determine the variation of bus voltages with varying system operating parameters. The methods used in analyzing the dynamic voltage stability include bifurcation analysis, small signal stability analysis, time domain simulations and energy function method [31,32,33,34]. Static voltage stability is based on power flow equations and can point out the mechanisms of voltage collapse for different operating conditions. This method takes less computational time and yields most of the required information concerning voltage stability of the system [35]. Since the system dynamics that influence voltage stability are slow, many aspects can be analyzed by use of static methods which determine the viability of equilibrium point represented by a given operation of the power system [36]. The methods used in static voltage analysis include; Q-V curves, bus sensitivities and P-V curves [35].

Due to the effects on power quality arising from connection of these renewable energy sources to the grid, several mitigation methods have been used in literature. Flexible AC transmission systems (FACTS) have been used to improve voltage profile in grids affected by connection of renewable energy sources. FACTS refers to a family of power electronic devices that can control the flow of active and reactive powers [37,38]. These FACTS devices can either provide series compensation or shunt compensation. Series compensation devices include Thyristor controlled series capacitor (TCSC), Thyristor controlled phase shift transformer (TCPST) and static synchronous series compensator (SSSC) [39] while the commonly used shunt compensators include fixed or variable capacitors [39,40] static compensators (STATCOMs) and static VAR compensators (SVCs). Literatures [41,42] review the use of dynamic voltage restorer (DVR) and STATCOMs in compensating voltage swells and sags. The combination of the DVR and STATCOM forms unified power quality compensator (UPQC) where DVR is used to supply series voltage in the event of voltage sag or swell while STATCOM is used to supply or absorb reactive power to maintain constant DC-link voltage.

Distribution FACTS devices are popularly used nowadays because they are smaller and less expensive than conventional FACTS devices [43,44]. STATCOM devices were used by [4,45] to support reactive power demand and improve voltage profile for a wind integrated grid. The performance of FACTS devices is done in literature [41]. Literature [42] compares the performance of STATCOM and SVC in improvement of the voltage profile after wind power integration. STATCOM is concluded to give better performance than SVC.

This paper analyzes the effects of connecting three renewable energy sources (solar PV, Wind and micro hydro) to the grid voltage levels. The sensitivities of the grid buses are also analyzed. A method for mitigating these effects is implemented and conclusions made. Solar PV system was connected to the grid through voltage source inverter to convert the DC power to AC power. Wind power was connected to the grid through voltage source converters, one to convert wind power from AC to DC for ease of control mechanisms and the other from DC to AC because the grid used was AC. Small hydro system was connected directly to the grid system.

Due to the effects of these renewable energy sources on the grid voltages and bus sensitivities, distribution static compensator (D-STATCOM) devices were connected to the affected grid buses in order to ensure the voltage levels are within the required standards as stated in IEEE standards. According to this standard, the voltage levels should always be within 5% above or below the nominal voltage value [46].

Figure 1 show the three renewable energy sources connected to the grid.

2. Mathematical Mode

2.1. Solar PV

The equivalent circuit of a PV cell is shown in Figure 2 [47].

The current source I_ph represents the cell photocurrent. R_sh and R_s are the intrinsic shunt and series resistances of the cell, respectively. Usually the value of R_sh is very large and that of R_s is very small, hence they may be neglected to simplify the analysis [48]. Practically, PV cells are grouped in larger units called PV modules and these modules are connected in series or parallel to create PV arrays which are used to generate electricity in PV generation systems. The equivalent circuit for PV array is shown in Figure 3 [49].

The voltage–current characteristic equation of a solar cell is provided in [50]:

Module photo-current I_ph:

$$I_{ph}=\left[I_{sc}+K_i\left(T-298\right)\right]\ast \frac{I_r}{1000I_{ph}}$$

(1)

where: $I_{ph}$ = photo-current in Amperes, $I_{sc}$ = short circuit current in Amperes, K_i = short-circuit current of cell at 25 °C and 1000 W/m², T = operating temperature in Kelvin, $I_r$ = solar irradiation (W/m²).

Module reverse saturation current I_rs:

$$I_{rs}=\frac{I_{sc}}{\left[\exp \left(q{V}_{OC}/N_{s}KnT\right)-1\right]}$$

(2)

where: q = electron charge, = 1.6 × 10⁻¹⁹ C; V_oc = open circuit voltage (V); N_s = number of cells connected in series; n: the ideality factor of the diode; K: Boltzmann’s constant, =1.3805 × 10⁻²³ J/K.

The module saturation current I₀ varies with the cell temperature, which is given by:

$$I_0=I_{rs}{\left[\frac{T}{T_r}\right]}^3\exp \left[\frac{q\ast E_{g0}}{nk}\left(\frac{1}{T}-\frac{1}{T_r}\right)\right]$$

(3)

where: $T_r$ = nominal temperature = 298.15 K; E_g0 = band gap energy of the semiconductor = 1.1 eV; The current output of PV module is:

$$I=N_p{I}_{ph}-N_p{I}_0\left[\exp \frac{V/N_s+I{R}_s/N_p}{n{V}_t}-1\right]-I_{sh}$$

(4)

with

$$V_t=\frac{kT}{q}$$

(5)

and

$$I_{sh}=\frac{V\ast N_p/N_s+I{R}_s}{R_{sh}}$$

(6)

where: $N_p$ = number of PV modules connected in parallel; $R_s$ = series resistance (Ω); $R_{sh}$ = shunt resistance (Ω); $V_t$ = diode thermal voltage (V).

The output power of PV panels depends on the current produced due to irradiation of solar rays on the module. Thus the output power can be written as a function of insolation which is the power produced per unit square meter of the panel. Considering panels of size 1 m², total power is the product of insolation, number of panels and the efficiency of the panel to effectively convert the solar irradiation into electric power. Thus the output power of PV panels can be mathematically expressed as:

$$P_s=\eta I{S}_n$$

(7)

where: η = energy conversion efficiency, I = Current produced due to irradiation and $S_n$ = generating power per 1 m² for 1 MJ/m².

In this paper, three PV systems were modeled with the aim of replacing three conventional generators in the IEEE 39 bus system. The PV parameters are shown in

Table 1. PV parameters.

Parameter	Value
Power	82.99 MW, 60.04 MW and 100.07 MW
Voltage	10 kV
Power factor	0.757

.

2.2. Doubly Fed Induction Generator (DFIG) for Wind Power

DFIGs have separate active and reactive control mechanism, hence they are the mostly used generators in wind farms as more than 85% of wind turbines utilize them. Furthermore, DFIG’s converter rating is only 30% of the total generator rating which makes it attractive in the economic point of view [51,52]. The stator voltage and flux of a DFIG can be expressed as [53];

$$\begin{array}{l}{V}_s=R_s{I}_s+\frac{d{\psi }_s}{dt}\\ {\psi }_s=L_s{I}_s+L_m{I}_r\end{array}$$

(8)

where V_s is the stator voltage, $R_s$ = stator winding resistance, $I_s$ is the stator current, ${\psi }_s$ is the stator flux linkage, $L_s$ is the stator inductance, $L_m$ is the maximum mutual inductance and $I_r$ is the rotor current.

The rotor voltage ($V_r$) and rotor flux (${\psi }_r$) are given by;

$$\begin{array}{l}{V}_r=R_r{I}_r+\frac{d{\psi }_r}{dt}-j{\omega }_m{\psi }_r\\ {\psi }_r=L_r{I}_r+L_m{I}_s\end{array}$$

(9)

where ω_m is the rotor mechanical speed and L_r is the rotor inductance.

From Equations (8) and (9), the following expressions can be obtained:

$$\begin{array}{l}\frac{d{I}_s}{dt}=-\frac{L_r{R}_s+j{\omega }_m{L}^2{}_m}{L_r{L}_s-L^2{}_m}{I}_s-\frac{j{\omega }_m{L}_r{L}_m-L_m{R}_r}{L_r{L}_s-L_m^2}{I}_r\\ +\frac{L_r}{L_r{L}_s-L_m^2}{V}_s-\frac{L_m}{L_r{L}_s-L_m^2}{V}_r\\ \frac{d{I}_r}{dt}=-\frac{L_m{R}_s+j{\omega }_m{L}_m{L}_s}{L_r{L}_s-L^2{}_m}{I}_s-\frac{j{\omega }_m{L}_r{L}_s-L_s{R}_r}{L_r{L}_s-L_m^2}{I}_r\\ +\frac{L_m}{L_r{L}_s-L_m^2}{V}_s-\frac{L_s}{L_r{L}_s-L_m^2}{V}_r\end{array}$$

(10)

The magnitudes and parameters are all referred to the stator [53]. The angular stator frequency and rotor frequency are related by:

$${\omega }_r={\omega }_s-{\omega }_m$$

(11)

where ${\omega }_r$ is the rotor electrical speed and ${\omega }_s$ is the electric synchronous speed.

The rotor and stator voltages in the stationary reference frame are given by:

$$\begin{array}{l}{V}_r=R_r{I}_r+sj{\omega }_s{L}_{\sigma r}{I}_r+sj{\omega }_s{L}_m(I_r+I_s)\\ V_s=R_r{I}_s+sj{\omega }_s{L}_{\sigma r}{I}_s+sj{\omega }_s{L}_m(I_r+I_s)\end{array}$$

(12)

where $L_{\sigma r}$ is the rotor leakage inductance?

The three phase active power losses for the stator ($P_s$) and rotor ($P_r$) of the DFIG machine are given by;

$$\begin{array}{l}{P}_s\left(losses\right)=\frac{3}{2}{R}_s{I}_s{}^2\\ P_r\left(losses\right)=\frac{3}{2}{R}_r{I}_r{}^2\end{array}$$

(13)

The active power for the stator and rotor are given by;

$$\begin{array}{l}{P}_s=\frac{3}{2}\mathrm{Re}\left(V_s\ast I_s{}^{*}\right)=\frac{3}{2}{R}_s{I}_s{}^2+\frac{3}{2}{\omega }_s{L}_m\mathrm{Re}\left(j(I_r\ast I_s{}^{*})\right)\\ P_r=\frac{3}{2}\mathrm{Re}\left(V_r\ast I_r{}^{*}\right)=\frac{3}{2}{R}_r{I}_r{}^2+\frac{3}{2}s{\omega }_s{L}_m\mathrm{Re}\left(j(I_r\ast I_s{}^{*})\right)\end{array}$$

(14)

The mechanical power of DFIG is given by;

$$\begin{array}{l}{P}_{mec}=P_s+P_r-P_s(losses)-P_r(losses)\\ =\frac{3}{2}{\omega }_s{L}_m\mathrm{Re}\left[j\left(I_r\ast I_s{}^{*}\right)+\left(s{I}_s\ast I_r{}^{*}\right)\right]\end{array}$$

(15)

The parameters used in modeling the DFIG are shown in

Table 2. DFIG parameters.

Parameter	Value
Power (2 DFIGs)	15 MW, 15 MW
Voltage	3.3 kV
Frequency	50 Hz
Speed	1494.2 rev/min
Power factor	0.85498
Slip	0.388
Efficiency	0.99
Pole pairs	2

.

2.3. Small Hydro System

The hydraulic power from a hydro system is given by [54];

$$P_h=g\rho WH\mathrm{watts}$$

(16)

where W = water discharge through the turbine in m/s, ρ = density in Kg/m³, H = Head in meters and g = gravitational acceleration = 9.81 m/s².

Since the density of water is 1000 Kg/m³ then the power is given by;

$$P_h=9.81WH\mathrm{kilowatts}$$

(17)

Total potential of water can be calculated from;

$$P_{total}=P_h•n_t•n_g\mathrm{kW}$$

(18)

where: $P_h$ is the hydraulic power, $n_t$ is the turbine efficiency and $n_g$ is the generator efficiency.

2.4. Voltage Stability

Voltage stability analysis can be done using time simulations that capture the events that lead to instability or by use of static methods that examine the viability of a balance point that is represented by specified parameters of the power system. There are 4 static methods for voltage stability analysis: V-Q Sensitivity Analysis, Q-V Modal Analysis, V-Q Curves and P-V Curves. These static analysis methods allow examination of a wide range of system conditions can provide information about the nature of the problem and can identify the key contributing factors [55].

This paper utilizes the static methods to assess the effects of connecting solar PV, wind power and small hydro into the grid.

2.4.1. Q-V Sensitivity Analysis

This method calculates the relationship between voltage change and reactive power change [56];

$$\Delta U=J_R^{-1}•\Delta Q$$

(19)

where: $\Delta U$ = incremental change in bus voltage magnitude (vector), $\Delta Q$ = incremental change in bus reactive power injection (vector), $J_R$ = reduced Jacobian matrix.

The V-Q sensitivities are found from the elements of the inverse of the reduced Jacobian matrix $J_R$ while the diagonal components are the self-sensitivities given by;

$$\frac{\partial U_i}{\partial Q_i}$$

(20)

The non-diagonal elements are the mutual sensitivities

$$\frac{\partial U_k}{\partial Q_i}$$

(21)

The sensitivities of voltage controlled buses are equal to zero since their voltages are assumed to be constant. V-Q sensitivities can either be; Positive or negative. Positive sensitivities shows that the system is under stable operation, the smaller the sensitivity, the more stable the system. As stability decreases, the magnitude of the sensitivity increases, becoming infinite at the stability limit. Negative sensitivities show unstable operation. At this region, the system is uncontrollable.

2.4.2. Q-V Modal Analysis

This modal analysis approach provides more information regarding the mechanism of instability. Voltage stability characteristics of the system are identified by determining the eigenvalues and eigenvectors of the reduced Jacobian matrix $J_R$ [56].

$$J_R={\xi }_i\Lambda \eta$$

(22)

where: $\Lambda$ = diagonal eigenvalue matrix, $\xi$ = right eigenvector matrix, $\eta$ = left eigenvector matrix, ${\xi }_i$ = the i^th right eigenvector, i^th column of right eigenvector matrix, ${\eta }_i$ = is the i^th left eigenvector, ith row of left eigenvector matrix.

Using modal analysis techniques Equation (19) becomes;

$$u={\Lambda }^{-1}•q$$

(23)

where: $u=\eta •\Delta U$ is the vector of modal voltage variations, $q=\eta •\Delta Q$q = η ΔQ is the vector of modal reactive power variations.

The inverse transformation of (23) is given by;

$$\begin{gathered} \Delta U=\xi •u \\ \Delta Q=\xi •q \end{gathered}$$

(24)

For U-Q modal analysis, Positive eigenvalue shows that the system is voltage stable. The smaller the magnitude, the closer the i^th modal voltage is to being unstable. The magnitude of the eigenvalues can provide a relative measure of the proximity to instability. Zero eigenvalue shows that the i^th modal voltage collapses because any change in that modal reactive power causes infinite change in the modal voltage. Negative eigenvalue shows that the system is voltage unstable. Zero reactive power is assumed for buses without load elements.

Bus participation factors give the relative participation of a bus in a certain mode. They are used to determine voltage weak areas or unstable (not controllable) areas. The sum of all the bus participations for each mode is equal to unity. The size of bus participation in a given mode indicates the effectiveness of remedial actions applied at that bus in stabilizing that mode [56].

2.4.3. Q-V Curves

Reactive-Voltage (Q-V) curve is one of the methods used in determining the stability of an electrical system. From Q-V curves, reactive power margin is measured as a distance between the lowest MVAr point and Voltage axis as shown in Figure 4 [57].

Therefore, reactive power margin indicates how further the loading on a particular bus can be increased before its loading limit is exhausted and voltage collapse takes place [58]. Literature [59] used reactive power margins to evaluate voltage instability problems for coherent bus groups. These margins are based on the reactive reserves on generators, SVCs and synchronous condensers that exhaust reserves in the process of computing a Q-V curve at any bus in a coherent group or voltage control area. This paper uses Q-V curves to analyze how the reactive power margins change with integration of different renewable energy sources to the grid.

2.5. Distribution Static Compensator (D-STATCOM)

D-STATCOM is a static synchronous generator operating as a Static Var Compensator (SVC) connected in parallel with the output current (capacitive or inductive) that can be controlled independently of the AC voltage network. The principle functions of a D-STATCOM are to mitigate the impact of voltage dips and voltage peaks of sensitive loads, voltage regulation, harmonic compensation and reactive power control. Its function in compensating reactive power and therefore regulating the bus bar voltage where it is connected is applied in this research paper. The basic structure for a static compensator is depicted in Figure 5 [60,61].

The voltage of D-STATCOM, $V_{sh}$ is injected in phase with the line voltage V_t, and in this case there is no exchange of energy with the active network, but only reactive power to be injected (or absorbed) by the D-STATCOM.

The reactive power exchange with the network is done by varying the amplitude of the output voltages [61].

The output voltage of the gate turn-off thyristor (GTO) converter ($V_{sh}$) is controlled in phase with the system voltage ($V_t$). The output current of the D-STATCOM ($I_q$) varies depending on $V_{sh}$ [61]. If $V_t$ < $V_{sh}$ then the phase angle of $I_q$ is leading with respect to the phase angle of $V_t$ by 90 degrees. This leads to reactive power flowing from the D-STATCOM (capacitive mode). When $V_t$ > $V_{sh}$ then the phase angle of $I_q$ is lagging with respect to $V_t$ by 90 degrees; the D-STATCOM consumes reactive power. When $V_t=V_{sh}$ then no reactive power is delivered to the power system. As a result, lagging reactive power flows into the D-STATCOM (inductive mode).

The amount of the reactive power is proportional to the voltage difference between $V_t$ and $V_{sh}$. The variation of the output voltages amplitude is achieved by varying the direct voltage across the capacitor. The D-STATCOM can deliver a capacitive or inductive current independent of the network voltage. So it can provide the maximum capacitive current even at low voltage values. Its ability to support the supply voltage is better than the SVC.

The advantage of this device is in its ability to exchange energy nature (capacitive or inductive) only with an inductor. Unlike SVC, there is no capacitive element that can cause resonances with inductive elements of the network. The structure and operational characteristic is shown in Figure 6. The D-STATCOM smoothly and continuously controls voltage from $V_1$ to $V_2$. However, if the system voltage exceeds a low-voltage ($V_1$) or high voltage limit ($V_2$), the D-STATCOM acts as a constant current source by controlling the converter voltage ($V_1$) appropriately [61].

The equivalent circuit for D-STATCOM is shown in Figure 7.

Taking $\overline{V_{sh}}=V_{sh}\angle {\delta }_{sh}$ as the reference phase and the fundamental component of the voltage source converter as $\overline{V_s}=V_s\angle 0$. The active and reactive power exchanged with the bus is given by;

$$\begin{array}{l}P=\frac{V_{sh}{V}_s}{X_t}\sin {\delta }_{sh}\\ Q=\frac{V_s^2}{X_t}-\frac{V_{sh}{V}_s}{X_t}\cos {\delta }_{sh}\end{array}$$

(25)

The current injected to the busbar by the STATCOM is given by;

$$I_{sh}=\frac{V_{sh}-V_t}{j{X}_t}$$

(26)

When all the quantities are in three phase;

$$\overline{V}=\left[\begin{array}{c}{V}_a\\ V_b\\ V_c\end{array}\right],\overline{V_{sh}}=\left[\begin{array}{c}{V}_{ash}\\ V_{bsh}\\ V_{csh}\end{array}\right],\overline{I_{sh}}=\left[\begin{array}{c}{I}_{sha}\\ I_{shb}\\ I_{shc}\end{array}\right]$$

(27)

The power injected to the busbar is given by;

$$\overline{S}=\overline{V_{sh}}•\overline{I_{sh}}=\frac{\overline{V_t}\left(\overline{V_{sh}{}^{*}}-\overline{V_t^{*}}\right)}{-j{X}_t}=\frac{\overline{V_t}•\overline{V_{sh}}-\overline{V_t{}^2}}{-j{X}_t}$$

(28)

The active and reactive power injected by the D-STATCOM is given by;

$$\begin{array}{l}{P}_{sh}=-V_t\cdot V_{sh}\cdot \sin \left({\theta }_t-{\theta }_{sh}\right)\\ Q_{sh}=V_t\left(V_{sh}\cos \left({\theta }_t-{\theta }_{sh}\right)-V_t\right)/X_t\end{array}$$

(29)

2.6. Sizing and Placement of D-STATCOM

There are various criteria for determining the required size of STATCOM devices [62] and [63]. STATCOM devices can be sized considering the ratings of the renewable energy systems connected to the gridas presented in [64]. In this study, the amount of reactive power needed for compensation is assumed to be equal to the sum of Wind turbine systems, PV systems and Small hydro systems ratings’ depending on which one is integrated at a given time.

Table 3. D-STATCOM sizes.

Type Integrated	D-STATCOM Size
Wind alone (2 DFIGs)	15 MVar
PV alone (3 PV systems)	180.24 MVar + 29.15 MVar + 379.31 MVar
Wind + PV	593 MVar
DFIG + PV + Small Hydro	598 MVar

shows STATCOM sizes connected for different connections of renewable energy types.

Literature [65] made comparisons of placement of STATCOM devices at the weakest buses of a network. The comparison is made on aggregated placement and dispersed placement at the weakest buses. The dispersed placement is preferred over the aggregated placement since it results to both lowest power losses and increase loadability of the network. Thus, considering this, this paper places the designed STATCOM devices on the weakest buses of the IEEE 39 bus test grid to improve the voltage stability with influx of the power from the renewable energy sources.

3. Simulation and Results

After modeling the three renewable energy sources (Solar PV, wind and small hydro) their powers were injected into the IEEE 39 bus system for analysis of voltage profile, V-Q sensitivities and Q-V curves. Firstly, wind power was injected at bus 12 (15 MW) and bus 28 (15 MW) and analysis done. Secondly, three generators of the test system were replaced by solar power with varying insolation (from 1 kW/m² to 0.7 kW/m²) at bus 30 (80 MW), at bus 32 (60 MW) and at bus 38 (100 MW) and analysis done. Thirdly, analysis was done with penetration of both wind power and solar power. Lastly, a small hydropower (10 MW) was injected at bus 03 and analysis done when the system is penetrated by all the three; solar power, wind power and small hydro power.

In order to improve the voltage levels to the required standards, the modeled D-STATCOM was connected to buses 12 and 07 and the results analyzed in comparison with those before compensation.

The IEEE 39 bus test system used in this work is shown in Figure 8.

3.1. Weak Buses of the IEEE 39 Bus System

The weakest buses of the IEEE 39 test bus system were determined using bus participation factors and are shown in Figure 9. The weakest buses are buses 12, 07 and 08.

3.2. Voltage Profile

3.2.1. Voltage Profile before Varying Reactive Power

Table 4. Voltage profile analysis with standard loads for IEEE 39 bus system.

Voltage Profile before Varying Reactive Power
Bus No.	Before Penetration		After Wind Penetration		After PV Penetration		PV + Wind Penetration		PV + Wind + Small Hydro
T	V	%V	V	%V	V	%V	V	%V	V	%V
N01	10.474	104.74	10.472	104.72	10.465	104.65	10.466	104.66	10.468	104.68
N02	10.487	104.87	10.485	104.85	10.419	104.19	10.423	104.23	10.426	104.26
N03	10.302	103.02	10.299	102.99	10.152	101.52	10.062	100.62	10.069	100.69
N04	10.039	100.39	10.037	100.37	9.501	95.01	9.52	95.2	9.531	95.31
N05	10.053	100.53	10.053	100.53	9.354	93.54	9.376	93.76	9.39	93.9
N06	10.077	100.77	10.077	100.77	9.357	93.57	9.379	93.79	9.393	93.93
N07	9.97	99.7	9.97	99.7	9.277	92.77	9.299	92.99	9.312	93.12
N08	9.96	99.6	9.96	99.6	9.289	92.89	9.31	93.1	9.323	93.23
N09	10.282	102.82	10.282	102.82	9.986	99.86	9.996	99.96	10.002	100.02
N10	10.172	101.72	10.17	101.7	9.694	96.94	9.71	97.1	9.72	97.2
N11	10.127	101.27	10.126	101.26	9.568	95.68	9.586	95.86	9.597	95.97
N12	10.002	100.02	9.996	99.96	9.467	94.67	9.484	94.84	9.495	94.95
N13	10.143	101.43	10.142	101.42	9.664	96.64	9.68	96.8	9.69	96.9
N14	10.117	101.17	10.116	101.16	9.652	96.52	9.669	96.69	9.679	96.79
N15	10.154	101.54	10.152	101.52	9.871	98.71	9.882	98.82	9.889	98.89
N16	10.318	103.18	10.316	103.16	10.122	101.22	10.13	101.3	10.135	101.35
N17	10.336	103.36	10.334	103.34	10.112	101.12	10.122	101.22	10.129	101.29
N18	10.309	103.09	10.307	103.07	10.076	100.76	10.086	100.86	10.093	100.93
N19	10.499	104.99	10.498	104.98	10.427	104.27	10.43	104.3	10.431	104.31
N20	9.912	99.12	9.911	99.11	9.872	98.72	9.874	98.74	9.875	98.75
N21	10.318	103.18	10.317	103.17	10.18	101.8	10.185	101.85	10.189	101.89
N22	10.498	104.98	10.497	104.97	10.424	104.24	10.427	104.27	10.429	104.29
N23	10.448	104.48	10.447	104.47	10.371	103.71	10.375	103.75	10.377	103.77
N24	10.373	103.73	10.372	103.72	10.195	101.95	10.202	102.02	10.207	102.07
N25	10.576	105.76	10.576	105.76	10.385	103.85	10.392	103.92	10.398	103.98
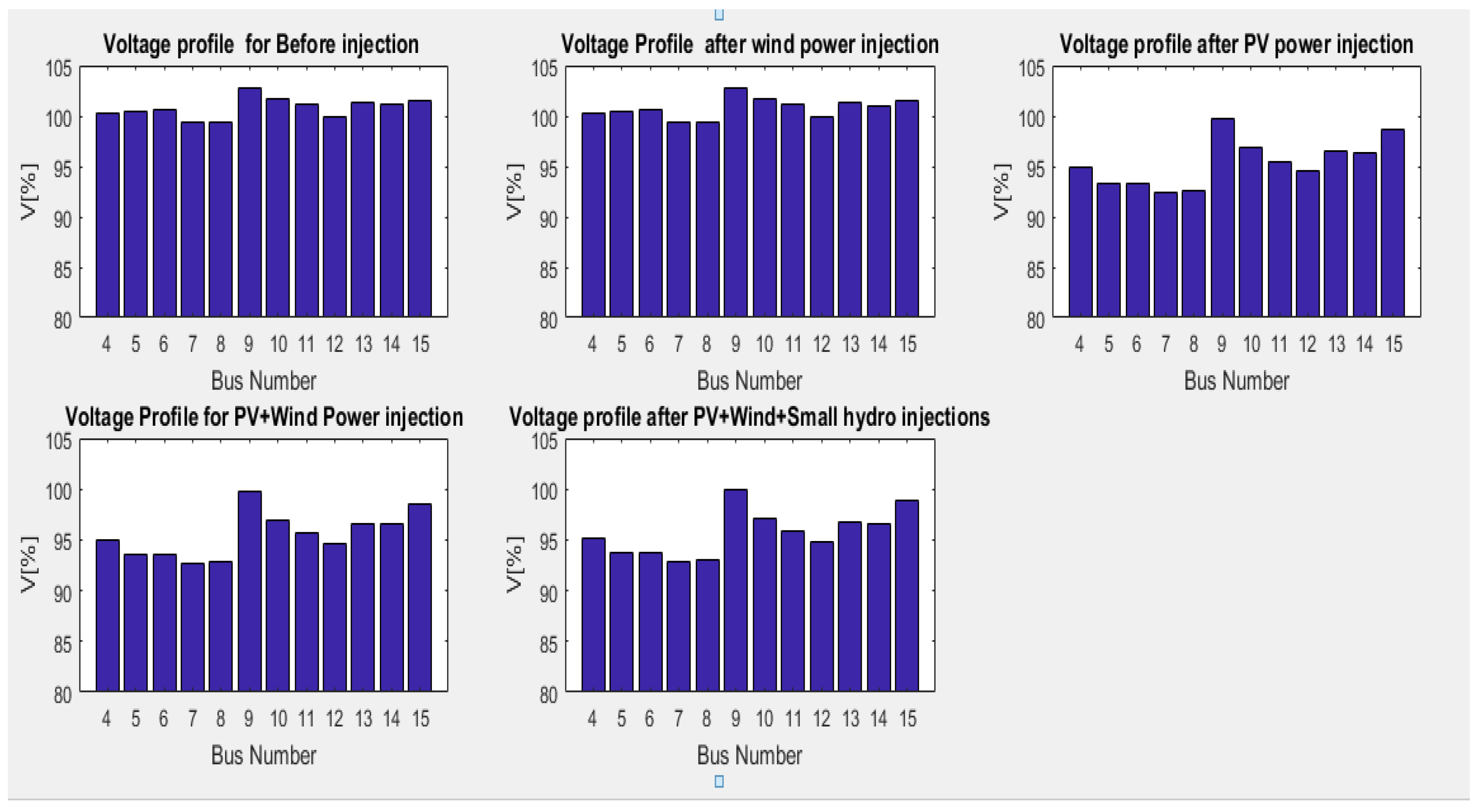
N26	10.521	105.21	10.517	105.17	10.338	103.38	10.349	103.49	10.358	103.58

and Figure 10 (considering the weak buses of the system) show the voltage profile of the IEEE 39 bus system before injecting any of the modeled systems into it, when wind power is injected at buses 12 and 28, when solar PV power alone is injected into buses 30, 32 and 38, when both solar power(injected at buses 30, 32 and 38) and wind power (injected at buses 12 and 28) and when all the three are injected to the grid; (solar power at buses 30, 32 and 38, Wind power (at buses 12 and 28) and small hydro power (at bus 03). Both Voltage levels and percentage of the nominal voltages are shown in Table 4 while the percentage voltage levels for the weakest buses of the system are depicted in Figure 10.

From the Table 4 and Figure 10, the voltage profile for the weak buses are seen to reduce when the system is penetrated with PV solar power then slightly improve with the connection of wind power and small hydro power into the system. The buses with the highest voltage drops when PV power is used to replace the three IEEE 39 bus test system were, bus 5 from 100.53% to 93.54%, bus 6 from 100.77% to 93.57%, bus 7 from 99.7% to 92.77% and bus 8 from 99.6% to 92.89%. Considering the weakest buses of the system (12 and 07) the voltage levels percentages for bus 12 are seen to change from 100.02% to 99.96% to 94.67% to 94.84% and 94.95% in the presented order while for Bus 07, the voltage profile percentages change from 99.7%, to 99.7% to 92.77% to 92.99% to 93.93% in that order.

3.2.2. Voltage Profile When Reactive Power on Bus 07 Is Varied

The reactive power consumed by the load on bus 07 was varied and voltage profile analyzed.

Table 5. Voltage profile when reactive power at the load at bus 07 is increased from 84 MVAR to 100MVAR.

Voltage Profile after Varying Reactive Power at Bus 07
Bus No.	Before Penetration		After Wind Penetration		After PV Penetration		PV + Wind Penetration		PV + Wind + Small Hydro
T	V	%V	V	%V	V	%V	V	%V	V	%V
N01	10.473	104.73	10.471	104.71	10.464	104.64	10.465	104.65	10.466	104.66
N02	10.485	104.85	10.483	104.83	10.416	104.16	10.42	104.2	10.423	104.23
N03	10.297	102.97	10.294	102.94	10.044	100.44	10.055	100.55	10.062	100.62
N04	10.028	100.28	10.026	100.26	9.486	94.86	9.504	95.04	9.516	95.16
N05	10.037	100.37	10.037	100.37	9.332	93.32	9.355	93.55	9.369	93.69
N06	10.061	100.61	10.061	100.61	9.335	93.35	9.358	93.58	9.372	93.72
N07	9.946	99.46	9.946	99.46	9.246	92.46	9.269	92.69	9.282	92.82
N08	9.94	99.4	9.939	99.39	9.262	92.62	9.283	92.83	9.296	92.96
N09	10.274	102.74	10.274	102.74	9.975	99.75	9.985	99.85	9.991	99.91
N10	10.162	101.62	10.161	101.61	9.68	96.8	9.696	96.96	9.706	97.06
N11	10.115	101.15	10.114	101.14	9.551	95.51	9.57	95.7	9.581	95.81
N12	9.99	99.9	9.985	99.85	9.451	94.51	9.469	94.69	9.48	94.8
N13	10.133	101.33	10.132	101.32	9.65	96.5	9.666	96.66	9.676	96.76
N14	10.108	101.08	10.107	101.07	9.639	96.39	9.655	96.55	9.666	96.66
N15	10.149	101.49	10.147	101.47	9.864	98.61	9.875	98.75	9.882	98.82
N16	10.314	103.14	10.313	103.13	10.117	101.17	10.125	101.25	10.131	101.31
N17	10.332	103.32	10.33	103.3	10.107	101.07	10.117	101.17	10.123	101.23
N18	10.305	103.05	10.303	103.03	10.069	100.69	10.08	100.8	10.087	100.87
N19	10.497	104.97	10.497	104.97	10.425	104.25	10.428	104.28	10.43	104.3
N20	9.911	99.11	9.911	99.11	9.871	98.71	9.873	98.73	9.874	98.74
N21	10.315	103.15	10.314	103.44	10.176	101.76	10.182	101.82	10.186	101.86
N22	10.497	104.97	10.496	104.96	10.422	104.22	10.425	104.25	10.427	104.27
N23	10.447	104.47	10.446	104.46	10.37	103.7	10.373	103.73	10.375	103.75
N24	10.37	103.7	10.369	103.69	10.19	101.9	10.198	101.98	10.202	102.02
N25	10574	105.74	10.574	105.74	10.382	103.82	10.39	103.9	10.395	103.95
N26	10.519	105.19	10.515	105.15	10.335	103.35	10.346	103.46	10.355	103.55

and Figure 11, show the voltage profile for the system when the reactive power of the load at bus 07 is increased from 84.0 MVAR to 100.0 MVAR.

3.2.3. Voltage Profile When Reactive Power on Bus 12 Is Varied

The reactive power consumed by the load on bus 07 was varied and voltage profile analyzed.

Table 6. Voltage profile when reactive power at the load at bus 07 is increased from 84 MVAR to 100MVAR.

Bus No.	Before Penetration		After Wind Penetration		After PV Penetration		PV + Wind Penetration		PV + Wind + Small Hydro
	V	%V	V	%V	V	%V	V	%V	V	%V
N01	10.473	104.73	10.471	104.71	10.464	104.64	10.466	104.66	10.467	104.67
N02	10.486	104.86	10.483	104.83	10.416	104.16	10.421	104.21	10.424	104.24
N03	10.298	102.98	10.295	102.95	10.046	100.46	10.057	100.57	10.064	100.64
N04	10.031	100.31	10.029	100.29	9.491	94.91	9.509	95.09	9.521	95.21
N05	10.045	100.45	10.044	100.44	9.343	93.43	9.365	93.65	9.378	93.78
N06	10.068	100.68	10.068	100.68	9.345	93.45	9.367	93.67	9.381	93.81
N07	9.962	99.62	9.962	99.62	9.266	92.66	9.288	92.88	9.301	93.01
N08	9.952	99.52	9.952	99.52	9.278	92.78	9.299	92.99	9.312	93.12
N09	10.279	102.79	10.279	102.79	9.982	99.82	9.991	99.91	9.997	99.97
N10	10.16	101.6	10.159	101.59	9.68	96.8	9.696	96.96	9.706	97.06
N11	10.115	101.15	10.113	101.13	9.553	95.53	9.571	95.71	9.582	95.82
N12	9.962	99.62	9.956	99.56	9.422	94.22	9.44	94.4	9.451	94.51
N13	10.13	11.3	10.129	101.29	9.648	96.48	9.664	96.64	9.674	96.74
N14	10.108	101.08	10.106	101.06	9.64	96.4	9.657	96.57	9.667	96.67
N15	10.149	101.49	10.147	101.47	9.865	98.65	9.876	98.76	9.883	98.83
N16	10.315	103.15	10.313	103.13	10.118	101.18	10.126	101.26	10.131	101.31
N17	10.332	103.32	10.33	103.3	10.108	101.08	10.118	101.18	10.125	101.25
N18	10.306	103.06	10.304	103.04	10.071	100.71	10.081	100.81	10.088	100.88
N19	10.497	104.97	10.497	104.97	10.425	104.25	10.428	104.28	10.43	104.3
N20	9.911	99.11	9.911	99.11	9.872	98.72	9.873	98.73	9.874	98.4
N21	10.315	103.15	10.314	103.14	10.177	101.77	10.183	101.83	10.186	101.86
N22	10.497	104.97	10.496	104.96	10.423	104.23	10.426	104.26	10.428	104.28
N23	10.447	104.47	10.446	104.46	10.37	103.7	10.373	103.73	10.375	103.75
N24	10.37	103.7	10.369	103.69	10.191	101.91	10.198	101.98	10.203	102.03
N25	10.574	105.74	10.575	105.75	10.383	103.83	10.391	103.91	10.396	103.96
N26	10.519	105.19	10.516	105.16	10.335	103.35	10.346	103.46	10.355	103.55

shows the voltage profile for the system when the reactive power of the load at bus 07 is increased from 84.0 MVAR to 100.0 MVAR. Figure 12 shows the voltage profile for the weakest buses of the IEEE 39 bus system.

From Table 5 and Table 6 and Figure 11 and Figure 12, there is a reduction in the voltage levels when PV penetrates the grid and the voltage levels improve as wind and small hydro powers are injected to the grid. From Table 5, The buses with the highest voltage drops when PV power is used to replace the three IEEE 39 bus test system were, bus 4 from 100.28% to 94.88%, bus 5 from 100.37% to 93.32%, bus 6 from 100.61% to 93.35%, bus 7 from 99.46% to 92.46% and bus 8 from 99.4% to 92.62%. From Table 6, the buses with the highest voltage drops when PV power is used to replace the three IEEE 39 bus test system were, bus 4 from 100.31 to 94.91, bus 5 from 100.45% to 93.43%, bus 6 from 100.68% to 93.45%, bus 7 from 99.62% to 92.66% and bus 8 from 99.52% to 92.68% and bus 12 99.62% to 94.22%. Considering buses 04 and 05, from Table 5; the voltage levels changed 100.28% to100.26% to 94.86% to 95.04% to 95.16% for bus 04 and from 100.37% to 100.37% to 93.32% to 93.55% to 93.69% for bus 05 respectively. From Table 6 the voltage levels changed from 100.31% to 100.29% to 94.91% to 95.09% to 95.21% for Bus 04 and from 100.45% to 100.44% to 93.43% to 93.65% to 93.78% for bus 05 respectively.

3.3. Q-V Sensitivity Analysis

3.3.1. Q-V Sensitivities before Varying Reactive Power

The bus sensitivities were determined using the standard loads of the IEEE 39 bus system and the results are shown in

Table 7. Q-V sensitivity analysis for standard IEEE load parameters.

Bus Sensitivities before Varying Reactive Power
Bus No.	Before Penetration	After Wind Power Penetration	After PV Power Penetration	After PV + Wind Power Penetration	After PV + Wind + Small Hydro Power Penetration
N12	0.0332	0.0333	0.0369	0.0367	0.0366
N28	0.0215	0.0215	0.0215	0.0215	0.0215
N27	0.0175	0.0176	0.0183	0.0182	0.0182
N09	0.0170	0.0170	0.0180	0.0179	0.0179
N01	0.0161	0.0161	0.0161	0.0161	0.0161
N26	0.0156	0.0156	0.0162	0.0161	0.0161
N07	0.0150	0.0149	0.0191	0.0189	0.0188
N08	0.0146	0.0146	0.0185	0.0183	0.0182
N15	0.0138	0.0138	0.0147	0.0147	0.0146
N18	0.0135	0.0135	0.0142	0.0142	0.0142
N21	0.0128	0.0128	0.0131	0.0131	0.0131
N29	0.0126	0.0126	0.0124	0.0124	0.0124
N14	0.0126	0.0126	0.0145	0.0144	0.0143
N04	0.0125	0.0125	0.0150	0.0149	0.0149
N24	0.0122	0.0122	0.0126	0.0126	0.0126
N13	0.0120	0.0120	0.0139	0.0138	0.0138
N11	0.0113	0.0113	0.0138	0.0137	0.0136
N03	0.0113	0.0113	0.0120	0.0120	0.0120
N17	0.0112	0.0112	0.0118	0.0118	0.0118
N05	0.0112	0.0112	0.0150	0.0149	0.0148
N20	0.0106	0.0106	0.0106	0.0106	0.0106
N10	0.0104	0.0104	0.0121	0.0120	0.0120
N06	0.0103	0.0103	0.0143	0.0141	0.0140
N23	0.0100	0.0100	0.0101	0.0101	0.0101
N25	0.0090	0.0090	0.0093	0.0093	0.0093
N16	0.0087	0.0087	0.0091	0.0091	0.0091

.

From Table 7, Q-V sensitivities increase with PV replacement of the conventional sources then start reducing as wind power and small hydro power are connected to the grid. Considering buses 12 and 07; the sensitivities change from 0.0332 to 0.0333 to 0.0369 to 0.0367 to 0.0366 for bus 12 and from 0.0150 to 0.10149 to 0.0191 to 0.0189 to 0.0188 for bus 07 respectively.

3.3.2. Q-V Sensitivities when Reactive Power at Buses 07 Is Varied

The reactive power consumed by the load on bus 07 was varied and bus sensitivities determined.

Table 8. Q-V sensitivity analysis when reactive power at the load at bus 07 is increased from 84 MVAR to 100MVAR.

Bus Sensitivities after Varying Reactive Power at Bus 07
Bus No.	Before Penetration	After Wind Power Penetration	After PV Power Penetration	After PV + Wind Power Penetration	After PV + Wind + Small Hydro Power Penetration
N12	0.0332	0.0333	0.0370	0.0368	0.0367
N28	0.0215	0.0215	0.0215	0.0215	0.0215
N27	0.0176	0.0176	0.0183	0.0183	0.0182
N09	0.0170	0.0170	0.0180	0.0180	0.0179
N01	0.0161	0.0161	0.0161	0.0161	0.0161
N26	0.0156	0.0156	0.0162	0.0161	0.0161
N07	0.0150	0.0150	0.0193	0.0191	0.0190
N08	0.0147	0.0147	0.0187	0.0185	0.0184
N15	0.0138	0.0138	0.0147	0.0147	0.0147
N18	0.0135	0.0135	0.0142	0.0142	0.0142
N21	0.0128	0.0128	0.0131	0.0131	0.0131
N29	0.0126	0.0126	0.0124	0.0124	0.0124
N14	0.0126	0.0126	0.0145	0.0144	0.0144
N04	0.0126	0.0126	0.0151	0.0150	0.0149
N24	0.0122	0.0122	0.0126	0.0126	0.0126
N13	0.0121	0.0121	0.0140	0.0139	0.0138
N11	0.0114	0.0118	0.0139	0.0138	0.0137
N03	0.0113	0.0113	0.0121	0.0120	0.0120
N17	0.0112	0.0112	0.0119	0.0118	0.0118
N05	0.0112	0.0112	0.0151	0.0150	0.0149
N20	0.0106	0.0106	0.0106	0.0106	0.0106
N10	0.0104	0.0104	0.0122	0.0121	0.0120
N06	0.0104	0.0103	0.0144	0.0142	0.0141
N23	0.0100	0.0100	0.0101	0.0101	0.0101
N25	0.0090	0.0090	0.0093	0.0093	0.0093
N16	0.0087	0.0087	0.0091	0.0091	0.0091

shows the bus sensitivities for the system when the reactive power of the load at bus 07 is increased from 84.0 MVAR to 100.0 MVAR.

3.3.3. Q-V Sensitivities when Reactive Power at Buses 12 Is Varied

The reactive power consumed by the load on bus 12 was varied and sensitivities of the buses determined.

Table 9. Q-V sensitivity analysis when reactive power at the load at.

Bus Sensitivities after Varying Reactive Power at Bus 07
Bus No.	Before Penetration	After Wind Power Penetration	After PV Power Penetration	After PV + Wind Power Penetration	After PV + Wind + Small Hydro Power Penetration
N12	0.0335	0.0336	0.0372	0.0371	0.0370
N28	0.0215	0.0215	0.0215	0.0215	0.0215
N27	0.0176	0.0176	0.0183	0.0183	0.0182
N09	0.0170	0.0170	0.0180	0.0179	0.0179
N01	0.0161	0.0161	0.0161	0.0161	0.0161
N26	0.0156	0.0156	0.0162	0.0161	0.0161
N07	0.0150	0.0150	0.0192	0.0190	0.0189
N08	0.0146	0.0146	0.0186	0.0184	0.0183
N15	0.0138	0.0138	0.0147	0.0147	0.0147
N18	0.0135	0.0135	0.0142	0.0142	0.0142
N21	0.0128	0.0128	0.0131	0.0131	0.0131
N29	0.0126	0.0126	0.0124	0.0124	0.0129
N14	0.0126	0.0126	0.0145	0.0144	0.0144
N04	0.0126	0.0126	0.0151	0.0150	0.0149
N24	0.0122	0.0122	0.0126	0.0126	0.0126
N13	0.0121	0.0121	0.0140	0.0139	0.0138
N11	0.0114	0.0114	0.0139	0.0138	0.0137
N03	0.0113	0.0113	0.0121	0.0120	0.0119
N17	0.0112	0.0112	0.0118	0.0118	0.0118
N05	0.0112	0.0112	0.0151	0.0149	0.0148
N20	0.0106	0.0106	0.0106	0.0106	0.0106
N10	0.0104	0.0104	0.0122	0.0121	0.0120
N06	0.0103	0.0103	0.0144	0.0142	0.0141
N23	0.0100	0.0100	0.0101	0.0101	0.0101
N25	0.0090	0.090	0.0093	0.0093	0.0093
N16	0.0087	0.0087	0.0091	0.0091	0.0091

shows the bus sensitivities for the system when the reactive power of the load at bus 12 is increased from 88.0 MVAR to 100.0 MVAR.

From Table 8 and Table 9 the V-Q sensitivities increase when the reactive power is increased compared to those on Table 4. The V-Q sensitivities are highest when PV alone is injected to the grid but reduce with wind and solar penetration. From Table 5, the highest sensitivities change from 0.0332 to 0.0333 to 0.0370 to 0.0368 to 0.0367. From Table 6, the highest sensitivities change from 0.0335 to 0.0336 to 0.0372 to 0.0371 to 0.0370 in that order.

3.4. Q-V Curves

The Q-V curves for the system with standard IEEE 39 parameters, with wind power injection alone, with PV power injection alone, with PV and wind power injection and with PV, wind and small hydro power injections are shown in Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17 respectively

From Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17, considering bus 07, it is noted that the reactive power margins for the system increased with Wind power injection alone from 1530 MVar to 1531 MVar, reduced with PV injection alone (from 1530 MVar to 800 MVar) then increased to 836 MVar for PV + Wind and to 851 MVar PV + Wind + small hydro for bus 07.

3.5. Voltage Profile after Connecting D-STATCOM

3.5.1. Before Varying Reactive Power

Table 10. Voltage profile after static compensation on buses 07 and 12 for standard parameters.

Bus No.	After PV Penetration		PV + Wind Penetration		PV + Wind + Small Hydro
	V	%V	V	%V	V	%V
N01	10.482	104.82	10.483	104.83	10.484	104.84
No2	10.463	104.63	10.466	104.66	10.469	104.69
N03	10.158	101.58	10.165	101.65	10.171	101.71
N04	9.719	97.19	9.732	97.32	9.741	97.41
N05	9.641	96.41	9.656	96.56	9.666	96.66
N06	9.644	96.44	9.66	96.6	9.67	96.7
N07	9.651	96.51	9.666	96.66	9.676	96.76
N08	9.623	96.23	9.638	96.38	9.648	96.48
N09	10.126	101.26	10.132	101.32	10.137	101.37
N10	9.918	99.18	9.927	99.27	9.933	99.33
N11	9.825	98.25	9.836	98.36	9.843	98.43
N12	9.899	98.99	9.899	98.99	9.899	98.99
N13	9.895	98.95	9.904	99.04	9.91	99.1
N14	9.856	98.56	9.866	98.66	9.874	98.74
N15	9.986	99.86	9.993	99.93	9.999	99.99
N16	10.195	101.95	10.201	102.01	10.206	102.06
N17	10.189	101.89	10.197	101.97	10.204	102.04
N18	10.164	101.64	10.172	101.72	10.179	101.79
N19	10.453	104.53	10.456	104.56	10.457	104.57
N20	9.887	98.87	9.888	98.88	9.889	98.89
N21	10.231	101.31	10.235	102.35	10.239	102.39
N22	10.452	104.52	10.454	104.54	10.456	104.56
N23	10.4	104.0	10.402	104.02	10.404	104.04
N24	10.261	102.61	10.266	102.66	10.271	102.71
N25	10.42	104.2	10.427	104.27	10.433	104.33
N26	10.382	103.82	10.392	103.92	10.405	104.05

and Figure 18 show the voltage profile after connecting STATCOM on buses 07 and 12 in order to improve the voltage levels before varying reactive power.

3.5.2. After Varying the Reactive Power on the Load at Bus 07

Figure 19 and

Table 11. Voltage profile after static compensation on buses 07 and 12 with varying reactive power at bus 12.

Bus No.	After PV Penetration		PV + Wind Penetration		PV + Wind + Small Hydro
	V	%V	V	%V	V	%V
N01	10.481	104.81	10.482	104.82	10.484	104.84
No2	10.461	104.61	10.464	104.64	10.469	104.69
N03	10.152	101.52	10.16	101.6	10.171	101.71
N04	9.708	97.08	9.721	97.21	9.741	97.41
N05	9.624	96.24	9.64	96.4	9.666	96.66
N06	9.628	96.28	9.644	96.44	9.67	96.7
N07	9.626	96.26	9.641	96.41	9.676	96.76
N08	9.601	96.01	9.616	96.16	9.648	96.48
N09	10.117	101.17	10.123	101.23	10.137	101.37
N10	9.91	99.1	9.919	99.9	9.933	99.33
N11	9.815	98.15	9.825	98.25	9.843	98.43
N12	9.899	98.99	9.899	98.99	9.899	98.99
N13	9.888	98.88	9.897	98.97	9.91	99.1
N14	9.848	98.48	9.858	98.58	9.874	98.74
N15	9.981	99.81	9.988	99.88	9.999	99.99
N16	10.192	101.92	10.198	101.98	10.206	102.06
N17	10.186	101.86	10.193	101.93	10.204	102.04
N18	10.16	101.6	10.168	101.68	10.179	101.79
N19	10.452	104.52	10.454	104.54	10.457	104.57
N20	9.886	98.86	9.888	98.88	9.889	98.89
N21	10.229	102.29	10.233	102.33	10.239	102.39
N22	10.45	104.5	10.453	104.53	10.456	104.56
N23	10.399	103.99	10.401	104.01	10.404	101.04
N24	10.258	102.58	10.264	102.64	10.271	102.71
N25	10.418	104.18	10.425	104.25	10.433	104.33
N26	10.38	103.8	10.39	103.9	10.405	104.05

show the voltage profile of the IEEE 39 bus system when the reactive power of the load at bus 07 is changed from 84 MVar to 100 MVar.

3.5.3. After Varying the Reactive Power on the Load at Bus 12

Table 12. Voltage profile after static compensation on buses 07 and 12 with varying reactive power at bus 12.

Bus No.	After PV Penetration		PV + Wind Penetration		PV + Wind + Small Hydro
	V	%V	V	%V	V	%V
N01	10.482	104.82	10.483	104.83	10.483	104.83
No2	10.463	104.63	10.467	104.67	10.466	104.66
N03	10.158	101.58	10.166	101.66	10.165	101.65
N04	9.719	97.19	9.73	97.3	9.732	97.32
N05	9.641	96.41	9.65	96.5	9.656	96.56
N06	9.644	96.44	9.654	96.54	9.66	96.6
N07	9.651	96.51	9.651	96.51	9.666	96.66
N08	9.623	96.23	9.626	96.26	9.638	96.38
N09	10.126	101.26	10.128	101.28	10.132	101.32
N10	9.918	99.18	9.925	99.25	9.927	99.27
N11	9.825	98.25	9.833	98.33	9.836	98.36
N12	9.899	98.99	9.899	98.99	9.899	98.99
N13	9.895	98.95	9.903	99.03	9.904	99.04
N14	9.856	98.56	9.865	98.65	9.866	98.66
N15	9.986	99.86	9.994	99.94	9.993	99.93
N16	10.195	101.95	10.203	102.03	10.201	102.01
N17	10.189	101.89	10.2	102.0	10.197	101.97
N18	10.164	101.64	10.174	101.74	10.172	101.72
N19	10.453	104.53	10.456	104.56	10.456	104.56
N20	9.887	98.87	9.889	98.89	9.888	98.88
N21	10.231	102.31	10.237	102.37	10.235	102.35
N22	10.452	104.52	10.455	104.55	10.454	104.54
N23	10.4	104.0	10.403	104.03	10.402	104.02
N24	10.261	102.61	10.268	102.68	10.266	102.66
N25	10.42	104.2	10.431	104.31	10.427	104.27
N26	10.382	103.82	10.402	104.02	10.392	103.92

and Figure 20 show the voltage profile of the IEEE 39 bus system when the reactive power of the load at bus 12 is changed from 88 MVar to 100 MVar.

From Table 10, Table 11 and Table 12 and Figure 18, Figure 19 and Figure 20, it can be seen that after connection of D-STATCOM at buses 07 and 12, all the voltage levels of all the buses were in the required standard i.e., within 5% above or below the nominal value for all the three cases; with PV penetration alone, with PV and Wind power penetration and with PV, wind power and small hydro penetration.

4. Conclusions

This paper has dealt with the analysis and mitigation of voltage stability on a grid highly penetrated by power from renewable energy sources. Determination of buses that need mitigation of voltage profile effects after integrating power from different renewable energy sources into IEEE 39 bus system network has been done. This has been done by analyzing voltage profiles, Q-V bus sensitivities and reactive power margins from Q-V curves. D-STATCOM was modeled and used to improve the voltage profiles. From the analysis, it was noted that connection of the modeled wind power alone while maintaining the conventional sources helped in stabilizing the system voltages as seen from the increase in reactive power margis from Q-V curves. When some of the conventional sources were replaced by PV systems the stability of the voltages in the grid was affected. It was further noted that connecting more than one energy source to the grid slightly improves the voltage levels and stability. In order to ensure that all the voltage levels meet the required standards, D-STATCOM was used. After connection of the D-STATCOM, the voltage levels for all the buses were improved to the required standards.