Two-Phase Smoothed Particle Hydrodynamics Modelling of Hydrodynamic-Aerodynamic and Wave-Structure Interaction
Abstract
:1. Introduction
2. Brief Outline of the Computational Model
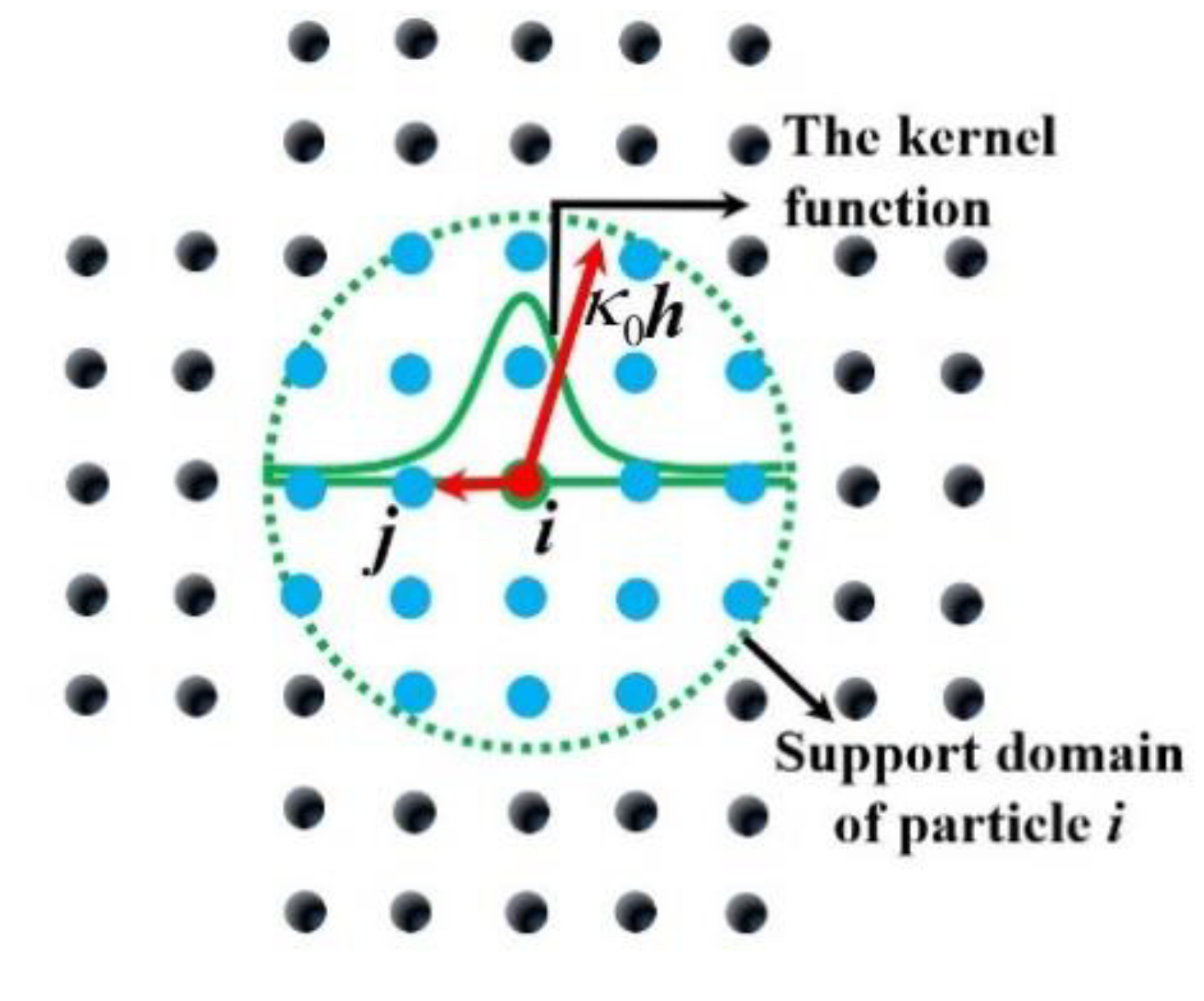
2.1. Smoothed Particle Hydrodynamics
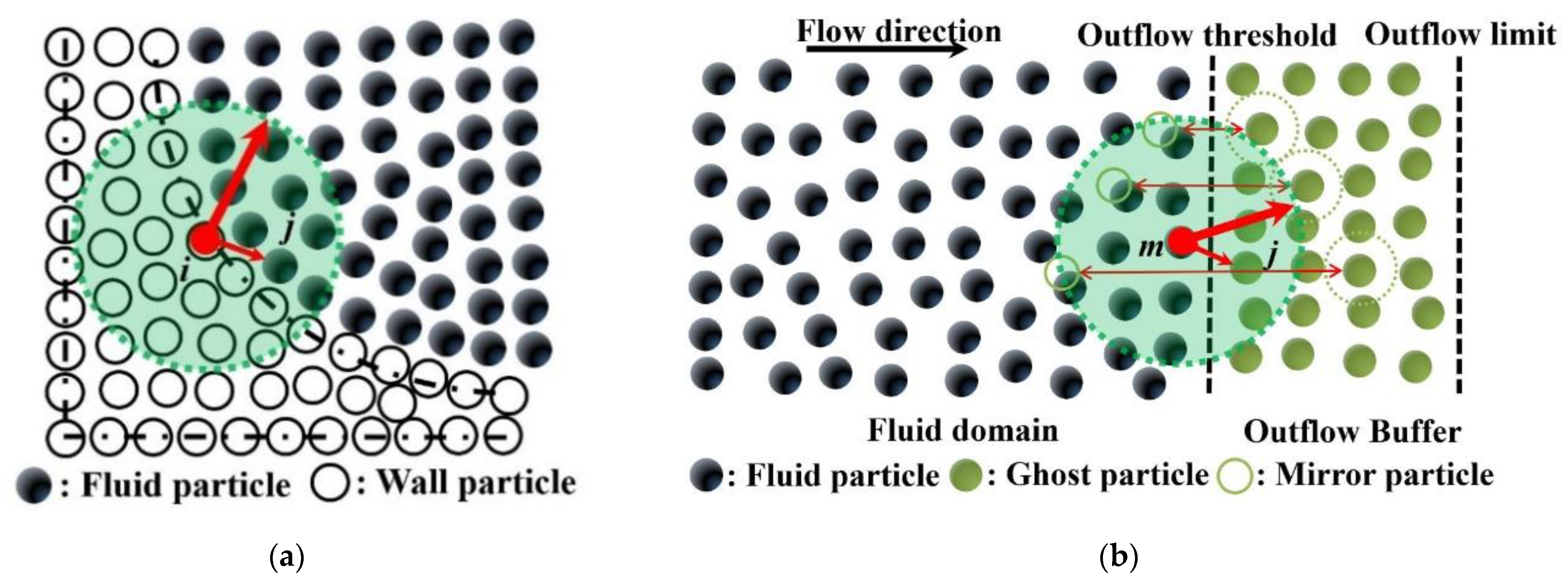
2.2. Boundary Conditions
2.3. Time Integration Schemes
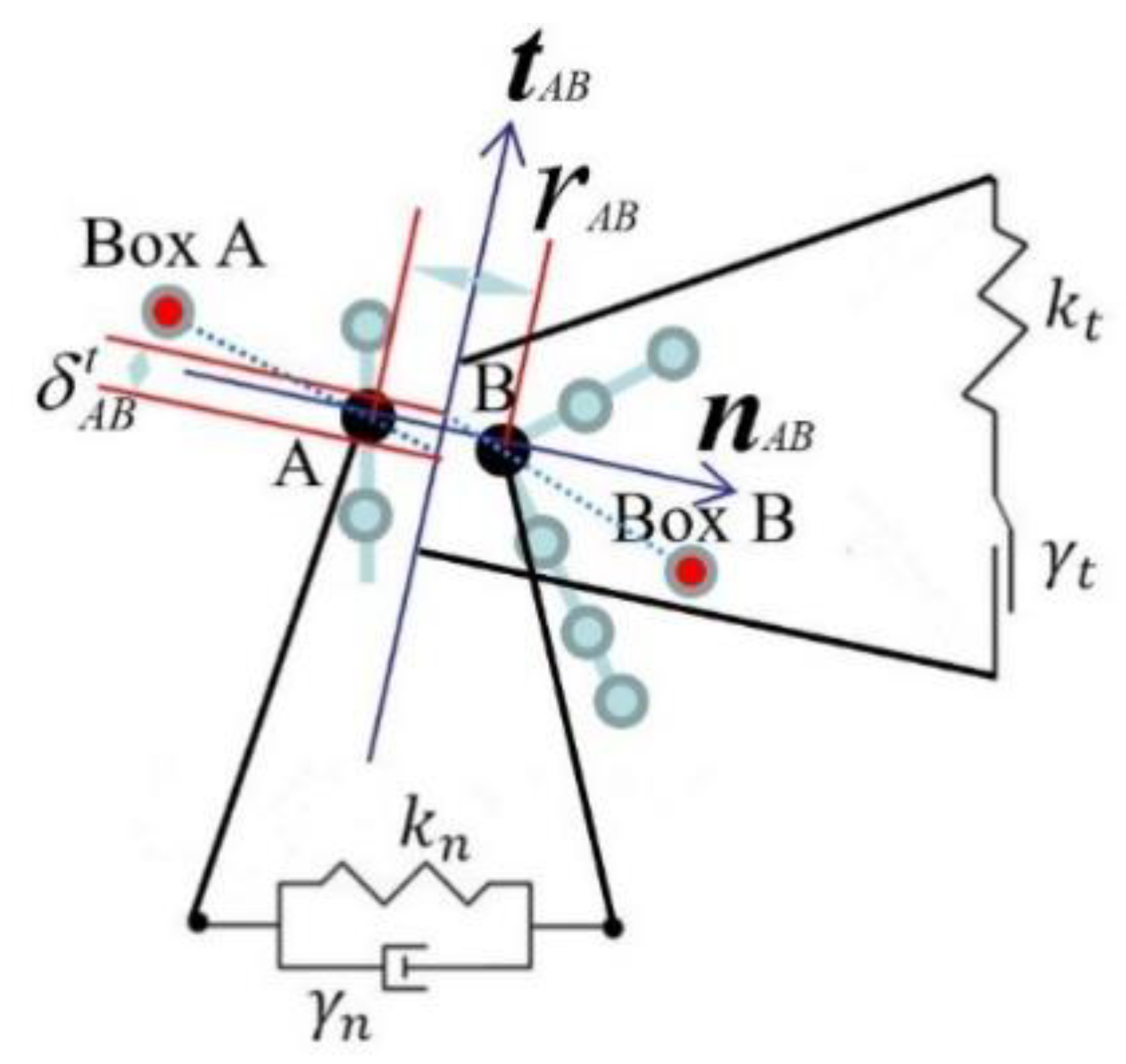
2.4. Collision Force Model
3. Numerical Results and Discussion
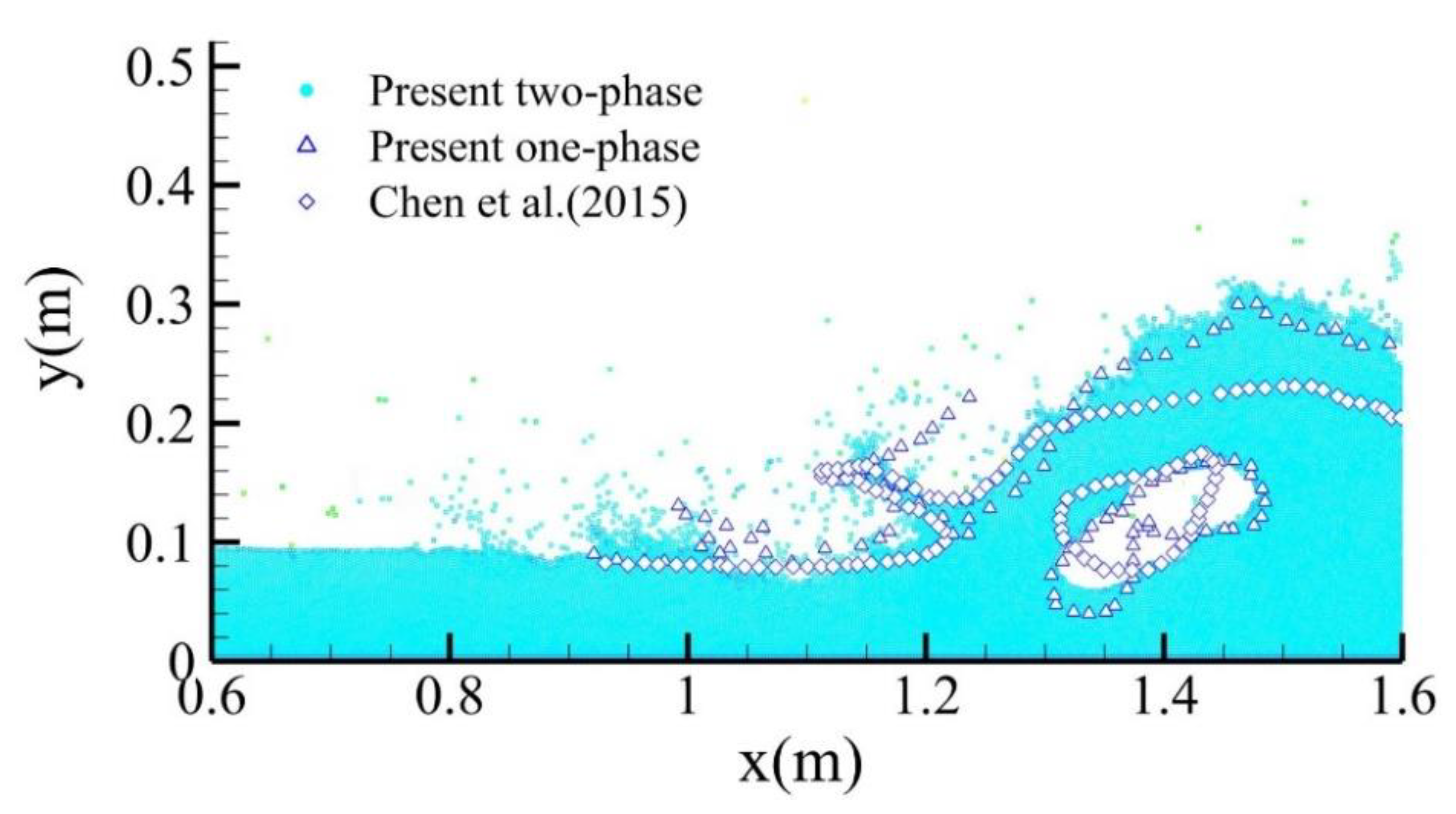
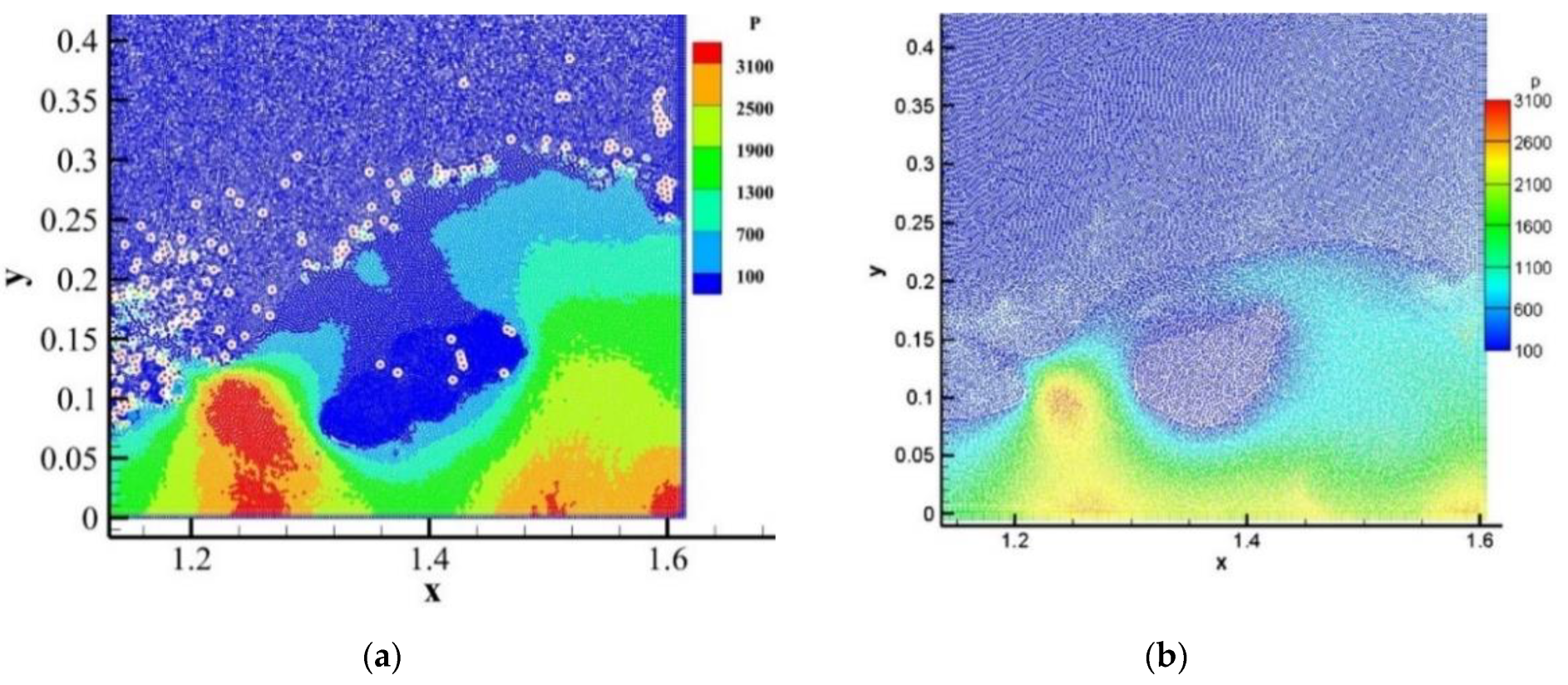
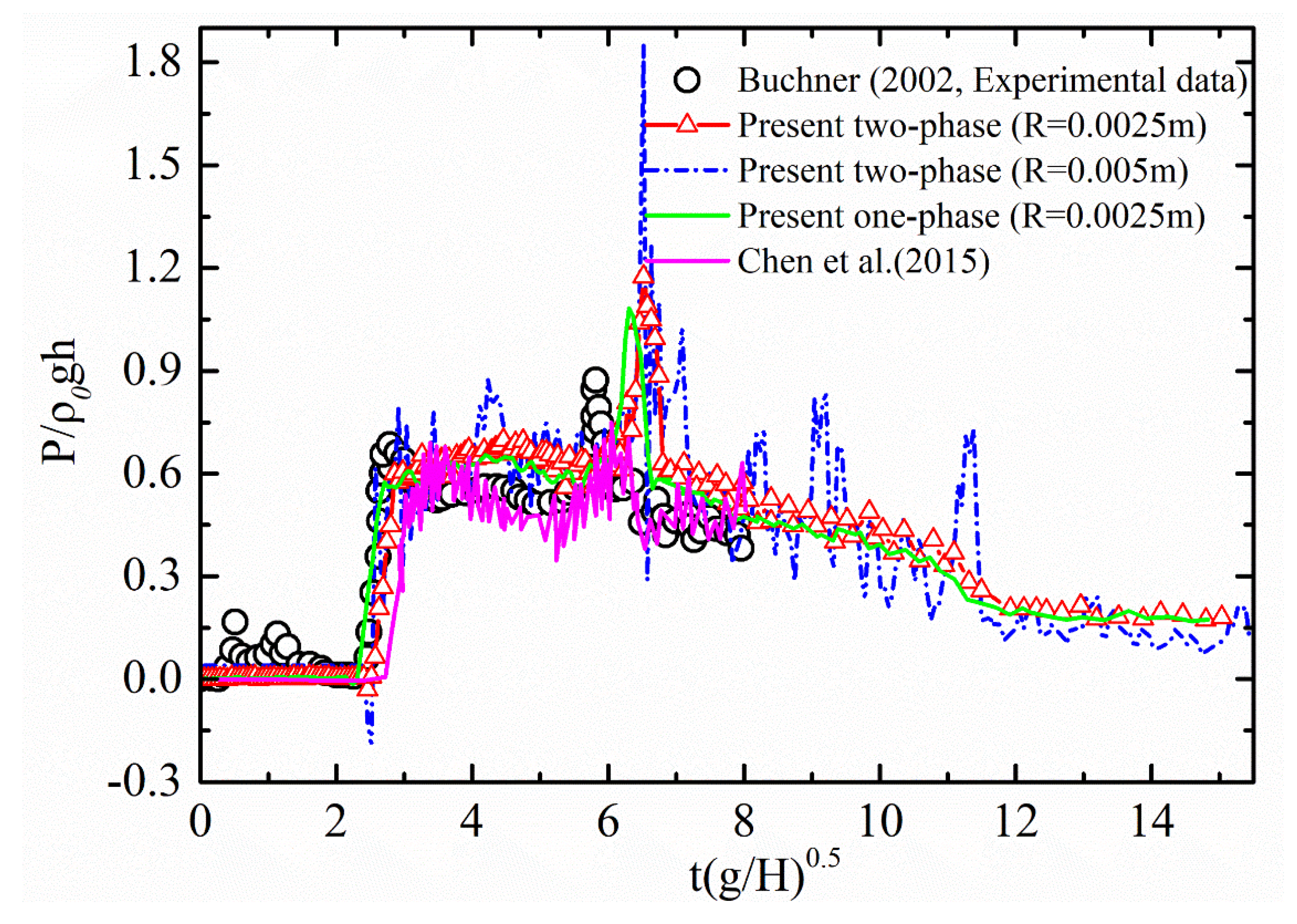
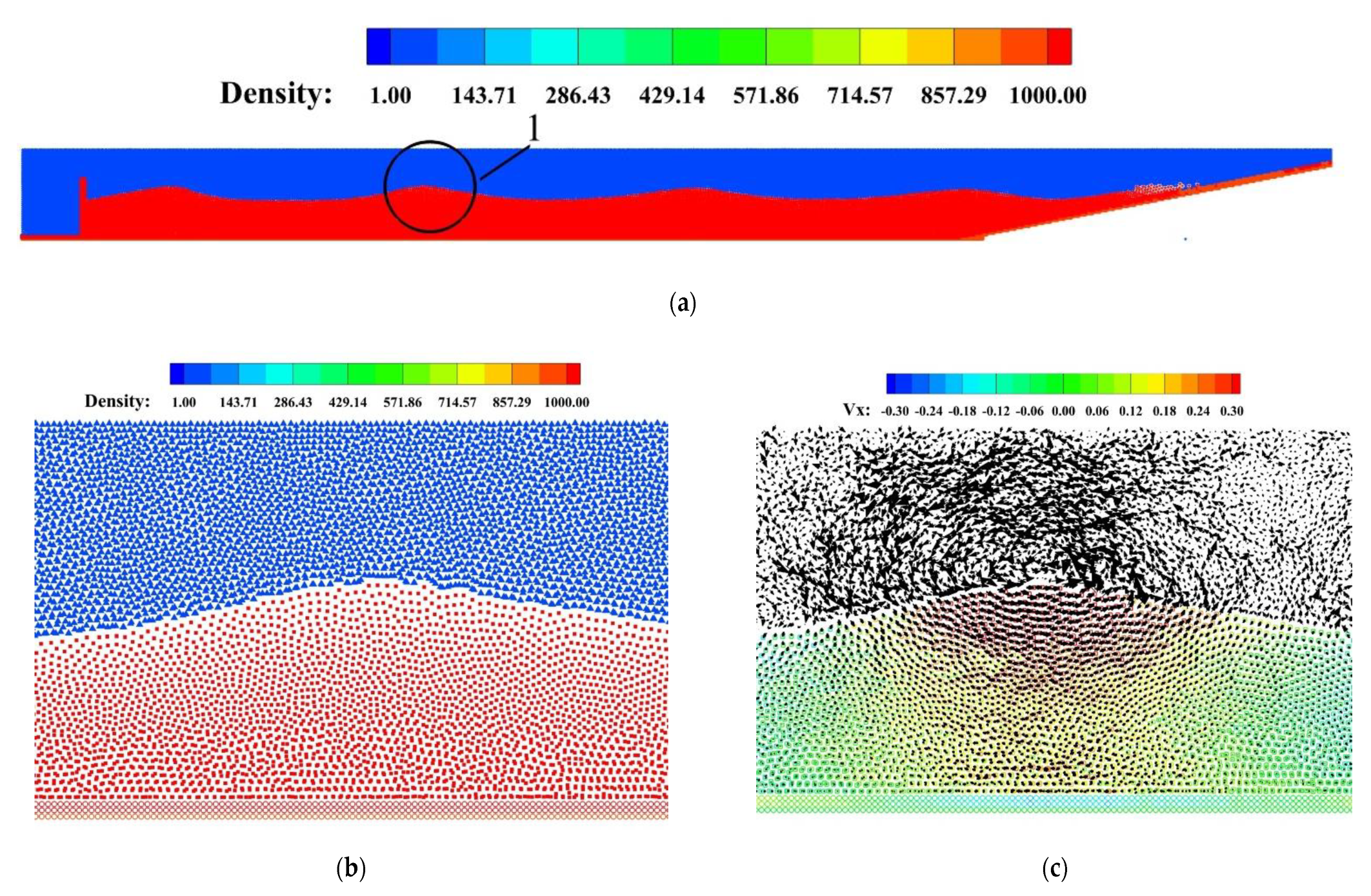
3.1. SPH Simulation of Dam-Breaking
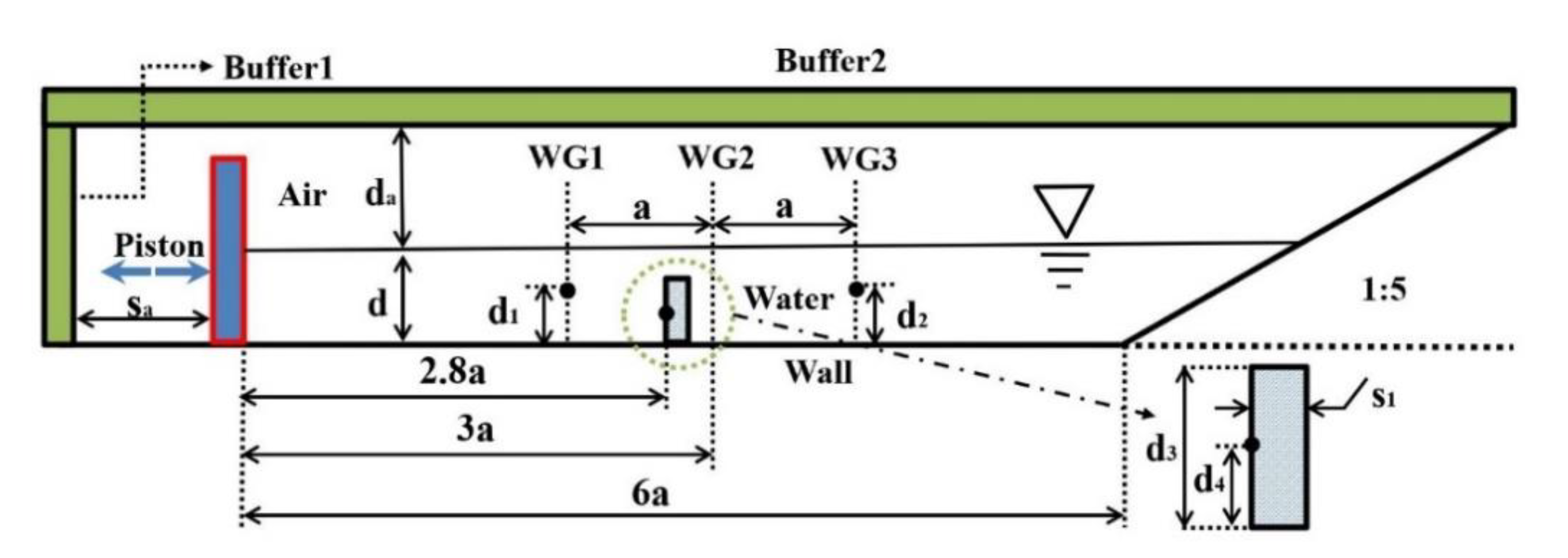
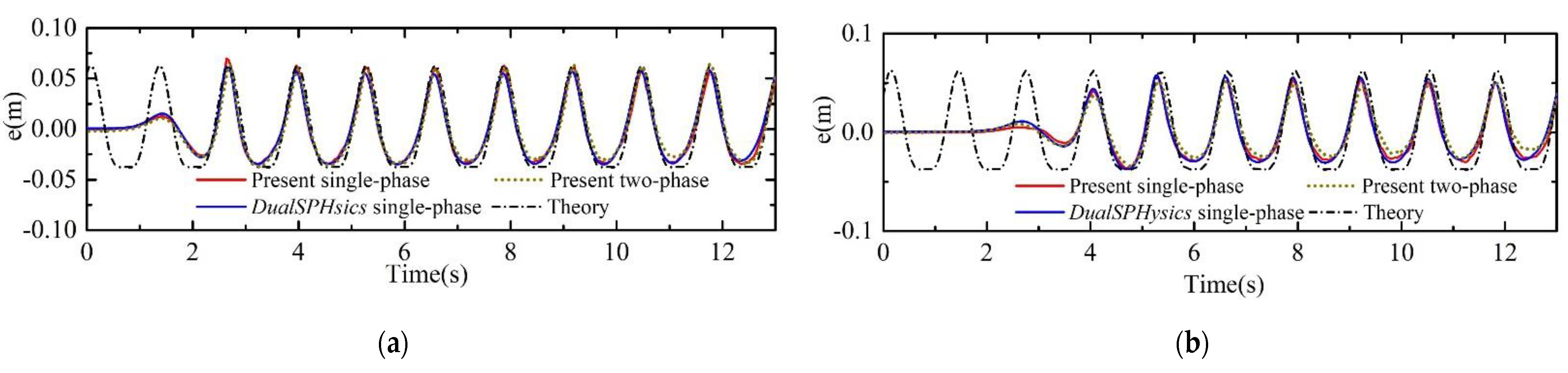
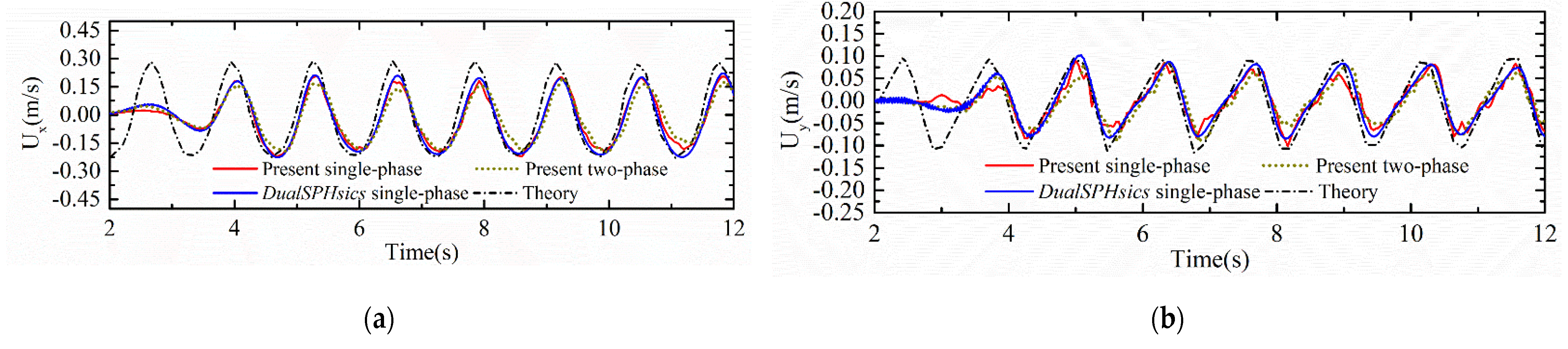
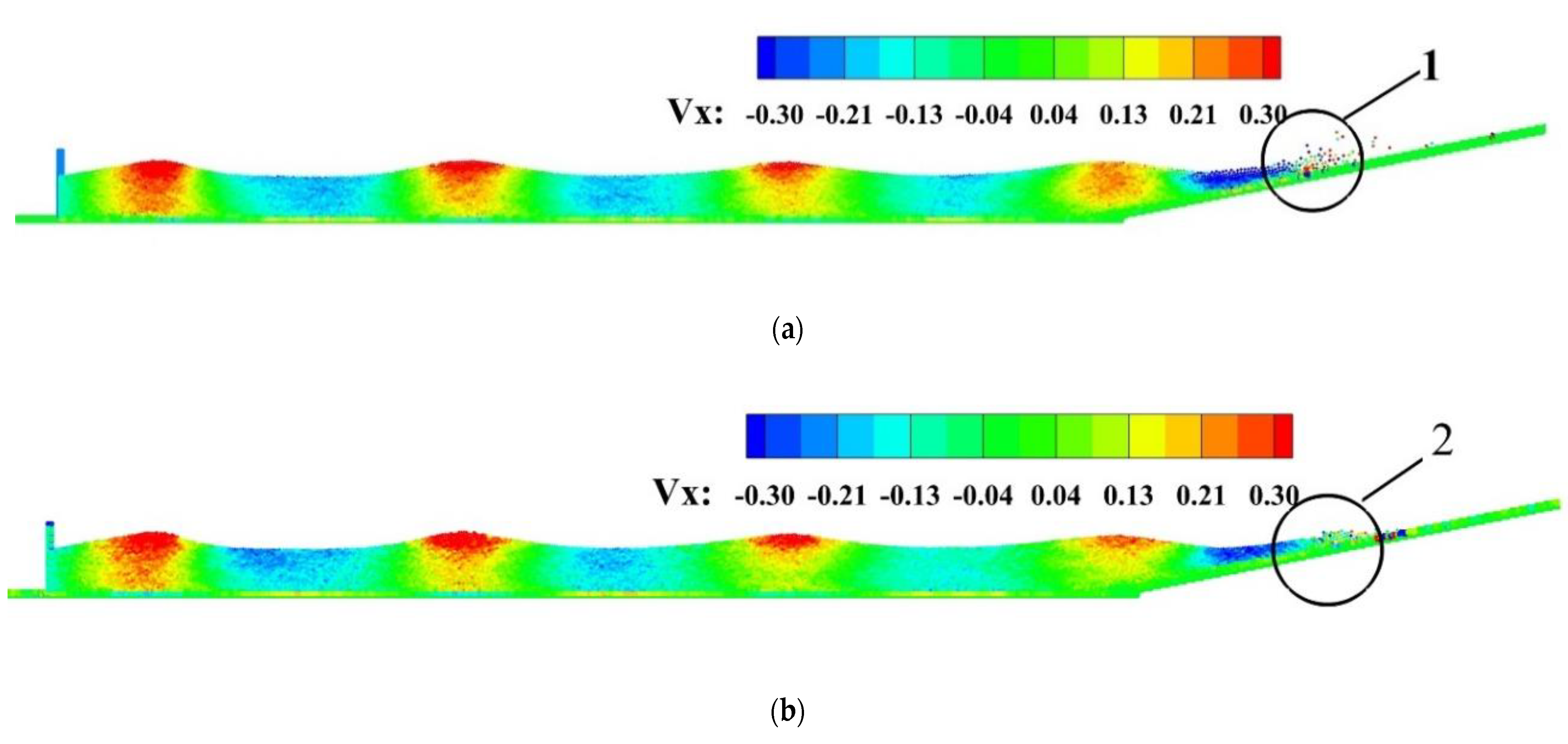
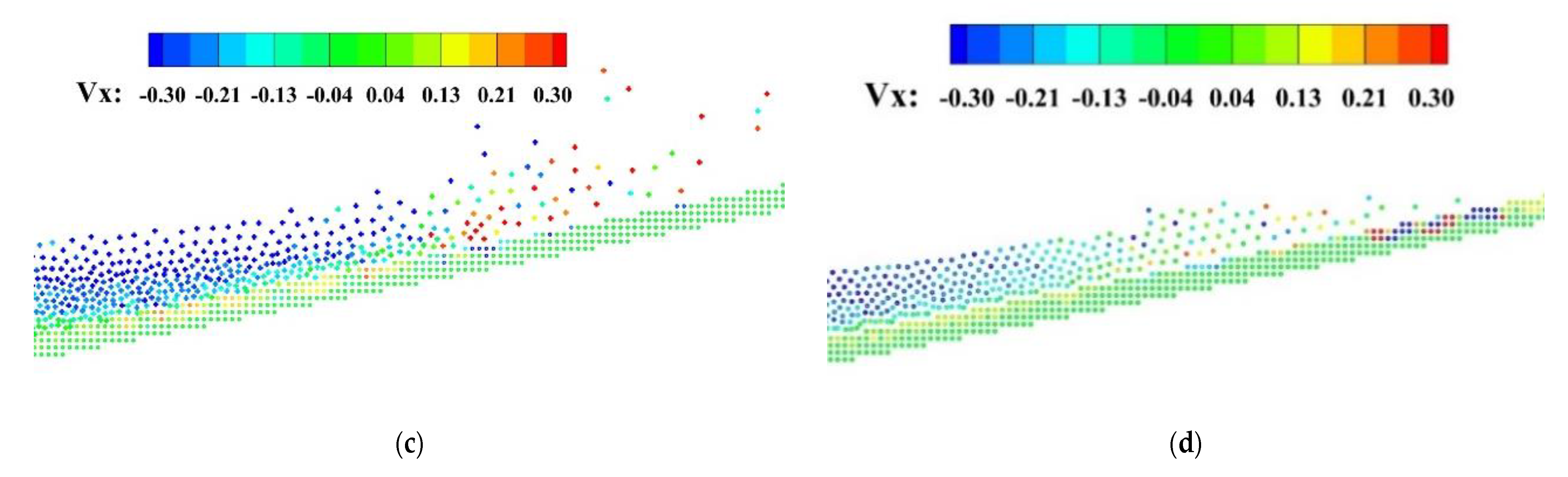
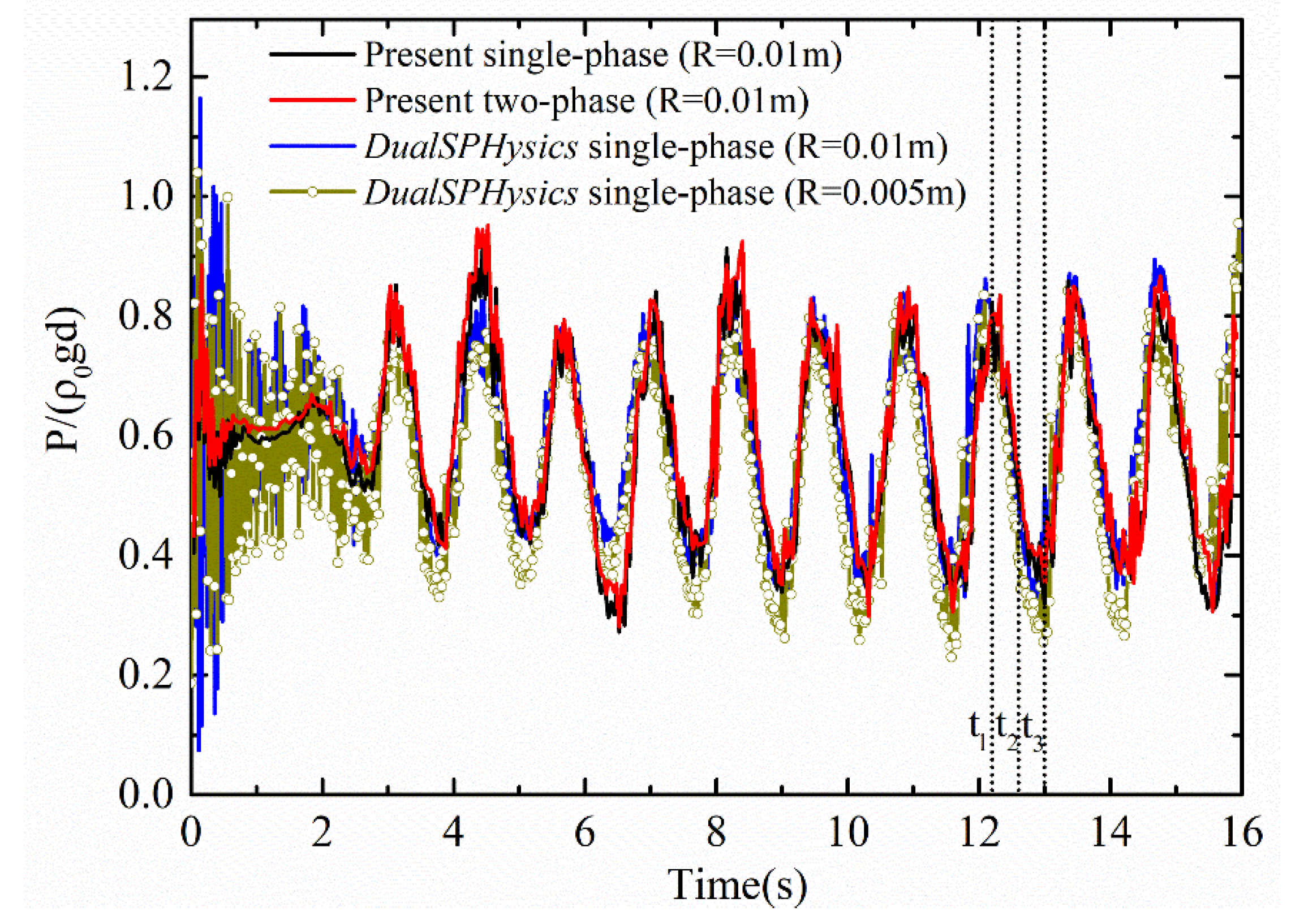
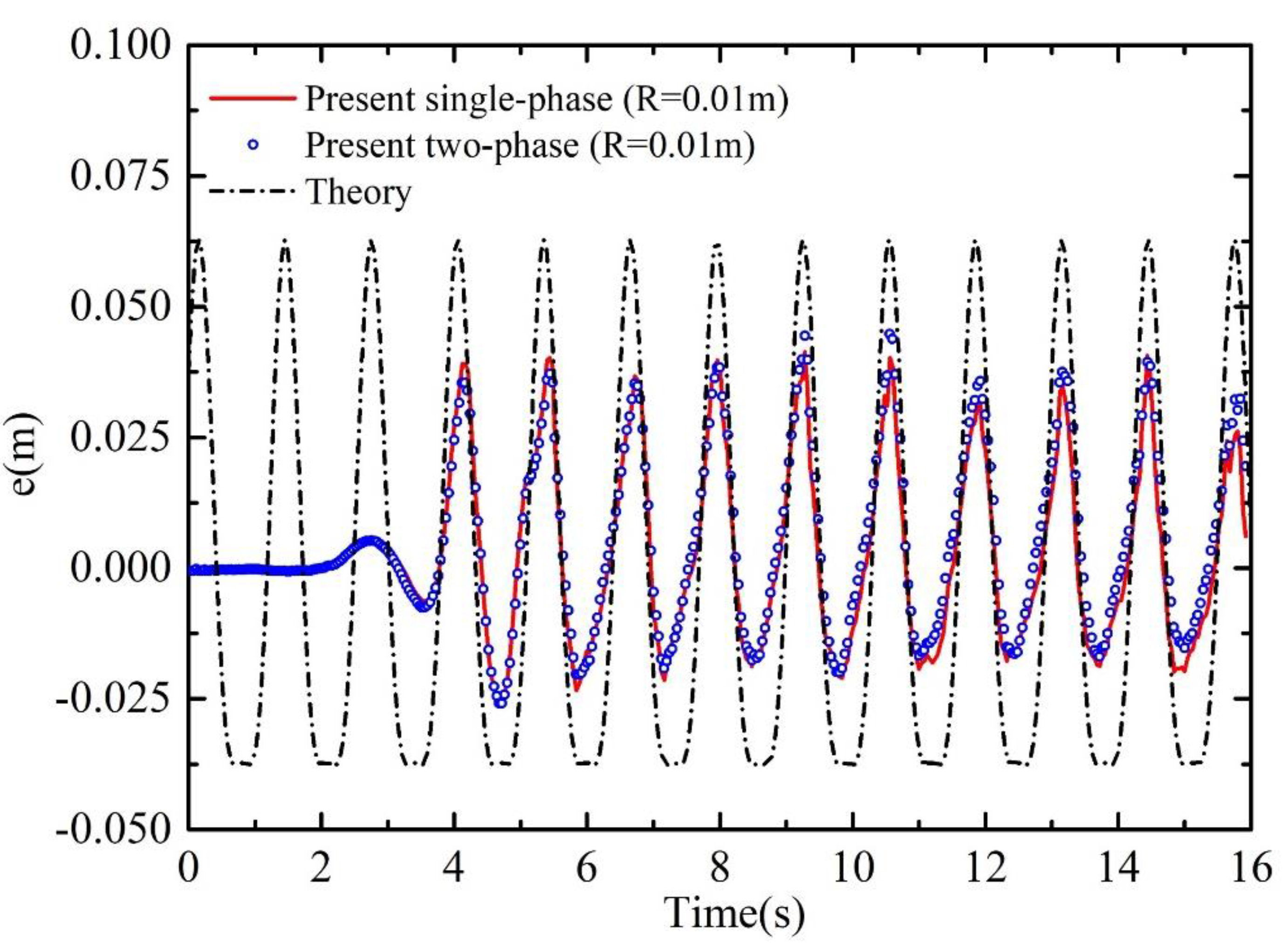
3.2. Two-Phase Wave Generation in a Wave Basin
3.3. Two-Phase SPH Simulation of the Wave-Rigid Beam Interaction
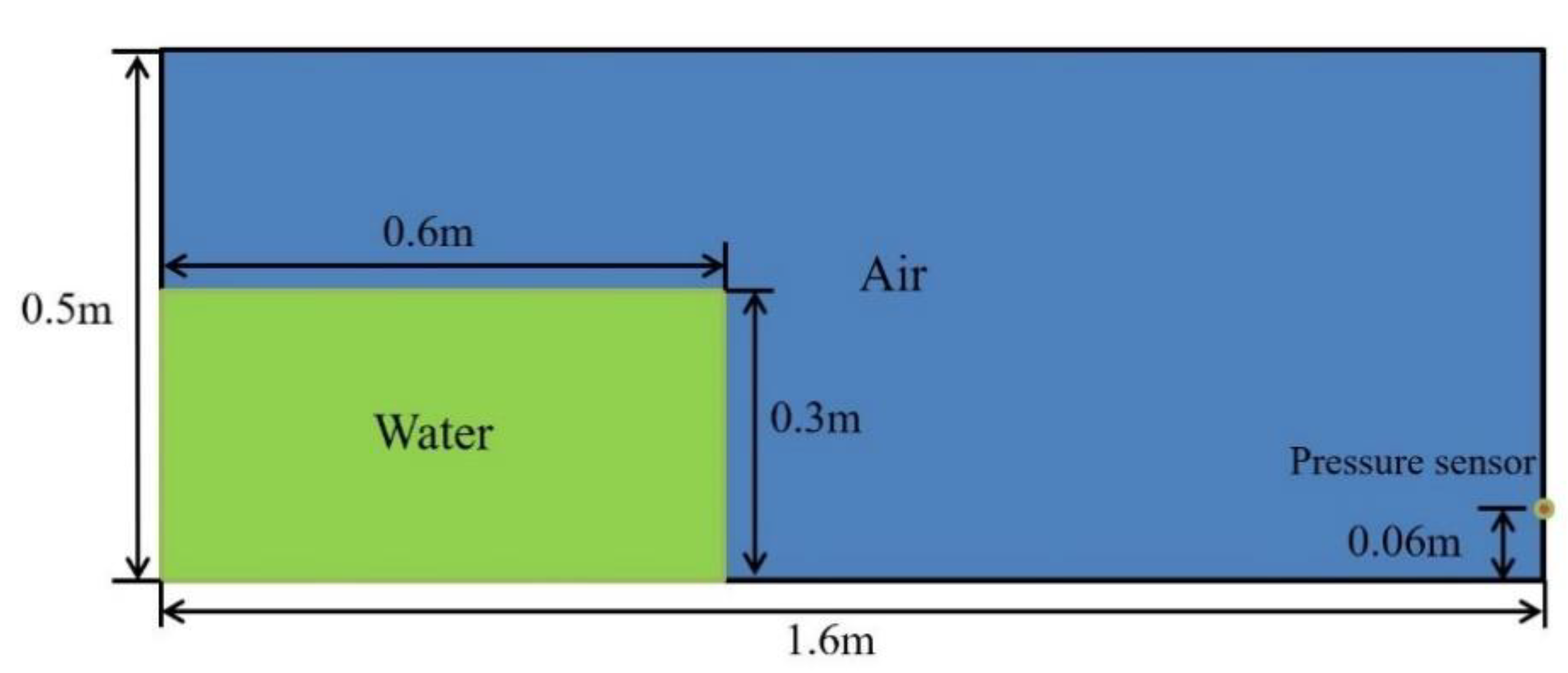
3.4. Two-Phase SPH Simulation of Wave Interaction with a Freely Floating Box in a Wave Basin
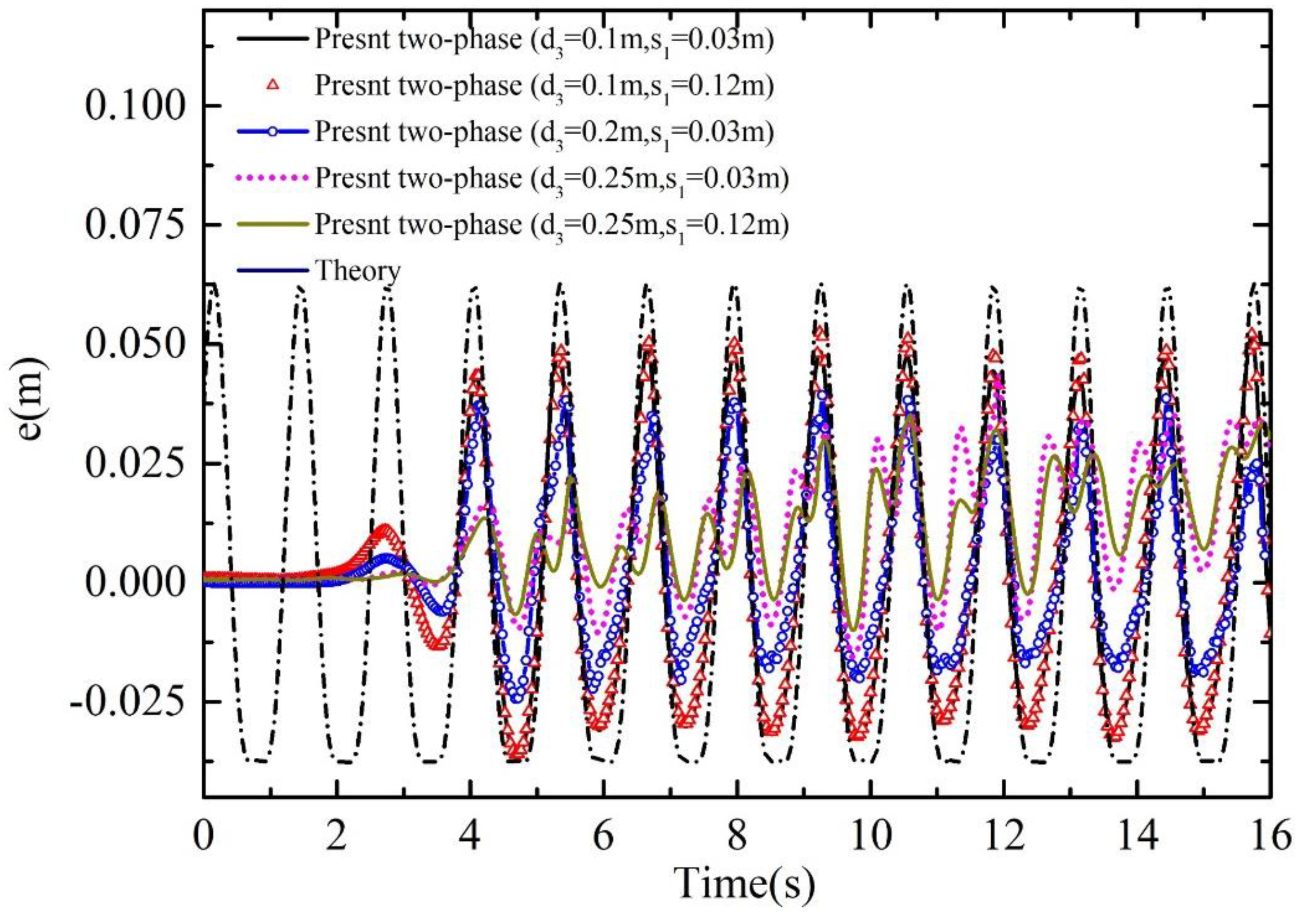
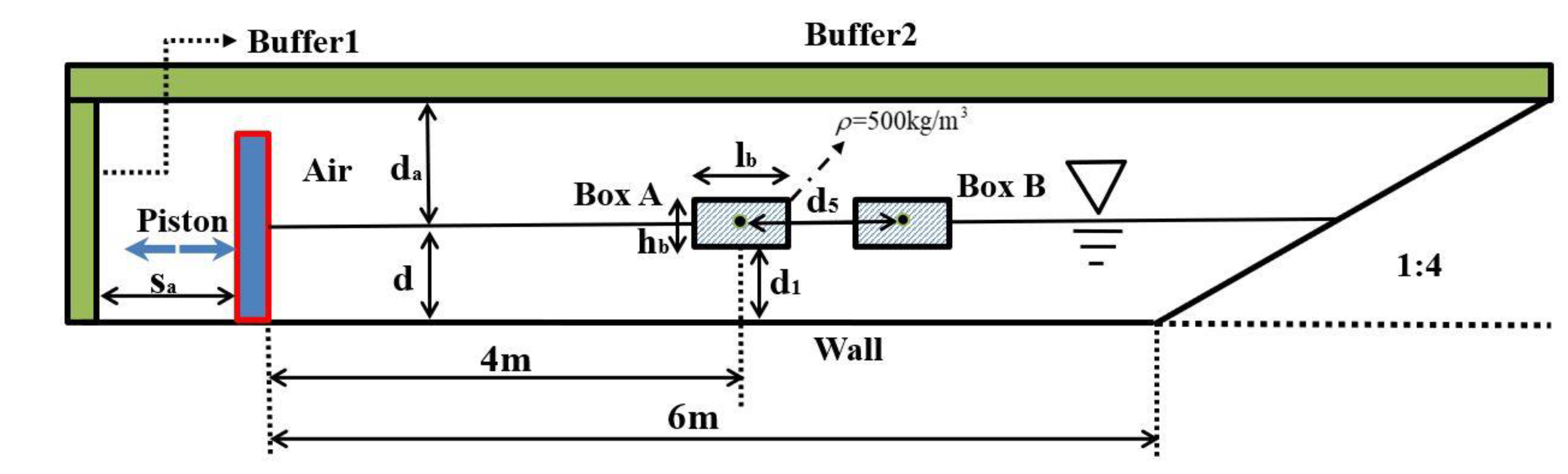
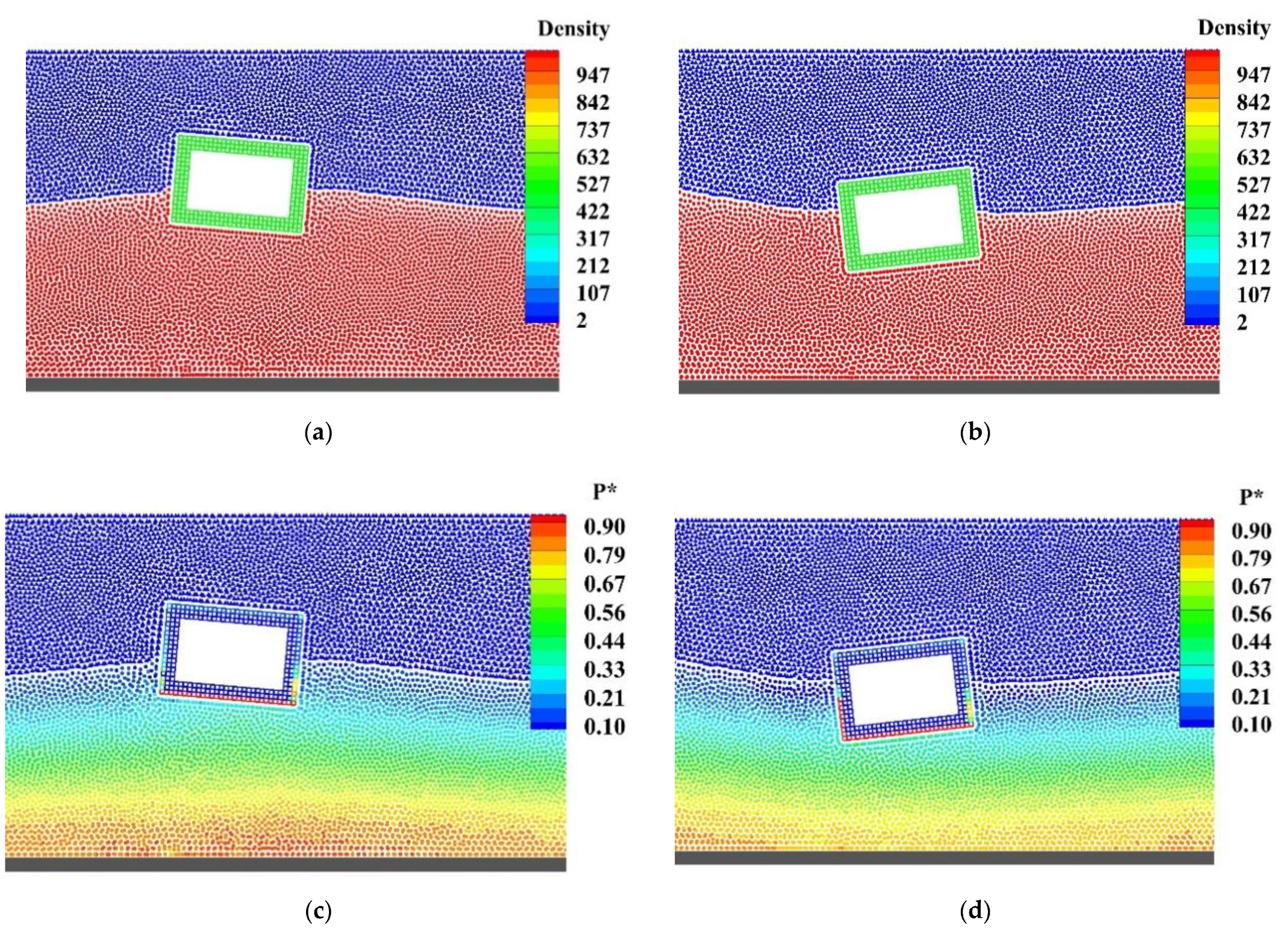
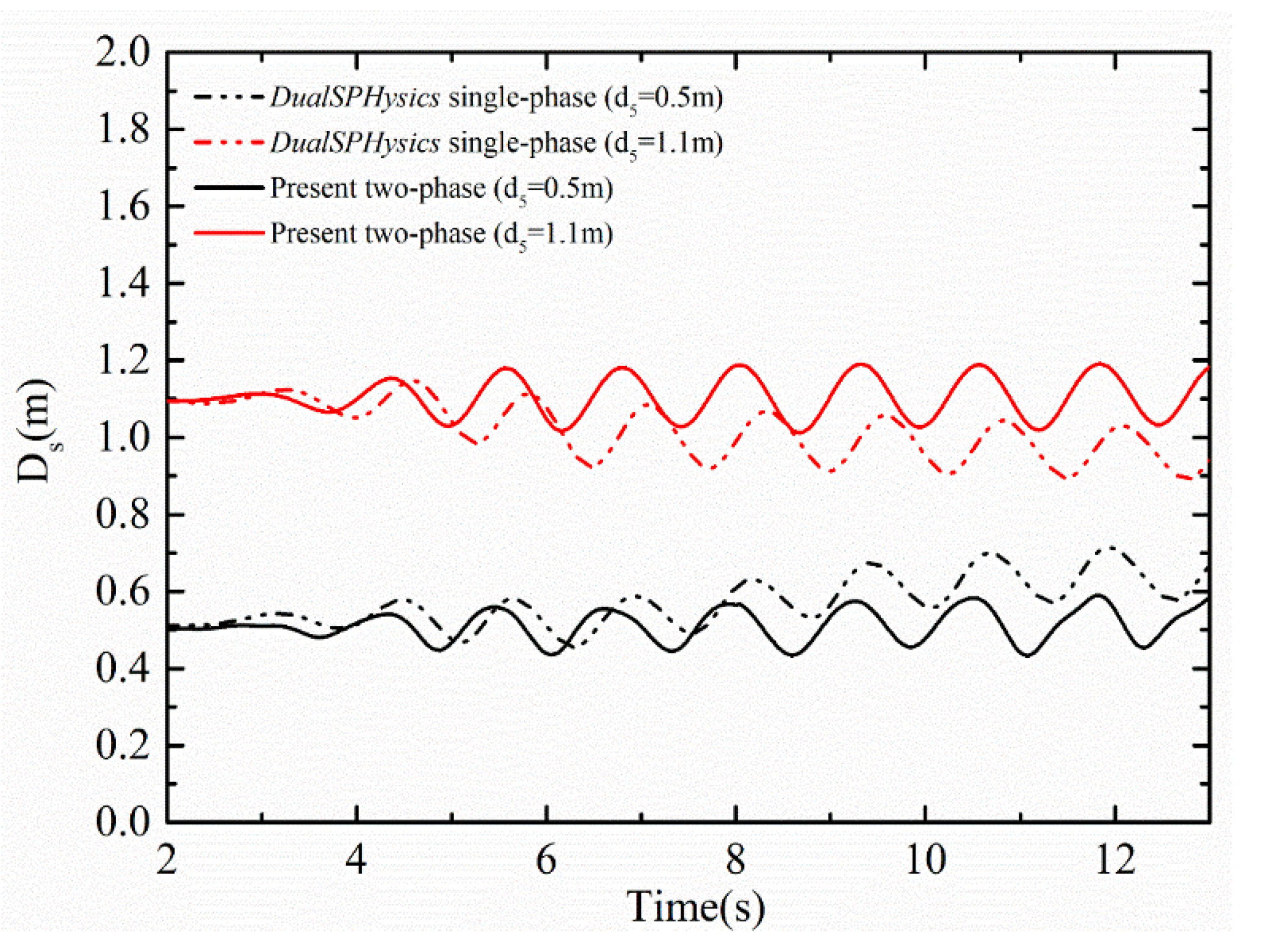
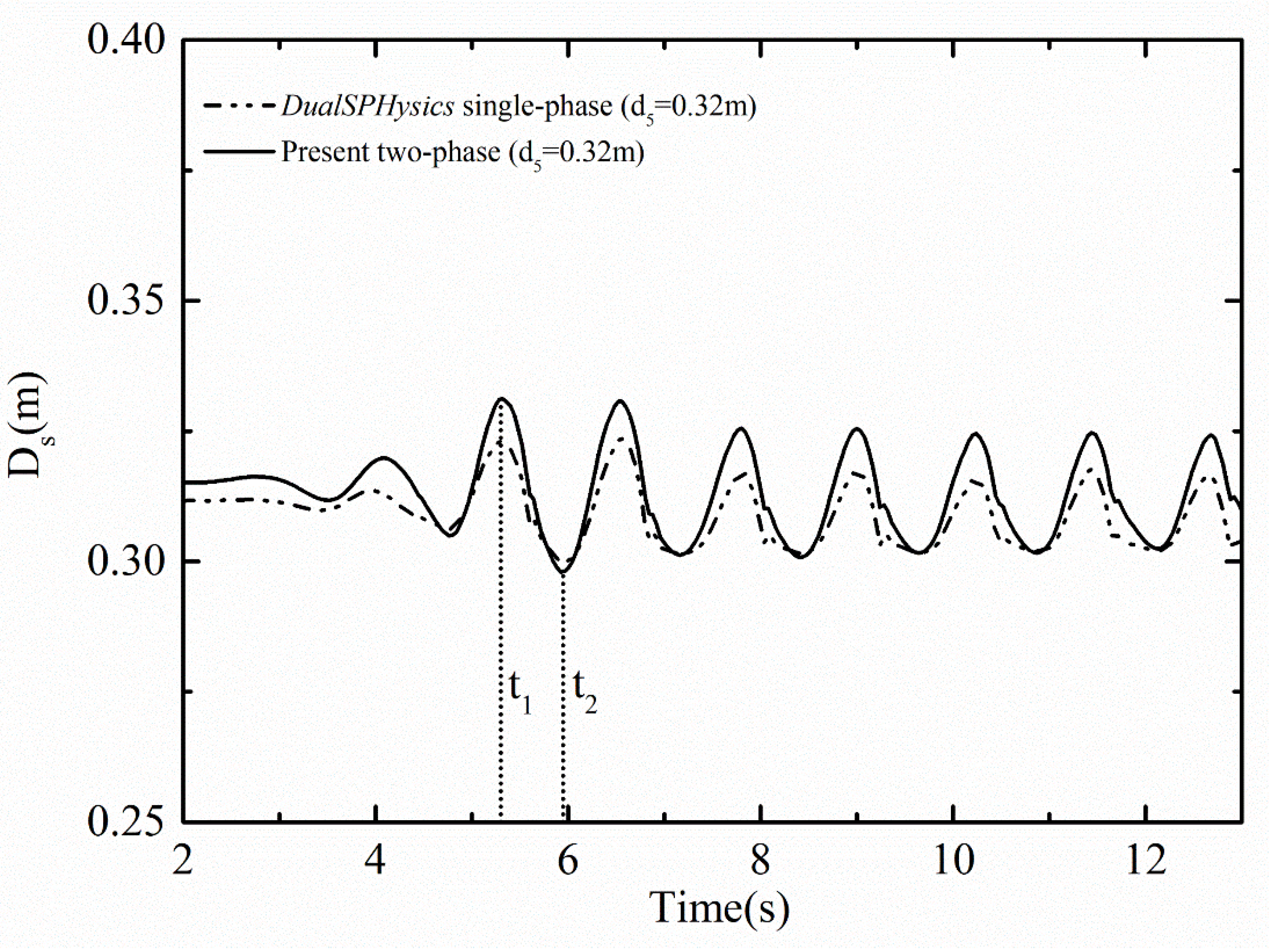
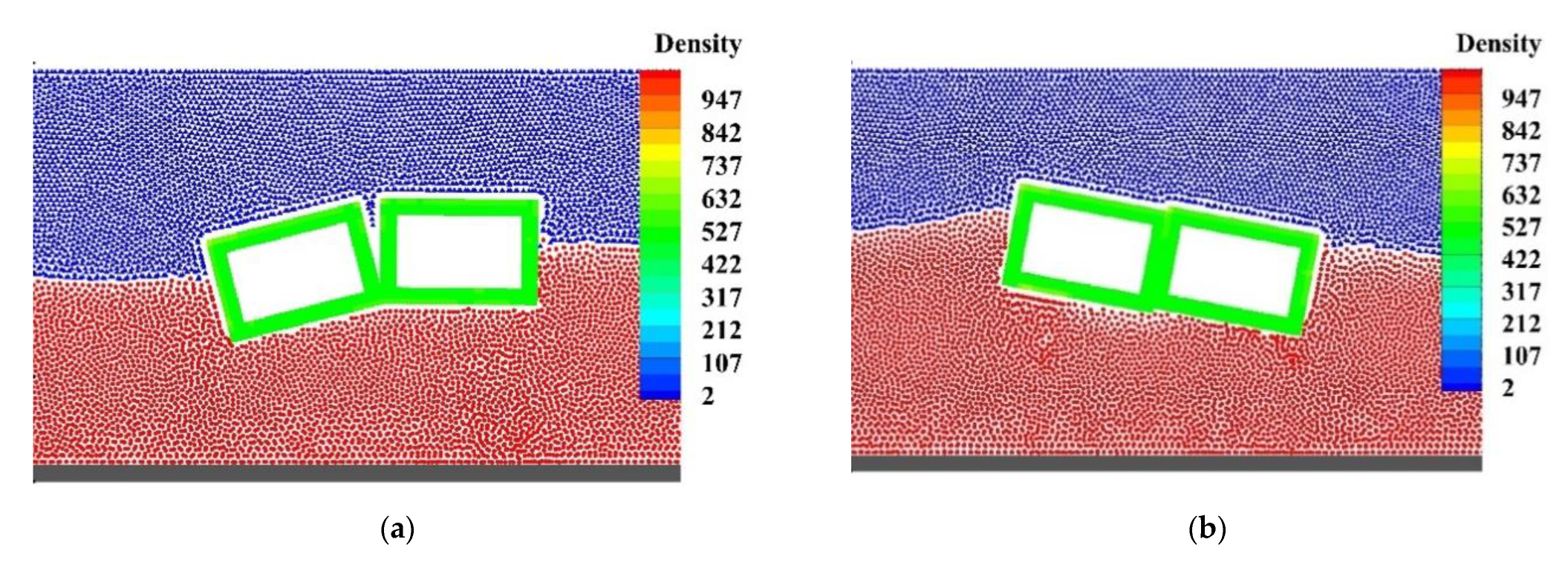
3.5. Wave Interaction with Two Freely Floating Boxes in a Basin
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, Z.; Li, Y.; Liu, Y. Hydraulic performance and wave loadings of perforated/slotted coastal structures: A review. Ocean. Eng. 2011, 38, 1031–1053. [Google Scholar] [CrossRef]
- Lamas-Pardo, M.; Iglesias, G.; Carral, L. A review of very large floating structures (VLFS) for coastal and offshore uses. Ocean. Eng. 2015, 109, 677–690. [Google Scholar] [CrossRef]
- Wang, C.; Tay, Z. Very large floating structures: Applications, research and development. Procedia Eng. 2011, 14, 62–72. [Google Scholar] [CrossRef] [Green Version]
- Chakrabarti, S.K. (Ed.) Numerical Models in Fluid Structure Interaction, Advances in Fluid Mechanics; WIT Press: Southampton, UK, 2005; Volume 42. [Google Scholar]
- Weymouth, G.; Dommermuth, D.G.; Hendrickson, K.; Yue, D.K.P. Advances in Cartesian-grid Methods for Computational Ship Hydrodynamics. In Proceedings of the 26th Symposium on Naval Hydrodynamics, Rome, Italy, 17–22 September 2006. [Google Scholar]
- Chau, F.P.; Taylor, R.E. Second-order wave diffraction by a vertical cylinder. J. Fluid Mech. 1992, 240, 571. [Google Scholar] [CrossRef]
- Stansberg, C.T.; Kristiansen, T. Non-linear scattering of steep surface waves around vertical columns. Appl. Ocean. Res. 2005, 27, 65–80. [Google Scholar] [CrossRef]
- Walker, D.; Eatock Taylor, R.; Taylor, P.; Zang, J. Wave diffraction and near-trapping by a multi-column gravity-based structure. Ocean. Eng. 2008, 35, 201–229. [Google Scholar] [CrossRef]
- Zang, J.; Gibson, R.; Taylor, P.H.; Eatock Taylor, R.; Swan, C. Second order wave diffraction around a fixed ship-shaped body in unidirectional steep waves. J. Offshore Mech. Arct. Eng. 2006, 128, 89–99. [Google Scholar] [CrossRef]
- Hadžić, I.; Hennig, J.; Perić, M.; Xing-Kaeding, Y. Computation of flow-induced motion of floating bodies. Appl. Math. Model. 2005, 29, 1196–1210. [Google Scholar] [CrossRef]
- Hu, C.; Kashiwagi, M. Two-dimensional numerical simulation and experiment on strongly non-linear wave–body interactions. J. Mar. Sci. Technol. 2008, 14, 200–213. [Google Scholar] [CrossRef]
- Chen, L.; Zang, J.; Hillis, A.; Morgan, G.; Plummer, A. Numerical investigation of wave–structure interaction using OpenFOAM. Ocean. Eng. 2014, 88, 91–109. [Google Scholar] [CrossRef] [Green Version]
- Hu, Z.Z.; Greaves, D.; Raby, A. Numerical wave tank study of extreme waves and wave-structure interaction using OpenFoam®. Ocean. Eng. 2016, 126, 329–342. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Ong, M.C.; Tang, T. A numerical toolbox for wave-induced seabed response analysis around marine structures in the OpenFOAM® framework. Ocean. Eng. 2020, 195, 106678. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Ni, X.Y.; Feng, W.B. Numerical simulation of wave overtopping based on DualSPHysics. Appl. Mech. Mater. 2013, 405, 1463–1471. [Google Scholar] [CrossRef]
- Wen, H.; Ren, B.; Dong, P.; Wang, Y. A SPH numerical wave basin for modeling wave-structure interactions. Appl. Ocean. Res. 2016, 59, 366–377. [Google Scholar] [CrossRef] [Green Version]
- Altomare, C.; Domínguez, J.; Crespo, A.; González-Cao, J.; Suzuki, T.; Gómez-Gesteira, M.; Troch, P. Long-crested wave generation and absorption for SPH-based DualSPHysics model. Coast. Eng. 2017, 127, 37–54. [Google Scholar] [CrossRef]
- Meringolo, D.D.; Aristodemo, F.; Veltri, P. SPH numerical modeling of wave–perforated breakwater interaction. Coast. Eng. 2015, 101, 48–68. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, D.; Si, Y.; Shi, Y.; Lin, Y. Coupled finite particle method for simulations of wave and structure interaction. Coast. Eng. 2018, 140, 147–160. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Lattanzio, J.C. A refined particle method for astrophysical problems. Astron. Astrophys. 1985, 149, 135–143. [Google Scholar]
- Antuono, M.; Colagrossi, A.; Marrone, S. Numerical diffusive terms in weakly-compressible SPH schemes. Comput. Phys. Commun. 2012, 183, 2570–2580. [Google Scholar] [CrossRef]
- Hu, X.; Adams, N. An incompressible multi-phase SPH method. J. Comput. Phys. 2007, 227, 264–278. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Morris, J.P.; Fox, P.J.; Zhu, Y. Modeling low Reynolds number incompressible flows using SPH. J. Comput. Phys. 1997, 136, 214–226. [Google Scholar] [CrossRef]
- Aami, S.; Hu, X.; Adams, N. A generalized wall boundary condition for smoothed particle hydrodynamics. J. Comput. Phys. 2012, 231, 7057–7075. [Google Scholar] [CrossRef]
- Tafuni, A.; Domínguez, J.; Vacondio, R.; Crespo, A. A versatile algorithm for the treatment of open boundary conditions in smoothed particle hydrodynamics GPU models. Comput. Methods Appl. Mech. Eng. 2018, 342, 604–624. [Google Scholar] [CrossRef]
- Liu, M.; Liu, G. Restoring particle consistency in smoothed particle hydrodynamics. Appl. Numer. Math. 2006, 56, 19–36. [Google Scholar] [CrossRef]
- Verlet, L. Computer “Experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Newmark, N. A Method of Computation for Structural Dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Canelas, R.B.; Crespo, A.J.; Domínguez, J.M.; Ferreira, R.M.; Gómez-Gesteira, M. SPH–DCDEM model for arbitrary geometries in free surface solid–fluid flows. Comput. Phys. Commun. 2016, 202, 131–140. [Google Scholar] [CrossRef]
- Kuwabara, G.; Kono, K. Restitution coefficient in a collision between two spheres. Jpn. J. Appl. Phys. 1987, 26, 1230–1233. [Google Scholar] [CrossRef]
- Lemieux, M.; Léonard, G.; Doucet, J.; Leclaire, L.; Viens, F.; Chaouki, J.; Bertrand, F. Large-scale numerical investigation of solids mixing in a V-blender using the discrete element method. Powder Technol. 2008, 181, 205–216. [Google Scholar] [CrossRef]
- Vetsch, F.D. Numerical Simulation of Sediment Transport with Meshfree Methods. Doctoral Dissertation, ETH Zurich, Zurich, Switzerland, 2012. [Google Scholar]
- Gong, K.; Shao, S.; Liu, H.; Wang, B.; Tan, S. Two-phase SPH simulation of fluid–structure interactions. J. Fluids Struct. 2016, 65, 155–179. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Zong, Z.; Liu, M.; Zou, L.; Li, H.; Shu, C. An SPH model for multiphase flows with complex interfaces and large density differences. J. Comput. Phys. 2015, 283, 169–188. [Google Scholar] [CrossRef]
- Buchner, B. Green Water on Ship-Type Offshore Structures. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2002. [Google Scholar]
- Biesel, F.; Suquet, F. Etude theorique d’un type d’appareil a la houle. Houille Blanche 1951, 6, 152–165. [Google Scholar]
- Frigaard, P.; Andersen, T. Technical Background Material for the Wave Generation Software AwaSys 5; Aalborg University: Aalborg, Denmark, 2010; Available online: https://core.ac.uk/display/60460686 (accessed on 6 February 2021).
- Madsen, O.S. On the generation of long waves. J. Geophys. Res. 1971, 76, 8672–8683. [Google Scholar] [CrossRef]
- Ren, B.; He, M.; Dong, P.; Wen, H. Non-linear simulations of wave-induced motions of a freely floating body using WCSPH method. Appl. Ocean. Res. 2015, 50, 1–12. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Crespo, A.J.; Hall, M.; Altomare, C.; Wu, M.; Stratigaki, V.; Troch, P.; Cappietti, L.; Gómez-Gesteira, M. SPH simulation of floating structures with moorings. Coast. Eng. 2019, 153, 103560. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouyang, Z.; Khoo, B.C. Two-Phase Smoothed Particle Hydrodynamics Modelling of Hydrodynamic-Aerodynamic and Wave-Structure Interaction. Energies 2022, 15, 3251. https://doi.org/10.3390/en15093251
Ouyang Z, Khoo BC. Two-Phase Smoothed Particle Hydrodynamics Modelling of Hydrodynamic-Aerodynamic and Wave-Structure Interaction. Energies. 2022; 15(9):3251. https://doi.org/10.3390/en15093251
Chicago/Turabian StyleOuyang, Zhenyu, and Boo Cheong Khoo. 2022. "Two-Phase Smoothed Particle Hydrodynamics Modelling of Hydrodynamic-Aerodynamic and Wave-Structure Interaction" Energies 15, no. 9: 3251. https://doi.org/10.3390/en15093251
APA StyleOuyang, Z., & Khoo, B. C. (2022). Two-Phase Smoothed Particle Hydrodynamics Modelling of Hydrodynamic-Aerodynamic and Wave-Structure Interaction. Energies, 15(9), 3251. https://doi.org/10.3390/en15093251





