Investigating the Impact of Triangle and Quadrangle Mesh Representations on AGV Path Planning for Various Indoor Environments: With or Without Inflation

Abstract

In a factory with different kinds of spatial atmosphere (warehouses, corridors, small or large workshops with varying sizes of obstacles and distribution patterns), the robot’s generated paths for navigation tasks mainly depend on the representation of that environment. Hence, finding the best representation for each particular environment is necessary to forge a compromise between length, safety, and complexity of path planning. This paper aims to scrutinize the impact of environment model representation on the performance of an automated guided vehicle (AGV). To do so, a multi-objective cost function, considering the length of the path, its complexity, and minimum distance to obstacles, is defined for a perfect circular robot. Unlike other similar studies, three types of representation, namely quadrangle, irregular triangle, and varying-size irregular triangle, are then utilized to model the environment while applying an inflation layer to the discretized view. Finally, a navigation scenario is tested for different cell decomposition methods and an inflation layer size. The obtained results indicate that a nearly constant coarse size triangular mesh is a good candidate for a fixed-size robot in a non-changing environment. Moreover, the varying size of the triangular mesh and grid cell representations are better choices for factories with changing plans and multi-robot sizes due to the effect of the inflation layer. Based on the definition of a metric, which is a criterion for quantifying the performance of path planning on a representation type, constant or variable size triangle shapes are the only and best candidate for discretization in about 59% of industrial environments. In other cases, both cell types, the square and the triangle, can together be the best representation.

1. Introduction

Automated guided vehicles (AGVs) have been used for several decades [1,2]. They mostly rely on predefined routes to move from one point to another. However, the flexibility and agility introduced by industry 4.0 [3] are pushing these technologies towards a complete autonomous navigation capability [4]. The required autonomy forces the AGVs to know the environment prior to moving intelligently and safely. Therefore, one of the most important tasks for these vehicles is to model the navigation environment as accurately as possible [5]. In indoor navigation on a planar floor of a factory, a 2D model of the environment, including the specifications of the obstacle-free area, is required to perform path planning. Abstracting, encoding, and saving this type of information is called ‘mapping’ in mobile robots [6]. A mobile robot uses this map repeatedly to find a path between the current position and the goal position. The essential information for constructing the environment model is usually obtained from raw sensor data with the help of data structures. There are different types of data structures for saving and reading necessary spatial information in navigation. After saving the information, path planning uses this information via queries (by means of the data structure) to perform a task. Therefore, the data structure types, spatial models, and the resulting map all play decisive roles in the performance of the global planners.

One of the most well-known mapping methods, which has gained special attention due to its simplicity and robustness, is the occupancy grid technique [7]. This method is composed mainly of uniform grids with simple square shapes, which are made cell by cell, independently. Other shapes such as triangles (with application in polygonal mesh [8], reconstruction [9], etc.) can be used for the discretization of the environment. Squares and triangles are the most famous cell types in a planar application. The analogy between the occupancy grid map and a triangular mesh is the creation of a discretized environment model using the cell concept. Their difference, though, lies on the shape and number of cells, as well as their connection rules (topology) in forming a complete and accurate free space model. By utilizing such a model, a global path planner, e.g., cell decomposition method [10], can be used to find an efficient path between two points.

The efficiency of the path planning algorithm is highly dependent on the environment model, which in turn is impacted by the representation type (cell’s shape, number, and topology). For instance, according to the number of cells, it may take a shorter or a longer time to find a path. Moreover, the realized path may have different lengths and distances to the obstacles considering the cell shape and size in the environment. An efficient path should consider all of these essential parameters (such as length, distance, and computational time) [11]. Another aspect worth noting is that, when the conditions of an environment change (new distribution of obstacles), a new representation (discretized model) may lead to a more efficient path. However, investigating the influence of environment model representation on generating a suitable path has escaped the attention of many researchers. Works such as [12,13] have tried to define the environment’s difficulty based on parameters such as obstacle shape and distribution or distance to the nearest obstacles. Nevertheless, they did not consider the effect of a navigation scenario (position of start and goal points) and map representation, and they did not propose any solution to consider this difficulty. Recently, valuable work such as that of [14] tried to relate this difficulty to the robot’s traversal time in navigation benchmarking. However, this work focused on the overall performance of the navigation platform and does not consider the global planner effect. In a similar task, [14] only considers the effect of cell shape and size on computational efficiency and does not consider their effect on the path length and safety. In addition, ref. [13] defines some metrics and compares different path planning methods only on grid-type cells. Other works such as [15], which uses an adaptive mesh for risk-aware path planning, do not mention important parameters such as distance to the nearest obstacle and the effect of robot size. When the environment is cluttered, to our knowledge, there is no straightforward method to select the most appropriate navigation environment approach. For consideration of robot size in path planning, there are various methods. The first strategy applies offset to the boundary of the obstacles, then uses this scaled view as an input for discretization [16]. This strategy is unsuitable when it is necessary to modify the map according to changes in the environment or when the real model of the obstacles is necessary for manipulation. The second strategy is used in the game industry (famous as navigation mesh [17]) and checks each triangle for the input and output edge’s length as a possibility of robot passage [18,19]. The third strategy is map generation based on the actual boundary, then applying the inflation layer on the discretized view (the offset or inflation layer is the robot’s radius plus any optional value for safety, such as the method implemented in the ROS (Robot operating System) [20]). In addition, it is usual to build an inflated map on top of the metric map in robotic applications [21]. Nevertheless, no specific study has been carried out to select the best environment representation based on the effect of this inflation. Therefore, the main contributions of this paper are:

• Showing that the type of environment representation has a direct impact on path planning, and quantifying this by a metric.
• Presenting the results showing the pros and cons of each representation when considering the inflation layer

By considering the points discussed, this paper explores the effect of the environment representation on the performance of an AGV. In this regard, a multi-objective cost function is developed, and three kinds of cell decomposition (quadrangle, irregular triangle, and varying-size irregular triangle) are used for environment modeling. Furthermore, the robot size is considered through an inflation layer imposed on the model. To the best of the authors’ knowledge, this is one of the first attempts to explore the impact of different cell decomposition techniques and robot size on the performance of an AGV. A specific platform is used to generate the three representations with different applicable sizes [22]. Then, a performance comparison is performed for each representation using a fixed scenario obtained by a global planner [13,14].

The rest of the paper is organized as follows. Section 2 depicts the problem formulation and assumptions. Section 3 introduces some common concepts concerning cells and neighbors regarding all the representations. In Section 4, the methodology for all representations is explained by a mathematical formulation. Section 5 discusses all the results, corresponding to the simulation tests on various environments and representations. Section 6 summarizes the outcomes and puts forward future directions.

2. Problem Formulation and Assumption

An AGV (Automated guided vehicle), denoted by A, navigates in a factory as workspace W_s. The workspace contains obstacles, B_i, with $\mathrm{i}\in \left\{1,2,3,\dots ,{\mathrm{N}}_{\mathrm{o}}\right\}$ and ${\mathrm{N}}_{\mathrm{o}}$, the number of obstacles. The obstacle boundaries (Γ(B_i)) are generated by a LIDAR (Light Detection and Ranging) placed on the AGV [23]. These can be polygonal or curvilinear curves. The W_s is divided into W_B, the union of all obstacles, and W_free, the free space. S and G are the start point and the goal point of A, respectively, in the W_free. According to the distribution of B_is and the size of A, various paths ($\mathsf{\tau }$) can be traversed to get to G from S. From an economic point of view, $\mathsf{\tau }$ must be realized quickly, be as short as possible, and keep a safe distance to B_is. If $\mathsf{\tau }$ does not satisfy one of these properties, AGV cannot be used reliably for a long time. In this regard, an optimal path (${\mathsf{\tau }}_{\mathrm{opt}}$) is the one that has the best of the properties mentioned. It is typically determined by a global planner with the help of encoding W_free to an environment map (${\mathrm{M}}_{\mathrm{reps}}$). The subscript “$\mathrm{reps}$” denotes the encoding types or representations, which have a significant impact on finding ${\mathsf{\tau }}_{\mathrm{opt}}$.

This study assumes a perfect circular robot without any sensor noise and environment modeling uncertainty, in order to be able to map spatial information into various representation formats. The index for comparing different representations is a multi-objective cost function ($\mathrm{f}$) which takes the length of ${\mathsf{\tau }}_{\mathrm{opt}}$, the complexity of finding the ${\mathsf{\tau }}_{\mathrm{opt}}$ (correlated with running time), and minimum distance to obstacles into account [24]. Furthermore, no post-processing on the generated path, such as path smoothing [25], has been performed, since this work studies the behavior of various representations on a global planner (as in the deliberative approach concept, in which information is complete before starting the navigation) [26]). The next section discusses common concepts regarding the environment representation types used in mapping and navigation.

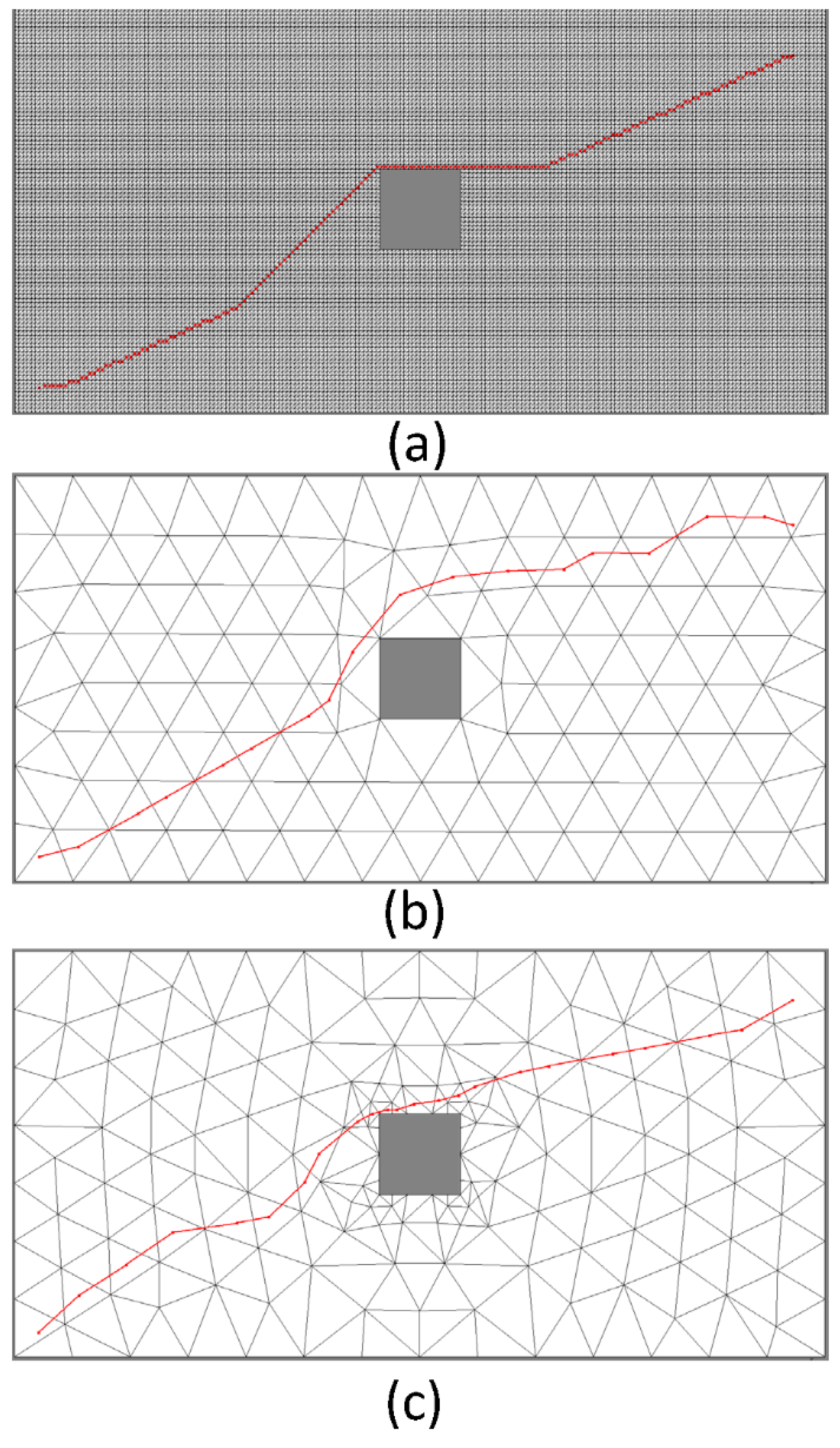
3. Environment Modelling for Navigation

The simplest required information to perform navigation in an environment is the W_free. In this regard, one of the best-known methods is cell decomposition, in which W_free is converted into digitized cells or a graph of cells. Various shapes can be used for the discretization of the environment. In the planar application, squares and triangles are the most famous cell types. Another practical cell type is the irregular triangular mesh (ITM), used extensively in computer graphics and gaming [17,18] as well as outdoor robotics applications [27]. Using these cells for navigation needs the definition of the neighbor types as either common-edge and common-node neighbors. In a quadrangle (QUAD) cell in a general condition (far from the obstacle), the number of common-edge neighbors and common-node neighbors is four and four. However, in an ITM, these numbers are generally three for common-edge neighbors or a variable number, depending on the degree of nodes.

As is clear, a QUAD cell with the edges parallel to the global frame of an environment cannot be flexible enough to show the boundary of obstacles in the environment except for shapes parallel with the global frame. This limitation causes some inaccuracy in the definition of the area around obstacles and presents limitations to accessing this area. Solving this problem requires a fine square, which, on the other hand, increases the computational burden. An ITM cell, with the flexibility of an edge’s direction, can accurately show the boundaries of obstacles. Nevertheless, their irregular shape requires the saving of topological and geometrical information, which makes the map larger. Therefore, each cell shape has its own pros and cons. These features can affect the performance of the algorithm that uses the encoded information of these cells.

The cell decomposition method takes a point as the representative of a cell in a navigation task in order to model the W_free. The cell’s center can be a simple selection for square cells, in order to calculate properties such as the nearest distance to an obstacle, or as a reference for the position of cells and for moving between cells. After obtaining a representative for each cell, a path can be defined as the lines connecting the start and goal points through the center of cells, if they exist. For a fair comparison between QUAD and ITM, the center of the triangle is selected as the representative of each cell in this study (other methods like that of [28] consider the middle of the edges, with lower computational time but with a longer path). Optimal searching in this graph is performed according to criteria such as the cost and the heuristic of each cell with respect to start and goal points. Since the building block of this graph is a cell, the selection of its size is an effective parameter for the construction and searching of the graph. Small cells give more information than large cells after digitizing, but increase the computational effort of the agent. In addition to cell size, the rules of neighboring, which are different for each cell shape, can change the graph. Hence, finding a good path presents the challenge of finding contradictory parameters. The selection of a suitable cell shape and size can help find a reasonable solution. In the next section, the methodology for studying the effects of these various representations will be described.

4. Methodology

The performed analysis in this study is divided into two parts. First, the effect of representation is considered regardless of the robot size. Second, the robot size is considered using the concept of inflation layer. This concept generates the map based on the real boundary. Then, it applies an inflation layer to the discretized view. In fact, the offset or inflation layer is the radius of the robot plus any optional value for safety [20]. This strategy has already been implemented in the ROS (Robot Operating System) [20]. In what follows, the decomposition methods are described.

4.1. Pure Decomposition

The geometry and the physical size of the robot are not considered in this section. Furthermore, the discretized cell is general and does not depend on the specific type of representation. For navigation on a planar surface by cell decomposition method, it is necessary to encode and abstract the environment information into a map representation, ${\mathrm{M}}_{\mathrm{reps}}$.

$${\mathrm{M}}_{\mathrm{reps}}=\{\mathrm{All}{ \mathrm{c}}_{\mathrm{i}} \left(\mathrm{i}=1,2,\dots \mathrm{N}\right) ; {\displaystyle \sum }{\mathrm{c}}_{\mathrm{i}}\approx {\mathrm{W}}_{\mathrm{free}}\}$$

(1)

where ${\mathrm{c}}_{\mathrm{i}}$ denotes the i^th cell and implies that the union of all discretized cells (finite number of N) can approximately estimate the free space W_free. Each path between S and G points in the map is defined as $\mathsf{\tau }$, which is a set of cells:

$$\mathsf{\tau }=\{{\mathrm{c}}_{\mathrm{s}},{\mathrm{c}}_1,{\mathrm{c}}_2,\dots ,{\mathrm{c}}_{\mathrm{g}}\},\mathrm{g}\le \mathrm{N}$$

(2)

A set of cells as a path is divided into several segments ${\mathrm{S}}_{\mathrm{ij}}$ between successive cells ${\mathrm{c}}_{\mathrm{i}}$ and ${\mathrm{c}}_{\mathrm{j}}$ in $\mathsf{\tau }$. This leads to:

$$\mathsf{\tau }=\{{\mathrm{S}}_{\mathrm{s}1},{\mathrm{S}}_{12},{\mathrm{S}}_{23},\dots ,{\mathrm{S}}_{\mathrm{ij}},\dots ,{\mathrm{S}}_{\mathrm{ig}}\},\mathrm{g}\le \mathrm{N},\mathrm{i}=\mathrm{g}-1$$

(3)

where ${\mathrm{S}}_{\mathrm{i}\mathrm{j}}$ is generally a curve connecting two cells (${\mathrm{c}}_{\mathrm{i}}$ and ${\mathrm{c}}_{\mathrm{j}}$) together with all the possible points inside the cells. This segment will be a building unit of movement for AGV according to its controller. So, each movement between ${\mathrm{c}}_{\mathrm{i}}$ and ${\mathrm{c}}_{\mathrm{j}}$ is a line segment between their centers. However, linear movement between the centers of two neighbors does not always guarantee safety near the obstacles. Therefore, it is necessary to check the feasibility of movement for some cells near obstacles. To do so, $\mathrm{Mov}({\mathrm{c}}_{\mathrm{i}},{\mathrm{c}}_{\mathrm{j}})$ is defined as:

$$\mathrm{Mov}\left({\mathrm{c}}_{\mathrm{i}},{\mathrm{c}}_{\mathrm{j}}\right)=\{\begin{array}{c}\mathrm{True} \mathrm{if} \forall \mathrm{p}\in \mathrm{Line}\left(\mathrm{cent}\left({\mathrm{c}}_{\mathrm{i}}\right),\mathrm{cent}\left({\mathrm{c}}_{\mathrm{j}}\right)\right)⟹\mathrm{p}\in {\mathrm{W}}_{\mathrm{free}}\\ \mathrm{False} \mathrm{if} \exists \mathrm{p}\in \mathrm{Line}\left(\mathrm{cent}\left({\mathrm{c}}_{\mathrm{i}}\right),\mathrm{cent}\left({\mathrm{c}}_{\mathrm{j}}\right)\right)⟹\mathrm{p}\notin {\mathrm{W}}_{\mathrm{free}}\end{array}$$

(4)

If $\mathrm{Mov}({\mathrm{c}}_{\mathrm{i}},{\mathrm{c}}_{\mathrm{j}})$ is true, it shows that the movement between the centers of ${\mathrm{c}}_{\mathrm{i}}$ and ${\mathrm{c}}_{\mathrm{j}}$ is feasible. Otherwise, there is the possibility of collision between agents and obstacles. In the geometrical view, if the combination of neighbor’s vertices is convex, then the linear segment will be inside the union of cells, and the movement is safe. Nevertheless, if the combination of ${\mathrm{c}}_{\mathrm{i}}$ and ${\mathrm{c}}_{\mathrm{j}}$’s vertices is concave, then the movement is not permitted. This is because it increases the possibility of collision with an obstacle. To include this extra condition into $\mathsf{\tau }$:

$$\mathsf{\tau }=\left\{\right\{{\mathrm{c}}_{\mathrm{s}},{\mathrm{c}}_1,{\mathrm{c}}_2,\dots ,{\mathrm{c}}_{\mathrm{g}}\},\forall { \mathrm{c}}_{\mathrm{i}}{ \mathrm{and} \mathrm{c}}_{\mathrm{j} }⟹\mathrm{Mov}\left({\mathrm{c}}_{\mathrm{i}},{\mathrm{c}}_{\mathrm{j}}\right)=\mathrm{True}\}$$

(5)

Checking the movement feasibility is simple for QUAD cells as the common-edge neighbor produces a convex shape. However, in ITM, it is possible to have a concave shape even for common-edge neighbors near obstacles. Hence, the movement feasibility needs to be checked in this mesh. This extra checking enhances the computational effort of this mesh type [29].

Among all possible $\mathsf{\tau }$, finding ${\mathsf{\tau }}_{\mathrm{opt}}$ is of great interest. According to the discretized nature of the path, it is possible to convert cells and movement between them into vertices and edges of a graph. Then a graph search algorithm can be used to find ${\mathsf{\tau }}_{\mathrm{opt}}$ between the start and goal cells. A*, as a popular graph search method [30], is employed in this study. This method uses Euclidean distance for calculating the cost and heuristic criterion between start and goal [31]. The cost of cell $ℊ\left({\mathrm{c}}_{\mathrm{i}}\right)$ is given by:

$$ℊ\left({\mathrm{c}}_{\mathrm{i}}\right)={\displaystyle \sum }\parallel \mathrm{cent}({\mathrm{c}}_{\mathrm{i}}),\mathrm{cent}\left(\mathrm{par}\left({\mathrm{c}}_{\mathrm{i}}\right)\right)\parallel$$

(6)

where $\mathrm{cent}\left({\mathrm{c}}_{\mathrm{i}}\right)$ stands for the center of the cell, Symbol $\parallel \mathrm{a},\mathrm{b}\parallel$ is the Euclidean distance between point a and point b, which are the center of two successive cells, and par(${\mathrm{c}}_{\mathrm{i}}$) is the parent of ${\mathrm{c}}_{\mathrm{i}}$. This cost starts from S and, in each sequence, accumulates the Euclidean distance between the current cell and its parent in a graph. The heuristic criterion of the cell (h$\left({\mathrm{c}}_{\mathrm{i}}\right)$) is calculated by:

$$\mathrm{h}\left({\mathrm{c}}_{\mathrm{i}}\right)=\parallel \mathrm{cent}\left({\mathrm{c}}_{\mathrm{i}}\right),\mathrm{goal}\parallel$$

(7)

The result of A* is a $\mathsf{\tau }$ with the minimum cost between two cells containing start and goal points. This $\mathsf{\tau }$ is shown by ${\mathsf{\tau }}_{\mathrm{opt}}$:

$${\mathsf{\tau }}_{\mathrm{opt}}=\left\{\right\{{\mathrm{c}}_{\mathrm{s}},{\mathrm{c}}_1,{\mathrm{c}}_2,\dots ,{\mathrm{c}}_{\mathrm{g}}\},\forall { \mathrm{c}}_{\mathrm{i}}{ \mathrm{and} \mathrm{c}}_{\mathrm{j}},$$

$${\mathrm{c}}_{\mathrm{i}}=\mathrm{par}\left({\mathrm{c}}_{\mathrm{j}}\right)⟹{ \mathrm{L}}_{{\mathsf{\tau }}_{\mathrm{opt}}}\approx \min \left({\mathrm{L}}_{\mathsf{\tau }}\right)$$

(8)

where ${\mathrm{L}}_{\mathsf{\tau }}$ denotes the length of a path.

As stated earlier, in this study, the utilized multi-objective cost function is composed of three metrics. These are the complexity of A* algorithm for finding ${\mathsf{\tau }}_{\mathrm{opt}}$, length of ${\mathsf{\tau }}_{\mathrm{opt}}$, and minimum distance between AGV and obstacles when it follows ${\mathsf{\tau }}_{\mathrm{opt}}$.

Herein, the complexity (${\mathrm{C}}_{\mathrm{reps}}$) is defined by counting the number of visited (In A*, visited cells go to a list named open list, so ${\mathrm{C}}_{\mathrm{reps}}$ = size (Open list)) nodes during A*.

$${\mathrm{C}}_{\mathrm{reps}}={\mathrm{Number} \mathrm{of} \mathrm{visited} \mathrm{cells} \mathrm{in} \mathrm{A}}^{\ast }$$

(9)

The length of the optimal path (${\mathrm{L}}_{{\mathsf{\tau }}_{\mathrm{opt}, \mathrm{reps}}}$) is calculated as follows:

$${\mathrm{L}}_{{\mathsf{\tau }}_{\mathrm{opt}, \mathrm{reps}}}={\displaystyle \sum }_{\mathrm{i}=\mathrm{S}}^{\mathrm{i}=\mathrm{G}}\parallel \mathrm{cent}\left({\mathrm{c}}_{\mathrm{i}}\right),\mathrm{cent}(\mathrm{par}\left({\mathrm{c}}_{\mathrm{i}}\right)\parallel$$

(10)

The minimum distance to the nearest obstacle is calculated with the help of the Euclidean distance grid, as explained in [32,33].

$$\mathrm{DT}\left(\mathrm{p}\right)={\mathrm{d}}_{\mathrm{k}}, \mathrm{p}\in { \mathrm{c}}_{\mathrm{RG},\mathrm{k}}$$

(11)

where $\mathrm{DT}\left(\mathrm{p}\right)$ is a function for mapping each point of free space p into a cell ${\mathrm{c}}_{\mathrm{RG},\mathrm{k}}$ in the reference grid ($\mathrm{RG}$), which is a Euclidean distance transform on a 200 × 100 grid. ${\mathrm{c}}_{\mathrm{RG},\mathrm{k}}$ contains the value of distance to the nearest obstacle as ${\mathrm{d}}_{\mathrm{k}}$.

Therefore, ${\mathrm{D}}_{\min ,\mathrm{reps}}$, as the minimum distance between all agent’s distances to the nearest obstacles, is given by:

$$\begin{gathered} {\mathrm{D}}_{\min ,\mathrm{reps}}=\min \left(\mathrm{DT}\left(\mathsf{\tau }\right)\right) \\ \mathrm{which} \forall {\mathrm{c}}_{\mathrm{i}}\in \mathsf{\tau } \bigwedge \mathrm{cent}\left({\mathrm{c}}_{\mathrm{i}}\right)\in {\mathrm{c}}_{\mathrm{RG},\mathrm{k}} \end{gathered}$$

(12)

In triangular representation, as shown in Figure 1, there are some free points near obstacles that are not placed inside any cells in the $\mathrm{RG}$. In this situation, the Euclidean distance between the point and other nodes and edges, which are tagged as the obstacle, is calculated. Then, the minimum value is returned as the minimum distance. This value may be smaller and larger than the previous distance value of the path and must be compared to the current minimum distance.

After calculating the three normalized metrics, a linear weighted sum approach is utilized to define the cost function for each representation.

$$\{\begin{array}{c}{\mathrm{LN}}_{\mathrm{reps}}=\frac{{\mathrm{L}}_{{\mathsf{\tau }}_{\mathrm{opt}, \mathrm{reps}}}}{{\mathrm{L}}_{\max }}\\ {\mathrm{CN}}_{\mathrm{reps}}=\frac{{\mathrm{C}}_{\mathrm{reps}}}{{\mathrm{C}}_{\max }}\\ {\mathrm{DN}}_{\mathrm{reps}}=\frac{{\mathrm{D}}_{\min }}{{\mathrm{D}}_{\min ,\mathrm{reps}}}\end{array}$$

(13)

where ${\mathrm{LN}}_{\mathrm{reps}}$ is the normalized optimal length, ${\mathrm{CN}}_{\mathrm{reps}}$ is the normalized complexity for finding optimal length, ${\mathrm{DN}}_{\mathrm{reps}}$ is the minimum distance of agent to the nearest obstacle when following the optimal path, ${\mathrm{L}}_{{\mathsf{\tau }}_{\mathrm{opt},\mathrm{reps}}}$ is the optimal length obtained by (10), ${\mathrm{C}}_{\mathrm{reps}}$ is the calculated complexity from (9), ${\mathrm{D}}_{\min ,\mathrm{reps}}$ is the minimum distance of the optimal path from (12), and ${\mathrm{L}}_{\max }$, ${\mathrm{C}}_{\max }$, and ${\mathrm{D}}_{\min }$ are the maximum lengths between start and goal, maximum complexity to find this maximum length path, and the minimum possible distance between agent and obstacle, respectively. Finally, the multi-objective cost function (${\mathrm{f}}_{\mathrm{reps}}$) is formulated as:

$${\mathrm{f}}_{\mathrm{reps}}={\mathsf{\omega }}_1\times { \mathrm{LN}}_{\mathrm{reps}}+{\mathsf{\omega }}_2\times { \mathrm{CN}}_{\mathrm{reps}}+{ \mathsf{\omega }}_3\times { \mathrm{DN}}_{\mathrm{reps}}$$

(14)

where ${\mathsf{\omega }}_1,{ \mathsf{\omega }}_2{ \mathrm{and} \mathsf{\omega }}_3$ are the weights. For simplicity, equal importance is considered for all weights: $\mathsf{\omega }$₁ = $\mathsf{\omega }$₂ = $\mathsf{\omega }$₃ = 0.333.

4.2. Decomposition of Inflation Layer

In this sub-section, the robot size is integrated into the inflation layer. The inflation layer is defined as follows:

$$\mathrm{Inflation} \mathrm{layer} =\left\{\forall \mathrm{p}\in {\mathrm{W}}_{\mathrm{free}}, \mathrm{DT}\left(\mathrm{p}\right)<\left({\mathrm{r}}_{\mathrm{AGV}}+\mathrm{SD}\right)\right\}$$

(15)

where ${\mathrm{r}}_{\mathrm{AGV}}$ is the radius of AGV, and $\mathrm{SD}$ is an optional value for a safe distance between the AGV and an obstacle. According to (15), the inflation layer is formed by all the points in W_free whose distance to the nearest obstacle is lower than a specific value. With this definition, the resulting map considering this inflation will be:

$${\mathrm{M}}_{\mathrm{reps}}=\{\forall {\mathrm{c}}_{\mathrm{i}}\left(\mathrm{i}=1,2,\dots \mathrm{N}\right); {\displaystyle \sum }{\mathrm{c}}_{\mathrm{i}}\approx {\mathrm{W}}_{\mathrm{free}};\mathrm{cent}\left({\mathrm{c}}_{\mathrm{i}}\right)\not\subset \mathrm{inflation} \mathrm{layer}\}$$

(16)

5. Results and Discussion

This section presents the results regarding the AGV performance in different conditions. After this, the considered case studies and the utilized platform are first explained. Subsequently, the results concerning environment representation and the inflation layer are discussed.

5.1. Platform for Experiment

The intended comparative study is expected to clarify the best representation (${\mathrm{M}}_{\mathrm{reps}}$) for each obstacle’s distribution (W_s) according to the above-explained multi-objective cost function ($\mathrm{f}$). In this regard, a fixed scenario (a path planning between S and G) is utilized for various ${\mathrm{M}}_{\mathrm{reps}}$ and W_s. The following types of representation (${\mathrm{M}}_{\mathrm{reps}}$) are considered in this study:

• QUAD mesh (GRID Nx × Ny): four cell sizes (GRID 100 × 50, GRID 120 × 60, GRID 160 × 80, and GRID 200 × 100) are considered for this mesh where Nx and Ny are the number of cells in horizontal and vertical directions.
• ITM: four cell sizes (ITM-700, ITM-500, ITM-300, ITM-100) are also considered for this mesh. ITM-100 refers to a triangle with an average of 100 mm edges. For some environments where this was not applicable, larger triangles and smaller ones were used.
• Varying-size ITM (VITM): Concerning this mesh, ITM-100-700 is utilized. This size refers to a triangular mesh with an average edge size of 700 mm, which has been refined to size 100 mm in some places. When confronting narrow passages, VITM-50-700 or VITM-30-700 have also been utilized.

Concerning various factory environments, the following W_s are taken into account (see Figure A1):

• Area with single obstacle: Map_1 (small-size obstacle), Map_2 (medium-size polygonal obstacle), Map_3 (medium-size circular obstacle)
• Space with dividers (Map_4)
• Narrow passage (Map_5)
• Curvilinear passage: Map6
• Area with regular multi-obstacles: Map_7, Map_8 (two groups), Map_9 (different size)
• Area with irregular multi-obstacles: Map_10, Map_11 (two groups), Map_12 (circular), Map_13 (different shapes)
• Hybrid with wide space: Map_14
• Corridor and dividers: Map_15
• Hybrid narrow space environments: Map_16, Map_17 (including all the previous environments)

In this study, a research platform developed by our team (ERICCA, Equipe de Recherche en Integration Cao-CAlcul) is utilized to perform the mesh generation for different environments. This platform is based on the Unified Topological Model [22] and automatic meshing and remeshing tools, as explained in [34,35,36,37]. The computer for using this platform and simulation was Intel Core i7-4790 RAM 32GiB. Since the main task is to study the effect of the discretized cell types and sizes on the generated path by the global planner, the required map preprocessing is performed by the operator. For instance, an STP file (the STP is a standard format for exchange of modelling data) is used to define the boundary edges of obstacles and the exterior frame of the environment. This preprocess is similar to changing a point cloud, as sensor data, into a continuous curve of the obstacle’s boundary. Using the STP file as an input, various representations (QUAD, ITM, and VITM) with different sizes can be produced by the mentioned platform. A rectangle area of 10,000 × 5000 (mm) is utilized as the environment for all the performed simulations. Various types of obstacle distribution (single and multi-obstacles) are carried out regularly and randomly in this environment. A fixed scenario, navigation between points (300, 300) as the start and (9600, 4400) as the goal, is utilized for all the tests. The reason for selecting this path is that AGV needs to turn around the obstacles to pass the optimal length. After the generation of each map, the UTM platform makes it possible to perform global path planning and find the length, distance, and complexity in order to calculate the cost function for different representations. The running time of the utilized search algorithm is calculated by means of the number of visited cells in the graph search. This strategy is selected in order to be independent of coding details while comparing different cases.

5.2. Result—Environment and Representations

Consider an environment with a single medium obstacle as an example, which has been discretized by the three representations (QUAD, ITM, and VITM) with different sizes. Figure 2 represents the optimal path obtained by A* solely for one size of each representation. The scenario is to find a path between the start (300, 300) and goal (9600, 4400) points without considering inflation.

Table 1. The length, minimum distance to obstacle, complexity, and cost function values for three sample representations for a sample map with a fixed scenario.

	Representations		Calculated Parameters			f (Single Criteria)
Item	Type	Size	Length (mm)	Min Distance (mm)	Complexity	Cost Function
1	QUAD	GRID 200 × 100	10,992	25	8323	0.145
2	ITM	700	10,749	155	134	0.006
3	VITM	100_700	10,521	19	177	0.007

reports the length, minimum distance to obstacles, complexity, and cost of each case. From this table, ITM-700 has reached the lowest cost followed by VITM-100-700 while the GRID 200 × 100 has led to the highest cost. Therefore, ITM-700 and VITM-100-700 perform better than GRID 200 × 100 in terms of finding an optimal path in an environment with medium-size obstacles in parallel with the global frame.

Similar scenarios have been performed for various environments and cell sizes, as shown in Figure A2. The considered environments are the different distributions variously mentioned in Section 5.1. Moreover, different cell sizes of QUAD, ITM, and VITM, as explained earlier, are considered. The complete result is presented in

Table A1. The length, minimum distance to obstacle, complexity, and cost function values for all representations without considering the inflation layer in the same scenario.

Map Name	Representations		S (300, 300) G (9600, 4400)	Parameters			Single Criteria
	Type	Size	Inflation	Length mm	Min Distance mm	Complexity	f Cost Function
Map_1	QUAD	GRID 100 × 50	0	10,986	75	2269	0.042
	QUAD	GRID 120 × 60	0	11,022	125	3160	0.056
	QUAD	GRID 160 × 80	0	11,007	75	5463	0.095
	QUAD	GRID 200 × 100	0	10,992	25	8359	0.143
	ITM	700	0	10,451	133	114	0.005
	ITM	500	0	10,433	275	168	0.006
	ITM	300	0	10,381	46	358	0.010
	ITM	100	0	10,329	275	1644	0.031
	VITM	100_700	0	10,292	1	118	0.008
Map_2	QUAD	GRID 100 × 50	0	10,986	25	2251	0.042
	QUAD	GRID 120 × 60	0	11,022	25	3206	0.058
	QUAD	GRID 160 × 80	0	11,007	25	5452	0.097
	QUAD	GRID 200 × 100	0	10,992	25	8323	0.145
	ITM	700	0	10,749	155	134	0.006
	ITM	500	0	10,375	25	153	0.006
	ITM	300	0	10,484	46	369	0.010
	ITM	100	0	10,570	125	3030	0.055
	VITM	100_700	0	10,521	19	177	0.007
Map_3	QUAD	GRID 100 × 50	0	10,986	25	2255	0.042
	QUAD	GRID 120 × 60	0	11,022	25	3049	0.056
	QUAD	GRID 160 × 80	0	11,007	25	5269	0.093
	QUAD	GRID 200 × 100	0	10,992	25	8117	0.141
	ITM	700	0	10,521	17	106	0.006
	ITM	500	0	10,559	75	190	0.007
	ITM	300	0	10,456	3	444	0.012
	ITM	100	0	10,399	19	2191	0.041
	VITM	100_700	0	10,394	40	173	0.007
Map_4	QUAD	GRID 100 × 50	0	12,416	25	2695	0.051
	QUAD	GRID 120 × 60	0	12,409	25	3707	0.069
	QUAD	GRID 160 × 80	0	12,340	25	6468	0.117
	QUAD	GRID 200 × 100	0	12,293	25	10,078	0.179
	ITM	700	0	12,565	116	164	0.007
	ITM	500	0	12,438	75	295	0.010
	ITM	300	0	12,222	75	747	0.017
	ITM	100	0	12,031	13	5613	0.102
	VITM	100_700	0	11,953	15	412	0.012
Map_5	QUAD	GRID 100 × 50	0	10,986	75	2102	0.039
	QUAD	GRID 120 × 60	0	11,022	25	2917	0.053
	QUAD	GRID 160 × 80	0	11,007	25	5064	0.090
	QUAD	GRID 200 × 100	0	10,992	25	7812	0.136
	ITM	700	0	10,294	87	92	0.005
	ITM	500	0	10,285	125	153	0.006
	ITM	300	0	10,339	133	308	0.009
	ITM	100	0	10,379	116	2316	0.043
	VITM	100_700	0	10,404	125	220	0.007
Map_6	QUAD	GRID 100 × 50	0	11,630	25	1579	0.053
	QUAD	GRID 120 × 60	0	11,657	25	2134	0.070
	QUAD	GRID 160 × 80	0	11,592	25	3726	0.116
	QUAD	GRID 200 × 100	0	11,519	25	5740	0.175
	ITM	700	0	11,109	46	94	0.009
	ITM	500	0	11,403	75	188	0.012
	ITM	300	0	11,048	46	360	0.017
	ITM	100	0	11,065	14	2859	0.091
	VITM	100_700	0	11,052	25	275	0.015
Map_7	QUAD	GRID 100 × 50	0	12,386	25	2289	0.066
	QUAD	GRID 120 × 60	0	12,380	25	2995	0.085
	QUAD	GRID 160 × 80	0	12,327	25	5502	0.150
	QUAD	GRID 200 × 100	0	12,173	25	8388	0.225
	ITM	700	0	12,760	46	190	0.012
	ITM	500	0	12,357	20	226	0.013
	ITM	300	0	12,233	11	552	0.021
	ITM	100	0	11,798	0.4	4428	0.130
	VITM	100_700	0	12,031	45	513	0.020
Map_8	QUAD	GRID 100 × 50	0	11,566	25	2224	0.054
	QUAD	GRID 120 × 60	0	11,640	25	3418	0.080
	QUAD	GRID 160 × 80	0	11,521	25	5532	0.126
	QUAD	GRID 200 × 100	0	11,511	25	8836	0.199
	ITM	700	0	11,938	20	167	0.009
	ITM	500	0	11,465	27	242	0.011
	ITM	300	0	11,444	39	611	0.019
	ITM	100	0	11,181	0	4737	0.117
	VITM	100_700	0	11,584	5	435	0.015
Map_9	QUAD	GRID 100 × 50	0	11,408	25	1705	0.046
	QUAD	GRID 120 × 60	0	11,461	25	2483	0.064
	QUAD	GRID 160 × 80	0	11,373	25	4069	0.102
	QUAD	GRID 200 × 100	0	11,343	25	6520	0.160
	ITM	700	0	11,207	31	120	0.008
	ITM	500	0	11,108	2	190	0.011
	ITM	300	0	10,921	13	379	0.015
	ITM	100	0	10,878	10	2793	0.072
	VITM	100_700	0	10,925	17	315	0.013
Map_10	QUAD	GRID 100 × 50	0	11,239	25	1458	0.037
	QUAD	GRID 120 × 60	0	11,189	25	2252	0.055
	QUAD	GRID 160 × 80	0	11,222	25	3771	0.089
	QUAD	GRID 200 × 100	0	11,201	25	5759	0.132
	ITM	700	0	11,105	14	119	0.008
	ITM	500	0	11,149	45	209	0.010
	ITM	300	0	11,292	2	583	0.020
	ITM	100	0	10,814	3	2507	0.061
	VITM	100_700	0	10,854	32	440	0.015
Map_11	QUAD	GRID 100 × 50	0	11,156	25	1650	0.036
	QUAD	GRID 120 × 60	0	11,120	25	2498	0.053
	QUAD	GRID 160 × 80	0	11,119	25	4214	0.086
	QUAD	GRID 200 × 100	0	11,119	25	6395	0.128
	ITM	700	0	10,500	13	95	0.006
	ITM	500	0	10,615	45	140	0.007
	ITM	300	0	10,519	32	356	0.011
	ITM	100	0	10,550	18	2998	0.062
	VITM	100_700	0	10,596	21	317	0.010
Map_12	QUAD	GRID 100 × 50	0	11,069	25	1651	0.039
	QUAD	GRID 120 × 60	0	11,091	25	2321	0.053
	QUAD	GRID 160 × 80	0	11,058	25	4066	0.089
	QUAD	GRID 200 × 100	0	11,033	25	6316	0.135
	ITM	700	0	10,531	4	94	0.007
	ITM	500	0	10,454	24	153	0.008
	ITM	300	0	10,369	29	230	0.009
	ITM	100	0	10,522	24	2026	0.046
	VITM	100_700	0	10,398	42	299	0.011
Map_13	QUAD	GRID 100 × 50	0	11,239	25	1479	0.036
	QUAD	GRID 120 × 60	0	11,189	25	2366	0.055
	QUAD	GRID 160 × 80	0	-	-	-	-
	QUAD	GRID 200 × 100	0	11,201	25	5999	0.132
	ITM	700	0	11,048	12	126	0.008
	ITM	500	0	11,026	44	160	0.008
	ITM	300	0	11,011	23	494	0.015
	ITM	100	0	10,891	14	3802	0.086
	VITM	100_700	0	11,063	21	254	0.010
Map_14	QUAD	GRID 100 × 50	0	11,903	25	3025	0.060
	QUAD	GRID 120 × 60	0	11,855	25	4270	0.083
	QUAD	GRID 160 × 80	0	11,918	25	7623	0.145
	QUAD	GRID 200 × 100	0	11,892	25	11,932	0.225
	ITM	700	0	11,568	42	214	0.008
	ITM	500	0	11,469	46	327	0.010
	ITM	300	0	11,573	46	771	0.019
	ITM	100	0	11,346	9	5936	0.114
	VITM	100_700	0	11,590	5	298	0.010
Map_15	QUAD	GRID 100 × 50	0	17,192	25	3118	0.068
	QUAD	GRID 120 × 60	0	17,246	25	4422	0.093
	QUAD	GRID 160 × 80	0	17,031	25	7472	0.153
	QUAD	GRID 200 × 100	0	16,769	25	11,676	0.235
	ITM	700	0	17,764	31	209	0.011
	ITM	500	0	18,192	46	353	0.014
	ITM	300	0	17,480	29	919	0.025
	ITM	100	0	16,593	8	7053	0.145
	VITM	100_700	0	16,786	1	403	0.020
Map_16	QUAD	GRID 200 × 100	0	29,830	25	13,978	0.303
	ITM	100	0	30,072	0	8215	0.219
	VITM	28_700	0	30,183	5	1538	0.045
Map_17	QUAD	GRID 120 × 60	0	32,876	25	5157	0.119
	QUAD	GRID 160 × 80	0	32,308	25	9484	0.206
	QUAD	GRID 200 × 100	0	32,075	25	15,000	0.318
	ITM	300	0	32,204	5	1207	0.039
	ITM	100	0	31,732	3	2455	0.064
	ITM	50	0	30,498	0	9232	0.216
	VITM	100_700	0	31,494	1	1095	0.037

, and for simplicity, only the best representation of each environment (minimum f values among others) is shown in

Table 2. Best representation for each environment according to f, cost function values without inflation.

MAP	Environment Description	Representation with the Lowest f Value	MAP	Environment Description	Representation with the Lowest f Value
Map_1	Small obstacle	ITM-700	Map_9	Regular different size	ITM-700
Map_2	Medium polygonal obstacle	ITM-700	Map_10	Irregular obstacles	ITM-700
		ITM-500
		VITM-100-700
Map_3	Medium circular obstacle	ITM-700	Map_11	Irregular two groups	ITM-700
		ITM-500
		VITM-100-700
Map_4	Space with dividers	ITM-700	Map_12	Irregular circular obstacles	ITM-700
Map_5	narrow passage	ITM-700	Map_13	Irregular different shape obstacles	ITM-700
Map_6	Curvilinear passage	ITM-700	Map_14	Hybrid with wide-spaced obstacles	ITM-700
Map_7	Regular obstacles	ITM-700	Map_15	Corridor and dividers	ITM-700
Map_8	Regular two groups	ITM-700	Map_16,17	Hybrid narrow-space environments	VITM-28-700
					VITM-100-700

. According to this table, a coarse ITM (like ITM-700 or ITM-500) seems to be a good candidate for almost all environments except the hybrid environment where a VITM (VITM-100-700) shows better performance. It is worth reminding the reader that the detailed results, as in Table 1, are presented in the Appendix for all environments. The discussed results have been obtained by considering the pure decomposition effect without an inflation layer. In the next sub-section, the results concerning the effect of robot size or inflation layer are explored.

5.3. Result—Inflation Effect on the Representations

In practice, it is necessary to consider the robot size in path planning. This is normally done by imposing an inflation layer around the obstacles. In this regard, the tests performed in the previous sub-section are repeated herein, considering the inflation layer.

Firstly, the test regarding the environment with medium-size obstacles is repeated by considering a robot size diameter of 354 mm (turtle bot 2 [38]). Figure 3 shows the obtained optimal path for this new case. The red layer around the obstacle and exterior boundary is not accessible by the robot. Therefore, the movements between the neighbors are affected by this layer, and the results will be changed. The new values considering this limitation are given in

Table 3. The length, minimum distance to obstacle, complexity, and cost function values for three sample representations considering the inflation layer.

	Representations		Calculated Parameters			F (Single Criteria)
Item	Type	Size	Length (mm)	Min Distance (mm)	Complexity	Cost Function
1	QUAD	GRID 200 × 100	10,992	22	7555	0.132
2	ITM	700	10,878	98	532	0.013
3	VITM	100_700	10,469	48	327	0.009

for the three different representations. From this table, VITM-100-700 reaches the best performance ($f_{reps}:$ 0.009) compared to the other two cases. This shows that considering the inflation layer influences the choice of the best representation, due to the change in complexity.

Secondly, all the previously considered environments of different types and sizes are repeated, considering the inflation layer. The obtained results are shown in

Table 4. Best representation for each environment according to f, cost function values with consideration of the inflation layer.

MAP	Environment Description	Representation with the Lowest f Value	MAP	Environment Description	Representation with the Lowest f Value
Map_1	Small obstacle	ITM-500	Map_9	Regular different size	ITM-700
		VITM-100-700			GRID 100 × 50
Map_2	Medium polygonal obstacle	VITM-100-700	Map_10	Irregular obstacles	VITM-30-700
Map_3	Medium circular obstacle	ITM-700	Map_11	Irregular two groups	ITM-500
Map_4	Space with dividers	ITM-700	Map_12	Irregular circular obstacles	ITM-700
Map_5	narrow passage	VITM-50-700	Map_13	Irregular different shape obstacles	VITM-100-700
					GRID 100 × 50
Map_6	Curvilinear passage	VITM-50-700	Map_14	Hybrid with wide-spaced obstacles	ITM-700
Map_7	Regular obstacles	GRID 100 × 50	Map_15	Corridor and dividers	VITM-50-700
					GRID 100 × 50
Map_8	Regular two groups	VITM-100-700	Map_16,17	Hybrid narrow-space environments	GRID 120 × 60
					VITM-28-700
		GRID 100 × 50			VITM-50-700
					GRID 160 × 80

. In this new analysis, as opposed to the case in which inflation was ignored, it is seen that many ITM representations have not been able to find the path, and they have been replaced by the VITM and QUAD representations. Furthermore, it has been necessary for the VITM to use finer triangles in the narrow passages that have not been blocked completely. Decreasing the size of triangles (increasing their number) can increase the chance of finding more triangles whose centers are inside the free space, and movement between them and their children is possible. Some of the generated paths are presented in Figure 4. According to Table 4, coarse ITM shows the best performance for a single obstacle or hybrid environment, with enough wide space (for Map_1, Map_3, and Map_14). Regarding the corridor and regular multi-obstacles, the coarse grid is the best method. In irregular multi-obstacles and a curvilinear passage, a VITM indicates the best performance.

To find the effect of inflation on each type of representation,

Table 5. Average of cost function value on all environments, without and with inflation, and its ratio.

Reps	fwithout_infl	fwith_infl	fwith/fwithout
QUAD	0.114	0.089	0.78
ITM	0.038	0.217	5.71
VITM	0.016	0.036	2.25

shows the average cost function (f values) for all environments in two conditions, without inflation and with an inflation layer. Their ratio shows that ITM is more sensitive to the inflation layer, and misses its benefit. QUAD representation shows better behavior when using inflation.

To compare the complexity of finding a path for each type of representation, we have calculated the average complexity (number of visited cells when graph searching) of each type of representation in

Table 6. Average of complexity value for all environments and each representation type.

Reps	QUAD	ITM	VITM
Average Complexity	3958	4244	1453

. If any size could not give a path, a smaller size has been used to produce one. Overall, VITM shows the lowest complexity as compared to other types.

5.4. Results—Discussion

Finding the best representation for an AGV inside a factory according to different environment encounters during its navigation is an important part of the use of autonomous agents. Different representations give different path. A good path has a short length with a maximum distance to obstacles that can be calculated quickly. Without knowing this path, a mobile robot can be an unfeasible solution for a factory, along with increasing energy consumption due to a less than optimal path, lowering efficiency by inappropriate planning time and increased cost due to the high risk of an inadequate distance to obstacles (high probability of collision). By considering all these important parameters of path planning, this work defined a single criterion and checked it for different types and sizes of representation for the various environments inside a factory.

The obtained results show that for various types of environments, such as single or multi obstacles and corridor-like, some level of coarse ITM is the predominant strategy for achieving a compromise solution for length, safety, and computation time; this verifies the work in [14], which shows that refinement is not necessary for some motion planning. However, what has not been considered is that, when considering the inflation layer around obstacles, VITM and GRID representations are better. It is clear that, by increasing the resolution or decreasing the cell size, the complexity increases, and in most cases, the nearest distance to the obstacles decreases, with some average improvement in length. According to this result, when the robot is of a fixed size in a static environment, and it is possible to apply first the robot size to the map, it is better to use the ITM method with coarse size like [16] in which inflation has been applied as offset during the first mapping. However, when there are the following situations, it is better to use VITM or GRID representations:

• In multi-robot sizes conditions, when is not possible to apply the offsetting method.
• Some changes in the environment make it necessary to apply online inflation to the map, and not by offsetting the obstacles in the primary map.
• There are narrow passages for a robot which makes ITM representation useless.

This benchmark also demonstrated that varying the size of the triangular mesh with a different strategy for refinement could be a competitive method when ITM cannot find the answer. Of course, this needs to be more refined when using the elements in an area with narrow passages. The other benefit of VITM is the more straightforward implementation relative to the quadtree method for neighbor finding, such as regular triangulation.

Robotic navigation in a real factory with multi AGVs with non-circular shapes is a more complicated task. This paper surveyed the effect of environment and map representation types on path planning considering a single circular AGV. Although a circle can cover any shape as a peripheral circle, it cannot obtain a path in some narrow passages. According to the robot’s footprint, this limitation leads to consideration of a more complex definition of the inflation layer. In addition, to show the clear behavior of various cell shapes in response to A* search graph, we did not consider any path smoothing, which causes a non-optimal path from the point of energy consumption.

6. Conclusions and Future Work

In using an AGV as a feasible solution in a factory in response to the fourth industrial revolution, it is necessary to consider a flexible multi-objective path planner to give better answers according to the changes in the environment. Hence, this paper investigates the impact of two important factors, environment model representation and robot size, on the performance of an AGV. In this regard, a multi-objective cost function, considering length, complexity, and minimum distance to obstacles, is formulated for a perfect circular robot with a fixed path. Subsequently, three types of representation, namely QUAD, ITM, and VITM, with different cell sizes are employed to model the environment. Moreover, an inflation layer is imposed on the discretized view to check its influence on the performance. A* is utilized to find the optimal path for the different cell representations and sizes with and without the inflation layer. The obtained results show that a coarse ITM is a good candidate for a relatively unchanging environment with fixed robot size and wide space. However, when it is possible to repeatedly change the factory’s plan and use different ‘robot sizes, VITM and GRID representations give better performance by applying an inflation layer, especially in narrow spaces. In comparing triangle and square representations, in about 59% of industrial environments, constant or variable size triangle shapes are the only best for the discretization of that specific environment.

Future work can pursue the following paths, which will bring important practical application in the field of AGV environment modeling and navigation. Consideration of dynamic environments will enrich the optimization function with more complex criteria using a solution such as right-hand traffic, and applying some simultaneous constraints on the navigation of a narrow passage. Furthermore, the results of this paper can be used as an efficient map server that selects the best representation according to the environment. This can bring a smarter AGV platform to industry.