1. Introduction
Model reduction in chemical kinetics is an important issue in numerical simulations of reactive flows involving high-dimensional detailed reaction mechanisms with multiple time scales [
1]. Also, for complexity reduction of chemical reaction mechanisms [
2] and biochemical networks [
3], insight into the multiple time scale structure is often useful.
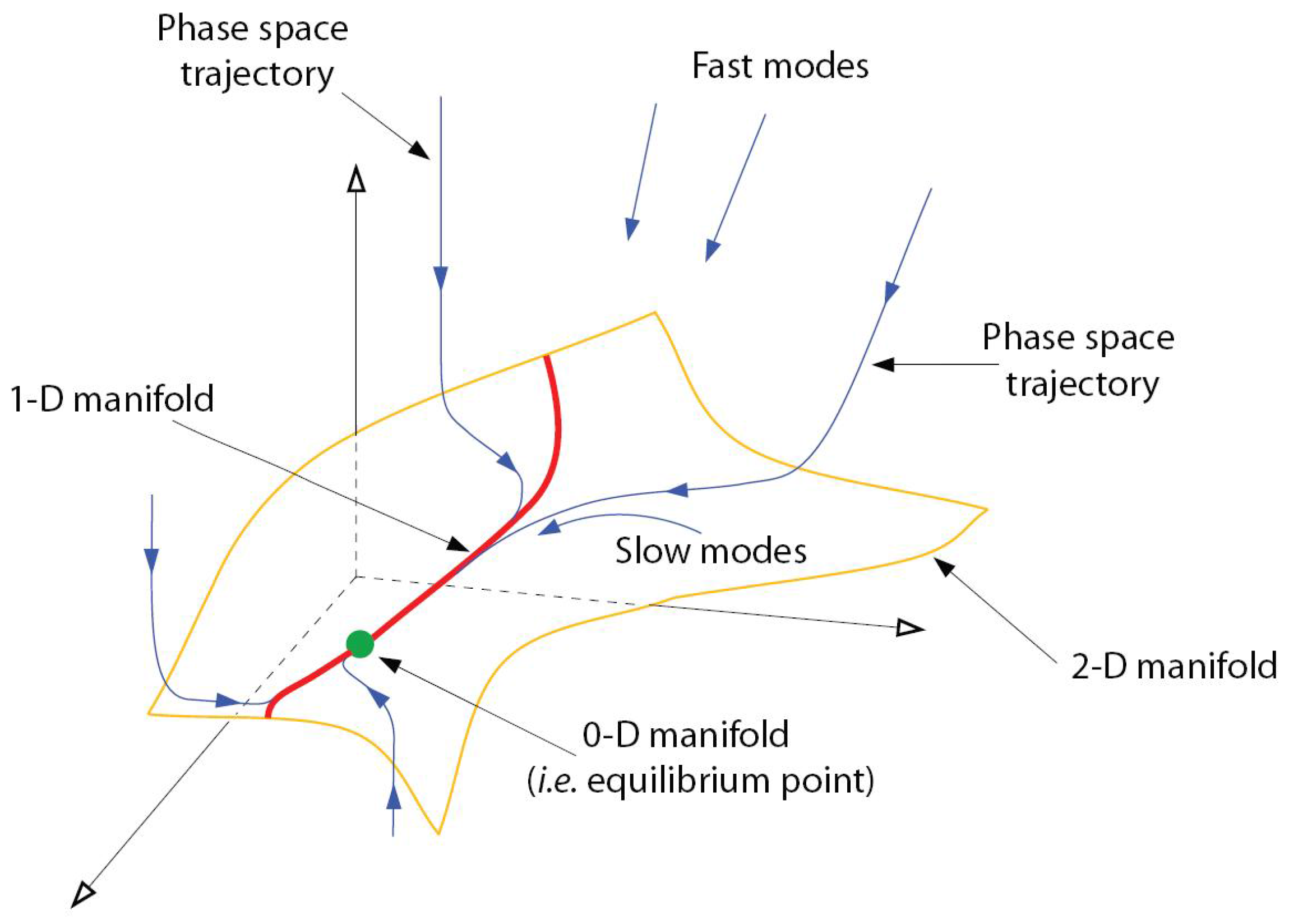
Figure 1.
Illustration of trajectories relaxing onto a 2-D manifold and successively a 1-D manifold while converging to stable equilibrium point. Figure courtesy of A.N. Al-Khateeb, J.M. Powers, S. Paolucci (private communication).
Figure 1.
Illustration of trajectories relaxing onto a 2-D manifold and successively a 1-D manifold while converging to stable equilibrium point. Figure courtesy of A.N. Al-Khateeb, J.M. Powers, S. Paolucci (private communication).
In dissipative ordinary differential equation (ODE) systems modeling chemical reaction kinetics, different time scales cause anisotropic phase volume contraction along solution trajectories. This leads to a bundling of trajectories near “manifolds of slow motion” of successively lower dimension as time progresses (see
Figure 1). Model reduction methods exploit a time scale separation into fast and slow modes by computing a dimension-reduced model via elimination of fast modes enslaving them to the slow ones and projecting the system dynamics from the full state space to a slow manifold.
Prominent numerical techniques are the ILDM-method [
4,
5], computational singular perturbation (CSP) [
6,
7], Fraser’s algorithm [
8,
9,
10], the method of invariant grids [
11,
35], the zero derivative principle (ZDP) [
13,
14], the rate-controlled constrained equilibrium (RCCE) method [
15], the invariant constrained equilibrium edge pre-image curve (ICE-PIC) method [
16,
17], flamelet-generated manifolds [
18,
19] and finite time Lyapunov exponents [
20].
Dissipation and the bundling of trajectories on slow manifolds are closely related to the concept of entropy. The term “entropy” is used in various contexts in chemistry, physics and dynamical systems theory, but all definitions follow the same basic idea related to information loss or gain and increase or decrease in complexity. Here, we will refer to the chemical definition of entropy production rate and the general concepts of topological and metric entropy of dynamical systems which measure the increase in dynamical complexity during time evolution. At the core of the thermodynamic point of view of entropy is Gibbs’ variational principle and Boltzmann’s microscopic interpretation of the entropy S as with the thermodynamic probability W measuring the number of microscopic states being consistent with a macroscopic property of a system. Postulating equal a priori probabilities of each microstate the thermodynamic probability of a macroscopic state to be implemented in this picture is proportional to the number of microstates being consistent with that macrostate.
Here, we review and discuss the recently proposed use of entropy-related concepts to formulate a variational principle suitable to characterize trajectories on, respectively near, slow invariant manifolds of chemical kinetic systems. In analogy to the classical thermodynamic point of view the slow manifold can be interpreted as a “macroscopic” view of the system and a variational principle is supposed to distinguish this “slow” macrostate from all other possible macrostates being consistent with a chosen parameterization of a low-dimensional manifold.
2. Entropy Concepts
For an elementary reaction step with reaction rates
and
for forward and backward reactions the chemical entropy production rate can be calculated from
where
R is the universal gas constant. Since the total entropy production rate is additive for several elementary steps, it can be computed from purely kinetic information for arbitrary reaction systems using (
1) if the detailed elementary step mechanism is known and the kinetic rate coefficients are available. For isolated systems with constant internal energy and volume, the entropy is a Lyapunov function of the dynamical system following the
Second Law of Thermodynamics.
In [
21,
22], numerical approximations of slow attracting manifolds are obtained by computation of trajectories along which the total (time integral over entropy production rate) entropy production (
1) summing over all elementary reaction steps is minimal while chemical equilibrium is approached as time progresses. The approach yields approximations of slow manifolds, however, they lack invariance. Here, we will discuss the extension and improvement of this fundamental idea to more general entropy-related extremum principles tracing trajectories of a dissipative dynamical system
backwards in time and point out relations to entropy concepts in dynamical systems theory. In the latter context, entropy can generally be interpreted as a measure of the rate of increase in dynamical complexity, e.g., the rate of dissipation. We propose that an extremum principle suitable to characterize trajectories on slow attracting manifolds should incorporate in some sense the idea of minimum dissipativeness (in the sense of “maximum slowness”) of a dynamical system along these trajectories.
In this section, we provide an overview of relevant entropic concepts in dynamical systems theory and in the next section we will try to illustrate how these general concepts qualitatively relate to and provide a motivation for the criteria we choose for the purpose of computing slow attracting manifold by proposing an entropy-related extremum principle for trajectories.
A standard reference for the following definitions and theorems is [
23]. Our presentation partially follows that of Young [
24].
Definition 1 [Topological entropy] [
23] Let
X be a compact metric space and
be the time-one map associated with the flow of the dynamical system defined by the vector field
of the ODE
.
is called a
-separated set,
, if
The topological entropy
of
g is defined as
with
denoting the maximum cardinality of all
-separated sets.
The illustrative meaning of this entropy concept is the following: ϵ determines the resolution scale above which two points are considered separated. counts the number of n-orbits (an orbit of “length n” corresponds to the time-n map ) through whose end points are separated in the sense of Definition 1. Thus the limit characterizes the overall divergence of trajectories. According to Definition 1 the number of (on the ϵ-scale) distinguishable orbits grows with n like .
It follows directly from Definition 1 that and if g is a differentiable map of a compact d-dimensional manifold with the differential .
Definition 2 [Metric entropy] [
23] Let
be a probability space with the
σ-algebra
, an appropriately chosen probability measure
μ such that
is a measure-preserving, i.e.
, time-one map diffeomorphism induced by the flow of the dynamical system defined by
. Let
be a finite partition of X,
and
j is called the
α-address of
if
. For two partitions
we define
, so that elements of
are sets of the form
for index tuples
which are called the
α-addresses of the
n-orbit through
x. With
the metric (or measure-theoretic) entropy
is defined as
From an illustrative point of view can be interpreted as a measure of “average uncertainty” in trying to predict the α-addresses of an arbitrary point in phase space. The following variational principle makes the connection between topological and metric entropy.
Theorem 1 [
25] Let
be a continuous map of a compact metric space
X. Then
over all
g-invariant probability measures
μ.
Metric entropy can also be interpreted as the rate of “loss of information” on the proximity of nearby orbits:
Theorem 2 [
24] Let
be ergodic. Then for
μ-almost every
x it holds
with
.
There is an interesting relation between the above entropy definitions and the concept of Lyapunov exponents characterizing the divergence of trajectories:
Theorem 3 [Ruelle’s Inequality] [
26] Let
be a
-diffeomorphism of a compact Riemannian manifold
M and
μ a
g-invariant ergodic probability measure. With the
r distinct Lyapunov exponents
of
and the linear subspaces
corresponding to
with the dimension
of the multiplicity of
, it holds
Theorem 4 [Pesin’s Formula] [
27] If
μ is equivalent to the Riemannian measure on
M it holds
Finally, topological entropy is related to volume growth caused by the phase flow. Let
M be a compact
m-dimensional
manifold and
a
-mapping and let
with
be the set of
mappings
with the
l-dimensional unit cube
and
the
l-dimensional volume of the image of
σ in
M counted with multiplicity (if
σ is not a one-to-one mapping and the images of several parts coincide, then the set will be counted as many times as it is covered by the image of
σ). For
define
and
Theorem 5- a)
[
28] If
g is
, then
- b)
[
29] For
it holds
For
a) and b) imply
.
In the case , is related to the rate of growth of volumes of -images of embedded sub-manifolds. Reduced models of chemical kinetics (generally approximating slow attracting invariant manifolds) are represented by such embedded sub-manifolds and intuitively their slowness property should be related to minimum growth of volumes when projected into the tangent bundle of these manifolds. This conceptual point of view will be taken when discussing extremum principles for trajectories supposed to be on, respectively close to, slow invariant manifolds.
3. Extremum Principle for Trajectories Approximating Slow Manifolds
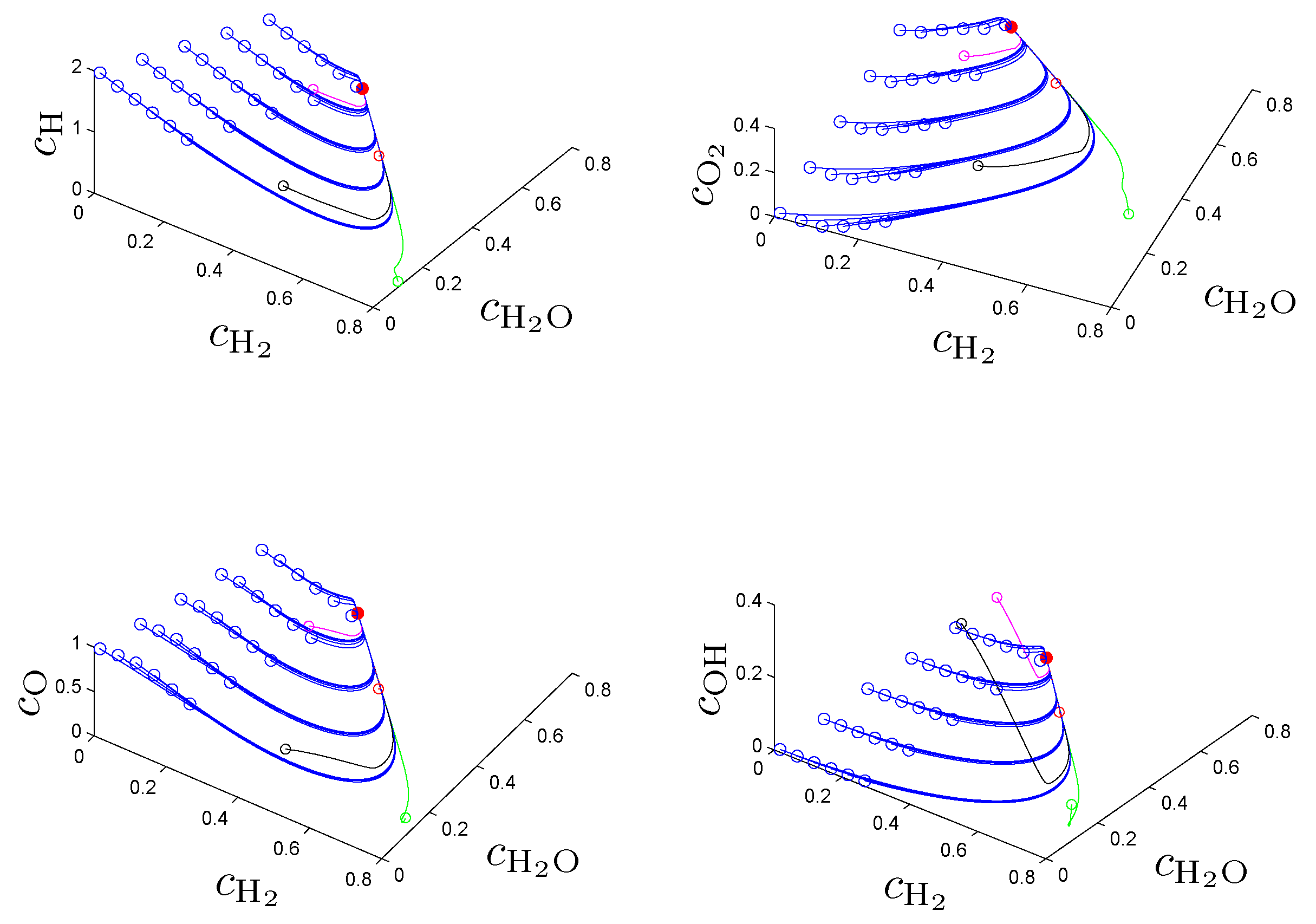
The key of our model reduction approach is based on the goal to exploit non-local phase space information on dissipativeness contained in the behavior of trajectories in time parameterization. This information can be used in a variational problem formulation aimed at a characterization of suitable reaction trajectories approximating slow invariant manifolds (SIM) in terms of an appropriate interpretation of minimum dissipativeness. The formulation of this idea as an ODE-constrained optimization problem allows the use of sophisticated and efficient optimization software for the numerical solution of the problem. The central issue is an objective functional implementing a variational principle for the identification of suitable trajectories which should reflect in a suitable sense minimum dissipation along the slow manifold. We suggest either time-integrated chemical entropy production rate (
1) or the norm of velocity change with time (see
section 3.1.) as a measure for the degree of dissipation. The latter is conceptually close to the notion of a
slow manifold.
We consider autonomous ODE systems of the form
modeling chemical reaction kinetics that have an asymptotically stable fixed point corresponding to chemical equilibrium. The variational problem can be formulated as
subject to
The variable
denotes the state vector and
is an index set that contains the indices of state variables (denoted as
reaction progress variables in chemical kinetics) with (at time
) fixed values chosen to parameterize the reduced model, i.e., the slow attracting manifold to be computed. The cardinality of the index set
equals the dimension of the slow manifold to be computed and has to be set a priori by the user. Thus, those state variables representing the actual degrees of freedom within the optimization problem are
. The process of determining
from
is known as
species reconstruction in model reduction of chemical kinetics and represents a function mapping the reaction progress variables to the full species composition by determining a point on the slow attracting manifold. The system dynamics (e.g., chemical kinetics determined by the reaction mechanism) are described by (2b) and enter the optimization problem as equality constraints. Hence an optimal solution of (2) always satisfies the system dynamics of the full ODE system and therefore represents a solution trajectory of (2b). Additional constraints (e.g. chemical element mass conservation relations in the case of chemical kinetics that have to be obeyed due to the law of mass conservation) are collected in the linear function
g in (2). The state variables chosen as parameterization of the SIM are fixed via the equality constraint (2d) at
. The function
in (2a) characterizes the variational principle that will be discussed in the next section.
The approximated SIM obtained by pointwise solution of problem (2) on a suitable grid of reaction progress variable values can be used as a reduced model of the underlying ODE model, for example via a look-up table for points on the slow manifold. This reduced model is parameterized by the reaction progress variables (coordinate system of the manifold) chosen to be an arbitrary set of variables that allow a unique parameterization of the manifold. Unfortunately, there is no systematic way to check for global uniqueness, however, in many applications physical insight into the system suggests an appropriate choice. In combustion chemistry, usually reaction products and/or intermediates with monotonic behavior during approach of equilibrium are chosen.
For continuously differentiable Φ it is easy to prove existence of a solution to (2) since the constraints (2b) and (2d) make the problem a finite-dimensional one with the initial values as free optimization variables and the linear constraint together with the inequality constraint define a closed and bounded subset of for the feasible initial values. Using the standard compactness argument, the existence of a solution follows. In order to prove uniqueness, convexity is required which cannot generally be assured for nonlinear Φ.
3.1. Optimization Criterion
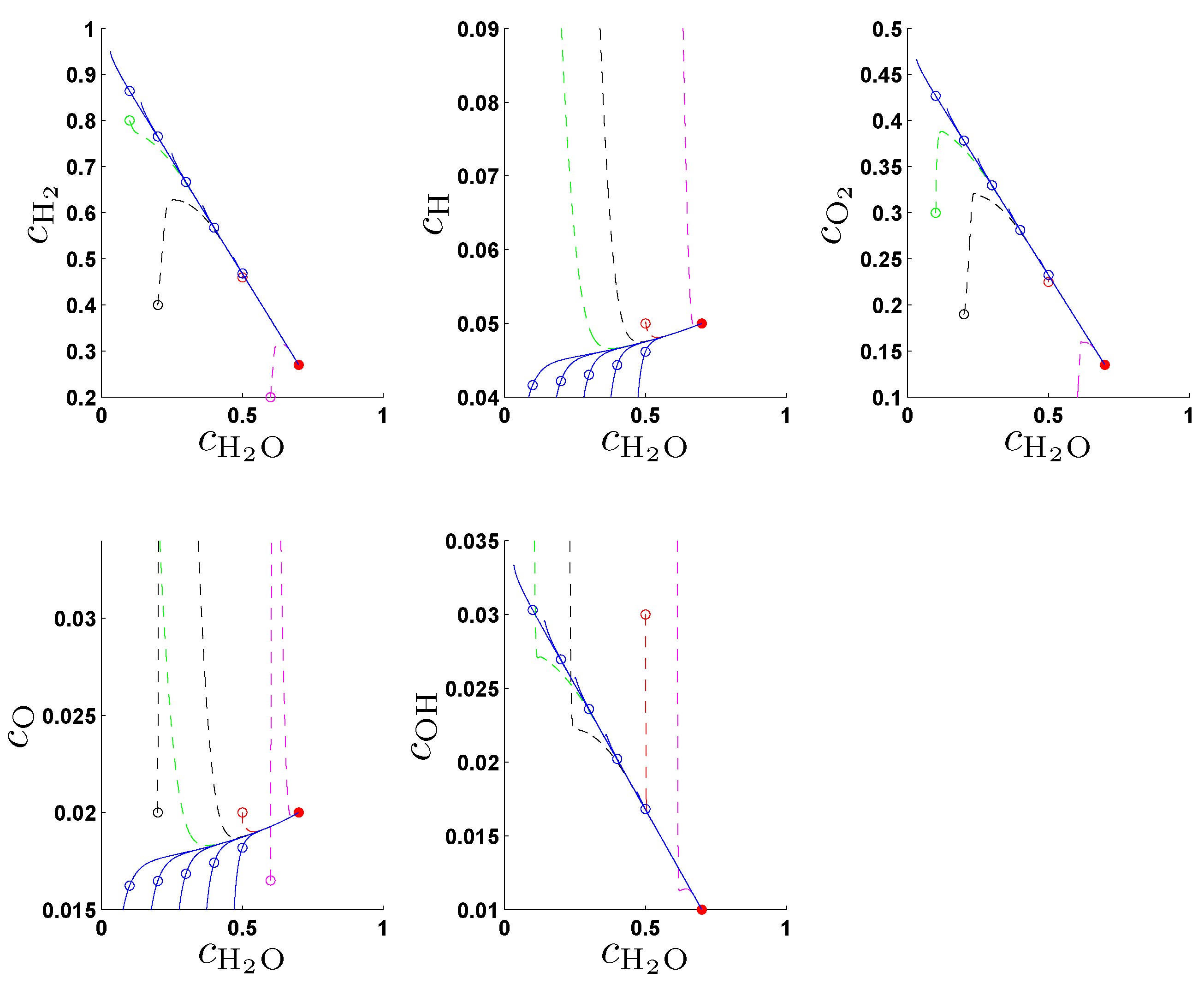
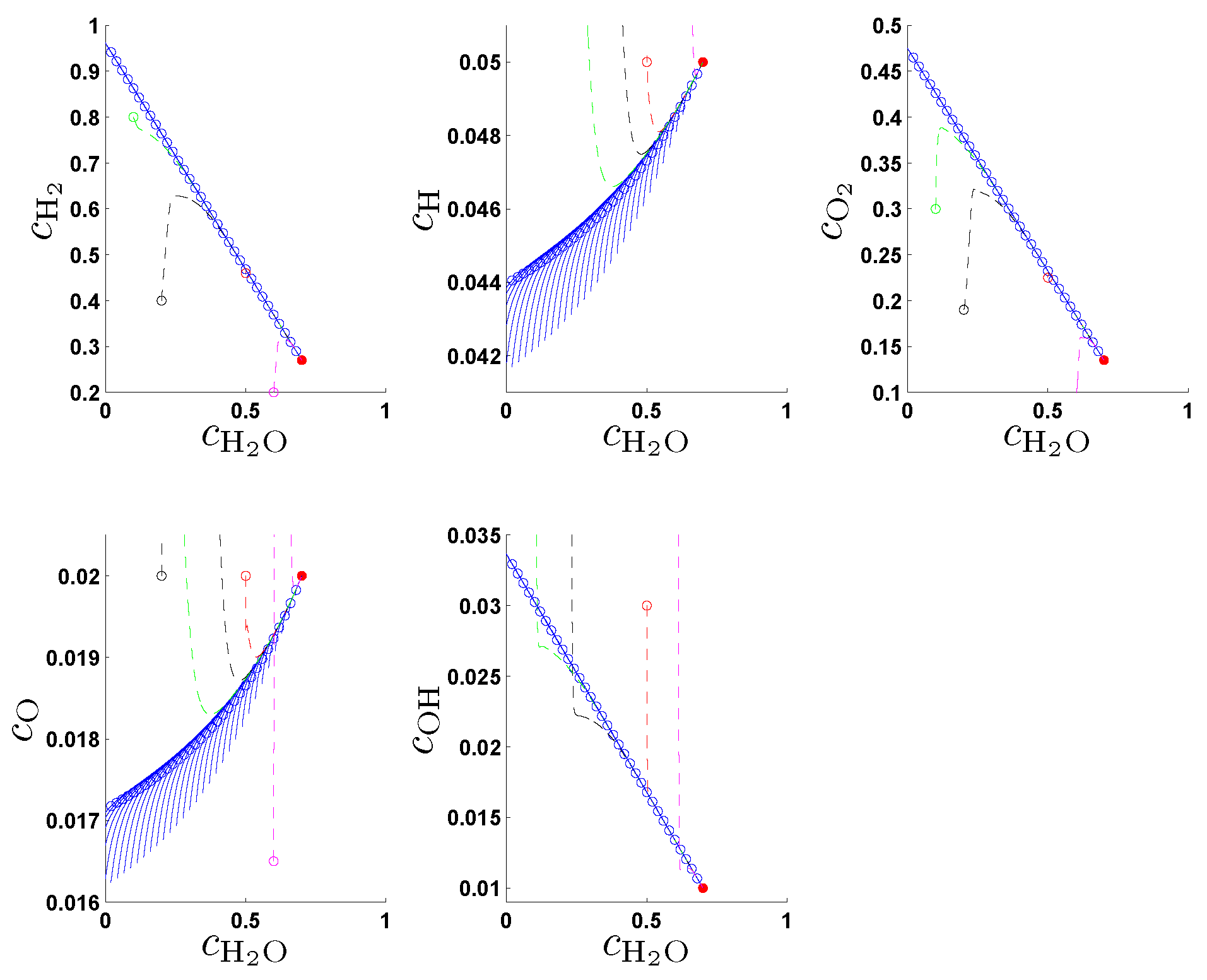
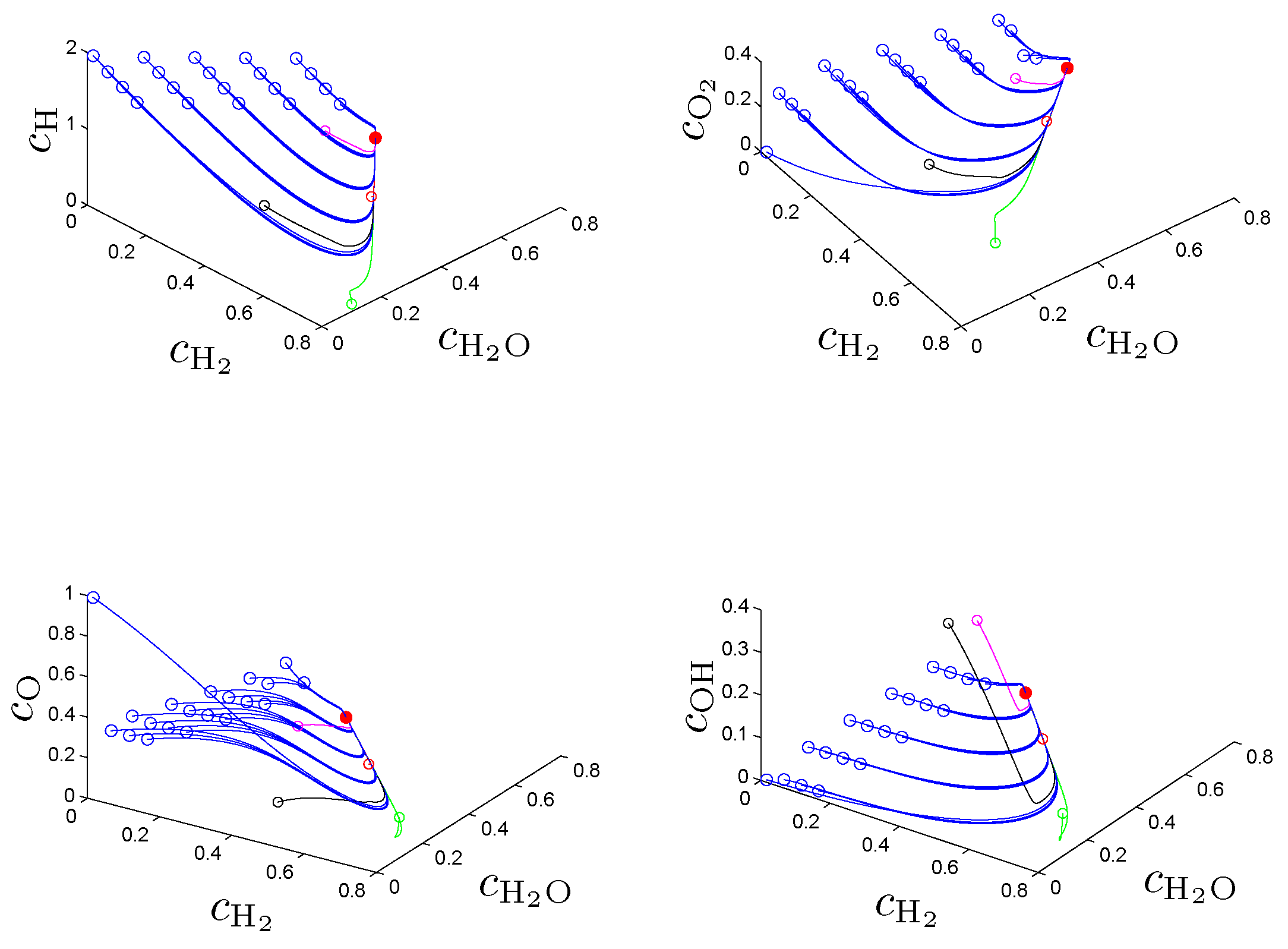
In the original work [
21] the entropy production rate (1) has been chosen as a criterion Φ in (2a) and following the fundamental idea to search for an entropy-related extremum principle that characterizes trajectories on or near slow attracting manifolds we discuss geometric criteria in [
31]. In
Section 4. we show that the latter are superior to the previously used entropy production rate and yield accurate approximations of slow invariant manifolds for an example model of chemical kinetics. We propose an appropriate characterization of maximum “slowness” in terms of an integral over suitably defined curvature (velocity change) of trajectories measured in the Euclidean norm. An attracting SIM is characterized by the property that all trajectories in its neighborhood converge faster (with exponential rates) to the manifold than to the attractor, the chemical equilibrium point. Adrover
et al. [
30] recently argued that this might be expressed as a ratio
of the local stretching (contraction) rate of vectors orthogonal to the manifold compared to those tangent to the manifold. Their local point of view comes close to our reasoning on the basis of a variational principle for trajectories.
The corresponding geometric objective functional (time integral over
) to be minimized in (2a) is supposed to incorporate essential characteristics of slow attracting manifolds. The successive relaxation of chemical forces causes curvature in the reaction trajectories (in the sense of velocity change along the trajectory). Therefore, in [
31,
32]
is proposed as a suitable criterion in (2a) with
being the Jacobian of the right hand side
f evaluated at
and
denoting the Euclidean norm.
The term
represents the rate of change of the reaction velocity vector in its own direction along a trajectory and can be interpreted as a specific definition of curvature in time parameterization of the curve:
The minimization of the time integral over Φ in (2a) incorporates the “maximum slowness” respectively “minimum dissipation” issue in terms of an average over suitably measured local curvature (in time parameterization) of a trajectory. The qualitative relation to the entropy concepts in dynamical systems theory reviewed in
section 2. becomes obvious when considering the time evolution of two nearby points
A and
B lying
ϵ-close to each other on the same trajectory defined by the optimal solution of (2) with (1) in the objective functional (2a) . Imagine now a phase flow field with constant velocity,
i.e.,
, along the trajectory. It follows
and the two points
A and
B are transported by the phase flow in backward time direction for some time
such that the end points after time
have the same distance as the initial points when measured in arc length of the trajectory piece connecting the two points. Increase in that distance between two
ϵ-close points
A and
B under this time-
map is obviously related to
. Along a trajectory with small
(a measure for velocity change in the interval
) the increase in distance between the two points
A and
B should be small as well along this particular trajectory. This relates to the ideas contained in the topological and metric entropy Definitions 1 and 2 in
section 2. implementing concepts to measure divergence, dissipation or information loss respectively and thus our criterion allows for a minimum entropy interpretation in terms of small distance growth between two points on the optimal trajectory for a given time horizon
. A stringent theoretical justification of the curvature criterion and its use for approximating slow attracting manifolds of 2-dimensional linear and nonlinear test models is provided in [
38] and beyond the scope of the present paper. Here, we restrict ourselves to the qualitative motivation related to entropy concepts.
3.2. Numerical Methods
Optimization problem (2) can be solved as a standard nonlinear programming problem (NLP), for example via the sequential quadratic programming (SQP) method [
33] or interior point methods (e.g., [
34]). However, one has to decide how to treat the differential equation constraint and the objective functional. The easiest way is a decoupled iterative approach, a full numerical integration of the ODE model with the current values of the variables subject to optimization. This is called the sequential (or single shooting) approach since it fully decouples simulation of the model and optimization. However, it is often beneficial to have an “all at once” approach that couples simulation and optimization via discretization of the ODE constraint. This simultaneous approach has the advantage of introducing more freedom into the optimization problem since the differential equation model does not have to be solved exactly in each iteration of the optimization. A fully discrete collocation approach and a numerical quadrature formula are appropriate for the treatment of the ODE constraints and the objective functional respectively. On a predefined time grid the collocation method constructs polynomials obeying the differential equation at a certain number of nodes depending on its degree. For the numerical solutions presented in this paper we use a Radau collocation method with linear, quadratic, or cubic polynomials, respectively. The resulting NLP is solved by use of the interior point algorithm implemented in the IPOPT-package [
34]. As in [
32] we use the invariance defect (see [
35,
36] and references therein) as a measure of “goodness” of the slow manifolds computed numerically. Restarting the optimization algorithm for parameter values corresponding to a point on a previously computed solution trajectory should yield the same trajectory in the case of invariance of the computed manifold.