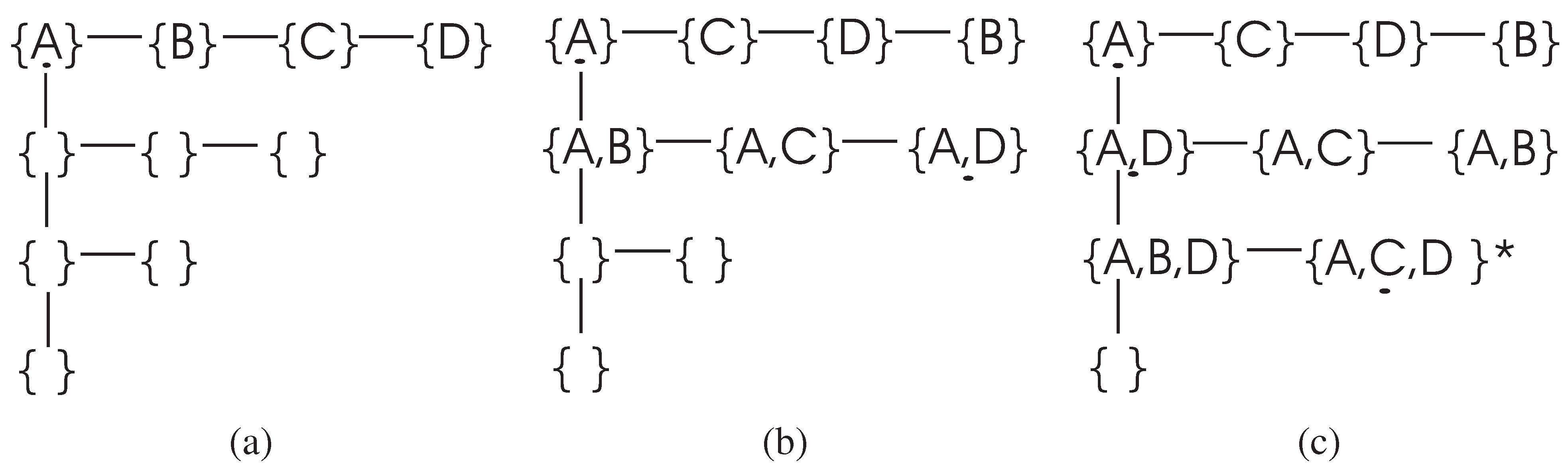3.1. Theoretic Motivation and Foundation
We restate the theorem about the relationship between the MI and the number of attributes in .
Theorem 3 ([35], p. 26) , with equality if and only if for all with .
Proof of Theorem 3 can be found in [
35]. In Theorem 3, it can be seen that {
will contain more or equal information about
Y as
does. To put it another way, the more variables, the more information is provided about another variable.
To measure which subset of features is optimal, we reformulate the following theorem, which is the theoretical foundation of our algorithm.
Theorem 4 If the MI between and Y is equal to the entropy of Y, i.e., , then Y is a function of .
It has been proved that if
, then
Y is a function of
X [
30]. Since
, it is immediate to obtain Theorem 4. The entropy
represents the diversity of the variable
Y. The MI
represents the dependence between vector
and
Y. From this point of view, Theorem 4 actually says that the dependence between vector
and
Y is very strong, such that there is no more diversity for
Y if
has been known. In other words, the value of
can fully determine the value of
Y.
satisfying Theorem 4 is defined as
essential attributes (EAs), because
essentially determines the value of
Y [
14].
3.2. Performing Feature Selection
The feature selection is often used as a preprocessing step before building models for classification. The aim of feature selection is to remove the irrelevant and redundant features, so that the induction algorithms can produce better prediction accuracies with more concise models and better efficiency.
From Theorem 1, the irrelevant features tend to share zero or very small MI with the class attribute in the presence of noise. Therefore, the irrelevant features can be eliminated by choosing those features with relatively large MI with the class attribute in modelling process.
When choosing candidate features, our approach maximizes the MI between the feature subsets and the class attribute. Suppose that
has already been selected at the step
, and the DFL algorithm is trying to add a new feature
to
. Specifically, our method uses the following criterion,
and
where
,
,
, and
. From Equation
14, it is obvious that the irrelevant features have lost the opportunity to be chosen as EAs of the classifiers after the first EA,
, is chosen, since
is very small if
is an irrelevant feature.
Next, we illustrate how to eliminate the redundant features. From Theorem 2, we have
In Equation
15, note that
does not change when trying different
. Hence, the maximization of
in our method is actually maximizing
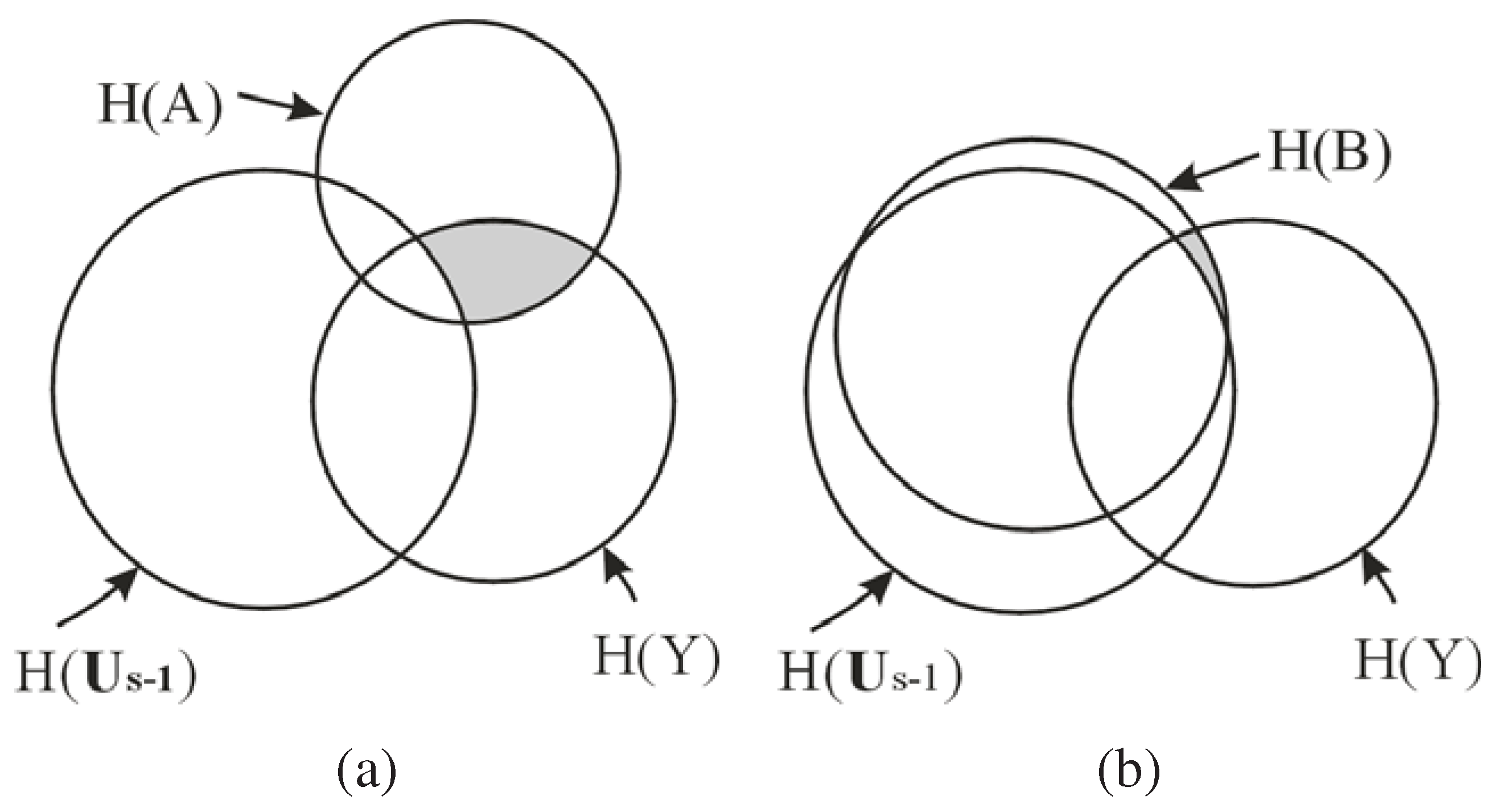
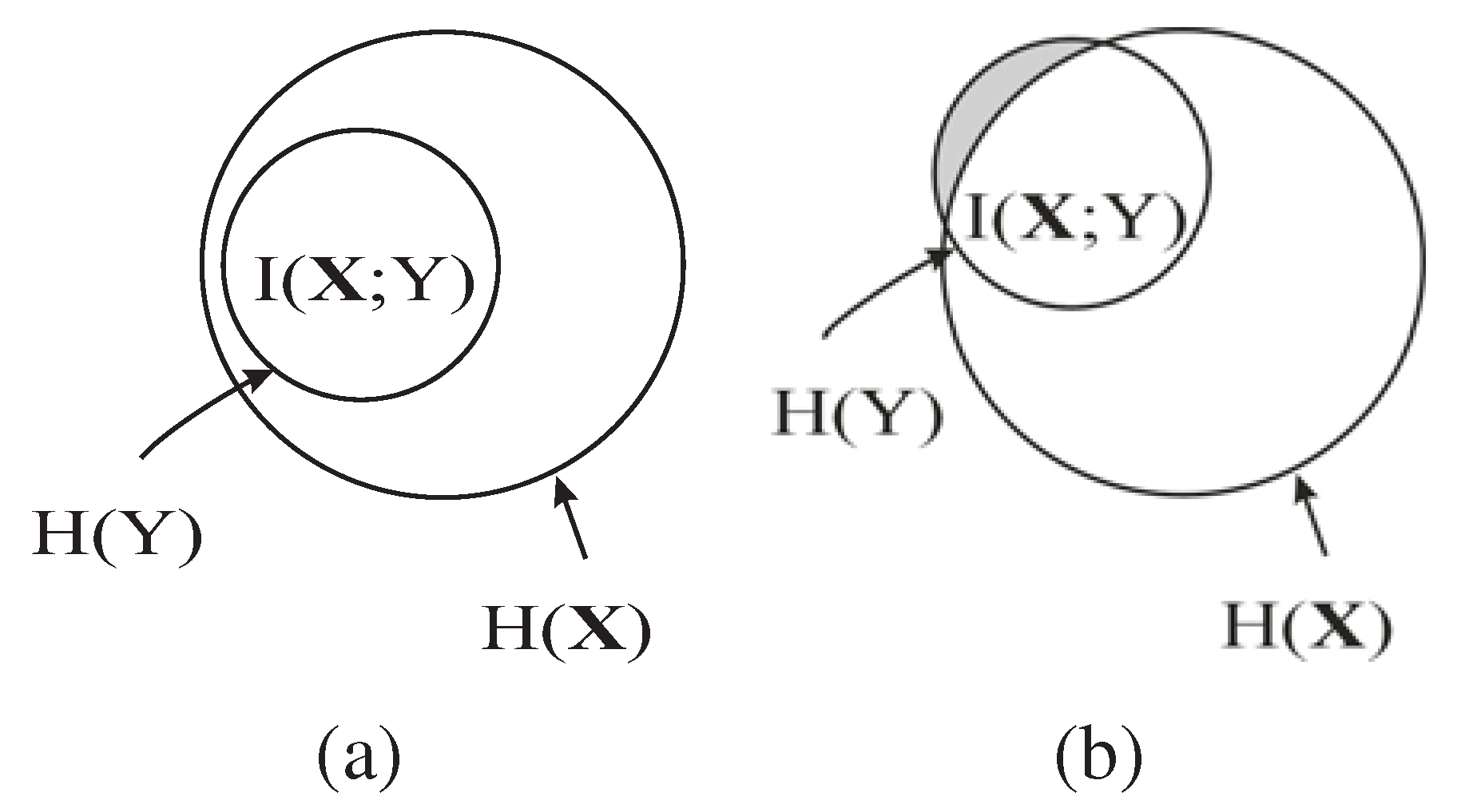
, as shown by the shaded region in
Figure 1, which is the conditional MI of
and
Y given the already selected features
,
i.e., the information of
Y not captured by
but carried by
. As shown in
Figure 1 (b), if the new feature
B is a redundant feature,
i.e.,
is large, then the additional information of
Y carried by
,
, will be small. Consequently,
B is unlikely to be chosen as an EA based on Equation
15. Hence, the redundant features are automatically eliminated by maximizing
.
From Theorem 4, if a feature subset
satisfies
=
, then Y is a deterministic function of
, which means that
is a complete and optimal feature subset. But the real data sets are often noisy. Thus, the DFL algorithm estimates the optimal feature subsets with the
ϵ value method to be introduced in
Section 4. by finding feature subsets to satisfy
.
In summary, the irrelevant and redundant features can be automatically removed, if the new candidate feature is evaluated with respect to the selected features as a vector by maximizing . Furthermore, the optimal subset of features can be determined by evaluating with respect to .
3.3. Relation to Markov Blanket
Conditional Independence (see [
36], p. 83) is a concept used in graphical models, especially Bayesian networks [
36].
Definition 1 (Conditional Independence) Let and be a joint probability function over the variables in . , and , the sets and are said to be conditional independent given
if
In other words, learning the value of
does not provide additional information about
, once we know
.
Markov Blanket [
36] is defined as follows.
Definition 2 (Markov Blanket) Let be some set of features(variables) which does not contain . We say that is a Markov Blanket
for if is conditional independent of [37] given , i.e.,A set is called a Markov boundary of , if it is a minimum Markov Blanket
of , i.e.
, none of its proper subsets satisfy Equation 17 (see [36], p. 97). From the definition of
Markov Blanket, it is known that if we can find a
Markov Blanket for the class attribute
Y, then all other variables in
will be statistically independent of
Y given
. This means that all the information that may influence the value of
Y is stored in values of
[
38]. In other words,
Markov Blanket has prevented other nodes from affecting the value of
Y.
Markov Blanket also corresponds to strongly relevant features [
39], as defined by Kohavi and John [
22]. Therefore, if we can find a
Markov Blanket of
Y as the candidate feature subsets,
should be the theoretical optimal subset of features to predict the value of
Y, as discussed in [
1,
39].
Next, let us discuss the relationship between our method and Markov Blanket. First, we restate Theorem 5 and 6, which is needed to prove Theorem 7.
Theorem 5 ([40], p. 36) Suppose that is a set of discrete random variables, and Y are a finite discrete random variables. Then, .
Theorem 6 ([30], p. 43) If , where is a set of discrete random variables, then .
Theorem 7 If , , , Y and are conditional independent given .
Proof 1 Let us consider ,
.
Firstly, Secondly, from Theorem 4, .
Then, from Theorem 6, .
So, Thus, .
From Theorem 5, we haveOn the other hand, from Theorem 3, we getFrom both Equation 18 and Equation 19, we obtain .
Again from Theorem 3, we get .
That is to say, Y and are conditional independent given .
Based on Theorem 7 and the concept of Markov Blanket, it is known that if , then is a Markov Blanket of Y. Formally, we have
Theorem 8 If , then is a Markov Blanket of Y.
Proof 2 Immediately from Theorem 7 and Definition 2.
As to be introduced in
Section 4.,
can be satisfied only when the data sets are noiseless. However, with the introduction of
ϵ method in
Section 4., the set that carries most information of
Y,
, is still a good estimation of the true
Markov Blanket of
Y. In addition, our method has competitive expected computational costs when compared to other methods for finding
Markov Blankets, such as in [
1,
39,
41,
42].
3.4. The Discrete Function Learning Algorithm
satisfying is a complete feature subsets in predicting Y based on Theorem 4. As also proved in Theorem 8, satisfying is a good feature subsets for predicting Y. Thus, we aim to find with from the training data sets for solving the problem of finding optimal feature subsets.
For n discrete variables, there are totally subsets. Clearly, it is NP-hard to examine all possible subsets exhaustively. It is often the case that there are some irrelevant and redundant features in the domain . Therefore, it is reasonable to reduce the searching space by only checking feature subsets with a predefined number of features. In this way, the problem can be solved in polynomial time.
Based on the above consideration, the DFL algorithm uses a parameter, the expected cardinality of EAs
K, to prevent the exhaustive searching of all subsets of attributes by checking those subsets with fewer than or equal to
K attributes, as listed in
Table 1 and
Table 2. The DFL algorithm has another parameter, the
ϵ value, which will be elaborated in
Section 4.
When trying to find the EAs from all combinations whose cardinalities are not larger than
K, the DFL algorithm will examine the MI between the combination of variables under consideration,
, and the class attribute,
Y. If
, then the DFL algorithm will terminate its searching process, and obtain the classifiers by deleting the non-essential attributes and duplicate instances of the EAs in the training data sets, which corresponds to step 5 in
Table 2. Meanwhile, the counts of different instances of
are stored in the classifiers and will be used in the prediction process. In the algorithm, we use the following definitions.
Definition 3 (δ Superset) Let be a subset of , then of is a superset of so that and .
Definition 4 (Δ Supersets) Let be a subset of , then of is the collective of all and .
Definition 5 (Searching Layer of ) Let , then the ith layer of all subsets of is, , .
Definition 6 (Searching Space) The searching space of functions with a bounded indegree K is .
From Definition 5, it is known that there are subsets of in . And there are subsets of in .
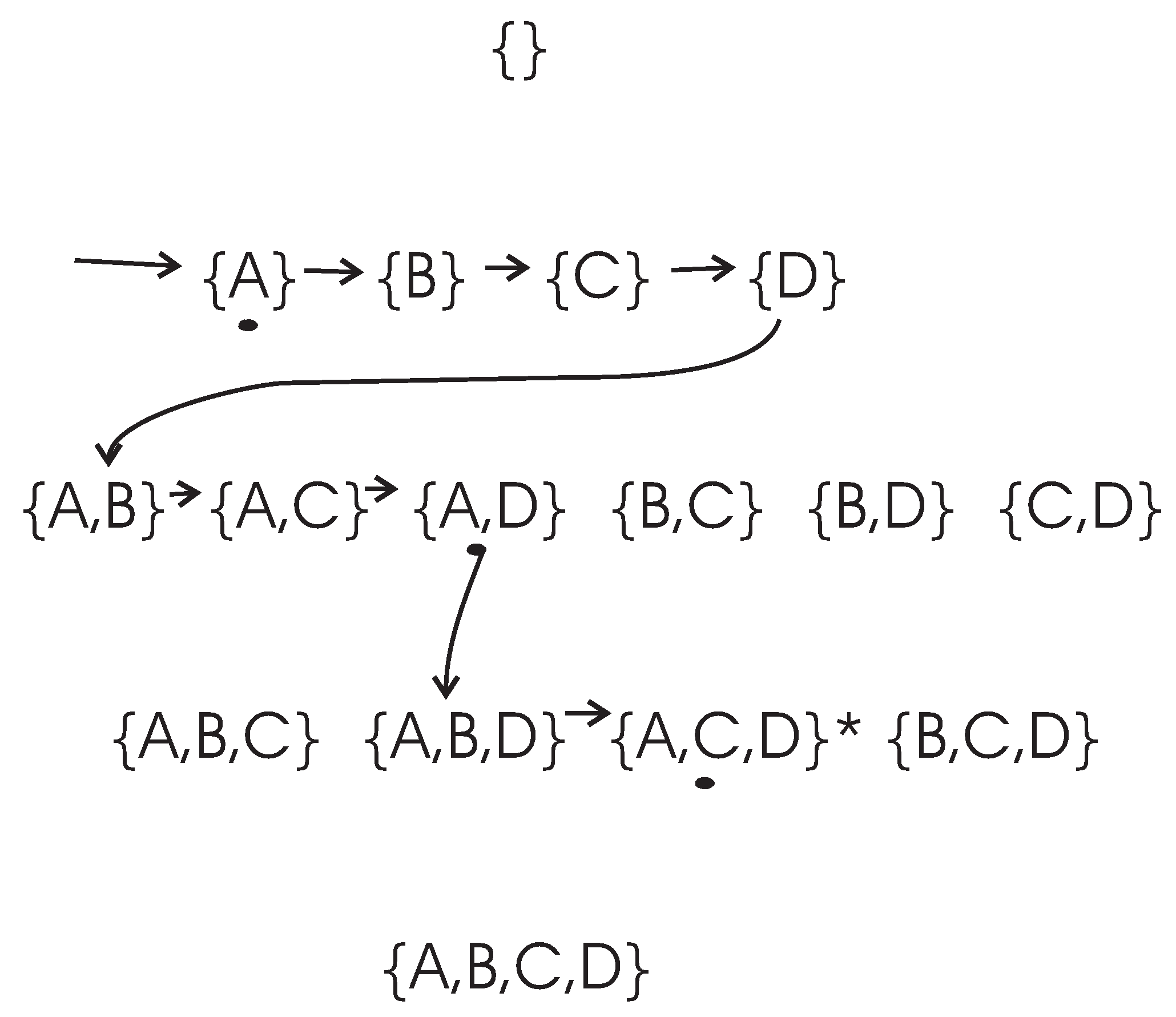
To clarify the search process of the DFL algorithm, let us consider an example, as shown in
Figure 2. In this example, the set of attributes is
and the class attribute is determined with
, where “·" and “+" are logic AND and OR operation respectively. The expected cardinality
K is set to
for this example. However, there are only three real relevant features. We use
k to represent the actual cardinality of the EAs, therefore,
in this example. The training data set
of this example is shown in
Table 3.
The search procedure of the DFL algorithm for this example is shown in
Figure 2. In the learning process, the DFL algorithm uses a data structure called
to store the Δ supersets in the searching process. For instance, the
when the DFL algorithm is learning the
Y is shown in
Figure 3.
As shown in
Figure 2 and
Figure 3, the DFL algorithm searches the first layer
, then it sorts all subsets according to their MI with
Y on
. Consequently, the DFL algorithm finds that
shares the largest MI with
Y among subsets on
.
Next, the
s are added to the second layer of
, as shown in
Figure 3. Similarly to
, the DFL algorithm finds that
shares the largest mutual information with
Y on
. Then, the DFL algorithm searches through
,
…,
, however it always decides the search order of
based on the calculation results of
. Finally, the DFL algorithm finds that the subset
satisfies the requirement of Theorem 4,
i.e.,
, and will construct the function
f for
Y with these three attributes.
To determine f, firstly, B is deleted from training data set since it is a non-essential attribute. Then, the duplicate rows of are removed from the training data set to obtain the final function f as the truth table of along with the counts for each instance of . This is the reason for which we name our algorithm as the Discrete Function Learning algorithm.
If the DFL algorithm still does not find the target subset, which satisfies the requirement of Theorem 4, in Kth layer , it will return to the first layer. Now, the first node on the and all its supersets have already been checked. In the following, the DFL algorithm continues to calculate the second node on the first layer (and all its supersets), the third one, and so on, until it reaches the end of and fulfills the exhaustive searching of .
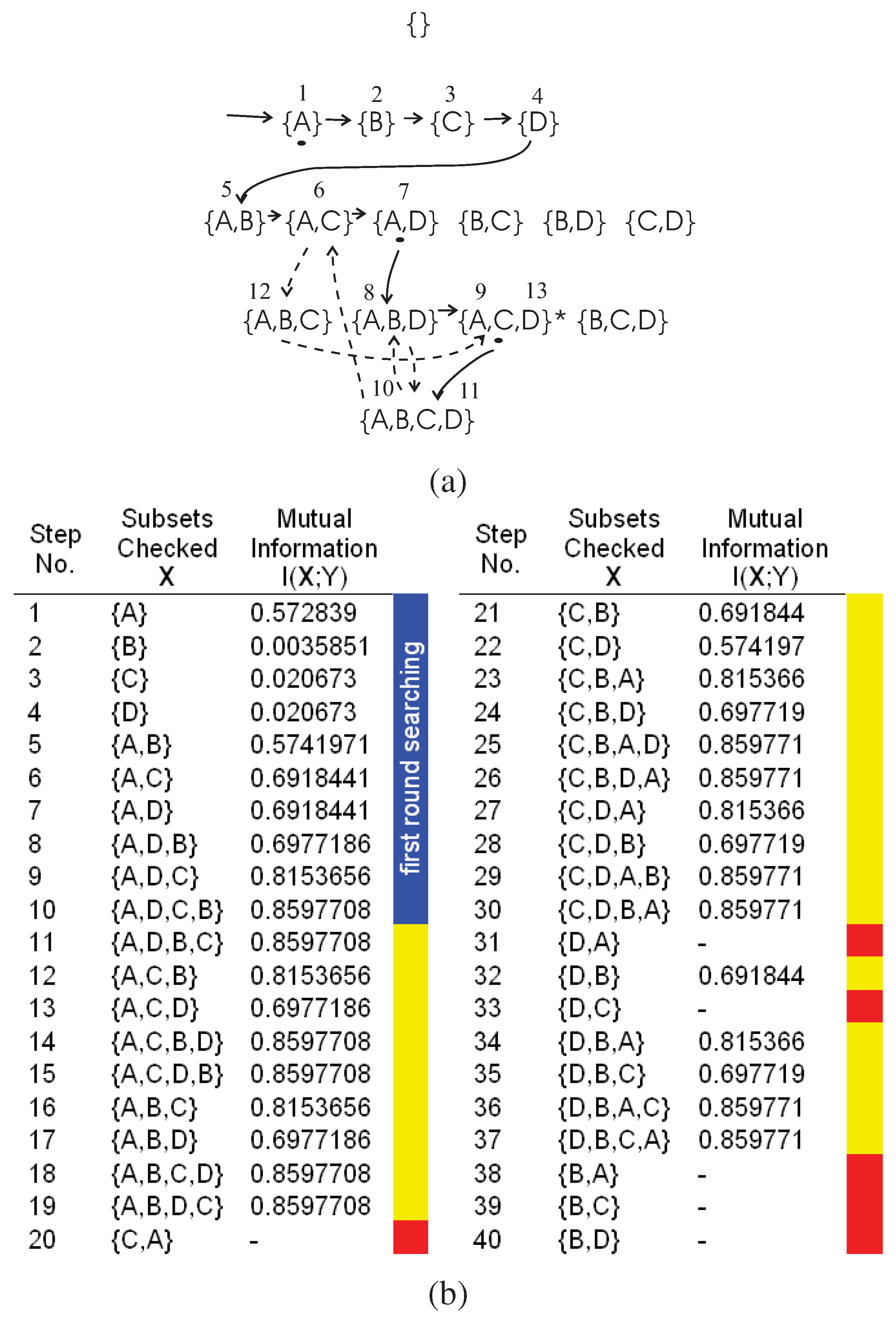
We use the example in
Figure 4 to illustrate the searching steps beyond the first round searching of the DFL algorithm. Note that the DFL algorithm is the same as the classical greedy forward selection algorithm [
43] and uses the mutual information
as the greedy measure before it returns to the
th layer from
Kth layer for the first time. We name the searching steps before this first return as the
first round searching of the DFL algorithm. As shown in
Figure 4 (a) and (b), this first return happens after step 10.
To produce the exhaustive searching, we add one noisy sample (1100,1) to the training data set in
Table 3. Then, we keep the same settings of
and
. As shown in
Figure 4 (b), the mutual information
of all subsets is not equal to
. Therefore, the DFL algorithm will exhaustively check all subsets and finally report “Fail to identify the model for
Y (the classifier) when
ϵ = 0".
In
Figure 4 (a), the first round searching is shown in the solid edges and the subsets checked in each step are shown in the blue region of
Figure 4 (b). In
Figure 4 (a), the dashed edges represent the searching path beyond the first round searching (only partly shown for the sake of legibility), marked as yellow regions in
Figure 4 (b). The red regions are the subsets, as well as their supersets, that will not be checked after deploying the redundancy matrix to be introduced in
Section B.1.
3.5. Complexity Analysis
First, we analyze the worst-case complexity of the DFL algorithm. As to be discussed in
Section 7.1, the complexity to compute the MI
is
, where
N is the number of instances in the training data set. For the example in
Figure 2,
will be visited twice from
and
in the worst case.
will be visited from
,
and
. Thus,
will be checked for
times in the worst case. In general, for a subset with
K features, it will be checked for
times in the worst case. Hence, it takes
to examine all subsets in
. Another computation intensive step is the sort step in line 7 of
Table 2. In
, there is only one sort operation, which takes
time. In
, there would be
n sort operations, which takes
time. Similarly, in
, the sort operation will be executed for
times, which takes
time. Therefore, the total complexity of the DFL algorithm is
in the worst case.
Next, we analyze the expected complexity of the DFL algorithm. As described in
Section 3.4, the actual cardinality of the EAs is
k. After the EAs with
k attributes are found in the subsets of cardinalities
, the DFL algorithm will stop its search. In our example, the
K is 4, while the
k is automatically determined as 3, since there are only 3 EAs in this example. Contributing to sort step in the line 7 of the subroutine, the algorithm makes the best choice on current layer of subsets. Since there are
supersets for a given single element subset,
supersets for a given two element subset, and so on. The DFL algorithm only considers
subsets in the optimal case. Thus, the expected time complexity of the DFL algorithm is approximately
, where
is for sort step in line 7 of
Table 2.
Next, we consider the space complexity of the DFL algorithm. To store the information needed in the search processes, the DFL algorithm uses two data structures. The first one is a linked list, which stores the value list of every variable. Therefore, the space complexity of the first data structure is
. The second one is the
, which is a linked list of length
K, and each node in the first dimension is itself a linked list. The
for the example in
Figure 2 is shown in
Figure 3. The first node of this data structure is used to store the single element subsets. If the DFL algorithm is processing
and its Δ supersets, the second node to the
Kth node are used to store
to
[
44] supersets of
. If there are
n variables, there would be
subsets in the
. To store the
, the space complexity would be
, since only the indexes of the variables are stored for each subsets. Therefore, the total space complexity of the DFL algorithm is
.
Finally, we consider the sample complexity of the DFL algorithm. Akutsu
et al. [
45] proved that
transition pairs are the theoretic lower bound to infer the Boolean networks, where
n is the number of genes (variables),
k is the maximum indegree of the genes, and a transition pair is
(
t is a time point). We further proved Theorem 9 when the genes have more than two discrete levels [
46,
47].
Theorem 9 ([46,47]) transition pairs are necessary in the worst case to identify the qualitative gene regulatory network models of maximum indegree and the maximum number of discrete levels for variables .
When considering the sample complexity in the context of feature selection (and classification), the transition pair should be replaced with . Because k, n and b in the context of feature selection (classification) are the same as those in learning gene regulatory network models, the number of samples N in training data set has the same theoretic lower bound of as in Theorem 9.