A Survey on Interference Networks: Interference Alignment and Neutralization
Abstract
:1. Introduction
1.1. Traditional Approaches

1.2. New Paradigms
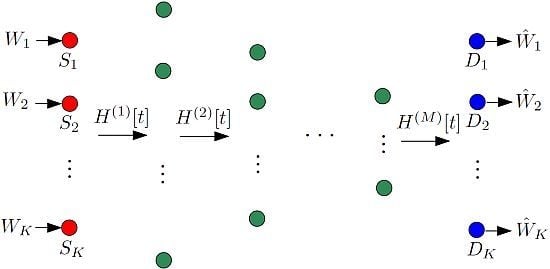
1.3. Layered Multi-Source Multi-Hop Networks

2. Single-Hop Networks: Interference Alignment
2.1. Signal-Space Interference Alignment


2.2. Ergodic Interference Alignment

2.3. Other Interference Alignment Techniques
3. Multi-Hop Networks: Interference Neutralization

3.1. Neutralization with Symbol Extension

3.2. Ergodic Interference Neutralization


4. Beyond Degrees of Freedom
4.1. Approximate Ergodic Capacity
5. Conclusions
Acknowledgments
References
- Cover, T.M.; El-Gamal, A. Capacity theorems for the relay channel. IEEE Trans. Inf. Theory 1979, IT-25, 572–584. [Google Scholar] [CrossRef]
- Carleial, A.B. A case where interference does not reduce capacity. IEEE Trans. Inf. Theory 1975, IT-21, 569–570. [Google Scholar] [CrossRef]
- Han, T.S.; Kobayashi, K. A new achievable rate region for the interference channel. IEEE Trans. Inf. Theory 1981, IT-27, 49–60. [Google Scholar] [CrossRef]
- Etkin, R.H.; Tse, D.N.C.; Wang, H. Gaussian interference channel capacity to within one bit. IEEE Trans. Inf. Theory 2008, 54, 5534–5562. [Google Scholar] [CrossRef]
- Minero, P.; Franceschetti, M.; Tse, D.N.C. Random access: An information-theoretic perspective. IEEE Trans. Inf. Theory 2012, 58, 909–930. [Google Scholar] [CrossRef]
- Cadambe, V.R.; Jafar, S.A. Interference alignment and degrees of freedom of the K-user interference channel. IEEE Trans. Inf. Theory 2008, 54, 3425–3441. [Google Scholar] [CrossRef]
- Maddah-Ali, M.; Motahari, A.; Khandani, A. Communication over MIMO X channels: Interference alignment, decomposition, and performance analysis. IEEE Trans. Inf. Theory 2008, 54, 3457–3470. [Google Scholar] [CrossRef]
- Cadambe, V.R.; Jafar, S.A. Interference alignment and the degrees of freedom of wireless X networks. IEEE Trans. Inf. Theory 2009, 54, 3893–3908. [Google Scholar] [CrossRef]
- Gou, T.; Jafar, S.A. Degrees of freedom of the K user M × N MIMO interference channel. IEEE Trans. Inf. Theory 2010, 56, 6040–6057. [Google Scholar] [CrossRef]
- Suh, C.; Ho, M.; Tse, D.N.C. Downlink interference alignments. IEEE Trans. Commun. 2011, 59, 2616–2626. [Google Scholar] [CrossRef]
- Suh, C.; Tse, D.N.C. Interference alignment for cellular networks. In Proceedings of the Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 23–26 September 2008.
- Cadambe, V.R.; Jafar, S.A. Degrees of freedom of wireless networks with relays, feedback, cooperation and full duplex operation. IEEE Trans. Inf. Theory 2009, 55, 2334–2344. [Google Scholar] [CrossRef]
- Annapureddy, V.S.; El-Gamal, A.; Veeravalli, V.V. Degrees of freedom of interference channels with CoMP transmission and reception. IEEE Trans. Inf. Theory 2012, 58, 5740–5760. [Google Scholar] [CrossRef]
- Ke, L.; Ramamoorthy, A.; Wang, Z.; Yin, H. Degrees of freedom region for an interference network with general message demands. IEEE Trans. Inf. Theory 2012, 58, 3787–3797. [Google Scholar] [CrossRef]
- Nazer, B.; Gastpar, M.; Jafar, S.A.; Vishwanath, S. Ergodic interference alignment. IEEE Trans. Inf. Theory 2012, 58, 6355–6371. [Google Scholar]
- Rankov, B.; Wittneben, A. Spectral efficient protocols for half- duplex fading relay channels. IEEE J. Select. Areas Commun. 2007, 25, 379–389. [Google Scholar] [CrossRef]
- Mohajer, S.; Diggavi, S.N.; Fragouli, C.; Tse, D.N.C. Approximate capacity region for a class of relay-interference networks. IEEE Trans. Inf. Theory 2011, 57, 2837–2864. [Google Scholar] [CrossRef]
- Gou, T.; Jafar, S.A.; Wang, C.; Jeon, S.-W.; Chung, S.-Y. Aligned interference neutralization and the degrees of freedom of the 2 × 2 × 2 interference channel. IEEE Trans. Inf. Theory 2012, 58, 4381–4395. [Google Scholar] [CrossRef]
- Jeon, S.-W.; Chung, S.-Y.; Jafar, S.A. Degrees of freedom region of a class of multisource Gaussian relay networks. IEEE Trans. Inf. Theory 2011, 57, 3032–3044. [Google Scholar] [CrossRef]
- Jeon, S.-W.; Wang, C.-Y.; Gastpar, M. Approximate Ergodic Capacity of a Class of Fading 2 × 2 × 2 Networks. In Proceedings of the Information Theory and Applications Workshop, San Diego, CA, USA, 5–10 February 2012.
- Jeon, S.-W.; Wang, C.-Y.; Gastpar, M. Approximate ergodic capacity of a class of fading 2-user 2-hop networks. In Proceedings of the IEEE International Symposium on Information Theory, Cambridge, MA, USA, 1–6 July 2012.
- Birk, Y.; Kol, T. Coding on demand by an informed source (ISCOD) for efficient broadcast of different supplemental data to caching clients. IEEE Trans. Inf. Theory 2006, 52, 2825–2830. [Google Scholar] [CrossRef]
- Suh, C.; Ramchandran, K. Exact-repair MDS code construction using interference alignment. IEEE Trans. Inf. Theory 2011, 57, 1425–1442. [Google Scholar] [CrossRef]
- Cadambe, V.R.; Jafar, S.A.; Maleki, H.; Ramchandran, K.; Suh, C. Asymptotic interference alignment for optimal repair of MDS codes in distributed storage. IEEE Trans. Inf. Theory 2011. Submitted. [Google Scholar] [CrossRef]
- Maleki, H.; Cadambe, V.R.; Jafar, S.A. Index Coding–An Interference Alignment Perspective. In Proceedings of the IEEE International Symposium on Information Theory, Cambridge, MA, USA, 1–6 July 2012.
- Choi, S.W.; Jafar, S.A.; Chung, S.-Y. On the beamforming design for efficient interference alignment. IEEE Commun. Lett. 2009, 13, 847–849. [Google Scholar] [CrossRef]
- Cadambe, V.R.; Jafar, S.A. Parallel Gaussian interference channels are not always separable. IEEE Trans. Inf. Theory 2009, 55, 3983–3990. [Google Scholar] [CrossRef]
- Sankar, L.; Shang, X.; Erkip, E.; Poor, H.V. Ergodic Two-User Interference Channels: Is Separability Optimal? In Proceedings of the Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 23–26 September 2008.
- Nazer, B.; Gastpar, M.; Jafar, S.A.; Vishwanath, S. Ergodic Interference Alignment. In Proceedings of the IEEE International Symposium on Information Theory, Seoul, Korea, 28 June–3 July 2009.
- Jeon, S.-W.; Chung, S.-Y. Capacity of a Class of Multi-Source Relay Networks. In Proceedings of the Information Theory and Applications Workshop, La Jolla, CA, USA, 8–13 February 2009.
- Koyluoglu, O.O.; El Gamal, H.; Lai, L.; Poor, H.V. Interference alignment for secrecy. IEEE Trans. Inf. Theory 2011, 57, 3323–3332. [Google Scholar] [CrossRef]
- Johnson, O.; Aldridge, M.; Piechocki, R. Delay–Rate Tradeoff in Ergodic Interference Alignment. In Proceedings of the IEEE International Symposium on Information Theory, Cambridge, MA, USA, 1–6 July 2012.
- Cadambe, V.R.; Jafar, S.A. Interference alignment with asymmetric complex signaling—Settling the Høst-Madsen–Nosratinia conjecture. IEEE Trans. Inf. Theory 2010, 56, 4552–4565. [Google Scholar] [CrossRef]
- Motahari, A.; Gharan, S.; Maddah-Ali, M.; Khandani, A. Real interference alignment: Exploiting the potential of single antenna systems. Available online: arxiv.org/abs/0908.2282/ (accessed on 28 September 2012).
- Motahari, A.; Gharan, S.; Khandani, A. Real interference alignment with real numbers. Available online: arXiv:cs.IT/0908.1208/ (accessed on 28 September 2012).
- Shomorony, I.; Avestimehr, A. S. Two-unicast wireless networks: Characterizing the degrees-of-freedom. IEEE Trans. Inf. Theory 2012. [Google Scholar] [CrossRef]
- Wang, C.; Gou, T.; Jafar, S.A. Multiple Unicast Capacity of 2-source 2-sink Networks. In Proceedings of the IEEE Global Telecommunications Conference, Houston, TA, USA, 5–9 December 2011.
- Vaze, C.S.; Varanasi, M.K. Beamforming and aligned interference neutralization achieve the degrees of freedom region of the 2 × 2 × 2 MIMO interference network. In Proceedings of the Information Theory and Applications Workshop, San Diego, CA, USA, 5–10 February 2012.
- Bresler, G.; Parekh, A.; Tse, D.N.C. The approximate capacity of the many-to-one and one-to-many Gaussian interference channels. IEEE Trans. Inf. Theory 2010, 56, 4566–4592. [Google Scholar] [CrossRef]
- Nam, W.; Chung, S.-Y.; Lee, Y.H. Capacity of the Gaussian two-way relay channel to within bit. IEEE Trans. Inf. Theory 2010, 56, 5488–5494. [Google Scholar] [CrossRef]
- Avestimehr, A.S.; Diggavi, S.N.; Tse, D.N.C. Wireless network information flow: A deterministic approach. IEEE Trans. Inf. Theory 2011, 57, 1872–1905. [Google Scholar] [CrossRef]
- Lim, S.H.; Kim, Y.-H.; El Gamal, A.; Chung, S.-Y. Noisy network coding. IEEE Trans. Inf. Theory 2011, 57, 3132–3152. [Google Scholar] [CrossRef]
- Nazer, B.; Gastpar, M. Compute-and-forward: Harnessing interference through structured codes. IEEE Trans. Inf. Theory 2011, 57, 6463–6486. [Google Scholar] [CrossRef]
- Niesen, U.; Nazer, B.; Whiting, P. Computation alignment: Capacity approximation without noise accumulation. In Proceedings of the Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 28–30 September 2011.
- Ordentlich, O.; Erez, U.; Nazer, B. The approximate sum capacity of the symmetric Gaussian K-user interference channel. In Proceedings of the IEEE International Symposium on Information Theory, Cambridge, MA, USA, 1–6 July 2012; pp. 2072–2076.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Jeon, S.-W.; Gastpar, M. A Survey on Interference Networks: Interference Alignment and Neutralization. Entropy 2012, 14, 1842-1863. https://doi.org/10.3390/e14101842
Jeon S-W, Gastpar M. A Survey on Interference Networks: Interference Alignment and Neutralization. Entropy. 2012; 14(10):1842-1863. https://doi.org/10.3390/e14101842
Chicago/Turabian StyleJeon, Sang-Woon, and Michael Gastpar. 2012. "A Survey on Interference Networks: Interference Alignment and Neutralization" Entropy 14, no. 10: 1842-1863. https://doi.org/10.3390/e14101842