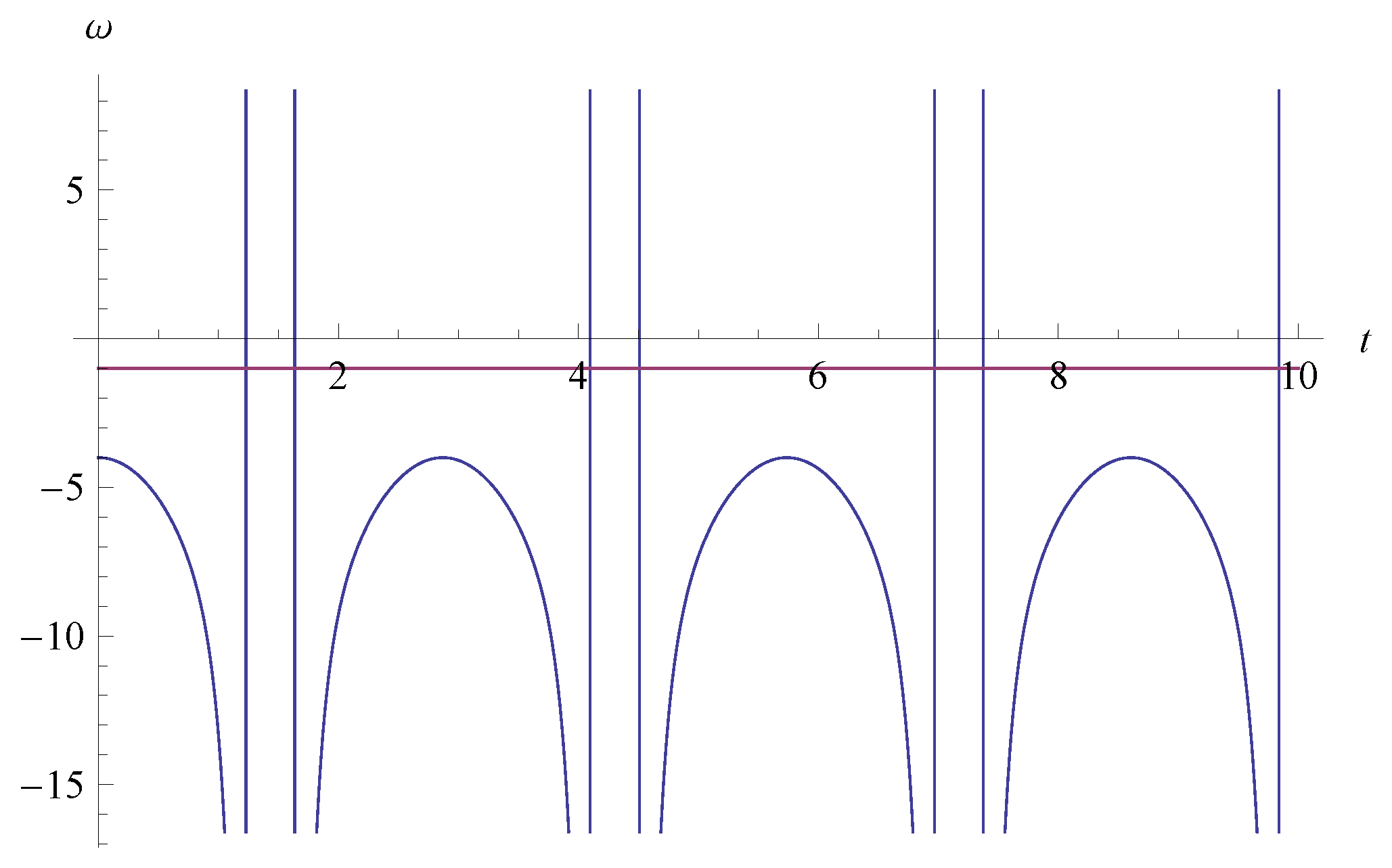
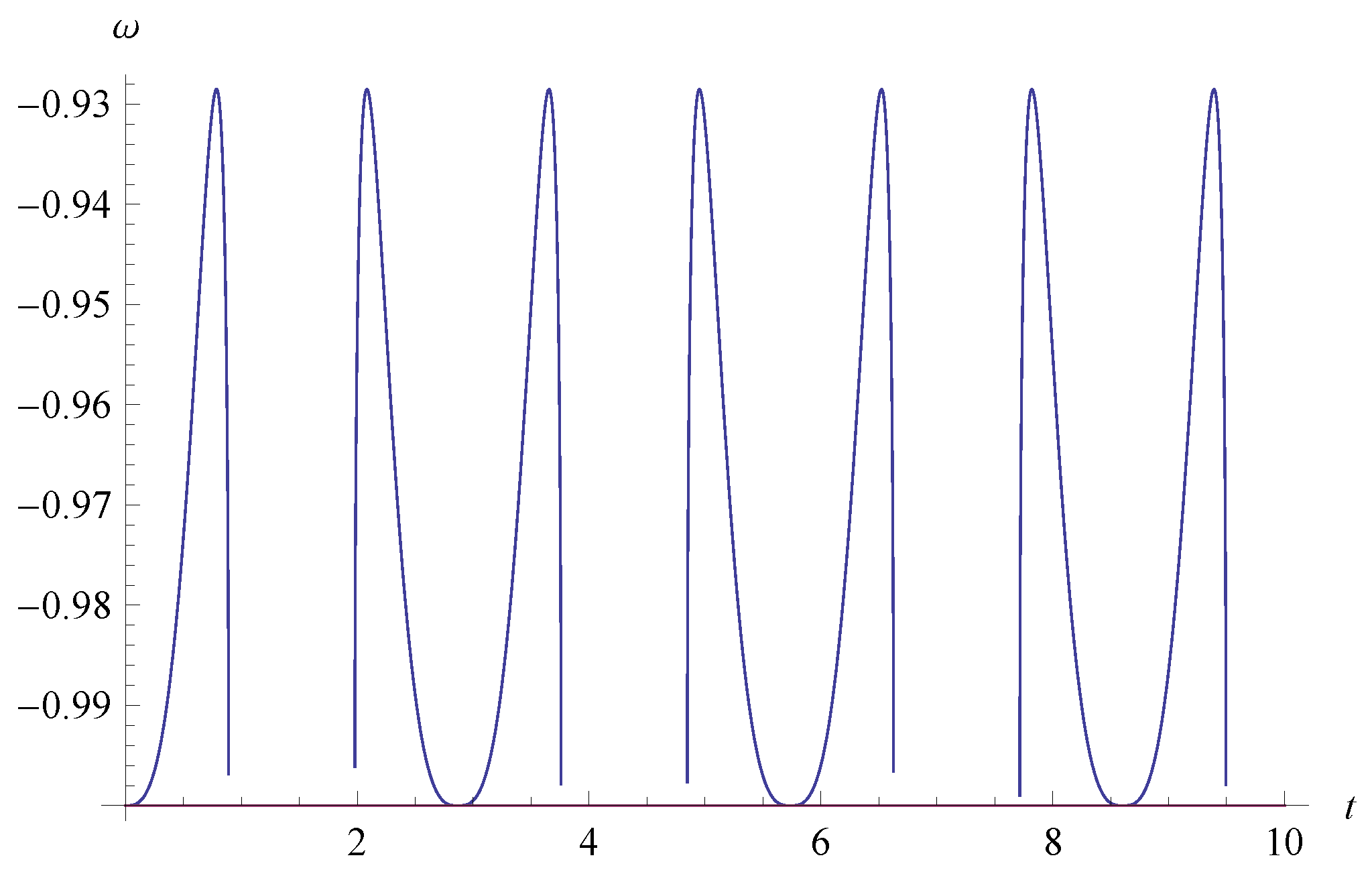
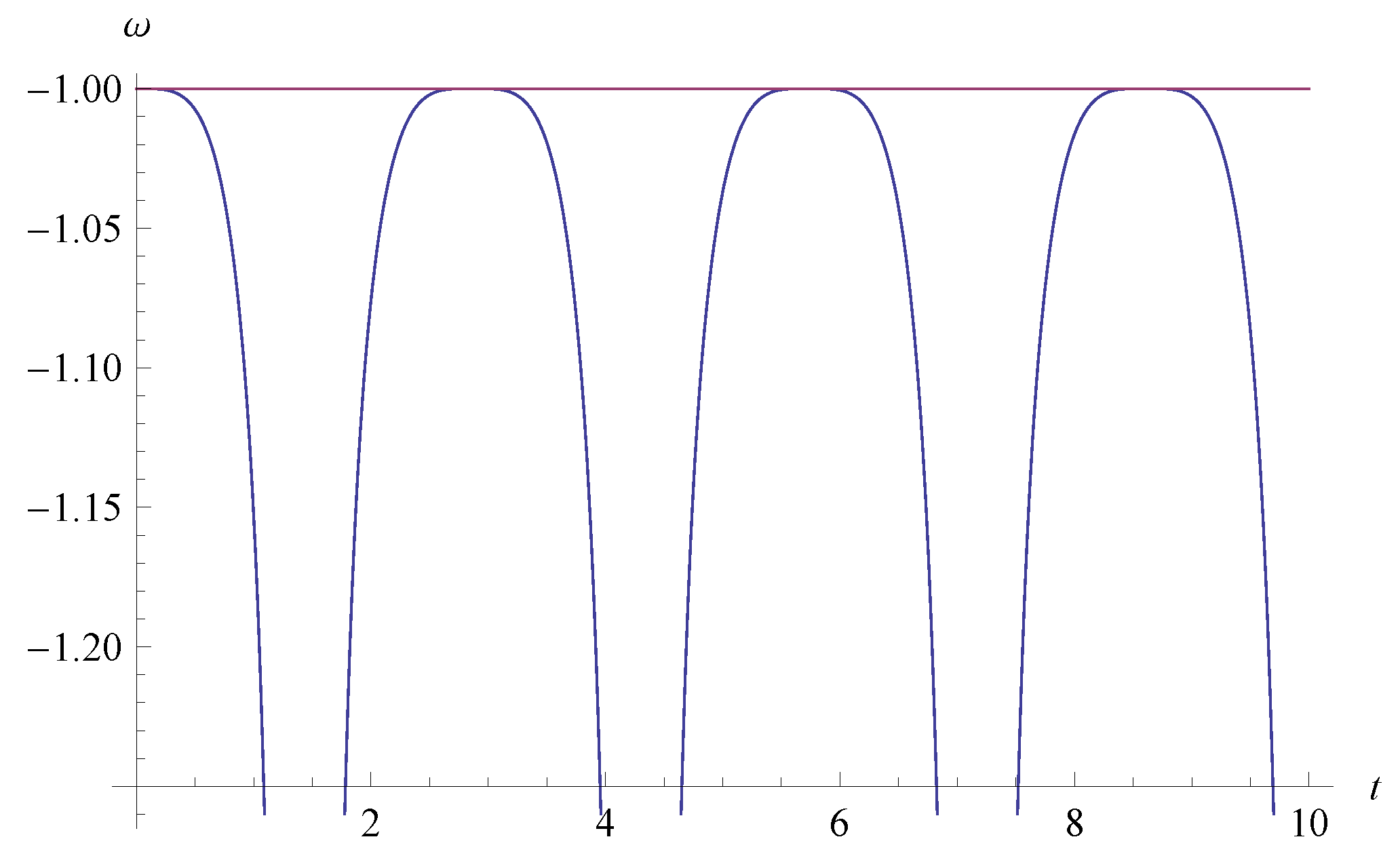
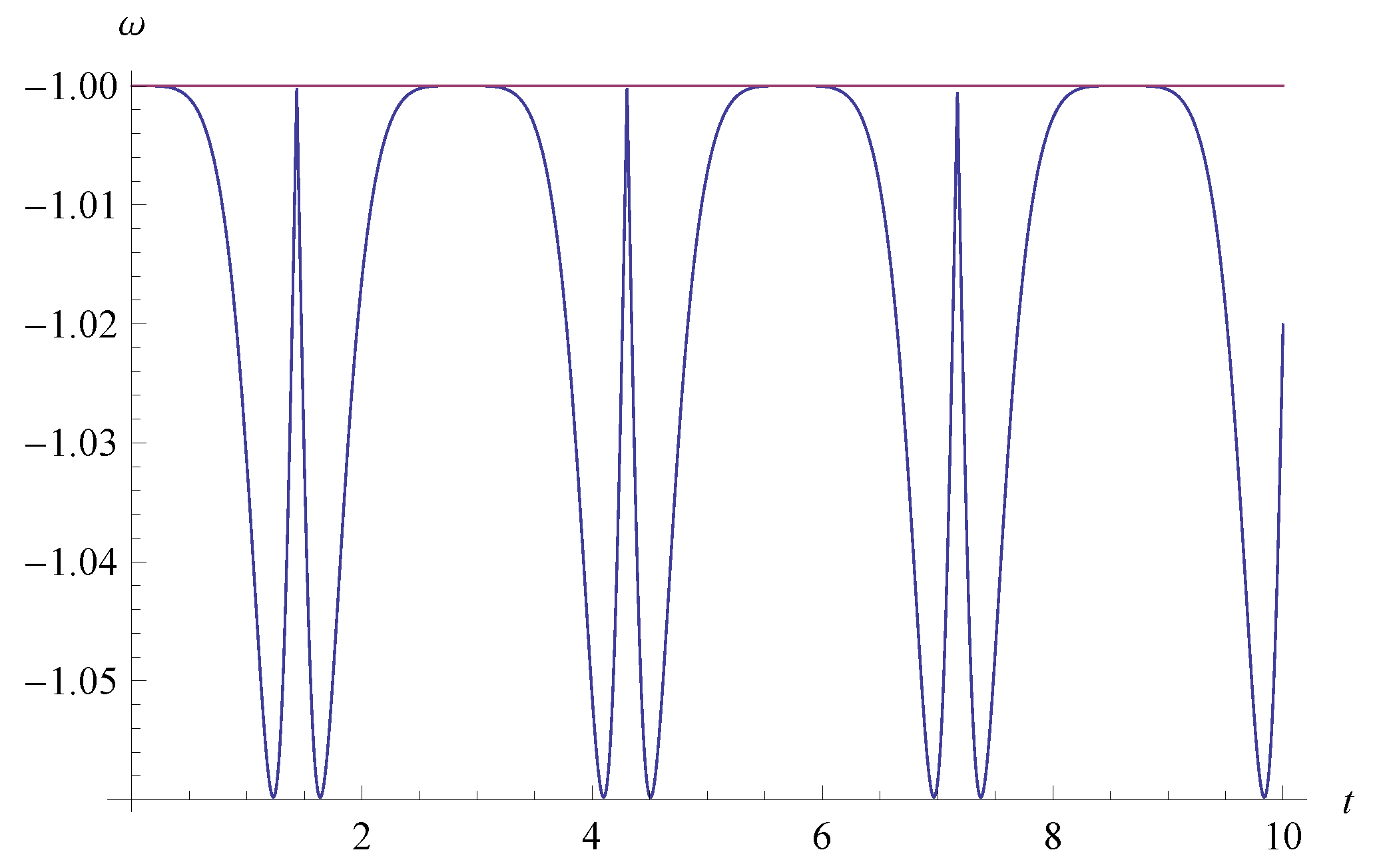
Periodic Cosmological Evolutions of Equation of State for Dark Energy
Abstract
:1. Introduction
2. Brief Review of the CG Type Models
3. Periodical and Quasi-periodical GCG Type Models
3.1. Periodical Generalizations
3.1.1. MG-XXI Model
3.1.2. MG-XXII Model
3.1.3. MG-XXIII Model
3.1.4. MG-XXIV Model
3.2. Quasi-periodical Generalizations
3.2.1. MG-XXV Model
3.2.2. MG-XXVI Model
3.2.3. MG-XXVII Model
4. Other Two Periodical FLRW Models
4.1. MG-XII Model

4.2. MG-XIII Model
4.3. MG-XIV Model
4.4. MG-XV Model
4.5. MG-XVI Model
4.6. MG-XVII Model
4.7. MG-XVIII Model
4.8. MG-XIX Model
4.9. MG-XX Model
4.10. MG-XXXIII Model
5. Conclusions
Acknowledgments
References
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters. Astrophys. J. Suppl. 2003, 148, 175–194. [Google Scholar] [CrossRef]
- Spergel, D.N.; Bean, R.; Dore, O.; Nolta, M.R.; Bennett, C.L.; Hinshaw, G.; Jarosik, N.; Komatsu, E.; Page, L.; Peiris, H.V.; et al. Wilkinson Microwave Anisotropy Probe (WMAP) three year results: Implications for cosmology. Astrophys. J. Suppl. 2007, 170, 377–408. [Google Scholar] [CrossRef]
- Komatsu, E.; Dunkley, J.; Nolta, M.R.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Limon, M.; Page, L.; et al. Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. Astrophys. J. Suppl. 2009, 180, 330–376. [Google Scholar] [CrossRef]
- Komatsu, E.; Smith, K.M.; Dunkley, J.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Nolta, M.R.; Page, L.; et al. Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. Astrophys. J. Suppl. 2011, 192, 18. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiattia, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Tegmark, M.; Strauss, M.A.; Blanton, M.R.; Abazajian, K.N.; Dodelson, S.; Sandvik, H.; Wang, X.; Weinberg, D.H.; Zehavi, I.; Bahcall, N.A.; et al. Cosmological parameters from SDSS and WMAP. Phys. Rev. D 2004. [Google Scholar] [CrossRef]
- Seljak, U.; Makarov, A.; McDonald, P.; Anderson, S.; Bahcall, N.; Brinkmann, J.; Burles, S.; Cen, R.; Doi, M.; Gunn, J.; Ivezic, Z.; et al. Cosmological parameter analysis including SDSS Ly-alpha forest and galaxy bias: Constraints on the primordial spectrum of fluctuations, neutrino mass, and dark energy. Phys. Rev. D 2005. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.; Tegmark, M.; Zheng, Z.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Jain, B.; Taylor, A. Cross-correlation Tomography: Measuring Dark Energy Evolution with Weak Lensing. Phys. Rev. Lett. 2003, 91, 141302. [Google Scholar] [CrossRef] [PubMed]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef]
- Durrer, R.; Maartens, R. Dark Energy and Dark Gravity. Gen. Rel. Grav. 2008, 40, 301–328. [Google Scholar] [CrossRef] [Green Version]
- Durrer, R.; Maartens, R. Dark Energy and Modified Gravity. In Dark Energy: Observational Theoretical Approaches; Ruiz-Lapuente, P., Ed.; Cambridge University press: Cambridge, UK, 2010; pp. 48–91. [Google Scholar]
- Cai, Y.F.; Saridakis, E.N.; Setare, M.R.; Xia, J.Q. Quintom Cosmology: Theoretical implications and observations. Phys. Rept. 2010, 493, 1–60. [Google Scholar] [CrossRef]
- Tsujikawa, S. Dark energy: investigation and modeling. 2010; arXiv:1004.1493 [astro-ph.CO]. [Google Scholar]
- Amendola, L.; Tsujikawa, S. Dark Energy; Cambridge University press: Cambridge, United Kingdom, 2010; pp. 1–491. [Google Scholar]
- Li, M.; Li, X.D.; Wang, S.; Wang, Y. Dark Energy. Commun. Theor. Phys. 2011, 56, 525–604. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: the equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: from F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Meth. Mod. Phys. 2007, 4, 115–146. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories Of Gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- Capozziello, S.; Faraoni, V. Beyond Einstein Gravity; Springer: London, UK, 2010; pp. 1–424. [Google Scholar]
- Capozziello, S.; de Laurentis, M. Extended Theories of Gravity. Phys. Rept. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Rel. 2010, 13, 3. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified Gravity and Cosmology. Phys. Rept. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Capozziello, S.; de Laurentis, M.; Odintsov, S.D. Hamiltonian dynamics and Noether symmetries in Extended Gravity Cosmology. Eur. Phys. J. C 2012, 72, 2068. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Kamionkowski, M.; Weinberg, N.N. Phantom Energy and Cosmic Doomsday. Phys. Rev. Lett. 2003. [Google Scholar] [CrossRef]
- McInnes, B. The dS/CFT correspondence and the big smash. J. High Energy Phys. 2002, 0208, 029. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Quantum deSitter cosmology and phantom matter. Phys. Lett. B 2003, 562, 147–152. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Effective equation of state and energy conditions in phantom / tachyon inflationary cosmology perturbed by quantum effects. Phys. Lett. B 2003, 571, 1–10. [Google Scholar] [CrossRef]
- Faraoni, V. Superquintessence. Int. J. Mod. Phys. D 2002, 11, 471–482. [Google Scholar] [CrossRef]
- Gonzalez-Diaz, P.F. K-essential phantom energy: Doomsday around the corner? Phys. Lett. B 2004, 586, 1–4. [Google Scholar] [CrossRef]
- Elizalde, E.; Nojiri, S.; Odintsov, S.D. Late-time cosmology in (phantom) scalar-tensor theory: Dark energy and the cosmic speed-up. Phys. Rev. D 2004. [Google Scholar] [CrossRef]
- Singh, P.; Sami, M.; Dadhich, N. Cosmological dynamics of phantom field. Phys. Rev. D 2003. [Google Scholar] [CrossRef]
- Csaki, C.; Kaloper, N.; Terning, J. Exorcising w < −1. Annals Phys. 2005, 317, 410–422. [Google Scholar]
- Wu, P.X.; Yu, H.W. Avoidance of Big Rip In Phantom Cosmology by Gravitational Back Reaction. Nucl. Phys. B 2005, 727, 355–367. [Google Scholar] [CrossRef]
- Nesseris, S.; Perivolaropoulos, L. The fate of bound systems in phantom and quintessence cosmologies. Phys. Rev. D 2004. [Google Scholar] [CrossRef]
- Sami, M.; Toporensky, A. Phantom Field and the Fate of Universe. Mod. Phys. Lett. A 2004, 19, 1509–1517. [Google Scholar] [CrossRef]
- Stefancic, H. Generalized phantom energy. Phys. Lett. B 2004, 586, 5–10. [Google Scholar] [CrossRef]
- Chimento, L.P.; Lazkoz, R. On the link between phantom and standard cosmologies. Phys. Rev. Lett. 2003. [Google Scholar] [CrossRef]
- Hao, J.G.; Li, X.Z. Generalized quartessence cosmic dynamics: Phantom or quintessence with de Sitter attractor. Phys. Lett. B 2005, 606, 7–11. [Google Scholar] [CrossRef]
- Elizalde, E.; Nojiri, S.; Odintsov, S. D.; Wang, P. Dark energy: Vacuum fluctuations, the effective phantom phase, and holography. Phys. Rev. D 2005. [Google Scholar] [CrossRef]
- Dabrowski, M.P.; Stachowiak, T. Phantom Friedmann cosmologies and higher-order characteristics of expansion. Annals Phys. 2006, 321, 771–812. [Google Scholar] [CrossRef]
- Lobo, F.S.N. Phantom energy traversable wormholes. Phys. Rev. D 2005. [Google Scholar] [CrossRef]
- Cai, R.G.; Zhang, H.S.; Wang, A. Crossing w = -1 in Gauss-Bonnet brane world with induced gravity. Commun. Theor. Phys. 2005, 44, 948–954. [Google Scholar] [CrossRef]
- Aref’eva, I.Y.; Koshelev, A.S.; Vernov, S.Y. Crossing of the w=-1 Barrier by D3-brane Dark Energy Model. Phys. Rev. D 2005. [Google Scholar] [CrossRef]
- Lu, H. Q.; Huang, Z.G.; Fang, W. Quantum and classical cosmology with Born-Infeld scalar field. 2005. [Google Scholar]
- Godlowski, W.; Szydlowski, M. Which cosmological model with dark energy - phantom or LambdaCDM. Phys. Lett. B 2005, 623, 10–16. [Google Scholar] [CrossRef]
- Sola, J.; Stefancic, H. Effective equation of state for dark energy: mimicking quintessence and phantom energy through a variable Lambda. Phys. Lett. B 2005, 624, 147–157. [Google Scholar] [CrossRef]
- Guberina, B.; Horvat, R.; Nikolic, H. Generalized holographic dark energy and the IR cutoff problem. Phys. Rev. D 2005. [Google Scholar] [CrossRef]
- Shtanov, Y.; Sahni, V. Unusual cosmological singularities in braneworld models. Class. Quant. Grav. 2002, 19, L101–L107. [Google Scholar] [CrossRef]
- Barrow, J.D. Sudden Future Singularities. Class. Quant. Grav. 2004, 21, L79–L82. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Quantum escape of sudden future singularity. Phys. Lett. B 2004, 595, 1–8. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. The final state and thermodynamics of dark energy universe. Phys. Rev. D 2004. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Inhomogeneous equation of state of the universe: Phantom era, future singularity and crossing the phantom barrier. Phys. Rev. D 2005. [Google Scholar] [CrossRef]
- Cotsakis, S.; Klaoudatou, I. Future singularities of isotropic cosmologies. J. Geom. Phys. 2005, 55, 306–315. [Google Scholar] [CrossRef]
- Dabrowski, M.P. Inhomogenized sudden future singularities. Phys. Rev. D 2005. [Google Scholar] [CrossRef]
- Fernandez-Jambrina, L.; Lazkoz, R. Geodesic behaviour of sudden future singularities. Phys. Rev. D 2004. [Google Scholar] [CrossRef]
- Fernandez-Jambrina, L.; Lazkoz, R. Singular fate of the universe in modified theories of gravity. Phys. Lett. B 2009, 670, 254–258. [Google Scholar] [CrossRef]
- Barrow, J.D.; Tsagas, C.G. New Isotropic and Anisotropic Sudden Singularities. Class. Quant. Grav. 2005, 22, 1563–1571. [Google Scholar] [CrossRef]
- Stefancic, H. ’Expansion’ around the vacuum equation of state: Sudden future singularities and asymptotic behavior. Phys. Rev. D 2005. [Google Scholar] [CrossRef]
- Cattoen, C.; Visser, M. Necessary and sufficient conditions for big bangs, bounces, crunches, rips, sudden singularities, and extremality events. Class. Quant. Grav. 2005, 22, 4913–4930. [Google Scholar] [CrossRef]
- Tretyakov, P.; Toporensky, A.; Shtanov, Y.; Sahni, V. Quantum effects, soft singularities and the fate of the universe in a braneworld cosmology. Class. Quant. Grav. 2006, 23, 3259–3274. [Google Scholar] [CrossRef]
- Balcerzak, A.; Dabrowski, M.P. Strings at future singularities. Phys. Rev. D 2006. [Google Scholar] [CrossRef]
- Sami, M.; Singh, P.; Tsujikawa, S. Avoidance of future singularities in loop quantum cosmology. Phys. Rev. D 2006. [Google Scholar] [CrossRef]
- Bouhmadi-Lopez, M.; Gonzalez-Diaz, P.F.; Martin-Moruno, P. Worse than a big rip? Phys. Lett. B 2008, 659, 1–5. [Google Scholar] [CrossRef]
- Yurov, A.V.; Astashenok, A.V.; Gonzalez-Diaz, P.F. Astronomical bounds on future big freeze singularity. Grav. Cosmol. 2008, 14, 205–212. [Google Scholar] [CrossRef]
- Koivisto, T. Dynamics of Nonlocal Cosmology. Phys. Rev. D 2008. [Google Scholar] [CrossRef]
- Barrow, J.D.; Lip, S.Z.W. The Classical Stability of Sudden and Big Rip Singularities. Phys. Rev. D 2009. [Google Scholar] [CrossRef]
- Bouhmadi-Lopez, M.; Tavakoli, Y.; Moniz, P.V. Appeasing the Phantom Menace? JCAP 2010, 1004, 016. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Tsujikawa, S. Properties of singularities in (phantom) dark energy universe. Phys. Rev. D 2005. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. The future evolution and finite-time singularities in F(R)-gravity unifying the inflation and cosmic acceleration. Phys. Rev. D 2008. [Google Scholar] [CrossRef]
- Bamba, K.; Nojiri, S.; Odintsov, S.D. The Universe future in modified gravity theories: Approaching the finite-time future singularity. JCAP 2008, 0810, 045. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Finite-time future singularities in modified Gauss-Bonnet and F(R,G) gravity and singularity avoidance. Eur. Phys. J. C 2010, 67, 295–310. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Turok, N. Cosmic evolution in a cyclic universe. Phys. Rev. D 2002. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Turok, N. A cyclic model of the universe. Science 2002, 296, 1436–1439. [Google Scholar] [CrossRef] [PubMed]
- Khoury, J.; Ovrut, B.A.; Steinhardt, P.J.; Turok, N. Density perturbations in the ekpyrotic scenario. Phys. Rev. D 2002. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Turok, N. The cyclic universe: An informal introduction. Nucl. Phys. Proc. Suppl. 2003, 124, 38–49. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Turok, N. A cyclic model of the universe. Science 2002, 296, 1436–1439. [Google Scholar] [CrossRef] [PubMed]
- Khoury, J.; Steinhardt, P.J.; Turok, N. Designing Cyclic Universe Models. Phys. Rev. Lett. 2004. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Turok, N. Why the cosmological constant is small and positive. Science 2006, 312, 1180–1182. [Google Scholar] [CrossRef] [PubMed]
- Saaidi, K.; Sheikhahmadi, H.; Mohammadi, A.H. Interacting New Agegraphic Dark Energy in a Cyclic Universe. Astrophys. Space Sci. 2012, 338, 355–361. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Saez-Gomez, D. Cyclic, ekpyrotic and little rip universe in modified gravity. AIP Conf. Proc. 2011, 1458, 207–221. [Google Scholar]
- Cai, Y.F.; Saridakis, E.N. Non-singular Cyclic Cosmology without Phantom Menace. J. Cosmol. 2011, 17, 7238–7254. [Google Scholar]
- Sahni, V.; Toporensky, A. Cosmological Hysteresis and the Cyclic Universe. Phys. Rev. D 2012. [Google Scholar] [CrossRef]
- Chung, D.Y. The Cyclic universe. 2001; arXiv:physics/0105064. [Google Scholar]
- Khoury, J.; Ovrut, B.A.; Steinhardt, P.J.; Turok, N. The ekpyrotic universe: Colliding branes and the origin of the hot big bang. Phys. Rev. D 2001. [Google Scholar] [CrossRef]
- Khoury, J.; Ovrut, B.A.; Steinhardt, P.J.; Turok, N. A brief comment on ’The pyrotechnic universe’. 2001; arXiv:hep-th/0105212. [Google Scholar]
- Donagi, R.Y.; Khoury, J.; Ovrut, B.A.; Steinhardt, P.J.; Turok, N. Visible branes with negative tension in heterotic M-theory. JHEP 2001, 0111, 041. [Google Scholar] [CrossRef]
- Khoury, J.; Ovrut, B.A.; Steinhardt, P.J.; Turok, N. Density perturbations in the ekpyrotic scenario. Phys. Rev. D 2002. [Google Scholar] [CrossRef]
- Page, D. N. A Fractal Set of Perpetually Bouncing Universes? Class. Quant. Grav. 1984, 1, 417–427. [Google Scholar] [CrossRef]
- Peter, P.; Pinto-Neto, N. Has the Universe always expanded? Phys. Rev. D 2001. [Google Scholar] [CrossRef]
- Peter, P.; Pinto-Neto, N. Primordial perturbations in a non singular bouncing universe model. Phys. Rev. D 2002. [Google Scholar] [CrossRef]
- Shtanov, Y.; Sahni, V. Bouncing braneworlds. Phys. Lett. B 2003, 557, 1–6. [Google Scholar] [CrossRef]
- Biswas, T.; Mazumdar, A.; Siegel, W. Bouncing universes in string-inspired gravity. J. Cosmol. Astropart. Phys. 2006, 0603, 009. [Google Scholar] [CrossRef]
- Cai, Y.F.; Qiu, T.; Piao, Y.S.; Li, M.; Zhang, X. Bouncing Universe with Quintom Matter. J. High Energ. Phys. 2007, 0710, 071. [Google Scholar] [CrossRef]
- Creminelli, P.; Senatore, L. A smooth bouncing cosmology with scale invariant spectrum. J. Cosmol. Astropart. Phys. 2007. [Google Scholar] [CrossRef]
- Piao, Y.S. Proliferation in Cycle. Phys. Lett. B 2009, 677, 1–5. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Z.G.; Piao, Y.S. Amplification of curvature perturbations in cyclic cosmology. Phys. Rev. D 2010. [Google Scholar] [CrossRef]
- Piao, Y.S. Design of a Cyclic Multiverse. Phys. Lett. B 2010, 691, 225–229. [Google Scholar] [CrossRef]
- Liu, Z.G.; Piao, Y.S. Scalar Perturbations Through Cycles. Phys. Rev. D 2012. [Google Scholar] [CrossRef]
- Novello, M.; Bergliaffa, S.E.P. Bouncing Cosmologies. Phys. Rept. 2008, 463, 127–213. [Google Scholar] [CrossRef]
- Myrzakulov, R. F(T) gravity and k-essence. To appear in Gen. Relativ. Gravit. 2012. [Google Scholar] [CrossRef]
- Myrzakulov, R. Knot Universes in Bianchi Type I Cosmology. Advances in High Energy Physics 2012, 2012, 868203. [Google Scholar] [CrossRef]
- Esmakhanova, K.; Myrzakulov, Y.; Nugmanova, G.; Myrzakulov, R. A note on the relationship between solutions of Einstein, Ramanujan and Chazy equations. Int. J. Theor. Phys. 2012, 51, 1204–1210. [Google Scholar] [CrossRef]
- Yesmakhanova, K.R.; Myrzakulov, N.A.; Yerzhanov, K.K.; Nugmanova, G.N.; Serikbayaev, N.S.; Myrzakulov, R. Some Models of Cyclic and Knot Universes. 2012; arXiv:1201.4360 [physics.gen-ph]. [Google Scholar]
- Gibbons, G.W.; Vyska, M. The Application of Weierstrass elliptic functions to Schwarzschild Null Geodesics. Class. Quant. Grav. 2012, 29, 065016. [Google Scholar] [CrossRef]
- Bochicchio, I.; Capozziello, S.; Laserra, E. The Weierstrass Criterion and the Lemaitre-Tolman-Bondi Models with Cosmological Constant Λ. Int. J. Geom. Meth. Mod. Phys. 2011, 8, 1653–1666. [Google Scholar] [CrossRef]
- Dimitrov, B.G. Cubic algebraic equations in gravity theory, parametrization with the Weierstrass function and non-arithmetic theory of algebraic equations. J. Math. Phys. 2003, 44, 2542–2578. [Google Scholar] [CrossRef] [Green Version]
- D’Ambroise, J. Applications of Elliptic and Theta Functions to Friedmann-Robertson-Lemaitre-Walker Cosmology with Cosmological Constant. 2009; arXiv:0908.2481 [gr-qc]. [Google Scholar]
- Bouhmadi-Lopez, M.; Garay, L.J.; Gonzalez-Diaz, P.F. Quantum behavior of FRW radiation-filled universes. Phys. Rev. D 2002. [Google Scholar] [CrossRef]
- Bamba, K.; Yesmakhanova, K.; Yerzhanov, K.; Myrzakulov, R. Reconstruction of the equation of state for the cyclic universes in homogeneous and isotropic cosmology. 2012; arXiv:1203.3401 [gr-qc]. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Inhomogeneous equation of state of the universe: Phantom era, future singularity and crossing the phantom barrier. Phys. Rev. D 2005. [Google Scholar] [CrossRef]
- Stefancic, H. ’Expansion’ around the vacuum equation of state: Sudden future singularities and asymptotic behavior. Phys. Rev. D 2005. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Moschella, U.; Pasquier, V. An Alternative to quintessence. Phys. Lett. B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas, accelerated expansion and dark energy matter unification. Phys. Rev. D 2002. [Google Scholar] [CrossRef]
- Benaoum, H.B. Accelerated universe from modified Chaplygin gas and tachyonic fluid. 2002; arXiv:hep-th/0205140. [Google Scholar]
- Saez-Gomez, D. Oscillating Universe from inhomogeneous EoS and coupled dark energy. Grav. Cosmol. 2009, 15, 134–140. [Google Scholar] [CrossRef]
- Sharif, M.; Yesmakhanova, K.R.; Rani, S.; Myrzakulov, R. Solvable K-essence Cosmologies and Modified Chaplygin Gas Unified Models of Dark Energy and Dark Matter. Eur. Phys. J. C 2012, 72, 2067. [Google Scholar] [CrossRef]
- Bamba, K.; Nojiri, S.; Odintsov, S.D.; Sasaki, M. Screening of cosmological constant for De Sitter Universe in non-local gravity, phantom-divide crossing and finite-time future singularities. Gen. Relativ. Gravit. 2012, 44, 1321–1356. [Google Scholar] [CrossRef]
- Alam, U.; Sahni, V.; Starobinsky, A.A. The case for dynamical dark energy revisited. J. Cosmol. Astropart. Phys. 2004, 0406, 008. [Google Scholar] [CrossRef]
- Alam, U.; Sahni, V.; Starobinsky, A.A. Exploring the Properties of Dark Energy Using Type Ia Supernovae and Other Datasets. J. Cosmol. Astropart. Phys. 2007, 0702, 011. [Google Scholar] [CrossRef]
- Nesseris, S.; Perivolaropoulos, L. Crossing the Phantom Divide: Theoretical Implications and Observational Status. J. Cosmol. Astropart. Phys. 2007, 0701, 018. [Google Scholar] [CrossRef]
- Wu, P.U.; Yu, H.W. Constraints on a variable dark energy model with recent observations. Phys. Lett. B 2006, 643, 315–318. [Google Scholar] [CrossRef]
- Jassal, H.K.; Bagla, J.S.; Padmanabhan, T. Understanding the origin of CMB constraints on Dark Energy. Mon. Not. Roy. Astron. Soc. 2010, 405, 2639–2650. [Google Scholar] [CrossRef]
- Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Abramowitz, M.; Stegun, l.A. (Eds.) Dover Publications: New York, NY, USA, 1965; pp. 1–1046.
- Zhao, G.B.; Xia, J.Q.; Li, M.; Feng, B.; Zhang, X. Perturbations of the quintom models of dark energy and the effects on observations. Phys. Rev. D 2005. [Google Scholar] [CrossRef]
- Chiba, T.; Okabe, T.; Yamaguchi, M. Kinetically driven quintessence. Phys. Rev. D 2000. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Damour, T.; Mukhanov, V.F. k-Inflation. Phys. Lett. B 1999, 458, 209–218. [Google Scholar] [CrossRef]
- Garriga, J.; Mukhanov, V.F. Perturbations in k-inflation. Phys. Lett. B 1999, 458, 219–225. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.F.; Steinhardt, P.J. A dynamical solution to the problem of a small cosmological constant and late-time cosmic acceleration. Phys. Rev. Lett. 2000, 85, 4438–4441. [Google Scholar] [CrossRef] [PubMed]
- Armendariz-Picon, C.; Mukhanov, V.F.; Steinhardt, P.J. Essentials of k-essence. Phys. Rev. D 2001. [Google Scholar] [CrossRef]
- de Putter, R.; Linder, E.V. Kinetic k-essence and Quintessence. Astropart. Phys. 2007, 28, 263–272. [Google Scholar] [CrossRef]
- Nicolis, A.; Rattazzi, R.; Trincherini, E. The Galileon as a local modification of gravity. Phys. Rev. D 2009. [Google Scholar] [CrossRef]
- Deffayet, C.; Esposito-Farese, G.; Vikman, A. Covariant Galileon. Phys. Rev. D 2009. [Google Scholar] [CrossRef]
- Deffayet, C.; Deser, S.; Esposito-Farese, G. Generalized Galileons: All scalar models whose curved background extensions maintain second-order field equations and stress-tensors. Phys. Rev. D 2009, 80. [Google Scholar] [CrossRef]
- Deffayet, C.; Deser, S.; Esposito-Farese, G. Arbitrary p-form Galileons. Phys. Rev. D 2010, 82, 061501-1–061501-5. [Google Scholar] [CrossRef]
- Shirai, N.; Bamba, K.; Kumekawa, S.; Matsumoto, J.; Nojiri, S. Generalized Galileon model: Cosmological reconstruction and the Vainshtein mechanism. Phys. Rev. D 2012. [Google Scholar] [CrossRef]
- Planck Science Team Home. Available online: http://www.sciops.esa.int/index.php?project=PL-ANCK (accessed on 17th November, 2012).
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bamba, K.; Debnath, U.; Yesmakhanova, K.; Tsyba, P.; Nugmanova, G.; Myrzakulov, R. Periodic Cosmological Evolutions of Equation of State for Dark Energy . Entropy 2012, 14, 2351-2374. https://doi.org/10.3390/e14112351
Bamba K, Debnath U, Yesmakhanova K, Tsyba P, Nugmanova G, Myrzakulov R. Periodic Cosmological Evolutions of Equation of State for Dark Energy . Entropy. 2012; 14(11):2351-2374. https://doi.org/10.3390/e14112351
Chicago/Turabian StyleBamba, Kazuharu, Ujjal Debnath, Kuralay Yesmakhanova, Petr Tsyba, Gulgasyl Nugmanova, and Ratbay Myrzakulov. 2012. "Periodic Cosmological Evolutions of Equation of State for Dark Energy " Entropy 14, no. 11: 2351-2374. https://doi.org/10.3390/e14112351