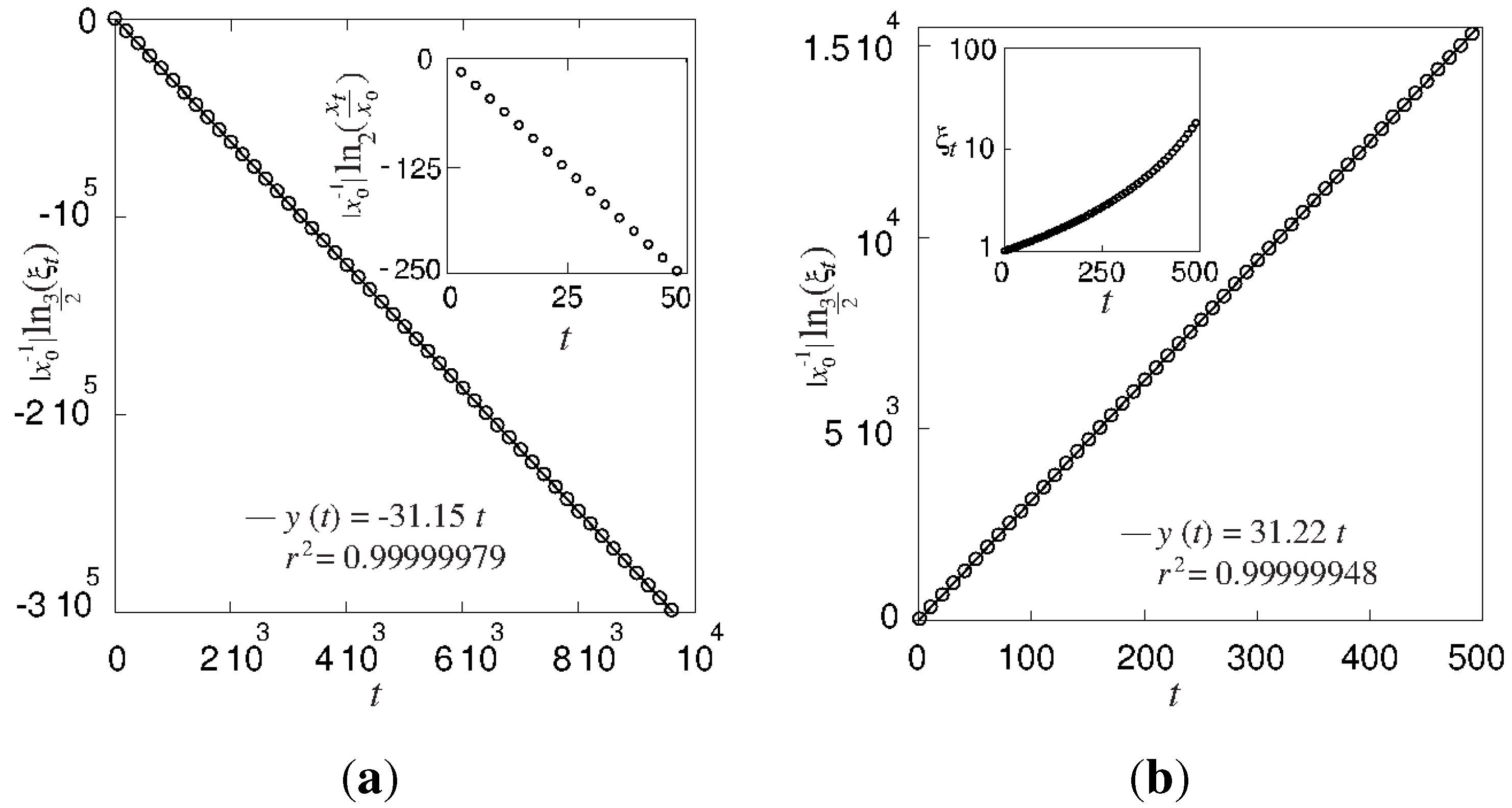
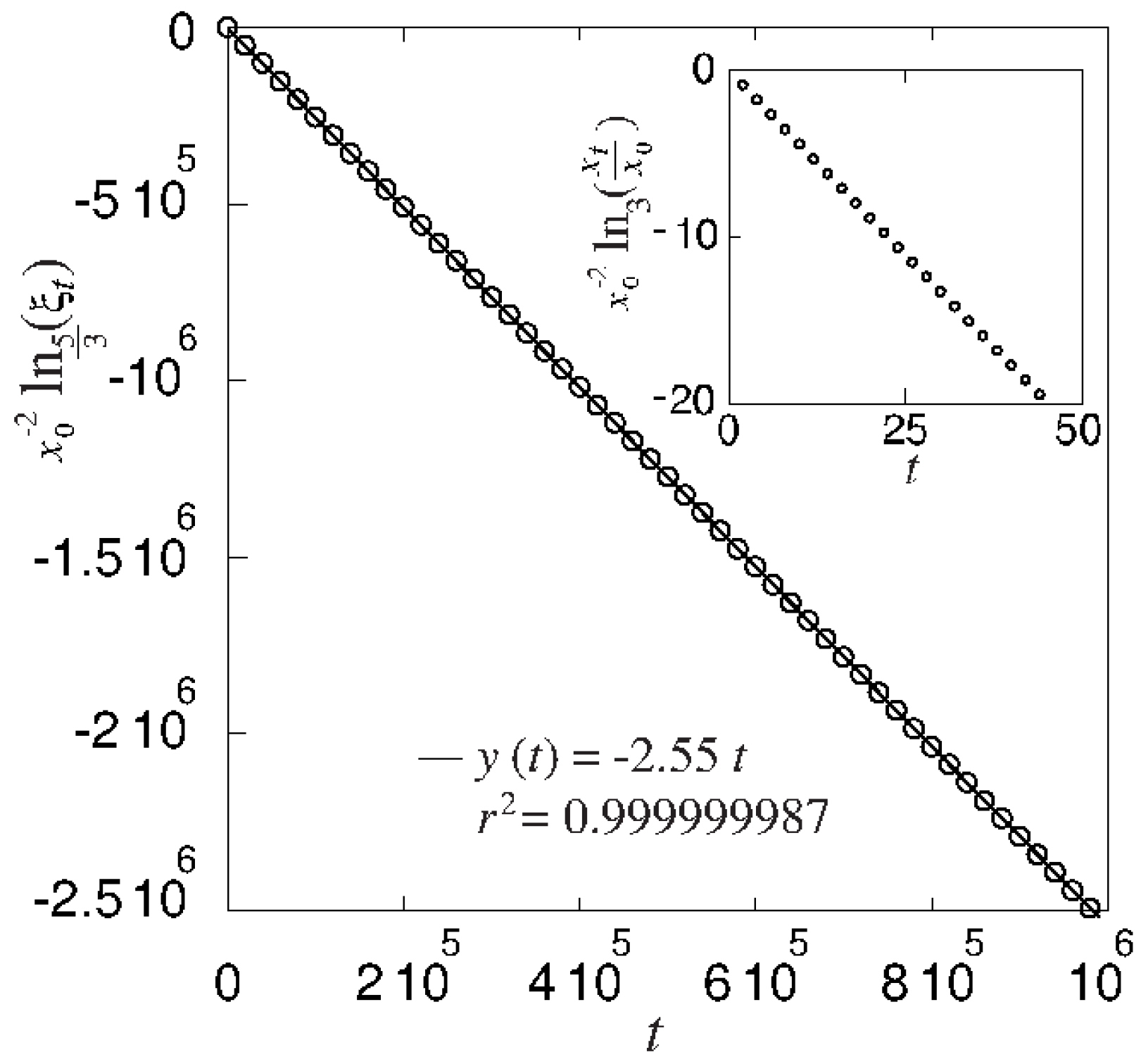
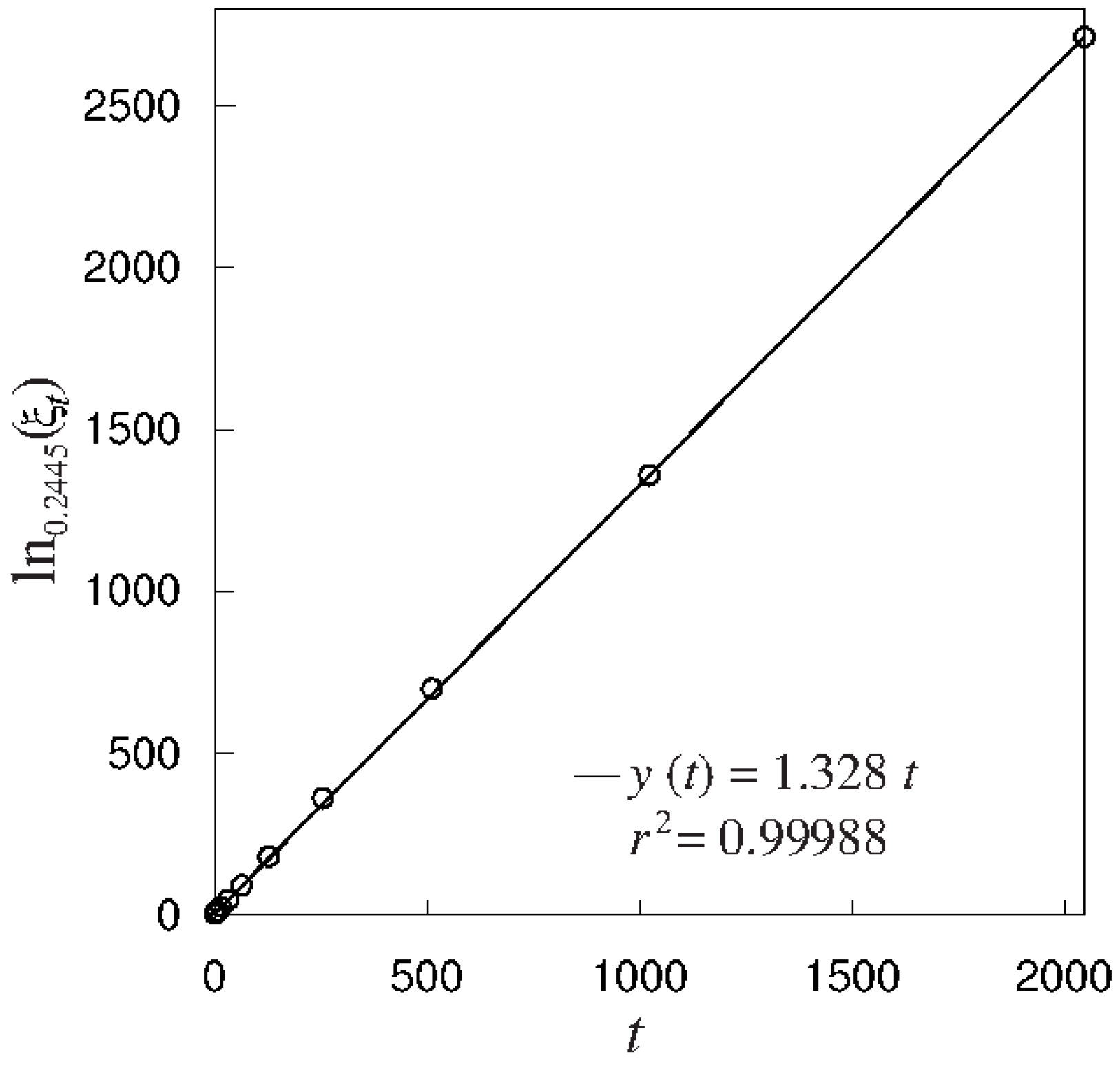
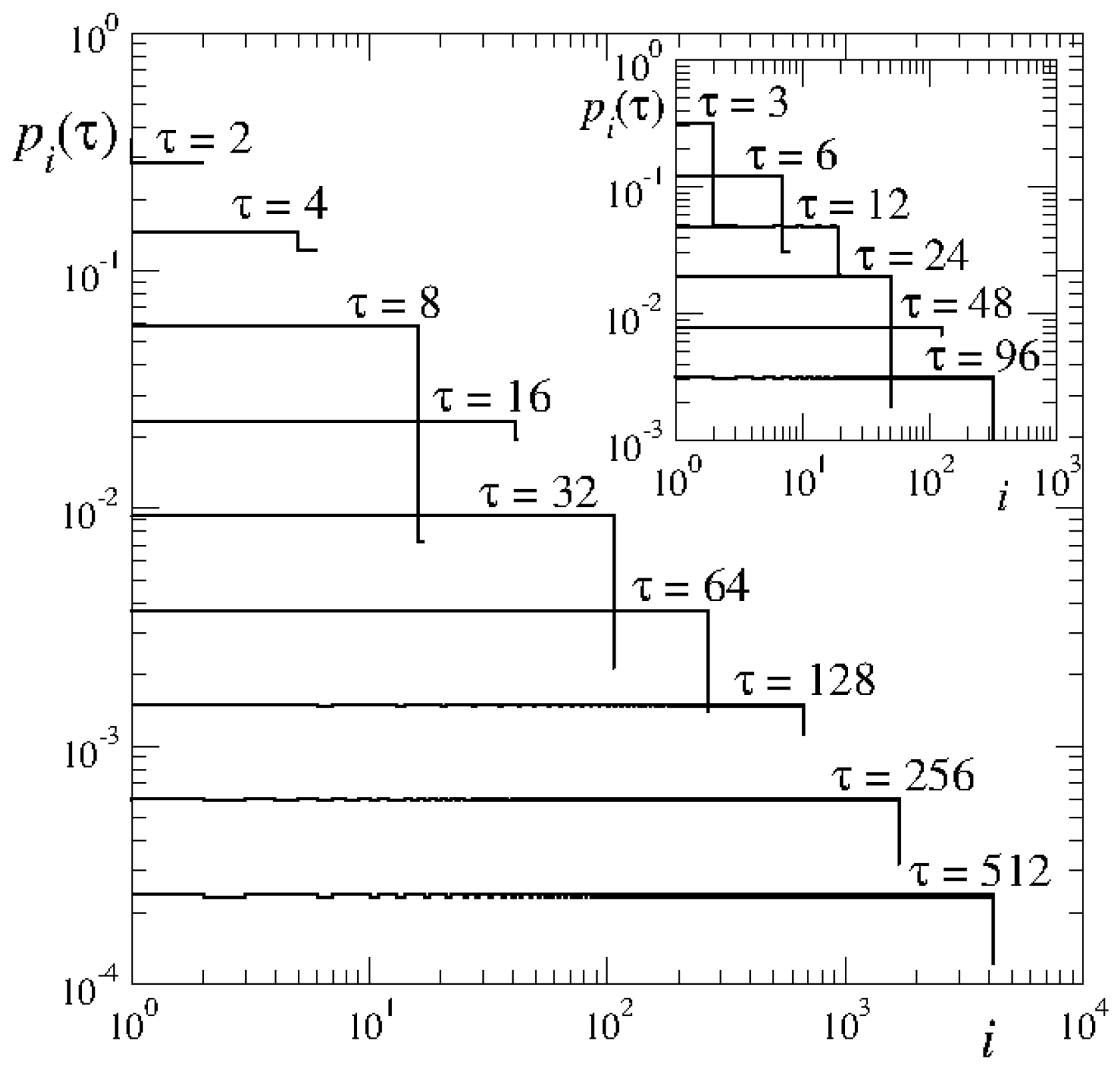
1. Introduction
Chaotic dynamical systems, such as chaotic attractors in one-dimensional nonlinear iterated maps, accept a statistical-mechanical description with an entropy expression of the Boltzmann–Gibbs (BG) type [
1]. The chaotic attractors generated by these maps have ergodic and mixing properties, and not surprisingly, they can be described by a thermodynamic formalism compatible with BG statistics [
1]. However, at the transition to chaos, such as the period-doubling accumulation point, the so-called Feigenbaum attractor, these two properties are lost, and this suggests the possibility of exploring the limit of validity of the BG structure in a precise, but simple enough, setting.
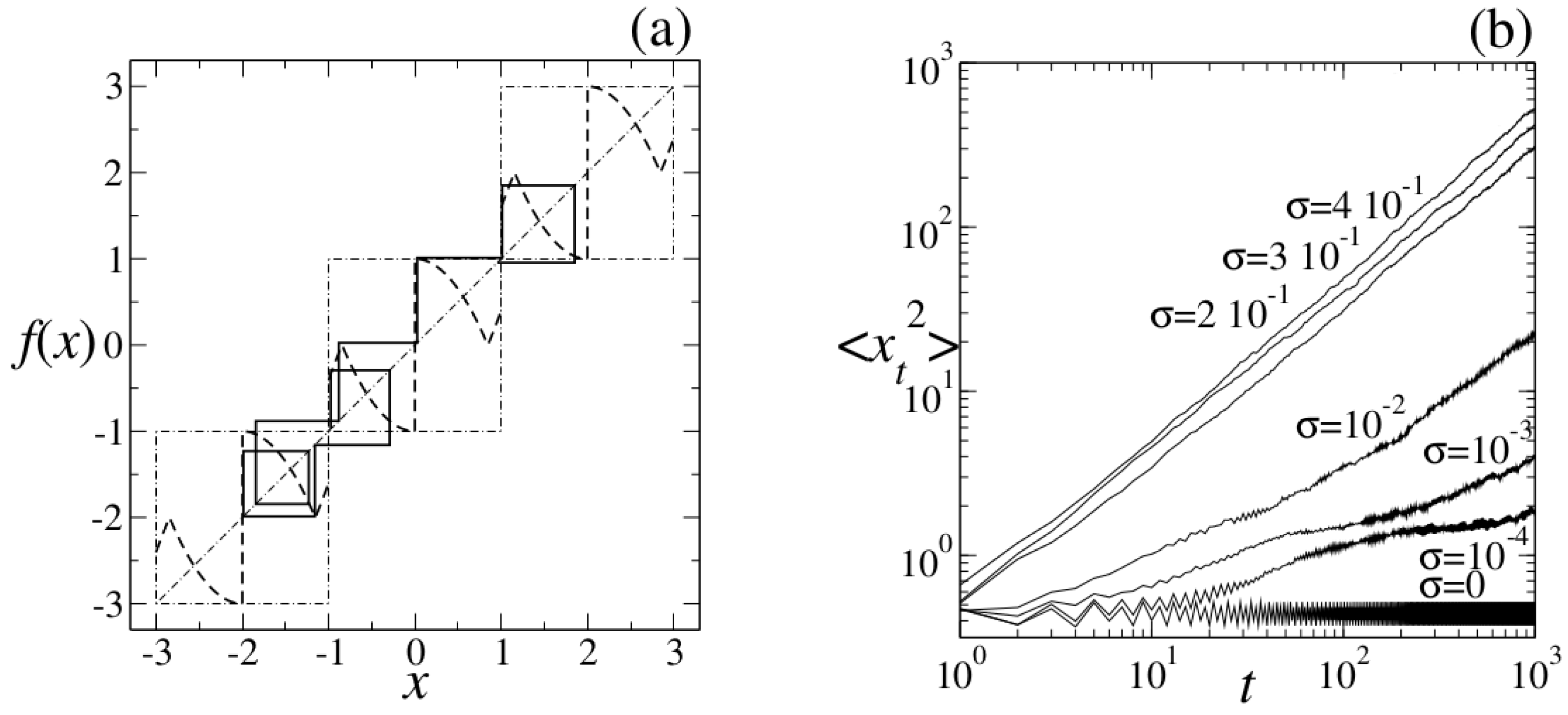
The attractors at the transitions to chaos in one-dimensional nonlinear maps (that we shall refer to as critical attractors) have a vanishing ordinary Lyapunov coefficient,
, and the sensitivity to initial conditions,
, for large iteration time
t ceases to obey exponential behavior, exhibiting, instead, power-law or faster than exponential growth behavior [
2,
3,
4,
5,
6,
7]. As it is generally suggested, the standard exponential divergence of trajectories in chaotic attractors provides a mechanism to justify the assumption of irreversibility in the BG statistical mechanics [
1]. In contrast, the onset of chaos in (necessarily dissipative) one-dimensional maps imprints memory preserving phase-space properties to its trajectories [
2], and we consider them here with a view to assess if generalized entropy expressions replace the usual BG expression. A simple type of attractor with
occurs at the transitions between periodic orbits, the so-called pitchfork bifurcations along the period-doubling cascades [
8,
9]. Another type, a critical attractor-repellor pair, occurs at the tangent bifurcation [
8,
9], a central feature for the intermittency route to chaos. Perhaps the most interesting types of critical attractors are geometrically involved (multifractal) sets of positions for which trajectories within them display an ever fluctuating non-exponential sensitivity,
[
2]. Important examples are the onset of chaos via period doubling and via quasiperiodicity, two other universal routes to chaos exhibited, respectively, by the prototypical logistic and circle maps [
8,
9].
There are two sets of properties associated with the attractors involved: those of the dynamics inside the attractors and those of the dynamics towards the attractors. These properties have been characterized in detail for the Feigenbaum attractor; both the organization of trajectories and the sensitivity to initial conditions are described in [
4], while the features of the rate of approach of an ensemble of trajectories to this attractor appears, explained in [
5]. The dynamics inside quasiperiodic critical attractors has also been determined by considering the so-called golden route to chaos in the circle map [
6]. The patterns formed by trajectories and the sensitivity,
, in this different case were found to share the general scheme displayed by these quantities for the Feigenbaum point, but with somewhat more involved features [
6]. On the contrary, the critical attractor-repellor set at the tangent bifurcation is a simpler finite set of positions with periodic dynamics that can be reduced to a single period-one attractor-repellor fixed point via functional composition, and the interesting properties of trajectories and sensitivity,
, correspond to the dynamics towards the attractor or away from the repellor [
3]. The search for generalized entropy properties in the dynamics of critical attractors has been two-fold. One focal point has been the determination of Pesin-like identities associated with the sensitivity,
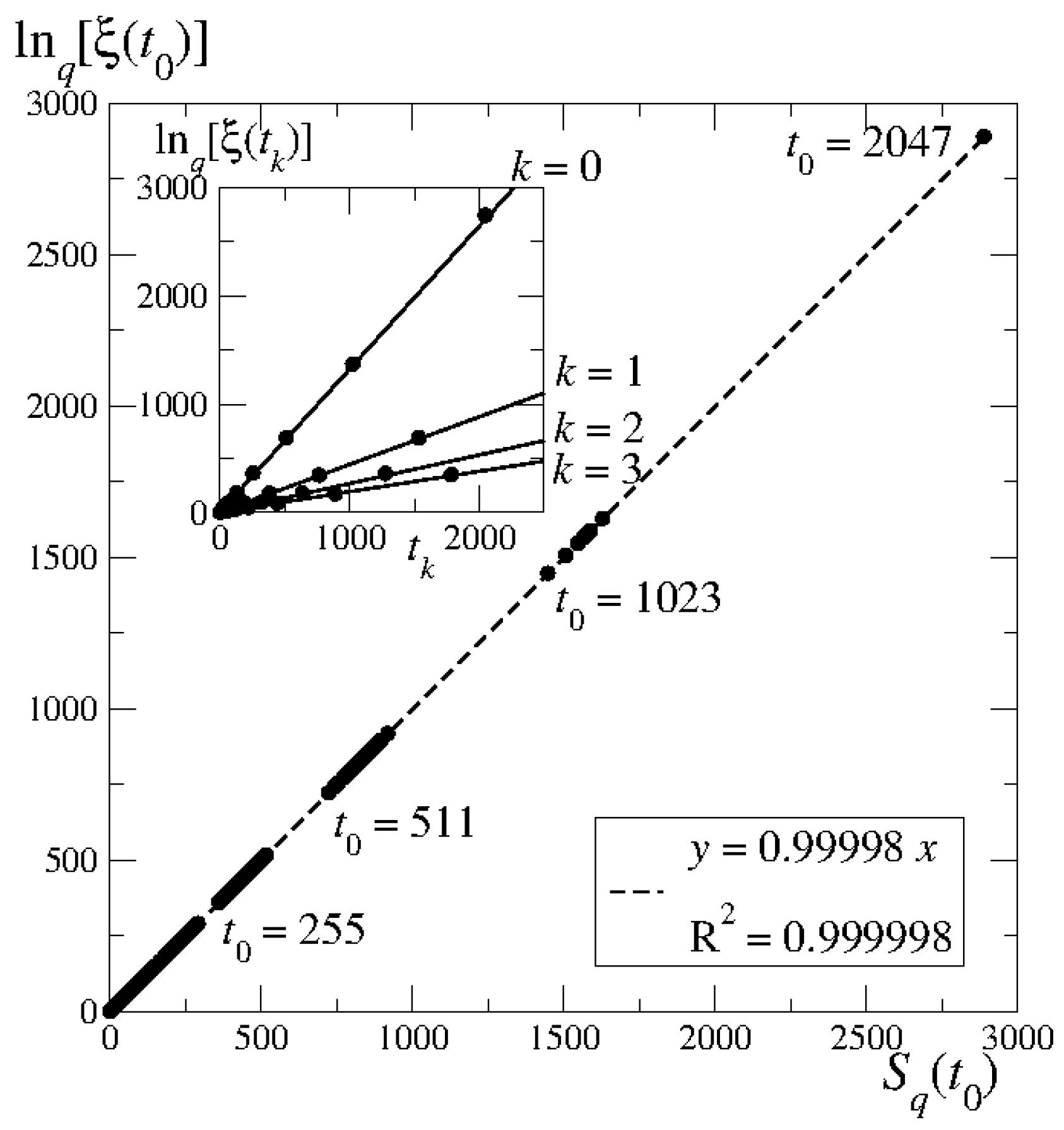
, within multifractal critical attractors for which the entropy expression involved is different from the BG expression. The second focal point is the determination of the relationship between the dynamics towards and the dynamics within multifractal critical attractors for which it has been found that the expression linking the two types of dynamics is statistical-mechanical in nature, one in which the configurational weights and the thermodynamical potential expressions differ from the BG ordinary exponential and logarithmic expressions. The simpler case of the tangent bifurcation also involves generalized entropy expressions linked to the trajectories and the sensitivity of the dynamics towards or away from the attractor-repellor fixed point.
The generalized entropy expressions were found to be of the Tsallis or
q -statistical type [
10,
11], involving the “
q-deformed” logarithmic function
, the functional inverse of the “
q-deformed” exponential function
. For the pitchfork and tangent bifurcations, the trajectories and the sensitivity,
(of their functional-composition renormalization-group (RG) fixed-point maps), are exactly expressible by
q-exponentials, and this leads to generalized
q-Lyapunov exponents
that are dependent on initial conditions [
3]. For multifractal critical attractors, the sensitivity,
, was found to be expressible in terms of an infinite set of
q-exponential functions, and from such
, one or several spectra of
q-generalized Lyapunov coefficients
were determined. The
are dependent on the initial position,
, and each spectrum can be examined by varying this position. The
satisfy a
q-generalized identity
of the Pesin type [
9], where
is an entropy production rate based on
q-statistical-type entropy expressions
[
4,
6]. In all cases, the presence of dual
q-indexes,
q and
, or
q and
, or a combination of them, have all well-defined dynamical meanings. If there is an entropy,
, or a coefficient,
, in the description of a critical attractor, the quantities,
and
, complement that description [
4,
6] . The partition function that describes the approach of trajectories to the Feigenbaum attractor contains an infinite set of
q-exponential weights (stemming from the infinite set of universal constants associated with the attractor), and the resulting thermodynamic potential involves another
q-index, which is the complicated outcome of all
q-indexes involved in the configurational terms [
5]. The generalized entropy in this case differs from the scheme contained in [
10,
11].
The manifestation of
q-statistics in complex condensed-matter systems can be explored via connections that have been established between the dynamics of critical attractors and the dynamics taking place in, for example, thermal systems under conditions when mixing and ergodic properties are not easily fulfilled. A relationship between intermittency and critical fluctuations suggested [
12,
13] that the dynamics in the proximity of a tangent bifurcation is analogous to the dynamics of fluctuations of an equilibrium state with well-known scaling properties [
14,
15]. We examine this connection with special attention to several unorthodox properties, such as, the extensivity of the
q-entropy
of fractal clusters of the order parameter and the anomalous (faster than exponential) sensitivity to initial conditions. A second example is that of the localization transition in electron transport in networks of scatterers. The use of a double Cayley tree model leads to an exact analogy with a nonlinear map that features two tangent bifurcations. The localization length is the inverse of the Lyapunov exponent,
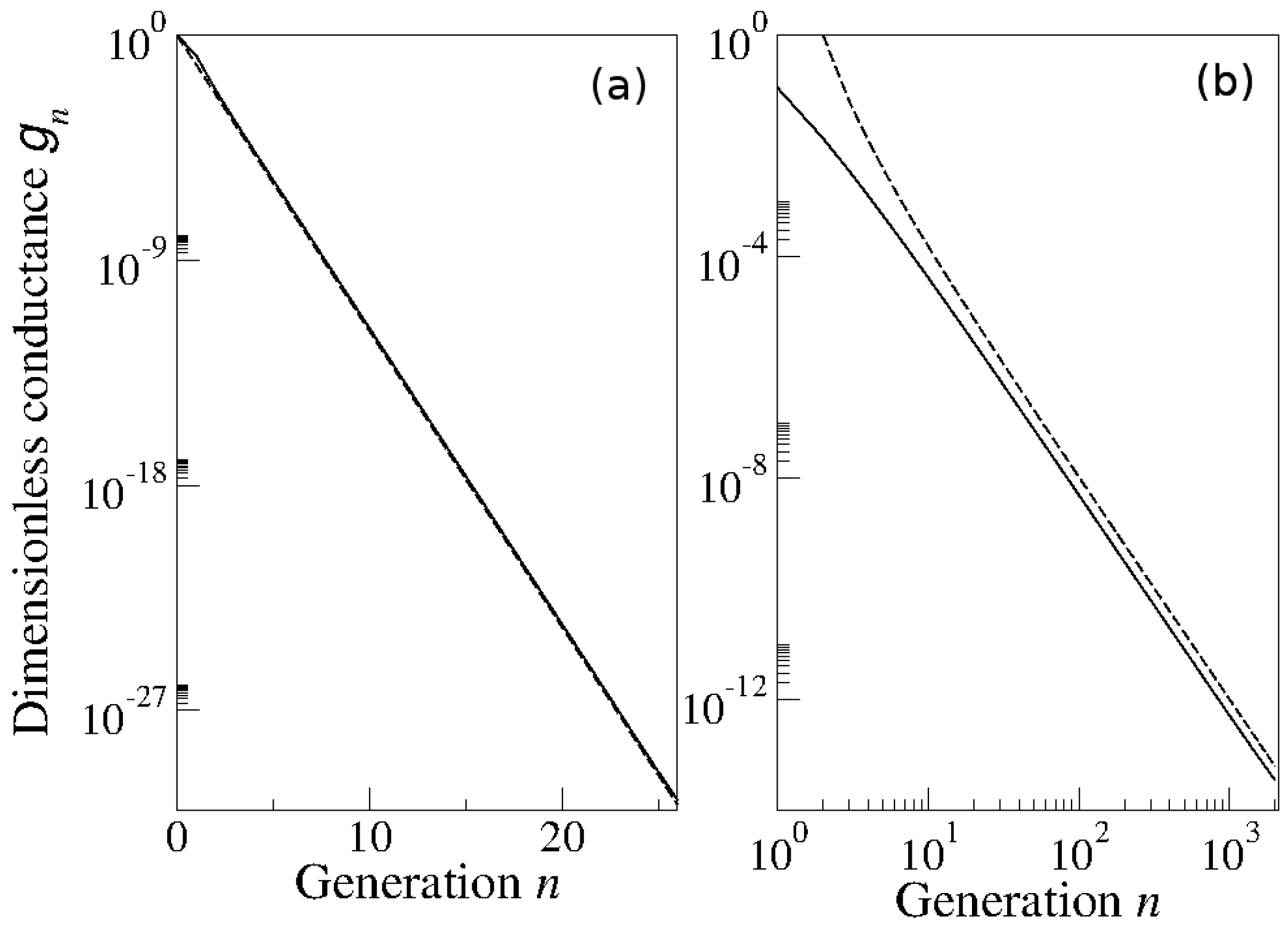
, and when this vanishes, we obtain a precise description of the mobility edge between insulating and conducting phases in terms of the
q-generalized exponent,
[
16]. As a third example, we describe our finding [
17,
18,
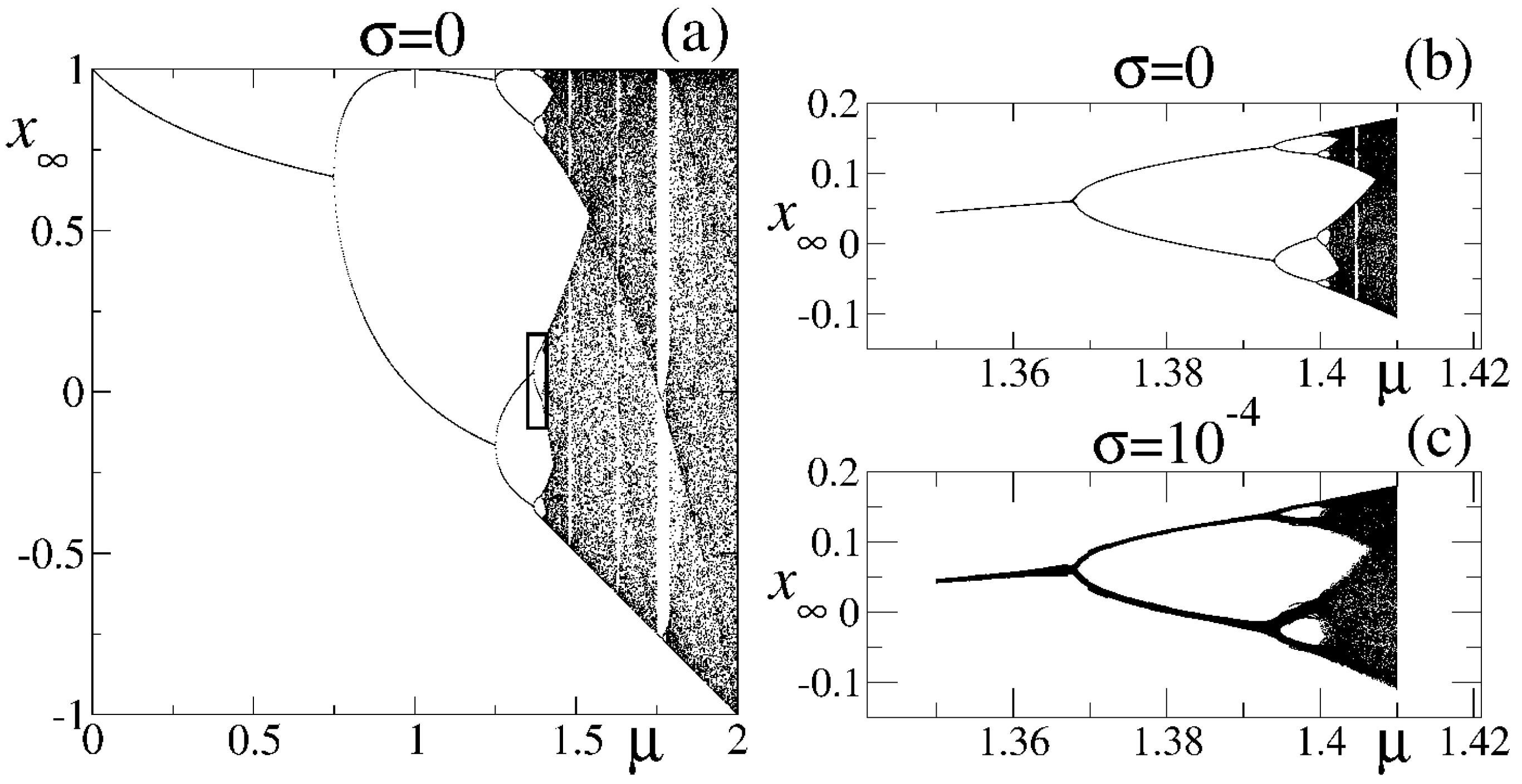
19] that the dynamics at the noise-perturbed period-doubling onset of chaos is analogous to that observed in supercooled liquids close to vitrification. We have demonstrated that four major features of glassy dynamics in structural glass formers are displayed by orbits with a vanishing Lyapunov coefficient. These are: two-step relaxation, a relationship between relaxation time and configurational entropy, aging scaling properties and evolution from a diffusive regime to arrest. The known properties in control-parameter space of the noise-induced bifurcation gap in the period-doubling cascade [
8] play a central role in determining the characteristics of dynamical relaxation at the chaos threshold.
The manifestations of
q-statistics in complex systems of a general or interdisciplinary nature have been and are currently being exposed and established. Two illustrations of general nature are provided: one corresponds to dynamical hierarchies with modular organization and emergent properties. We recall the demonstration that the dynamics towards multifractal attractors as illustrated by the Feigenbaum point fulfills the main features of such dynamical hierarchies [
20]. The other general topic is that of limit distributions of sums of deterministic variables, for which we describe and discuss the stationary distributions at the period-doubling transition to chaos and how they transform to Gaussian distributions for chaotic attractors. We consider both cases, that of an initial trajectory inside the attractor and that of an ensemble of trajectories uniformly distributed throughout all of phase space [
21,
22,
23]. We consider also two examples directed at more specific types of complex systems. One case corresponds to the large class of systems described by rank distributions. Their rank distributions are proved to be analogous to the dynamics at or near the tangent bifurcation [
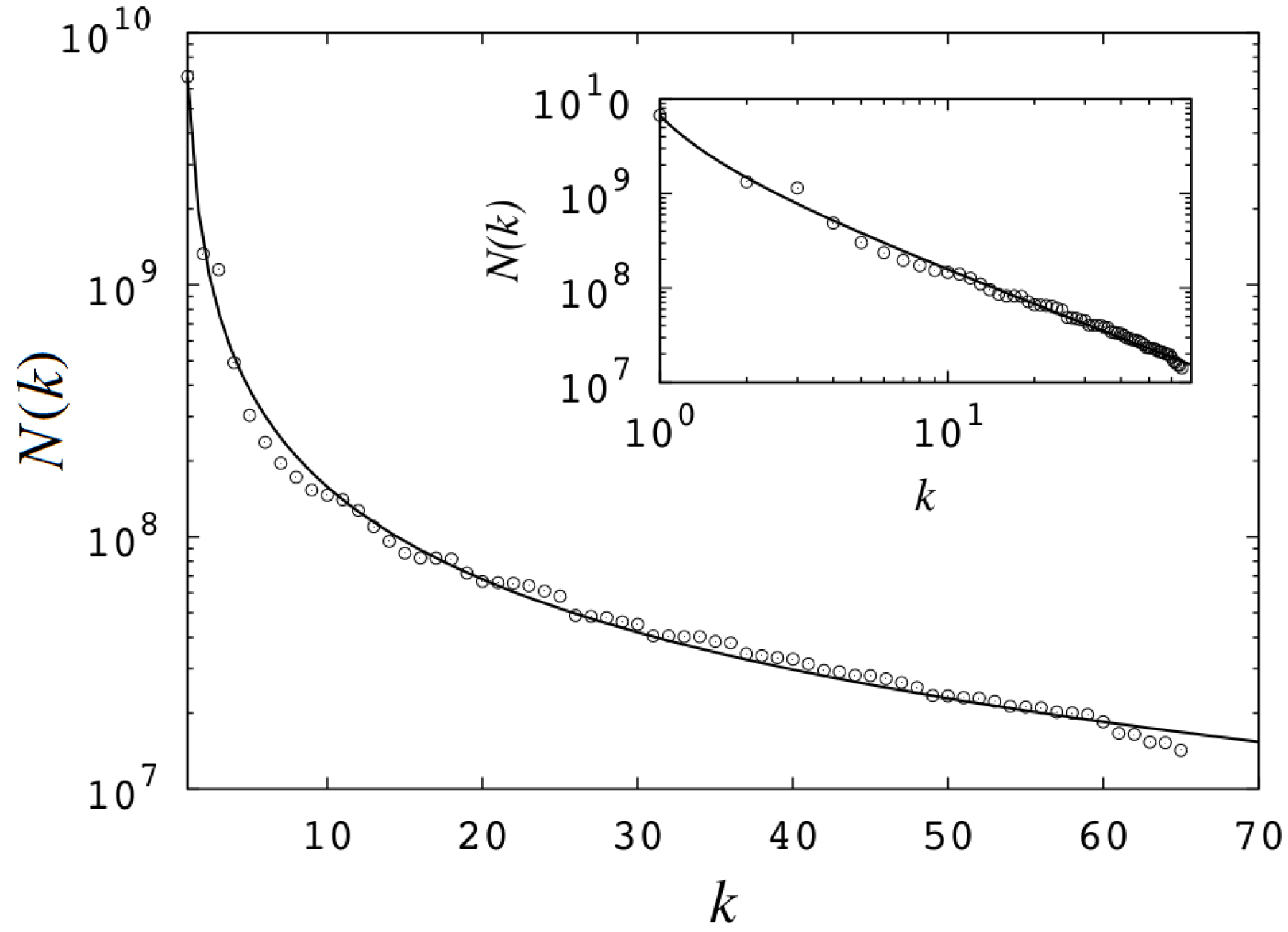
24]. Another set of studies correspond to the transcription of the time series formed by the trajectories generated by the critical attractors into networks via an appropriate algorithm known as the horizontal visibility method [
25]. Generalized entropies play an important role in understanding these applications.
The structure of the rest of article is as follows: In
Section 2, we provide the basic description of the anomalous dynamics at critical attractors that forms the core knowledge for the rest of the article. Of the three routes to chaos in one-dimensional nonlinear maps, we refer only to the intermittency and the period-doubling cases. For the sake of brevity, we do not provide a description of the quasiperiodic critical attractors and give only the relevant references. In
Section 3, we extend our description to the intricate dynamics towards the Feigenbaum attractor and refer to its hierarchical structure with modular organization. In
Section 4, we describe the stationary distributions produced by sums of positions in the dynamics associated with the Feigenbaum attractor and how they transform beyond the transition to chaos. In
Section 5, we present our applications to condensed-matter complex systems, whereas in
Section 6, we do so likewise for general or interdisciplinary complex systems. In
Section 7, we discuss our results and make clarifying remarks.
7. Discussion and Conclusions
The search and evaluation of the applicability of
q-statistics or other proposed generalizations of the BG canonical statistical mechanics involves an examination of the domain of validity of the BG formalism. The circumstances for which BG statistics fails to be applicable are believed to be associated with situations that lack the full degree of chaotic irregular dynamics that probes configurational phase space thoroughly, a requisite for true equilibrium. For the critical attractors of nonlinear one-dimensional maps, such anomalous circumstances are signaled by the vanishing of the Lyapunov coefficient,
, and the ergodic and mixing properties of chaotic
trajectories are no longer present when
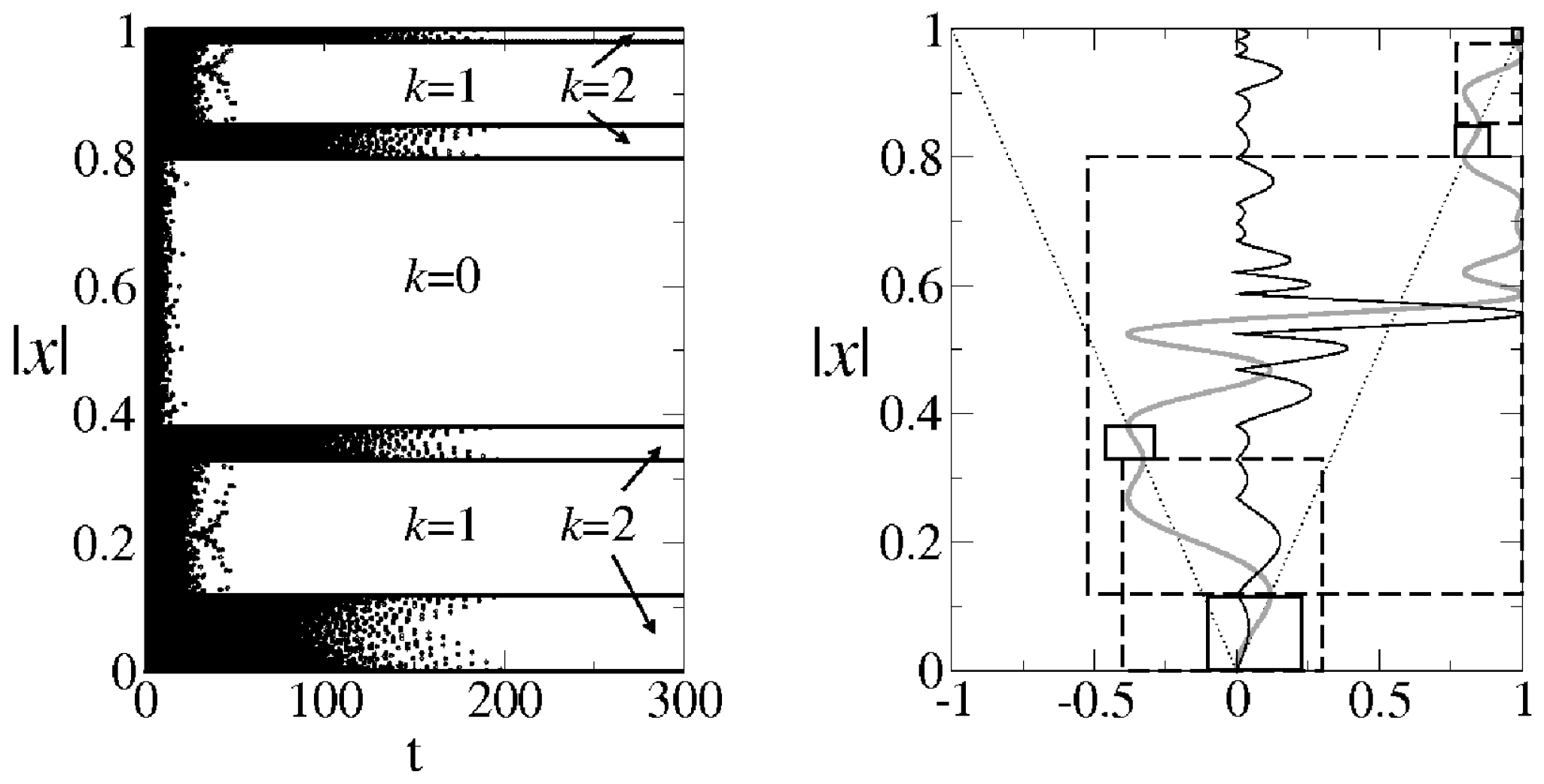
. At the period-doubling onset of chaos, the trajectories within the attractor, or those that have evolved a long time towards it, are confined to a multifractal subset of phase space with fractal dimension
. These trajectories possess boundless memory. The dynamics at the tangent bifurcation consists of either a monotonous evolution towards or away from the position of tangency. It does not consider the access of trajectories to an adjacent or neighboring chaotic region, as in the setting of [
33], or as in trajectories in conservative maps with weakly developed chaotic regions [
8,
9]. Hence, there is no reappearance of trajectories from chaotic regions that would cause the relaxation from the
q-statistical regime we have found to a BG regime at some crossover iteration time,
τ.
The manifestation of the anomalous dynamics at the onset of chaos in the properties of the condensed-matter physical systems and the complex systems we have studied implies ergodicity and/or mixing breakdown in their own nature or circumstances. As seen in
Section 5.1, the study of clusters at criticality in thermal systems by means of the saddle-point approximation in the LGW free energy model involves the retention of only one coarse-grained, but dominant, configuration. This, in turn, leads to physically reasonable cluster properties that appear to fall outside the limits of validity of the BG theory. On the other hand, it was found that the entropy expression that provides the property of extensivity for the estimate of the number of cluster configurations is not the usual BG expression, but that for the
q-statistics. The crossover from
to that for
is obtained when the system is taken out of criticality, because
makes
. The equivalence with the insulator-conductor transition in the model system described in
Section 5.2 with the transition to chaos along the intermittency route suggests ergodicity and mixing failure at the mobility edge. Furthermore, because of the precise analogy described in
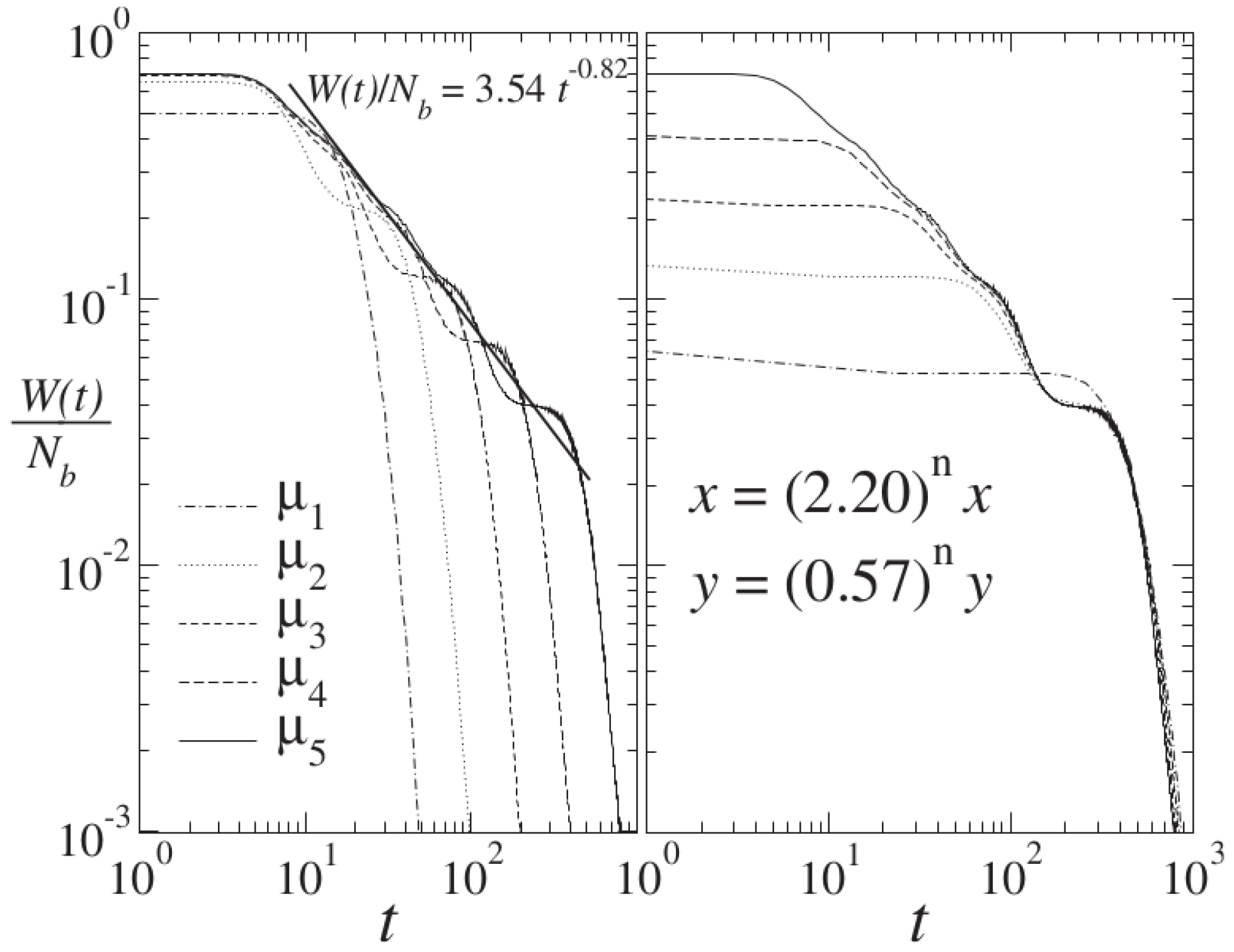
Section 6.1.1 between the dynamics at the tangent bifurcation and the stochastic problem of rank distributions, similar implications can be entertained for the ranking properties of these complex systems. We have seen that the dynamics of noise-perturbed logistic maps at the chaos threshold exhibits the most prominent features of glassy dynamics in supercooled liquids [
17,
18,
19]. The existence of this analogy cannot be considered accidental, since the limit of vanishing noise amplitude,
, involves, like in glass formation, loss of ergodicity. The occurrence of these properties in this simple dynamical system with degrees of freedom represented via a random noise term, and no reference to molecular interactions, suggests a universal mechanism lying beneath the dynamics of glass formation.
We have described the dynamical behavior at the pitchfork and tangent bifurcations of unimodal maps of arbitrary nonlinearity
. This was accomplished via the consideration of the solution to the RG functional composition for these types of critical attractors. Our studies have made use of the specific form of the
ζ-logistic map, but the results have a universal validity, as conveyed by the RG approach. The RG solutions are exact and have the analytical form of
q-exponentials; we have shown that they are the time (iteration number) counterpart of the RG fixed-point map expression found by Hu and Rudnick for the tangent bifurcations, and that is applicable also to the pitchfork bifurcations [
3]. The
q-exponential for the sensitivity,
, is exact, and we have straightforward predictions for
q and
in terms of the fixed-point map properties. We found that the index,
q, is independent of
ζ and takes one of two possible values according to whether the transition is of the pitchfork or the tangent type. The generalized Lyapunov exponent,
, is simply identified with the leading expansion coefficient,
u, together with the starting position,
.
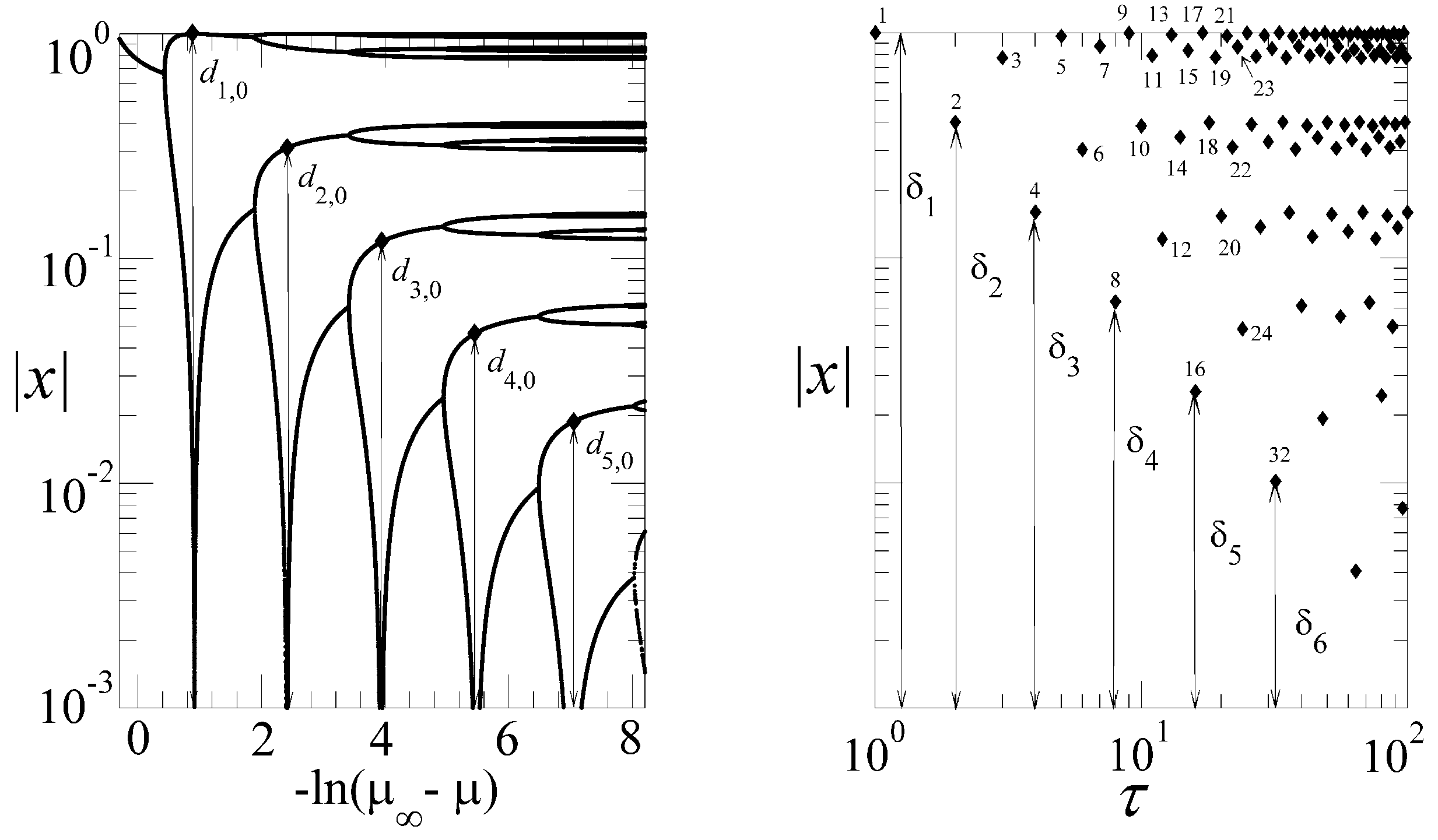
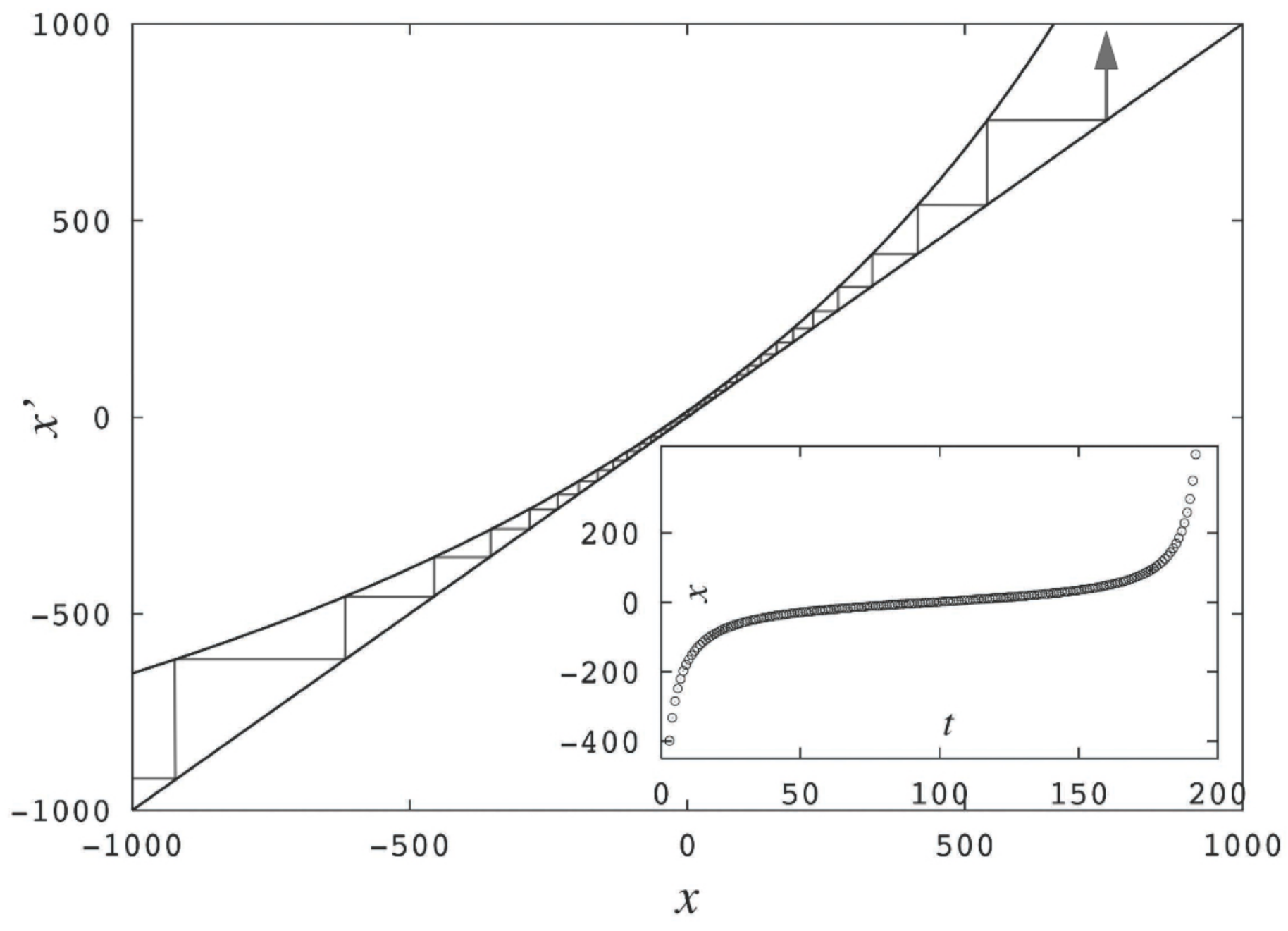
One of our most striking findings is that the dynamics at the period-doubling accumulation point is constituted by an infinite family of Mori’s
q-phase transitions, each associated with orbits that have common starting and finishing positions located at specific regions of the multifractal attractor. Each of these transitions is related to a discontinuity in the trajectory scaling function,
, or “diameters ratio” function, and this, in turn, implies a
q-exponential
and a spectrum of
q-Lyapunov coefficients for each set of orbits. The transitions come in pairs with specific conjugate indexes,
q and
, as these correspond to switching starting and finishing orbital positions. Since the amplitude of the discontinuities in
σ diminishes rapidly, in practical terms, there is only the need for the evaluation for the first few of them. The dominant discontinuity is associated with the most crowded and sparse regions of the attractor, and this alone provides a very reasonable description. Thus, the special values for the Tsallis entropic index,
q, in
are equal to the special values of the variable
in the formalism of Mori and colleagues at which the
q-phase transitions take place. We found that there is an infinite number of such special values, as there is an infinite number of universal discontinuities
. See [
4] for a wider discussion.
Then, we recall that the approach of an ensemble of trajectories to the Feigenbaum attractor leads to a rich hierarchical structure with a generalized statistical-mechanical expression as an emergent property, an expression that contains an infinite number of
q-indexes in the partition function linked to a thermodynamic potential also associated with a
q-deformed exponential. Again, the values of all of these
q-indexes are given in terms of the universal constants contained in the trajectory function,
. Both the trajectories within and those that approach the Feigenbaum attractor lead to stationary distributions for their sums of visited positions. As we have seen, these distributions capture the features of the dynamics associated with the multifractal attractor: the families of
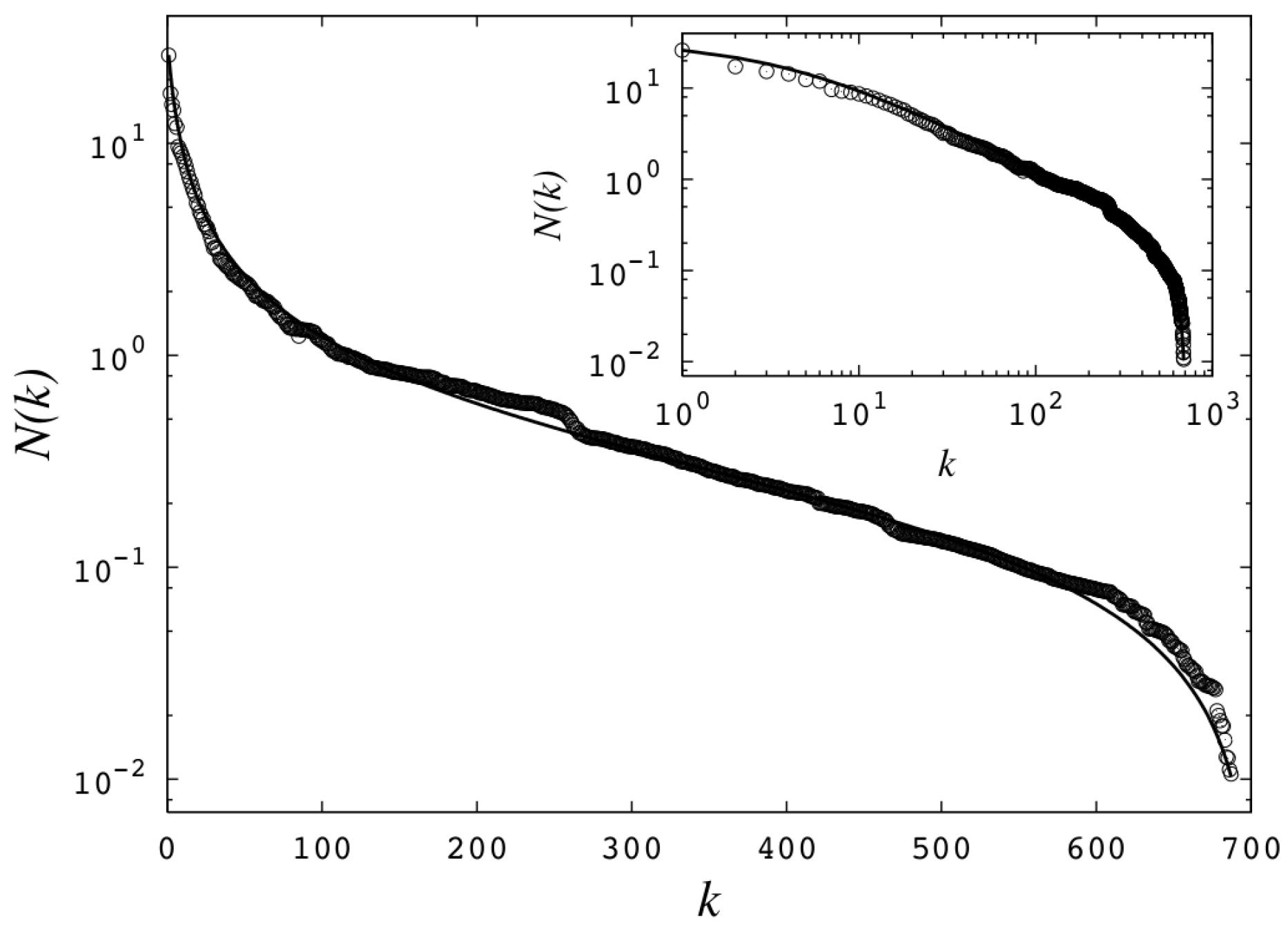
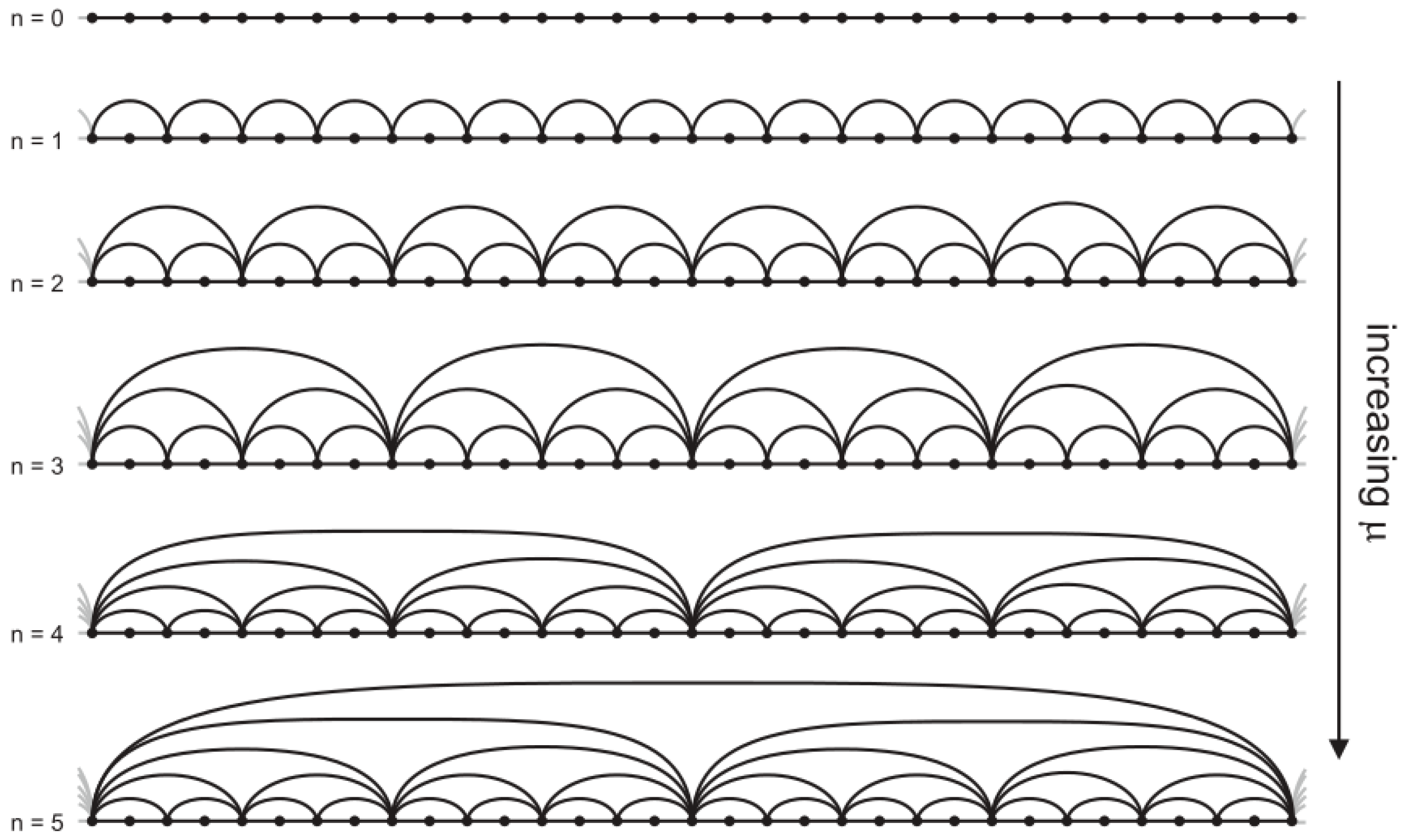
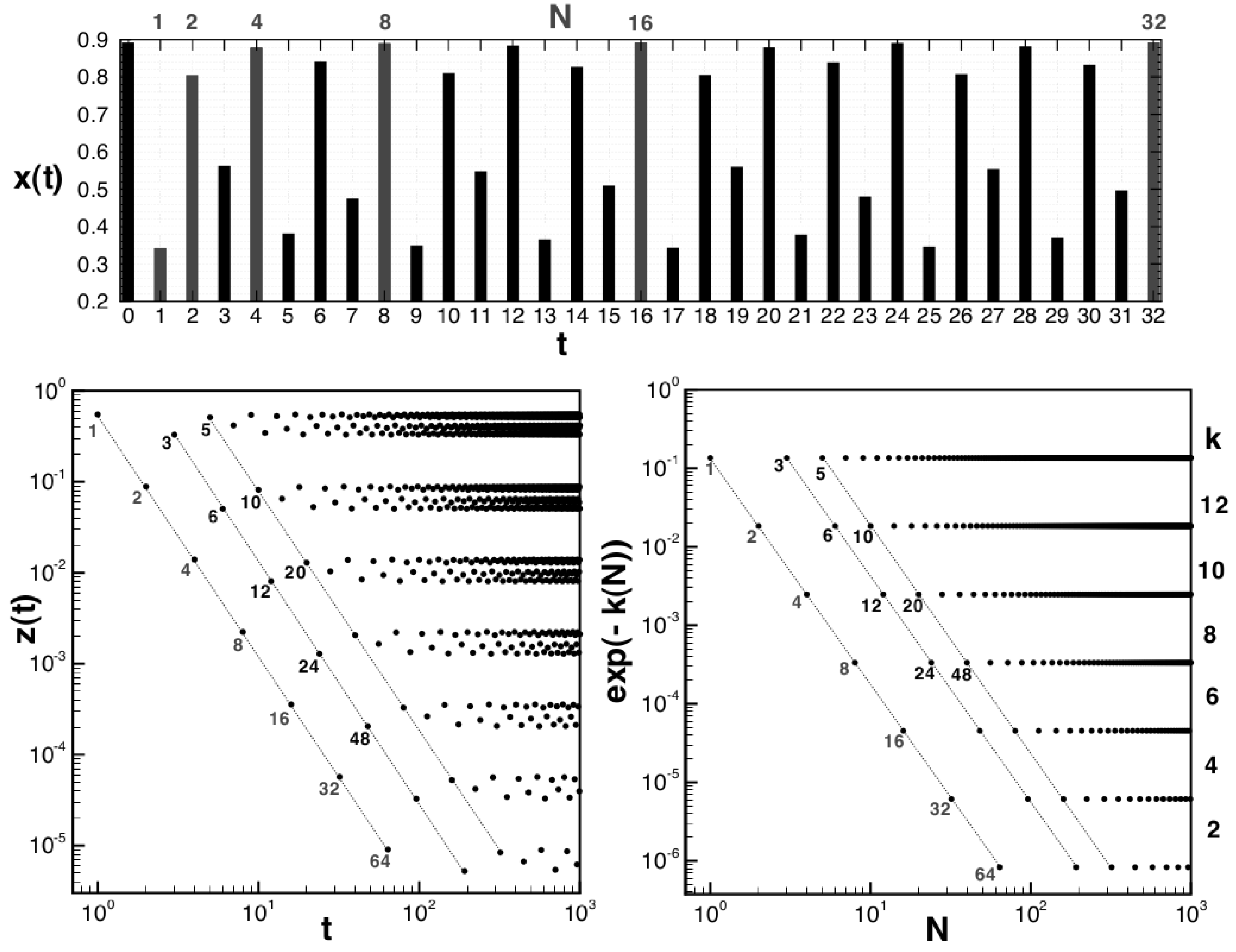
q-exponentials in the trajectory within the attractor (
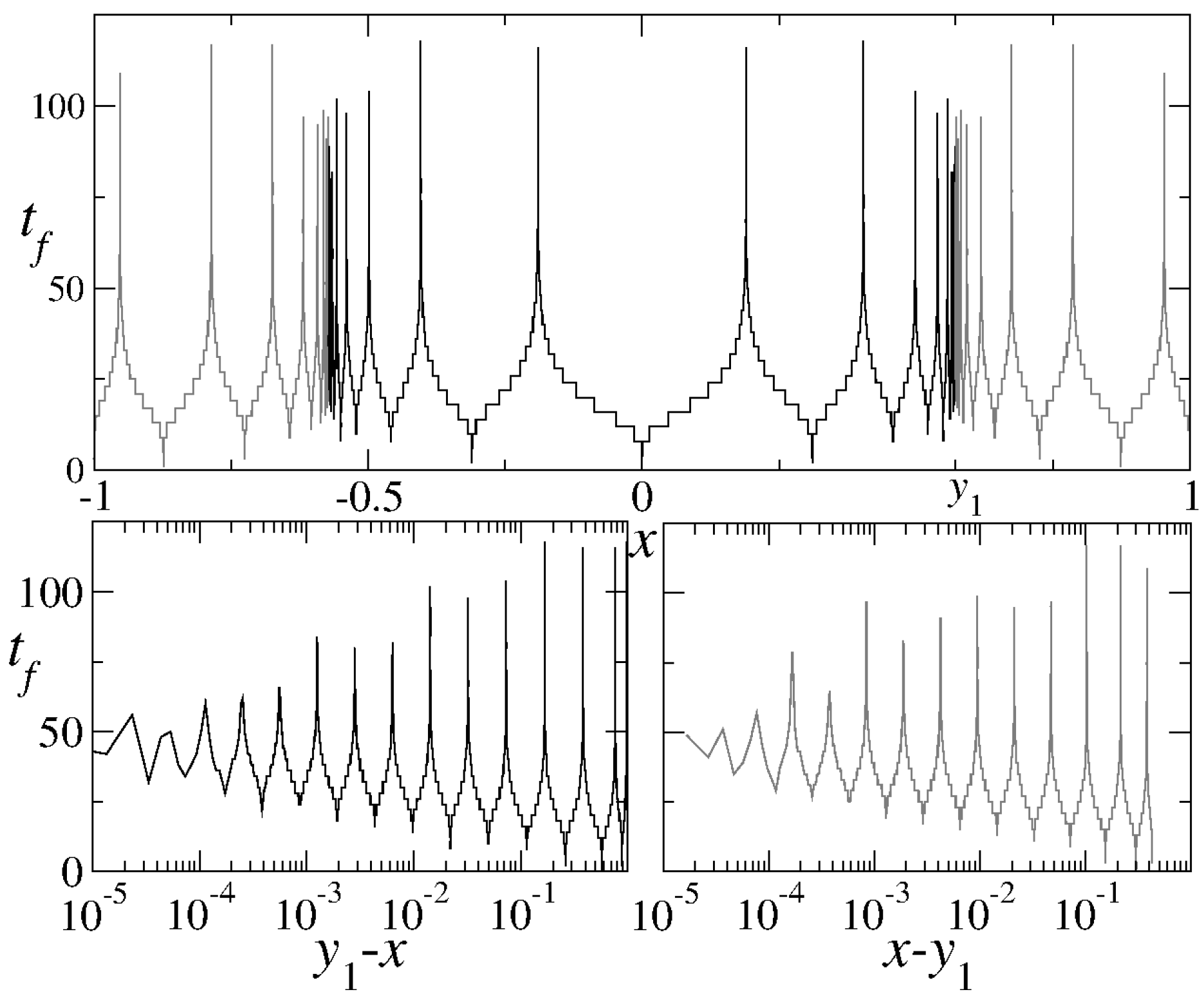
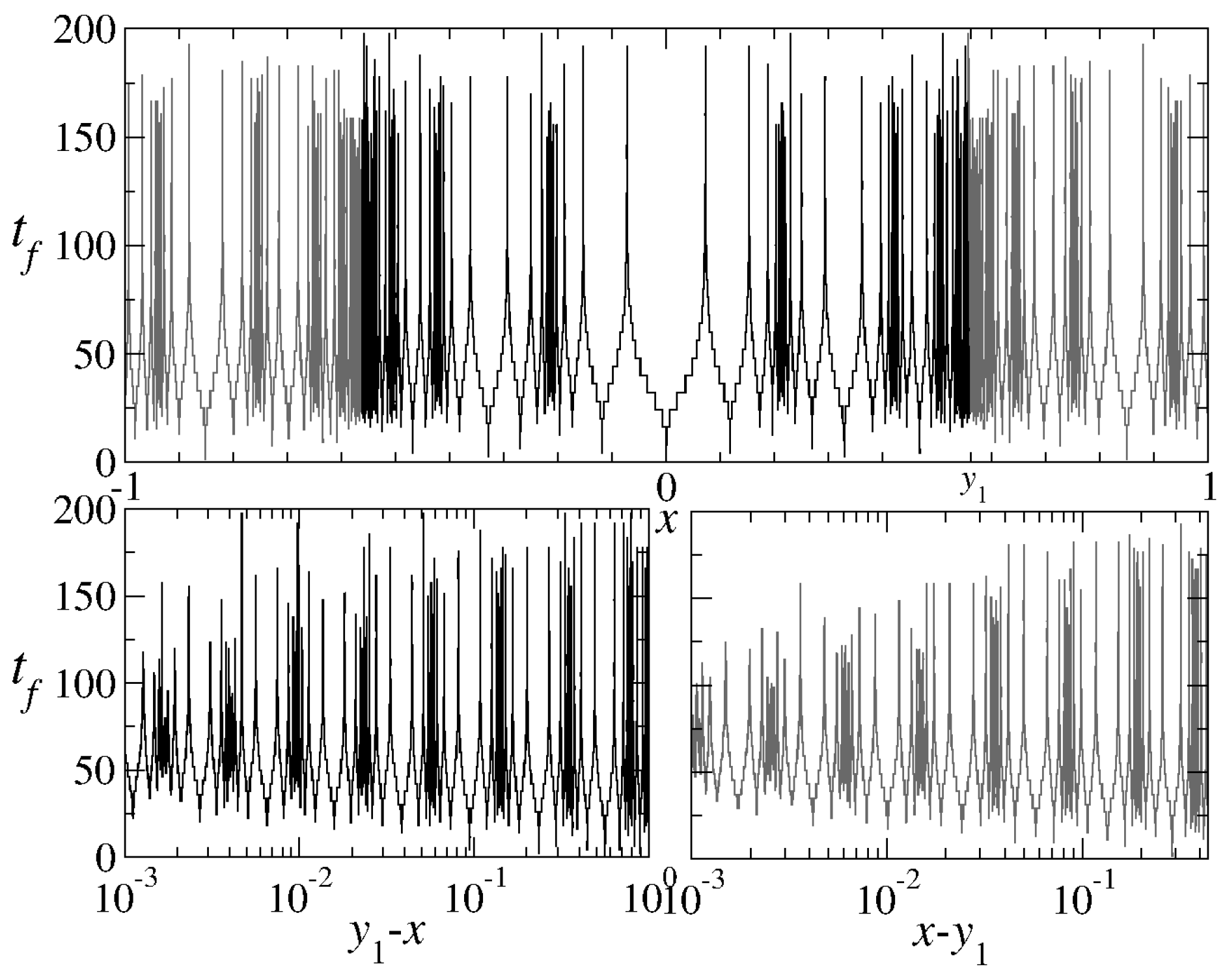
Figure 3), the formation of phase-space gaps (
Figure 9), the hierarchical arrangements of the repellor positions and their preimages (
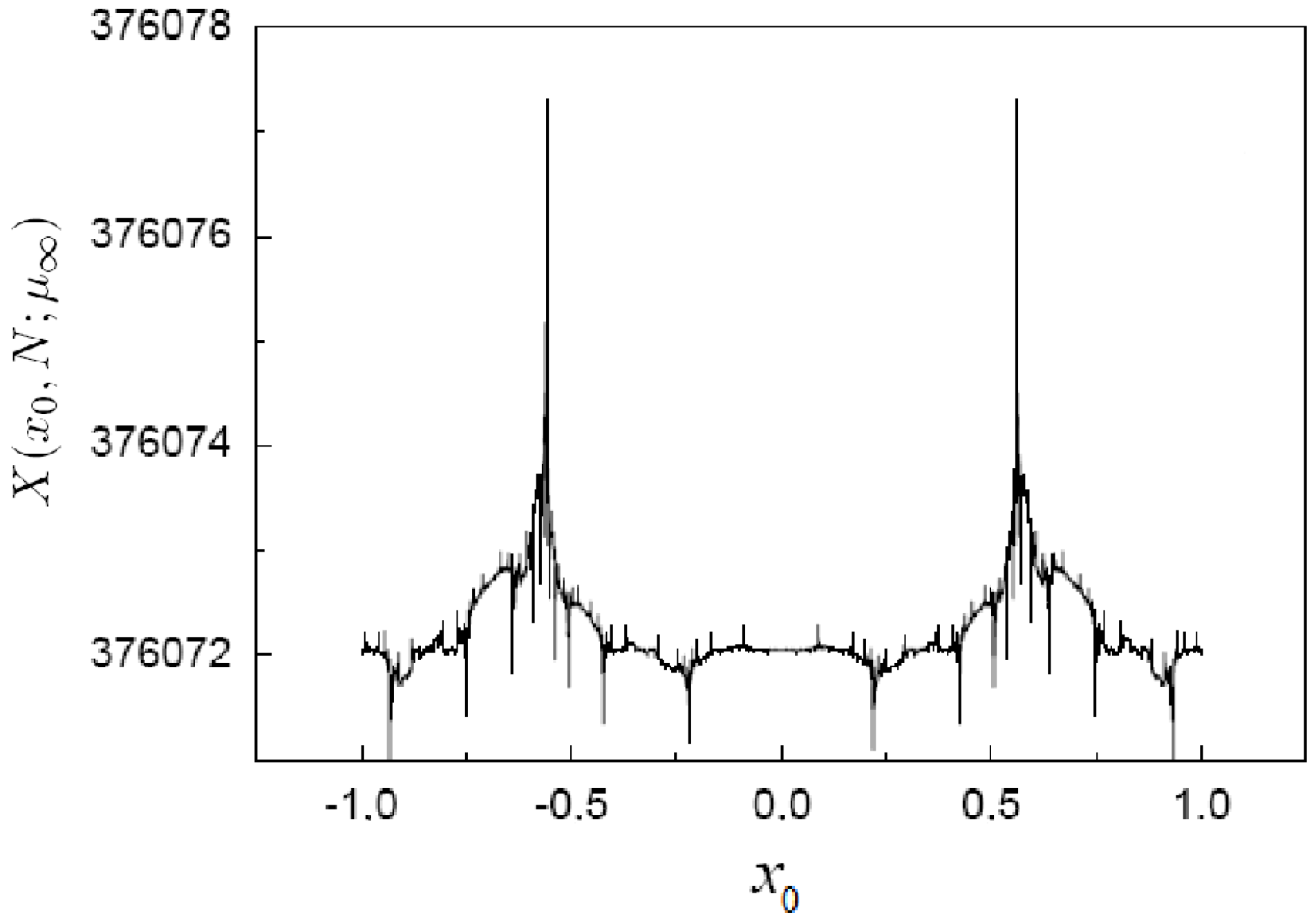
Figure 11 and
Figure 12).
In the case of the attractor-repellor fixed point that represents the tangent bifurcation, we have seen that there is a pure
q-statistical regime, for the trajectories,
, the sensitivity,
, and the time extensivity of the entropy,
. A single
q-index occurs (and naturally, also, its companion indexes,
and
). This is reflected in the physical systems that accept a description analogous to this dynamics, the critical clusters, the conductance at the mobility edge and the rank distributions. However, as we have seen, the multifractal nature of the period-doubling accumulation point (and, similarly, the critical attractors of the quasiperiodic route to chaos in circle maps [
6]) requires an infinite set of
q-indexes and their duals,
, each, of course, given by the infinite set of universal constants contained in the trajectory scaling function,
. As described, there are infinite families of
q-exponentials in the sensitivity within the attractor and in the configurational weights in the partition function. The anomalous dynamics within and towards this type of critical attractor cannot be described with a language simpler than that required to characterize the multifractal set itself. However, approximations can be introduced that reduce the infinite set of
q-indexes to a basic pair,
q and
. For the Feigenbaum attractor of the quadratic logistic map
, the dominance of the two largest discontinuities in
,
and
, which correspond, respectively, to the sparsest and tighter regions of the multifractal, suggests that a reasonable approximation is the consideration of only these two contributions, while the others are neglected. This approximation reduces the Feigenbaum attractor into a two-scale multifractal and a single index parameter
[
5,
39]. Furthermore, the time series transformation of the trajectories at the Feigenbaum attractor into a network via the HV algorithm reduces the multifractal nature in the dynamical properties into a single fractal description with only a single network generalized Lyapunov spectrum [
25].
Since the early days of
q-statistics, the presence of a duality in
q-indexes and
q-entropies have been noticed and documented. From a purely operational standpoint, their source is straightforward: the inverse of a
q-exponential or, equivalently, the inverse of the argument of a
q-logarithm, generates the dual indexes,
q and
. Differentiation of these functions give the twin indexes,
q and
, and a combination of both yields the pair
. Larger sets of related
q-indexes can be produced via iteration of these and other common algebraic and analytical procedures. Naturally, there appear dual physical quantities associated with them, e.g., generalized Lyapunov exponents and generalized Pesin identities. Their physical status and meanings can be answered by considering the results obtained for the different dynamical systems considered here. These point out that the view that between two possible entropy expressions, only one is to be a physical quantity, is inappropriate. We quote a statement from an earlier study [
34]: “An interesting observation about the structure of the nonextensive formalism is that the equiprobability entropy expression
can be obtained not only from
in:
but also from
where
. The inverse property of the
q exponential reads
for the
q logarithm and as pointed out introduces a pair of conjugate indices
with the consequence that, while some theoretical features are equally expressed by both
and
, some others appear only via the use of either
or
. For instance, the canonical ensemble maximization of
with the customary constraints
and
, where
and
U are configurational and average energies, respectively, leads to a
Q-exponential weight (with
when
). On the other hand, the partition function is obtained via the optimization of
. The mutual Equations (
52) and (
53) elegantly generalize the BG entropy.”
Recently [
55,
56], the two entropy expressions in Equations (
52) and (
53) have been formally examined in relation to the maximum entropy principle (MEP) under the assumption that only the first three Shannon–Kinchin axioms hold. The dual entropies are known to follow from optimization involving different constraints: one is that quoted above,
; and the other is related to the modified “average”
. It is clear that the two constraints leading to the two entropy expressions play a role in the dynamics with a single pair of dual indexes,
q and
, like in that associated with the tangent bifurcation and its manifestations in the description of critical clusters, mobility edge and rank distributions. However, for the case of a multifractal critical attractor, the MEP procedure calls for some generalization in order to accommodate the presence of an infinite set of
q-indexes.
The common tenet in the studies reviewed here is that the properties of the systems considered are first determined independently of any method that assumes a statistical-mechanical formalism (other than the ordinary LGW Hamiltonian in the BG formalism for critical clusters in
Subsection 5.1). That is, these properties are not derived under the supposition of the applicability of generalized entropy expressions or their implications. After that, the results obtained for these systems (trajectories, sensitivity, rates of approach,
etc., and their counterparts in condensed matter and other interdisciplinarily complex systems) are analyzed in relation to generalized entropy expressions or properties derived from them. Finally, we commented on pertinent conclusions.