1. Introduction
In recent years, opinion dynamics have aroused a lot of research interest, aiming to model the formation of collective phenomena by describing local interacting behavior in social systems [
1]. Statistical physics has become a widely used method to study how microscopic behavior causes different global complex properties. Initial opinion models originate from physical systems, using the analogy of ferromagnetic spins [
2]. These models can explain some collective social phenomena from the microscopic perspective, for instance, why an initial minority opinion could very quickly convince the whole population in a French referendum [
3]. In opinion models, individual opinions are initiated in the beginning, and then, agents update their opinions following nearest neighbors [
4]. Agents’ opinions can take one of several or an infinite number of available opinions, and therefore, a collection of opinion models contain discrete and continuous opinion models. In the discrete group, the voter model assumes agents are completely convinced by their neighbors, and adopt neighbors’ opinions randomly [
5]. The model is simple and can be analyzed by the mean-field approach [
6]. Other discrete opinion models also have been presented in terms of realistic systems, such as the majority model [
7,
8], and the Sznajd model [
9,
10]. In the continuous group, the bounded confidence is introduced to make agents trust only those neighbors who hold similar beliefs [
11,
12]. Martins [
13,
14,
15] presented a model with discrete actions and continuous opinions, in which individual opinions are latent, and neighbors are aware of agents’ actions. Furthermore, complex networks have been used to mediate opinion interaction, and the network structure has been found to play a significant part in the dynamics [
16,
17]. Relaxation time, average opinion and other global properties depend significantly on the underlying network [
18].
Agents’ personal characteristics and behavior patterns have been considered in opinion models, and these features affect local opinion updates [
19]. In [
20], the action of withdrawing from interaction for agents was taken into account, and agents had memory of historical actions, so they could take the best action. In that model, the convergence time relies heavily on the memory length. Other personal factors, such as contrarians [
21] and individual awareness [
22] have already been studied, and their influence on the final opinion distribution has proven to be notable. In actual social networks, the interaction among agents is not always symmetrical. In [
23], the authors proposed a PageRank model of opinion formation, in which connections between agents are weighted by a webpage ranking algorithm used by the Google search engine,
i.e., PageRank probability. Similarly, in [
24], opinion leaders with a strong convincing power were distinguished from ordinary people, and agents selected the weighted average of neighboring opinions. All in all, these nonlinear features were found to make the system enter different stationary regimes.
The kinetic opinion model [
25] has often been applied in social and economic systems to describe consensus formation or information diffusion. The kinetic opinion model has two parameters, considering agent’s self-confidence and neighbors’ influence [
26]. In many studies, individual conviction and influence are assignedat eachtime, and the distribution of conviction and influence is homogeneous. However, in an actual environment, especially in online communities, individual influence is often quite heterogeneous [
27]. Most agents are susceptible and have little impact on their neighbors, but a few agents are highly influential. For instance, on Twitter which is a well-known Internet social medium, a few users often have their posts retweeted over a large range, implying that their opinions have been accepted by a large number of users. The reasons are their abundant followers and the strong power they have for convincing their neighbors [
28]. Concerning this topic, the probability of persuading the same agent for different neighbors differs greatly. In [
29], based on the continuous opinion model, different tolerances of opinion discrepancy were defined by a given distribution for each agent, and results showed that heterogeneity does not always promote consensus. From empirical data, individual influence often correlates with underlying network structure [
30], so the dependence of opinion dynamics on realistic influence,
i.e., network-based influence, still need be explored. On the other hand, agents’ self-confidence is also heterogeneous and dynamic during the interaction [
31], and it is affected by social recognition [
32,
33]. Therefore, individual confidence and their opinions evolve together, and its effect on an agent’s decision at different time should be diverse. One may be concerned about the different effects of these two factors,
i.e., individual confidence and influence on the final state of the system. In this paper, we attempt to reveal how the heterogeneity of influencers affects the formation of public opinion and to explore the competition of heterogeneous conviction and influence in agents’ decisions and relaxation process.
In this paper, we propose a kinetic exchange model that includes dynamic self-confidence and heterogeneous influence. We conduct numerical simulations to investigate macroscopic characteristics of our model. Simulations results show that differently from traditional voter model, the system with heterogeneous conviction and influence does not have conserved average magnetization, but is driven to an ordered state in which one opinion becomes the majority opinion. However, due to the spontaneous formation of extremists, total consensus cannot occur. This result coincides with empirical analysis of the actual social interaction on Internet [
34], without the need of introducing highly specific post and reply mechanism. On online social media, consensus is always hard to reach [
35], and one opinion will be dominant in the population. Moreover, in our model, individual influence plays a subtle role in opinion dynamics when competing with agents’ conviction. The heterogeneity of individual influence accelerates the relaxation process, but it cannot lead to the convergence of average magnetization. This phenomenon can help in understanding why information diffuses and evolves more rapidly in online social networks.
The rest of the paper is structured as follows:
Section 2 proposes a voter model with heterogeneous individual conviction and influence. In
Section 3 simulation results and discussion about the model are provided. Our conclusions are presented in
Section 4.
2. The Model
In the kinetic opinion model, an agent updates its opinion according to its original opinion and a neighbor’s opinion. For the discrete case [
36], each agent has one of several opinions, and the parameters are also renormalized to discrete values. In an update event, an agent
i’s opinion evolves as:
where
Ci represents agent
i’s confidence level, meaning agents have the tendency to maintain their original opinions [
36]. The parameter
μij denotes neighbor’s influence with values of +1 or –1 for a given probability. The parameter
Ci as well as
μij hasthe same distribution for each agent. The parameters can be either annealed or quenched. The annealed parameters are assigned at each Monte Carlo step, but the quenched parameters are fixed during the evolution.
In many real situations, agents’ confidence and influence on others are heterogeneous. With a large individual influence, an agent has the ability to persuade more people to adopt and propagate its opinion. In [
27,
30], the authors analyzed the influence of agents in an actual social network. In their studies, agents’ influence is related to the underlying network structure, and agents that have a large degree or centrality in the network have more influence. They verified the validity of individual influence by calculating the average retweeting probability and other indicators. In this paper, we investigate the action of individual influence based on the network topology. We introduce our heterogeneous voter model as follows.
Assuming N agents constitute a system, and agents can have either of two opinions, i.e., σ = + 1 or σ = − 1. In an update event, an agent i is selected at random. Agent i’s conviction is defined as Ci, which is a continuous variable taking value from [0, 1]. With the probability Ci, agent i keeps its original opinion; otherwise, it will update its opinion following its neighbors. With the probability 1 − Ci, agent i selects a neighbor j according to the influence strength of its neighbors and adopts the neighbor’s opinion. The probability that agent i will choose one of its neighbors j is directly proportional to neighbor j’s influence. After N such update events, the time step is increased by 1. There are many methods to measure agents’ influence. For the sake of simplicity and without loss of generality, considering the network structure, we use node degree and betweenness as their individual influence.
Agent
i’s conviction
Ci does not always remain constant; instead, its conviction changes when its opinion is confirmed by neighbors. If most of neighbors support the agent’s opinion, its confidence about its opinion is increased; however, if many neighbors hold an opposite opinion, the agent may doubt its own opinion, so that its confidence declines. This phenomenon agrees with social reinforcement, and multiple sources of support are required to convince people about a given behavior [
37]. We assume that all agents have the same initial conviction
C0. When agent
i decides to follow its neighbor’s opinion, its confidence
Ci may change during the interaction. In each update event, if the neighbor
j that is selected in terms of its influence has the same opinion as agent
i, agent
i’s conviction
Ci increases linearly by
h, otherwise, its conviction decreases by
h. The variation
h satisfies 0 ≤
h < 1, and cannot be too large in order to avoid stopping the dynamics quickly. The variation of agents’ conviction may have many different forms. In Reference [
31], individual conviction of keeping its current state changes linearly with the interacting time elapsed. Similarly, here we use the linear variation
h of conviction for the sake of simplicity.
Now, we investigate the effect of individual influence on the final opinion. In this case, we assume individual confidence does not evolve with time, i.e., each agent’s conviction Ci is fixed at C0. The global density of opinion +1 for agents with degree k at time t is defined as f (k,t). Considering the degree-based influence, for each agent with degree k, a neighbor with degree ku is selected with the probability , where is the degree-degree correlation function.
Therefore, in any network, the transition rate of
f (
k,t) is given by
In the mean-field approach, the density of opinion +1 with different degree ku is identical, and then we get . Therefore, without the evolution of agents’ conviction, the average magnetization of the system is conserved in any network, in accordance with the standard voter model.
3. Simulation Results
We conduct Monte Carlo simulations to study the difference of effects between individual conviction and influence and how these dynamic individual characteristics affect the evolutionary process. We use both the Barabasi-Albert scale-free network and Erdos-Reyni random network as the interaction topology. All of the networks are constructed to have the same average degree
. In the creation of the scale-free network, 10 nodes are fully connected initially, and each time a new node is added to the network with five edges linking to different old nodes. As far as we know, the random network has a Poisson degree distribution, while the degree of a scale-free network decays as a power law.
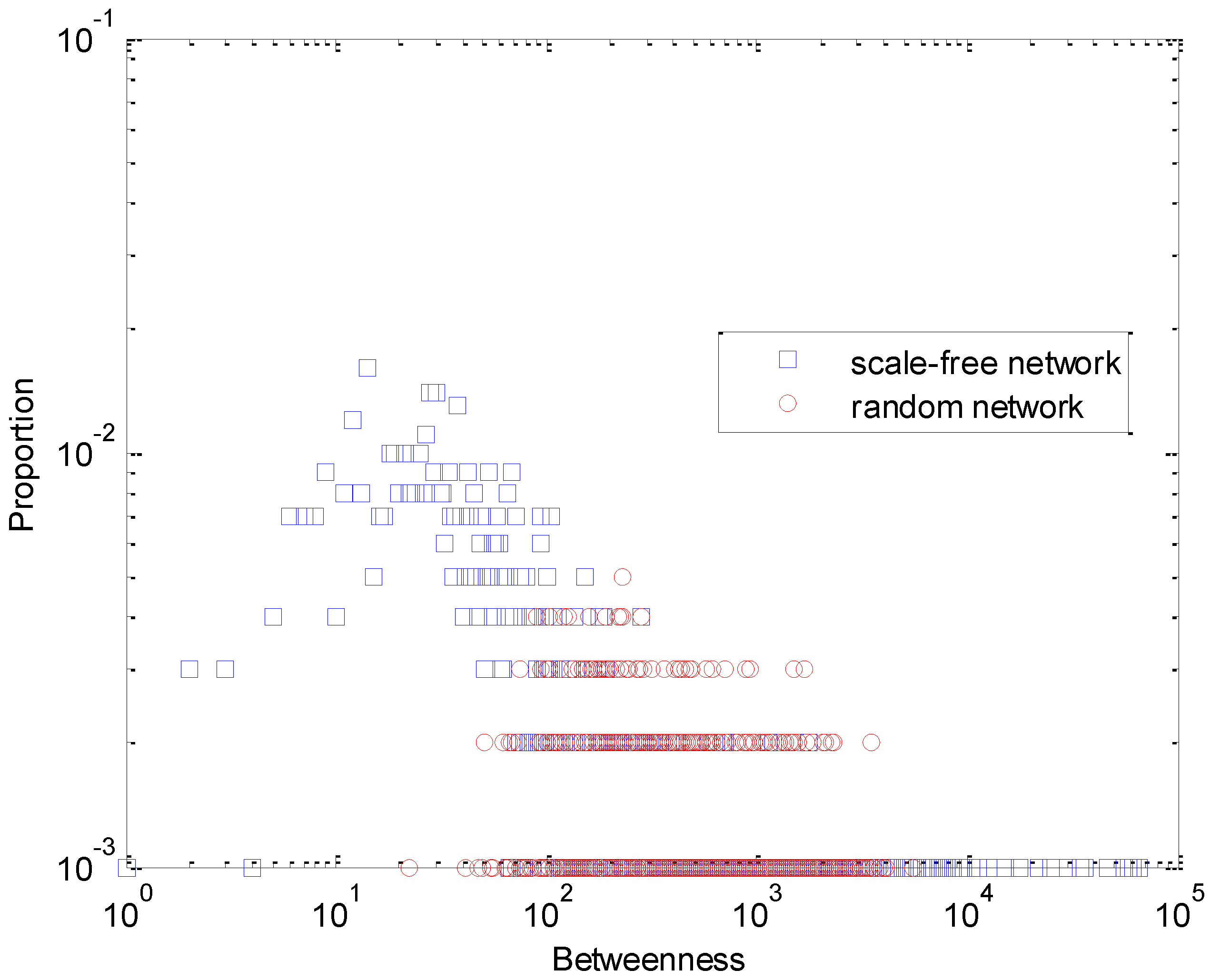
Figure 1 illustrates the distribution of betweenness for both networks. The betweenness of node
i refers to the number of shortest paths that pass through node
i between any two nodes. From
Figure 1, the betweenness in scale-free networks varies from 1 to about 10,000, with a maximal proportion around 12. Therefore, scale-free networks have a wider range of betweeeness than random networks. Obviously, compared with node degree, betweenness has a much more heterogeneous distribution.
Figure 1.
Distribution of betweenness in a scale-free network and random network. The average node degree is 10, and N = 1,000.
Figure 1.
Distribution of betweenness in a scale-free network and random network. The average node degree is 10, and N = 1,000.
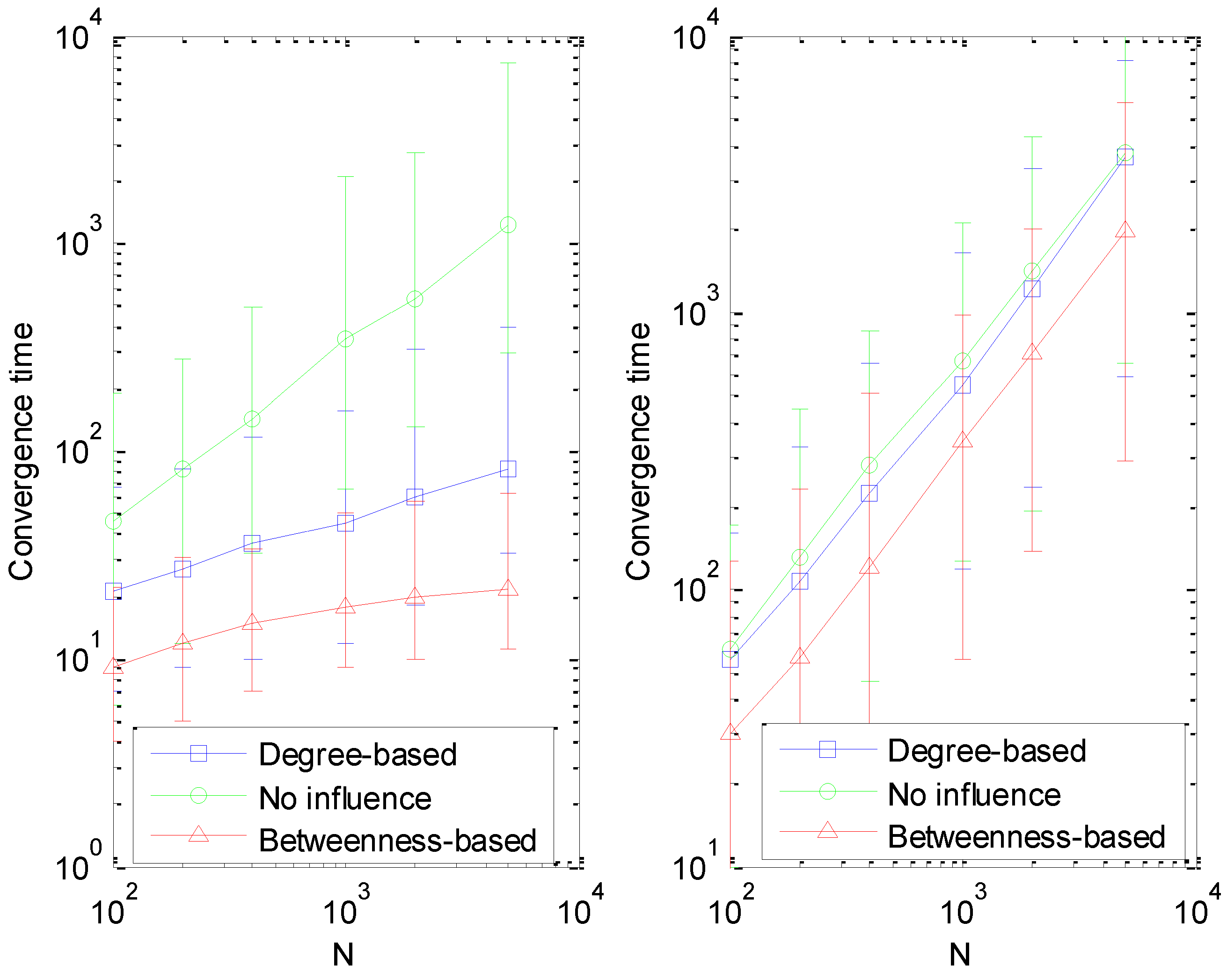
We have demonstrated that without the dynamic individual conviction, the system has conserved magnetization and will evolve to the consensus state in each realization. In that situation, individual influence does not change the final state of the system; instead, it changes the essential evolutionary process. Now, we omit agents’ conviction temporarily to investigate the convergence time under the action of individual influence. As shown in
Figure 2, the heterogeneous individual influence accelerates the opinion dynamics markedly. The average convergence time in scale-free networks is much less than that in random networks, especially when the betweenness-based influence is applied. The reason for this phenomenon is that the difference of degree and betweenness among nodes stays larger in scale-free networks, and very few agents have large power to affect others’ opinions. Therefore, the opinions of these influential agents are adopted by others frequently, reducing the fluctuations in the system and speeding up the evolution. In the traditional voter model, the convergence time
τ both in scale-free networks and random networks increases as the size
N of the system increases, following a power-law scaling,
i.e.,
[
6]. In contrast, in scale-free networks the convergence time with heterogeneous individual influence stays at a low level and increases very slowly with the size of the system, implying the action of agents’ influence is comparable with random fluctuations. However, in random networks, the system with degree-based influence has nearly the same relaxation speed as the traditional voter model, since the degree distribution of networks is relatively uniform. Moreover, opinions of the population under betweenness-based influence converge most rapidly in any network on average. Therefore, it is concluded that the heterogeneity of the frequency with which an agent’s idea is adopted by others makes the system stabilize faster.
Figure 2.
Convergence time as a function of system size N. Agents’ conviction is not considered in this figure. In the beginning, opinions are assigned uniformly at random. In the left plot, the underlying topology is scale-free networks, and in the right plot, random networks mediate the interaction. Every plot is an average of 200 different simulations.
Figure 2.
Convergence time as a function of system size N. Agents’ conviction is not considered in this figure. In the beginning, opinions are assigned uniformly at random. In the left plot, the underlying topology is scale-free networks, and in the right plot, random networks mediate the interaction. Every plot is an average of 200 different simulations.
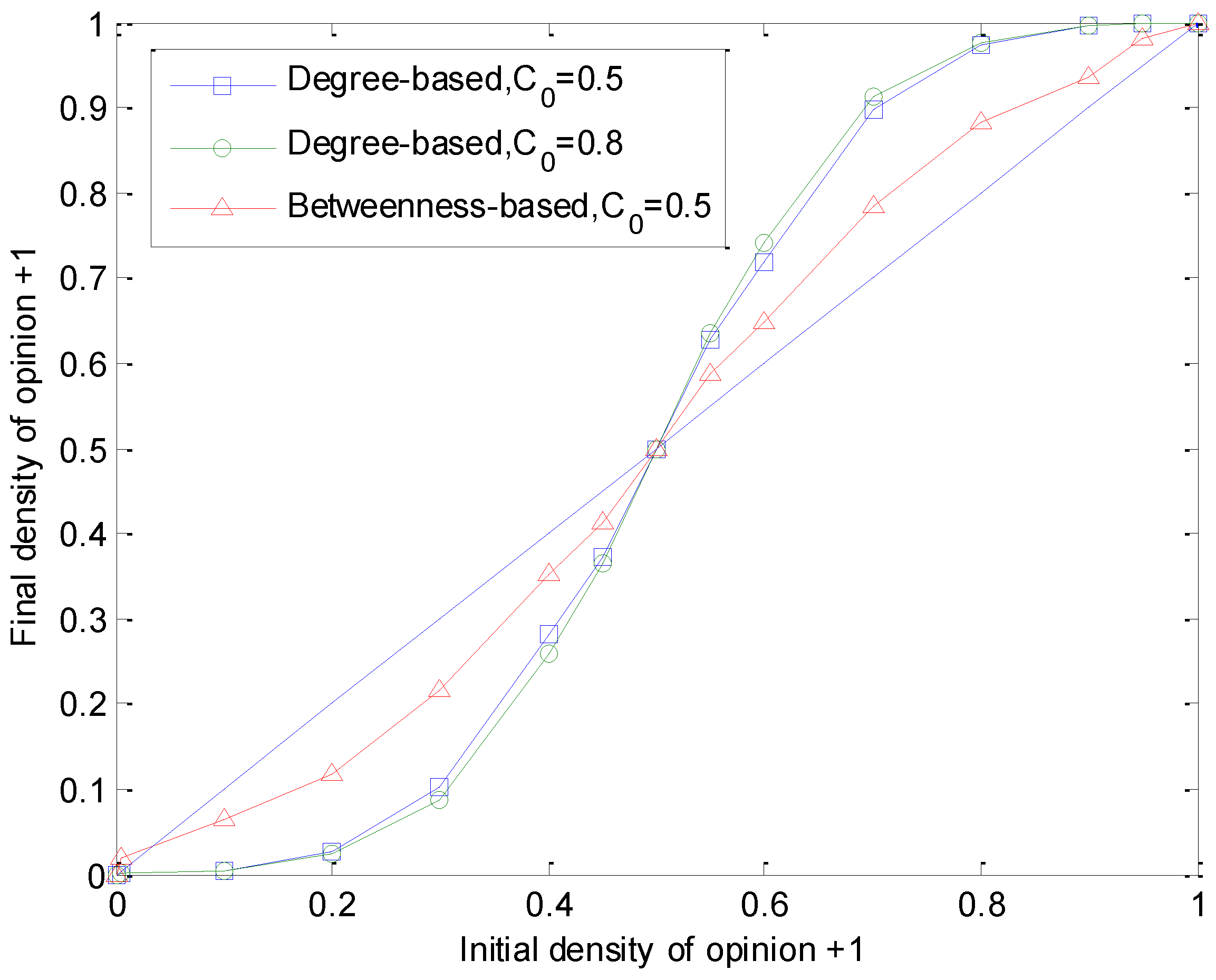
We explore the average magnetization to reveal the social entropy under the joint effect of individual conviction and influence.
Figure 3 shows the final density of opinion +1
with different initial conditions. Therefore, the average magnetization can be attained by
. From
Figure 3, under the impact of agents’ conviction and influence, the average magnetization conservation is broken, and the system is driven towards the direction of the consensus state. The difference in densities of two opinions is enlarged during the evolution process, since it is easier for agents with the majority opinion to strengthen their confidence. Finally, one opinion will dominate the population. However, due to the effect of strong personal confidence, total consensus is prevented by a few extremists holding the minority opinion. The heterogeneous individual influence has a significant role in opinion dynamics, but it cannot change the average magnetization without personal conviction. In
Figure 3, the system with betweenness-based influence almost approaches the traditional voter model, but the degree-based influence clearly changes the final average opinion. Although the betweenness distribution of the network is more heterogeneous and speed up the relaxation process effectively, agents’ conviction in this case is not strong enough to exert a dominating effect and support the initial majority opinion. Moreover, agents form their personal confidence gradually during the interaction, and therefore, initial conviction of each agent
C0 does not have any distinct impact on the average magnetization.
Figure 3.
Final density of opinion +1 versus initial density of opinion +1 f (0). The underlying topology is a scale-free network, N = 1,000 and h = 0.1. The results are averaged over 200 different simulations. The dotted curve refers to the standard voter model.
Figure 3.
Final density of opinion +1 versus initial density of opinion +1 f (0). The underlying topology is a scale-free network, N = 1,000 and h = 0.1. The results are averaged over 200 different simulations. The dotted curve refers to the standard voter model.
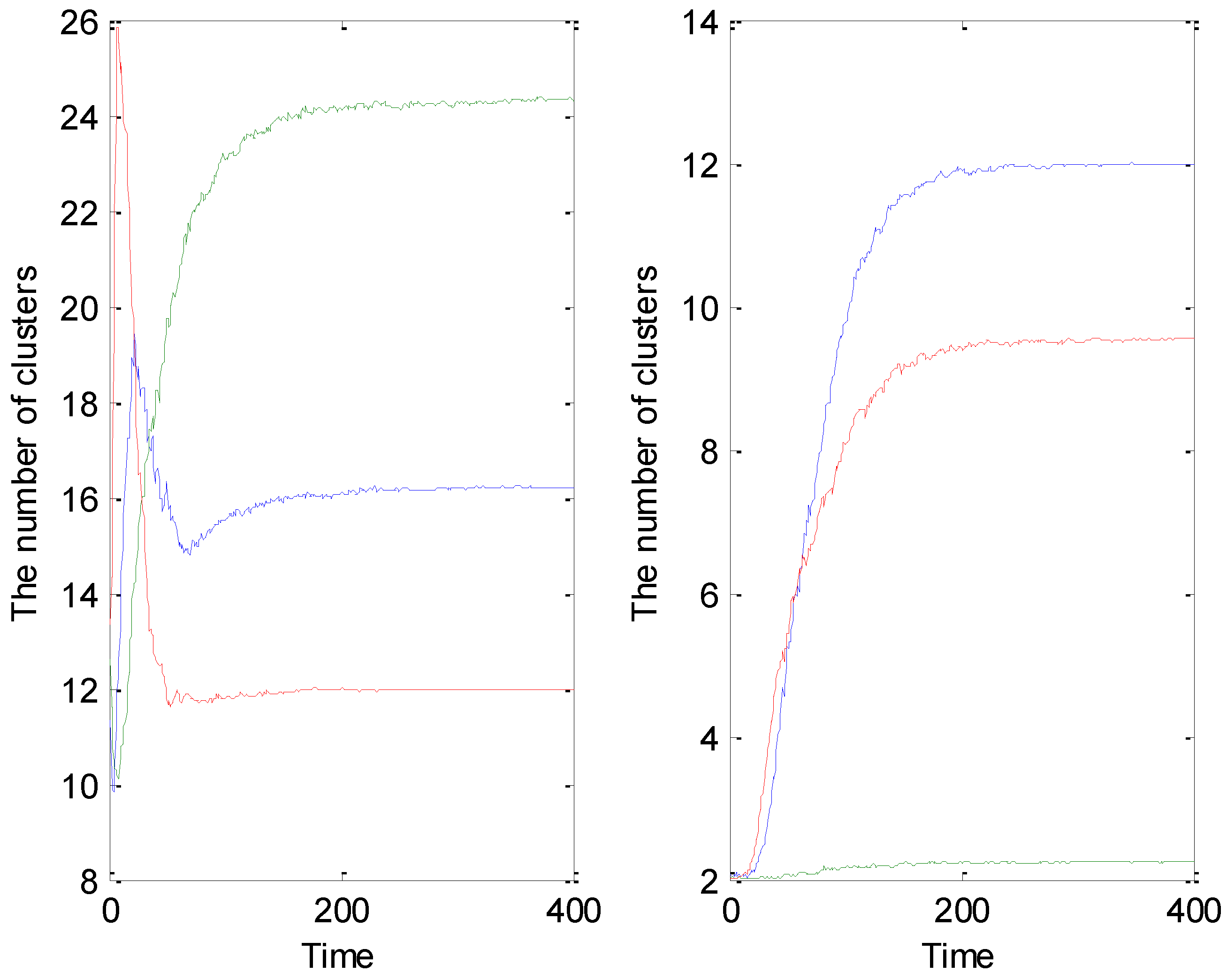
Figure 4 illustrates the time evolution of the number of opinion clusters. The variation ranges of final number of clusters for different realizations in the left plot of
Figure 4 (from top to bottom) are [10,61], [5,47] and [2,35] respectively, while those in the right plot are [2,24], [2,18] and [2,8] respectively. As in many opinion models, agents holding the same opinion gather together to form a cluster, and agents inside the cluster are not easy to persuade. As time passes, opinion clusters merge with each other, small clusters disappear, and macroscopic opinion clusters occur. Therefore, the number of clusters decreases with time. However, in our model, as shown in
Figure 4, the number of opinion clusters may increase with time during the dynamics. Agents’ rising conviction makes them reluctant to adopt others’ opinions, and more and more isolated agents with a minority opinion emerge. These agents have strong personal confidence and become extremists. Generally, the average number of clusters in random networks is smaller than that in scale-free networks, for shortcuts in random networks reduce the mean shortest distance so that agents can find their supporters more easily. Opinion clusters are fewer on average in the system with betweenness-based individual influence and the sizes of several macroscopic clusters are larger. We also find the evolution of opinion clusters has great fluctuations in scale-free networks. The number of clusters rises to a peak quickly and then declines to a stable value. With betweenness-based influence in scale-free networks, opinion clusters have the greatest fluctuation, but the number will gradually stabilize at a low level. Moreover, large initial conviction
C0 almost eliminates the fluctuation of clusters due to the instant occurrence of some extremists. Although the initial individual conviction does not affect the final average opinion, it changes the formation of opinion clusters greatly. Nontrivially, the system with large initial conviction in scale-free networks has the most clusters finally, but the number of clusters with the same condition in random networks is the smallest. The reason is that, even if agents’ conviction can become so strong within a quite short time, these agents in random networks still have some neighbors with the same opinion as a result of shortcuts of topology, and therefore, large-scale clusters are not split into fragments.
Figure 4.
The number of opinion clusters as a function of time. In the beginning opinions are assigned uniformly at random, h = 0.1 and N = 1,000. The blue solid curve indicates that the degree-based individual influence is used and C0 = 0.5. The green dotted curve describes the situation that agents have degree-based influence and C0 = 0.8. The red dash-dotted curve refers to the system with betweenness-based individual influence and C0 = 0.5 for both plots. The left plot uses a scale-free network as interacting topology, while the right plot is obtained from a random network. Every plot is an average of 100 different simulations.
Figure 4.
The number of opinion clusters as a function of time. In the beginning opinions are assigned uniformly at random, h = 0.1 and N = 1,000. The blue solid curve indicates that the degree-based individual influence is used and C0 = 0.5. The green dotted curve describes the situation that agents have degree-based influence and C0 = 0.8. The red dash-dotted curve refers to the system with betweenness-based individual influence and C0 = 0.5 for both plots. The left plot uses a scale-free network as interacting topology, while the right plot is obtained from a random network. Every plot is an average of 100 different simulations.
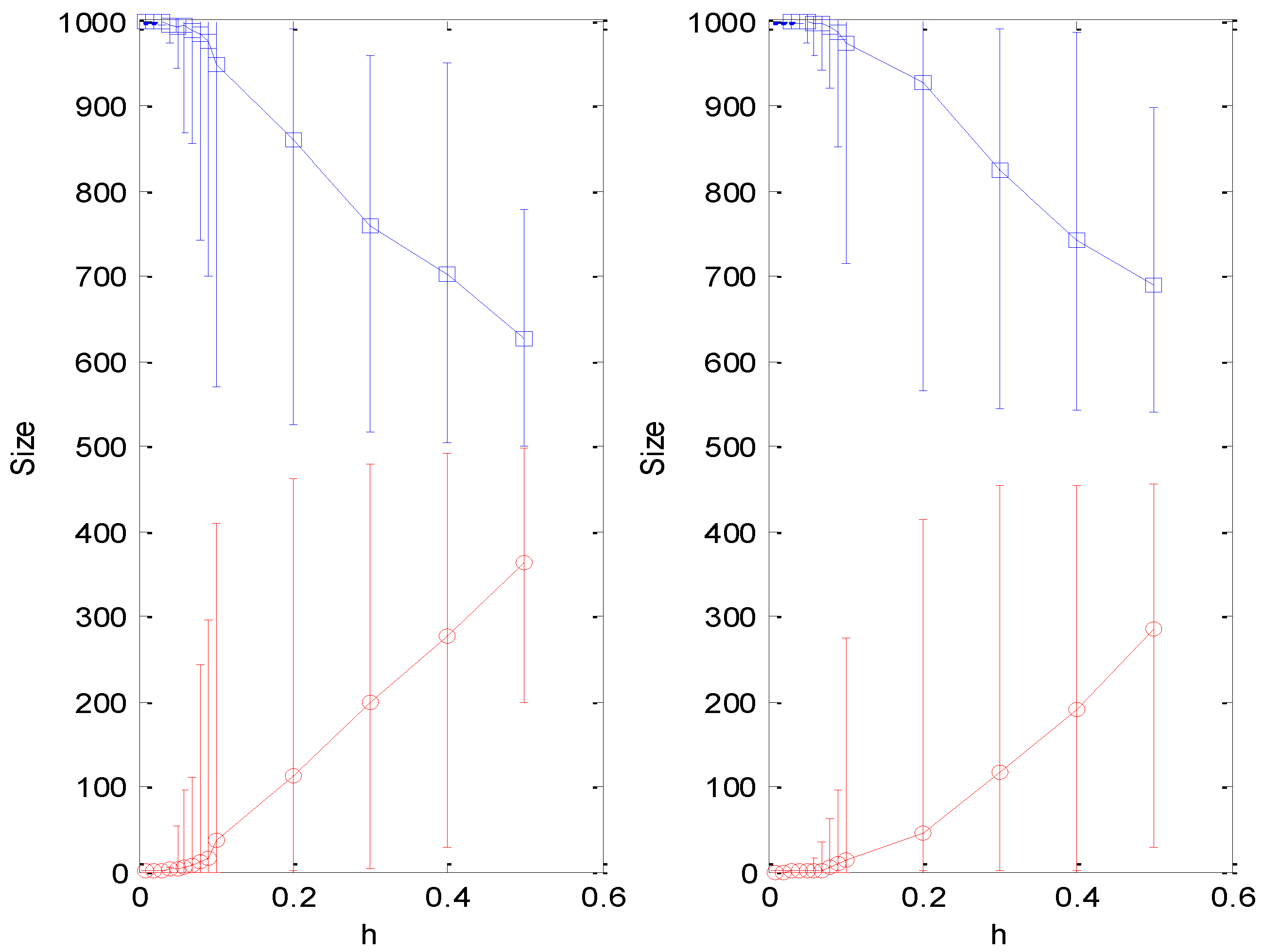
Figure 5 shows the final sizes of the largest and second largest opinion clusters with different individual conviction variation
h. From about
h = 0.1, the average change of the largest and second largest cluster’s size appears to be roughly linear in
h both for degree-based and betweenness-based influence. With a rapid increase in individual conviction, the largest cluster breaks up into some parts, and the system witnesses the appearance of several new macroscopic-size clusters. Clearly, the conviction variation
h has a threshold below which the largest cluster dominates the population absolutely and the formation of other large clusters is prohibited. The threshold is smaller for the system with degree-based individual influence. Meanwhile, the second largest cluster with degree-based influence is larger than that with betweenness-based influence on average, demonstrating that more heterogeneous individual influence makes a greater impression on cluster mergence when competing with self-confidence. In order to distinctly observe the different advantages of individual confidence and influence, we calculate the number of events when agents update their opinions following neighbors during the evolutionary process, compared with the total number of update events.
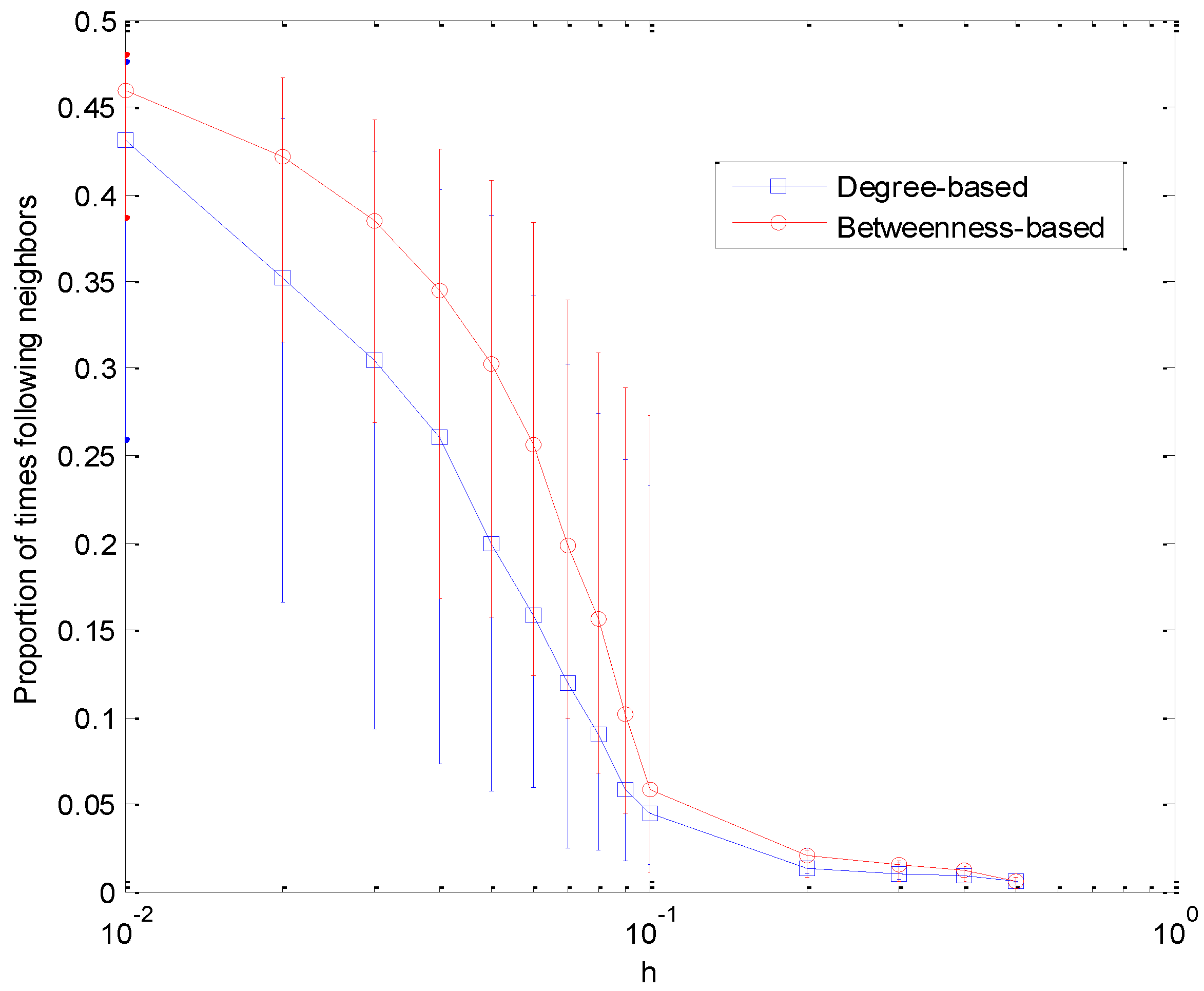
Figure 6 shows the proportion of adopting neighbor’s opinion with different
h. Obviously, betweenness-based influence plays a more important role in individual decisions, and when
h < 0.2, the effect of individual influence cannot be neglected.
Figure 5.
The size of largest (square line) and second largest (circle line) opinion clusters as a function of h. In the beginning opinions are assigned uniformly at random, C0 = 0.5 and N = 1,000. A scale-free network is used for both plots. In the left plot, the degree-based influence is used, while agents have betweenness-based influence in the right plot. Every plot is an average of 100 different simulations.
Figure 5.
The size of largest (square line) and second largest (circle line) opinion clusters as a function of h. In the beginning opinions are assigned uniformly at random, C0 = 0.5 and N = 1,000. A scale-free network is used for both plots. In the left plot, the degree-based influence is used, while agents have betweenness-based influence in the right plot. Every plot is an average of 100 different simulations.
Although individual influence means agents are able to affect local opinion interaction, they cannot exert a full action to persuade neighbors to change opinions, as shown in
Figure 6. Agents’ opinion distribution depends on their conviction and neighbors’ influence, as well as their network structure.
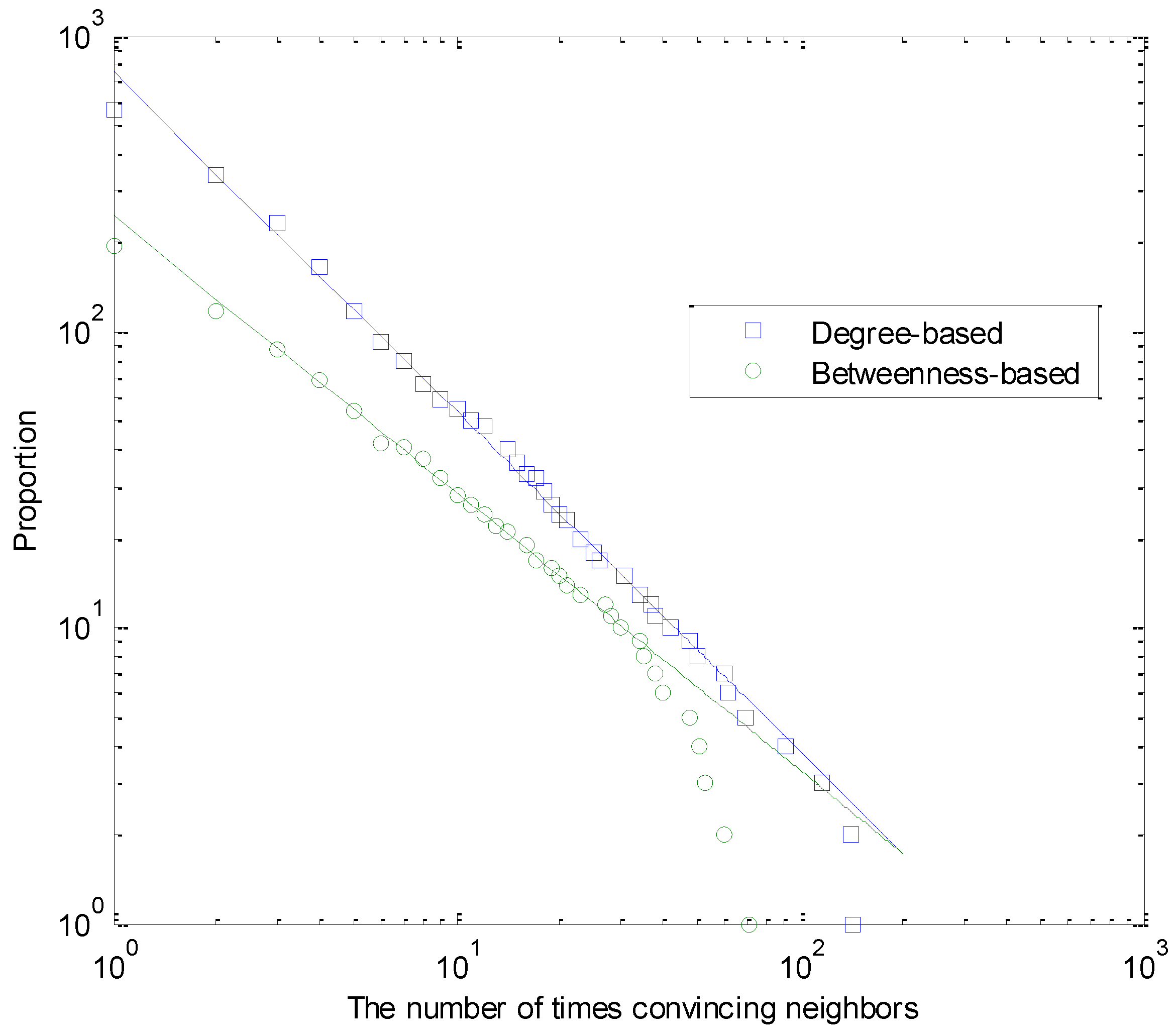
Figure 7 indicates the distribution of the number of times that each agent convinces neighbors to change opinions. A power-law form gives a good description for much of the data in
Figure 7 with the power exponent
for degree-based influence, and
for betweenness-based influence. The heterogeneity of individual influence changes the power exponent of the distribution, but the distribution for the effect of neighboring persuasiveness mainly relies on the network topology.
Figure 6.
The proportion of update events adopting neighbor’s opinion versus h in a scale-free network, and initial opinions are assigned uniformly at random. C0 = 0.5 and N = 1,000. Every plot is an average of 100 different simulations.
Figure 6.
The proportion of update events adopting neighbor’s opinion versus h in a scale-free network, and initial opinions are assigned uniformly at random. C0 = 0.5 and N = 1,000. Every plot is an average of 100 different simulations.
Figure 7.
The distribution of number of times persuading neighbors to change opinions for each agent in a scale-free network, C0 = 0.5 , h = 0.1 and N = 1,000. The exponents of power-law fitting for degree-based or betweenness-based influence are γ = −1.147, and γ = −0.937, respectively.
Figure 7.
The distribution of number of times persuading neighbors to change opinions for each agent in a scale-free network, C0 = 0.5 , h = 0.1 and N = 1,000. The exponents of power-law fitting for degree-based or betweenness-based influence are γ = −1.147, and γ = −0.937, respectively.
4. Conclusions
In online social networks, individual conviction and influence are quite heterogeneous. Previous empirical studies found individual influence on some social media often is related to the user network. In this paper, we explored the evolutionary agents’ self-confidence and inhomogeneous individual influence, and studied opinion interaction under these two factors. We presented a discrete opinion model with heterogeneous individual conviction and influence that depends on network structure. Agent’s confidence increases when neighbors hold the same opinion as the agent, but it decreases when the agent confronts opponents. We conducted numerical simulations of the average magnetization and opinion clusters, and analyzed the role of these two factors in opinion formation.
Simulation results show that, in both scale-free and random networks, the heterogeneity of individual influence speeds up the dynamics, but more heterogeneous influence doesn’t make the average magnetization more ordered when competing with personal conviction. The magnetization conservation is broken, and the system under the two factors is driven to a polarized state in which most of people hold the same opinion. However, the total convergence of the system is prevented by the appearance of extremists. In addition, more heterogeneous influence contributes more for individual opinion exchanges. The results of our study should be helpful in understanding some online social phenomena. For instance, consensus is almost never reached in an online environment, but instead, users that hold the majority or minority opinion confront each other; public opinion evolves rapidly in online social network; even if extremists are not specified in the beginning, they can occur spontaneously during the interaction.
Although we used node degree and betweenness as individual influence in the opinion model, the intrinsic evolutionary process does not depend on the concrete form of network-based influence, thereby maintaining the generality of the model. In addition, our model can be used in voter dynamics, as well as in the majority model and other opinion models.