Structural Patterns in Complex Systems Using Multidendrograms
Abstract
:1. Introduction
2. Multidendrograms Algorithm
- (1)
- Initialize n singleton clusters with one individual in each of them. Initialize also the distances between clusters with the values of the distances between individuals.
- (2)
- Find the minimum distance separating two different clusters.
- (3)
- Select two clusters separated by such minimum distance and merge them into a new supercluster.
- (4)
- Compute the distances (Depending on the criterion used to compute the distances, different agglomerative hierarchical clusterings are obtained: single linkage, complete linkage, unweighted average, weighted average, unweighted centroid, weighted centroid, and Ward’s method are the most commonly used.) between the new supercluster and each of the other clusters.
- (5)
- If all individuals are not yet in the same cluster, then go back to Step 2.
- When there are no ties, multidendrograms give the same result as the pair-group algorithm.
- It always gives a uniquely determined solution thanks to the implementation of the variable-group algorithm.
- In the multidendrogram representation of the results, the occurrence of ties during the agglomerative process can be explicitly observed, and a subsequent notion of the degree of heterogeneity inside the tied clusters is obtained.
3. Applications
3.1. Case Study: Vertex Similarity in Networks
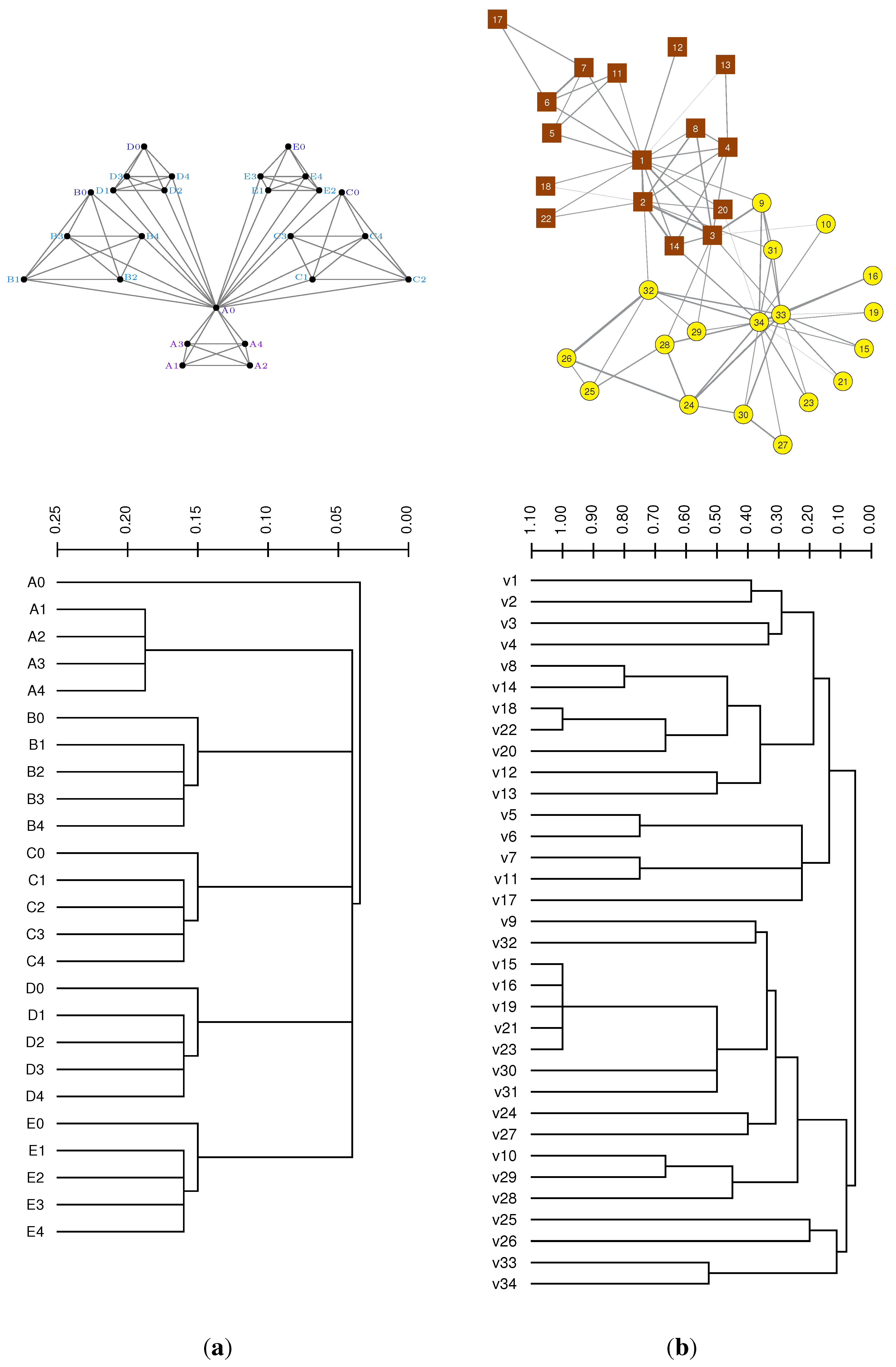
3.2. Case Study: Modular Node Similarity in Networks
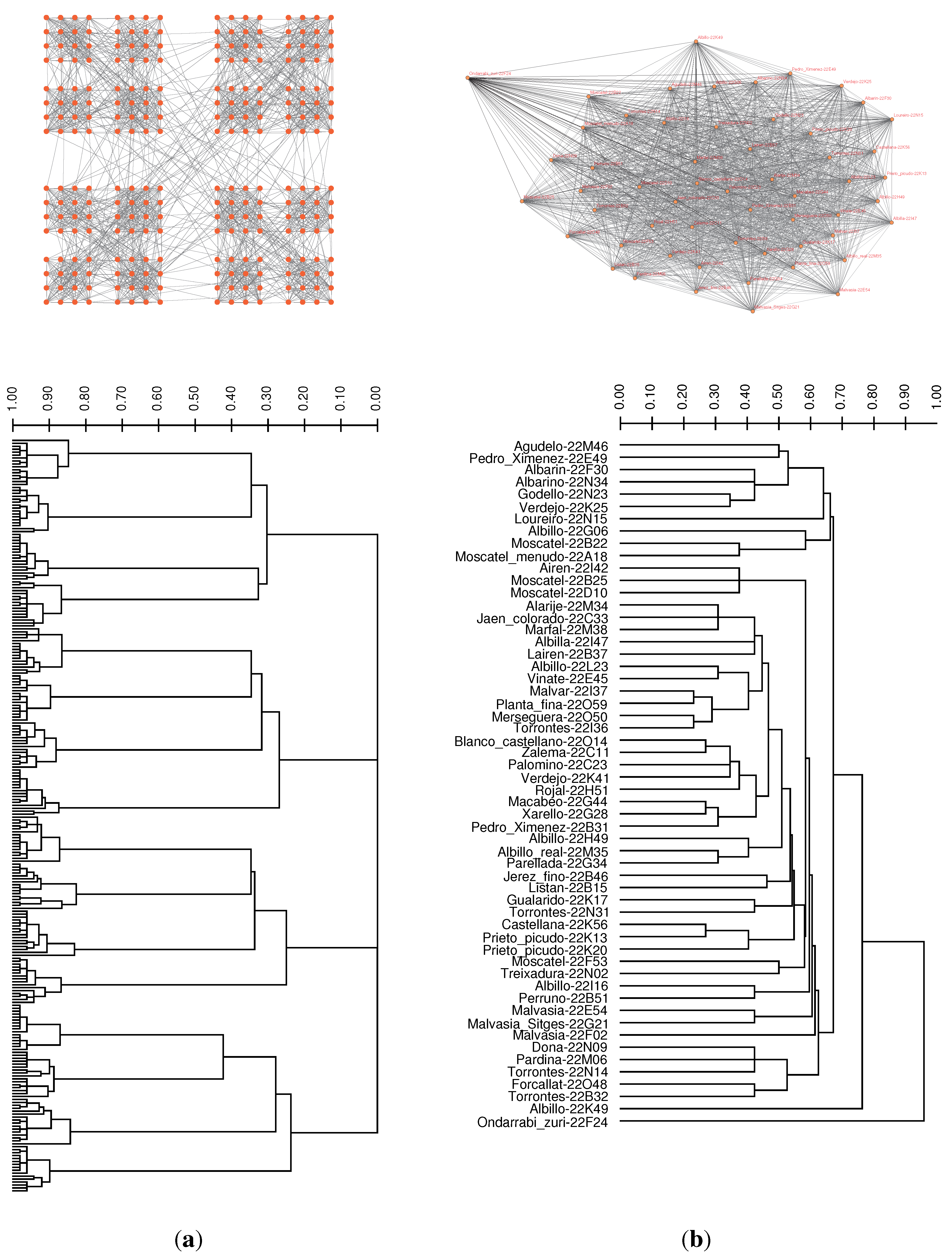
3.3. Case Study: Distance Similarities in Complete Weighted Networks
| Method | Precision = 3 | Precision = 4 | Precision = 5 |
|---|---|---|---|
| Unweighted Average | 17, 900 | 2, 208 | 2, 124 |
| Weighted Average | 9, 859 | 1, 709 | 1, 762 |
| Complete Linkage | >108 | >108 | >108 |
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Newman, M. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Arenas, A.; Fernández, A.; Gómez, S. Analysis of the structure of complex networks at different resolution levels. New J. Phys. 2008, 10, 053039. [Google Scholar] [CrossRef]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef]
- Leicht, E.; Holme, P.; Newman, M. Vertex similarity in networks. Phys. Rev. E 2006, 73, 026120. [Google Scholar] [CrossRef] [PubMed]
- Gordon, A. Classification, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 1999. [Google Scholar]
- Sneath, P.; Sokal, R. Numerical Taxonomy: The Principles and Practice of Numerical Classification; W.H. Freeman and Company: San Francisco, CA, USA, 1973. [Google Scholar]
- Eisen, M.; Spellman, P.; Brown, P.; Botstein, D. Cluster analysis and display of genome-wide expression patterns. Proc. Natl. Acad. Sci. USA 1998, 95, 14863–14868. [Google Scholar] [CrossRef] [PubMed]
- D’haeseleer, P. How does gene expression clustering work? Nat. Biotechnol. 2005, 23, 1499–1501. [Google Scholar] [CrossRef] [PubMed]
- Lazareva-Ulitsky, B.; Diemer, K.; Thomas, P. On the quality of tree-based protein classification. Bioinformatics 2005, 21, 1876–1890. [Google Scholar] [CrossRef] [PubMed]
- Loewenstein, Y.; Portugaly, E.; Fromer, M.; Linial, M. Efficient algorithms for accurate hierarchical clustering of huge datasets: Tackling the entire protein space. Bioinformatics 2008, 24, i41–i49. [Google Scholar] [CrossRef] [PubMed]
- Hart, G. The Occurrence of Multiple UPGMA Phenograms. In Numerical Taxonomy; Felsenstein, J., Ed.; Springer-Verlag: Berlin Heidelberg, Germany, 1983; pp. 254–258. [Google Scholar]
- Arnau, V.; Mars, S.; Marín, I. Iterative cluster analysis of protein interaction data. Bioinformatics 2005, 21, 364–378. [Google Scholar] [CrossRef] [PubMed]
- Van der Kloot, W.; Spaans, A.; Heiser, W. Instability of hierarchical cluster analysis due to input order of the data: The PermuCLUSTER solution. Psychol. Methods 2005, 10, 468–476. [Google Scholar] [CrossRef] [PubMed]
- MacCuish, J.; Nicolaou, C.; MacCuish, N. Ties in proximity and clustering compounds. J. Chem. Inf. Comput. Sci. 2001, 41, 134–146. [Google Scholar] [CrossRef] [PubMed]
- Morgan, B.; Ray, A. Non-uniqueness and inversions in cluster analysis. Appl. Statist. 1995, 44, 117–134. [Google Scholar] [CrossRef]
- Backeljau, T.; de Bruyn, L.; de Wolf, H.; Jordaens, K.; van Dongen, S.; Winnepennincks, B. Multiple UPGMA and neighbor-joining trees and the performance of some computer packages. Mol. Biol. Evol. 1996, 13, 309–313. [Google Scholar] [CrossRef]
- Fernández, A.; Gómez, S. Solving non-uniqueness in agglomerative hierarchical clustering using multidendrograms. J. Classif. 2008, 25, 43–65. [Google Scholar] [CrossRef]
- Gómez, S.; Fernández, A. MultiDendrograms: Software Application. Available online: http://deim.urv.cat/sgomez/multidendrograms.php (accessed on 9 October 2013).
- Holme, P.; Huss, M. Role-similarity based functional prediction in networked systems: Application to the yeast proteome. J. R. Soc. Interface 2005, 2, 327–333. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.H.; Gou, L.; Zhang, X.; Giles, C.L. Capturing Missing Edges in Social Networks Using Vertex Similarity. In K-CAP; Musen, M.A., Corcho, O., Eds.; ACM: New York, NY, USA, 2011; pp. 195–196. [Google Scholar]
- Jaccard, P. Distribution de la flore alpine dans le bassin des Dranses et dans quelques régions voisines. Bull. Soc. Vaudoise Sci. Nat. 1901, 37, 241–272. (in French). [Google Scholar]
- Ravasz, E.; Barabási, A.L. Hierarchical organization in complex networks. Phys. Rev. E 2003, 67, 026112. [Google Scholar] [CrossRef] [PubMed]
- Zachary, W. An information flow model for conflict and fission in small groups. J. Anthropol. Res. 1977, 33, 452–473. [Google Scholar]
- Granell, C.; Gómez, S.; Arenas, A. Mesoscopic analysis of networks: Applications to exploratory analysis and data clustering. Chaos 2011, 21, 016102. [Google Scholar] [CrossRef] [PubMed]
- Granell, C.; Gómez, S.; Arenas, A. Hierarchical multiresolution method to overcome the resolution limit in complex networks. Int. J. Bifurc. Chaos 2012, 22, 1250171. [Google Scholar] [CrossRef]
- Arenas, A.; Díaz-Guilera, A.; Pérez-Vicente, C.J. Synchronization reveals topological scales in complex networks. Phys. Rev. Lett. 2006, 96, 114102. [Google Scholar] [CrossRef] [PubMed]
- Ibáñez, J.; de Andrés, M.; Molino, A.; Borrego, J. Genetic study of key spanish grapevine varieties using microsatellite analysis. Am. J. Enol. Vitic. 2003, 54, 22–30. [Google Scholar]
- Gómez, S.; Jensen, P.; Arenas, A. Analysis of community structure in networks of correlated data. Phys. Rev. E 2009, 80, 016114. [Google Scholar] [CrossRef] [PubMed]
- Takezaki, N. Tie trees generated by distance methods of phylogenetic reconstruction. Mol. Biol. Evol. 1998, 15, 727–737. [Google Scholar] [CrossRef] [PubMed]
- Fatahi, R.; Ebadi, A.; Bassil, N.; Mehlenbacher, S.; Zamani, Z. Characterization of Iranian grapevine cultivars using microsatellite markers. Vitis 2003, 42, 185–192. [Google Scholar]
- Zdunić, G.; Preece, J.; Dangl, G.; Koehmstedt, A.; Mucalo, A.; Maletić, E.; Pejić, I. Genetic characterization of grapevine cultivars collected throughout the dalmatian region. Am. J. Enol. Vitic. 2013, 64, 285–290. [Google Scholar] [CrossRef]
- Almadanim, M.; Baleiras-Couto, M.; Pereira, H.; Carneiro, L.; Fevereiro, P.; Eiras-Dias, J.; Morais-Cecilio, L.; Viegas, W.; Veloso, M. Genetic diversity of the grapevine (Vitis vinifera L.) cultivars most utilized for wine production in Portugal. Vitis 2007, 46, 116–119. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gómez, S.; Fernández, A.; Granell, C.; Arenas, A. Structural Patterns in Complex Systems Using Multidendrograms. Entropy 2013, 15, 5464-5474. https://doi.org/10.3390/e15125464
Gómez S, Fernández A, Granell C, Arenas A. Structural Patterns in Complex Systems Using Multidendrograms. Entropy. 2013; 15(12):5464-5474. https://doi.org/10.3390/e15125464
Chicago/Turabian StyleGómez, Sergio, Alberto Fernández, Clara Granell, and Alex Arenas. 2013. "Structural Patterns in Complex Systems Using Multidendrograms" Entropy 15, no. 12: 5464-5474. https://doi.org/10.3390/e15125464
APA StyleGómez, S., Fernández, A., Granell, C., & Arenas, A. (2013). Structural Patterns in Complex Systems Using Multidendrograms. Entropy, 15(12), 5464-5474. https://doi.org/10.3390/e15125464





