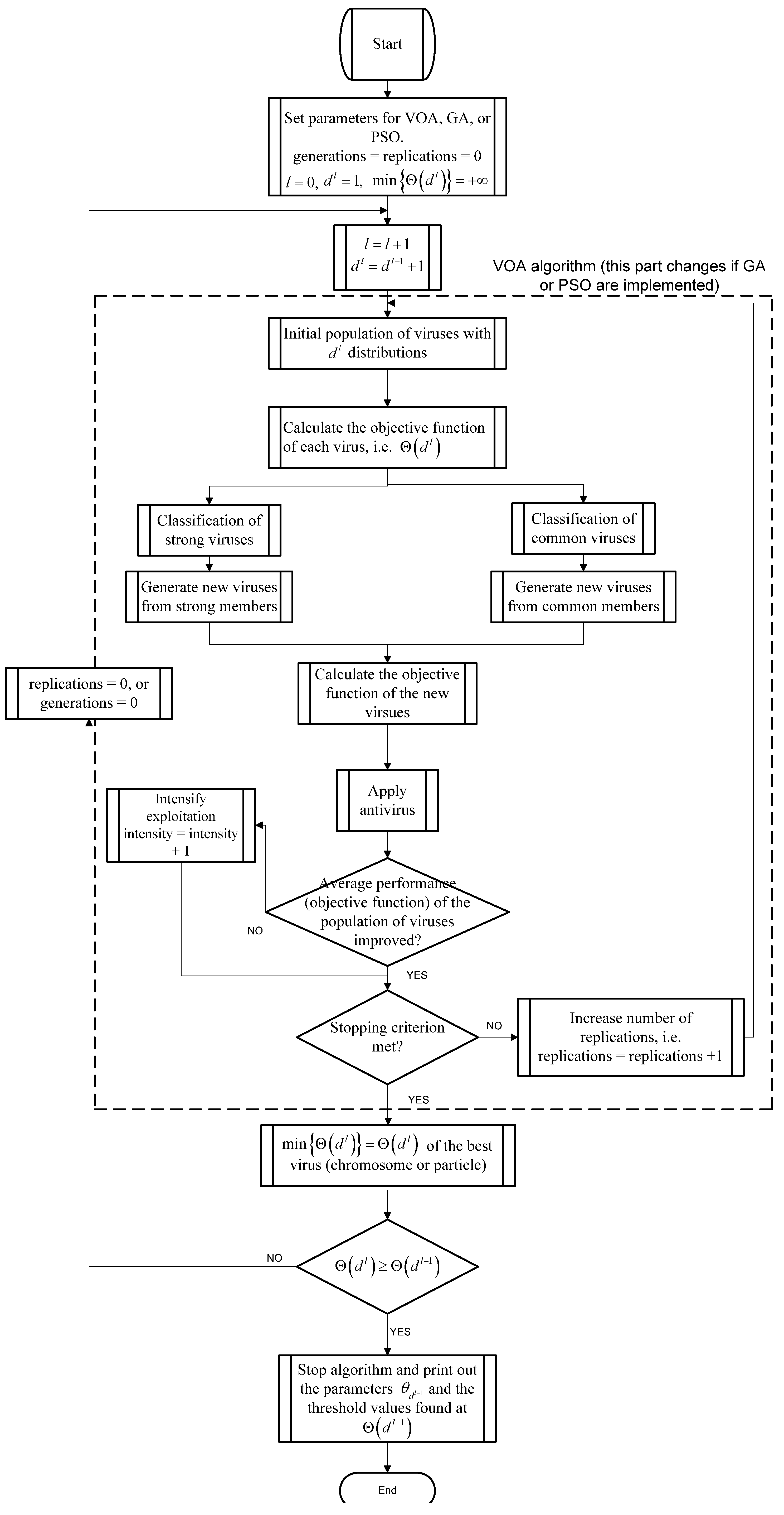
Figure 4.
Test image 1: (a) Original image; Thresholded image implementing (b) VOA, (c) GA, (d) PSO, and (e) Otsu’s method using three thresholds.
Figure 5.
Test image 2: (a) Original image; Thresholded image implementing (b) VOA, (c) GA, (d) PSO, and (e) Otsu’s method with two thresholds.
3.1. Algorithmic Setting (VOA, GA, and PSO)
The setting of VOA, GA, and PSO was determined by using Design of Experiments (DoE) [
19,
20] to know which values for the parameters are suitable when optimizing Equation (10). The full factorial design,
i.e., 3-levels factorial design was performed for the four parameters of the VOA; in other words, 3
4 combinations of the four parameters were tested.
Table 1 shows the results after performing DoE, where the final setting of the VOA is presented in bold.
Table 1.
Parameter values (factor levels) used during the for the VOA.
Table 1.
Parameter values (factor levels) used during the for the VOA.
| Parameter | Low Level | Medium Level | High Level |
|---|
| Initial population of viruses | 5 | 10 | 30 |
| Viruses considered as strong | 1 | 3 | 10 |
| Growing rate of strong viruses | 2 | 5 | 10 |
| Growing rate of common viruses | 1 | 3 | 6 |
Similarly, a 3
3 full factorial design was implemented in order to set the population size (
ps), crossover and mutation probabilities (
pc and
pm) respectively for GA.
Table 2 summarizes the experimental settings and the final setting (in bold) of the GA. As for PSO a 3
4 full factorial design determined the values for the swarm size, inertia weight (
w), cognitive and social parameters (
c1 and
c2) respectively.
Table 3 summarizes the experimental settings of the PSO algorithm and the final setting is also highlighted in bold.
Table 2.
Parameter values (factor levels) used during the DoE for the GA.
Table 2.
Parameter values (factor levels) used during the DoE for the GA.
| Parameter | Low Level | Medium Level | High Level |
|---|
| Population size (ps) | 5 | 10 | 30 |
| Probability of crossover (pc) | 0.8 | 0.9 | 0.99 |
| Probability of mutation (pm) | 0.05 | 0.1 | 0.15 |
Table 3.
Parameter values (factor levels) used during the DoE for the PSO.
Table 3.
Parameter values (factor levels) used during the DoE for the PSO.
| Parameter | Low Level | Medium Level | High Level |
|---|
| Swarm size | 5 | 10 | 30 |
| Inertia weight (w) | 0.5 | 0.8 | 0.99 |
| Cognitive parameter (c1) | 2 | 2.1 | 2.2 |
| Social parameter (c2) | 2 | 2.1 | 2.2 |
The basic idea of the DoE is to run the 34, 33, and 34, parameters combinations for VOA, GA, and PSO respectively, to later select which level (value) yielded the best performance (lower objective function value). Once the values for each parameter which delivered the best objective function value are identified, each test image is segmented by optimizing Equation (10) with each of the algorithmic tools used in this study.
The advantage of using DoE is that it is a systematic as well as well-known approach when deciding the setting yielding the best possible performance among all the combinations used during the full factorial design. In addition to the aforementioned, it is also a testing method that has been proven to be quite useful in many different areas such as tuning algorithm parameters [
20].
3.2. Segmentation Results for the Proposed Model Using Meta-Heuristics as Optimization Tools
A comprehensive study of the proposed model implementing the three meta-heuristics introduced above is detailed in this part of
Section 3. Additionally, a well-known segmentation method (Otsu’s) is implemented, where only the output image is observed in order to verify if the segmentation result given by the optimization algorithms used to minimize Equation (10) is as good as the one provided by Otsu’s method. The reason of the above mentioned, is because in terms of CPU time Otsu’s is a kind of exhaustive search approach; therefore, it is unfair to compare both ideas (the proposed approach and the Otsu’s method) in terms of computational effort.
Table 4,
Table 5,
Table 6,
Table 7 and
Table 8 detail the performance of the methods used for optimizing Equation (10) over different images. The results (objective function, threshold values, means, variances, and weights) are averaged over 50 independent runs, where the standard deviations of those 50 runs are not shown because they are in the order of 10
−17.
By testing the image in
Figure 4a it is observed that implementing the three meta-heuristics previously introduced for the optimization of Equation (10), the correct number of thresholds needed for segmenting the image is achieved (which is three). The computational effort and parameters of each Gaussian distribution (
) are summarized in
Table 4. Here, the number of iterations for the algorithms were four,
i.e., the proposed method optimized By testing the image in
Figure 4a it is observed that implementing the three meta-heuristics previously introduced for the optimization of Equation (10), the correct number of thresholds needed for segmenting the image is achieved (which is 3).
Table 4.
Thresholding results over 50 runs for the test image 1.
Table 4.
Thresholding results over 50 runs for the test image 1.
| Algorithm | Number of Thresholds | Objective Function | Threshold Values | Means | Variances | Weights | CPU Time per Iteration (s) | Total CPU Time for the Proposed Approach (s) |
|---|
| VOA | 1 | 2.410 | 244 | 66.808 | 3836.212 | 0.637 | 0.026 | 0.507 |
| 251.391 | 37.709 | 0.363 |
| 2 | 0.976 | 62, 244 | 33.209 | 12.892 | 0.483 | 0.071 |
| 175.849 | 1298.019 | 0.167 |
| 252.452 | 0.616 | 0.350 |
| 3 | 0.826 | 44, 145, 246 | 33.123 | 11.272 | 0.480 | 0.117 |
| 78.128 | 390.079 | 0.021 |
| 187.900 | 186.987 | 0.149 |
| 252.469 | 0.482 | 0.350 |
| 4 | 0.896 | 55, 97, 163, 246 | 33.178 | 12.123 | 0.482 | 0.294 |
| 75.522 | 119.910 | 0.017 |
| 128.441 | 258.119 | 0.003 |
| 185.922 | 82.920 | 0.142 |
| 252.158 | 6.177 | 0.356 |
| GA | 1 | 2.410 | 244 | 69.838 | 4226.048 | 0.650 | 0.106 | 0.658 |
| 252.452 | 0.616 | 0.350 |
| 2 | 0.994 | 65, 242 | 33.239 | 13.806 | 0.483 | 0.147 |
| 176.018 | 1256.142 | 0.166 |
| 252.440 | 0.736 | 0.351 |
| 3 | 0.857 | 45, 111, 242 | 33.131 | 11.350 | 0.481 | 0.195 |
| 74.412 | 187.027 | 0.019 |
| 186.725 | 207.543 | 0.150 |
| 252.440 | 0.736 | 0.351 |
| 4 | 0.882 | 44, 143, 155, 247 | 33.123 | 11.272 | 0.480 | 0.211 |
| 77.924 | 377.966 | 0.021 |
| 150.013 | 12.387 | 0.001 |
| 188.193 | 191.885 | 0.149 |
| 252.477 | 0.431 | 0.349 |
| PSO | 1 | 2.384 | 247 | 70.158 | 4274.185 | 0.651 | 0.083 | 0.584 |
| 252.477 | 0.431 | 0.349 |
| 2 | 0.955 | 65, 247 | 33.239 | 13.806 | 0.483 | 0.118 |
| 176.672 | 1288.421 | 0.167 |
| 252.477 | 0.431 | 0.349 |
| 3 | 0.857 | 45, 111, 242 | 33.131 | 11.350 | 0.481 | 0.172 |
| 74.412 | 187.027 | 0.019 |
| 186.725 | 207.543 | 0.150 |
| 252.440 | 0.736 | 0.351 |
| 4 | 0.880 | 42, 135, 154, 247 | 33.097 | 11.070 | 0.479 | 0.211 |
| 74.922 | 381.817 | 0.022 |
| 144.535 | 35.001 | 0.001 |
| 188.161 | 192.778 | 0.149 |
| 252.477 | 0.431 | 0.349 |
The computational effort and parameters of each Gaussian distribution (
) are summarized in
Table 4. Here, the number of iterations for the algorithms were 4,
i.e., the proposed method optimized Equation (10) for
d = [1, 2, 3, 4] before reaching the stopping criterion.
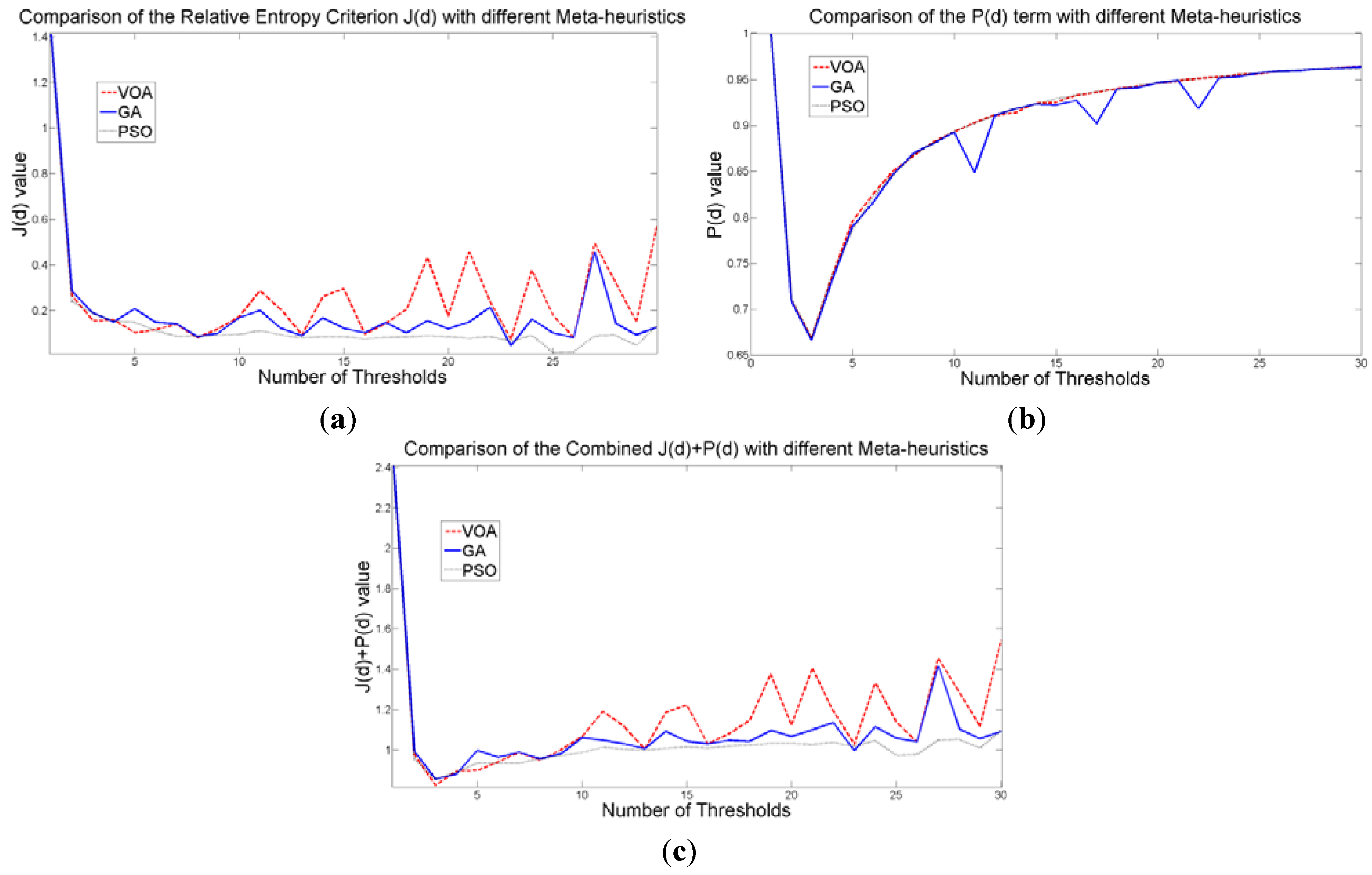
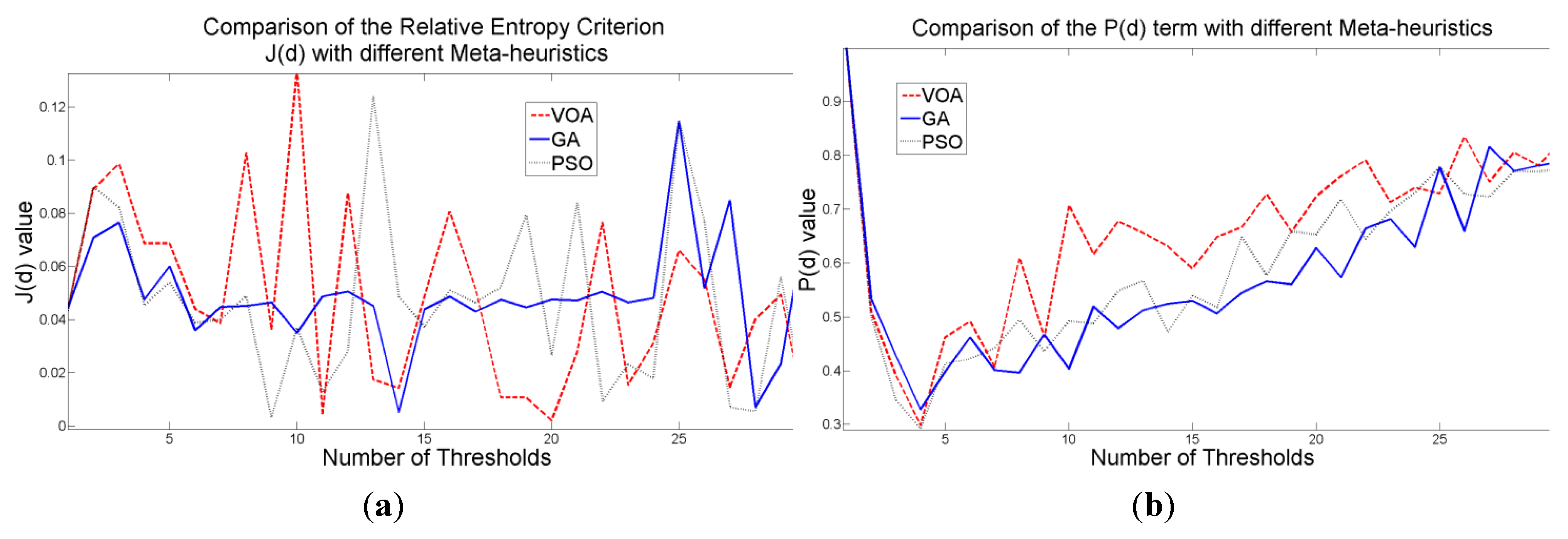
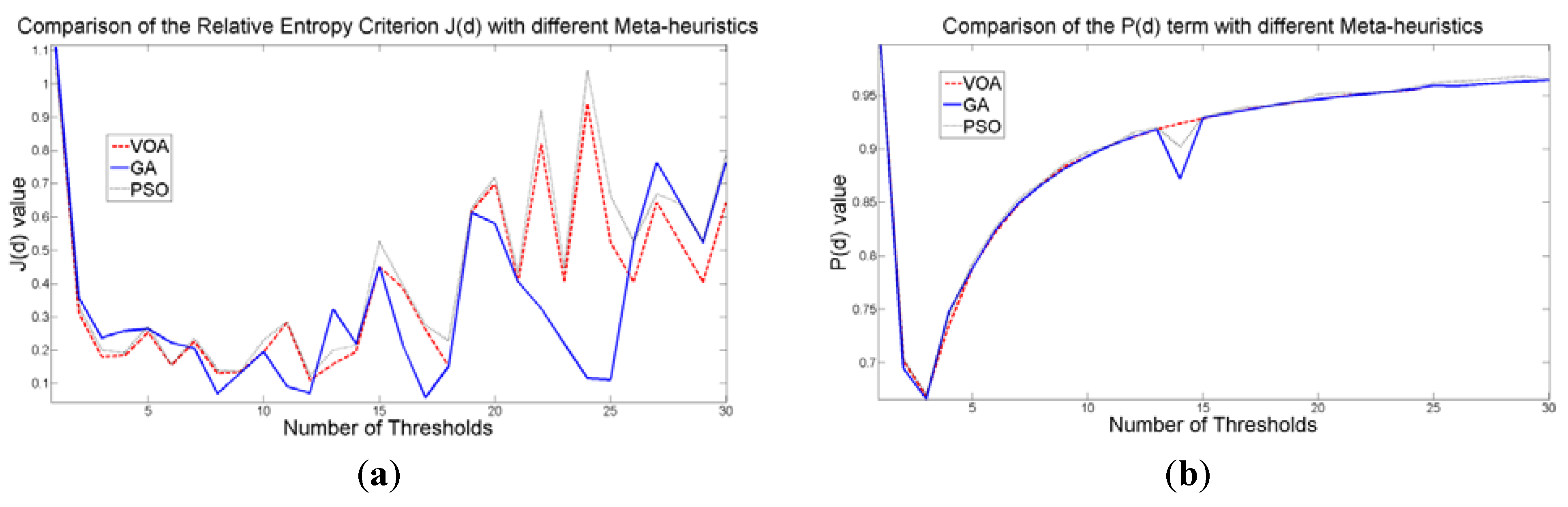
The behavior of the Relative Entropy function (
Figure 7a) reveals its deficiency in detecting an appropriate number of distributions that will have a good description of the image histogram (
Figure 8). The aforementioned is because as more distributions or thresholds are added into the mixture, it is impossible to identify a true minimum for the value of
J(
d) when implementing the three different meta-heuristic tools.
The additional function
P(
d) on the other hand shows a minimum value when a suitable number of distributions (which is the same as finding the number of thresholds) is found (
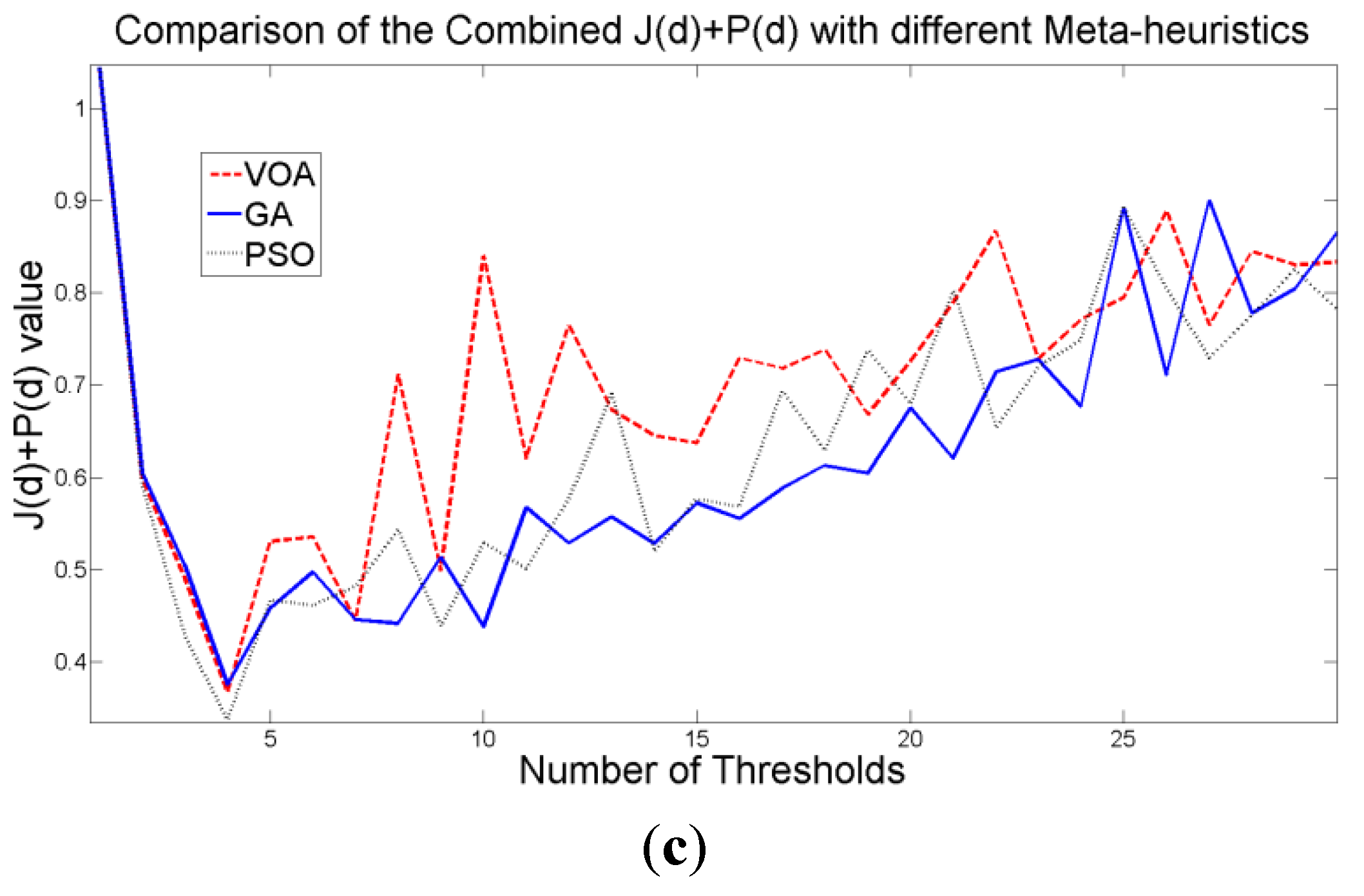
Figure 7b), since its value shows an increasing pattern when more distributions are added to the mixture model. The combination of these two functions
J(
d) and
P(
d) shows that the optimal value for Θ(
d) (
Figure 7c) will be when the number of thresholds is three as
P(
d) suggested. Note that the purpose of
J(
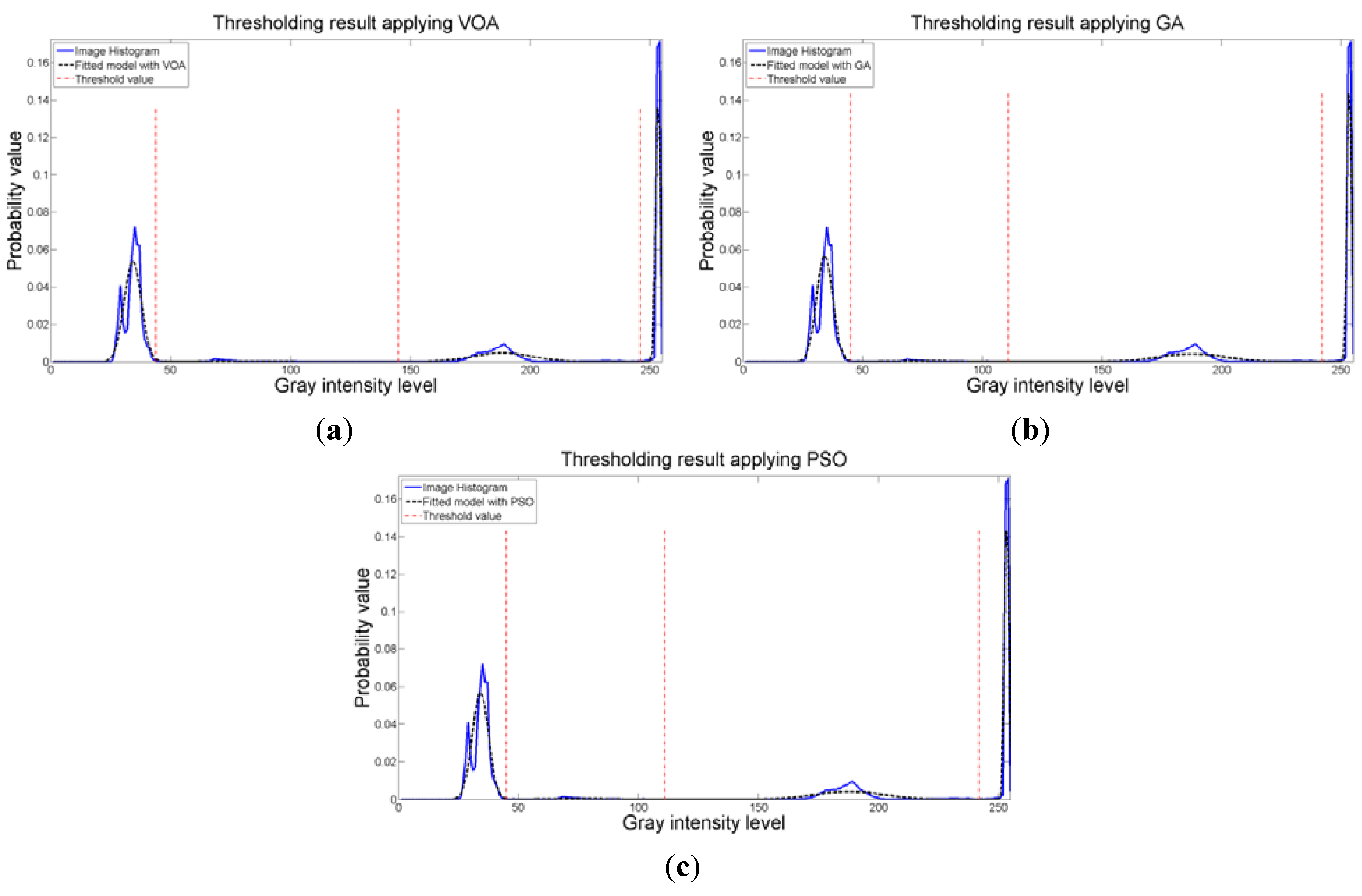
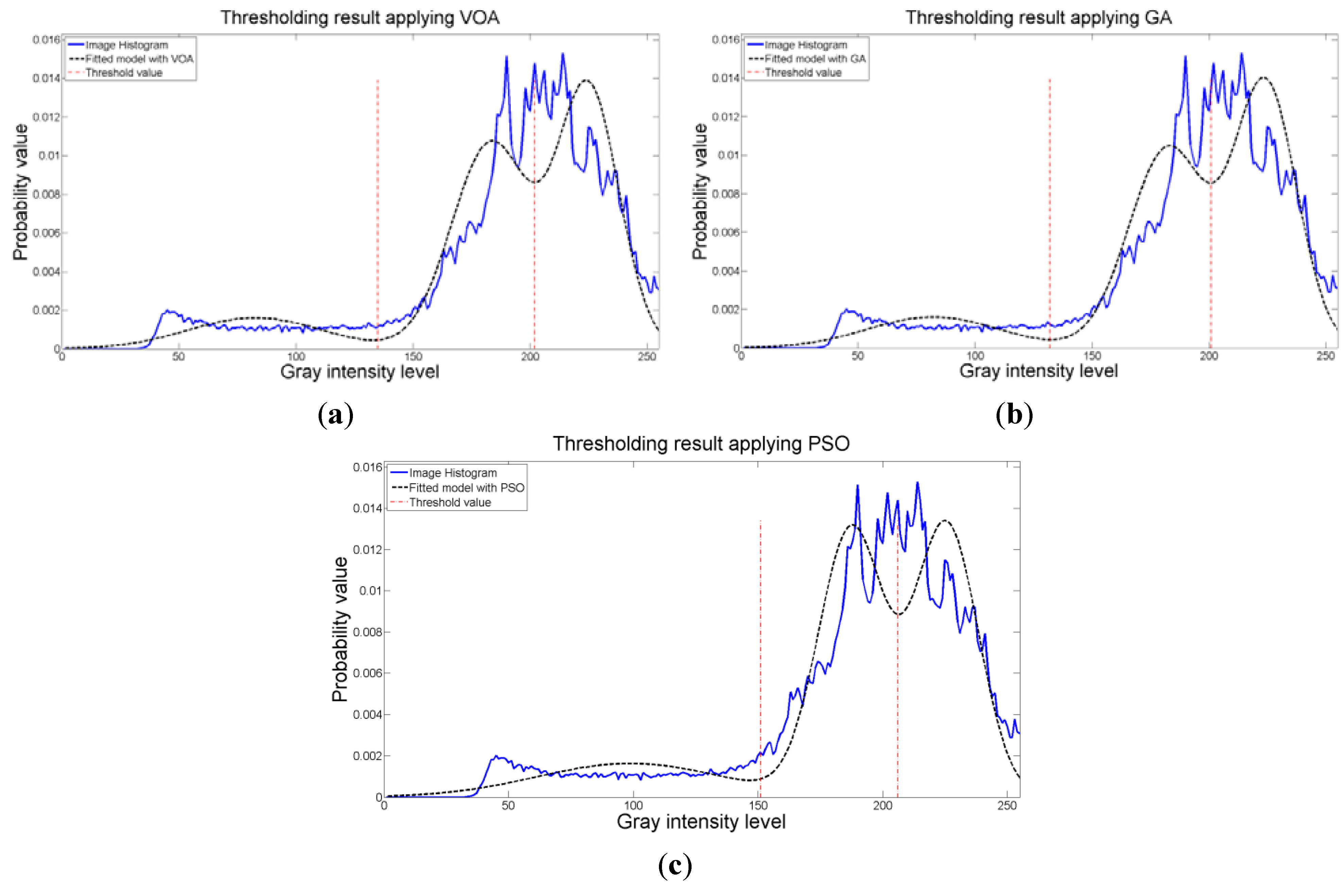
d) is to find the best possible fitting with the suitable number of distributions (thresholds), and this is observed at
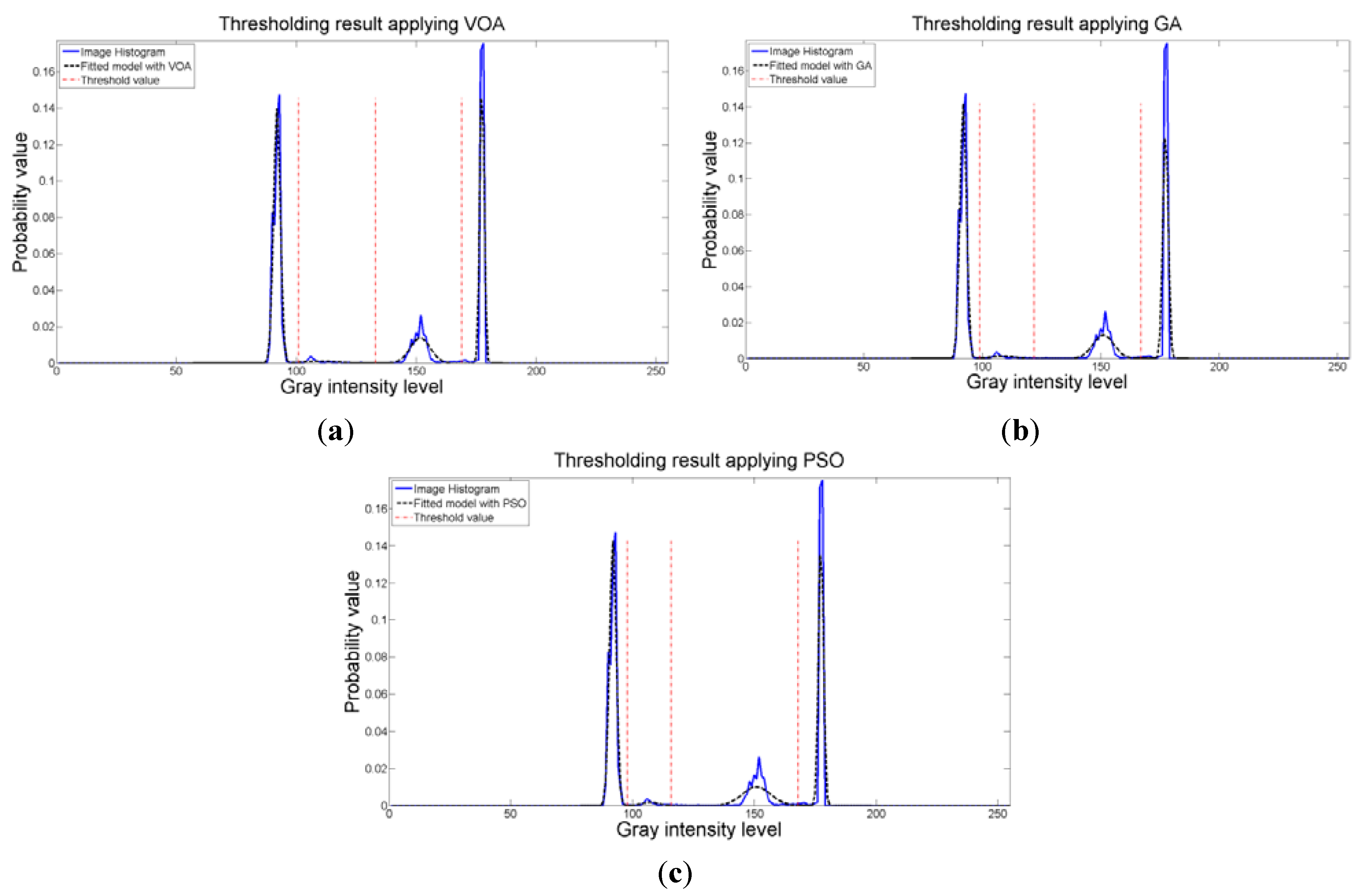
Figure 8 where the fitted model (dotted line) provides a very good description of the original histogram (solid line) given by the image. The vertical dashed lines in
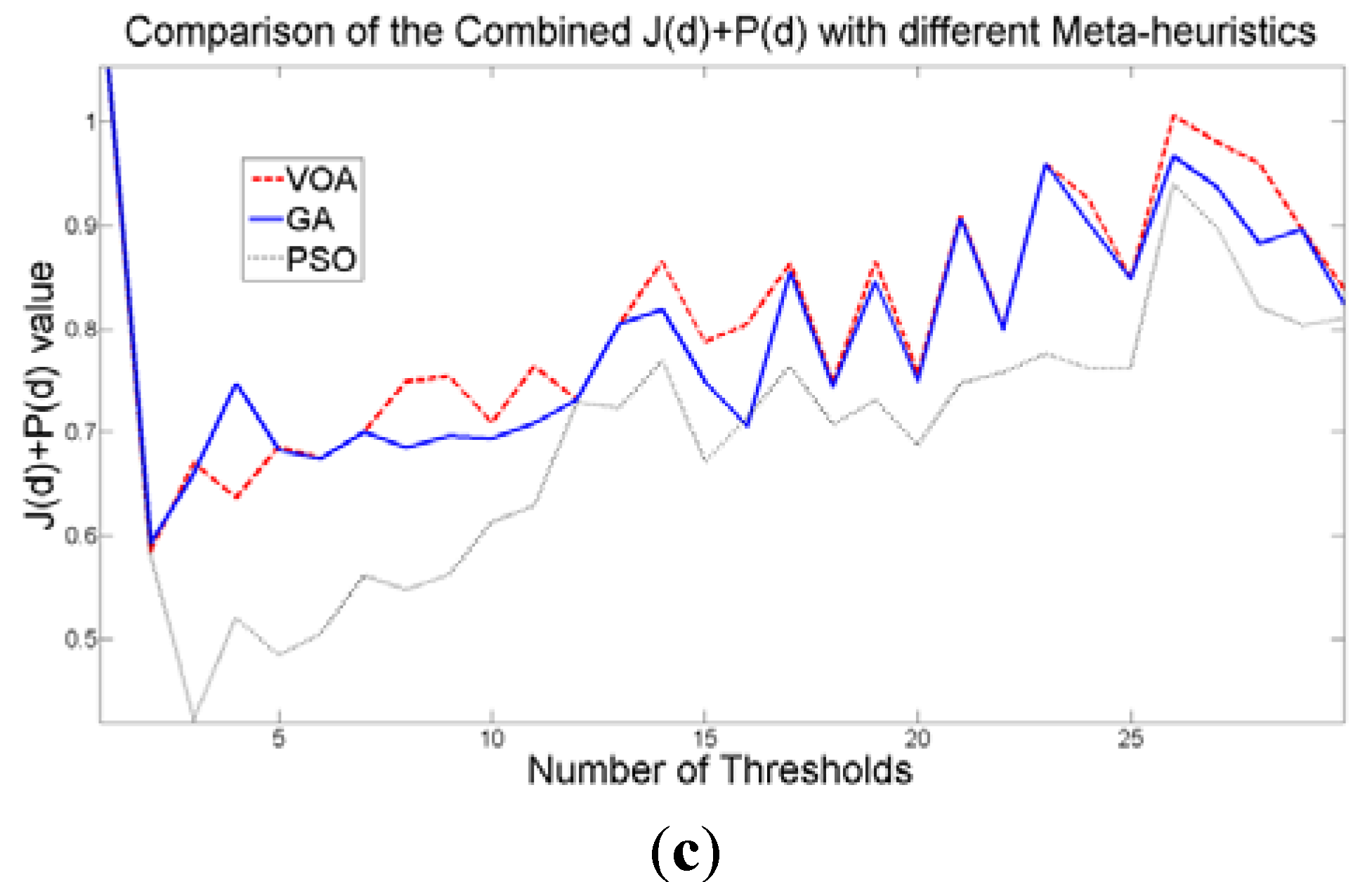
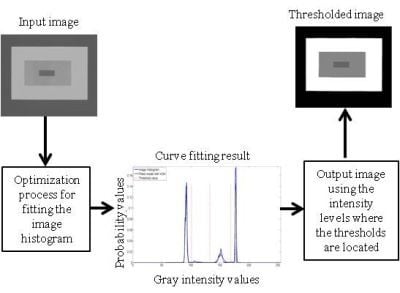
Figure 8 are the values of the threshold found. In addition to the thresholding result, it was observed that VOA provides both, the smallest CPU time as well as the best objective function value among the three algorithms.
Figure 7.
Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA and PSO on test image 1.
Figure 7.
Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA and PSO on test image 1.
Figure 8.
Fitting of the histogram of the test image 1 implementing (a) VOA, (b) GA, and (c) PSO.
Figure 8.
Fitting of the histogram of the test image 1 implementing (a) VOA, (b) GA, and (c) PSO.
When implementing Otsu’s method, it is rather impressive to observe that the output image delivered by the algorithms when optimizing Equation (10) resembles the one given by Otsu’s method (
Figure 4e). The aforementioned, confirms the competitiveness of the proposed idea in segmenting a gray scale image given a number of distributions in the mixture model. Additionally, the main contribution is that we do not need to look at the histogram to determine how many thresholds will provide a good segmentation, and by implementing optimization tools such as the ones presented in this study, we can provide satisfactory results in a short period of time, where methods such as Otsu’s would take too long.
Table 5.
Thresholding results over 50 runs for the test image 2.
Table 5.
Thresholding results over 50 runs for the test image 2.
| Algorithm | Number of Thresholds | Objective Function | Threshold Values | Means | Variances | Weights | CPU Time per Iteration (s) | Total CPU Time for the Proposed Approach (s) |
|---|
| VOA | 1 | 1.051 | 143 | 87.326 | 1015.901 | 0.127 | 0.057 | 0.237 |
| 203.855 | 603.462 | 0.873 |
| 2 | 0.585 | 133, 205 | 81.590 | 808.054 | 0.114 | 0.089 |
| 182.352 | 280.586 | 0.448 |
| 223.915 | 170.129 | 0.438 |
| 3 | 0.670 | 104, 174, 209 | 67.393 | 370.007 | 0.082 | 0.091 |
| 150.866 | 385.486 | 0.153 |
| 192.994 | 90.775 | 0.378 |
| 226.231 | 146.602 | 0.386 |
| GA | 1 | 1.051 | 142 | 86.658 | 991.336 | 0.126 | 0.109 | 0.480 |
| 203.746 | 609.117 | 0.874 |
| 2 | 0.593 | 132, 204 | 81.075 | 790.076 | 0.113 | 0.145 |
| 181.537 | 279.992 | 0.436 |
| 223.310 | 176.642 | 0.451 |
| 3 | 0.659 | 142, 149, 206 | 86.658 | 991.336 | 0.126 | 0.226 |
| 145.121 | 3.989 | 0.011 |
| 185.213 | 205.948 | 0.440 |
| 224.558 | 163.332 | 0.423 |
| PSO | 1 | 1.051 | 143 | 87.326 | 1015.901 | 0.127 | 0.072 | 0.453 |
| 203.855 | 603.462 | 0.873 |
| 2 | 0.573 | 156, 206 | 97.751 | 1389.414 | 0.153 | 0.141 |
| 186.458 | 170.789 | 0.424 |
| 224.558 | 163.332 | 0.423 |
| 3 | 0.619 | 101, 180, 211 | 66.048 | 335.944 | 0.079 | 0.240 |
| 155.144 | 453.146 | 0.195 |
| 195.932 | 76.337 | 0.366 |
| 227.489 | 134.942 | 0.359 |
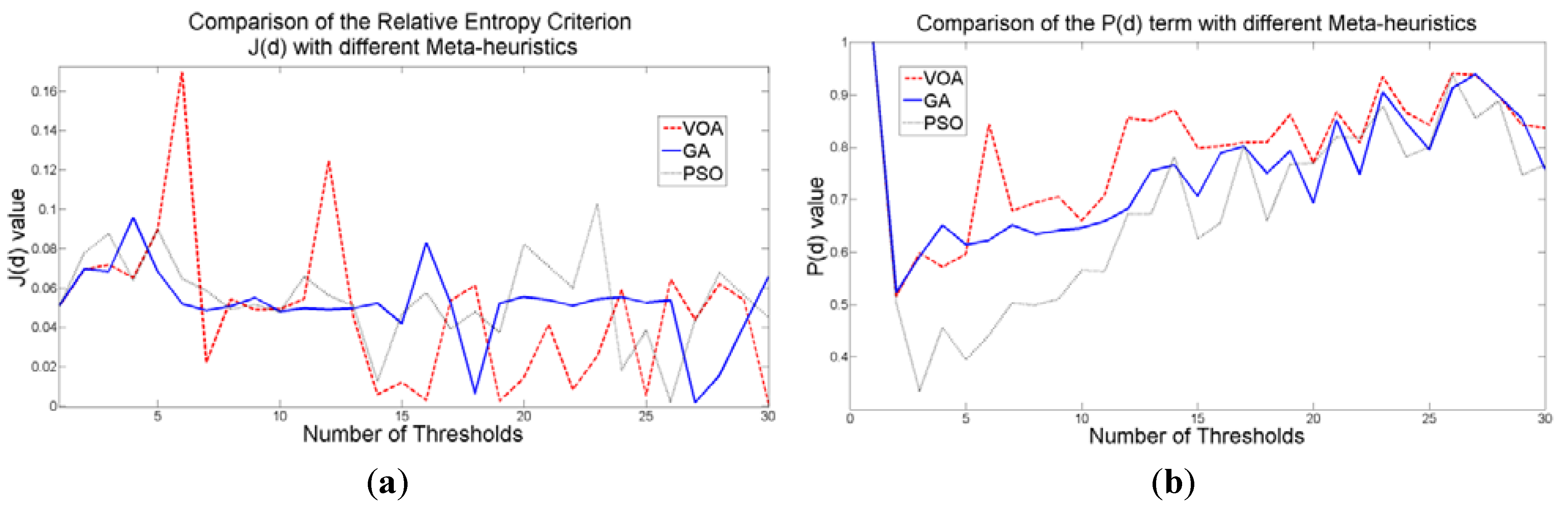
When an image containing text on a wrinkled paper (
Figure 5a) is tested, two thresholds (or three Gaussian distributions) give the best objective function value for Equation (10) as observed in
Figure 9c.
Table 5 summarizes the thresholding results,
i.e., Θ(
d), computational effort and Gaussian parameters, for the three meta-heuristics implemented. As for the fitting result,
Figure 10 shows that even though three Gaussian distributions do not provide an exact description of the image histogram, it is good enough to recognize all the characters on the thresholded image (
Figure 5b–d).
Figure 9.
Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA and PSO on test image 2.
Figure 9.
Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA and PSO on test image 2.
The outstanding performance of the three meta-heuristics is observed once again when comparing with the Otsu’s method (
Figure 5e), where the computational effort shows the feasibility of optimizing the proposed mathematical model with heuristic optimization algorithms.
Figure 10.
Fitting of the histogram of the test image 2 implementing (a) VOA, (b) GA, and (c) PSO.
Figure 10.
Fitting of the histogram of the test image 2 implementing (a) VOA, (b) GA, and (c) PSO.
The thresholding results of the Lena image (
Figure 6a) shows that four thresholds (five Gaussian distributions) have the best objective function value, which is detailed in
Table 6. Visually, the thresholded images (
Figure 6b–d) obtain most of the details from the original one, and in terms of objective function behavior (
Figure 11) there is no need to add more distributions into the mixture model (
i.e., more thresholds) because they do not provide a better objective function value.
Table 6.
Thresholding results over 50 runs for the test image 3.
Table 6.
Thresholding results over 50 runs for the test image 3.
| Algorithm | Number of Thresholds | Objective Function | Threshold Values | Means | Variances | Weights | CPU Time per Iteration (s) | Total CPU Time for the Proposed Approach (s) |
|---|
| VOA | 1 | 1.043 | 63 | 48.917 | 51.398 | 0.159 | 0.046 | 1.009 |
| 138.048 | 1442.095 | 0.841 |
| 2 | 0.575 | 59, 138 | 47.598 | 40.100 | 0.143 | 0.128 |
| 104.785 | 484.361 | 0.430 |
| 168.523 | 538.213 | 0.428 |
| 3 | 0.454 | 99, 140, 183 | 65.002 | 369.233 | 0.302 | 0.198 |
| 120.137 | 147.621 | 0.287 |
| 157.234 | 130.155 | 0.295 |
| 201.595 | 109.646 | 0.116 |
| 4 | 0.367 | 86, 126, 154, 199 | 57.243 | 192.433 | 0.236 | 0.210 |
| 106.550 | 126.938 | 0.236 |
| 139.629 | 67.666 | 0.241 |
| 170.694 | 173.733 | 0.218 |
| 208.851 | 42.459 | 0.068 |
| 5 | 0.466 | 68, 104, 134, 156, 190 | 50.380 | 68.188 | 0.175 | 0.428 |
| 88.813 | 108.622 | 0.165 |
| 120.054 | 77.656 | 0.203 |
| 145.072 | 39.845 | 0.192 |
| 168.597 | 90.400 | 0.167 |
| 204.364 | 77.722 | 0.098 |
| GA | 1 | 1.044 | 66 | 49.794 | 60.874 | 0.169 | 0.103 | 0.904 |
| 138.924 | 1393.456 | 0.831 |
| 2 | 0.606 | 69, 139 | 50.671 | 72.095 | 0.178 | 0.136 |
| 109.090 | 368.075 | 0.402 |
| 169.106 | 530.358 | 0.419 |
| 3 | 0.504 | 96, 140, 179 | 62.664 | 315.826 | 0.282 | 0.182 |
| 118.590 | 171.180 | 0.307 |
| 156.168 | 110.243 | 0.282 |
| 199.453 | 139.510 | 0.129 |
| 4 | 0.474 | 46, 99, 136, 169 | 40.698 | 14.583 | 0.051 | 0.225 |
| 69.954 | 296.623 | 0.251 |
| 118.032 | 124.129 | 0.256 |
| 151.053 | 77.603 | 0.267 |
| 192.624 | 235.736 | 0.175 |
| 5 | 0.584 | 65, 87, 128, 152, 205 | 49.504 | 57.550 | 0.166 | 0.258 |
| 76.023 | 40.415 | 0.074 |
| 108.258 | 138.292 | 0.250 |
| 139.533 | 49.522 | 0.205 |
| 171.707 | 244.613 | 0.257 |
| 211.824 | 28.018 | 0.049 |
| PSO | 1 | 1.044 | 64 | 49.212 | 54.387 | 0.163 | 0.096 | 0.887 |
| 138.353 | 1424.978 | 0.837 |
| 2 | 0.575 | 68, 140 | 50.380 | 68.188 | 0.175 | 0.128 |
| 109.403 | 387.984 | 0.414 |
| 169.718 | 522.330 | 0.411 |
| 3 | 0.446 | 97, 141, 191 | 63.440 | 333.741 | 0.288 | 0.170 |
| 119.639 | 170.199 | 0.309 |
| 159.625 | 168.784 | 0.308 |
| 204.790 | 73.728 | 0.095 |
| 4 | 0.337 | 79, 121, 148, 184 | 54.216 | 131.179 | 0.210 | 0.220 |
| 101.036 | 126.541 | 0.225 |
| 134.327 | 60.474 | 0.225 |
| 161.866 | 95.355 | 0.227 |
| 202.037 | 103.844 | 0.113 |
| 5 | 0.478 | 60, 115, 117, 147, 186 | 47.926 | 42.582 | 0.147 | 0.273 |
| 90.827 | 237.679 | 0.255 |
| 115.514 | 0.250 | 0.010 |
| 132.322 | 71.331 | 0.240 |
| 161.755 | 107.986 | 0.240 |
| 202.782 | 94.639 | 0.108 |
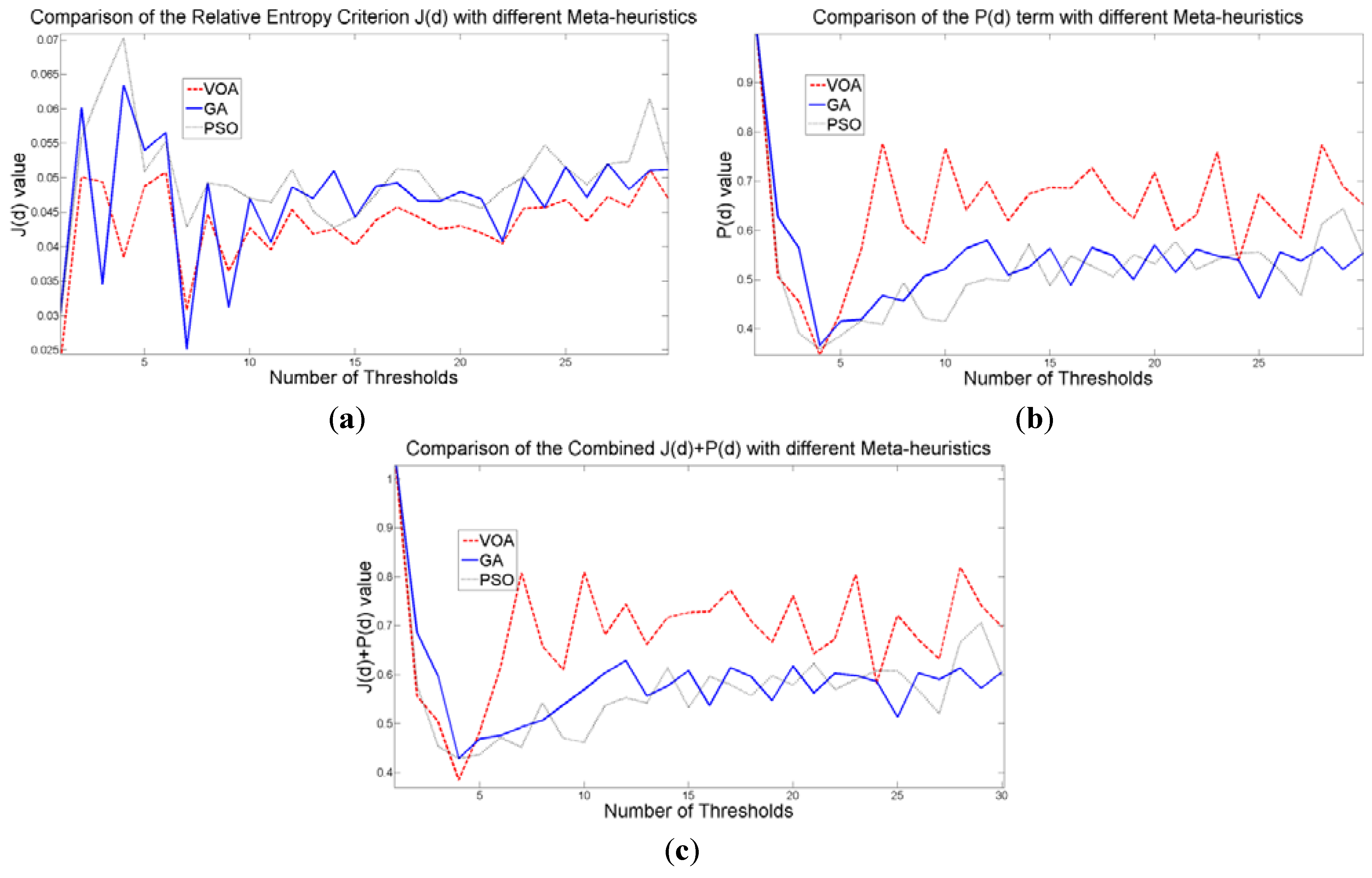
Figure 11.
Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA and PSO on test image 3.
Figure 11.
Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA and PSO on test image 3.
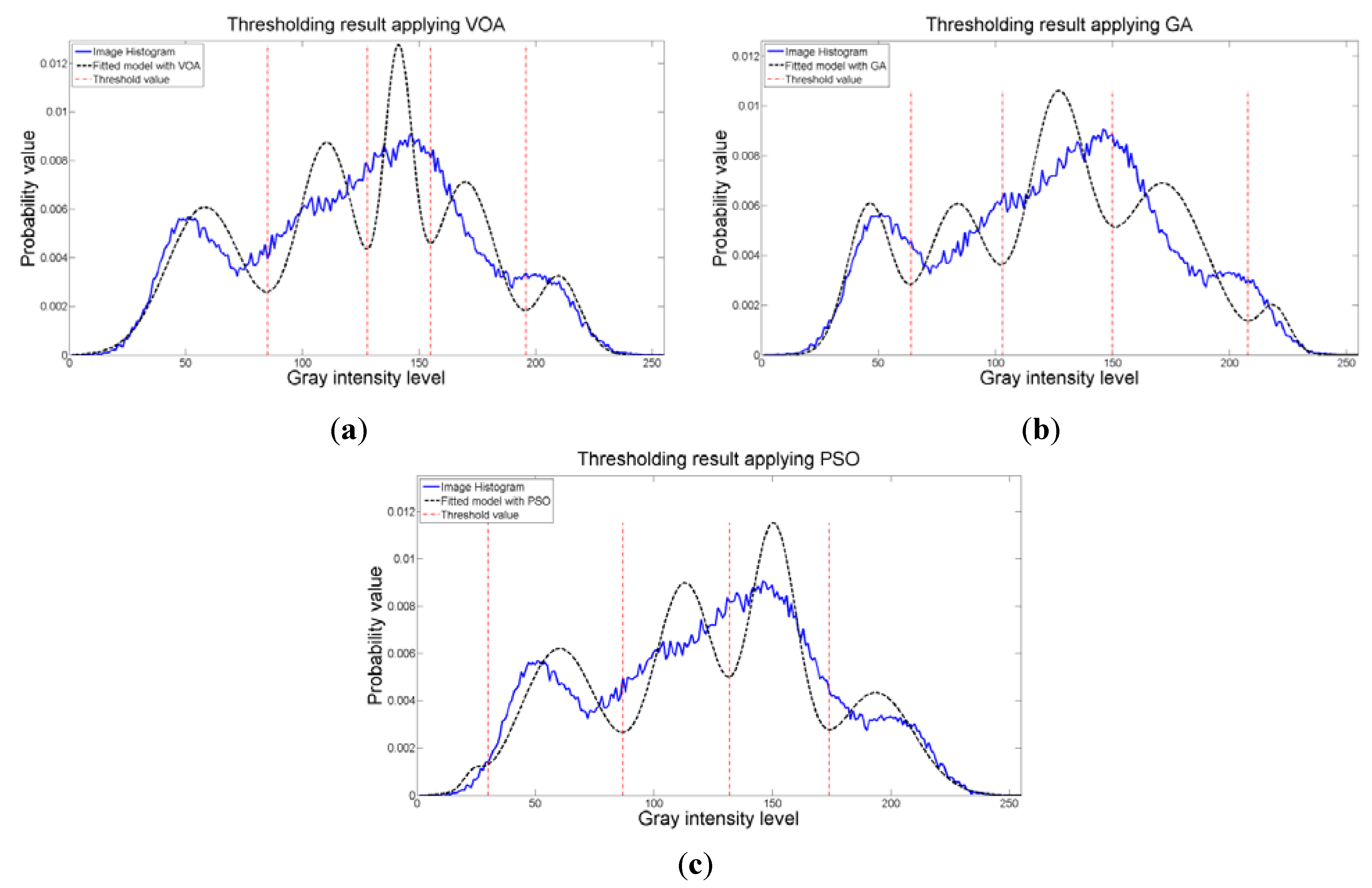
Once again, the fitting provided by the mixture model (
Figure 12) might not be the best; however, it is good enough to provide most of the details from the original image. It is interesting to observe that all the algorithmic tools are able to find satisfactory results in no more than 1.009 seconds in the case of VOA which is the slowest one, even though the algorithmic tools had to optimize Equation (10) for
d = [1, 2, 3, 4].
Figure 12.
Fitting of the histogram of the test image 3 implementing (a) VOA, (b) GA, and (c) PSO.
Figure 12.
Fitting of the histogram of the test image 3 implementing (a) VOA, (b) GA, and (c) PSO.
To further test the proposed method an image with low contrast is used as illustrated in
Figure 13a. It is observed that all the algorithmic tools are able to segment the image providing the correct number of thresholds which is three. Additionally, when comparing the output image given by Otsu’s method and the idea proposed in this study, we are able to observe that despite its novelty the proposed method provides stable and satisfactory results for a low contrast image.
Three thresholds are suggested after the optimization of Equation (10) is performed, which is good enough for successfully segmenting the image under study (
Figure 13b–d), though the fitting of the image histogram was not a perfect one (
Figure 15). More importantly, the addition of more than four distributions (
i.e., three thresholds) to the mathematical model Equation (10) does not achieve a better result according to
Figure 14c; therefore, the power of the proposed approach is shown once again with this instance. As for the Otsu’s method, even though the correct number of thresholds is provided, the low contrast causes defect in the output image (seen at the light gray region in the middle of
Figure 13e.
Table 7.
Thresholding result over 50 runs for the test image 4.
Table 7.
Thresholding result over 50 runs for the test image 4.
| Algorithm | Number of Thresholds | Objective Function | Threshold Values | Means | Variances | Weights | CPU Time per Iteration (s) | Total CPU Time for the Proposed Approach (s) |
|---|
| VOA | 1 | 2.112 | 98 | 102.027 | 504.595 | 0.612 | 0.045 | 0.213 |
| 174.622 | 36.165 | 0.388 |
| 2 | 1.014 | 105, 169 | 91.007 | 2.994 | 0.486 | 0.051 |
| 146.853 | 157.462 | 0.160 |
| 176.415 | 0.749 | 0.354 |
| 3 | 0.848 | 101, 133, 169 | 90.917 | 1.888 | 0.482 | 0.054 |
| 109.438 | 46.637 | 0.019 |
| 150.667 | 17.258 | 0.145 |
| 176.415 | 0.749 | 0.354 |
| 4 | 0.919 | 103, 117, 140, 169 | 90.929 | 2.009 | 0.483 | 0.064 |
| 107.796 | 17.853 | 0.016 |
| 126.818 | 25.714 | 0.002 |
| 150.202 | 9.141 | 0.139 |
| 176.271 | 2.326 | 0.359 |
| GA | 1 | 2.112 | 98 | 90.906 | 1.803 | 0.482 | 0.134 | 0.692 |
| 166.703 | 268.234 | 0.518 |
| 2 | 1.051 | 100, 166 | 90.914 | 1.861 | 0.482 | 0.153 |
| 145.534 | 191.624 | 0.161 |
| 176.349 | 1.354 | 0.357 |
| 3 | 0.903 | 99, 122, 167 | 90.910 | 1.832 | 0.482 | 0.179 |
| 107.759 | 23.640 | 0.018 |
| 150.171 | 19.452 | 0.144 |
| 176.364 | 1.203 | 0.356 |
| 4 | 0.998 | 109, 115, 139, 177 | 91.270 | 6.829 | 0.494 | 0.225 |
| 111.849 | 2.575 | 0.003 |
| 123.655 | 52.305 | 0.005 |
| 164.654 | 163.335 | 0.323 |
| 177.000 | 1.455 | 0.176 |
| PSO | 1 | 2.112 | 98 | 90.906 | 1.803 | 0.482 | 0.027 | 0.171 |
| 166.703 | 268.234 | 0.518 |
| 2 | 1.005 | 97, 168 | 90.902 | 1.780 | 0.481 | 0.035 |
| 145.505 | 204.582 | 0.163 |
| 176.393 | 0.931 | 0.355 |
| 3 | 0.873 | 98, 116, 168 | 90.906 | 1.803 | 0.482 | 0.045 |
| 106.393 | 12.956 | 0.016 |
| 149.899 | 33.945 | 0.147 |
| 176.393 | 0.931 | 0.355 |
| 4 | 0.911 | 98, 130, 138, 169 | 90.906 | 1.803 | 0.482 | 0.065 |
| 108.777 | 42.833 | 0.019 |
| 133.110 | 4.122 | 0.001 |
| 150.704 | 16.707 | 0.144 |
| 176.415 | 0.749 | 0.354 |
Figure 13.
Test image 4: (a) Original image; Thresholded image implementing (b) VOA, (c) GA, (d) PSO, and (e) Otsu’s method.
Figure 13.
Test image 4: (a) Original image; Thresholded image implementing (b) VOA, (c) GA, (d) PSO, and (e) Otsu’s method.
Figure 14.
Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA, and PSO on test image 4.
Figure 14.
Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA, and PSO on test image 4.
Figure 15.
Fitting of the histogram of the test image 4 implementing (a) VOA, (b) GA, and (c) PSO.
Figure 15.
Fitting of the histogram of the test image 4 implementing (a) VOA, (b) GA, and (c) PSO.
Table 8.
Thresholding result over 50 runs for the test image 5.
Table 8.
Thresholding result over 50 runs for the test image 5.
| Algorithm | Number of Thresholds | Objective Function | Threshold Values | Means | Variances | Weights | CPU Time per Iteration (s) | Total CPU Time for the Proposed Approach (s) |
|---|
| VOA | 1 | 1.023 | 67 | 48.328 | 119.083 | 0.172 | 0.060 | 0.435 |
| 138.301 | 1428.555 | 0.828 |
| 2 | 0.556 | 63, 137 | 46.555 | 100.292 | 0.155 | 0.075 |
| 104.962 | 436.410 | 0.421 |
| 168.426 | 564.154 | 0.424 |
| 3 | 0.504 | 88, 140, 206 | 57.730 | 278.208 | 0.254 | 0.082 |
| 115.780 | 221.287 | 0.346 |
| 165.005 | 334.790 | 0.358 |
| 214.735 | 50.956 | 0.042 |
| 4 | 0.481 | 87, 130, 151, 197 | 57.218 | 267.832 | 0.249 | 0.094 |
| 109.591 | 151.059 | 0.268 |
| 140.153 | 36.619 | 0.178 |
| 168.811 | 169.302 | 0.232 |
| 209.138 | 78.820 | 0.071 |
| 5 | 0.495 | 77, 116, 143, 158, 214, 255 | 52.347 | 176.710 | 0.208 | 0.124 |
| 97.798 | 120.079 | 0.210 |
| 129.636 | 59.464 | 0.208 |
| 149.842 | 18.471 | 0.128 |
| 180.649 | 270.308 | 0.226 |
| 220.581 | 34.873 | 0.020 |
| GA | 1 | 1.024 | 71 | 49.927 | 139.317 | 0.187 | 0.139 | 1.204 |
| 139.577 | 1363.879 | 0.813 |
| 2 | 0.669 | 76, 137 | 51.913 | 169.499 | 0.204 | 0.198 |
| 109.784 | 294.414 | 0.372 |
| 168.426 | 564.154 | 0.424 |
| 3 | 0.586 | 84, 138, 227 | 55.674 | 237.243 | 0.236 | 0.209 |
| 113.180 | 235.410 | 0.347 |
| 168.529 | 529.908 | 0.413 |
| 231.261 | 20.782 | 0.003 |
| 4 | 0.568 | 60, 103, 146, 211 | 45.138 | 87.633 | 0.141 | 0.259 |
| 82.720 | 165.607 | 0.195 |
| 125.553 | 152.188 | 0.316 |
| 170.644 | 343.107 | 0.320 |
| 218.253 | 40.308 | 0.028 |
| 5 | 0.573 | 57, 90, 130, 156, 212 | 43.635 | 76.301 | 0.126 | 0.400 |
| 72.881 | 99.772 | 0.138 |
| 110.800 | 131.973 | 0.254 |
| 142.590 | 55.391 | 0.220 |
| 178.408 | 270.837 | 0.237 |
| 219.035 | 38.368 | 0.025 |
| PSO | 1 | 1.023 | 66 | 47.900 | 114.220 | 0.168 | 0.034 | 0.373 |
| 137.948 | 1446.983 | 0.832 |
| 2 | 0.564 | 64, 137 | 47.023 | 104.922 | 0.159 | 0.060 |
| 105.419 | 421.751 | 0.416 |
| 168.426 | 564.154 | 0.424 |
| 3 | 0.413 | 97, 140, 182 | 63.047 | 390.706 | 0.300 | 0.073 |
| 119.448 | 154.217 | 0.300 |
| 157.206 | 130.606 | 0.281 |
| 201.012 | 152.773 | 0.119 |
| 4 | 0.410 | 28, 89, 133, 169 | 22.825 | 17.056 | 0.007 | 0.091 |
| 59.246 | 263.407 | 0.252 |
| 112.179 | 160.043 | 0.284 |
| 149.441 | 99.432 | 0.282 |
| 192.596 | 259.838 | 0.175 |
| 5 | 0.576 | 40, 70, 125, 159, 230 | 32.580 | 32.714 | 0.037 | 0.115 |
| 53.830 | 68.546 | 0.146 |
| 100.401 | 235.202 | 0.297 |
| 141.671 | 92.691 | 0.281 |
| 184.398 | 346.042 | 0.237 |
| 234.122 | 19.797 | 0.002 |
The Lena image in which a random noise is generated will be our last test instance (
Figure 16a), from this it is expected to provide clear evidence concerning robustness of the proposed method, where all the parameter values and computational results are summarized on
Table 8. By observing the thresholded images when implementing the proposed approach (
Figure 16b–d), we are able to conclude that random noise does not represent a major issue, even though different optimization tools are used.
The objective function behavior (
Figure 17c) proved once again that when a suitable number of thresholds is achieved, the addition of more distributions into the mixture model is not necessary, since it will always achieve a larger objective function value compared with the one given by having four thresholds (or five Gaussians). Additionally, the fitting of the histogram (
Figure 18) given by the image, even though is not a perfect one, is proved to be good enough to keep most of the relevant details from the original test instance.
Most of the relevant details from the original instance are kept. On the other hand, Otsu’s method (
Figure 16e) is not able to provide an output image as clear as the ones given by the proposed approach when implementing the meta-heuristic tools.
Figure 16.
Test image 5: (a) Original image; Thresholded image implementing (b) VOA, (c) GA, (d) PSO, and (e) Otsu’s method with 4 thresholds.
Figure 16.
Test image 5: (a) Original image; Thresholded image implementing (b) VOA, (c) GA, (d) PSO, and (e) Otsu’s method with 4 thresholds.
Figure 17.
Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA and PSO on test image 5.
Figure 17.
Behavior of (a) Relative Entropy function J(d), (b) P(d), and (c) Objective function Θ(d) over different numbers of thresholds with different meta-heuristics VOA, GA and PSO on test image 5.
Figure 18.
Fitting of the histogram of the test image 5 implementing (a) VOA, (b) GA, and (c) PSO.
Figure 18.
Fitting of the histogram of the test image 5 implementing (a) VOA, (b) GA, and (c) PSO.