A Five Species Cyclically Dominant Evolutionary Game with Fixed Direction: A New Way to Produce Self-Organized Spatial Patterns

Abstract

Cyclically dominant systems are hot issues in academia, and they play an important role in explaining biodiversity in Nature. In this paper, we construct a five-strategy cyclically dominant system. Each individual in our system changes its strategy along a fixed direction. The dominant strategy can promote a change in the dominated strategy, and the dominated strategy can block a change in the dominant strategy. We use mean-field theory and cellular automaton simulation to discuss the evolving characters of the system. In the cellular automaton simulation, we find the emergence of spiral waves on spatial patterns without a migration rate, which suggests a new way to produce self-organized spatial patterns.

1. Introduction

Cyclically dominant systems in Nature have recently become hot issues, especially in explaining biological diversity [1,2,3,4,5,6]. As the simplest cyclical interaction system that contains three species, the rock-paper-scissors game can explain typical population oscillatory behavior and other phenomena, ex., marine benthic systems [7], plant communities [8,9,10,11,12], microbial populations [2,13,14,15,16] and driven-dissipative quantum systems [17]. The rock-paper-scissors game is also reflected in the strategic choice in terms of biological methods, for example, the mating strategy of side-blotched lizards [18] and the regular oscillations of the numbers of collared lemmings [19] and Pacific salmon [20]. In other words, biological diversity can be interpreted by invasions among species [21,22]. Extensions of the classical rock-paper-scissors game to more than three strategies have been popular issues in recent research. Avelino et al. investigated the three-dimensional predator-prey model with four or five species, showing the spatial distribution of Z_N Lotka–Volterra competition models using stochastic and mean field theory simulations [23]. Dobrinevski et al. considered an asymmetric ecological model with four strategies, which contains a three-strategy cycle and a neutral alliance of two strategies, showing that the model exhibits a mobility-dependent selection of either the three-strategy cycle or the neutral pair [24]. Durney et al. discussed the evolution of characters of a cyclically competing predator-prey system with four or more species [25]. Feng et al. observed self-organization spiral waves of a cyclic five-species system using direct simulations and nonlinear partial differential equations [26]. Intoy et al. focused on the extinction processes in a cyclic four-species system [27]. In our previous work, we studied the evolution properties of a cyclic five-strategy system with two different invasion routes [28], and the group interactions of the system have been discussed [29,30,31]. Knebel et al. analyzed the coexistence and survival scenarios of Lotka–Volterra networks with both a cyclic four-species system and a cyclic five-species system [32]. Laird et al. provided numbers for possible competitive topologies for a cyclic five-species system, showing the different coexistences [33]. Li et al. analyzed the evolutionary properties of the N-species Jungle game, which is a special cyclic competing system in mean-field theory [34]. Andrae et al. analyzed the entropy production in the cyclic competing system [35].

What does “dominant” mean in cyclic dominant evolutionary games? In previous research, “dominant” always meant “alternative” or “study”. In ecological models, one population dominates another means the dominant population occupies the habitat of the weakness population. Similarly, in social game models, “dominant” means the losers study the strategies of the winners. However, in fact, the factors that cause the losers to change their strategies are not only the above. Consider, for example, the rock-paper-scissors game. If an individual playing paper loses to his opponent playing scissors, in the next game, he may play rock to defeat his opponent instead of learning the strategy of the opponent who played scissors. In this case, “dominant” causes the losers to change their strategies. Mobilia studies rock-paper-scissors games including studying mechanisms [36]. Sometimes, strategic choices are not arbitrary; for example, in a Texas Hold’Em game, players are not allowed to reduce the chips that they have already bet on.

Traditional Chinese medicine has been recognized in many fields in the world [37]. In traditional Chinese medicine, there are five elements, “Metal”, “Wood”, “Water”, “Fire” and “Earth”, in the five element theory. The relationships between two of the five elements are “generating interaction” and “overcoming interaction” [38]. The two relationships can be interpreted as dominant. Hence, the five element theory is similar to the rock-paper-scissors-lizard-Spock game [28]. In our paper, we construct a five-strategy cyclically dominant system based on the five element theory. “Generating interaction” is interpreted as the change in direction of strategy, and “overcoming interaction” is interpreted as the dominant that promotes the losers to change their strategies. Each individual in our system changes its strategy along a fixed direction. In other words, the dominant strategy can promote the changing of the dominated strategy, and the dominated strategy can block the changing of the dominant strategy.

In a homogeneous mixed environment, we construct the ordinary differential equations of this model. We discuss and prove the stability of the system in the case that the number of an individual’s neighbors is one. We analyze cases in which individuals have more than one neighbor using numerical solution. Then, we study the model on a two dimensional lattice by using the cellular automata simulations. We find the self-organization spatial distributions when the Moore neighborhood or six-cell neighborhood were used without moving. In this case, the distribution of individuals in the system forms spiral waves. However, when the Von Neumann neighborhood was used, there is no self-organization in this system. It should be noted that self-organization spatial distributions are important in the research of evolutionary games [39,40,41,42]. In previous studies, moving is one key factor that can promote the emergence of self-organization spatial distributions such as spiral waves [30,42].

2. Model

There are five strategies in our model: S₁, S₂, S₃, S₄ and S₅. The relationships between the five strategies are shown in Figure 1. S_i can translate into S_i+1, and S_i can dominate S_i+2. We set the following conditions: S_i can promote the transformation of S_i+2 and prevent the transformation of S_i+1. Each individual has K neighbors. The transformation rules are as follows. S_i converts to S_i+1 if more individuals use the S_i-2 strategy than S_i-1 of its neighbors; in other cases, the strategy will not change. For example, if an individual use strategy S₃ and there are more S₁ among its neighbors than S₂, then the individual converts its strategy to S₄.

The simulation runs as follows:

• Place individuals using different strategies randomly on the lattice;
• For each individual using the strategy S_i in the system, count the numbers of S_i-1 and S_i-2 respectively in its neighbors. If the number of S_i-2 in its neighbors is more than S_i-1, we label the individual S_i as “alterable”.
• Changing the labeled “alterable” individuals’ strategies from S_i to S_i+1.
• Repeat step 2.

3. Mean Field Theory

Mean-field theory is one of the major methods of studying cyclically dominant systems [43]. Let x_i denote the density of individuals who use strategy S_i. In mean-field theory, each individual adopts strategy S_i with the probability x_i. If there are enough individuals in the system, we obtain the equation:

$$\stackrel{·}{x_i}=-x_{i}f\left(x_{i-2},x_{i-1}\right)+x_{i-1}f\left(x_{i-3},x_{i-2}\right)$$

where:

$$f\left(x,y\right)={\displaystyle \sum _{i=1}^K{\displaystyle \sum _{j=0}^{\min \left\{i-1,K-i\right\}}{C}_K^i{C}_{K-i}^j{x}^i{y}^j{\left(1-x-y\right)}^{K-i-j}}}$$

represents the probability that more individuals choose strategy x than y among all of the K neighbors.

When K = 1, the equation is $\stackrel{·}{x_i}=-x_i{x}_{i-2}+x_{i-1}{x}_{i-3}$. Let $V=x_1{x}_2{x}_3{x}_4{x}_5$; we obtain $\frac{dV}{dt}=V\left(x_1^{-1}{x}_3{x}_5+x_1{x}_2^{-1}{x}_4+x_2{x}_3^{-1}{x}_5+x_1{x}_3{x}_4^{-1}+x_2{x}_4{x}_5^{-1}-1\right)\ge 0$. V can achieve its maximum value if and only if $x_1=x_2=x_3=x_4=x_5=1/5$. Thus, the equilibrium point (1/5, 1/5, 1/5, 1/5, 1/5) is globally asymptotically stable.

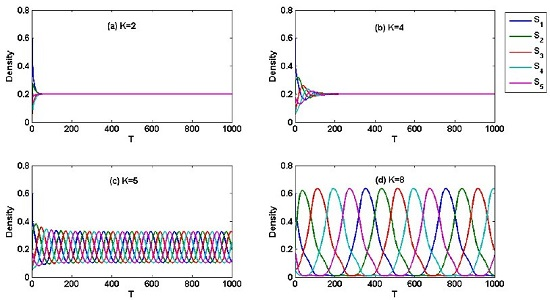
4. Numerical Result

For the case K > 1, the equation becomes too complicated for theoretical analysis. Thus, we use numerical solutions to solve the problem. Using the fourth-order Runge–Kutta method with four stages, the initial densities are ρ₁ = 0.6 and ρ₂ = ρ₃ = ρ₄ = ρ₅ = 0.1, as shown in Figure 2. We find that when K < 5, the solution converges to the internal equilibrium point (1/5, 1/5, 1/5, 1/5, 1/5). The larger the K, the slower the rate of convergence. When K > 4, the solutions of the equation become stable periodic fluctuations. The larger K, the larger the amplitude and the longer the period.

We can see from Figure 3 and Figure 4 that when the number of individuals’ neighbors are more than four, the densities fluctuate periodically and evolve through time. The amplitude increases with the increasing number of individuals’ neighbors; the minimum value of the densities approaches zero, and the maximum value of the densities approaches 0.8. The period grows exponentially with the increasing number of neighbors. The larger K is, the larger the degree of the differential equation is. Because in our model the parameter K must be an integer, we cannot prove whether bifurcations exist because the bifurcation parameter K is varied, especially the supercritical Hopf bifurcation.

5. Simulation

We consider a spatial environment as one that puts individuals on a square lattice of linear size L with periodic spatial boundary conditions. Each site can only be occupied by one individual. Interactions between individuals are based on Cellular Automata simulation.

The strategy of an individual changes from S_i to S_i+1 if its neighbors have more individuals using the strategy S_i-2 than S_i-1. As shown in Mean-field theory, the number of neighbors has enormous impacts on the system. We use the Von Neumann neighborhood, the four nearest neighbors, and the Moore neighborhood, the eight nearest neighbors, to simulate the system, respectively. The initial density of each species is ρ_i; in this case, i = 1, 2, 3, 4, 5.

Setting L = 200 and ρ₁ = ρ₂ = ρ₃ = ρ₄ = ρ₅ = 0.2 in the Moore neighborhood case, we obtain the steady-state densities of different strategies evolving through time, as shown in Figure 5. We find that the five strategies can coexist in this system and the densities fluctuate stably. Figure 6 shows the snapshots of the system in different time steps. In Figure 6, the individuals in the system form a self-organizing pattern; we find that there are spiral waves in the figure.

Considering the impact of different densities on the system, setting L = 200, ρ₁ = 0.6 and ρ₂ = ρ₃ = ρ₄ = ρ₅ = 0.1, we obtain the steady-state densities of different strategies evolving through time, as shown in Figure 7. We find that in this system, the five strategies can coexist and their densities fluctuate stably. However, the speed with which the system reaches a steady state is slow. Figure 8 shows the snapshots of the system. We can see from Figure 6 that spiral waves emerge in some regions. In other regions, ”dead regions” emerge; i.e., the strategies in these regions will not evolve through time. The formation of ‘dead regions’ is related to the initial distribution of species.

Setting L = 200, ρ₁ = 0.6 and ρ₂ = ρ₃ = ρ₄ = ρ₅ = 0.1 in the Von Neumann neighborhood case, we obtain the steady-state densities of different strategies evolving through time, as shown in Figure 9. The densities come to a steady state sooner than the case of eight neighbors. We can see from the snapshot that self-organizing spiral waves do not exist.

We can see from the simulation that the five strategies can coexist irrespective of whether we use a Moore neighborhood or a Von Neumann neighborhood. In the Von Neumann neighborhood model, the densities of species reach a steady state faster than in the Moore neighborhood. In the Moore neighborhood model, the system reaches a steady state faster when the initial distributions are uniform, and self-organizing spiral waves emerge in this uniform environment. When the initial environment is not uniform, some ”dead regions” may appear in the system. We can also see that spiral waves do not appear in the Von Neumann neighborhood.

Next, we consider the triangular lattice with six neighbors. Compared to the L × L square lattice with periodic boundary, we just need to move the sites in the odd-numbered lines in the right half of the unit. Setting L = 200 and ρ₁ = ρ₂ = ρ₃ = ρ₄ = ρ₅ = 0.2, we obtain the densities of the five strategies evolving through time as shown in Figure 10 and the spatial distribution as shown in Figure 11. We find that different from the Moore neighborhood and Von Neumann neighborhood, the system reaches the steady state more slowly. As shown in Figure 10, the system reaches the steady state after 900 time steps. We can also see from Figure 11 that obvious spiral waves appear in the system.

It should also be noted that there are no random factors in our model using the cellular automata method, except the initial conditions of the system. Therefore, the results of the simulations will be periodic, which is the weakness of the cellular automata method [44].The results of the simulation are influenced by the initial distributions of the system; thus, we ran more tests and obtained similar results. Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 are the results from one run, and our results in terms of diversity and self-organization are robust.

6. Conclusions

In this paper, we construct a five-strategy cyclically dominant system. Each individual changes its strategy along a fixed direction in this model. In other words, the dominant strategy can promote a change in the dominated strategy and the dominated strategy can block the change of the dominant strategy. The individuals can change their strategies based on their neighbors.

If an individual has K neighbors and the number of dominant strategies available to the chosen individual is more than the number of dominated strategies, the chosen individual can change its strategy. We use mean-field theory and cellular automaton to discuss the evolving characters of the system. We find that the five strategies in this system can coexist and the steady state of the system is based on the parameter K, which represents the number of neighbors.

In a homogeneous mixing environment, we use mean-field theory to describe the densities evolving through time. We construct an ordinary differential equation and show that when K = 1, the internal equilibrium of the equation is globally stable. That is to say, each individual changes its strategy based on another individual, and at the steady state, the individuals using five strategies tend to be equal.

When K > 1, we use numerical solutions to solve the problem. Using the fourth-order Runge–Kutta method with four stages, we find that if the number of neighbors is not more than 4, the individuals using five strategies tend to be equal. However, if the number is greater than 4, the five densities fluctuate periodically.

The larger the number of neighbors, the larger the amplitude and the longer the period. That is to say, the greater the number of neighbors of an individual that consider changing their strategies, the greater the difference between five strategies. The difference leads to the periodic fluctuation.

Considering the spatial structure, we use cellular automata to simulate the system on a two-dimensional lattice. We find that the number of neighbors has a huge influence on the system. In a Moore neighborhood model and triangular lattice model, self-organizing spiral waves emerge when the system is stable.

As shown in previous studies, the migration rate is the key factor that can lead to self-organization patterns [30,42]. However, in our model, we find a mechanism to produce self-organization patterns. This is interesting. It should be noted that there are no self-organization patterns in the Von Neumann neighborhood, K = 4.

Although spiral waves were found in this cellular automaton simulation, we do not quite understand the mechanism that produces the waves, which merits future study. Our model can be applied to systems with six or more strategies, which may also be worth studying.