1. Introduction
In the design of new generation electronic devices, the modern micro- and nanoelectronics industry has an increasing need for mathematical models to simulate devices before they are realized in the laboratory. In particular, the accurate modeling of energy transport in semiconductors is necessary in order to describe high-field phenomena, such as hot electron propagation, impact ionization and heat generation in the bulk material. Semiclassically, the most effective way to describe these phenomena makes use of the semiclassical Boltzmann Transport Equation (BTE) [
1]. However, solving the BTE is a daunting computational task, both using an indirect stochastic approach by Monte Carlo methods and direct numerical schemes based on discontinuous Galerkin methods or finite differences [
2]. This is the reason why, in many cases, it is desirable to have simpler macroscopical models, known as hydrodynamical-like models, which are highly useful for computer aided design (CAD) purposes. These models are obtained from the infinite set of moment equations of the BTE by a suitable truncation procedure. It is well-known that a closure assumption is required in order to have a closed system of evolution equations. In the past, various closure assumptions have been made for the semiconductor transport moment systems, leading to various classes of hydrodynamical models, see e.g., [
3,
4,
5]. However, these various closure assumptions are, at best, only phenomenological and often a consistent physical and mathematical justification is lacking. Lately, a closure assumption based on the Maximum Entropy Principle of extended thermodynamics [
6,
7] has been successfully applied, both in the parabolic and non-parabolic band approximation, to various types of semiconductors [
8,
9,
10,
11,
12,
13]. The resulting models, which differ for the choice of the moments to assume as field variables, are, in fact, able to describe charge transport due both to electrons and holes and also heat transport due to phonons. All the main scattering mechanisms between carriers and phonons and among phonons themselves are taken into account. The models also have nice mathematical properties, being symmetric hyperbolic. In particular, this assures the well-posedness of the Cauchy problems and the finite velocity of the propagation of disturbances [
14].
Due to the increasing shrinking of modern device dimensions, quantum effects are beginning to play a relevant role in charge transport. In the framework of the moment method and of Maximum Entropy Principle (MEP), a strategy to take into account these effects has been proposed in [
15] and consists of using the moment system arising from the Wigner equation. The starting point is to expand the Wigner function and the relative transport equation with respect to the squared reduced Planck constant
. The zero-order part of the collision operator is supposed to be the same as the semiclassical one, while the first-order contribution is supposed to act only on the
correction of the Wigner function and is modeled in a relaxation form. Therefore, at zero order, the Wigner function is given by the solution of the semiclassical Boltzmann equation, which is approximated with the standard maximum entropy method, while the
order correction is obtained with a Chapman–Enskog expansion in the high field scaling.
In the description of charge transport in some devices, such as double gate metal oxide semiconductor field effect transistors (DG-MOSFETs), where quantum effects are relevant only along one direction, called the confinement or transversal direction, another strategy can be used. One can adopt a quasi-static description along the confining direction based on a coupled Schrödinger–Poisson system which leads to a subband decomposition of the electron energy levels, while the transport along the longitudinal directions can be described by a semiclassical Boltzmann equation for each subband [
16]. Therefore, a complete description can be done in terms of a coupled Schrödinger–Poisson–Boltzmann system. However, the numerical integration of the transport part, which has been performed by employing Monte Carlo or deterministic methods [
16,
17], is also in this case very expensive, from a computational point of view, for CAD purposes. Consequently, it can be convenient to substitute the Boltzmann equations with macroscopic models again obtained by using the moment method and closing the moment equations with MEP [
18,
19,
20].
In this paper, we will give a review of all the above-mentioned models according to the following plan. In
Section 2, the 3D semiclassical macroscopic models are presented, showing how they are closed by using MEP and in
Section 3 their quantum correction is discussed. In
Section 4, the case of quantum confinement is described. Eventually in
Section 5, some numerical simulations are sketched.
2. The 3D Semiclassical Macroscopic Models
In the semiclassical description, roughly speaking, the charge and heat transport in semiconductors can be described by modeling them as consisting of a mixture of gases of electrons and phonons. As regards electrons, those which mainly contribute to the current flow occupy states near to the lowest minima of the lowest conductions bands and to the highest maxima of the highest valence bands. The latter contribution can be conveniently treated in terms of pseudo-particles called holes (missing electrons), which have electric charge, crystal momentum and energy opposite to those of the missing electrons in the considered valence band [
1,
21,
22]. An electron/hole population for each neighborhood of the lowest/highest minima/maxima of the lowest/highest conduction/valence bands is taken into account. The neighborhoods of the minima/maxima are usually called valleys. The electron/hole state is characterized by the index of the band it occupies, by its wave vector and spin state.
The dependence of the carrier energy on the wave vector in each valley can be analytically approximated by non-parabolic dispersion relations of the following form [
1,
9]
where
is the carrier energy in the
A-th valley measured from the bottom of the valley, the index A running over the considered valleys,
is the carrier quasi-wave vector, referred, for each valley, to the minimum or maximum of the valley [
1],
,
is the non-parabolicity factor, and
is the free electron mass.
For electrons, if one uses the ellipsoidal approximation, the dependence of
on
is given by
where
are the diagonal elements (eigenvalues) of the inverse effective mass tensor of the A-th valley, multiplied by
, referred to an orthonormal basis of the tensor.
Analogously, for holes, one has
in the case of warped bands, with
φ and
θ the azimuthal and polar angle of the wave vector respectively, and
,
and
inverse valence band parameters.
In the analytic approximations, for each valley, the domain of the wave-vector is extended to all
and the volume element in the
-space can be written as (henceforth we omit the valley index unless there is a possibility of confusion)
where the prime denotes a derivative with respect to the argument of the function, and
is the solid angle element. The charge carrier velocity, given by
, has the following expression in terms of the energy and the angular variables
Similarly, for phonons that are used to describe the crystal vibrations and strongly influence charge transport, one population for each branch has to be considered [
23]. The number of branches is equal to
,
ν being the total number of atoms per unit cell of the crystal lattice, and
a is the lattice constant. Among the most used analytic approximations for the phonon dispersion relation, we report the one which is isotropic and quadratic in the phonon wave vector
where
is the phonon energy,
and
,
, are suitable constants depending on the material under consideration, and
p varies over the
phonon branches. The Einstein and the Debye approximations are particular cases of (2), respectively obtained for
and
.
At the kinetic level, the state of the electrons, holes and phonons can be described by their one-particle distribution functions
,
(electron),
h (hole),
indicating the valleys occupied by
β-carriers (
), and
, with
, whose time evolution is determined by the Boltzmann–Bloch–Peierls (BBP) system (see [
24] and references therein)
where
is the charge of the particles,
with
q absolute value of the elementary charge,
is the complement of
β with respect to the set
is the phonon group velocity,
is the material permittivity,
V and
are the electric potential and field,
η labels the type of scattering among phonons themselves (see below),
and
are the acceptor and donor concentrations, while
n is the total electron density
and
p the total hole density
The Boltzmann Equation (3A) is coupled among them through the Poisson Equation (3C) and some of the collision operators which appear at the right-hand side of (3A) and (3B).
The operator
[
1] takes into account scatterings between carriers and impurities and is elastic and intravalley, which means that the initial and the final state of the carrier lie in the same valley. Its form is
the impurity scattering transition rate being given by
with
the inverse Debye length and
, where
Z is the impurity charge number,
the lattice temperature and
the Boltzmann constant. According to whether interactions with donors or acceptors are considered,
or
, and
or
have to be taken.
The collision operators
describe interactions between carriers of the same type and phonons. These scatterings can be intravalley (intraband) (
), or intervalley (intraband or interband) (
) [
1], which means that the initial and final state belong to different valleys. These operators read [
24]
where
is the sphere of radius
, which approximates the first Brillouin zone
in the case of isotropic approximations for the phonon dispersion relations, and, for example, the integrands are given by
being the
p-phonon density of states,
δ the Dirac delta function, and
a vector of the Brillouin zone, whose presence is due to the fact that the total wave vector is conserved up to it. The scattering functions
are characteristic of the type of interaction of carriers, for example with acoustic and non-polar optical phonons for elemental semiconductors such as Si and Ge, and also with polar optical phonons for compound semiconductors, such as GaAs and SiC. The previous expressions of the scattering rates
w are valid in the case when only conduction electrons are involved; for all the other cases as well as for the expressions of the scattering functions, we refer the interested reader to [
1,
8,
9].
The generation-recombination collision operators
include several mechanisms, among which the most important are the Auger and the Schockley–Read–Hall (SRH) processes. In a relaxation time approximation and in the simpler case of a single conduction and a single valence band, the operators read [
25]
where
or
p according to whether the A-th valley is populated by electrons or holes, the
’s are the Maxwellians normalized to unit,
and
are the Auger electron and hole constant coefficients,
and
are the carrier lifetimes, and
is the intrinsic concentration [
1].
The collision operators which appear in the Boltzmann–Peierls equations for phonons, relative to their interactions with carriers, read [
24]
The other interactions of phonons can be distinguished into intrinsic ones, arising from the anharmonicity of the interatomic forces, and extrinsic ones, due to phonon scatterings at the boundaries of the crystal and at various types of crystal defects and imperfections. In their turn, the anharmonic scatterings can be normal processes (
N-processes), in which the phonon total momentum after the interaction is conserved, and umklapp processes (
U-processes) for which the total momentum changes by a reciprocal lattice vector multiplied by
ℏ after a collision. On the other hand, all extrinsic processes do not conserve the total momentum after a collision and, together with the umklapp ones, are usually called resistive processes. For the expressions of the corresponding collision operators, we refer the interested readers to [
23] and references therein.
Macroscopic models can be constructed starting from the BBP system by taking a suitable number of moments of the distribution functions [
14]. The most common choice is that of considering the following functions of the carrier and phonon wave vectors
and
, to which the following macroscopic state variables correspond:
which are the carrier number densities, the average energies, velocities and energy-fluxes per carrier, and the phonon average energies and energy-fluxes, respectively. The above choice involves the minimal number of moments necessary for describing the thermal energy transport, but this number, if required by the physical problem under study, can be easily extended to cover, for example, an arbitrary number of scalar and vector moments both for carriers and phonons, by taking into account, e.g., higher microscopic energy powers in the functions
ψ [
7,
26].
The evolution equations for the state variables (7) and (8) can be obtained directly from the Boltzmann equations by integration:
In the above equations, the extra-fluxes and production terms relative to charges respectively read
with
, while for the phonons, we have
In the evolution equations, the number of the unknowns is greater than that of the equations, therefore constitutive equations are needed for the extra-variables
,
,
. A systematic way to find these relations is founded on a universal physical principle: the maximum entropy principle [
6,
14,
27,
28]. It states that, if a certain number of moments is known, then the least biased distribution functions, which can be used for evaluating the unknown moments, are those maximizing the total entropy functional under the constraint that they reproduce the known moments. In the case under consideration, neglecting the mutual interactions among the subsystems and degeneration effects (the degeneracy case can be tackled in the same way; we present the non-degenerate case only for the sake of simplicity), the total entropy is
with
the charge density of states, while the constraints are given by (7) and (8). Let us introduce the functional spaces
Given the values of the moments
and
, MEP amounts to solve the following optimization problem:
under the constraints
where time and position are considered fixed and omitted for the sake of simplifying the notation. The solution of this maximization problem is given by [
29]
which, linearized with respect to the vector variables (small anisotropy assumption) [
8,
9,
27], becomes
where the Λ’s are Lagrange multipliers, related to the state variables by means of the constraint relations (7) and (8). Linearization is made in order to simplify the inversion of the constraints, otherwise it has to be done numerically [
29]. After inversion, the dependence of the distribution functions on
will only be through the state variables, and substituting the distributions into the integrals defining the extra-variables, the needed closure relations can be obtained. It can be proven that the balance equations with the closure relations given by MEP form a quasilinear hyperbolic system in the relevant physical region of the field variables.
Following this procedure, mathematical models for the description of charge transport in unipolar and bipolar silicon devices have been constructed, see for example [
10,
30], while results relative to Si thermal properties can be found in [
23,
31]. The procedure has also been applied to compound semiconductors such as GaAs, GaN and SiC [
8,
9].
3. Quantum Corrections to the Semiclassical Models
Based on the previous considerations, a natural way to get a quantum macroscopic model is to use MEP in a quantum framework to close the moment system arising from the Wigner equations. The general guidelines can be found in [
32,
33]. This approach has been followed in [
34] (see also [
35] and references therein). However, one has to deal with operatorial equations which are very complex and therefore hard to be solved numerically. Moreover, drastic simplifications of the collision terms are introduced in order to make the problem tractable.
Another strategy can be adopted to close the moment system arising from the Wigner equation. According to this strategy, the Wigner function and the relative transport equation are expanded with respect to . The zero-order part of the collision operator is supposed to be the same as the semiclassical one, while the first-order contribution is supposed to act only on the correction of the Wigner function and is modeled in a relaxation form. Therefore, at the zero order, the Wigner function is given by the solution of the semiclassical Boltzmann equation, which is approximated with the standard maximum entropy method, while the order correction is obtained with a Chapman–Enskog expansion in the high field scaling.
The typical physical situation which can be described in this way is that when the main contribution to the charge transport is semiclassical, the quantum effects enter as small perturbations. For example, this is reasonable for devices such as MOSFETs of characteristic length of about ten nanometers subjected to strong electric fields.
The main assumption is that there is a balance between the drift and collision terms. This can be motivated by the fact that the collision frequency of the semiclassical scatterings tends to increase as the energy rises. Therefore, quantum effects are expected to be relevant at high fields; in such conditions, there should be high energies with consequently high collision frequencies.
The starting point for our derivation of the quantum corrections to the semiclassical model is the single particle Wigner–Poisson system, which represents the quantum analogue of the semiclassical Boltzmann–Poisson system (for the sake of simplicity, only the case of a single valley in the conduction band is considered),
where
is the electron effective mass, the potential
V usually is the sum of a self-consistent part
, solution of the Poisson equation, and an additional part which models the potential barriers in heterostructures. The unknown function
, depending on the position
, crystal momentum
and time
t, is the Wigner quasi-distribution, defined as
Here,
is the density matrix, which is related to the wave function
by
The operator
denotes the Fourier transform, given for a function
by
with
i the imaginary unit, and
denotes the inverse Fourier transform
The terms
and
represent the pseudo-differential operators
As is well known,
is not in general positive definite. However, it is possible to calculate the macroscopic quantities of interest as expectation values (moments) of
in the same way as in the semiclassical case, e.g.,
The operator
represents the quantum collision term. Its formulation is itself an open problem. Some attempts can be found in [
36,
37], but a derivation suitable for applications in electron devices is still lacking. In [
15], an expression has been proposed which is a perturbation of the semiclassical collision term, useful for the formulation of macroscopic models.
As a general guideline,
should drive the system towards the equilibrium. Let us consider the electrons in a thermal bath at the lattice temperature
. The equilibrium Wigner function
for an arbitrary energy band, up to
terms, reads [
38,
39]
where
We suppose that the expansion
holds. By proceeding in a formal way, as
the Wigner equation gives the semiclassical Boltzmann equation
While, at the first order in
, we have (Einstein’s convention is used: summation with respect to repeated dummy indices is understood.)
with
to be modeled. We make the following
Remark 1. At variance with other approaches, only the correction to the collision term has a relaxation form. This assures that as one gets the semiclassical scattering of electrons with phonons and impurities. We note that and therefore the semiclassical expression of the collision term makes sense.
The value of the quantum collision frequency ν is a fitting parameter that can be determined by comparing the results with the experimental data.
We require that conserves the electron density, that is we make the following
Proposition 1. The collision operator of the form (24) satisfies up to terms , the following properties:- 1.
is given by the quantum Maxwellianwith the classical Maxwellian. - 2.
- 3.
Moreover, the equality holds if and only if w is the quantum Maxwellian, defined above.
Properties 1 and 3 are straightforward. Property 2 is based on the proof in [
40,
41,
42] valid in the classical case.
3.1. Quantum Corrections in the High Field Approximation
In the case of high electric fields and effective mass approximation for the dispersion relation
it is possible to find an approximation for
by a suitable Chapman–Enskog expansion. Let us introduce the dimensionless variables
with
,
and
the typical length, time and velocity. Let
be the characteristic length of the electrical potential and
the characteristic collision frequency. After scaling the collision frequency according to
, Equation (23) can be rewritten as
We will continue to denote the scaled variables as the unscaled ones in order to simplify the notation.
Let us introduce the characteristic length associated with the quantum correction of the collision term (a kind of mean free path in a semiclassical context)
Let us assume that the quantum effects occur in the high field and collision dominated regime, where drift and collision mechanisms have the same characteristic length. Therefore, we set formally
and observe that, in the high frequency regime, the Knudsen number
is a small parameter. Substituting it in the previous equation, we get
The zero order in
α gives
and by Fourier transforming, one has
Approximating
with MEP distribution function, we obtain
For example, in the 8-moment case, using the
found in [
10], the following explicit approximation for the Wigner function is obtained
which can be used for evaluating the unknown quantities in the moment system, associated with the Wigner equation. The vectors
and
represent the velocity and the energy-flux at zero order in
.
3.2. The Quantum Moment Equations
In analogy with the semiclassical case, multiplying (13) by suitable weight functions
ψ, depending, in the physically relevant cases, on the velocity
, and integrating over the velocity space, one has the balance equations for the macroscopic quantities of interest
In the 8-moment model, the basic variables are the macroscopic density, velocity, energy and energy-flux, that are the moments relative to the weight functions 1, , , .
By evaluating (31) for
, under the assumption that the necessary moments of
and
with respect to
exist, one has
obtaining the continuity equation
In order to get the other moment equations, we observe that from (27) it follows that
for any weight function
such that the integrals exist.
By taking into account (33), multiplying Equation (13) by the weight functions
,
,
, and after integration, one finds the balance equations for velocity, energy and energy-flux
Here,
,
and
are the zero-order components of the average velocity, energy and energy-flux. The components of the flux of the velocity and the flux of the energy-flux are defined as
The production terms are defined as
Remark 2. The quantum corrections affect only the free streaming part, while the drift and production terms appear only at the zero order.
Therefore, , and are the same as in the semiclassical case.
In the system (32), (34)–(36) are not closed for the presence of the unknown quantities , , , and . We solve the closure problem with the approximation (29), assuming a collision dominated high field regime for the quantum effects.
In order to evaluate the unknown quantities present in the moment equations, the following formal lemmas are useful
The proof follows by a simple computation. With the aid of these lemmas, we get the following closure relations:
In the previous relationships, parentheses indicate symmetrization, e.g.,
Remark 3. The zero order in is the same as that obtained in [10,30]. Remark 4. Sincewe havethat is the assumption (25) is fulfilled. Remark 5. In the limit of high frequency one has the simplified model From Equation (28), one sees that in the limit
,
reduces to the quantum correction of the equilibrium Wigner function
. The resulting quantum corrections to the tensor
are the same as those obtained in [
43] by using a shifted Wigner function, but with the semiclassical contribution which also contains a heat flux, not added ad hoc.
Remark 6. Under the assumption (see [43]) that the equilibrium relationis valid, one can recover a formulation of the quantum corrections of density gradient type. The density gradient version is more familiar because the quantum corrections take a form similar to the Bohm potential arising in the Madelung model of quantum fluids in the zero temperature limit. Moreover, some numerical experiments [
43] lead to it being considered more robust than the original formulation in terms of the derivatives of the electric potential. In the limit
, the closure relations in the density gradient form explicitly read as
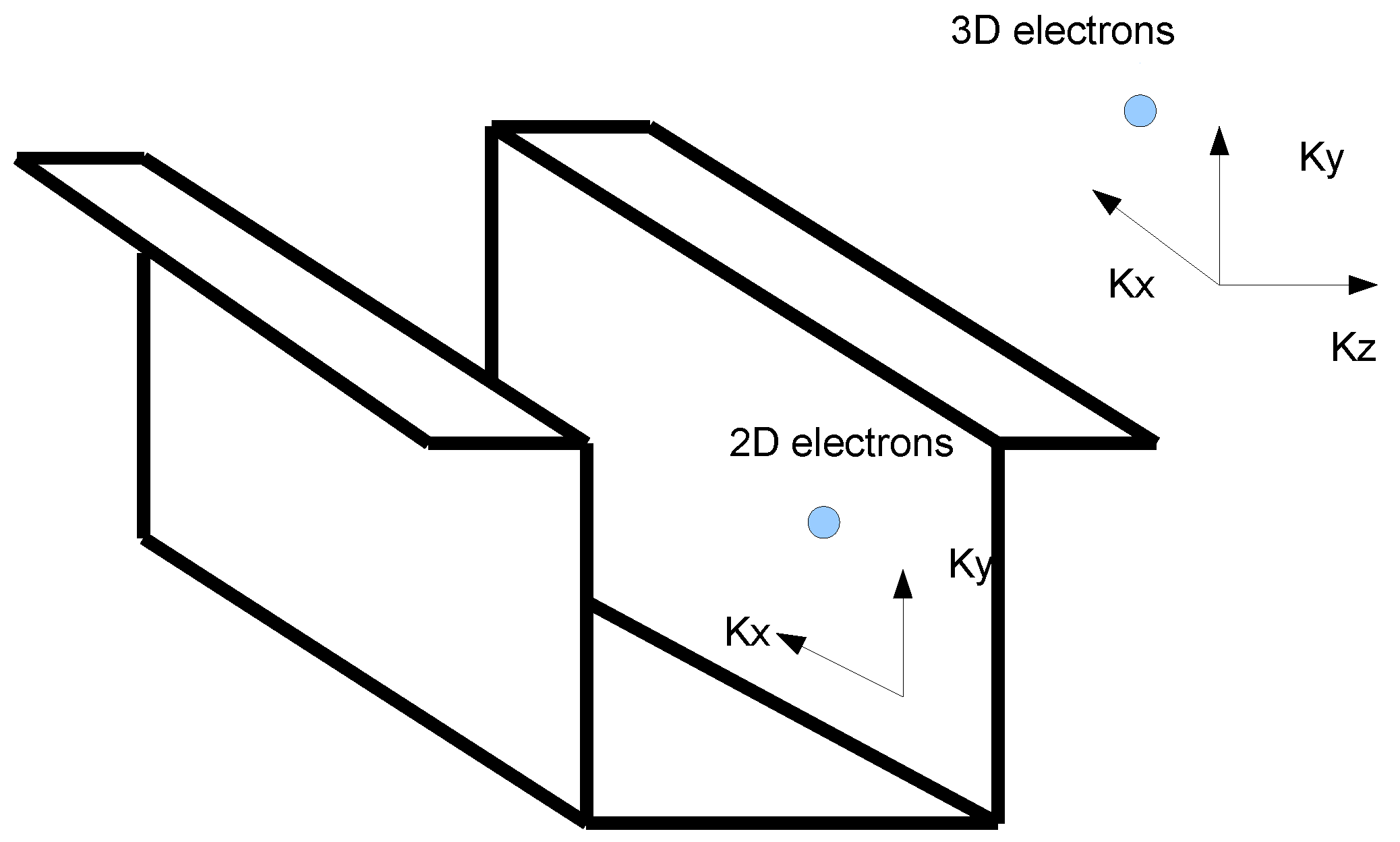
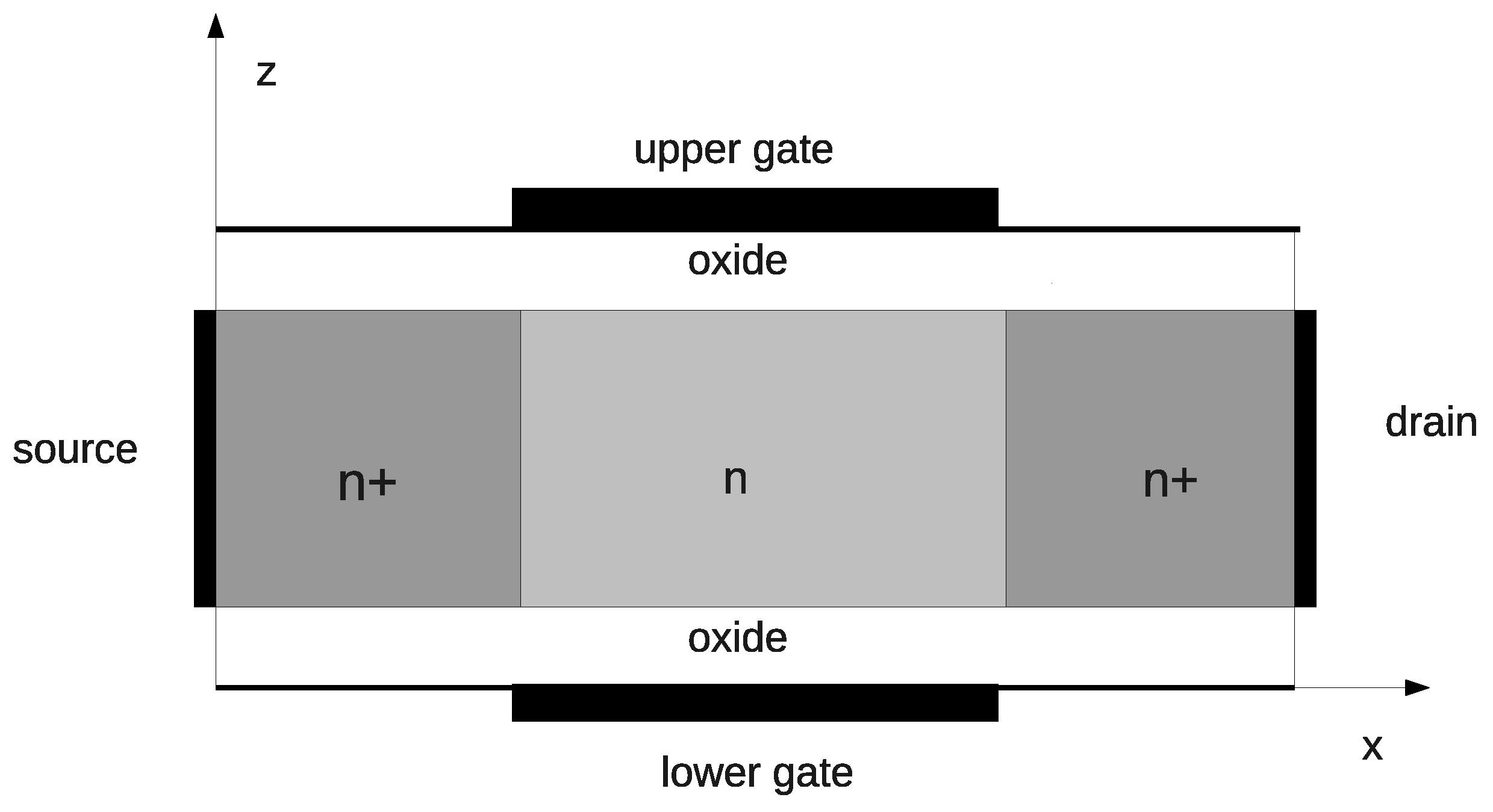
4. Two-Dimensional Electron Gases: The Case of Quantum Confinement
In this section, we consider the case of an ensemble of electrons (the treatment of holes would be analogous) confined along one dimension, called quasi 2Delectron gas (2DEG) [
16,
18,
19,
20,
44]. This situation arises when the length scale in one (the confined) space direction of the semiconductor device under study is of the order of de Broglie wavelength of electrons, while the nonconfined directions have a much bigger length scale. In other words, electrons are in a quantum regime in the confined direction and exhibit a classical behaviour in the nonconfined ones [
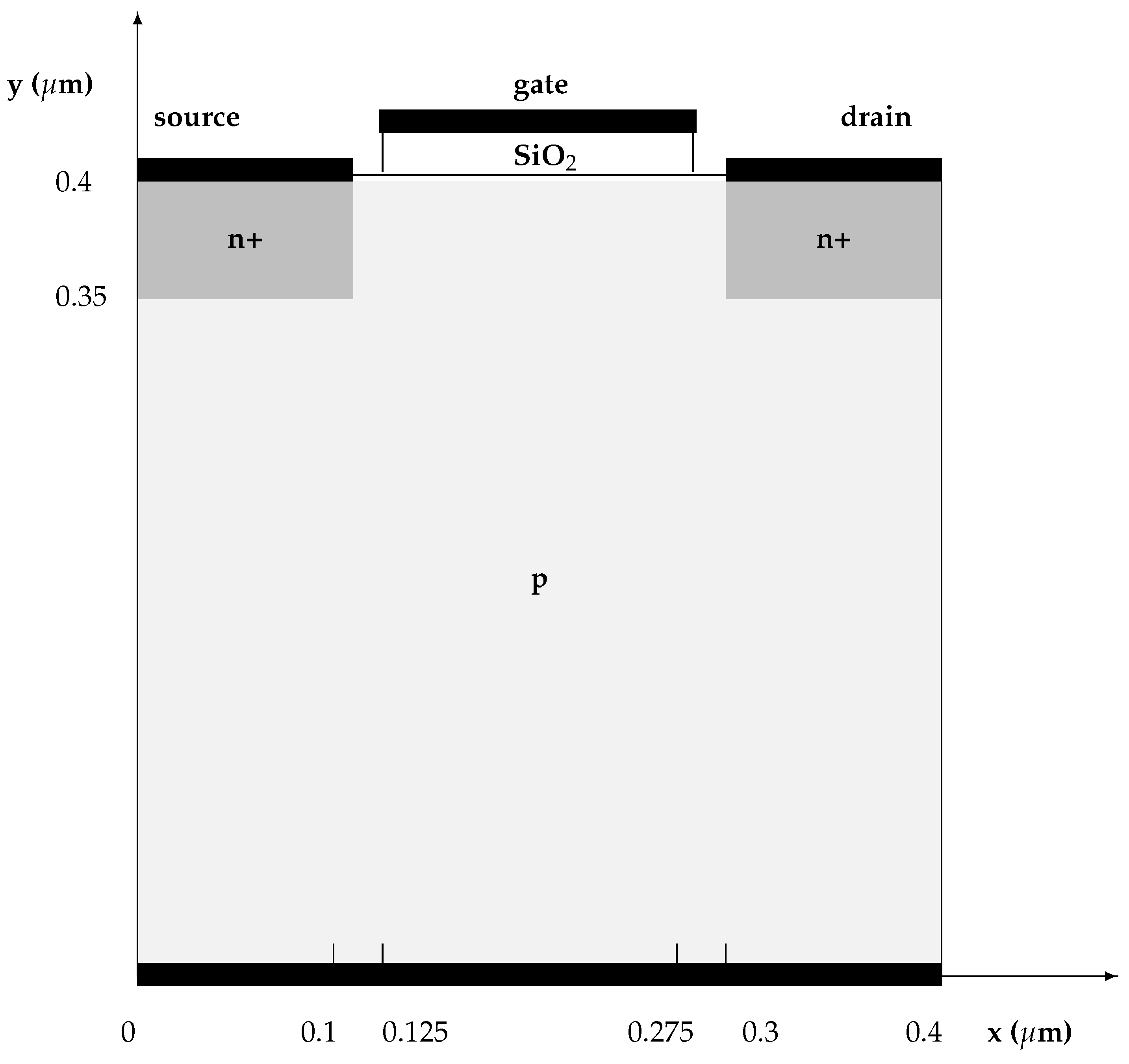
16] as shown in
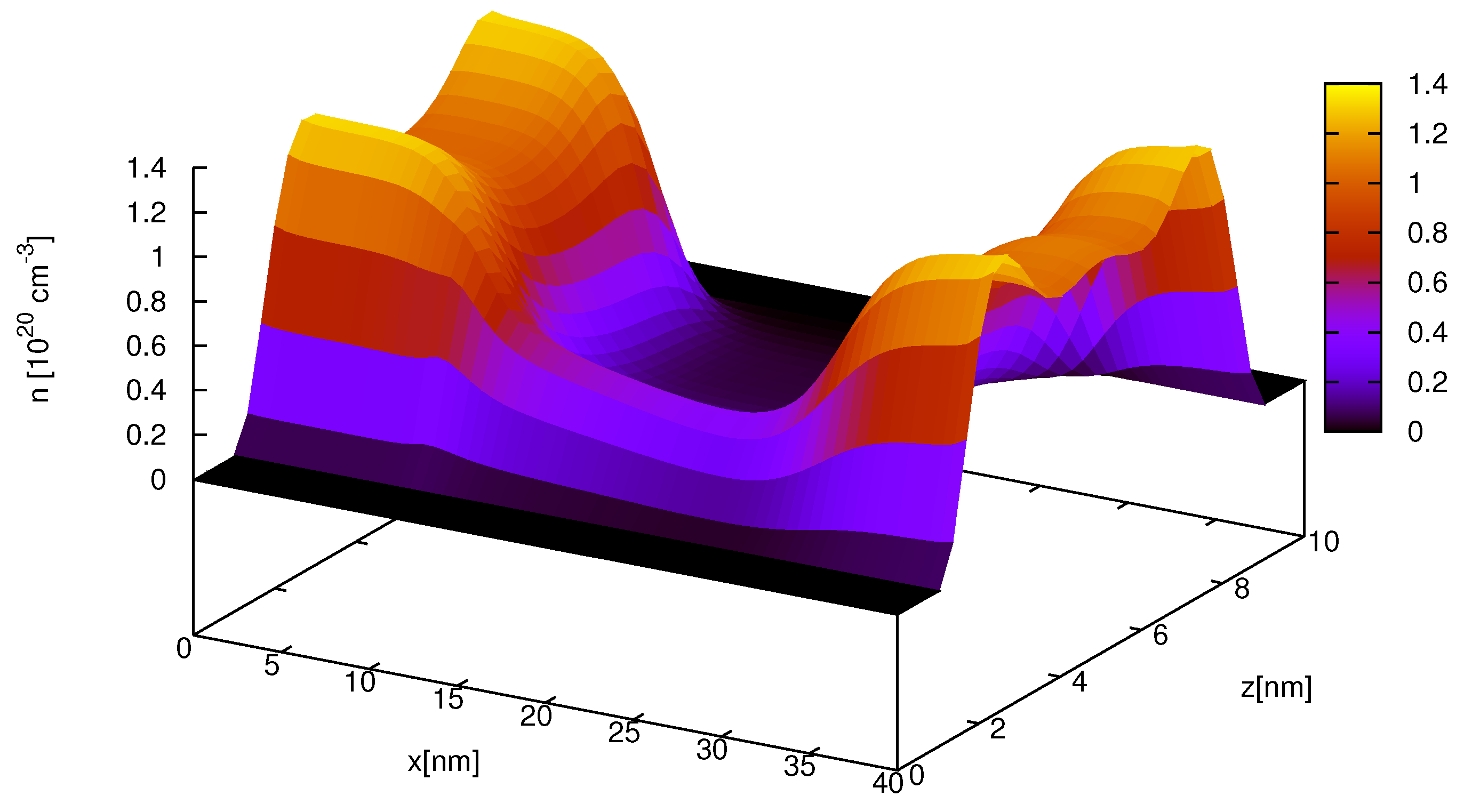
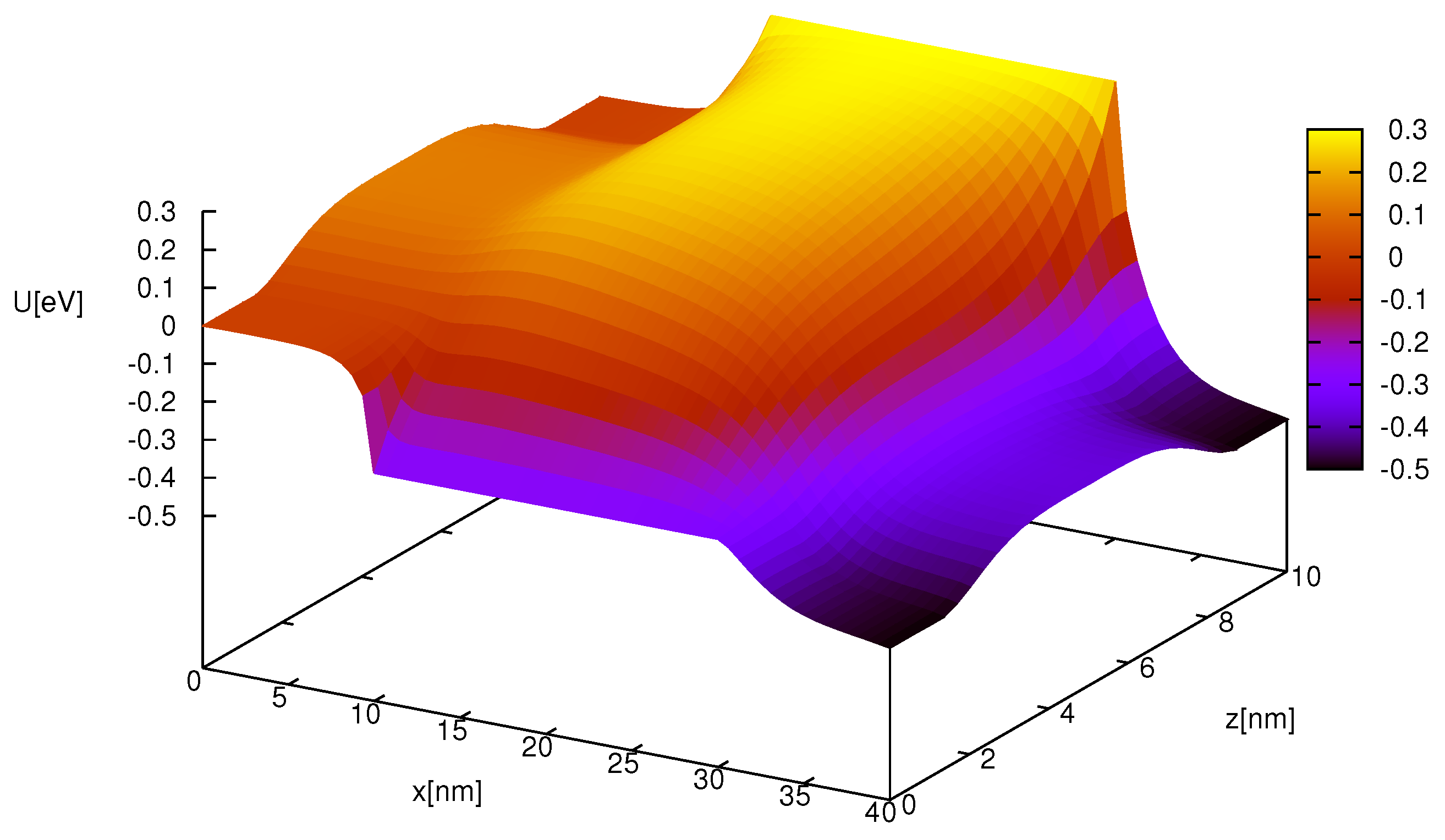
Figure 1.
Let us suppose that electrons are quantized along one direction, which we choose as the z direction, and free to move in the orthogonal x-y plane. Let be the spatial domain. Here, , , are fixed. More general cases with a variable confining direction can be easily incorporated.
Let us introduce the parameter
σ defined as the ratio between the transversal (perpendicular to the
x-
y plane) typical length scale
and the longitudinal typical length scale
and assume that
. Moreover, as is customary, let us assume the following ansatz about the electron wave function
with
and
denoting the longitudinal components of the wave-vector
and the position vector
, respectively, and
being the area of the
x-
y cross-section. The previous wave function is inserted into the stationary Schrödinger equation in the effective mass approximation
where
is the electron effective mass,
is the conduction band minimum,
, with
the confining potential and
the self-consistent electrostatic potential.
Under the assumption that the confining potential is so high that it gives rise to a barrier which can be considered infinite, it enters into the equations only through the boundary conditions
and
is taken.
Therefore, introducing the slowly varying variable
and inserting (62) into (63), one has
In the limit
, one formally gets that the envelope function
φ must solve the reduced Schrödinger equation
with boundary conditions
The solution of (64) and (65) depends only parametrically on
(and in a slow way), and more in general also on time
t if a non-steady-state solution is considered. In fact, electrons as waves achieve equilibrium along the confined direction in a time which is much shorter than the typical transport time, so that one can adopt a quasi-static description along the
z-direction. The couple (64) and (65) constitutes a one dimensional Sturm–Liouville problem, which admits a countable set of eigen-pairs (subbands)
, whose eigenvalues are simple and do not cross. The potential
V is obtained from the Poisson equation
where the electron density
n is given by
with
the (areal) density of electrons of the
νth subband and for simplicity an n–doped material has been considered. Of course, the Schrödinger and Poisson equations are coupled and must be solved simultaneously.
For devices with longitudinal characteristic length of a few tens of nanometers, the transport of electrons in the longitudinal direction is semi-classical within a good approximation. Therefore, electrons in each subband can be considered as different populations, the state of each of them being described by a semiclassical distribution function
, and electron transport along the longitudinal direction being determined by adding to the Schrödinger–Poisson system the following system of coupled Boltzmann equations
where
, and the electron energy in each subband
is the sum of a transversal contribution
and a longitudinal one
where
α is the non-parabolicity parameter. Consequently, the longitudinal electron velocity is
A formal justification of Equation (67) can be found in [
45]. Regarding the collision operator, in the non-degenerate approximation, each contribution has the general form [
18,
19,
20]
where
is the two-dimensional Brillouin zone. When
, the scattering is intra-subband; when
, it is the inter-subband. We recall that inter-subband transitions may also happen in the absence of phonons, by quantum mechanical tunneling induced by the presence of a static field as has been shown for example in [
46]. The term
is the transition rate from the longitudinal state with wave-vector
, belonging to the
μth subband, to the longitudinal state with wave-vector
, belonging to the
νth subband, and
. In Si, the relevant 2D scattering mechanisms are the acoustic phonon scattering, and the non-polar optical phonon scattering. Their expressions are the 2D version of those shown in
Section 2 and can be found in [
18,
19,
20,
47]. Attempts to directly solve the Schrödinger–Poisson–Boltzmann system can be found, for example, in [
16,
17,
48] where numerical schemes based on finite differences have been employed. However, the direct numerical approach is a daunting computational task and requires very long computing times. This has again prompted the development of simpler macroscopic models for CAD purposes. These models can be obtained as moment equations of the Boltzmann transport equations under suitable closure relations [
18,
19,
20]. The moment of the
ν-th subband distribution with respect to a weight function
reads
In particular, analogously to the previous cases, we take as basic moments
The corresponding moment system reads
where
Also in this case, the above written fluxes and production terms are extra-variables for which closure relations are needed. In order to employ MEP, a suitable expression of the entropy for the system under consideration has to be found. Neglecting the mutual interaction of electrons in different subbands, considering the phonon gas as a thermal bath and assuming the electron gas is sufficiently dilute, in each subband the expression of the entropy is the semiclassical limit of that arising from the Fermi statistics. Eventually, for obtaining the total entropy, one has to consider that electrons have a quantum behaviour along the
z-direction, therefore
we define the entropy density of the system asRemark 7. The proposed expression of the entropy has been introduced for the first time in [20,47]. It combines quantum effects and semiclassical transport along the longitudinal direction, weighting the contribution of each subband with the square modulus of the ’s arising from the Schrödinger–Poisson block. According to MEP, the
’s are estimated by means of the distributions
’s that
,
solve the problem:
where the
’s are the basic moments (69)–(72) and
is the space of the summable function with respect to
such that the moments appearing in the system (73)–(76) exist.
With the above choice of the functions
, the resulting maximum entropy distribution functions read (the factor
has been included into the multipliers)
In order to complete the procedure, similarly to the previous case, one has to insert the
’s into the constraints (69)–(72) and express the Lagrange multipliers as functions of the basic moments
,
,
,
. In general, in the case considered in this section as well as in that considered in
Section 2, it is not possible to assure that such a procedure can be accomplished. The solvability of the MEP problem depends on the band structure and on the choice of the moments, as well known already in gas-dynamics [
14,
49]. For example, if the parabolic case (where the energy is a quadratic function of the wave vector) is considered, the same drawbacks of classical gas-dynamics arise regarding the lack of integrability of the MEP distribution function. In the case of the Kane dispersion relation, the solvability of the MEP problem is guaranteed by the following property, proven in [
49].
Proposition 3. When the Kane model for the energy band is employed, the corresponding maximum entropy models are symmetric hyperbolic systems with convex domains of definition and the equilibria are interior points, guaranteeing the validity of expansions around equilibrium states.
The proof has been given for a 3D electron gas, but it can be extended to a 2DEG in a straightforward way.
For the 2DEG case, the final expressions of the extra-fluxes and production terms, obtained by using linearized MEP distribution functions, can be found in [
18,
47] for the parabolic approximation and in [
19,
20] for the non-parabolic one. The resulting moment system has been used to simulate double-gate MOSFETs in [
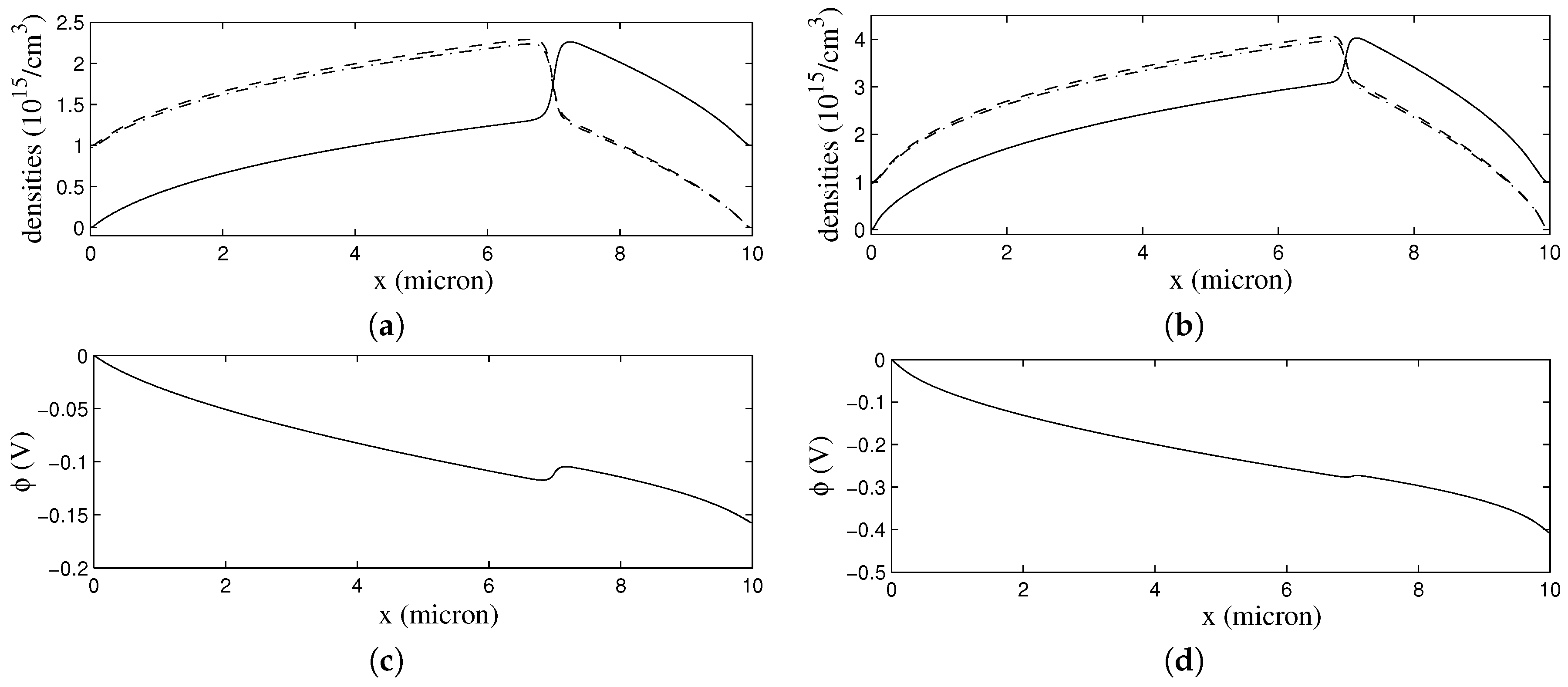
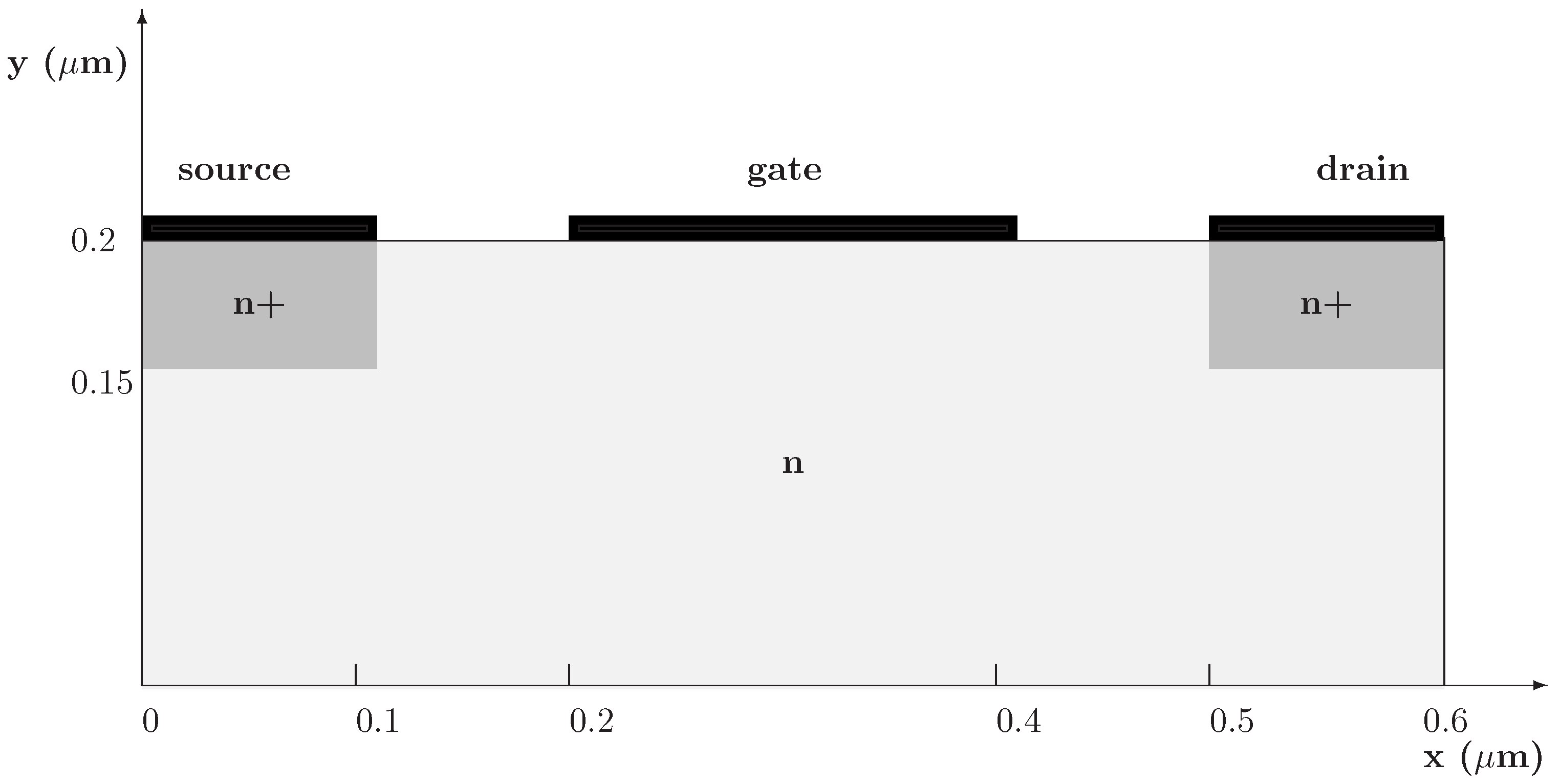
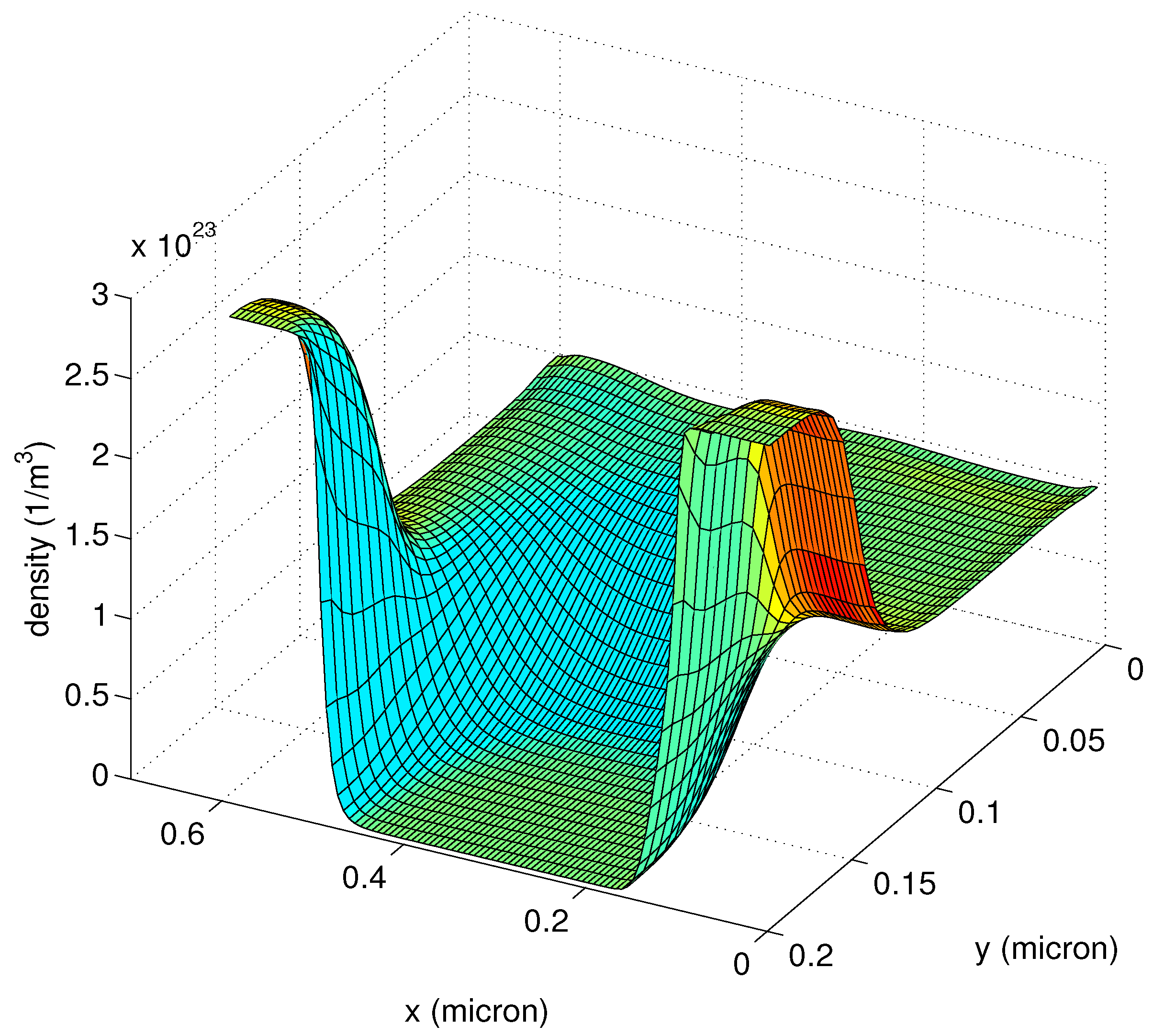
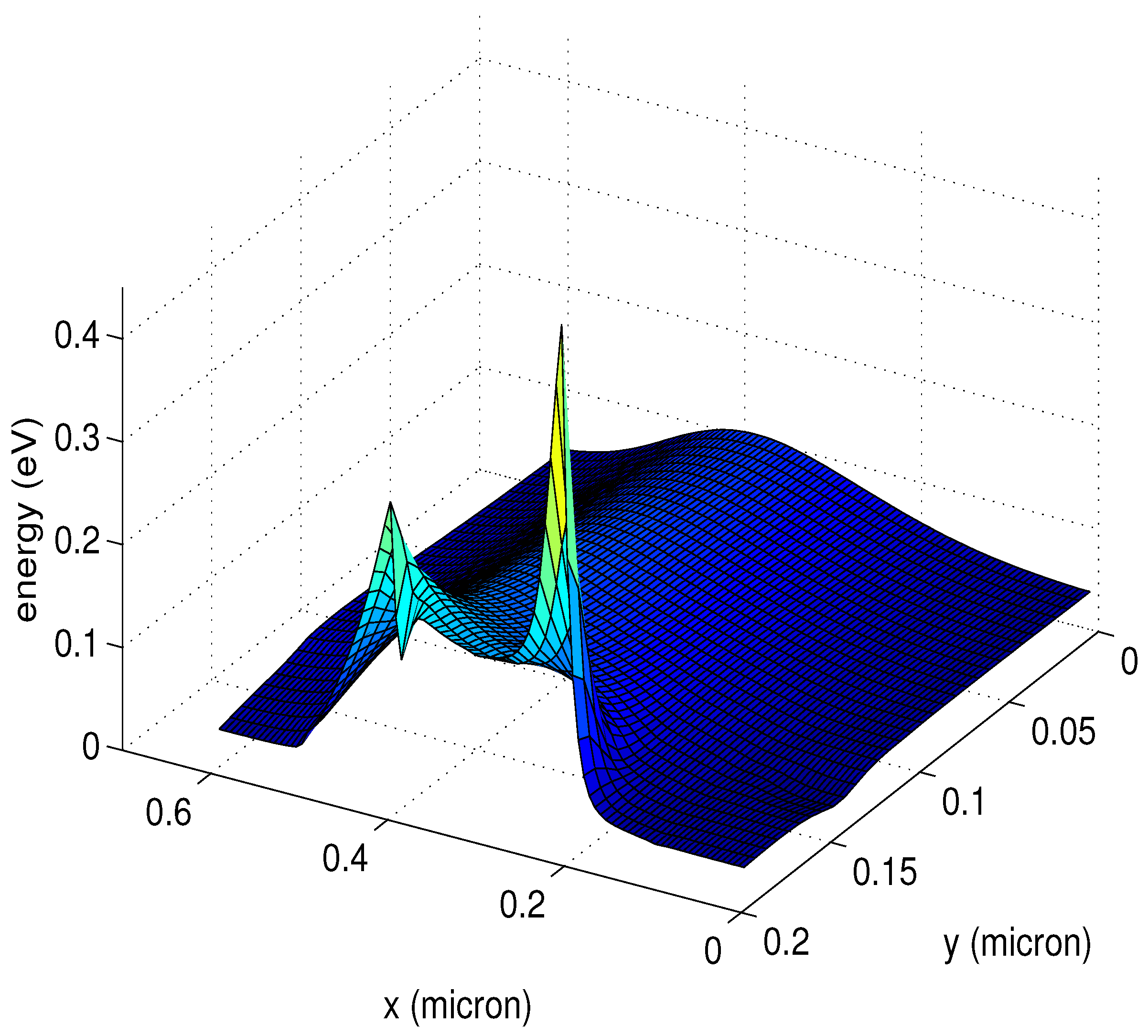
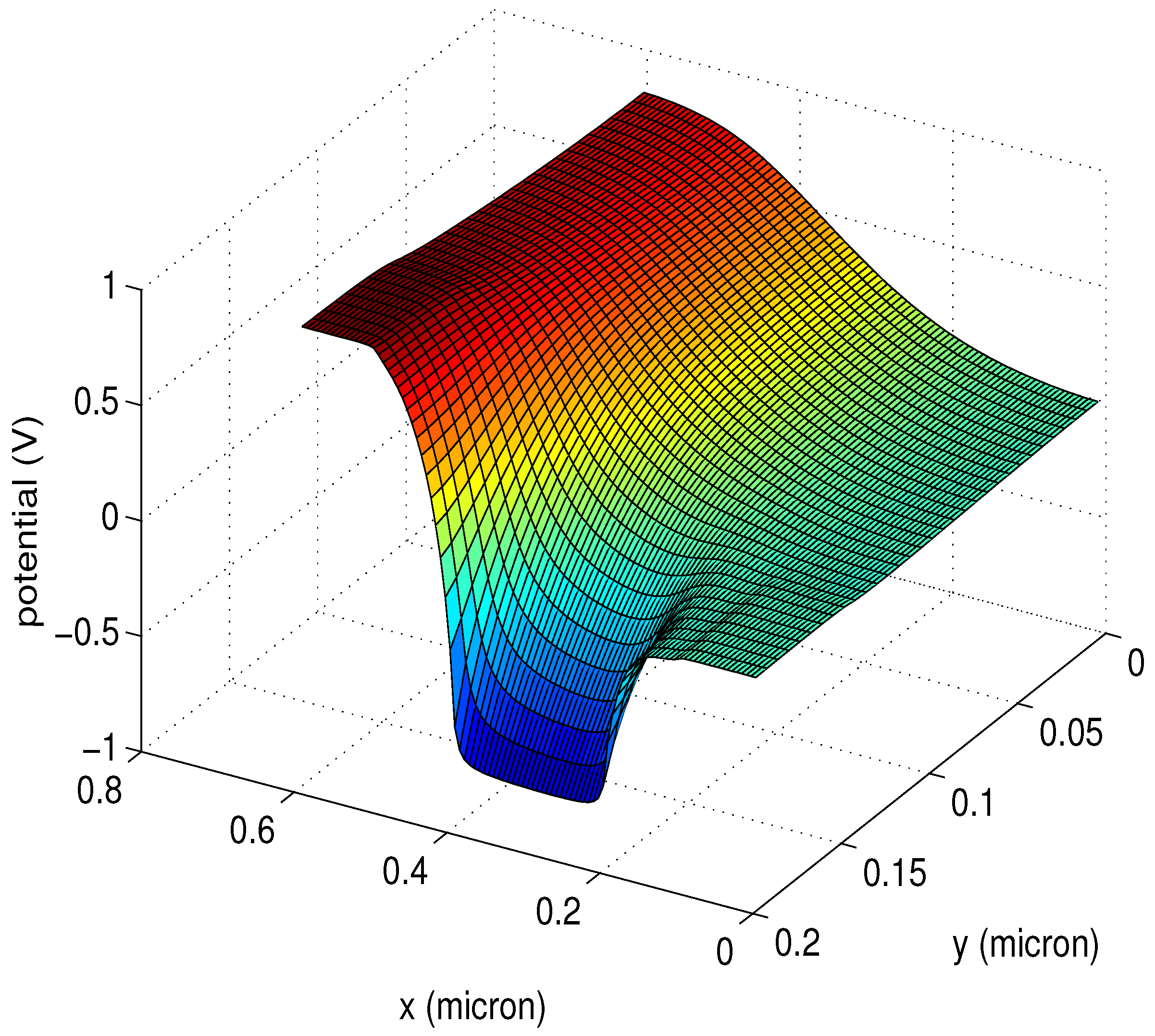
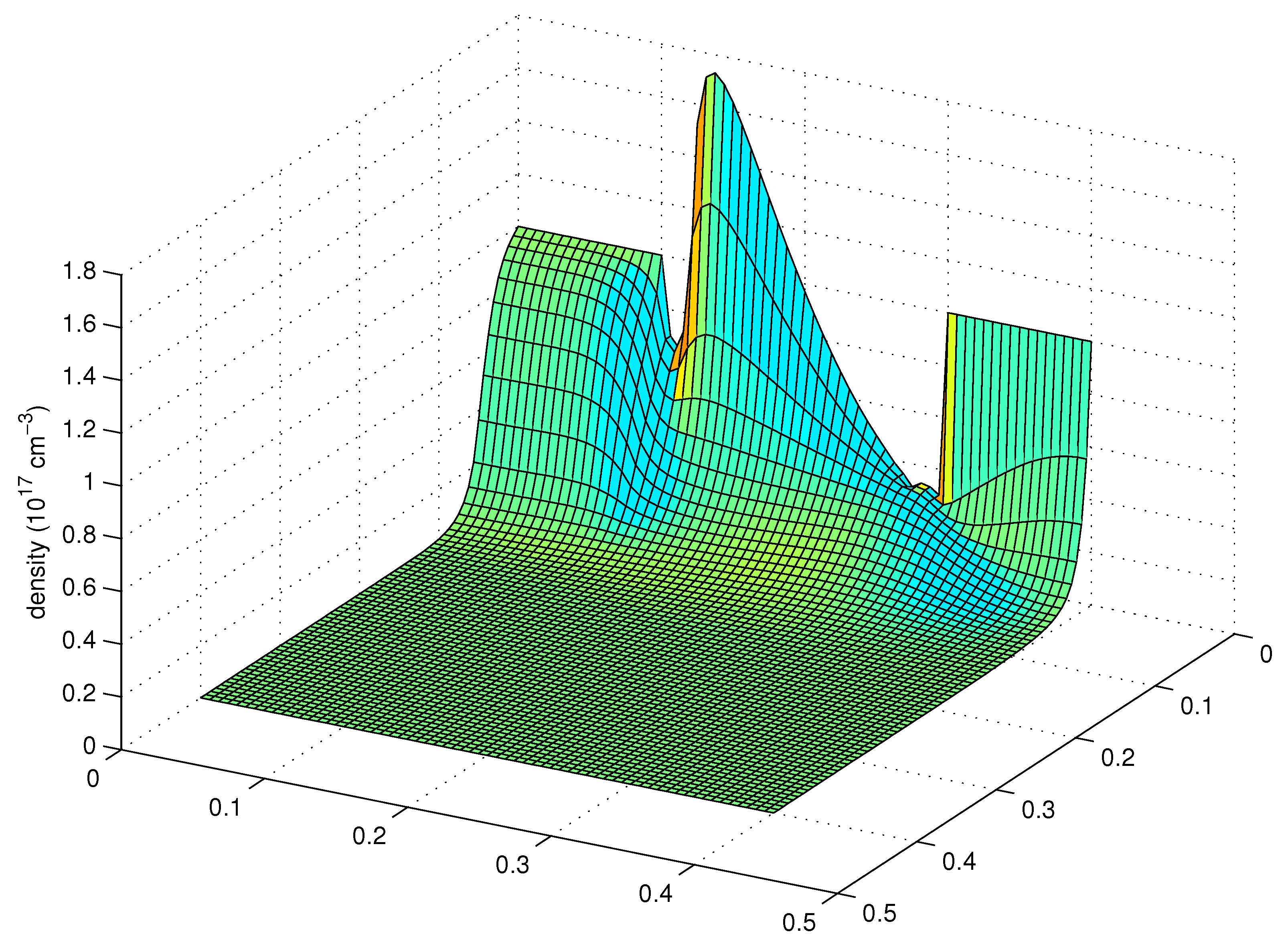
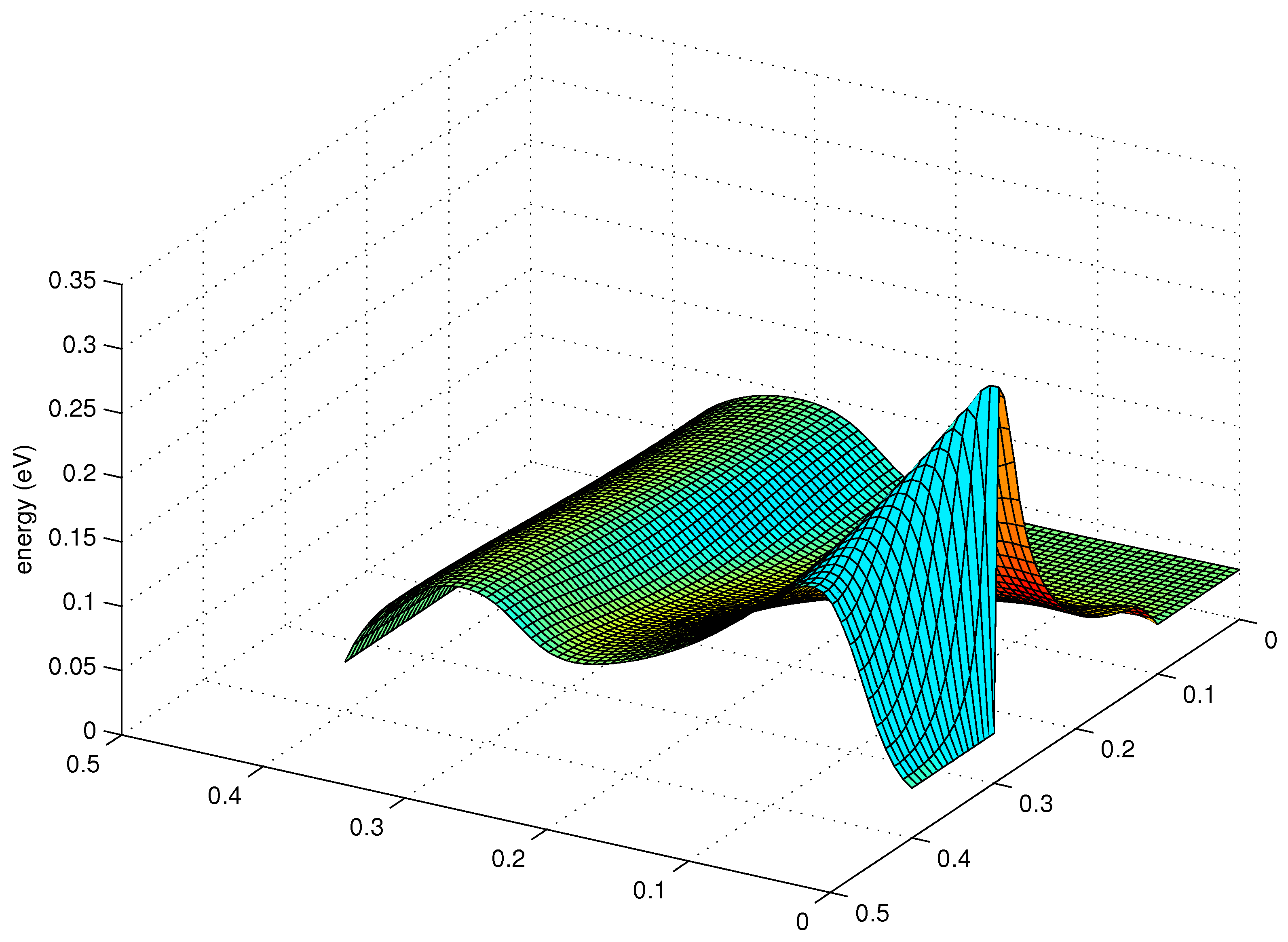
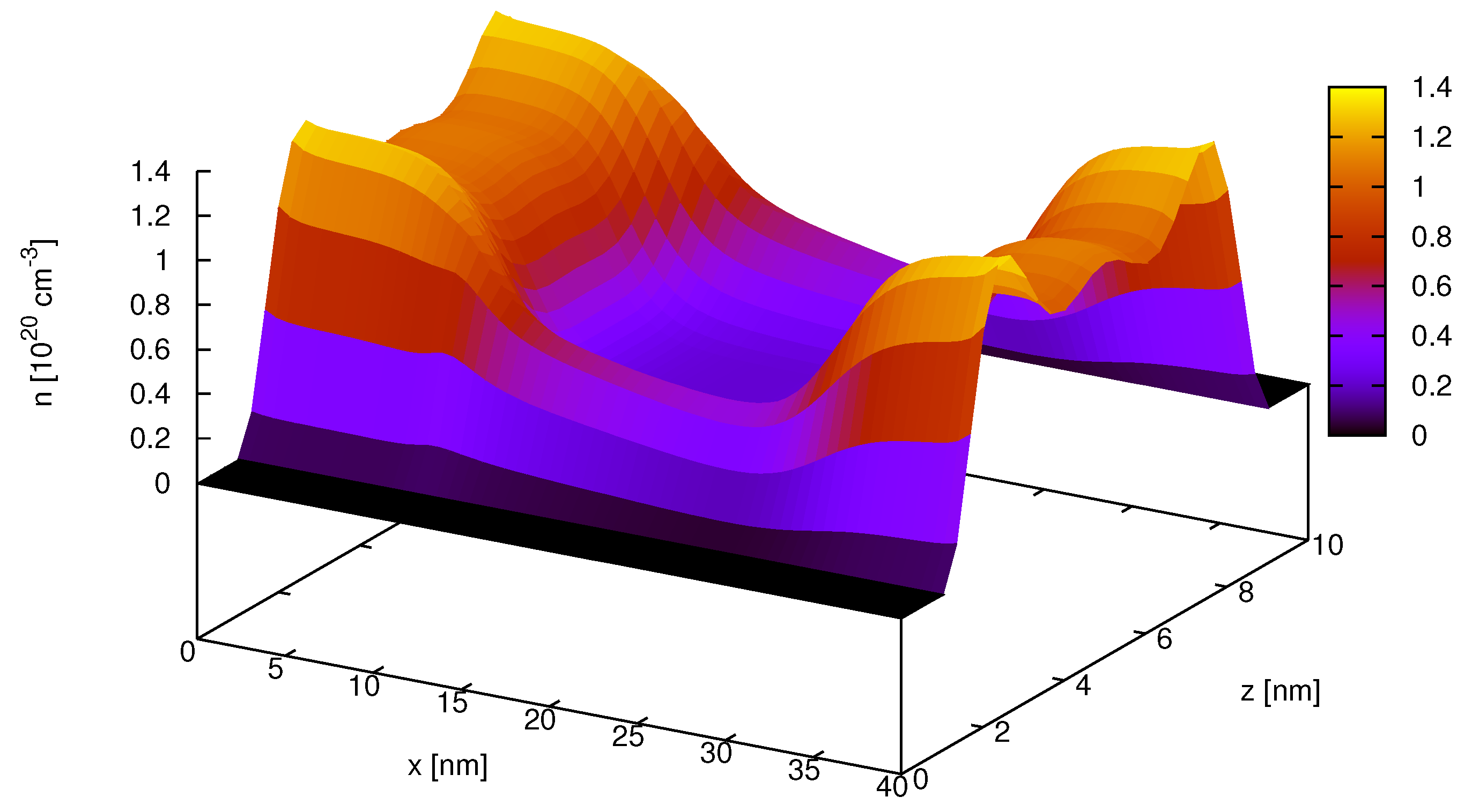
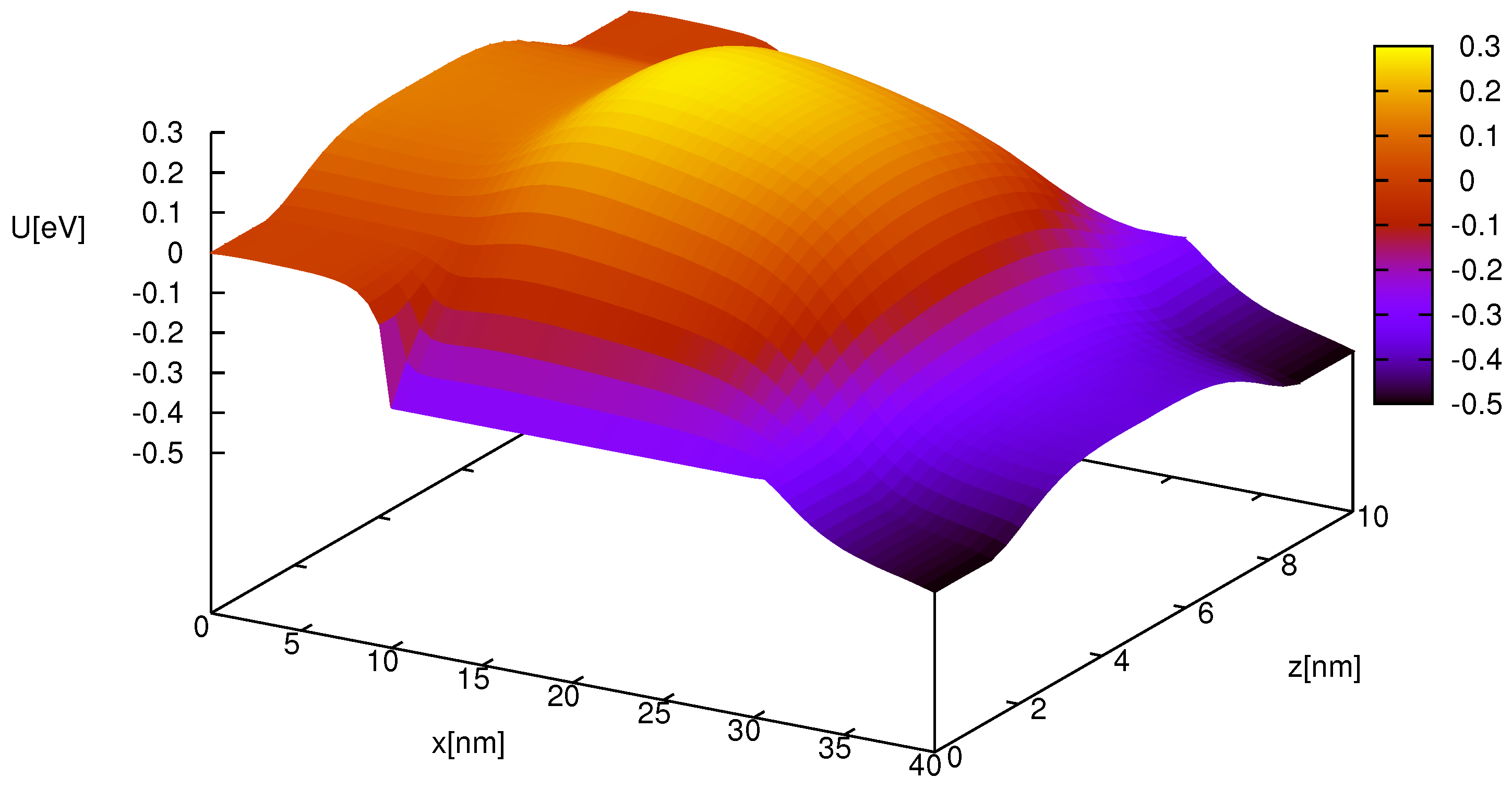
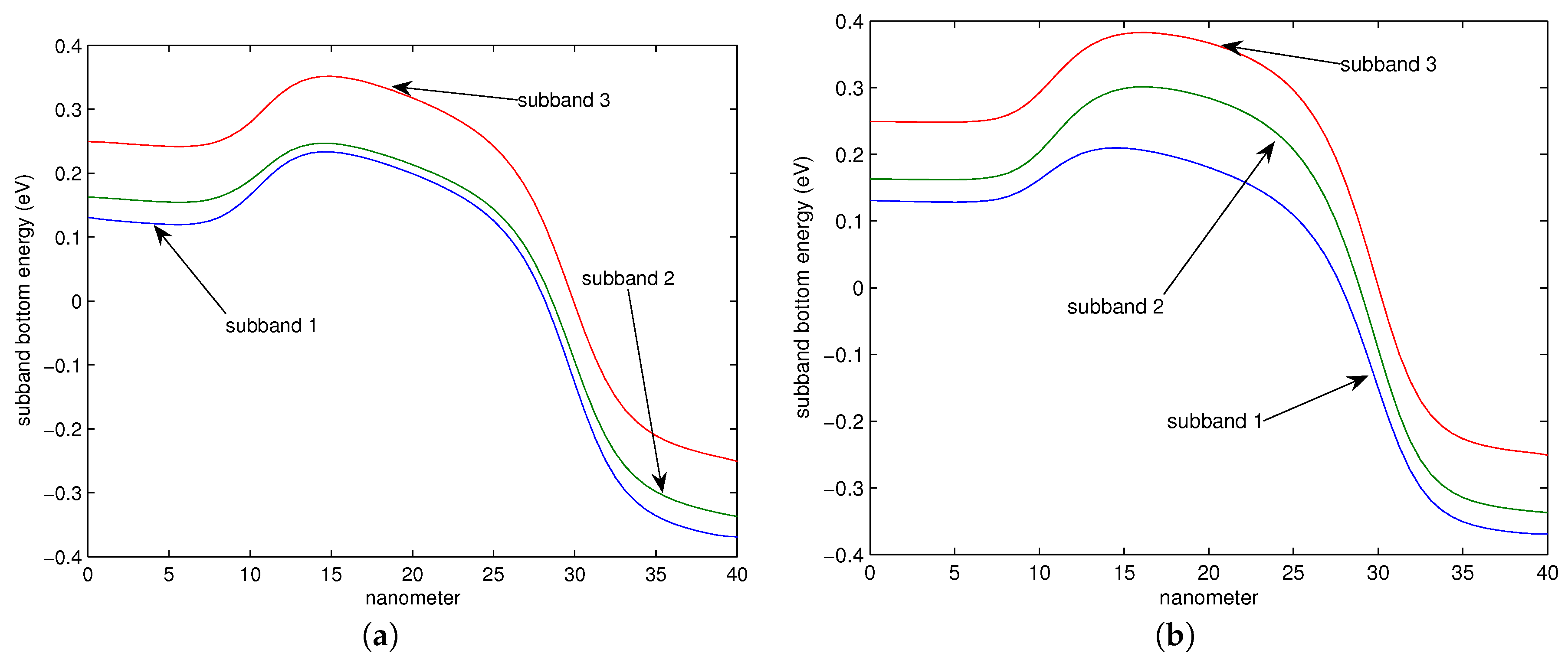
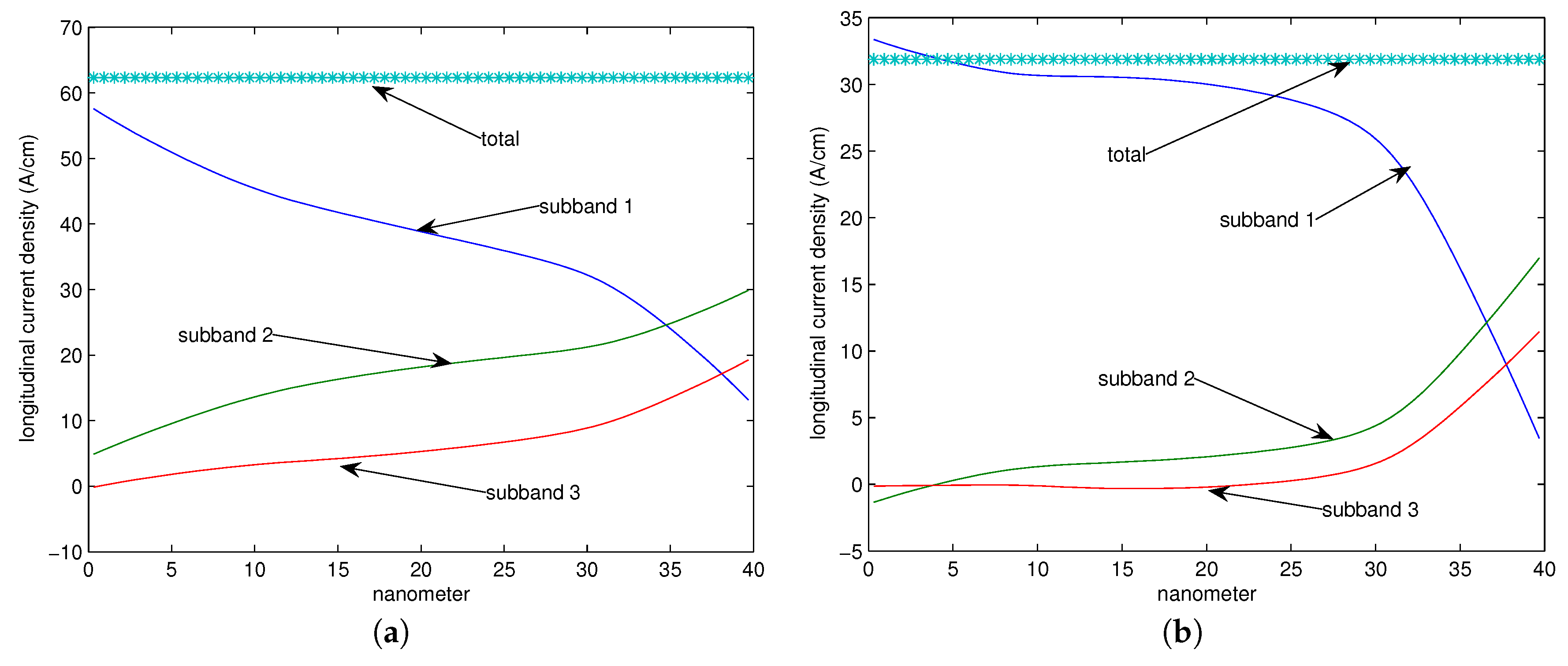
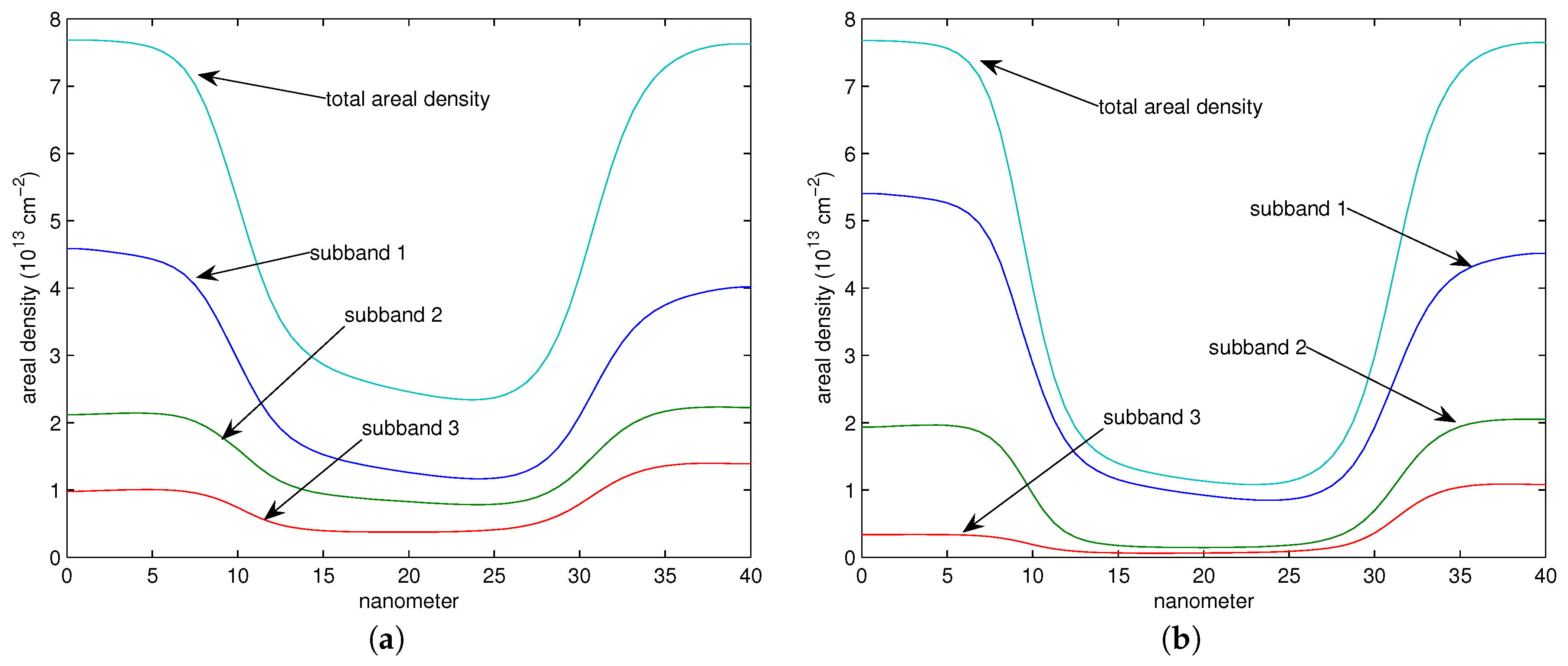
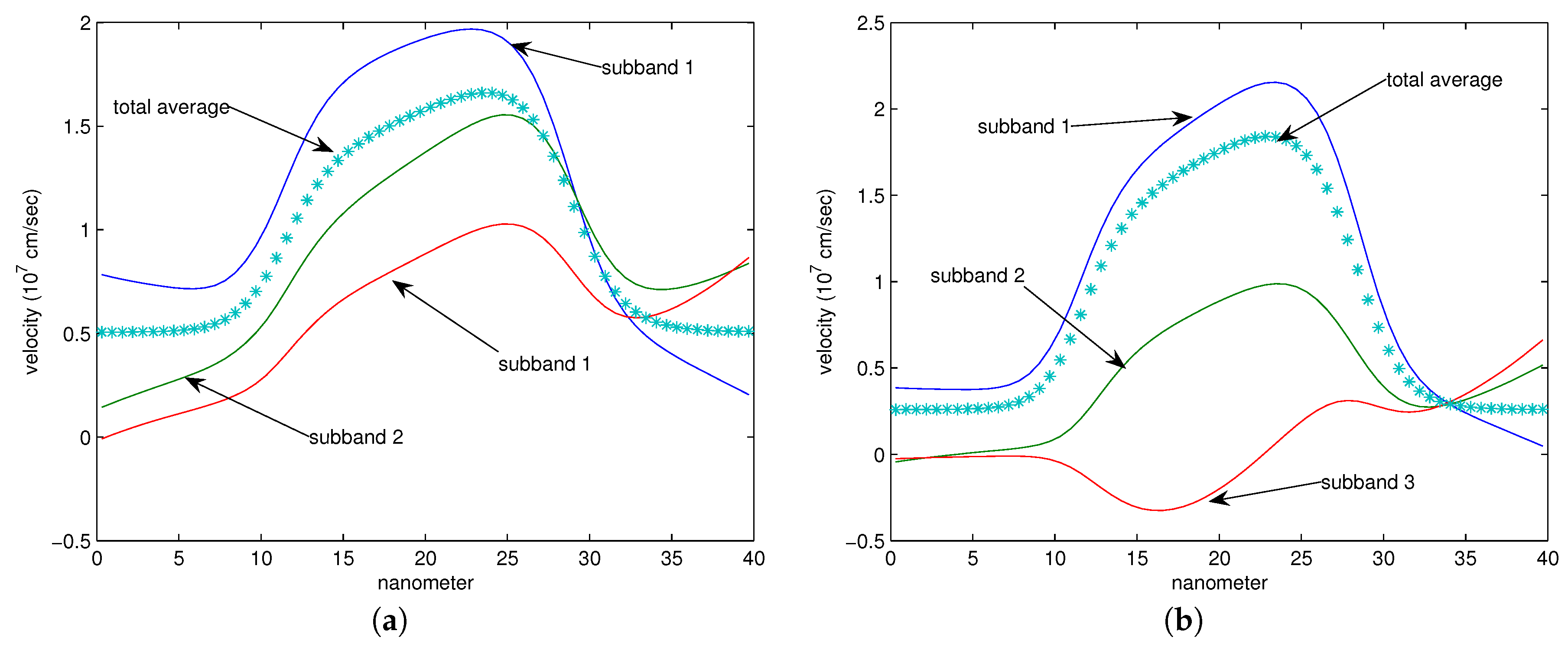
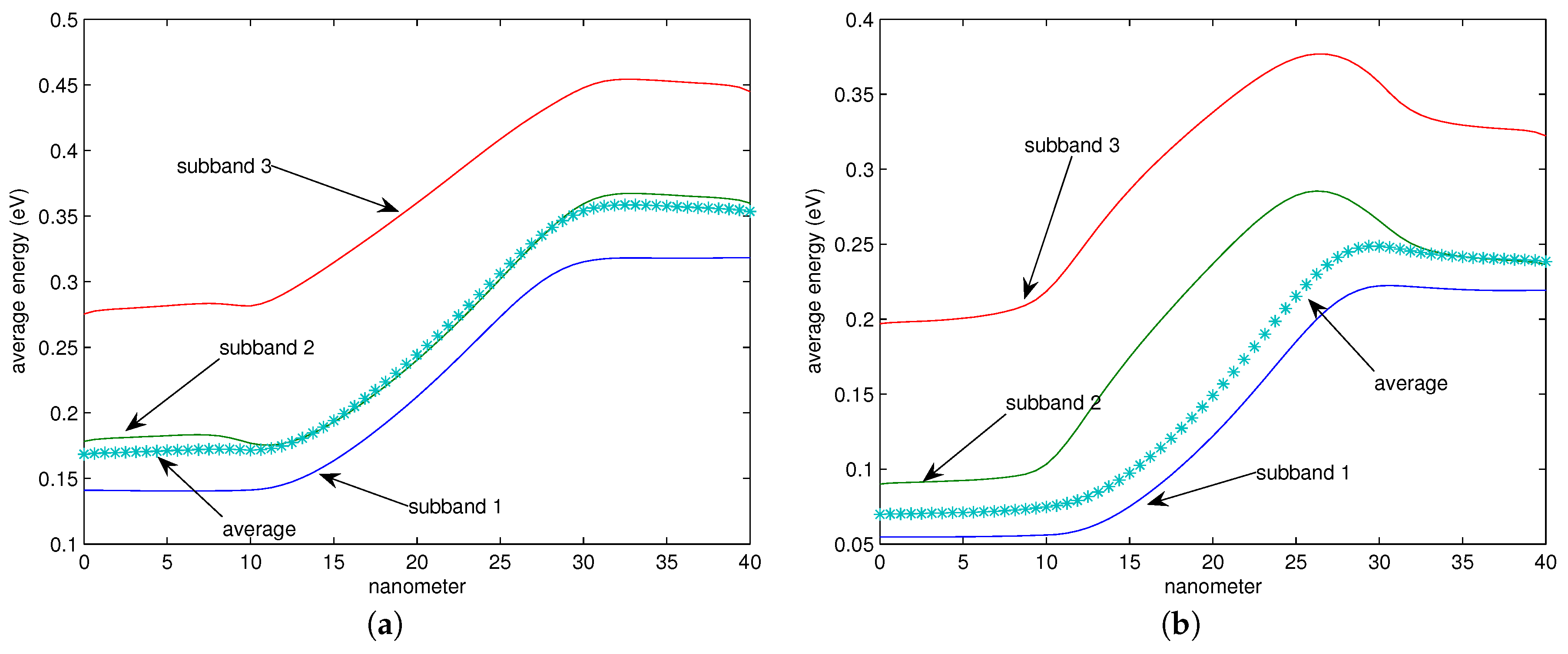
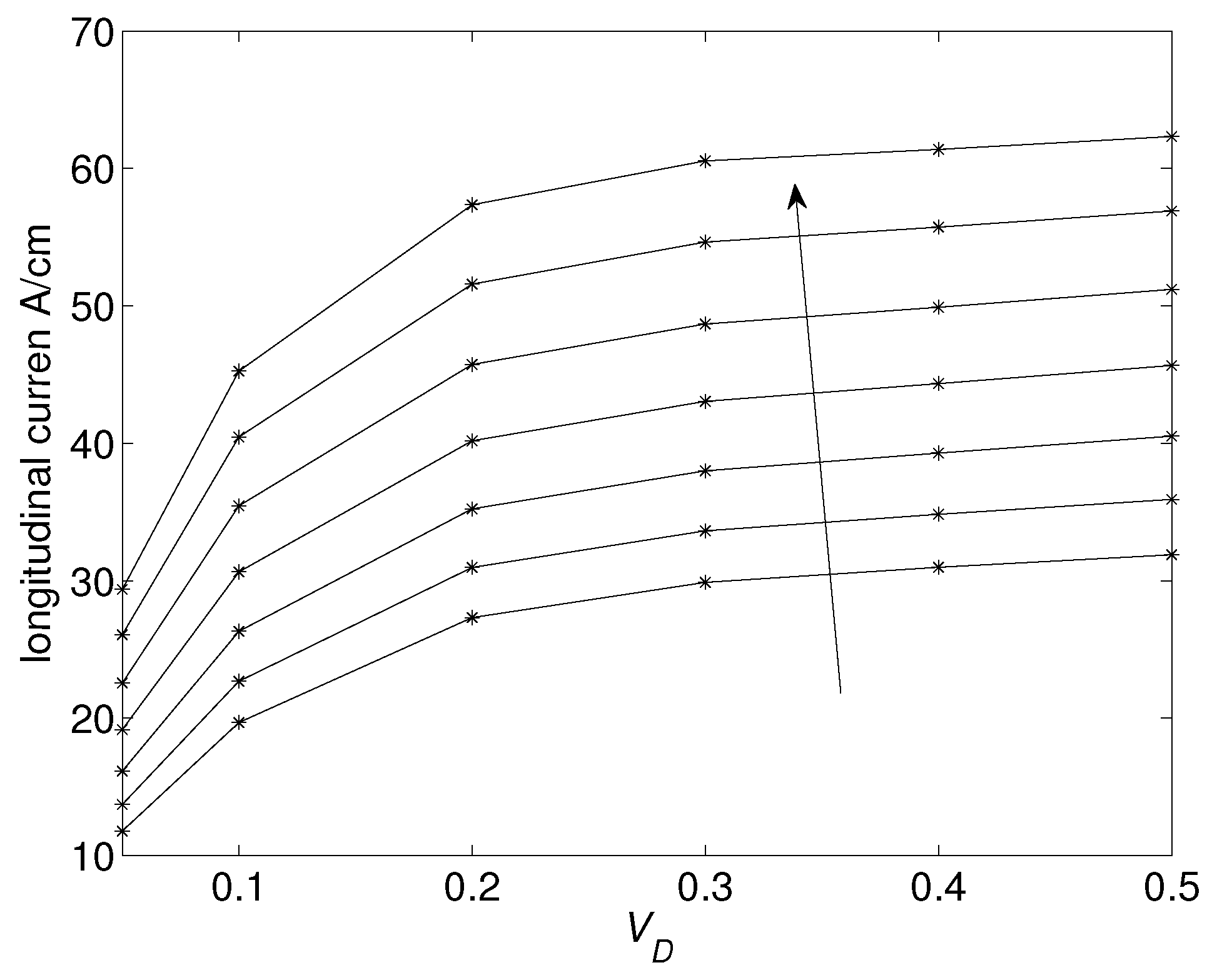
18,
19].