Comparison of Two Entropy Spectral Analysis Methods for Streamflow Forecasting in Northwest China
Abstract
:1. Introduction
2. Derivation and Evaluation of Maximum Entropy Spectral Analysis Prediction Model
2.1. Maximum Entropy Model
2.2. Constraints for Model
2.3. Determination of Spectral Density
2.4. Solution of the BESA Model
2.5. Determination of Model Order
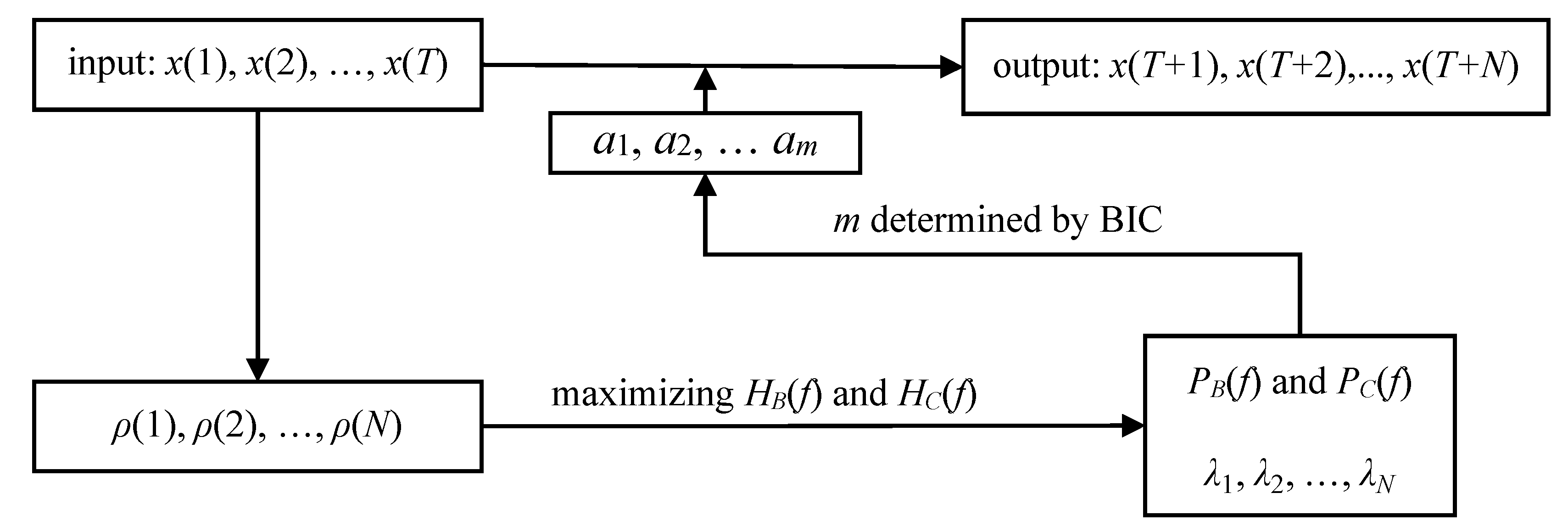
2.6. Procedure for Streamflow Forecasting
2.7. Evaluation of Model Forecast Performances
3. Application to Streamflow Forecasting
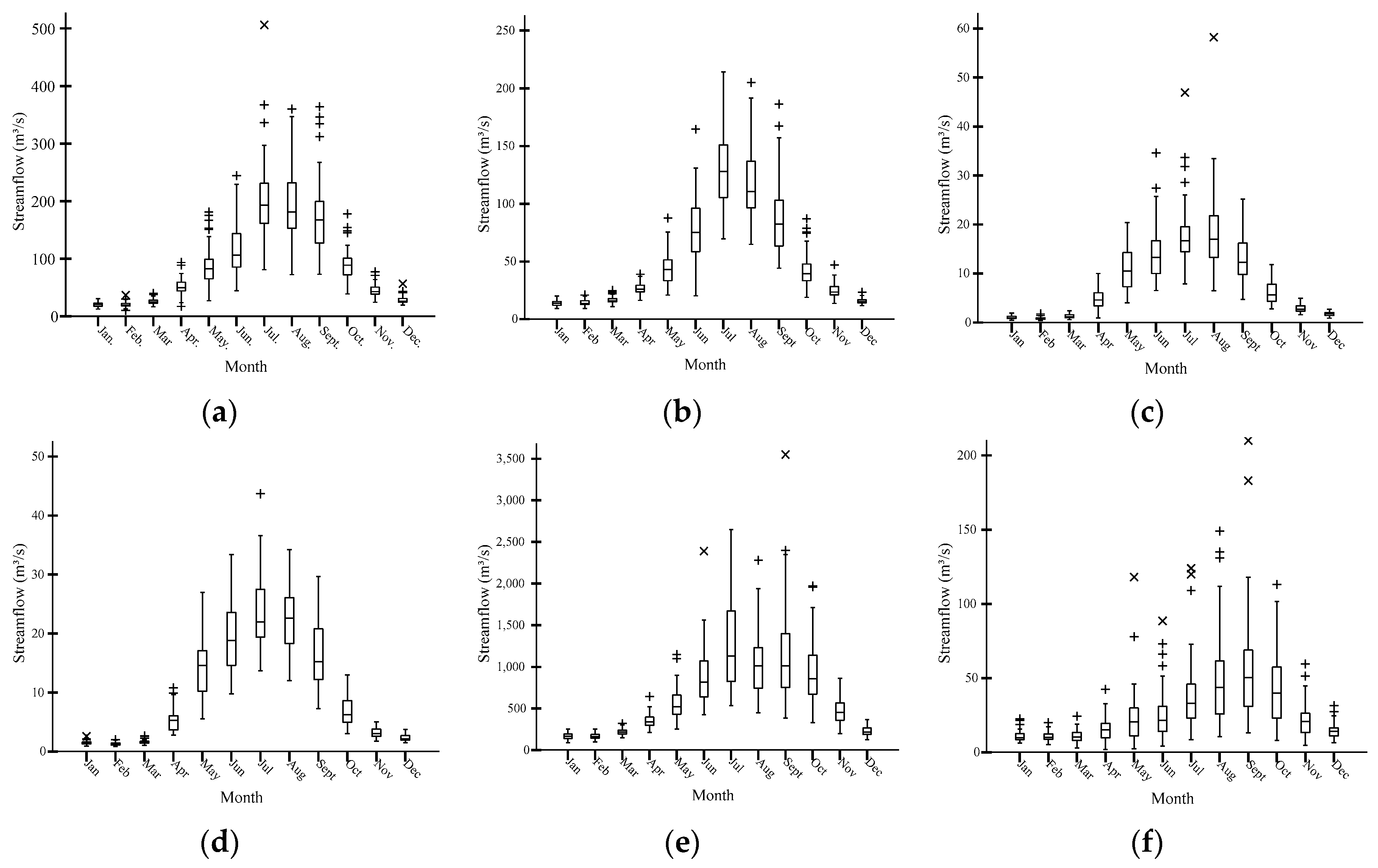
3.1. Observed Data and Characteristics
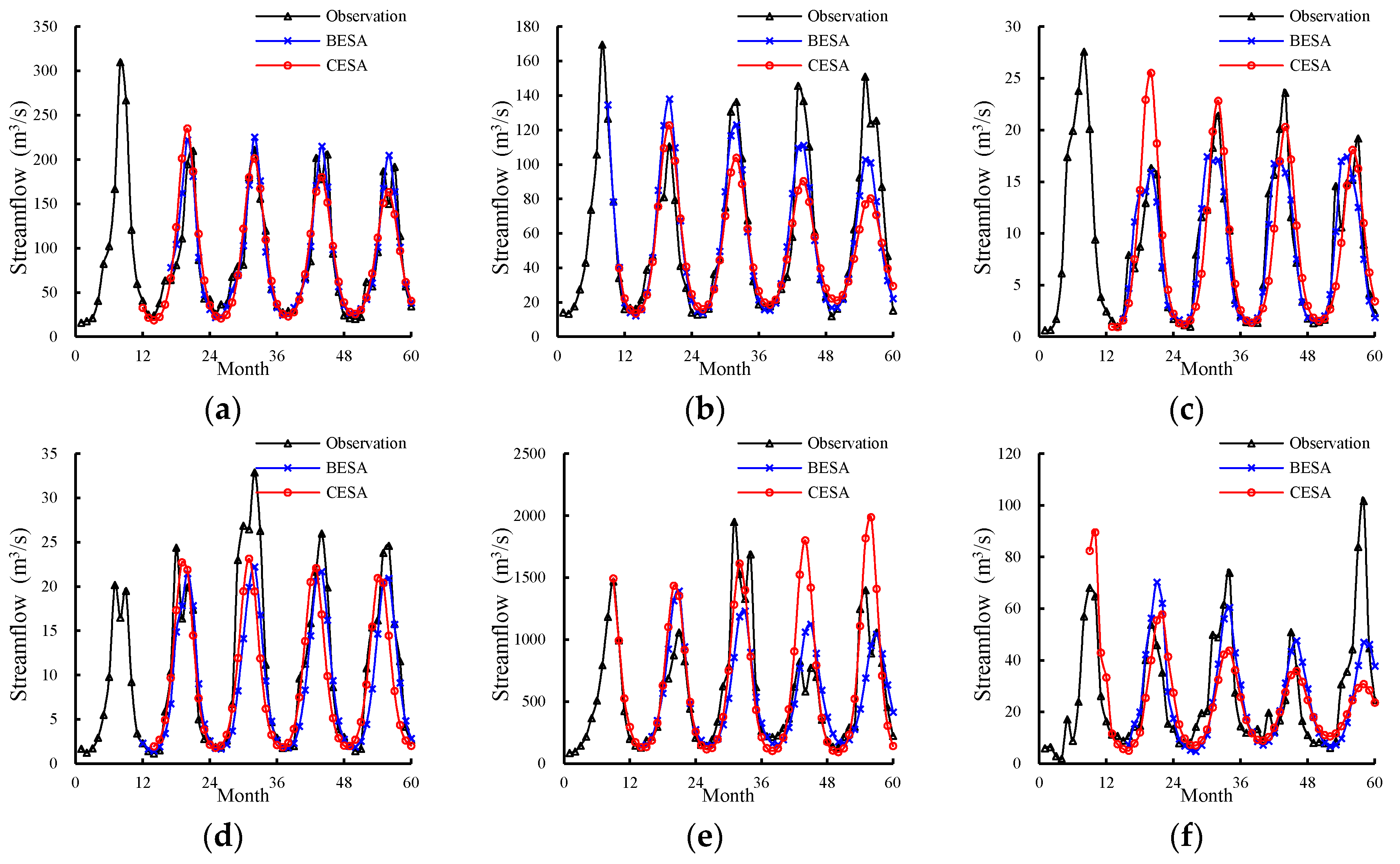
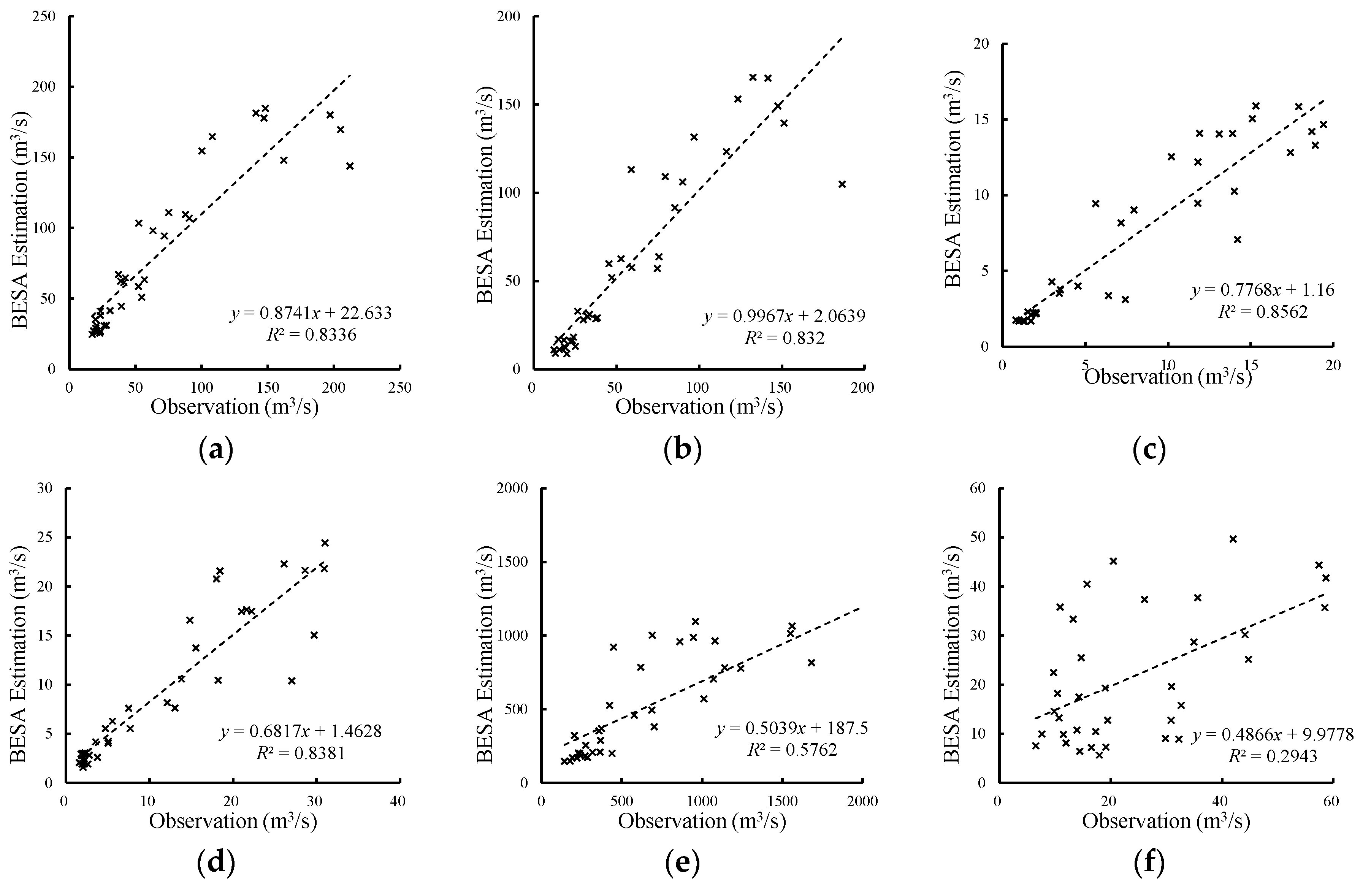
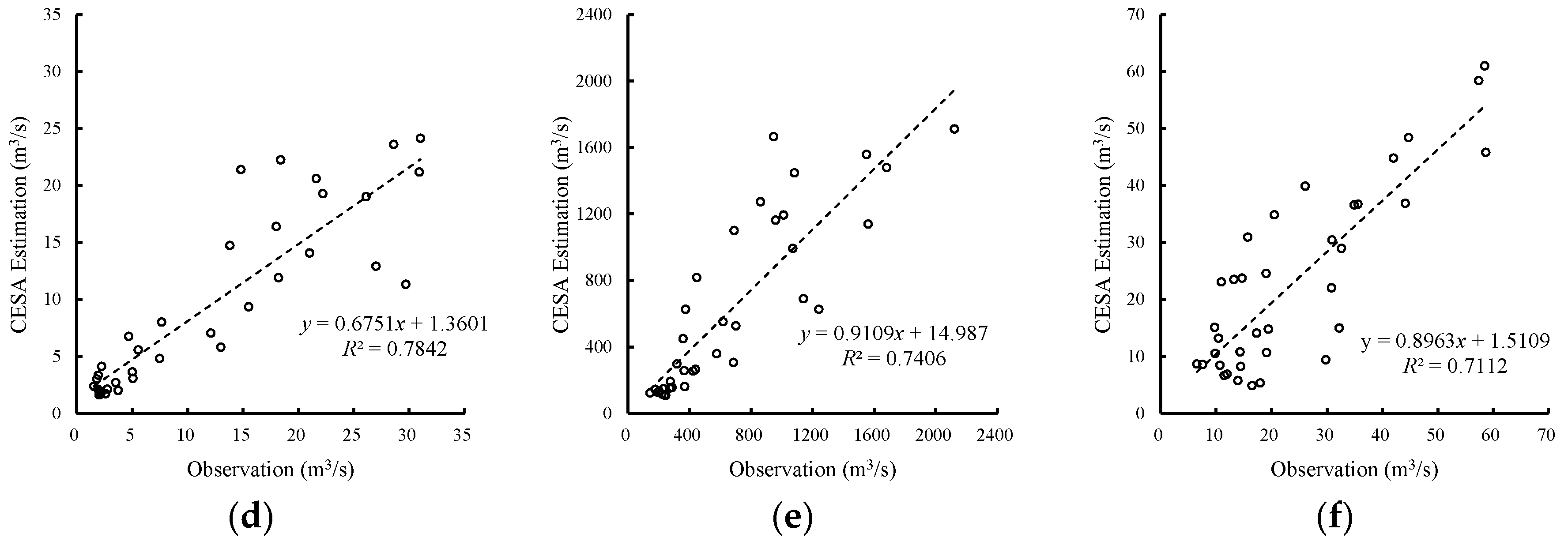
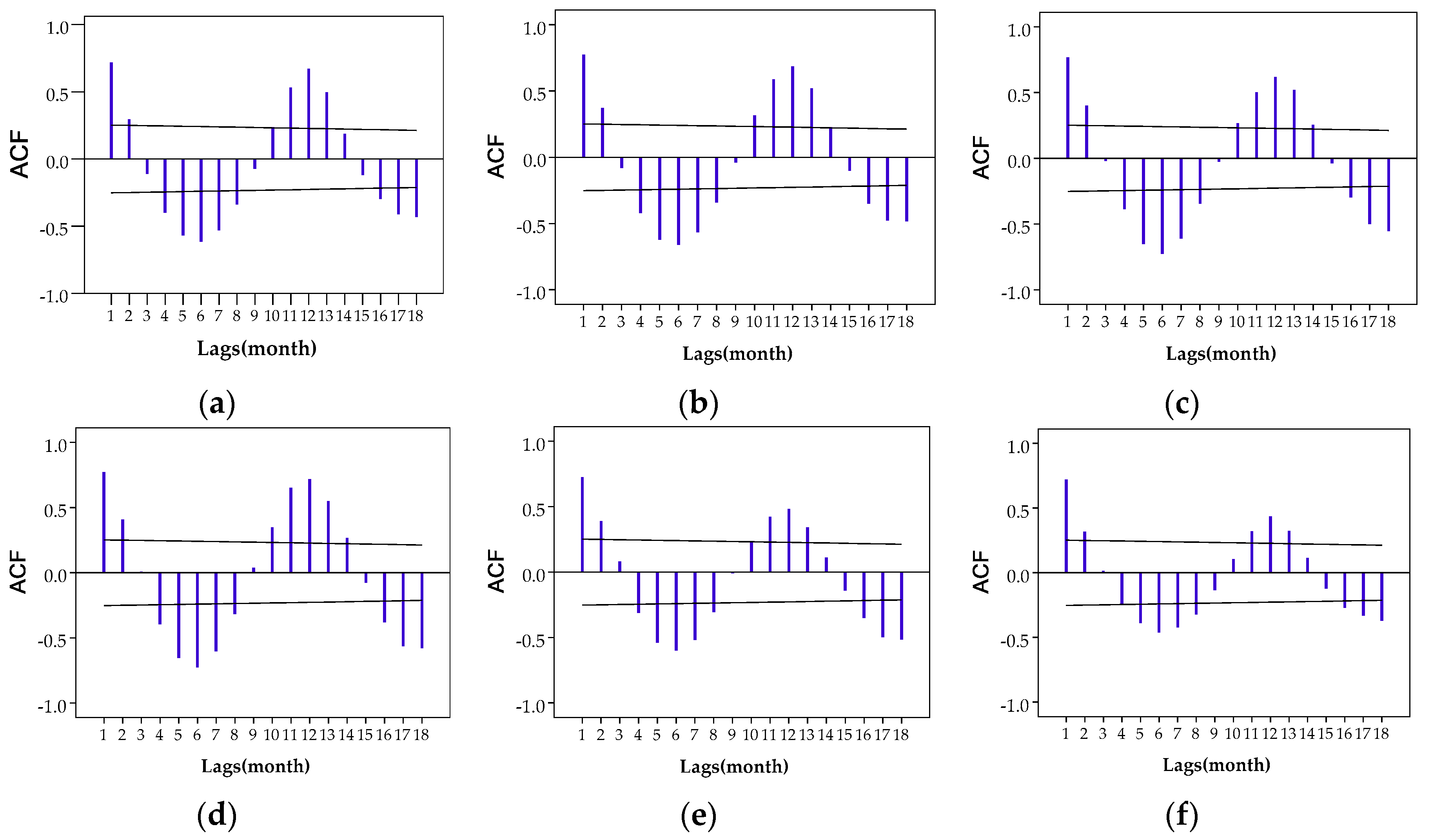
3.2. Comparison the Results of BESA and CESA
3.3. Comparison with Other Autocorrelation Models
4. Discussion
5. Conclusions
- The autoregressive coefficients obtained by maximizing Burg entropy and configurational entropy leads to more reliable than those by Levinson-Durbin algorithm. So, the streamflow forecasted by BESA and CESA is more accurate than that of the AR and SAR models.
- For the streamflow with strong correlation, both BESA and CESA forecast monthly streamflow well. The R2 and NSE were over 0.84 and 0.68, respectively. The forecast accuracy of BESA is higher than that of CESA. For the streamflow with weak correlation, the conclusion is the opposite.
- The time of peak flow forecasted by both models (BESA and CESA) may be either earlier or later than observed. The peak flow is generally underestimated by both models. BESA accurately forecasted the bi-modal values of the flood season for the lead time, while CESA had better forecast results for the streamflow data with weak correlation.
- In Northwest China, streamflow in the flood periods is principally composed of precipitation. The month with maximum precipitation is not fixed. Hence, the study of streamflow characteristics and spectral pattern associated with the precipitation can be used as the next research direction.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Box, G.E.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden-Day: Oakland, CA, USA, 1976. [Google Scholar]
- Carlson, R.F.; Maccormick, A.J.A.; Watts, D.G. Application of linear random models to four annual streamflow series. Water Resour. Res. 1970, 6, 1070–1078. [Google Scholar] [CrossRef]
- Hipel, K.W.; McLeod, A.I. Time Series Modelling of Water Resources and Environmental Systems; Elsevier: Amsterdam, The Netherlands, 1994; Volume 45. [Google Scholar]
- Haltiner, J.P.; Salas, J.D. Development and testing of a multivariate, seasonal ARMA (1,1) model. J. Hydrol. 1988, 104, 247–272. [Google Scholar] [CrossRef]
- Elshorbagy, A.; Simonovic, S.; Panu, U. Noise reduction in chaotic hydrologic time series: Facts and doubts. J. Hydrol. 2002, 256, 147–165. [Google Scholar] [CrossRef]
- Singh, V.P.; Cui, H. Entropy theory for streamflow forecasting. Environ. Process. 2015, 2, 449–460. [Google Scholar] [CrossRef]
- Fleming, S.W.; Marsh Lavenue, A.; Aly, A.H.; Adams, A. Practical applications of spectral analysis to hydrologic time series. Hydrol. Process. 2002, 16, 565–574. [Google Scholar] [CrossRef]
- Ghil, M.; Allen, M.; Dettinger, M.; Ide, K.; Kondrashov, D.; Mann, M.; Robertson, A.W.; Saunders, A.; Tian, Y.; Varadi, F. Advanced spectral methods for climatic time series. Rev. Geophys. 2002, 40. [Google Scholar] [CrossRef]
- Labat, D. Recent advances in wavelet analyses: Part 1. A review of concepts. J. Hydrol. 2005, 314, 275–288. [Google Scholar] [CrossRef]
- Labat, D.; Ronchail, J.; Guyot, J.L. Recent advances in wavelet analyses: Part 2—Amazon, Parana, Orinoco and Congo discharges time scale variability. J. Hydrol. 2005, 314, 289–311. [Google Scholar] [CrossRef]
- Marques, C.; Ferreira, J.; Rocha, A.; Castanheira, J.; Melo-Goncalves, P.; Vaz, N.; Dias, J. Singular spectrum analysis and forecasting of hydrological time series. Phys. Chem. Earth Parts A/B/C 2006, 31, 1172–1179. [Google Scholar] [CrossRef]
- Burg, J.P. Maximum entropy spectral analysis. In Proceedings of the 37th Annual International Meeting, Oklahoma, OK, USA, 31 October 1967. [Google Scholar]
- Currie, R.G. Geomagnetic line spectra-2 to 70 years. Astrophys. Space Sci. 1973, 21, 425–438. [Google Scholar] [CrossRef]
- Pardo-Igúzquiza, E.; Rodríguez-Tovar, F.J. Maximum entropy spectral analysis of climatic time series revisited: Assessing the statistical significance of estimated spectral peaks. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Hasanean, H. Fluctuations of surface air temperature in the eastern mediterranean. Theor. Appl. Climatol. 2001, 68, 75–87. [Google Scholar] [CrossRef]
- Wang, D.; Chen, Y.-F.; Li, G.-F.; Xu, Y.-H. Maximum entropy spectral analysis for annual maximum tide levels time series of the changjiang river estuary. J. Coast. Res. 2004, 43, 101–108. [Google Scholar]
- Dalezios, N.R.; Tyraskis, P.A. Maximum entropy spectra for regional precipitation analysis and forecasting. J. Hydrol. 1989, 109, 25–42. [Google Scholar] [CrossRef]
- Huang, Z.S. The application of spectrum analysis method in hydrogy. Hydrology 1983, 3, 101–108. [Google Scholar]
- Krstanovic, P.; Singh, V.P. A univariate model for long-term streamflow forecasting. Stoch. Hydrol. Hydraul. 1991, 5, 173–188. [Google Scholar] [CrossRef]
- Krstanovic, P.; Singh, V.P. A real-time flood forecasting model based on maximum-entropy spectral analysis: I. Development. Water Resour. Manag. 1993, 7, 109–129. [Google Scholar] [CrossRef]
- Krstanovic, P.; Singh, V.P. A real-time flood forecasting model based on maximum-entropy spectral analysis: II. Application. Water Resour. Manag. 1993, 7, 131–151. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy Theory and Its Application in Environmental and Water Engineering, 1st ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Singh, V.P. Entropy Theory in Hydrologic Science and Engineering; McGraw-Hill: New York, NY, USA, 2015. [Google Scholar]
- Huo, C. Use of auto-regression model of time series in the simulation and forecast of groundwater dynamic in irrigation areas. Geotech. Investig. Surv. 1990, 1, 36–38. [Google Scholar]
- Wang, D.; Zhu, Y.S. Research on cryptic period of hydrologic time series based on mem1spectral analysis. Hydrology 2002, 2, 19–23. [Google Scholar]
- Shen, H.F.; Li, M.S.; Luo, F. Strict maximum entropy spectral estimation based on recursive algorithm. Radar Sci. Technol. 2008, 4, 288–291. [Google Scholar]
- Boshnakov, G.N.; Lambert-Lacroix, S. A periodic levinson–durbin algorithm for entropy maximization. Comput. Stat. Data Anal. 2012, 56, 15–24. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. Configurational entropy theory for streamflow forecasting. J. Hydrol. 2015, 521, 1–17. [Google Scholar] [CrossRef]
- Frieden, B.R. Restoring with maximum likelihood and maximum entropy. J. Opt. Soc. Am. 1972, 62, 511–518. [Google Scholar] [CrossRef] [PubMed]
- Gull, S.F.; Daniell, G.J. Image reconstruction from incomplete and noisy data. Nature 1978, 272, 686–690. [Google Scholar] [CrossRef]
- Wu, N.L. An explicit solution and data extension in the maximum entropy method. IEEE Trans. Acoust. Speech Signal Process. 1983, 31, 486–491. [Google Scholar]
- Nadeu, C. Finite length cepstrum modelling—A simple spectrum estimation technique. Signal Process. 1992, 26, 49–59. [Google Scholar] [CrossRef]
- Katsakos-Mavromichalis, N.; Tzannes, M.; Tzannes, N. Frequency resolution: A comparative study of four entropy methods. Kybernetes 1986, 15, 25–32. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models partI—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Men, B.; Long, R.; Zhang, J. Combined forecasting of streamflow based on cross entropy. Entropy 2016, 18, 336. [Google Scholar] [CrossRef]
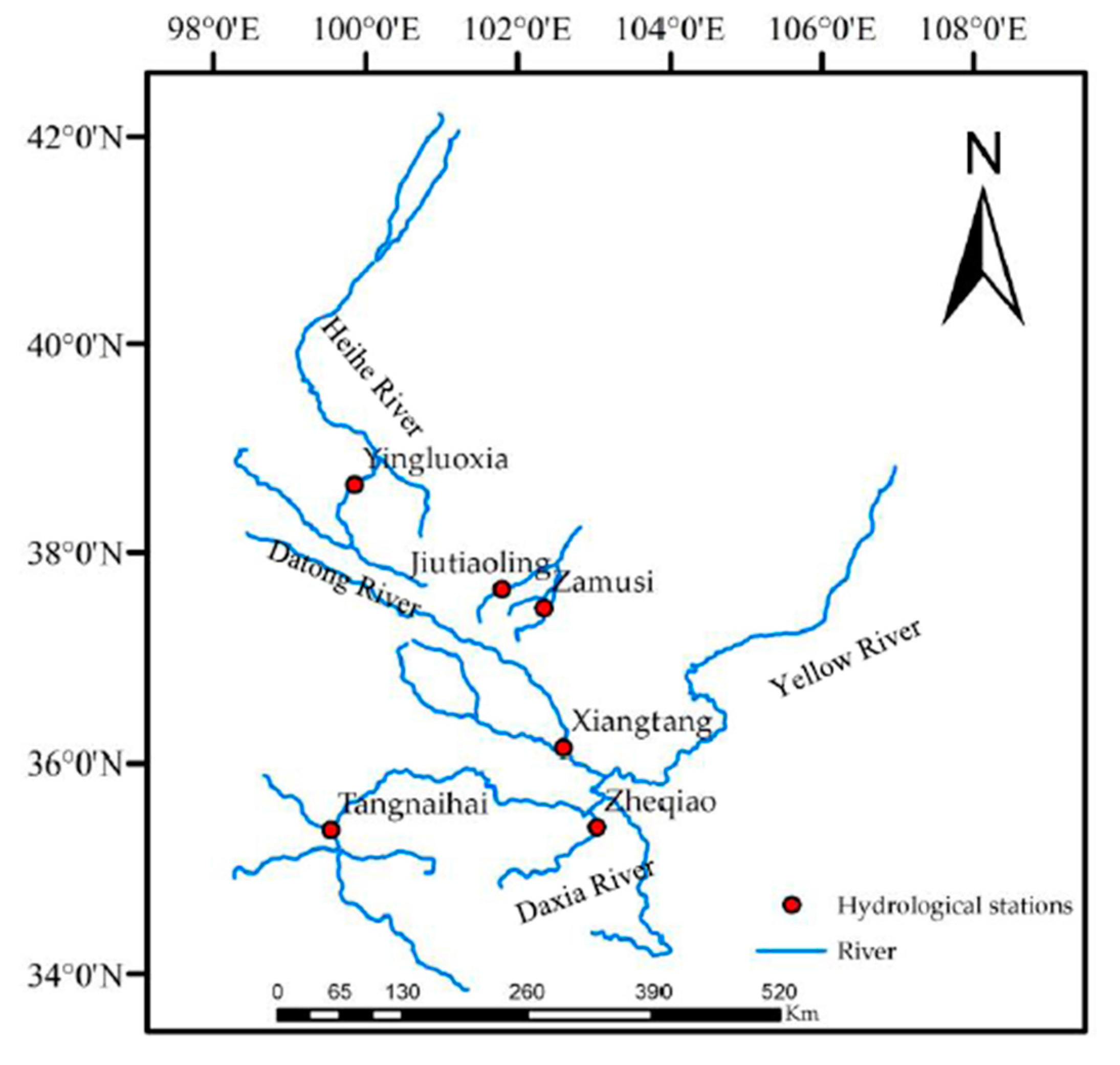


| No. | Station | Longitude | Latitude | River | Basin Area (km2) | Catchment Area (km2) | Record Length | Average (m3/s) | Peak (m3/s) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Xiangtang | 102°51′E | 36°22′N | Datong | 15133 | 15,126 | 1950–2016 | 88 | 506 |
| 2 | Yingluoxia | 100°11′E | 38°48′N | Heihe | 130,000 | 10,009 | 1954–2012 | 51 | 214 |
| 3 | Zamusi | 102°34′E | 37°42′N | Zamu | 851 | 851 | 1952–2010 | 8 | 58.2 |
| 4 | Jiutiaoling | 102°03′E | 37°52′N | Xiying | 1120 | 1077 | 1972–2010 | 10 | 43.7 |
| 5 | Tangnaihai | 100°09′E | 35°30′N | Yellow | 752,443 | 121,972 | 1956–2016 | 633 | 3550 |
| 6 | Zheqiao | 103°16′E | 35°38′N | Daxia | 7154 | 6843 | 1963–2016 | 27 | 210 |
| Station | Model | Model Order | Training Time (2003–2007) | Lead Time (2008–2010) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RE | RMSE | R2 | NSE | RE | RMSE | R2 | NSE | |||
| xiangtang | BESA | 16 | 0.169 | 19.4 | 0.953 | 0.904 | 0.376 | 27.3 | 0.913 | 0.773 |
| CESA | 11 | 0.231 | 24.5 | 0.920 | 0.840 | 0.405 | 28.1 | 0.890 | 0.760 | |
| yingluoxia | BESA | 8 | 0.202 | 17.3 | 0.915 | 0.834 | 0.235 | 21.2 | 0.912 | 0.798 |
| CESA | 10 | 0.267 | 22.8 | 0.874 | 0.708 | 0.185 | 21.1 | 0.917 | 0.801 | |
| zamusi | BESA | 14 | 0.207 | 2.7 | 0.913 | 0.832 | 0.268 | 2.5 | 0.925 | 0.838 |
| CESA | 12 | 0.316 | 3.7 | 0.864 | 0.690 | 0.382 | 3.5 | 0.840 | 0.684 | |
| jiutiaoling | BESA | 11 | 0.229 | 4.5 | 0.920 | 0.768 | 0.245 | 4.9 | 0.915 | 0.755 |
| CESA | 13 | 0.346 | 5.1 | 0.868 | 0.697 | 0.318 | 5.4 | 0.886 | 0.707 | |
| tangnaihai | BESA | 13 | 0.312 | 303.3 | 0.750 | 0.548 | 0.295 | 354.8 | 0.759 | 0.482 |
| CESA | 8 | 0.335 | 340.3 | 0.805 | 0.447 | 0.360 | 273.0 | 0.861 | 0.693 | |
| zheqiao | BESA | 15 | 0.362 | 19.0 | 0.621 | 0.255 | 0.291 | 9.1 | 0.876 | 0.618 |
| CESA | 8 | 0.466 | 17.8 | 0.640 | 0.365 | 0.369 | 8.6 | 0.843 | 0.659 | |
| Station | BESA | CESA | AR | SAR | ||||
|---|---|---|---|---|---|---|---|---|
| NSE of TT | NSE of LT | NSE of TT | NSE of LT | NSE of TT | NSE of LT | NSE of TT | NSE of LT | |
| xiangtang | 0.904 | 0.773 | 0.840 | 0.760 | 0.686 | 0.666 | 0.564 | 0.631 |
| yingluoxia | 0.834 | 0.798 | 0.708 | 0.801 | 0.612 | 0.755 | 0.429 | 0.624 |
| zamusi | 0.832 | 0.838 | 0.690 | 0.684 | 0.644 | 0.524 | 0.479 | 0.540 |
| jiutiaoling | 0.768 | 0.755 | 0.697 | 0.707 | 0.585 | 0.511 | 0.456 | 0.466 |
| tangnaihai | 0.548 | 0.482 | 0.447 | 0.693 | 0.495 | 0.34 | 0.403 | 0.373 |
| zheqiao | 0.255 | 0.618 | 0.365 | 0.659 | 0.485 | 0.144 | 0.364 | 0.728 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Ju, J.; Su, X.; Singh, V.P.; Zhang, G. Comparison of Two Entropy Spectral Analysis Methods for Streamflow Forecasting in Northwest China. Entropy 2017, 19, 597. https://doi.org/10.3390/e19110597
Zhou Z, Ju J, Su X, Singh VP, Zhang G. Comparison of Two Entropy Spectral Analysis Methods for Streamflow Forecasting in Northwest China. Entropy. 2017; 19(11):597. https://doi.org/10.3390/e19110597
Chicago/Turabian StyleZhou, Zhenghong, Juanli Ju, Xiaoling Su, Vijay P. Singh, and Gengxi Zhang. 2017. "Comparison of Two Entropy Spectral Analysis Methods for Streamflow Forecasting in Northwest China" Entropy 19, no. 11: 597. https://doi.org/10.3390/e19110597





