A Sparse Multiwavelet-Based Generalized Laguerre–Volterra Model for Identifying Time-Varying Neural Dynamics from Spiking Activities
Abstract
:1. Introduction
2. Methodology
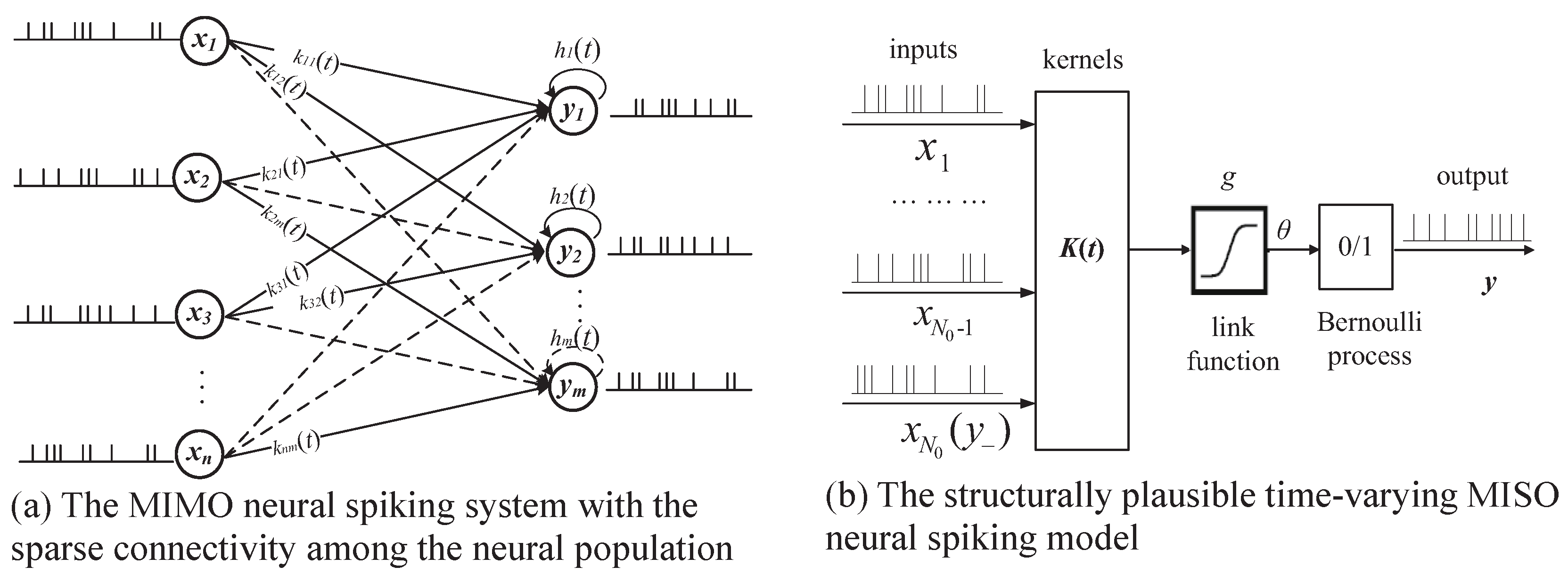
2.1. Time-Varying Generalized Volterra Model
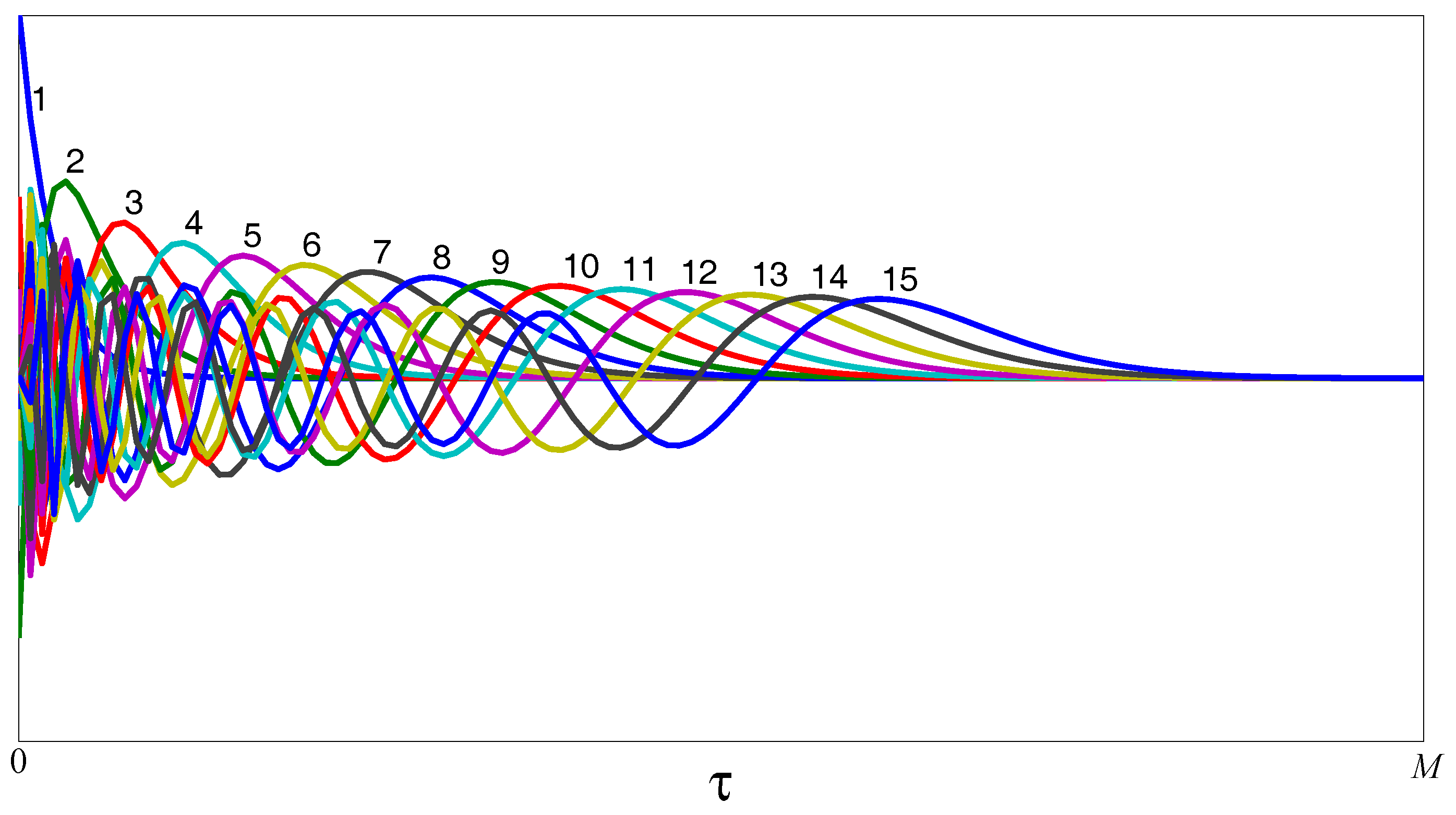
2.2. Time-Varying Generalized Laguerre–Volterra Model
2.3. Functional Sparsity Based on a Group Regularization Method
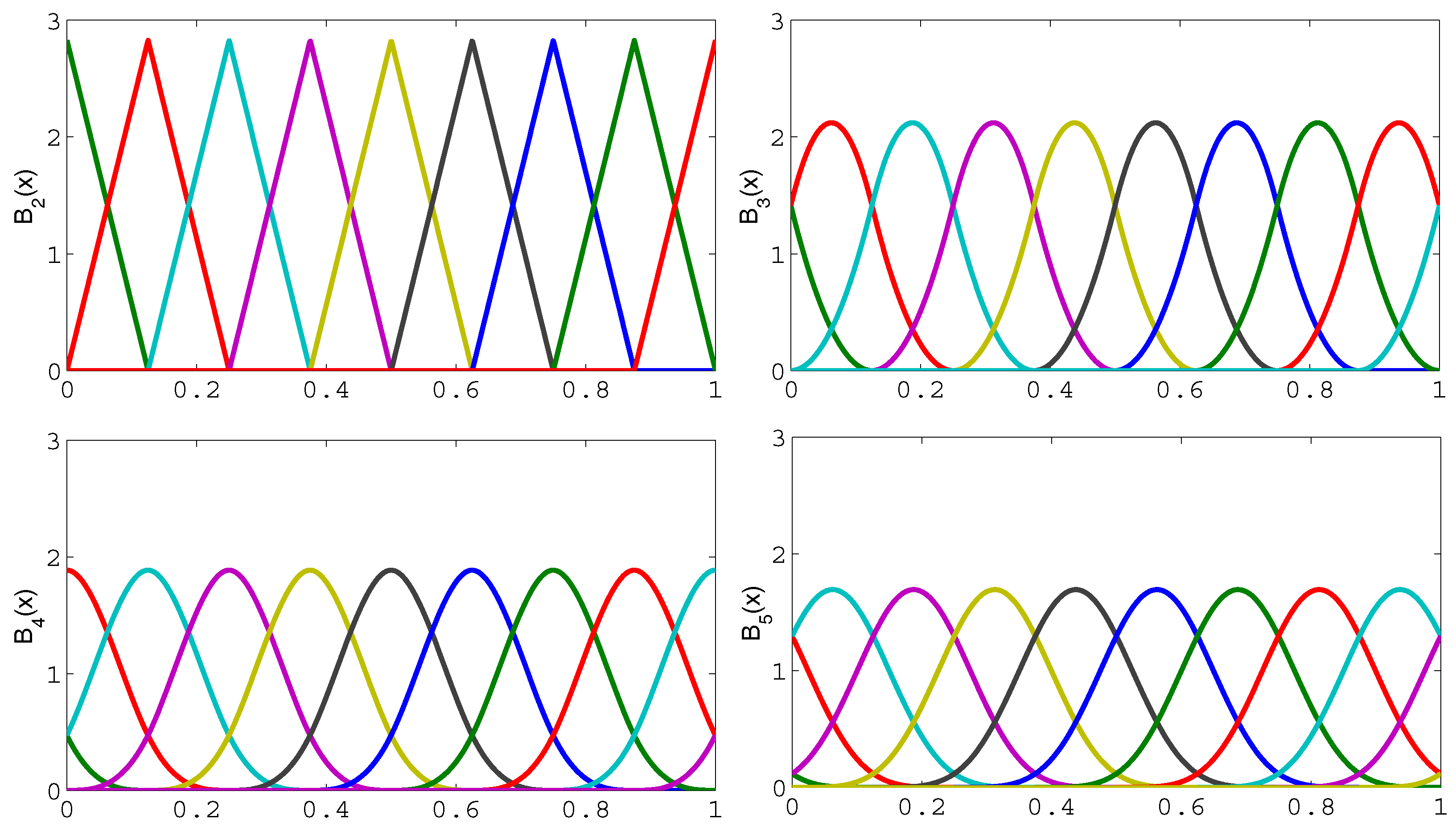
2.4. Sparse Multiwavelet-Based Generalized Laguerre–Volterra Model
2.5. Model Structure Selection
2.6. Parameter Estimation and Tuning Parameter Optimization
2.7. Kernel Reconstruction and Interpretation
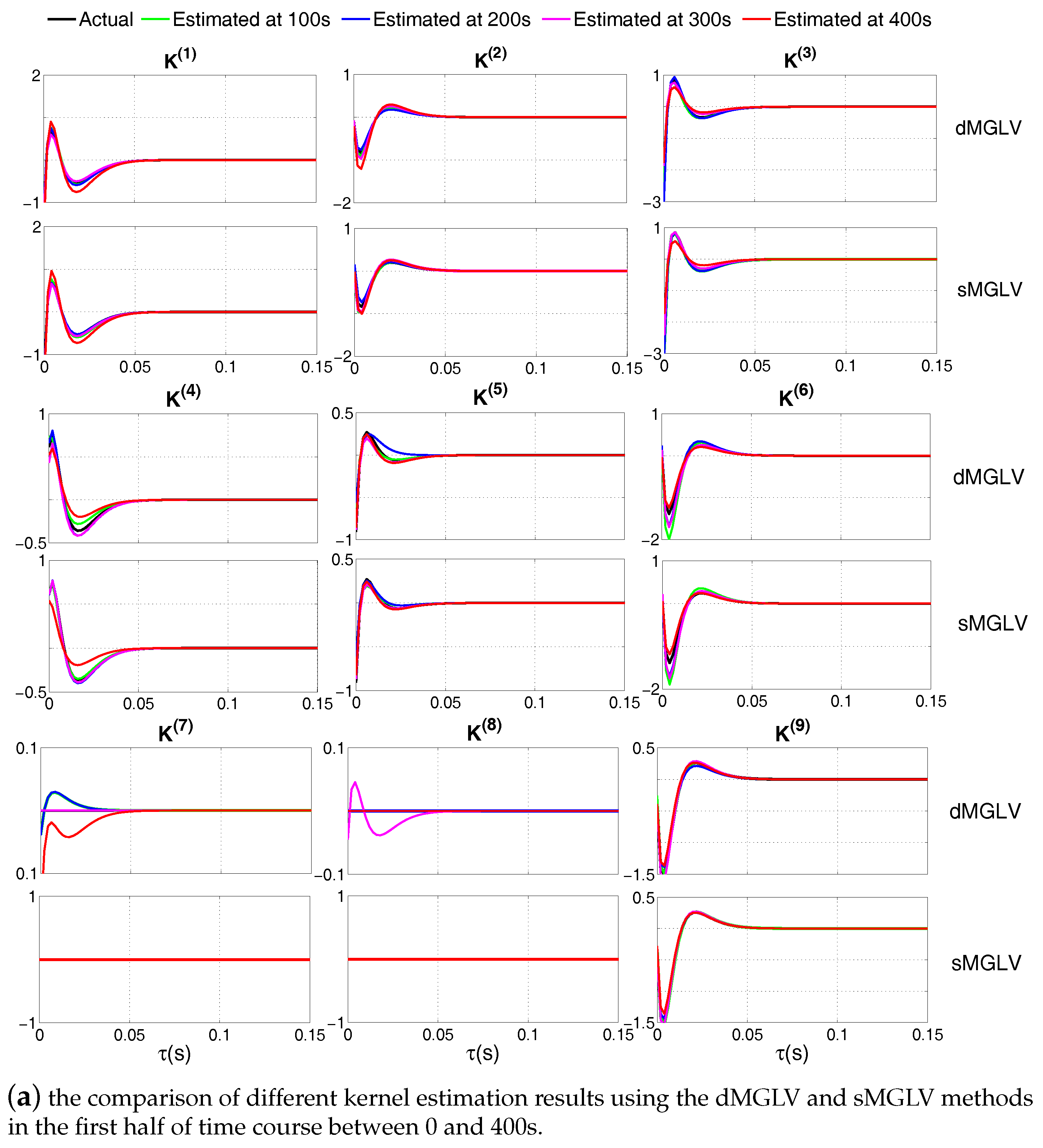
3. Simulation Studies
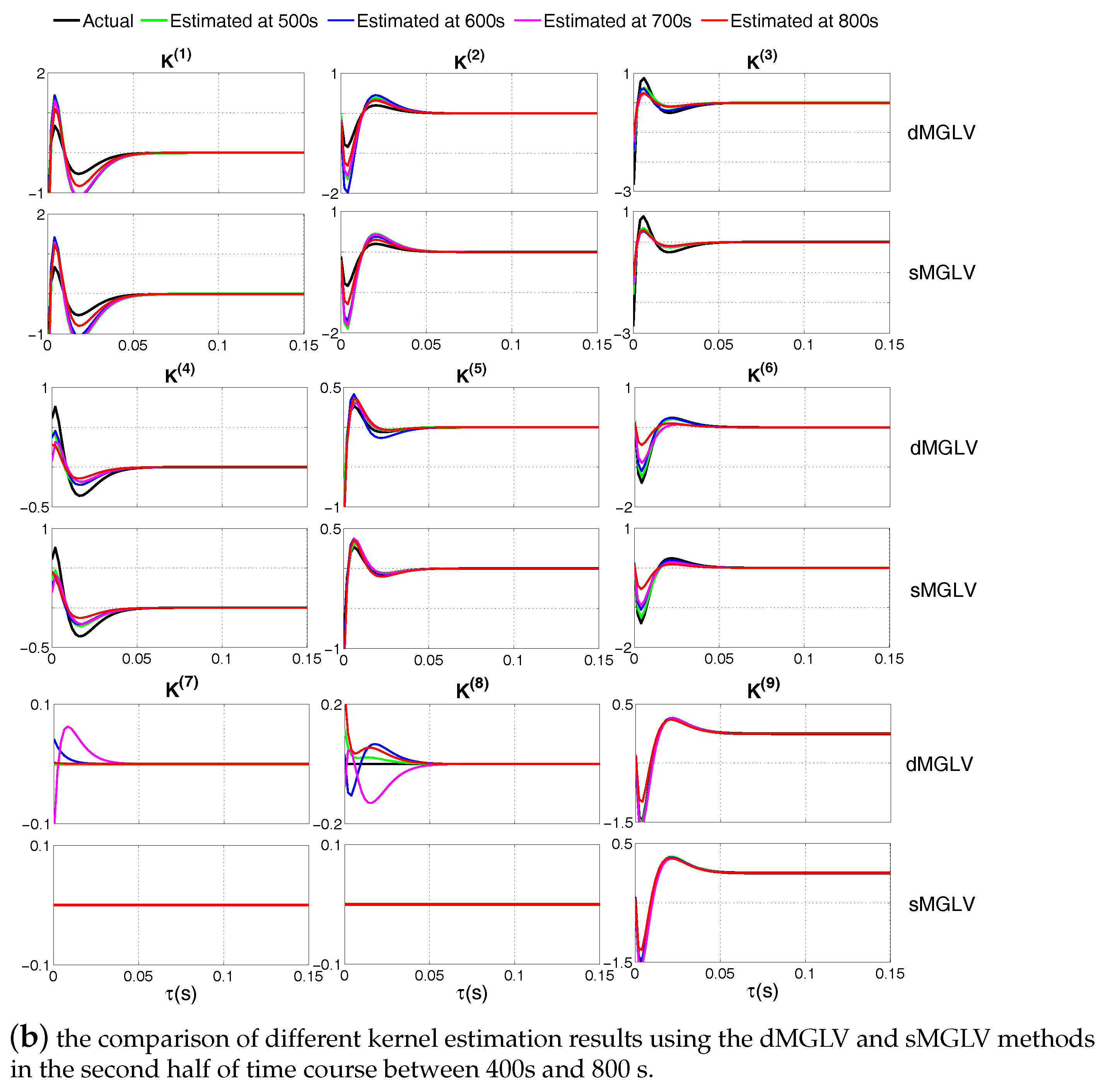
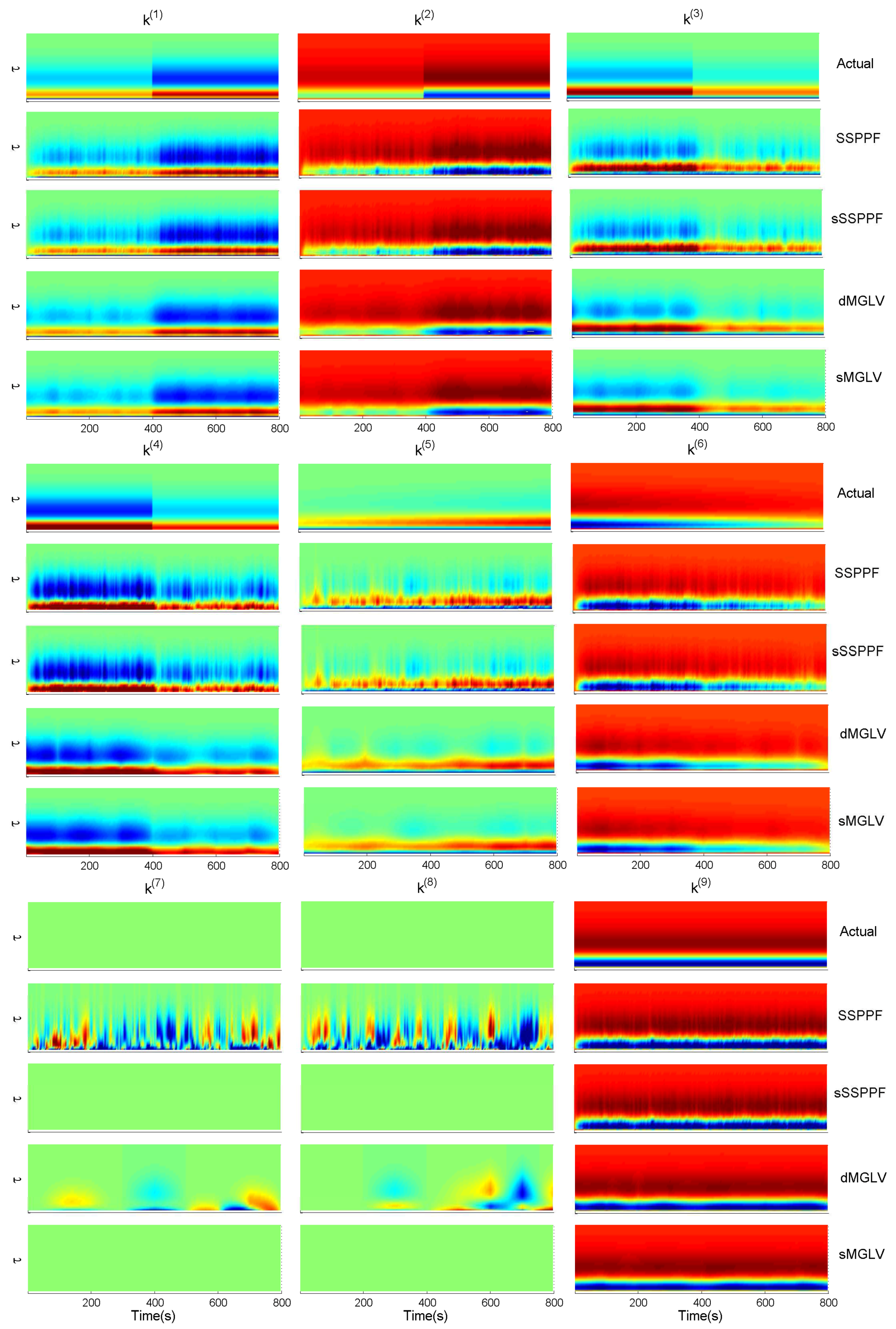
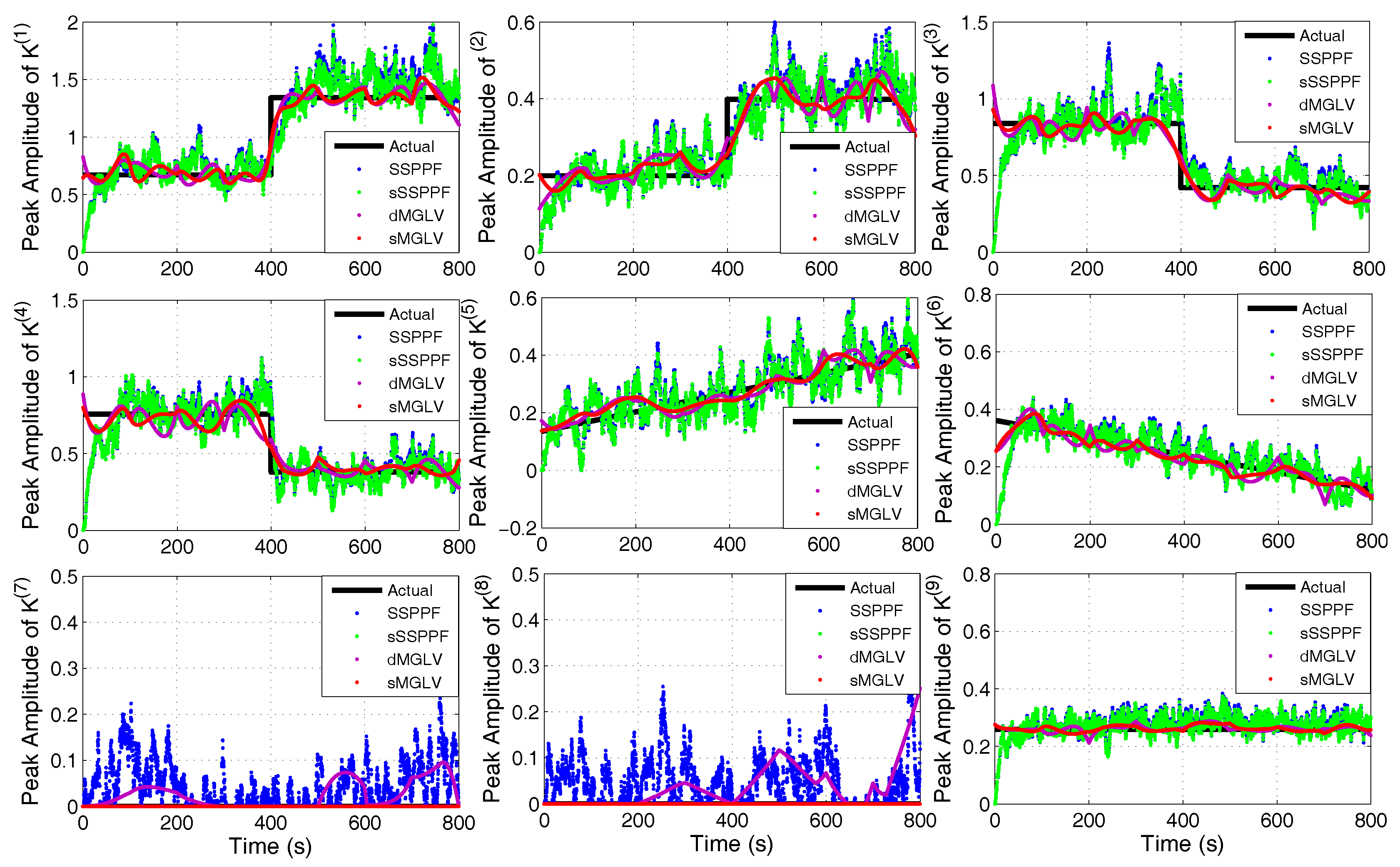
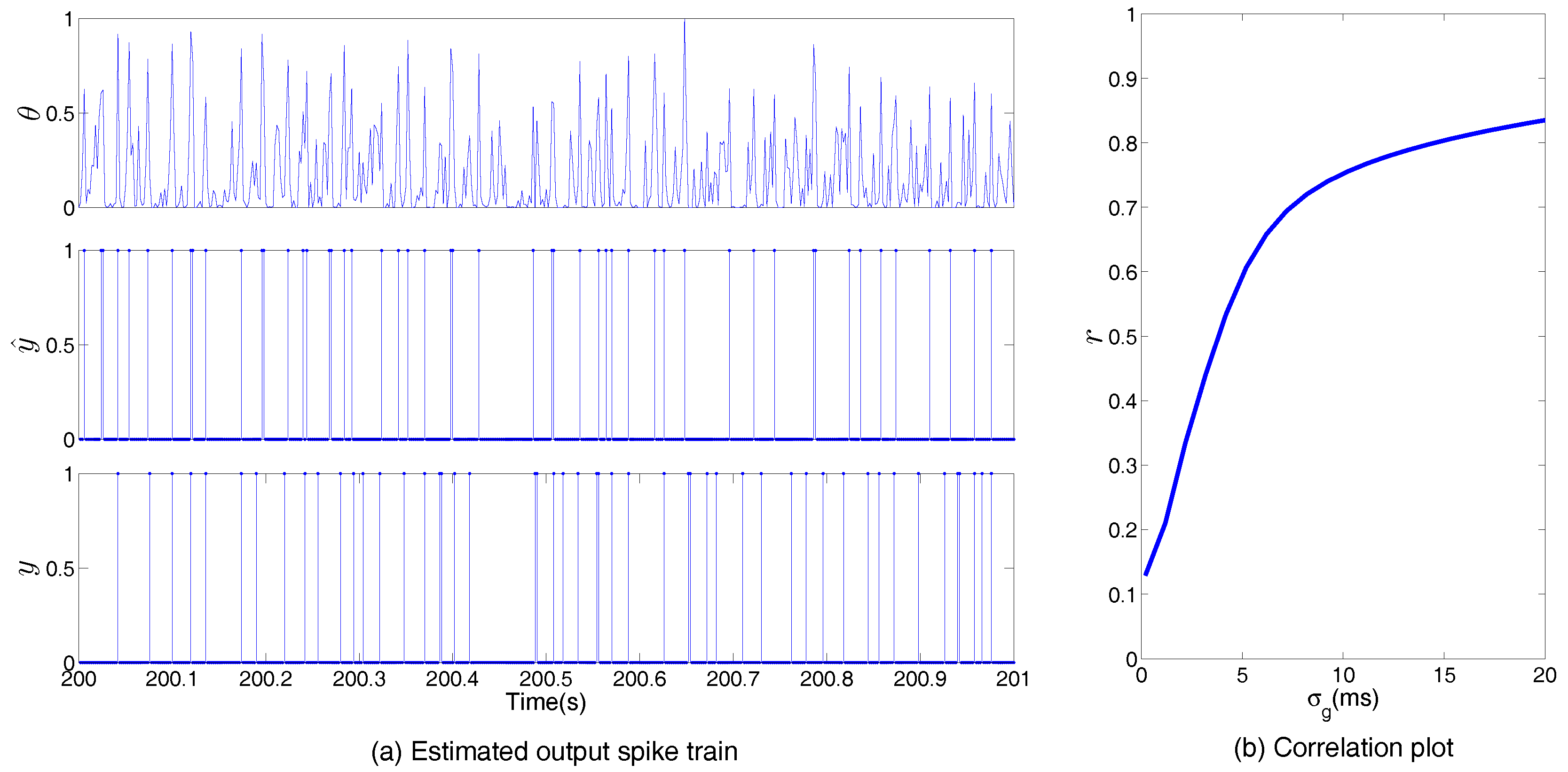
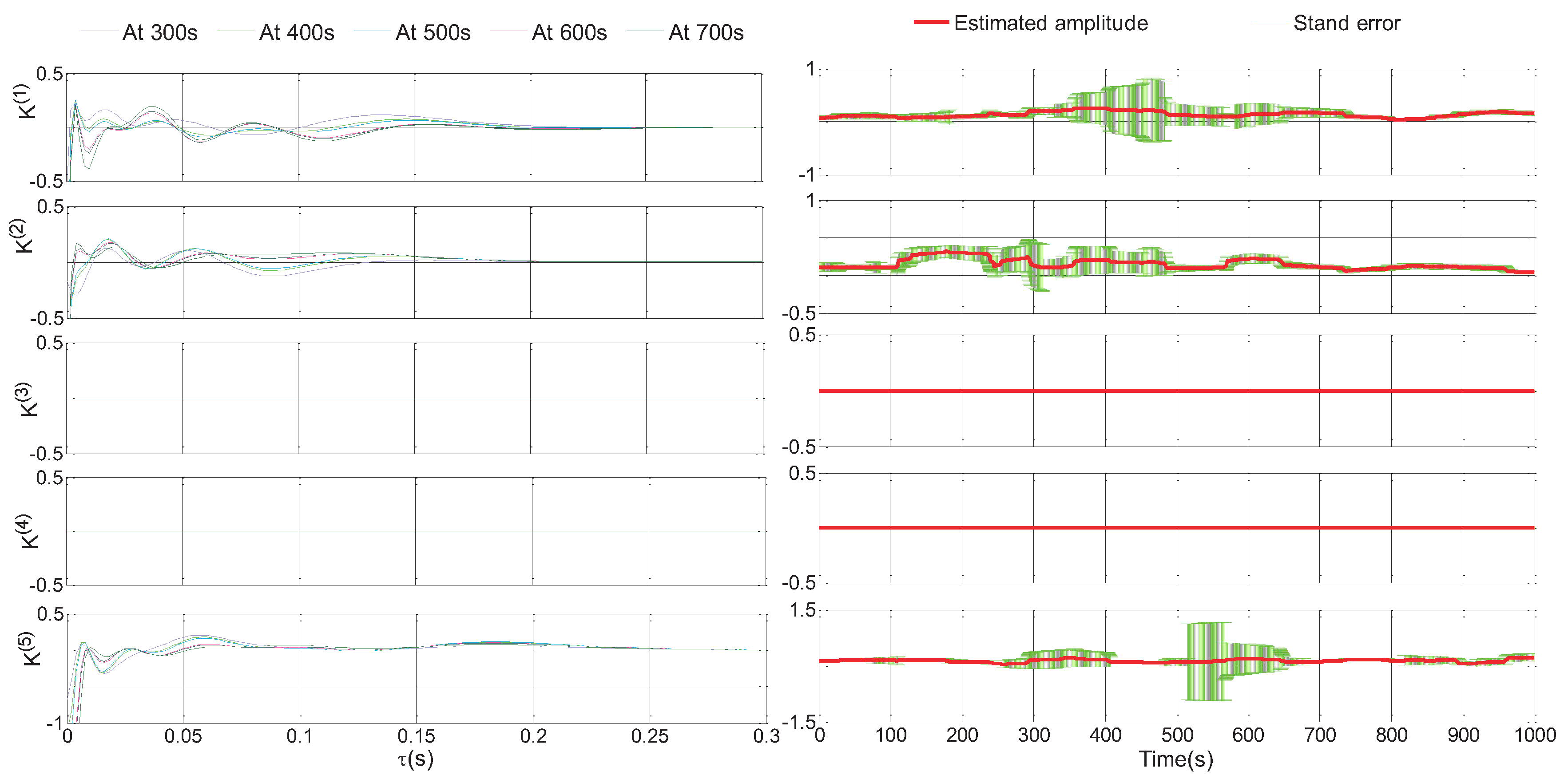
4. Application to Functional Connectivity Analysis of Retinal Neural Spikes
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chan, R.H.; Song, D.; Berger, T.W. Nonstationary modeling of neural population dynamics. Proeedings of the 31st Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 2–6 September 2009. [Google Scholar]
- Nasser, H.; Cessac, B. Parameter estimation for spatio-temporal maximum entropy distribu- tions: Application to neural spike trains. Entropy 2014, 16, 2244–2277. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Park, I.; Seth, S.; Sanchez, J.; Príncipe, J. Functional connectivity dynamics among cortical neurons: A dependence analysis. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 20, 18–30. [Google Scholar] [CrossRef] [PubMed]
- Dahl, G.; Yu, D.; Deng, L.; Acero, A. Context-dependent pre-trained deep neural networks for large-vocabulary speech recognition. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 30–42. [Google Scholar] [CrossRef]
- Coulibaly, P.; Baldwin, C. Nonstationary hydrological time series forecasting using non-linear dynamic methods. J. Hydrol. 2005, 307, 164–174. [Google Scholar] [CrossRef]
- Iatrou, M.; Berger, T.W.; Marmarelis, V.Z. Modeling of nonlinear nonstationary dynamic systems with a novel class of artificial neural networks. IEEE Trans. Neural Netw. 1999, 10, 327–339. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wen, Y.; Gou, Y.; Ye, Z.; Chen, H. Fractional-order gradient descent learning of bp neural networks with caputo derivative. Neural Netw. 2017, 89, 19–30. [Google Scholar] [CrossRef] [PubMed]
- Sayed, A.H. Fundamentals of Adaptive Filtering; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Seáñez-González, I.; Mussa-Ivaldi, F.A. Cursor control by kalman filter with a non- invasive body–Machine interface. J. Neural Eng. 2014, 11, 056026. [Google Scholar] [CrossRef] [PubMed]
- Eden, U.; Frank, L.; Barbieri, R.; Solo, V.; Brown, E. Dynamic analysis of neural encoding by point process adaptive filtering. Neural Comput. 2004, 16, 971–998. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liu, Q.; Tan, S.; Chan, R.M. High-resolution time-frequency analysis of eeg signals using multiscale radial basis functions. Neurocomputing 2016, 195, 96–103. [Google Scholar] [CrossRef]
- Zou, R.; Chon, K.H. Robust algorithm for estimation of time-varying transfer functions. IEEE Trans. Biomed. Eng. 2004, 51, 219–228. [Google Scholar] [CrossRef] [PubMed]
- Martel, F.; Rancourt, D.; Chochol, C.; St-Amant, Y.; Chesne, S.; Rémond, D. Time-varying torsional stiffness identification on a vertical beam using chebyshev polynomials. Mech. Syst. Signal Process. 2015, 54, 481–490. [Google Scholar] [CrossRef]
- Clement, P.R. Laguerre functions in signal analysis and parameter identification. J. Frankl. Inst. 1982, 313, 85–95. [Google Scholar] [CrossRef]
- Niedzwiecki, M. Identification of Time-Varying Processes; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Su, W.C.; Liu, C.Y.; Huang, C.S. Identification of instantaneous modal parameter of time-varying systems via a wavelet-based approach and its application. Comput. Aided Civ. Infrastruct. Eng. 2014, 29, 279–298. [Google Scholar] [CrossRef]
- Li, Y.; Luo, M.; Li, K. A multiwavelet-based time-varying model identification approach for time-frequency analysis of eeg signals. Neurocomputing 2016, 193, 106–114. [Google Scholar] [CrossRef]
- Windeatt, T.; Zor, C. Ensemble pruning using spectral coefficients. IEEE Trans. Neural netw. Learn. Syst. 2013, 24, 673–678. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, S.; Li, Y.; Wang, X.; Chan, R.H. Identification of time-varying neural dynamics from spiking activities using chebyshev polynomials. In Proceedings of the 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Orlando, FL, USA, 16–20 August 2016. [Google Scholar]
- Chon, K.H.; Zhao, H.; Zou, R.; Ju, K. Multiple time-varying dynamic analysis using multiple sets of basis functions. IEEE Trans. Biomed. Eng. 2005, 52, 956–960. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wei, H.; Billings, S.A.; Sarrigiannis, P.G. Time-varying model identification for time- frequency feature extraction from eeg data. J. Neurosci. Methods, 2011, 196, 151–158. [Google Scholar] [CrossRef] [PubMed]
- Dorval, A.D. Estimating neuronal information: Logarithmic binning of neuronal inter-spike intervals. Entropy 2011, 13, 485–501. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wei, H.; Billings, S.A. Identification of time-varying systems using multi-wavelet basis functions. IEEE Trans. Control Syst. Technol. 2011, 19, 656–663. [Google Scholar] [CrossRef]
- Xu, S.; Li, Y.; Guo, Q.; Yang, X.; Chan, R.M. Identification of time-varying neural dyna- mics from spike train data using multiwavelet basis functions. J. Neurosci. Methods 2017, 278, 46–56. [Google Scholar] [CrossRef] [PubMed]
- He, F.; Wei, H.; Billings, S. Identification and frequency domain analysis of nonsta- tionary and nonlinear systems using time-varying narmax models. Int. J. Syst. Sci. 2015, 46, 2087–2100. [Google Scholar] [CrossRef]
- She, Q.; Chen, G.; Chan, R.M. Evaluating the small-world-ness of a sampled network: Fun- ctional connectivity of entorhinal-hippocampal circuitry. Sci. Rep. 2016, 6, 21468. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Chen, G. Complex networks: Small-world, scale-free and beyond. IEEE Circuits Syst. Mag. 2003, 3, 6–20. [Google Scholar] [CrossRef]
- Gong, C.; Tao, D.; Fu, K.; Yang, J. Fick’s law assisted propagation for semisupervised learning. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2148–2162. [Google Scholar] [CrossRef] [PubMed]
- Tu, C.; Song, D.; Breidt, F.; Berger, T.; Wang, H. Functional model selection for sparse binary time series with multiple inputs. In Economic Time Series: Modeling and Seasonality; Chapman and Hall/CRC: Boca Raton, FL, USA, 2012. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. stat. Assoc. 2001, 96, 348–1360. [Google Scholar] [CrossRef]
- Yuan, M.; Li, Y. Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. B Stat. Methodol. 2006, 68, 49–67. [Google Scholar] [CrossRef]
- Huang, J.; Ma, S.; Xie, H.; Zhang, C. A group bridge approach for variable selection. Biometrika 2009, 96, 339–355. [Google Scholar] [CrossRef] [PubMed]
- Song, D.; Wang, H.; Tu, C.; Marmarelis, V.; Hampson, R.; Deadwyler, S.A.; Berger, T. Identification of sparse neural functional connectivity using penalized likelihood estimation and basis functions. J. Comput. Neurosci. 2013, 35, 335–357. [Google Scholar] [CrossRef] [PubMed]
- Brown, E.; Nguyen, D.; Frank, L.; Wilson, M.; Solo, V. An analysis of neural receptive field plasticity by point process adaptive filtering. Proc. Natl. Acad. Sci. USA 2001, 98, 12261–12266. [Google Scholar] [CrossRef] [PubMed]
- Song, D.; Chan, R.M.; Marmarelis, V.; Hampson, R.; Deadwyler, S.; Berger, T. Nonlinear modeling of neural population dynamics for hippocampal prostheses. Neural Netw. 2009, 22, 1340–1351. [Google Scholar] [CrossRef] [PubMed]
- Song, D.; Chan, R.M.; Robinson, B.; Marmarelis, V.; Opris, I.; Hampson, R.; Deadwyler, S.; Berger, T. Identification of functional synaptic plasticity from spiking activities using nonlinear dynamical modeling. J. Neurosci. Methods 2015, 244, 123–135. [Google Scholar] [CrossRef] [PubMed]
- Berger, T.; Song, D.; Chan, R.M.; Marmarelis, V.; LaCoss, J.; Wills, J.; Hampson, R.; Deadwyler, S.; Granacki, J. A hippocampal cognitive prosthesis: Multi-input, multi- output nonlinear modeling and vlsi implementation. IEEE Trans. Neural Syst. Rehabil. Eng. 2012, 20, 198–211. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Cui, W.; Guo, Y.; Huang, T.; Yang, X.; Wei, H. Time-varying system identification using an ultra-orthogonal forward regression and multiwavelet basis functions with applications to EEG. IEEE Trans. Neural Netw. Learn. Syst. 2017. [Google Scholar] [CrossRef] [PubMed]
- Kukreja, S.L.; Löfberg, J.; Brenner, M.J. A least absolute shrinkage and selection operator (lasso) for nonlinear system identification. IFAC Proc. Vol. 2006, 39, 814–819. [Google Scholar] [CrossRef]
- Rasouli, M.; Westwick, D.T.; Rosehart, W.D. Reducing induction motor identified parameters using a non- linear lasso method. Electr. Power Syst. Res. 2012, 88. [Google Scholar] [CrossRef]
- Li, Z.; Sillanpää, M.J. Overview of lasso-related penalized regression methods for quantitative trait mapping and genomic selection. Theor. Appl. Genet. 2012, 125, 419–435. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wee, C.; Jie, B.; Peng, Z.; Shen, D. Sparse multivariate autoregressive modeling for mild cognitive impairment classification. Neuroinformatics 2014, 12, 455–469. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Wei, H.; Coca, D.; Billings, S. Model term selection for spatio-temporal system identification using mutual information. Int. J. Syst. Sci. 2013, 44, 223–231. [Google Scholar] [CrossRef]
- Li, Y.; Cui, W.; Luo, M.; Li, K.; Wang, L. High-resolution time–frequency representation of eeg data using multi-scale wavelets. Int. J. Syst. Sci. 2017, 48. [Google Scholar] [CrossRef]
- Stafford, B.; Sher, A.; Litke, A.; Feldheim, D. Spatial-temporal patterns of retinal waves underlying activity-dependent refinement of retinofugal projections. Neuron 2009, 64, 200–212. [Google Scholar] [CrossRef] [PubMed]
- Heuberger, P.C.; van den Hof, P.J.; Wahlber, B. Modelling and Identification with Rational Orth-Ogonal Basis Functions; Springer: London, UK, 2005. [Google Scholar]

| Symbols | Meanings |
|---|---|
| y | Output signal |
| X | Equivalent input signals set |
| M | Memory length of signals |
| Link function of the model | |
| Zeroth-order kernel function | |
| First-order kernel function of the n-th input at lag | |
| Time-Varying Laguerre expansion coefficient of the l-th basis function of the n-th kernel | |
| The l-th order Laguerre basis function | |
| L | Number of Laguerre basis functions |
| Laguerre parameter | |
| P | Composite penalty function |
| Regularization parameter | |
| Time-invariant multiwavelet expansion coefficients | |
| The m-th order Bspline basis function | |
| j | The scale parameter of Bspline basis function |
| m | The order parameter of Bspline basis function |
| p | The number of selected significant model terms |
| Performance Indicators | Estimated Kernels | Identification Methods | |||
|---|---|---|---|---|---|
| SSPPF | sSSPPF | dMGLV | sMGLV | ||
| MSE | 0.1409 | 0.1310 | 0.0592 | 0.0536 | |
| 0.0453 | 0.0435 | 0.0330 | 0.0259 | ||
| 0.0980 | 0.0922 | 0.0483 | 0.0416 | ||
| 0.0911 | 0.0882 | 0.0521 | 0.0408 | ||
| 0.0525 | 0.0529 | 0.0260 | 0.0217 | ||
| 0.0405 | 0.0387 | 0.0222 | 0.0162 | ||
| 0.0431 | 0.0000 | 0.0250 | 0.0000 | ||
| 0.0467 | 0.0000 | 0.0371 | 0.0000 | ||
| 0.0317 | 0.0288 | 0.0078 | 0.0078 | ||
| NRMSE | 0.1987 | 0.1894 | 0.0847 | 0.0791 | |
| 0.2315 | 0.2243 | 0.1472 | 0.1187 | ||
| 0.2337 | 0.2177 | 0.1101 | 0.0991 | ||
| 0.2307 | 0.2229 | 0.1212 | 0.0952 | ||
| 0.2848 | 0.2821 | 0.1270 | 0.1137 | ||
| 0.2370 | 0.2316 | 0.1284 | 0.0875 | ||
| * | - | - | - | - | |
| * | - | - | - | - | |
| 0.1634 | 0.1533 | 0.0425 | 0.0384 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Li, Y.; Huang, T.; Chan, R.H.M. A Sparse Multiwavelet-Based Generalized Laguerre–Volterra Model for Identifying Time-Varying Neural Dynamics from Spiking Activities. Entropy 2017, 19, 425. https://doi.org/10.3390/e19080425
Xu S, Li Y, Huang T, Chan RHM. A Sparse Multiwavelet-Based Generalized Laguerre–Volterra Model for Identifying Time-Varying Neural Dynamics from Spiking Activities. Entropy. 2017; 19(8):425. https://doi.org/10.3390/e19080425
Chicago/Turabian StyleXu, Song, Yang Li, Tingwen Huang, and Rosa H. M. Chan. 2017. "A Sparse Multiwavelet-Based Generalized Laguerre–Volterra Model for Identifying Time-Varying Neural Dynamics from Spiking Activities" Entropy 19, no. 8: 425. https://doi.org/10.3390/e19080425





