Performance Analysis of a Proton Exchange Membrane Fuel Cell Based Syngas
Abstract
1. Introduction
2. The Auxiliary Systems outside a PEM Fuel Cell
2.1. The Heat Needed in HE1 and HE2
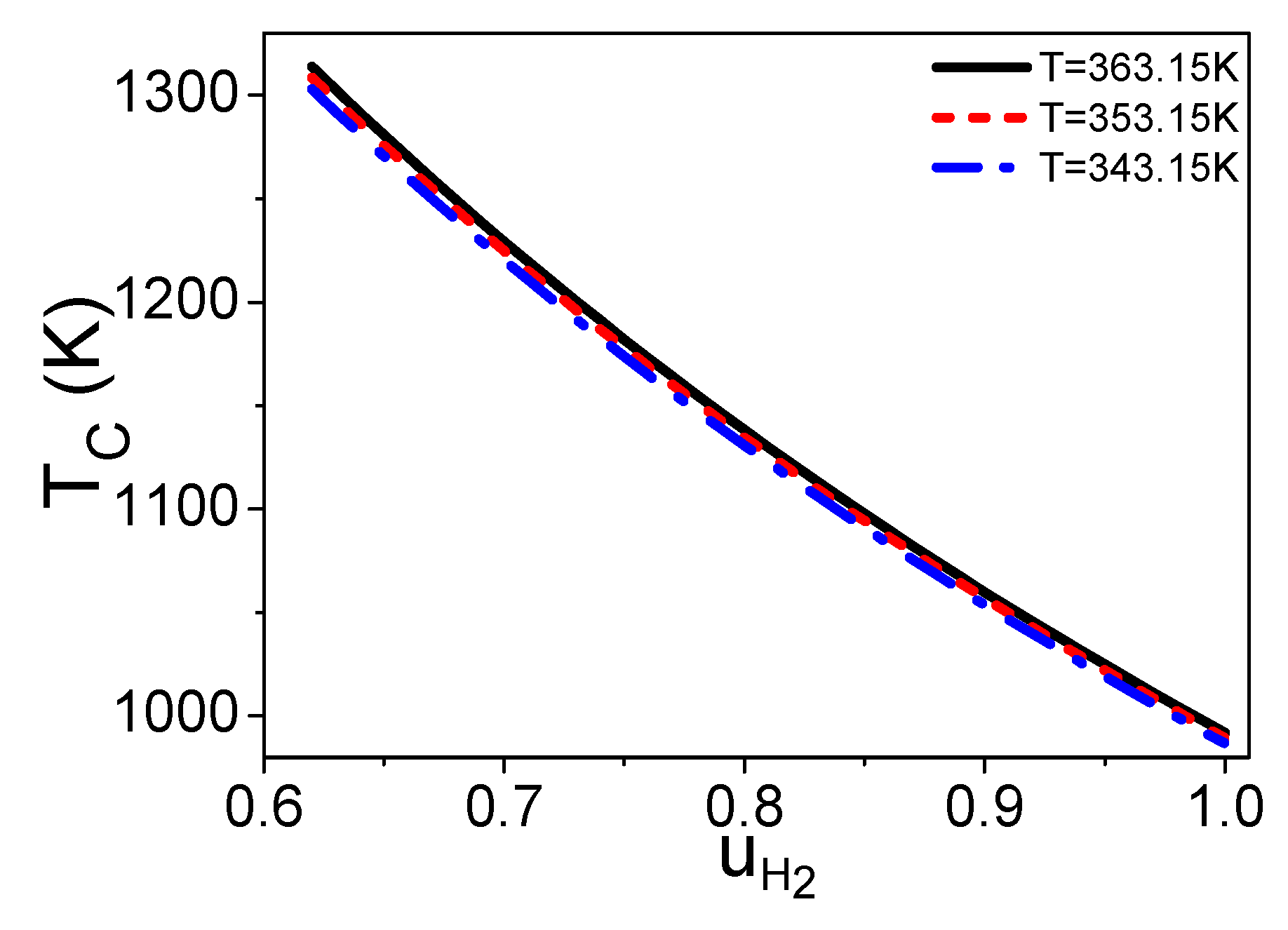
2.2. The Molar Ratio of Syngas into the Burner and Steam Reformer
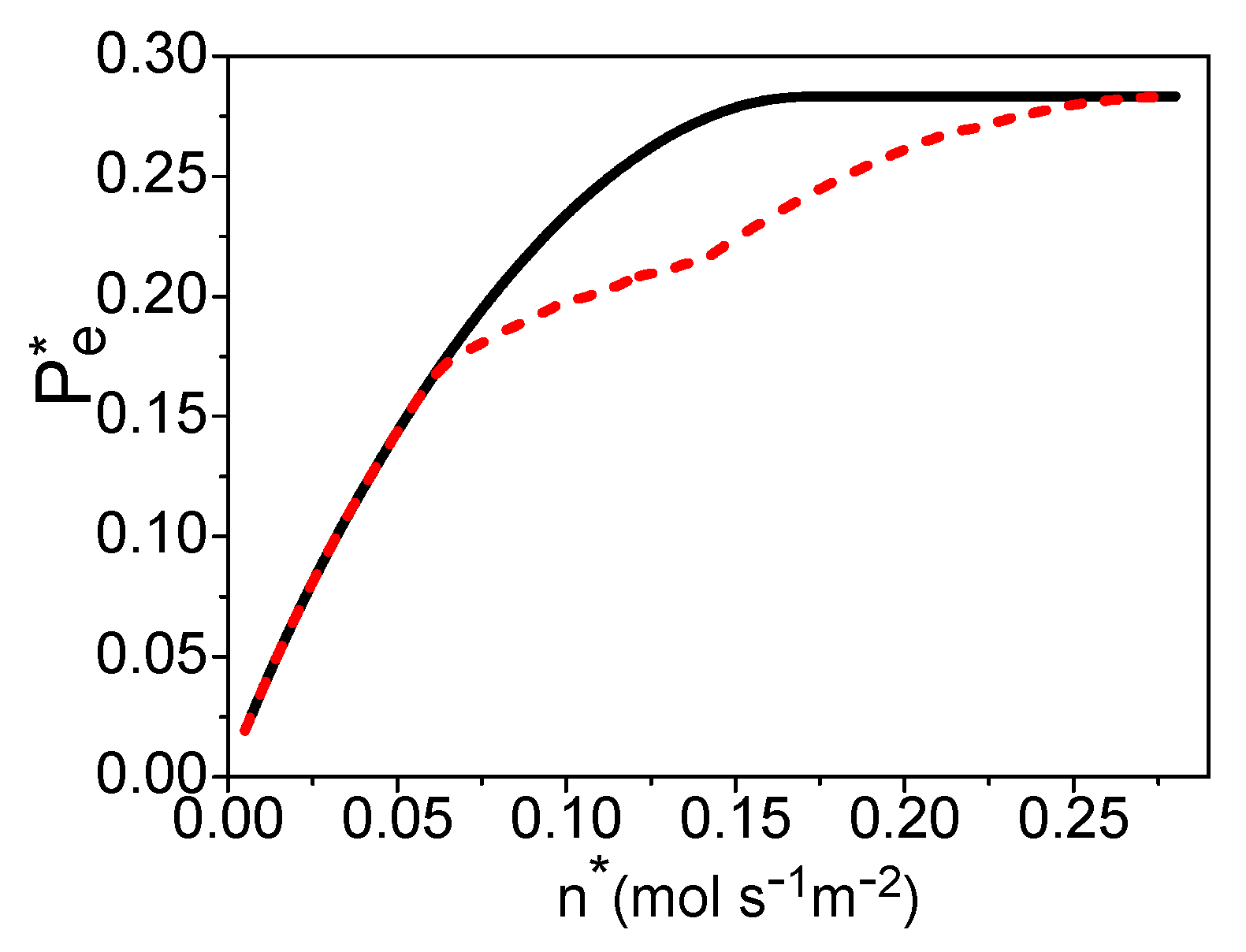
3. The Electric Power of a PEM Fuel Cell Based Syngas
4. The Total Energy Conversion Efficiency
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Effective surface area of the bipolar plate | |
| Charge transfer coefficient at anode | |
| Charge transfer coefficient at cathode | |
| Parameter in the expression of overpotential | |
| Constant in the expression of overpotential | |
| Molar heat capacity of k | |
| Enthalpy change of gases | |
| Enthalpy change of gases | |
| Gibbs function change of gases | |
| Entropy change of gases | |
| Stoichiometry coefficient | |
| Stoichiometry coefficient | |
| Membrane thickness | |
| Faraday constant | |
| Efficiency of the hybrid system | |
| Molar enthalpy of k at 600 °C | |
| Molar enthalpy of k at 25 °C | |
| Molar enthalpy of k at temperature T | |
| Enthalpy of gases leaving the fuel cell | |
| Enthalpy of gases into burner | |
| Enthalpy of gases leaving the burner | |
| Electric current of a PEM fuel cell | |
| Exchange current density of the electrodes | |
| Current density of a PEM fuel cell | |
| Limiting current density of a PEM fuel cell | |
| Latent heat of one mole water | |
| Water content | |
| Mole flow rate of syngas into HE1 | |
| Mole rate of water added into syngas | |
| Mole flow rate of syngas into HE1 unit area | |
| Number of electrons | |
| Electric power density of a PEM fuel cell | |
| Electric power of a PEM fuel cell | |
| Pressure at the cathode | |
| Pressure at the anode | |
| Saturation pressure of water | |
| Partial pressure of k at the electrode | |
| The heat needed in HE2 unit time | |
| The heat needed in HE1 unit time | |
| Lower heating value of k per molar | |
| Universal gas constant | |
| Molar entropy of k at 25°C | |
| Membrane conductivity | |
| Operating temperature of a PEM fuel cell | |
| Combustion temperature | |
| Temperature | |
| Temperature of gases leaving HE1 | |
| Hydrogen utilization factor in a fuel cell | |
| Activation overpotential | |
| Ohm overpotential | |
| Concentration overpotential | |
| Dry gas molar ratio at cathode | |
| Dry gas molar ratio at anode | |
| The molar ratio | |
| Molar fraction of k in syngas |
References
- Brey, J.J.; Carazo, A.F.; Brey, R. Exploring the marketability of fuel cell electric vehicles in terms of infrastructure and hydrogen costs in Spain. Renew. Sustain. Energy Rev. 2018, 82, 2893–2899. [Google Scholar] [CrossRef]
- Ham, S.W.; Jo, S.Y.; Dong, H.W.; Jeong, J.W. A simplified PEM fuel cell model for building cogeneration applications. Energy Build. 2015, 107, 213–225. [Google Scholar] [CrossRef]
- Izurieta, E.M.; Adrover, M.E.; Pedernera, M.N.; López, E. Ethanol processor design for hydrogen production. Kinetic analysis and process integration. Ind. Eng. Chem. Res. 2018, 57, 13615–13626. [Google Scholar] [CrossRef]
- Maximini, M.; Engelhardt, P.; Brenner, M.; Beckmann, F.; Moritz, O. Fast start-up of a diesel fuel processor for PEM fuel cells. Int. J. Hydrog. Energy 2014, 39, 18154–18163. [Google Scholar] [CrossRef]
- Peng, W.X.; Wang, L.S.; Mirzaee, M.; Ahmadi, H.; Esfahani, M.J.; Fremaux, S. Hydrogen and syngas production by catalytic biomass gasification. Energy Convers. Manag. 2017, 135, 270–273. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, W.; Deng, Y.; Zhu, J.Y. Low-temperature microbial and direct conversion of lignocellulosic biomass to electricity: Advances and Challenges. Renew. Sustain. Energy Rev. 2017, 71, 268–282. [Google Scholar] [CrossRef]
- Guan, T.; Chutichai, B.; Alvfors, P.; Arpornwichanop, A. Biomass-fuelled PEM FC systems: Evaluation of two conversion paths relevant for different raw materials. Energy Convers. Manag. 2015, 106, 1183–1191. [Google Scholar] [CrossRef]
- Wess, R.; Nores-Pondal, F.; Laborde, M.; Giunta, P. Single stage H2 production, purification, and heat supply by means of sorption-enhanced steam reforming of glycerol. A thermodynamic analysis. Chem. Eng. Sci. 2015, 134, 86–95. [Google Scholar] [CrossRef]
- Shin’ya, O.; Itaru, T.; Shunsuke, K.; Akira, H.; Seizi, S. Exergy analysis of the woody biomass Stirling engine and PEM-FC combined system with exhaust heat reforming. Int. J. Hydrog. Energy 2008, 33, 2289–2299. [Google Scholar]
- Purnima, P.; Jayanti, S. A high-efficiency, auto-thermal system for on-board hydrogen production for low temperature PEM fuel cells using dual reforming of ethanol. Int. J. Hydrog. Energy 2016, 41, 13800–13810. [Google Scholar] [CrossRef]
- Salemme, L.; Menna, L.; Simeone, M.; Volpicelli, G. Energy efficiency of membrane-based fuel processors-PEM fuel cell systems. Int. J. Hydrog. Energy 2010, 35, 3712–3720. [Google Scholar] [CrossRef]
- Comas, J.; Dieuzeide, M.; Baronetti, G.; Laborde, M.; Amadeo, N. Methane steam reforming and ethanol steam reforming using a Ni(II)-Al(III) catalyst prepared from lamellar double hydroxides. Chem. Eng. J. 2006, 118, 11–15. [Google Scholar] [CrossRef]
- Ersoz, A.; Olgun, H.; Ozdogan, S. Reforming options for hydrogen production from fossil fuels for PEM fuel cells. J. Power Sources 2006, 154, 67–73. [Google Scholar] [CrossRef]
- Ito, H.; Heo, Y.; Ishida, M.; Nakano, A.; Someya, S.; Munakata, T. Application of a self-supporting micro-porous layer to gas diffusion layers of proton exchange membrane fuel cells. J. Power Sources 2017, 342, 393–404. [Google Scholar] [CrossRef]
- Mishra, A.K.; Bose, S.; Kuila, T.; Kim, N.H.; Lee, J.H. Silicate-based polymer-nanocomposite membranes for polymer electrolyte membrane fuel cells. Prog. Polym. Sci. 2012, 37, 842–869. [Google Scholar] [CrossRef]
- Chien, H.C.; Tsai, L.D.; Lai, C.M.; Lin, J.N.; Zhu, C.Y.; Chang, F.C. Characteristics of high-water-uptake activated carbon/Nafion hybrid membranes for proton exchange membrane fuel cells. J. Power Sources 2013, 226, 87–93. [Google Scholar] [CrossRef]
- Kim, H.; Kim, K. Numerical study on the effects of gas humidity on proton-exchange membrane fuel cell performance. Int. J. Hydrog. Energy 2016, 41, 11776–11783. [Google Scholar] [CrossRef]
- Liu, J.X.; Guo, H.; Ye, F.; Ma, C.F. Two-dimensional analytical model of a proton exchange membrane fuel cell. Energy 2017, 119, 299–308. [Google Scholar]
- Kahraman, H.; Orhan, M.F. Flow field bipolar plates in a proton exchange membrane fuel cell: Analysis & modeling. Energy Convers. Manag. 2017, 133, 363–384. [Google Scholar]
- Zhang, X.; Wang, Y.; Liu, T.; Chen, J. Theoretical basis and performance optimization analysis of a solid oxide fuel cell-gas turbine hybrid system with fuel reforming. Energy Convers. Manag. 2014, 86, 1102–1109. [Google Scholar] [CrossRef]
- Shin, Y.; Park, W.; Chang, J.; Park, J. Evaluation of the high temperature electrolysis of steam to produce hydrogen. Int. J. Hydrog. Energy 2007, 32, 1486–1491. [Google Scholar] [CrossRef]
- Zhang, X.; Li, G.; Li, J.; Feng, Z. Numerical study on electric characteristics of solid oxide fuel cells. Energy Convers. Manag. 2007, 48, 977–989. [Google Scholar] [CrossRef]
- Strahl, S.; Costa-Castelló, R. Temperature control of open-cathode PEM fuel cells. IFAC-PapersOnLine 2017, 50-1, 11088–11093. [Google Scholar]
- Zhang, X.; Ni, M.; He, W.; Dong, F. Theoretical analysis and optimum integration strategy of the PEM fuel cell and internal combustion engine hybrid system for vehicle applications. Int. J. Energy Res. 2015, 39, 1664–1672. [Google Scholar] [CrossRef]
- Rowe, A.; Li, X. Mathematical modeling of proton exchange membrane fuel cells. J. Power Sources 2001, 102, 82–96. [Google Scholar] [CrossRef]
- Zhang, Y.; Mawardi, A.; Pitchumani, R. Numerical studies on an air-breathing proton exchange membrane (PEM) fuel cell stack. J. Power Sources 2007, 173, 264–276. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, J.; Chen, J. The parametric optimum analysis of a proton exchange membrane (PEM) fuel cell and its load matching. Energy 2010, 35, 5294–5299. [Google Scholar] [CrossRef]
- Chan, S.H.; Low, C.F.; Ding, O.L. Energy and exergy analysis of simple solid-oxide fuel-cell power systems. J. Power Sources 2002, 103, 188–200. [Google Scholar] [CrossRef]
- Larminie, J.; Dicks, A. Fuel Cell Systems Explained; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Ay, M.; Midilli, A.; Dincer, I. Exergetic performance analysis of a PEM fuel cell. Int. J. Energy Res. 2006, 30, 307–321. [Google Scholar] [CrossRef]
- Pukrushpan, J.; Stefanopoulou, A.; Peng, H. Modeling and control for PEM fuel cell stack system. In Proceedings of the American Control Conference, Anchorage, AK, USA, 8–10 May 2002; IEEE: Piscataway, NJ, USA, 2002. [Google Scholar]
- Wang, Y.; Chen, K.; Mishler, J.; Cho, S.; Adroher, X. A review of polymer electrolyte membrane fuel cells: Technology, applications, and needs on fundamental research. Appl. Energy 2011, 88, 981–1007. [Google Scholar] [CrossRef]





| Component k | ||||||
|---|---|---|---|---|---|---|
| Mole fraction of k in syngas: xk | 0.13 | 0.01 | 0.16 | 0.05 | 0.36 | 0.29 |
| Component | (J·mol−1) | (J·mol−1·K−1) | (J·mol−1) | Molar Heat Capacity (J·mol−1·K−1) |
|---|---|---|---|---|
| N2 | 0 | — | — | 29.12 |
| O2 | 0 | 205.138 | — | 25.8911 + 0.0129874t − 0.0000038644t2 |
| CH4 | −75,000 | — | — | 14.1555 + 0.0755466t − 0.0000180032t2 |
| CO2 | −393,800 | — | — | 26.0167 + 0.0435259t − 0.0000148422t2 |
| CO | −110,500 | — | — | 26.8742 + 0.006971t − 0.0000008206t2 |
| H2 | 0 | 130.695 | — | 29.0856 − 0.0008373t + 0.0000020138t2 |
| H2O (g) | −241,800 | — | — | 30 + 0.01071t + 33000/t2 |
| H2O (l) | −285,800 | 69.940 | 40,700 | 75.44 |
| Parameter | Value |
|---|---|
| Number of electrons, | 2 |
| Faraday constant, F (C mol−1) | 96485 |
| Universal gas constant, R (J·mol·K−1) | 8.314 |
| Pressure at the anode, (atm) | 3 [13] |
| Pressure at the cathode, (atm) | 5 [13] |
| Anode stoichiometry, | 1.5 [20] |
| Cathode stoichiometry, | 3 [20] |
| Dry gas molar ratio at anode, | [13] |
| Dry gas molar ratio at cathode, | 3.762 (air) |
| Charge transfer coefficient at the anode, | 0.5 [20] |
| Charge transfer coefficient at the cathode, | 1 [20] |
| Membrane thickness, (cm) | 0.018 [13] |
| 14 [21] | |
| Constant, | 2 [20] |
| Limiting current density, (A cm−2) | 2 [20] |
| T = 70 °C: (atm); | 0.3071; 0.2048 |
| (kJ mol−1): k = H2; CO; CH4 | 241.9; 283.2; 803.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Lin, Q.; Liu, H.; Chen, X.; Su, S.; Ni, M. Performance Analysis of a Proton Exchange Membrane Fuel Cell Based Syngas. Entropy 2019, 21, 85. https://doi.org/10.3390/e21010085
Zhang X, Lin Q, Liu H, Chen X, Su S, Ni M. Performance Analysis of a Proton Exchange Membrane Fuel Cell Based Syngas. Entropy. 2019; 21(1):85. https://doi.org/10.3390/e21010085
Chicago/Turabian StyleZhang, Xiuqin, Qiubao Lin, Huiying Liu, Xiaowei Chen, Sunqing Su, and Meng Ni. 2019. "Performance Analysis of a Proton Exchange Membrane Fuel Cell Based Syngas" Entropy 21, no. 1: 85. https://doi.org/10.3390/e21010085
APA StyleZhang, X., Lin, Q., Liu, H., Chen, X., Su, S., & Ni, M. (2019). Performance Analysis of a Proton Exchange Membrane Fuel Cell Based Syngas. Entropy, 21(1), 85. https://doi.org/10.3390/e21010085





