Extreme Interval Entropy Based on Symbolic Analysis and a Self-Adaptive Method
Abstract
:1. Introduction
2. Symbolic Analysis for Components
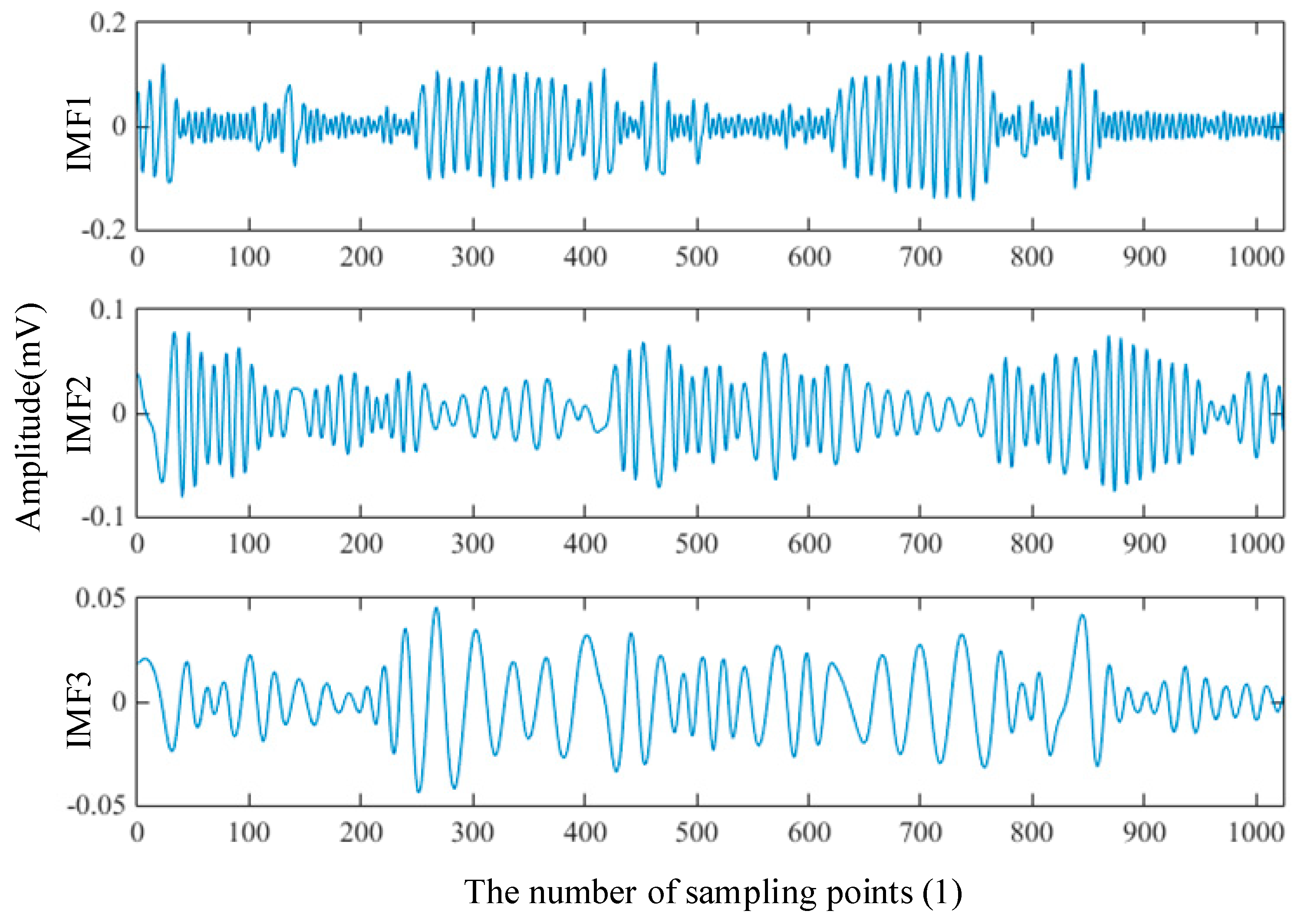
2.1. Intrinsic Mode Functions
- (1)
- Find the positions and amplitudes of all local maxima and minima, then denote them as and correspondingly.
- (2)
- Create the upper and lower envelopes by cubic spline interpolation of the local maxima and the local minima, respectively. Calculate the mean of both the upper and lower envelops;
- (3)
- The envelope is then subtracted from the signal using. If satisfies the two conditions of IMF conditions as follows, it can be obtained as an IMF. Otherwise, set and repeat processes (1)–(3) until the residual satisfies the stopping criterion.
- (4)
- Once IMF has been gotis obtained, should be replaced by the residual. The above process is repeated and the signal would be separated into n IMFs and a residue signal as in Equation (1). at last: Finally, the signal is decomposed into n number of IMFs and the residual signal.
2.2. Symbolic Analysis for IMF
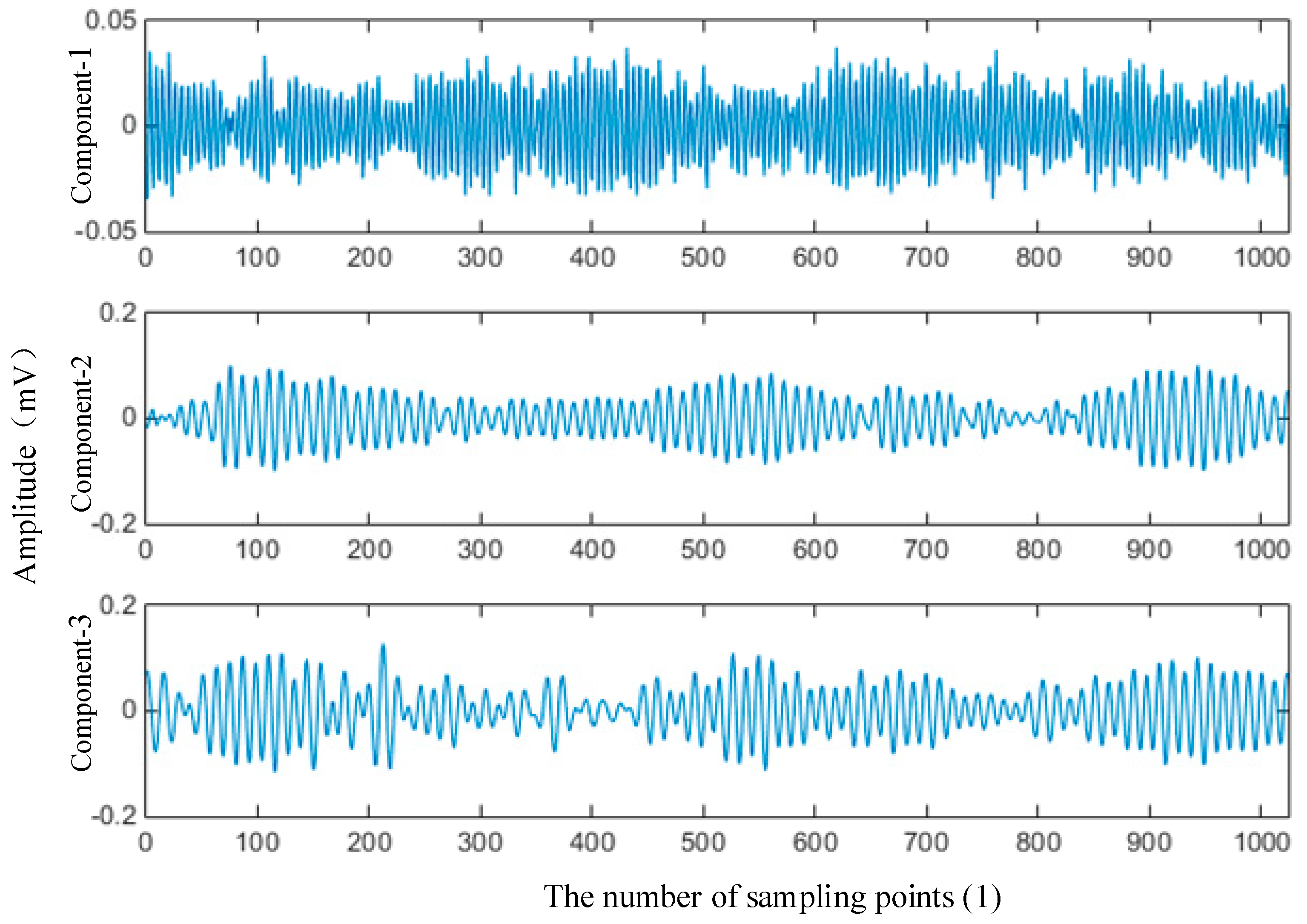
2.3. Symbolic Analysis of EWT
3. Experiment
3.1. Fault Diagnosis of Rolling Bearing with a Frequency of 12 kHz
3.2. Fault Diagnosis of Rolling Bearing with a Frequency of 48 kHz
3.3. Fault Diagnosis of Rolling Bearing in Printing Press
4. Conclusions
- (1)
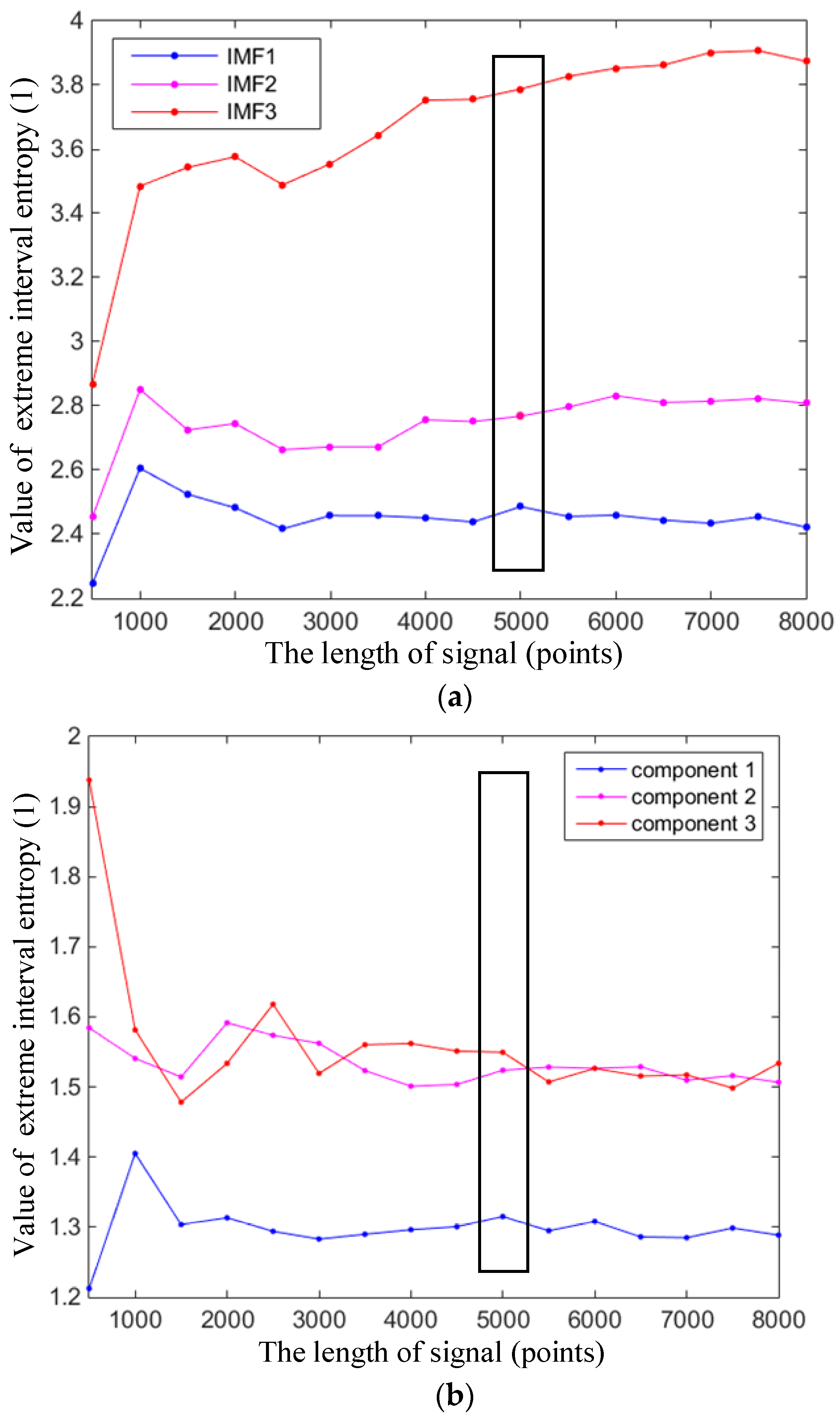
- A symbolized method was given to normalize the components from a self-adaptive perspective according to the positions of extreme values. With the symbolization, the components were simplified toin a large degree (only contains 1, −1, 0). Then, an improved feature for these simplified components, extreme interval entropy, was proposed and calculated for to similar self-adaptive components.
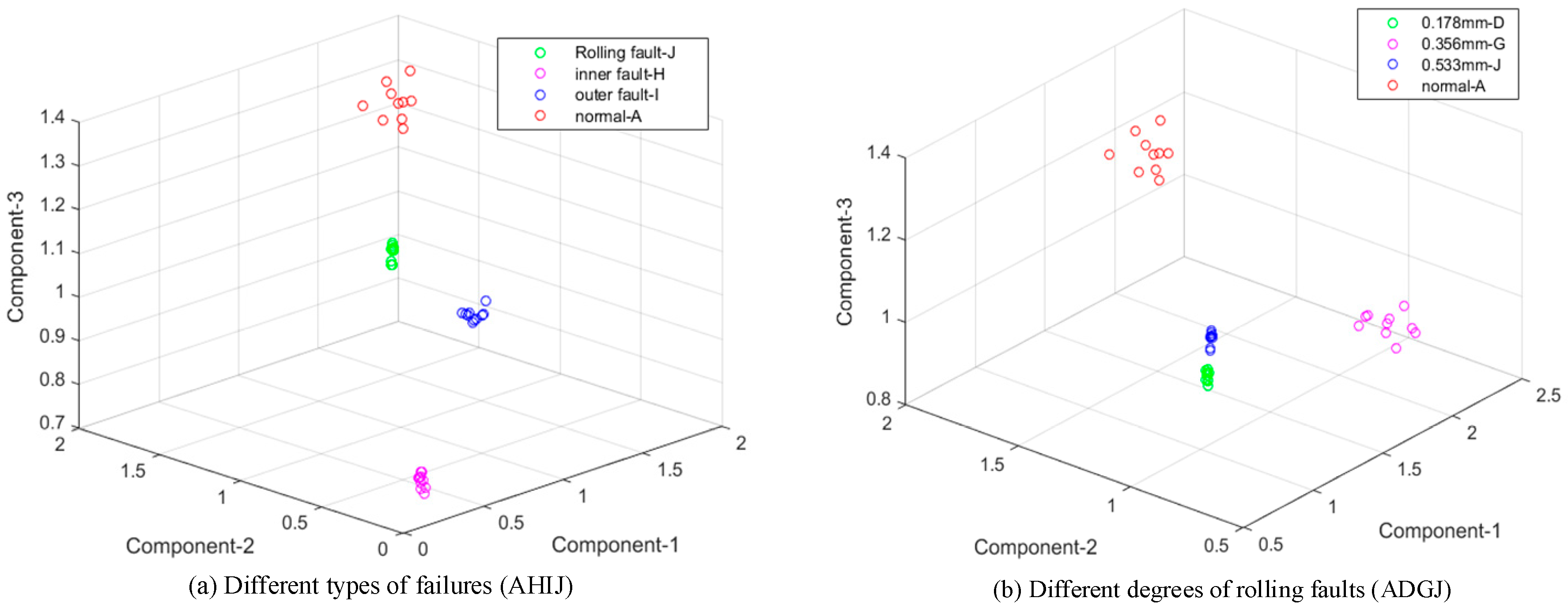
- (2)
- According to the identified result of three group experiments, the extreme interval entropies of high order components can be distinguished in a 3D figure. Both different fault kinds and degrees were distinguished well in Section 3.1 and Section 3.2 by the given method under sample frequencies of 12 kHz and 48 kHz. Extreme interval entropy was proved to be an effectively feature in this fault recognition. A cage fault in the rolling bearing of a printing press was also identified correctly in Section 3.3. Extreme interval entropy with EWT always has a better effect.
- (3)
- The effectiveness of the proposed method was evaluated with K-means cluster. The accuracy rate of fault diagnosis in rolling bearing was between 75% to 100% with EMD while 95% to 100% with EWT. In the experiment with thein printing press, the given method could reach to a 100% accuracy rate with EWT in identification of the normal bearing, fault bearing in 4 r/s and in 8 r/s (cannot distinguish normal samples atin different speeds). Extreme interval entropy was proved to be a reliable and effective tool for fault diagnosis and other similar applications.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Singh, D.S.; Zhao, Q. Pseudo-fault signal assisted EMD for fault detection and isolation in rotating machines. Mech. Syst. Signal Process. 2016, 81, 202–218. [Google Scholar] [CrossRef]
- Pang, B.; Tang, G.; Tian, T.; Zhou, C. Rolling bearing fault diagnosis based on an improved HTT transform. Sensors 2018, 18, 1203. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Gao, R.X.; Yan, R. Multi-scale enveloping order spectrogram for rotating machine health diagnosis. Mech. Syst. Signal Process. 2014, 46, 28–44. [Google Scholar] [CrossRef]
- Tsao, W.-C.; Li, Y.-F.; Du Le, D.; Pan, M.-C. An insight concept to select appropriate IMFs for envelope analysis of bearing fault diagnosis. Measurement 2012, 45, 1489–1498. [Google Scholar] [CrossRef]
- Wu, T.Y.; Chung, Y.L. Misalignment diagnosis of rotating machinery through vibration analysis via the hybrid EEMD and EMD approach. Smart Mater. Struct. 2009, 18, 095004. [Google Scholar] [CrossRef]
- Chen, J.; Li, Z.; Pan, J.; Chen, G.; Zi, Y.; Yuan, J.; Chen, B.; He, Z. Wavelet transform based on inner product in fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2016, 70–71, 1–35. [Google Scholar] [CrossRef]
- Yang, J.N.; Lei, Y.; Pan, S.; Huang, N. System identification of linear structures based on Hilbert–Huang spectral analysis. Part I: Normal modes. Earthq. Eng. Struct. Dyn. 2010, 32, 1533–1554. [Google Scholar] [CrossRef]
- Xue, Y.-j.; Zhang, J.; Chang, Q.; Zhang, L.-p.; Zou, F. Instantaneous Frequency Extraction Using the EMD-based Wavelet Ridge to Reveal Geological Features. Front. Earth Sci. 2018, 6, 65. [Google Scholar] [CrossRef]
- Agrawal, S.; Gupta, A. Fractal and EMD based removal of baseline wander and powerline interference from ECG signals. Comput. Biol. Med. 2013, 43, 1889–1899. [Google Scholar] [CrossRef] [PubMed]
- Jia, S.; Guo, Y.; Wang, Q.; Zhang, J. Trend Extraction and Similarity Matching of Financial Time Series Based on EMD Method. In Proceedings of the IEEE World Congress on Computer Science & Information Engineering, Los Angeles, CA, USA, 31 March–2 April 2009. [Google Scholar]
- Zhang, B.; Wang, J.; Fang, W. Volatility behavior of visibility graph EMD financial time series from Ising interacting system. Phys. A Stat. Mech. Appl. 2015, 432, 301–314. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 41. [Google Scholar] [CrossRef]
- Peng, Z.K.; Tse, P.W.; Chu, F.L. A comparison study of improved Hilbert-Huang transform and wavelet transform: Application to fault diagnosis for rolling bearing. Mech. Syst. Signal Process. 2005, 19, 974–988. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Z.; Chen, S.; Wang, J.; Zhang, X. Optimised ensemble empirical mode decomposition with optimised noise parameters and its application to rolling element bearing fault diagnosis. Insight Non-Destr. Test. Cond. Monit. 2016, 58, 494–501. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Zi, Y. A Comparative Study on the Local Mean Decomposition and Empirical Mode Decomposition and Their Applications to Rotating Machinery Health Diagnosis. J. Vib. Acoust. 2010, 132, 613–624. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Wahyu, C.; Tegoeh, T.; Buyung, K.; Kiet, T.A. Integrated condition monitoring and prognosis method for incipient defect detection and remaining life prediction of low speed slew bearings. Machines 2017, 5, 11. [Google Scholar]
- Rodriguez, N.; Cabrera, G.; Lagos, C.; Cabrera, E. Stationary wavelet Singular Entropy and Kernel Extreme Learning for Bearing Multi-Fault Diagnosis. Entropy 2017, 19, 541. [Google Scholar] [CrossRef]
- Gilles, J. Empirical Wavelet Transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Song, Y.; Zeng, S.; Ma, J.; Guo, J. A fault diagnosis method for roller bearing based on empirical wavelet transform decomposition with adaptive empirical mode segmentation. Measurement 2018, 117, 266–276. [Google Scholar] [CrossRef]
- Caesarendra, W.; Tjahjowidodo, T. A Review of Feature Extraction Methods in Vibration-Based Condition Monitoring and Its Application for Degradation Trend Estimation of Low-Speed Slew Bearing. Machines 2017, 5, 21. [Google Scholar] [CrossRef]
- Glowacz, A. Acoustic-Based Fault Diagnosis of Commutator Motor. Electronics 2018, 7, 299. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, Y.; Guo, Q.; Hu, C.; Peng, Z. Multi-dimensional variational mode decomposition for bearing-crack detection in wind turbines with large driving-speed variations. Renew. Energy 2018, 116, 55–73. [Google Scholar] [CrossRef]
- Glowacz, A. Fault diagnosis of single-phase induction motor based on acoustic signals. Mech. Syst. Signal Process. 2019, 117, 65–80. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, H.; Liu, J.; Hou, H. A Research on Maximum Symbolic Entropy from Intrinsic Mode Function and Its Application in Fault Diagnosis. Math. Probl. Eng. 2017, 2017, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Sánchez-López, C.; Fernández, F.V.; Tlelo-Cuautle, E.; Tan, S.X.-D. Pathological Element-Based Active Device Models and Their Application to Symbolic Analysis. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 1382–1395. [Google Scholar] [CrossRef] [Green Version]
- Daw, C.S.; Finney, C.E.A.; Tracy, E.R. A review of symbolic analysis of experimental data. Rev. Sci. Instrum. 2003, 74, 915. [Google Scholar] [CrossRef]
- Mingtao, G.; Jie, W.; Xiangyang, R. Fault Diagnosis of Rolling Bearings Based on EWT and KDEC. Entropy 2017, 19, 633. [Google Scholar] [Green Version]
- El Safty, S.; Elzonkoly, A. Applying wavelet entropy principle in fault classification. Int. J. Electr. Power Energy Syst. 2009, 31, 604–607. [Google Scholar] [CrossRef] [Green Version]
- Premjith, B.; Mohan, N.; Poornachandran, P.; Soman, K. Audio Data Authentication with PMU Data and EWT. Procedia Technol. 2015, 21, 596–603. [Google Scholar] [CrossRef] [Green Version]
- Loparo, K.A. Bearings Vibration Data Set; Case Western Reserve University. Available online: http://www.eecs.cwru.edu/laboratory/Bearing/download.htm (accessed on 1 October 2018).
- Li, C.; Zheng, C.; Tai, C. Detection of ECG characteristic points using wavelet transforms. IEEE Trans. Biomed. Eng. 1995, 42, 21–28. [Google Scholar] [PubMed]
- Mao, W.; Feng, W.; Liang, X. A novel deep output kernel learning method for bearing fault structural diagnosis. Mech. Syst. Signal Process. 2019, 117, 293–318. [Google Scholar] [CrossRef]
- Wang, W.; Golnaraghi, F.; Ismail, F. Condition Monitoring of Multistage Printing Presses. J. Sound Vib. 2005, 27, 755–766. [Google Scholar] [CrossRef]
- Sutanto, E.; Alleyne, A. A semi-continuous Roll-to-Roll (R2R) electrohydrodynamic jet printing system. Mechatronics 2015, 31, 243–254. [Google Scholar] [CrossRef]











| Sample | Bearing Condition | Diameter of Faults (mm) |
|---|---|---|
| A | Normal | --- |
| B | Inner fault | 0.178 |
| C | Outer fault | 0.178 |
| D | Rolling fault | 0.178 |
| E | Inner fault | 0.356 |
| F | Outer fault | 0.356 |
| G | Rolling fault | 0.356 |
| H | Inner fault | 0.533 |
| I | Outer fault | 0.533 |
| J | Rolling fault | 0.533 |
| Order | Sample | EMD | EWT | Sample | EMD | EWT |
|---|---|---|---|---|---|---|
| 1st | A | 2.404 | 1.310 | F | 1.227 | 1.013 |
| B | 1.258 | 1.015 | G | 0.986 | 0.965 | |
| C | 1.174 | 0.972 | H | 0.807 | 0.736 | |
| D | 0.921 | 1.058 | I | 1.231 | 1.001 | |
| E | 1.215 | 1.054 | J | 1.130 | 1.158 | |
| 2nd | A | 2.725 | 1.564 | F | 1.942 | 0.966 |
| B | 1.849 | 0.444 | G | 2.129 | 0.783 | |
| C | 1.343 | 0.825 | H | 1.924 | 0.283 | |
| D | 2.039 | 0.817 | I | 1.702 | 0.590 | |
| E | 1.609 | 0.878 | J | 1.928 | 0.785 | |
| 3rd | A | 3.619 | 1.539 | F | 2.787 | 0.817 |
| B | 2.388 | 0.669 | G | 2.867 | 1.999 | |
| C | 2.018 | 0.721 | H | 3.328 | 0.402 | |
| D | 2.945 | 0.754 | I | 2.302 | 1.043 | |
| E | 2.387 | 0.602 | J | 2.740 | 0.730 |
| Sample | EMD | EWT |
|---|---|---|
| A, H, I, J | 100.00% | 100.00% |
| A, D, G, J | 82.50% | 100.00% |
| A, B, E, H | 100.00% | 100.00% |
| A, C, F, I | 100.00% | 100.00% |
| Sample | Bearing Condition | Diameter of Faults (mm) |
|---|---|---|
| A | Normal | --- |
| B | Inner fault | 0.178 |
| C | Outer fault | 0.178 |
| D | Rolling fault | 0.178 |
| E | Inner fault | 0.356 |
| F | Outer fault | 0.356 |
| G | Rolling fault | 0.356 |
| H | Inner fault | 0.533 |
| I | Outer fault | 0.533 |
| J | Rolling fault | 0.533 |
| Sample | EMD | EWT |
|---|---|---|
| A, H, I, J | 100.00% | 95.00% |
| A, D, G, J | 75.00% | 97.50% |
| A, B, E, H | 95.00% | 100.00% |
| A, C, F, I | 75.00% | 100.00% |
| Sample | EMD | EWT | |
|---|---|---|---|
| A | Fault 4 r/s Fault 8 r/s Normal | 95.00% | 100.00% |
| B | Fault 4 r/s Fault 8 r/s Normal 4 r/s Normal 8 r/s | 72.50% | 77.50% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Shi, Y.; Zhao, Q.; Li, W.; Liu, K. Extreme Interval Entropy Based on Symbolic Analysis and a Self-Adaptive Method. Entropy 2019, 21, 238. https://doi.org/10.3390/e21030238
Xu Z, Shi Y, Zhao Q, Li W, Liu K. Extreme Interval Entropy Based on Symbolic Analysis and a Self-Adaptive Method. Entropy. 2019; 21(3):238. https://doi.org/10.3390/e21030238
Chicago/Turabian StyleXu, Zhuofei, Yuxia Shi, Qinghai Zhao, Wei Li, and Kai Liu. 2019. "Extreme Interval Entropy Based on Symbolic Analysis and a Self-Adaptive Method" Entropy 21, no. 3: 238. https://doi.org/10.3390/e21030238
APA StyleXu, Z., Shi, Y., Zhao, Q., Li, W., & Liu, K. (2019). Extreme Interval Entropy Based on Symbolic Analysis and a Self-Adaptive Method. Entropy, 21(3), 238. https://doi.org/10.3390/e21030238





