A Macroscopic Quantum Three-Box Paradox: Finding Consistency with Weak Macroscopic Realism
Abstract
:1. Introduction
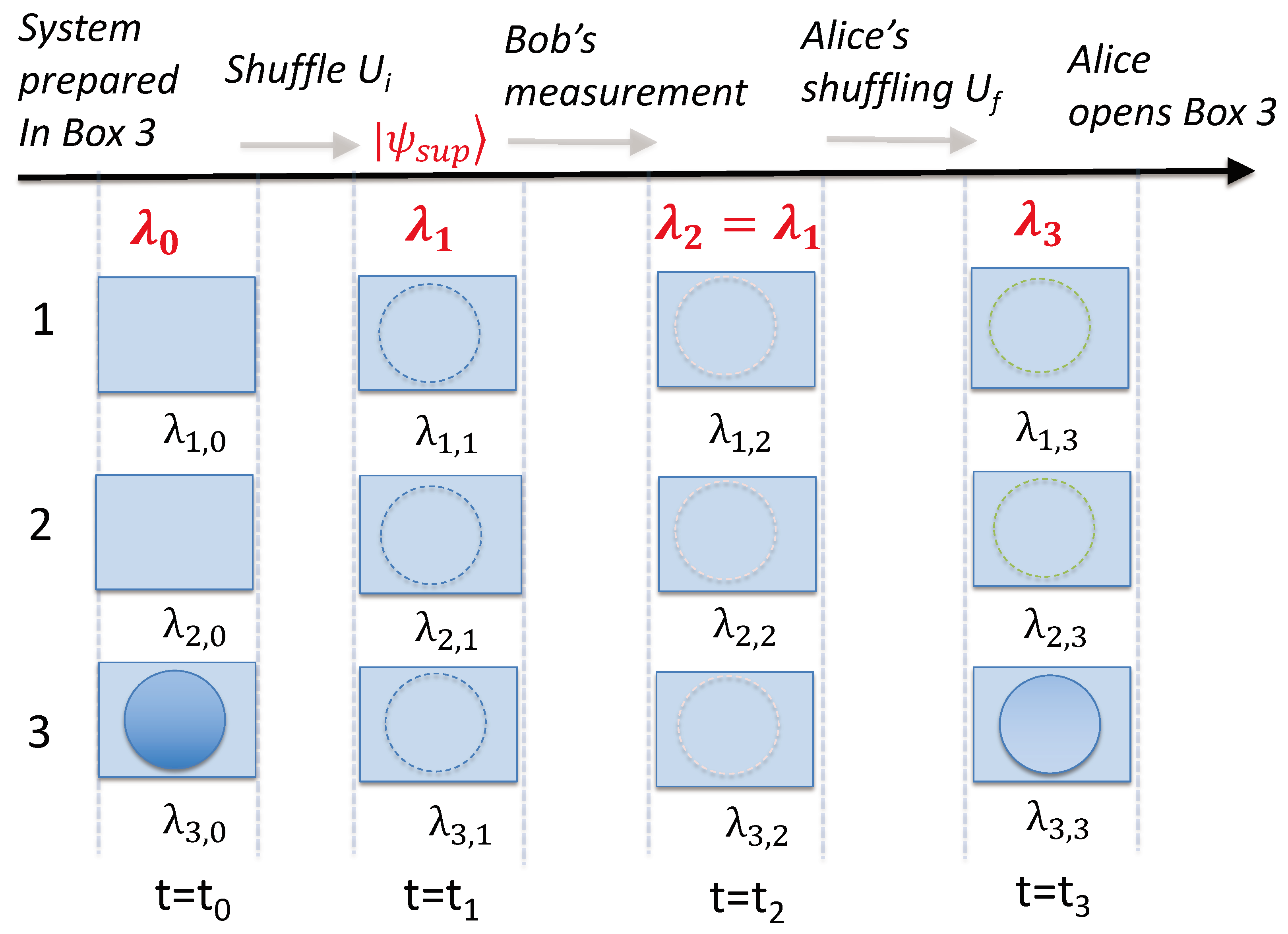
2. Three-Box Paradox
Experimental Realization
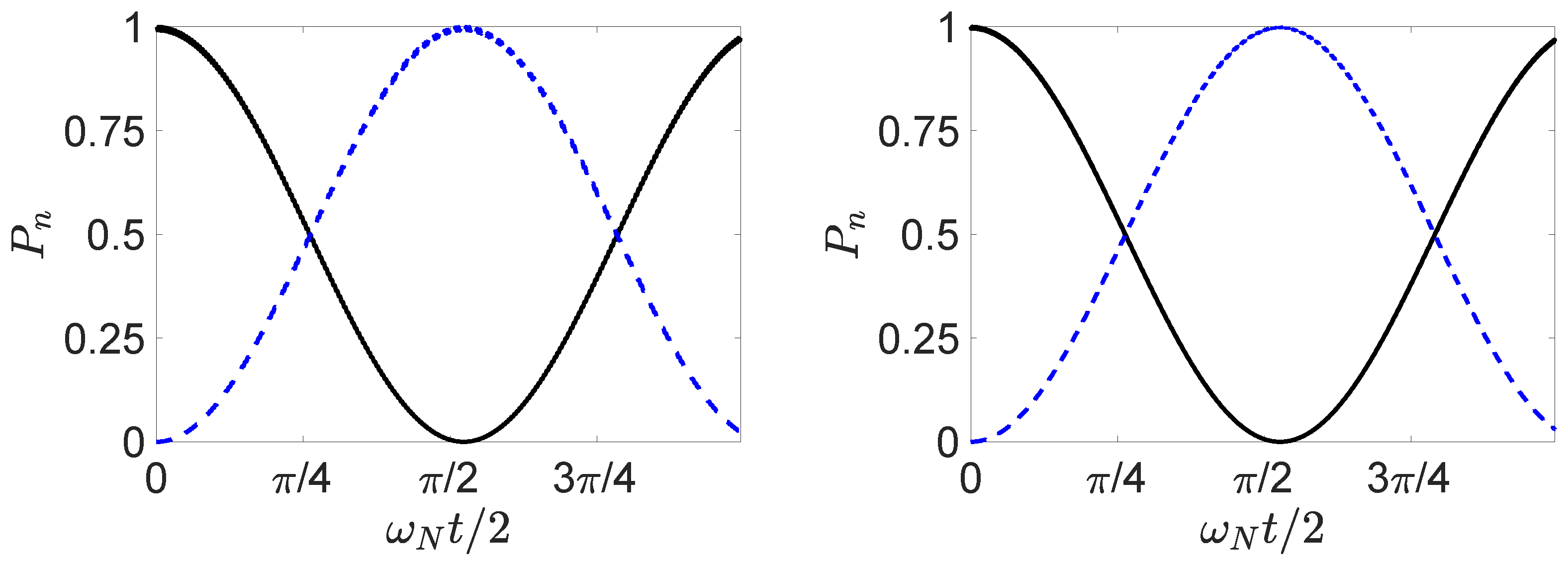
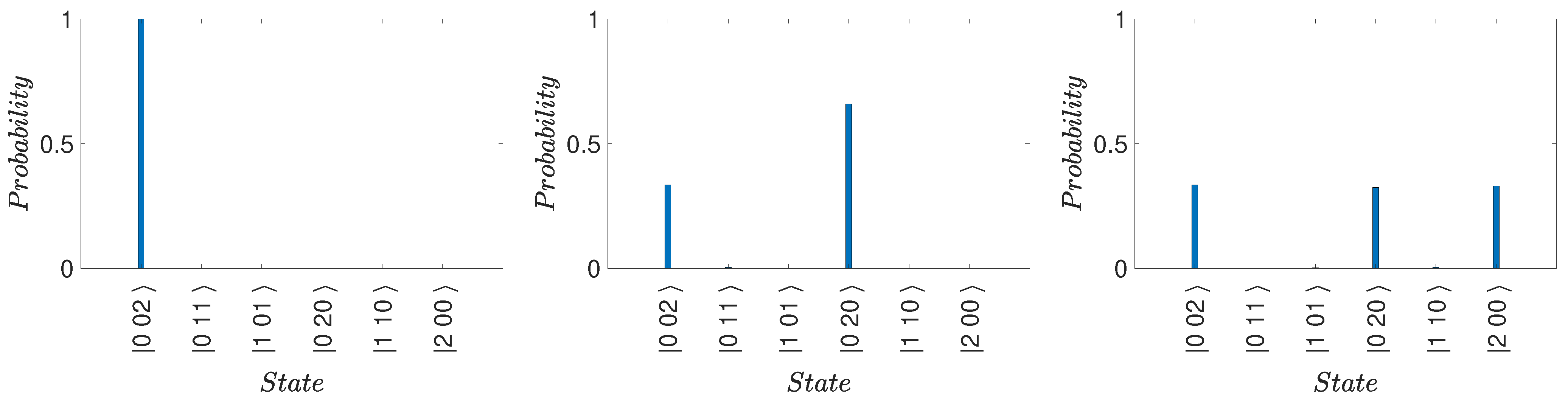
3. Mesoscopic Paradox
Number States
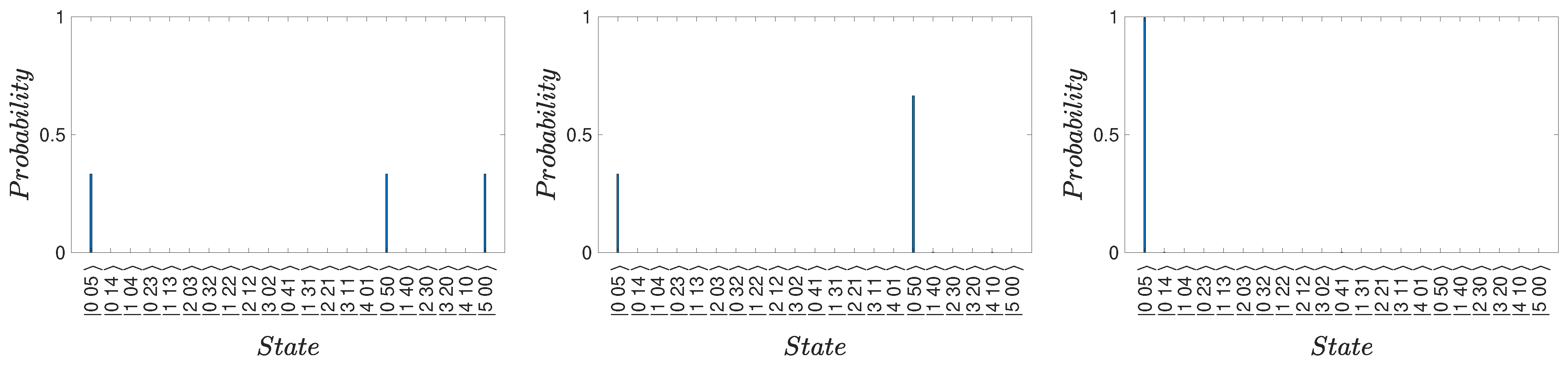
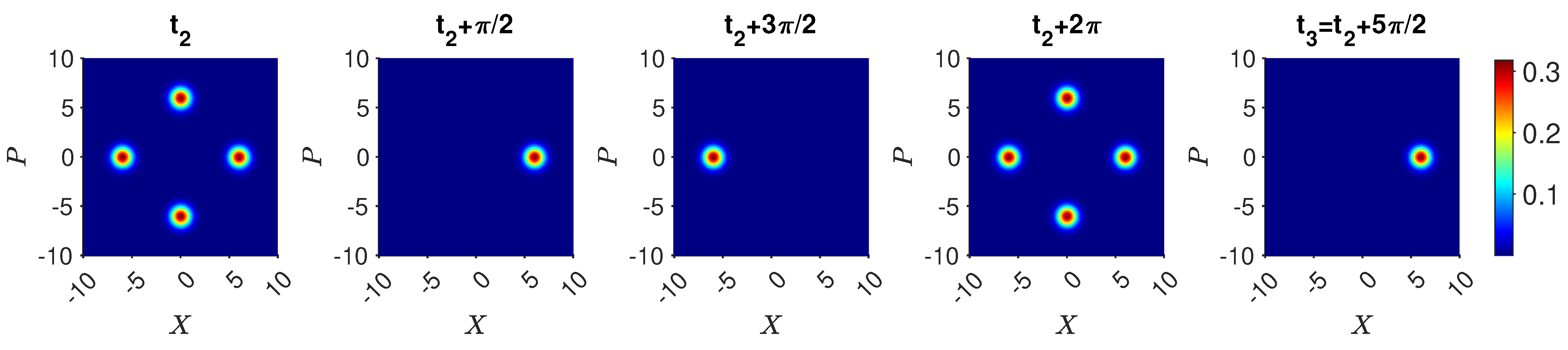
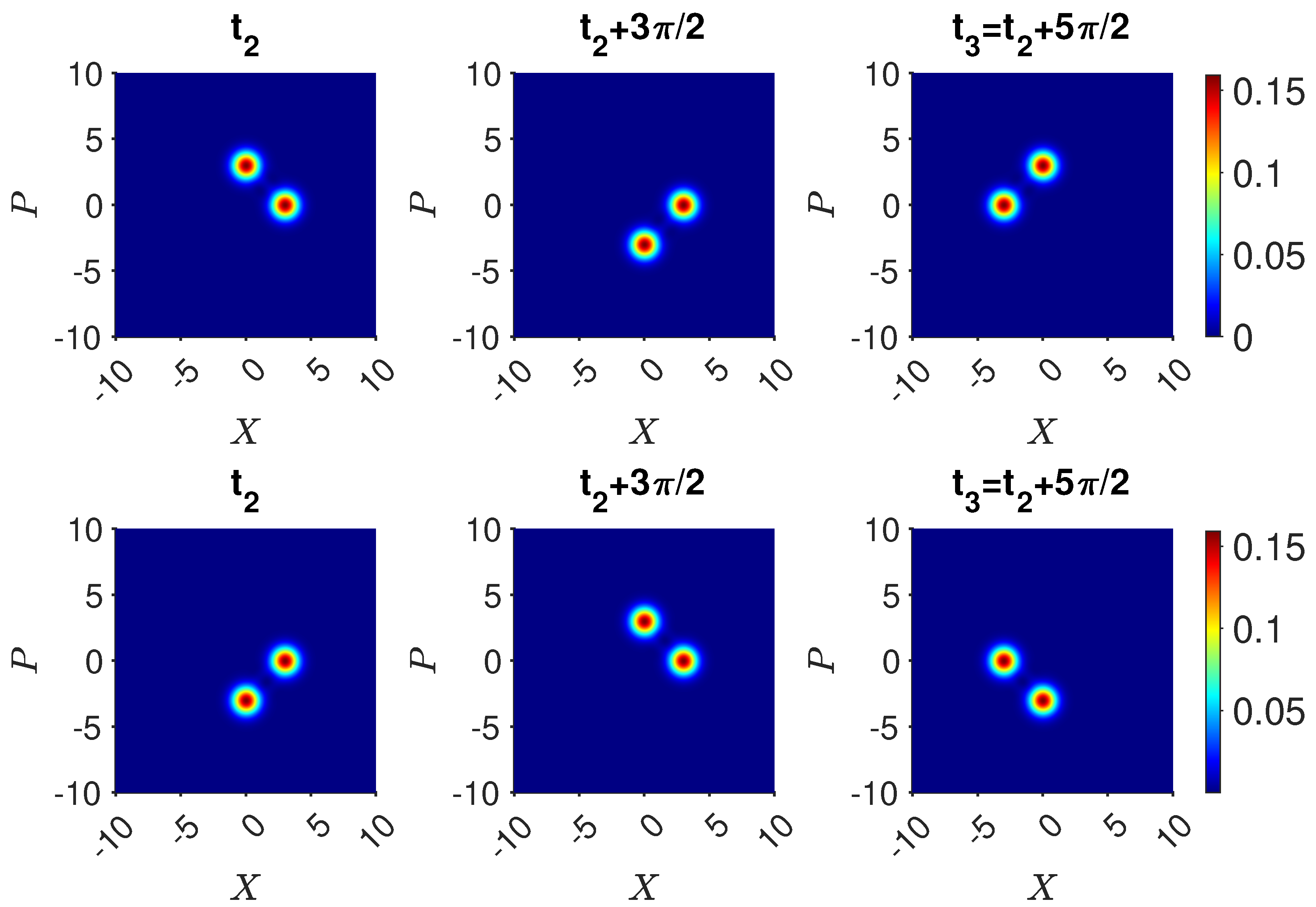
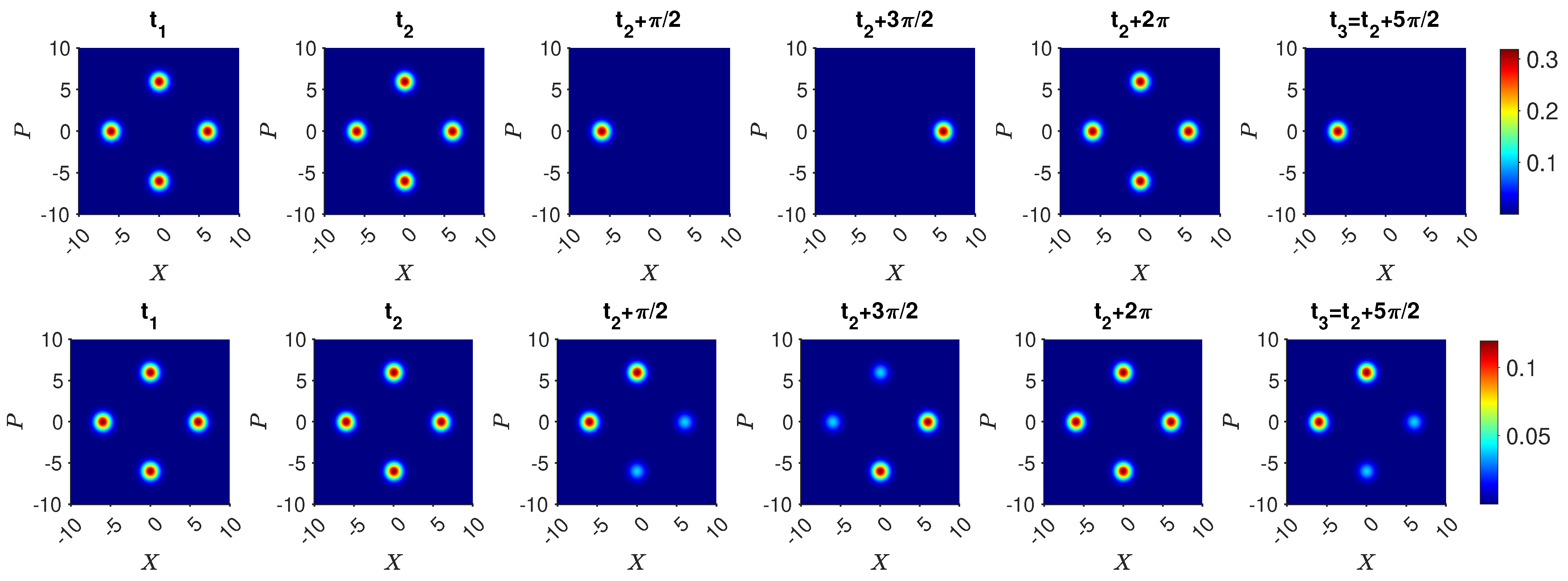
4. Macroscopic “Three-box” Paradox with Cat States
4.1. Coherent-State Model:
Experimental Realization
4.2. Coherent-State Model:
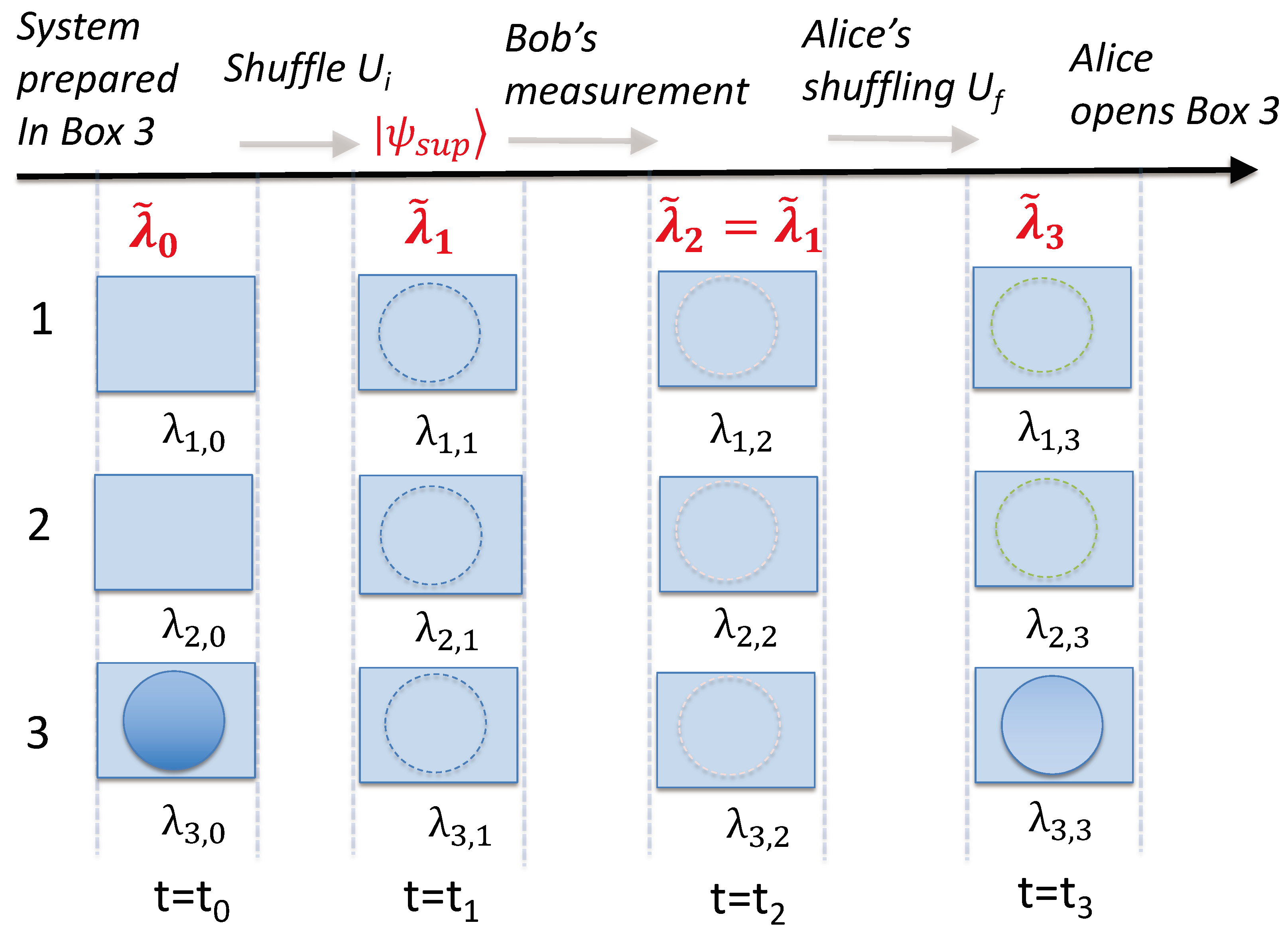
5. Finding Consistency with Weak Macroscopic Realism
5.1. The Weak Macroscopic Realism (wMR) Model
- (1)
- A real property for the pointer measurement:
- (2)
- A weak form of locality:
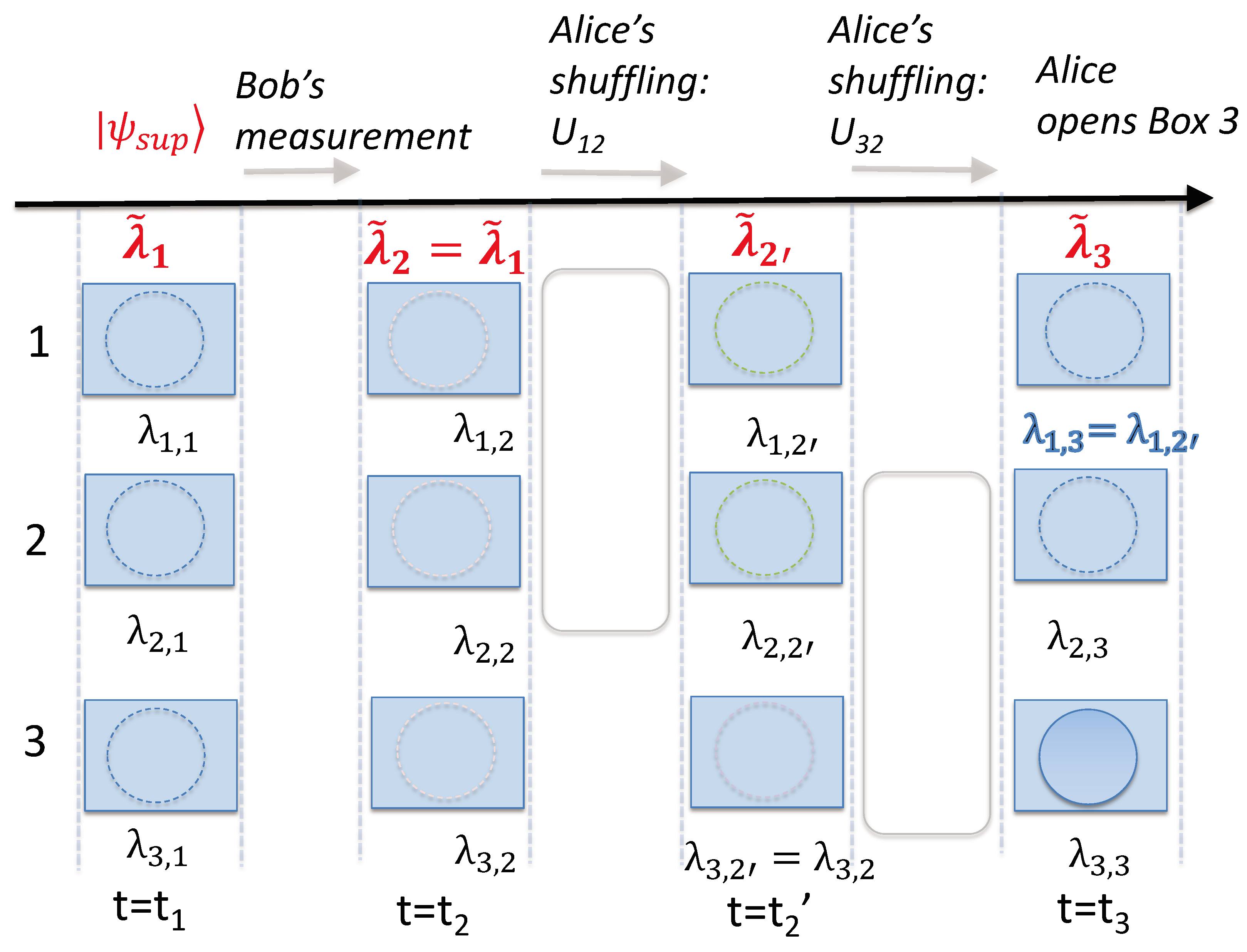
5.2. Finding Consistency with wMR
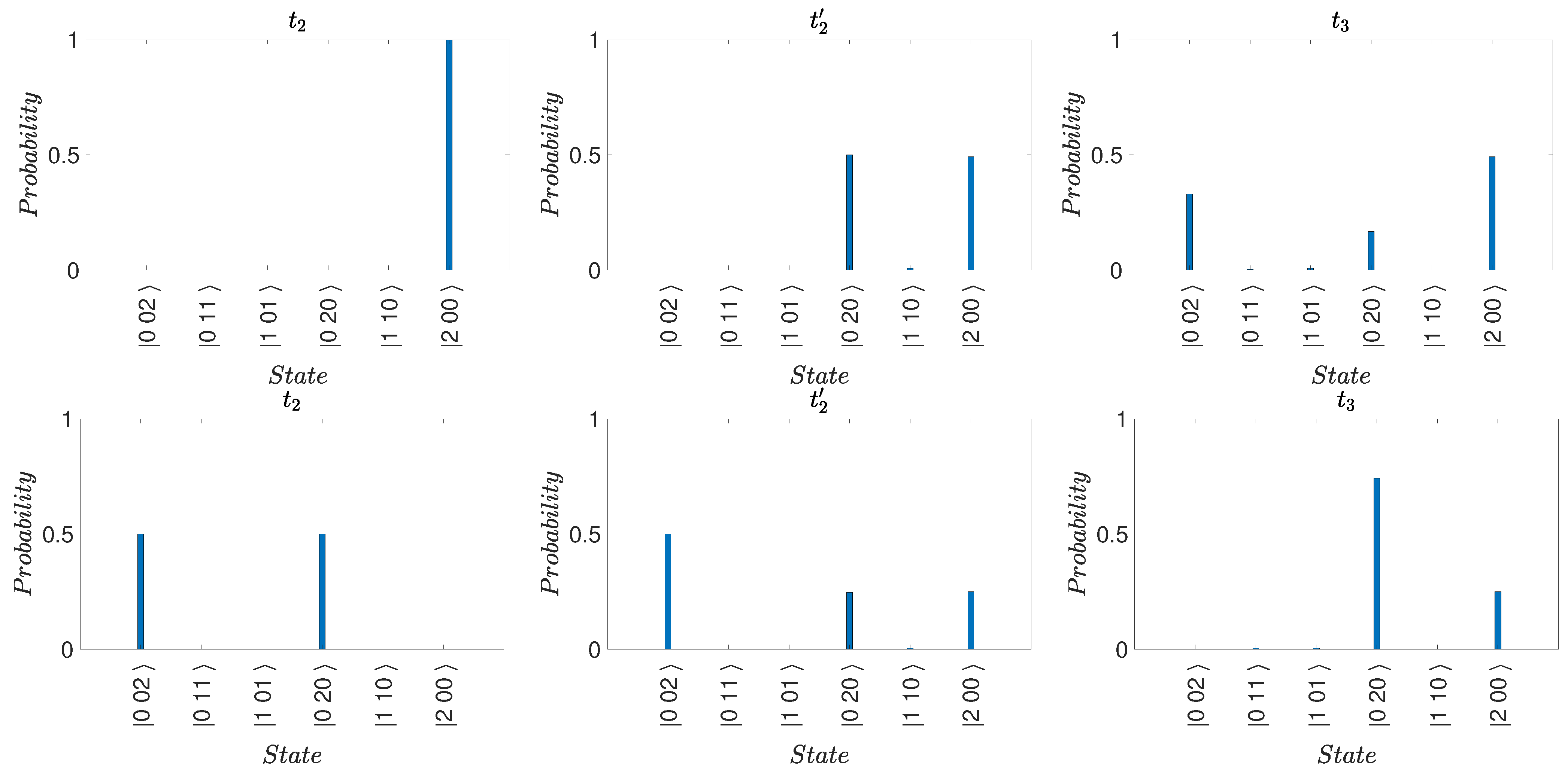
5.2.1. Three-Box Mesoscopic Paradox
5.2.2. Cat-State Paradox
5.2.3. Summary
6. Leggett–Garg Test of Macro-Realism
6.1. Weak Macroscopic Realism (wMR) and the Leggett–Garg Assumptions
6.2. Original Three-Box Paradox and the Mesoscopic Realization
6.3. Macroscopic Cat-State Realization of “Three-Box” Paradox
6.4. Finding Consistency with Weak Macroscopic Realism
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aharonov, Y.; Vaidman, L. Complete description of a quantum system at a given time. J. Phys. A Math. Gen. 1991, 24, 2315. [Google Scholar] [CrossRef]
- Aharonov, Y.; Bergmann, P.G.; Lebowitz, J.L. Time Symmetry in the Quantum Process of Measurement. Phys. Rev. B 1964, 134, 1410. [Google Scholar] [CrossRef]
- Kirkpatrick, K.A. Classical three-box ‘paradox’. J. Phys. A 2003, 36, 4891. [Google Scholar] [CrossRef]
- Leifer, M.S.; Spekkens, R.W. Logical Pre- and Post-Selection Paradoxes, Measurement-Disturbance and Contextuality. Int. J. Theor. Phys. 2005, 44, 1977. [Google Scholar] [CrossRef]
- Leifer, M.S.; Spekkens, R.W. Pre- and Post-Selection Paradoxes and Contextuality in Quantum Mechanics. Phys. Rev. Lett. 2005, 95, 200405. [Google Scholar] [CrossRef]
- Finkelstein, J. What is paradoxical about the “Three-box paradox”? arXiv 2006, arXiv:quant-ph/0606218. [Google Scholar]
- Ravon, T.; Vaidman, L. The three-box paradox revisited. J. Phys. A Math. Theor. 2007, 40, 2873. [Google Scholar] [CrossRef]
- Kirkpatrick, K.A. Reply to ’The three-box paradox revisited’ by T Ravon and L Vaidman. J. Phys. A 2007, 40, 2883. [Google Scholar] [CrossRef]
- Maroney, O.J.E. Measurements, disturbance and the three-box paradox. Stud. Hist. Philos. Sci. B Stud. Hist. Philos. Mod. Phys. 2017, 58, 41. [Google Scholar] [CrossRef]
- Kastner, R.E. The Three-box “Paradox” and Other Reasons to Reject the Counterfactual Usage of the ABL Rule. Found. Phys. 1999, 29, 851. [Google Scholar] [CrossRef]
- Vaidman, L. The Meaning of Elements of Reality and Quantum Counterfactuals: Reply to Kastner. Found. Phys. 1999, 29, 865. [Google Scholar] [CrossRef]
- Boyle, C.; Schafir, R. The N-box paradox in orthodox quantum mechanics. arXiv 2001, arXiv:quant-ph/0108113. [Google Scholar]
- Aharonov, Y.; Cohen, E.; Landau, A.; Elitzur, A.C. The Case of the Disappearing (and Re-Appearing) Particle. Sci. Rep. 2017, 7, 531. [Google Scholar] [CrossRef] [PubMed]
- Blasiak, P.; Borsuk, E. Causal reappraisal of the quantum three-box paradox. Phys. Rev. A 2021, 105, 012207. [Google Scholar] [CrossRef]
- Kolenderski, P.; Sinha, U.; Youning, L.; Zhao, T.; Volpini, M.; Cabello, A.; Laflamme, R.; Jennewein, T. Playing the Aharon-Vaidman quantum game with a Young type photonic qutrit. arXiv 2011, arXiv:1107.5828. [Google Scholar]
- Resch, K.J.; Lundeen, J.S.; Steinberg, A.M. Experimental Realization of the Quantum box Problem. Phys. Lett. A 2004, 324, 125. [Google Scholar] [CrossRef]
- George, R.E.; Robledo, L.M.; Maroney, O.J.E.; Blok, M.S.; Bernien, H.; Markham, M.L.; Twitchen, D.J.; Morton, J.J.L.; Briggs, G.A.D.; Hanson, R. Opening up three quantum boxes causes classically undetectable wavefunction collapse. Proc. Natl. Acad. Sci. USA 2013, 110, 3777. [Google Scholar] [CrossRef]
- Kirchmair, G.; Vlastakis, B.; Leghtas, Z.; Nigg, S.E.; Paik, H.; Ginossar, E.; Mirrahimi, M.; Frunzio, L.; Girvin, S.M.; Schoelkopf, R.J. Observation of the quantum state collapse and revival due to a single-photon Kerr effect. Nature 2013, 495, 205. [Google Scholar] [CrossRef]
- Vlastakis, B.; Kirchmair, G.; Leghtas, Z.; Nigg, S.E.; Frunzio, L.; Girvin, S.M.; Mirrahimi, M.; Devoret, M.H.; Schoelkopf, R.J. Deterministically encoding quantum information using 100-photon schrödinger cat states. Science 2013, 342, 607. [Google Scholar] [CrossRef]
- Thenabadu, M.; Reid, M.D. Bipartite Leggett–Garg and macroscopic Bell inequality violations using cat states: Distinguishing weak and deterministic macroscopic realism. Phys. Rev. A 2022, 105, 052207. [Google Scholar] [CrossRef]
- Fulton, J.; Teh, R.Y.; Reid, M.D. Argument for the incompleteness of quantum mechanics based on macroscopic and contextual realism: GHZ and Bohm-EPR paradoxes with cat states. arXiv 2022, arXiv:2208.01225. [Google Scholar]
- Fulton, J.; Thenabadu, M.; Teh, R.; Reid, M.D. Weak versus deterministic macroscopic realism, and elements of reality. arXiv 2021, arXiv:2101.09476. [Google Scholar]
- Joseph, R.R.; Thenabadu, M.; Hatharasinghe, C.; Fulton, J.; Teh, R.-Y.; Drummond, P.D.; Reid, M.D. Wigner’s Friend paradoxes: Consistency with weak-contextual and weak-macroscopic realism models. arXiv 2022, arXiv:2211.02877. [Google Scholar]
- Schrödinger, E. The Present Status of Quantum Mechanics. Die Naturwissenschaften 1935, 23, 807. [Google Scholar]
- Leggett, A.; Garg, A. Quantum mechanics versus macroscopic realism: Is the flux there when nobody looks? Phys. Rev. Lett. 1985, 54, 857. [Google Scholar] [CrossRef] [PubMed]
- Thenabadu, M.; Cheng, G.-L.; Pham, T.L.H.; Drummond, L.V.; Rosales-Zárate, L.; Reid, M.D. Testing macroscopic local realism using local nonlinear dynamics and time settings. Phys. Rev. A 2020, 102, 022202. [Google Scholar] [CrossRef]
- Thenabadu, M.; Reid, M.D. Leggett–Garg tests of macrorealism for dynamical cat states evolving in a nonlinear medium. Phys. Rev. A 2019, 99, 032125. [Google Scholar]
- Thenabadu, M.; Reid, M.D. Macroscopic delayed-choice and retrocausality: Quantum eraser, Leggett–Garg and dimension witness tests with cat states. Phys. Rev. A 2022, 105, 062209. [Google Scholar] [CrossRef]
- Dowling, J.P. Quantum optical metrology–the lowdown on high-n00n states. Contemp. Phys. 2008, 49, 125. [Google Scholar] [CrossRef]
- Lipkin, H.J.; Meshkov, N.; Glick, A.J. Validity of many-body approximation methods for a solvable model: Exact solutions and perturbation theory. Nucl. Phys. 1965, 62, 188. [Google Scholar] [CrossRef]
- Steel, M.; Collett, M.J. Quantum state of two trapped Bose-Einstein condensates with a Josephson coupling. Phys. Rev. A 1998, 57, 2920. [Google Scholar] [CrossRef]
- Carr, L.D.; Dounas-Frazer, D.; Garcia-March, M.A. Dynamical realization of macroscopic superposition states of cold bosons in a tilted double well. Europhys. Lett. 2010, 90, 10005. [Google Scholar]
- Fröwis, F.; Sekatski, P.; Dür, W.; Gisin, N.; Sangouard, N. Macroscopic quantum states: Measures, fragility, and implementations. Rev. Mod. Phys. 2018, 90, 025004. [Google Scholar]
- Yurke, B.; Stoler, D. Generating quantum mechanical superpositions of macroscopically distinguishable states via amplitude dispersion. Phys. Rev. Lett. 1986, 57, 13. [Google Scholar]
- Wineland, D.J. Nobel Lecture: Superposition, entanglement, and raising Schrödinger’s cat. Rev. Mod. Phys. 2013, 85, 1103. [Google Scholar] [CrossRef]
- Leghtas, Z.; Kirchmair, G.; Vlastakis, B.; Devoret, M.H.; Schoelkopf, R.J.; Mirrahimi, M. Deterministic protocol for mapping a qubit to coherent state superpositions in a cavity. Phys. Rev. A 2013, 87, 042315. [Google Scholar]
- Ourjoumtsev, A.; Jeong, H.; Tualle-Brouri, R.; Grangier, P. Generation of optical ‘Schrödinger cats’ from photon number states. Nature 2007, 448, 784. [Google Scholar]
- Wang, C.; Gao, Y.Y.; Reinhold, P.; Heeres, R.W.; Ofek, N.; Chou, K.; Axline, C.; Reagor, M.; Blumoff, J.; Sliwa, K.M.; et al. A Schrödinger cat living in two boxes. Science 2016, 352, 1087. [Google Scholar] [CrossRef]
- Wolinsky, M.; Carmichael, H.J. Quantum noise in the parametric oscillator: From squeezed states to coherent-state superpositions. Phys. Rev. Lett. 1988, 60, 1836. [Google Scholar]
- Hach Edwin, E., III; Gerry Christopher, C. Generation of mixtures of Schrödinger-cat states from a competitive two-photon process. Phys. Rev. A 1994, 49, 490. [Google Scholar] [CrossRef]
- Gilles, L.; Garraway, B.M.; Knight, P.L. Generation of nonclassical light by dissipative two-photon processes. Phys. Rev. A 1994, 49, 2785. [Google Scholar] [CrossRef] [PubMed]
- Teh, R.Y.; Sun, F.-X.; Polkinghorne, R.; He, Q.; Gong, Q.; Drummond, P.D.; Reid, M.D. Dynamics of transient cat states in degenerate parametric oscillation with and without nonlinear kerr interactions. Phys. Rev. A 2020, 101, 043807. [Google Scholar] [CrossRef]
- Ku, H.-Y.; Lambert, N.; Chan, F.-J.; Emary, C.; Chen, Y.-N.; Nori, F. Experimental test of non-macrorealistic cat states in the cloud. npj Quantum Inf. 2020, 6, 98. [Google Scholar] [CrossRef]
- Omran, A.; Levine, H.; Keesling, A.; Semeghini, G.; Wang, T.T.; Ebadi, S.; Bernien, H.; Zibrov, A.S.; Pichler, H.; Choi, S.; et al. Generation and manipulation of Schrödinger cat states in Rydberg atom arrays. Science 2019, 365, 570. [Google Scholar] [CrossRef] [PubMed]
- Wright, E.; Walls, D.; Garrison, J. Collapses and Revivals of Bose-Einstein Condensates Formed in Small Atomic Samples. Phys. Rev. Lett. 1996, 77, 2158. [Google Scholar] [CrossRef]
- Greiner, M.; Mandel, O.; Bloch, T.H.I. Collapse and revival of the matter wave field of a Bose-Einstein condensate. Nature 2002, 419, 51. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein-Podolsky-Rosen paradox. Physics 1964, 1, 195. [Google Scholar] [CrossRef]
- Bell, J.S. On the Problem of Hidden Variables in Quantum Mechanics. Rev. Mod. Phys. 1966, 38, 447–452. [Google Scholar] [CrossRef]
- Kochen, S.; Specker, E. The problem of hidden variables in quantum mechanics. J. Math. Andm. 1967, 17, 59. [Google Scholar] [CrossRef]
- Maroney, O.J.E.; Timpson, C.G. Quantum- vs. Macro- Realism: What does the Leggett–Garg Inequality actually test? arXiv 2017, arXiv:1412.6139. [Google Scholar]
- Bohm, D. A suggested interpretation of quantum theory in terms of “hidden” variables. Phys. Rev. 1952, 85, 166. [Google Scholar] [CrossRef]
- Budiyono, A.; Rohrlich, D. Quantum mechanics as classical statistical mechanics with an ontic extension and an epistemic restriction. Nat. Commun. 2017, 8, 1306. [Google Scholar] [CrossRef] [PubMed]
- Husimi, K. Some Formal Properties of the Density Matrix. Proc. Phys. Math. Soc. Jpn. 1940, 22, 264. [Google Scholar]

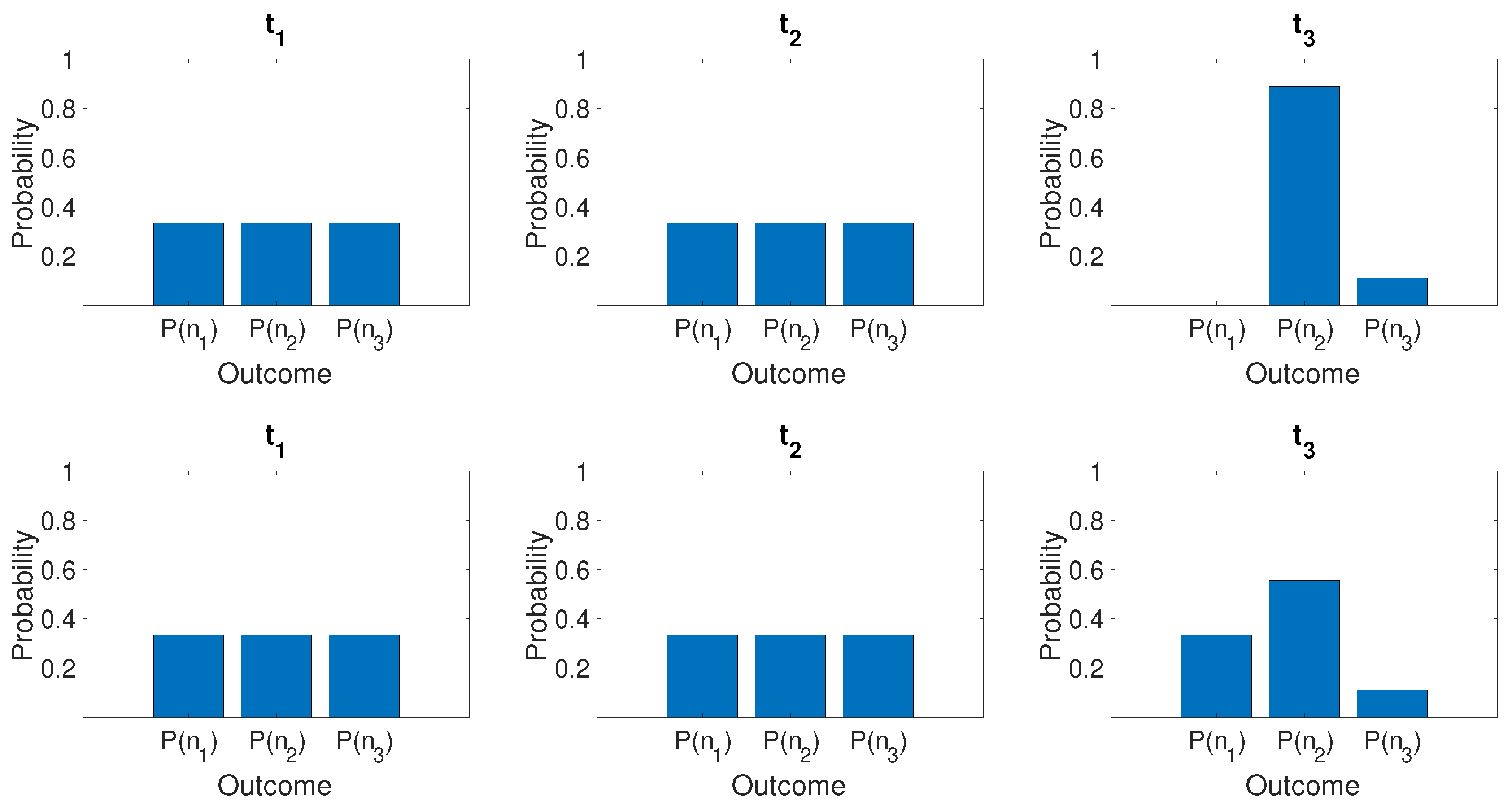
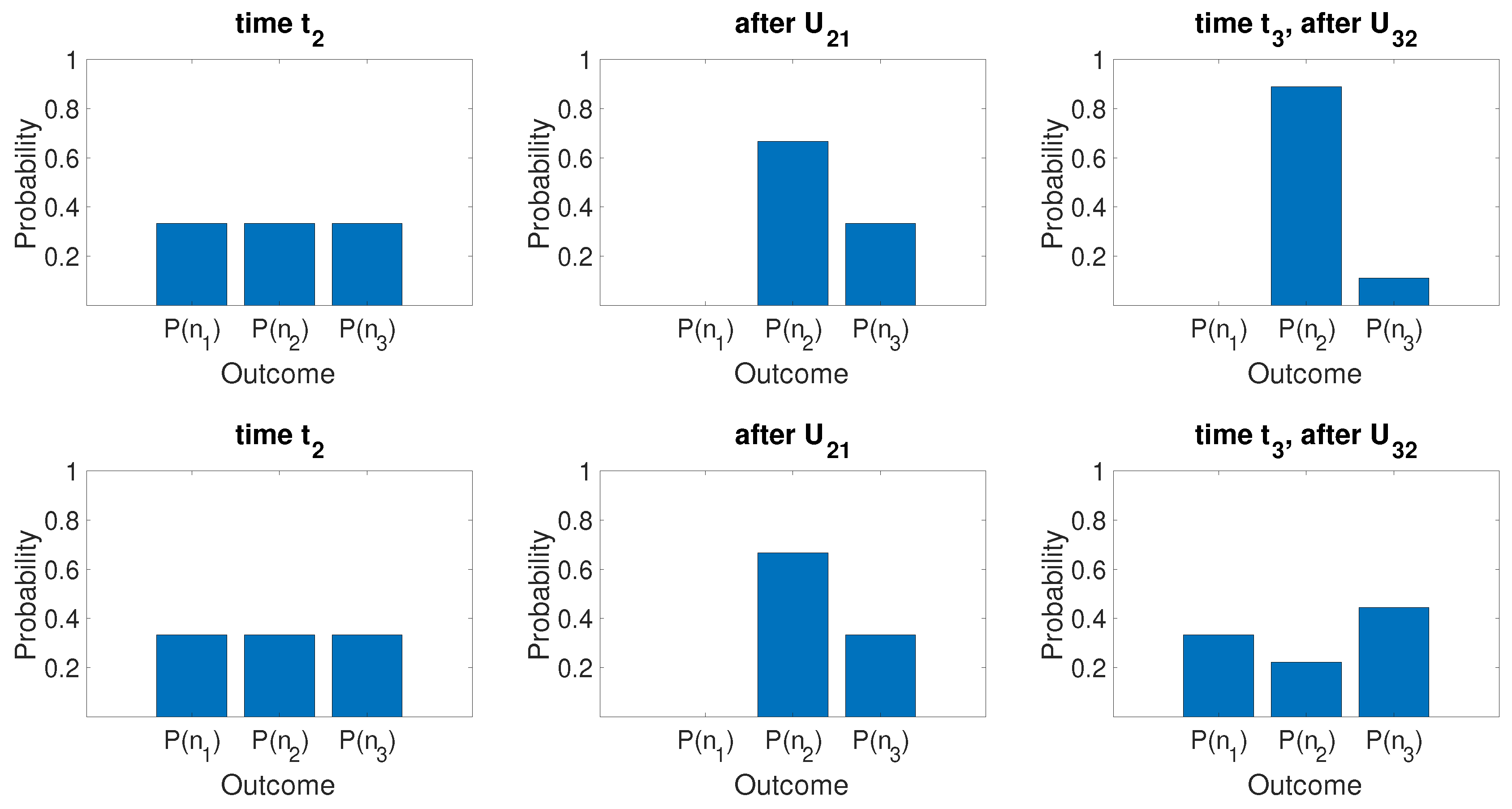

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hatharasinghe, C.; Thenabadu, M.; Drummond, P.D.; Reid, M.D. A Macroscopic Quantum Three-Box Paradox: Finding Consistency with Weak Macroscopic Realism. Entropy 2023, 25, 1620. https://doi.org/10.3390/e25121620
Hatharasinghe C, Thenabadu M, Drummond PD, Reid MD. A Macroscopic Quantum Three-Box Paradox: Finding Consistency with Weak Macroscopic Realism. Entropy. 2023; 25(12):1620. https://doi.org/10.3390/e25121620
Chicago/Turabian StyleHatharasinghe, Channa, Manushan Thenabadu, Peter D. Drummond, and Margaret D. Reid. 2023. "A Macroscopic Quantum Three-Box Paradox: Finding Consistency with Weak Macroscopic Realism" Entropy 25, no. 12: 1620. https://doi.org/10.3390/e25121620




