A Possible Extension of Shannon's Information Theory

Abstract

As a possible generalization of Shannon’s information theory, we review the formalism based on the non-logarithmic information content parametrized by a real number q, which exhibits nonadditivity of the associated uncertainty. Moreover it is shown that the establishment of the concept of the mutual information is of importance upon the generalization.

1 Introduction

The recent development of the statistical mechanics based on the non-Gibbsian entropy, or Tsallis’s nonextensive statistical mechanics [1] has intensified interests in search for a possible extension of Shannon information theory. This is mainly due to the similarity of the form of the entropy function involved. In fact one can develop the non-Shannon (but includes Shannon’s as a special case) information theory to some extent from a formal point of view. The quantitative measure of information is of importance when we transmit the strings of messages through a channel, moreover, coding and decoding the messages can be considered to be manipulation of the amount of information. Therefore we need a definition of the information content. Shannon wrote in his original paper[2]:

If the number of messages in the set is finite then this number or any monotonic function of this number can be regarded as a measure of the information produced when one message is chosen from the set, all choices being equally likely. As was pointed out by Hartley the most natural choice is the logarithmic function. Although this definition must be generalized considerably when we consider the influence of the statistics of the message and ...

Here it is worth to know the motivation of adopting the information measure introduced by Hartley[3]. He proposed that the information is to be proportional to the the number of possible events (the term ’selections’ is used in his original paper). By comparing the number of possible sequences of two systems, he states that to take the logarithm of the number is most practical. Therefore, Shannon provided the measure of uncertainty of information contained as an entropy which is the celebrated form − ∑_i p_i log p_i [2,4], where the p_i is the probability of the i-th state of the system considered.

We shall note that the above statement by Shannon may seem to allow some possibilities of generalized formalism for theory of communication, or information theory. Up to now, many forms of information function differed from Shannon have been devised with parameters[5,6,7]. Among them, let us mention that similar forms to Tsallis’s are that of Havrda et.al. and of Daróczy[6]. However the discussions about the coding theorem and other important elements for information theory based on such a generalized function seem to lacking. In this paper we assume that nonadditivity of the uncertainty of the system arises from a certain property of messages. We briefly shows the present trial of a possible extension of Shannon’s information theory.

2 Set up

Before we go into details, we first define the information source. This is common in both an additive source and a nonadditive one and described as follows. A source consists of a finite set called a source alphabet S = {x₁,…x_n} and of the probability set P = {p(x₁),…,p(x_n)} assigned to them. The entropy function H depends only on the P and not on the elements of the alphabets.

Here, it would be worth mentioning the following fact. I.e. the entropy function is uniquely determined as Shannon’s form due not to the definition of the mean value of the information but to the additivity of the uncertainty of the information that the source has. To see this clearly, let us take the following explanation. Let the elements S = {x₁,… x_n} partition into k nonempty disjoint groups G₁,…,G_k, each of which has the size |G_i| = G_i and ∑_i g_i = n. We first chose a group G_i with probability p(G_i) = g_i/n, then we pick an alphabet with equal probability from the group G_i. Since the conditional probability that a certain alphabet x_j is in G_m is given as

(1)

the probability of choosing x_j is written with Bayes’ relation as

(2)

Therefore we see that it is the same as the probability when we chose x_j directly from S with equal probability. Although a group that an element belongs has been identified, we still have the uncertainty involved in choosing the element from the group. The uncertainty in choosing an element from G_i is H(1/g_i,…,1/g_i). Here, suppose that the average uncertainty be given by taking e.g. an escort probability [8] with a parameter q ∈ $ℛ$ instead of the usual average

(3)

The case q = 1 means to take the usual average. On the other hand, we have the uncertainty in choosing one group G_i from k groups, that is H(g₁/n,…,g_k/n). When we impose the additivity of the uncertainty, the uncertainty in choosing directly from the source S with equal probability H(1/n,…,1/n) can be provided as the sum of the two uncertainties,

(4)

When g_i = l for all i = 1, …,k therefore l_k = n, no matter what the value q takes, r.h.s of the above relation reduces to H(l/n,…,l/n) + H(1/l,…,1/l). The proof of the uniqueness of the logarithmic form for H after this stage (with two more important properties:H is a continuous function of its argument {p_i}(p_i ∈ [0, 1]) for all i and we have greater uncertainty when there are more outcomes, can be seen in the standard textbook e.g. [9] . The important point in the above discussion is that the logarithmic form is not stem from the way we take the average of the uncertainty but from the additivity of uncertainties. The additivity postulate of the uncertainty leads to logarithmic property of the information acquired. It is worthwhile to note that the uniqueness theorem for Tsallis entropy has been discussed in Ref.[10,11]. These are not based on the additivity of the entropy function but on the pseudoadditivity[12]. We are concerned with the formulation when we discard the additivity postulate in the present consideration. As a starting point, we begin with the definition of the amount of information associated with the occurrence of a certain information from the source. Then we shall define the pertinent information entropy based on it. Upon the generalization of the information content parametrized with nonadditivity, there seem two unavoidable notions that we should bear in mind. First point is that we should retain Shannon’s (or Hartley’s) information as a special case. Second, the introduction of appropriate definition for the mutual information is needed to develop the channel coding theorem. We shall describe this point later in Section 3. Hereafter we change notations that denote elements of an alphabet to avoid burdensome suffixes: x belongs to an alphabet $\mathscr{H}$ and y to another $\mathcal{Y}$.

We borrow from the definition used in Tsallis nonextensive statistical mechanics. In Tsallis’s for- malism of statistical mechanics, we base our discussions on the q-logarithmic function [13,14,15]. Then we may regard the amount of information as the q-logarithm of the probability I_q(p) ≡ — ln_q p(x) where ln_q x = (x^1−q − 1)/(1 − q). In fact, I_q(p) is a monotonically decreasing function as − ln p is for all q. In this case, we measure the information not by bit but by nat. In the limit q → 1, the information content recovers − ln p.

One should also notice that the escort average or the normalized q−average[12] of the information content (information entropy) gives the modified form of Tsallis entropy[16,17,18]

(5)

We note that this form takes as the Tsallis one divided by a factor ∑_i $p_i^q$. We shall hereafter denote the entropy function by indexing q as H_q(X).

In a similar way, we define the joint entropy of X and Y and a nonadditive conditional entropy H_q(Y | x) as

(6)

where ${\langle \cdot \rangle }_q^{(X)}$ represents the escort average with respect to p(x). Let us next define the mutual information I_q(Y; X). Here, we shall follow the usual definition of the reduction in uncertainty due to another variable (the entropy subtracted by the conditional entropy). That is,

(7)

In order to be in consistent with the usual additive mutual information, we impose non-negativity for it. It also converges to the usual mutual information I(Y ; X) = H(Y) − H(Y | X) = H(X) + H(Y) − H(X,Y ) in the additive limit(q → 1). The mutual information of a random variable with itself is the entropy itself I_q(X; X) = H_q(X, and when X and Y are independent variables, I_q(Y ; X) = 0. Some people claim that the mutual information in any generic extension ought to obey symmetry under interchange of two variables(sender X and receiver Y ) and must vanish when the two events are statistically independent. However, there seems no clear reason to keep these properties when we measure the information as the non-logarithmic form. We could also say that since the pseudoadditivity states that the probability with factorized form does not construct the sum of the pertinent entropy, it may take a stand point that the mutual information may not possess the above two properties at the same time. We will discuss this point in the next Section.

We here only give the relations which the H_qsatisfies (the reader who has interest in proofs is referred to [18]).

where Z in the last relation denotes the third events. All these relations reduce to the ones which are satisfied in the usual Shannon’s information theory in the limit q → 1. Next, we give the generalized Kullbak-Leibler(KL) entropy between two probability distributions p_i(x) and $p_i^{\prime }$ as follows [18,19,20],

(8)

The KL entropy or the relative entropy is a measure of the distance between two probability distributions[21]. We note that the above generalized KL entropy satisfies the form invariant structure which has introduced in Ref.[17]. Then the following information inequality holds

(9)

with equality if and only if p(x) = p′(x) for all x ∈ $\mathscr{H}$ and D₀[p(x) ‖ p′(x)] = 0. The positivity in the case of q > 0 can be considered a necessary property to develop the information theory.

3 Source coding theorem

We review and give the nonadditive version of the Shannon’s source coding theorem. Source coding theorem together with the channel coding theorem can be considered a pillar of information theory today. We usually want to encode the source letters in such a way that the expected codeword length becomes as short as possible. We recapitulate how the source coding theorem is described by writing a usual Shannon’s case in a parallel way. We write expressions of the nonadditive version in parentheses in this section.

Let us denote codeword lengths of each letters as l₁,l₂,· · ·. We recall that any code which is uniquely decoded and satisfies prefix conditions over the alphabet size D must be content with the Kraft inequality[22]

(10)

where M is the number of codewords. The minimum expected codeword length can be achieved by using the Lagrange multiplier method with constraint of the Kraft inequality. The resulting optimal codeword length $l_i^{*}$ becomes q log_D p_i). The following property is crucial i.e., the codeword length can not be below the entropy,

(11)

with equality if and only if When we use an incorrect or a non-optimal information, we have more complexity in its description. In other words, the use of a wrong distribution, say r, involved in each source letter incurs a penalty (or an increment of the expected description length) of the relative entropy D[p ‖ r] (D_q[p ‖ r]) in the average codeword length,

(12)

In fact, the $l_i^{*}$’s may not be integers then we round them up to the smallest integers larger than $l_i^{*}$’s. We represent these codeword lengths as We can show that the average codeword length resides within 1 nat against H(p) + D[p ‖ r] (H_q(p) + D_q[p ‖ r]) due to the present definition of the l_i, that is, When we transmit a sequence of n letters from the source, each of which is generated independently and in identically distributed manner, the average codeword length per one letter 〈L_n〉 is bounded as H(X) ≤ 〈L_n〉 < H(X) + 1/n. This bound relation can be attributed to the additive property of the joint entropy H(X₁,…,X_n) = Σ_i H(X_i) = nH(X). In the nonadditive case, on the other hand, H(X) is replaced by This form arises from the property of H_q(x₁,…,X_n) we have listed in the previous section. This can be considered to complete the source coding theorem. We only mention the fact that the Fano’s inequality which provides an upper bound to the conditional entropy, when the system has a noisy channel, can be naturally generalized within the present formalism[18].

4 Mutual information and channel capacity

We address the generalized mutual information we have promised in the Section 2 and explore consequences of two alternative definitions of mutual information by calculating the simple model of information channel i.e., the binary symmetric channel(BSC). Recently, Landsberg et.al.[16] have focused on a possible constraint on the generalization of entropy concept and have compared channel capacities based on Shannon, Renyi, Tsallis, and another generalized entropy by applying to a BSC for a fixed error probability e of communication. It would be worth noting that the last generalized entropy introduced by Landsberg et al. was presented independently by Rajagopal et al.[17] from a consideration of a form invariant structure of nonadditive entropy.

The concept of the mutual information can be regarded as the important ingredient to evaluate a communication channel in information theory. The mutual information is a measure of the amount of information that one random variable contains about another random variable. In other wards, I_q(Y; X) expresses the reduction in uncertainty of Y due to the acquisition of knowledge of X[22]. In previous considerations in Section 2 and in Ref.[16], there is a point that should be investigated about the definition of the mutual information upon generalization. In Ref.[16] they devised to take the average of conditional entropy H(Y | X = x) using usual weighting p(x) from the requisition that the capacity based on the any information entropy should be 0 for e = 1/2 as Shannon’s case. However this selection possesses asymmetry of the mutual information in X and Y unless we choose the Shannon’s H(Y | X = x). The same applies to the case of the definition we have adopted.

Let us try to compare the two possible definitions of the generalized mutual information by checking the channel capacity of the BSC. The one holds symmetry in X and Y and the other is borrowed from the generalized KL entropy.

To capture and elucidate the present problem clearly let us review the usual mutual information by Shannon. The mutual information can be defined as the relative entropy between the joint probability distribution p(x, y) and the product of the two probability distributions p(x)p(y). That is, we can regard that the mutual information is a marker how far the joint probability deviates from the independence of the two i.e.,

(13)

Hence the mutual information is symmetric in X and Y , I (X; Y ) = I (Y ; X). Moreover its positivity can be proved. Here, the most remarkable feature associated with the later discussion is the fact that we can rewrite the I (X; Y ) from Eq.(13) as

(14)

Therefore we can take the definition of the mutual information either as H(X) − H(X | Y ) or as D[p(x, y) ‖ p(x)p(y)]. However, the situation totally differs in the context of the generalized mutual information. More specifically, the definition by the generalized KL entropy D_q[p(x, y) ‖ p(x)p(y)] [18] does not give the expression H_q(X) − H_q(X | Y). Accordingly we need to determine which standpoint we take as the definition.

Now we first consider the mutual information indexed by q as

(15)

Then we immediately see that the mutual information becomes symmetric in X and Y,

(16)

In BSC we have the alphabet $\mathscr{H}$ = {0, 1}. The input code x of 0 and 1 can be received as a 1 and a 0 of the output code y respectively with the error probability e due to the external noise[22]. Then the conditional probabilities p(y | x) are given as p(0 | 1) = p(1 | 0) = e and p(0 | 0) = p(1 | 1) = 1 − e respectively. If we write the input (output) probability which we observe a 0 and a 1 as p₀ and p₁ ($p_0^{\prime }$ and $p_1^{\prime }$) respectively, then we have the joint probabilities

Using this, the nonadditive joint entropy is calculated as We define a generalized channel capacity as follows

(17)

Since the output probabilities $p_0^{\prime }$ and $p_1^{\prime }$ are given as

(18)

respectively, the summation Σ_i p^q(y_i) is calculated with p₁ = 1 − p₀ as ((1 − 2e)p₀ + e)^q + ((2e − 1)p₀ + 1 − e)^q. Therefore from Eq(16) the mutual information is expressed as

(19)

where we have put . The I_q(X; Y ) can be taken its maximum when p₀ = p₁ = 1/2 for some ranges of q and e. Then the capacity is found to be

(20)

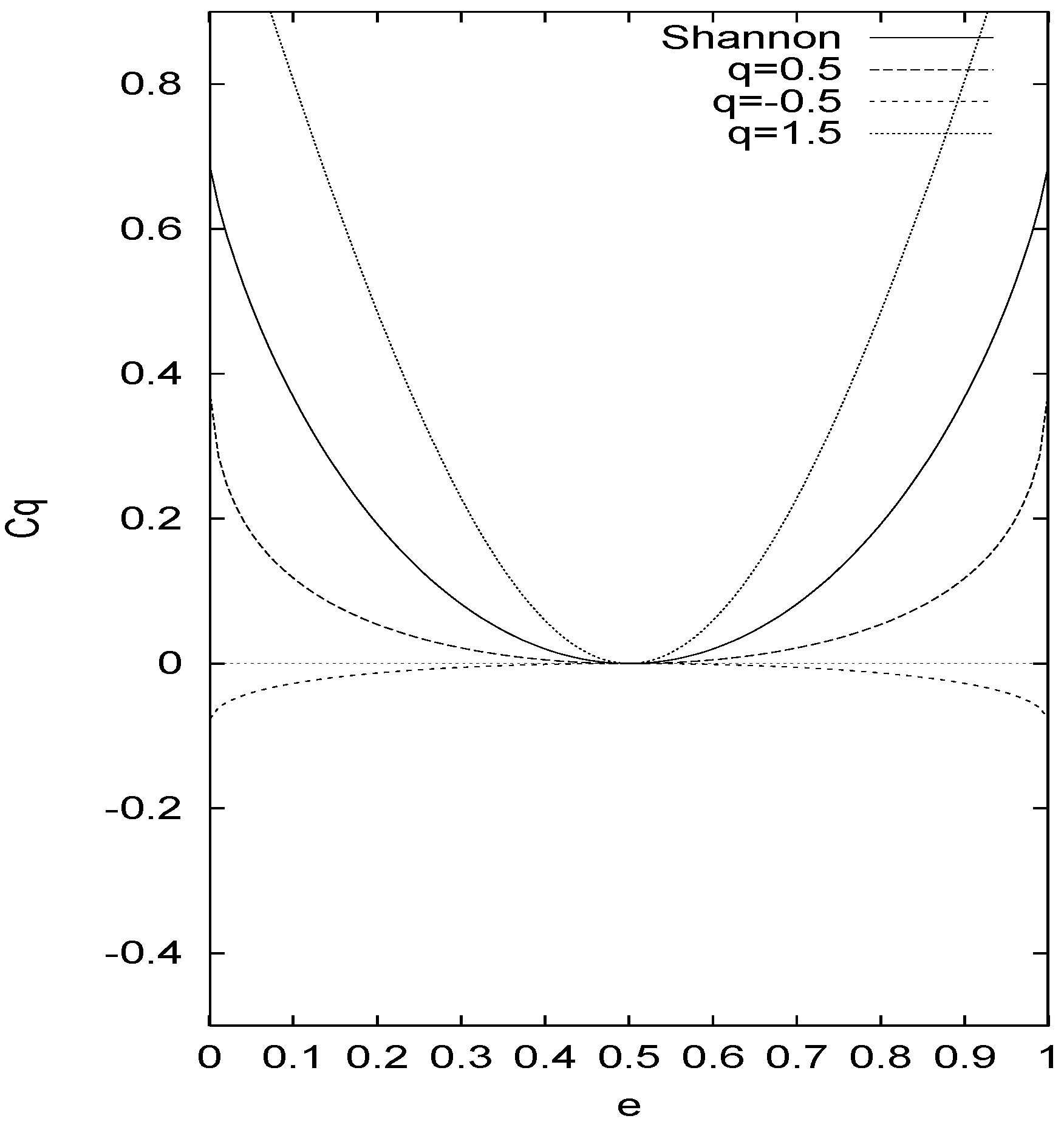
Figure 1. The channel capacity of BSC is plotted against the error probability for Shannon and some different values of q defined by Eq.(16).

Figure 1. The channel capacity of BSC is plotted against the error probability for Shannon and some different values of q defined by Eq.(16).

Fig.1 shows the channel capacity C_q against e for the case of Shannon and for different values of q. The capacity does not become zero for e = 1/2 except for Shannon. It exceeds the Shannon’s capacity for the intermediate noise level (q < 1) and is below Shannon when the channel is very noisy(or less noisy). We note that the capacity can be negative also for our new definition of the mutual information for some ranges of q and e and we can have the capacity above Shannon for extreme cases of e. However, the negative channel capacity has a difficulty to understand in the usual communication framework as pointed out in the definition of Ref.[16].

Next we take a stance where the generalized mutual information should be defined in terms of the generalized KL entropy[18] in a complete analogous manner to the Shannon’s case i.e.,

(21)

Then Eq.(21) in BSC is calculated as

(22)

where we have put and g(p₀, e) = [(1 − . Since the maximization of I_q(X; Y ) can be achieved when p₀ = p₁ = 1/2 as in the previous definition, we can calculate C_q as

(23)

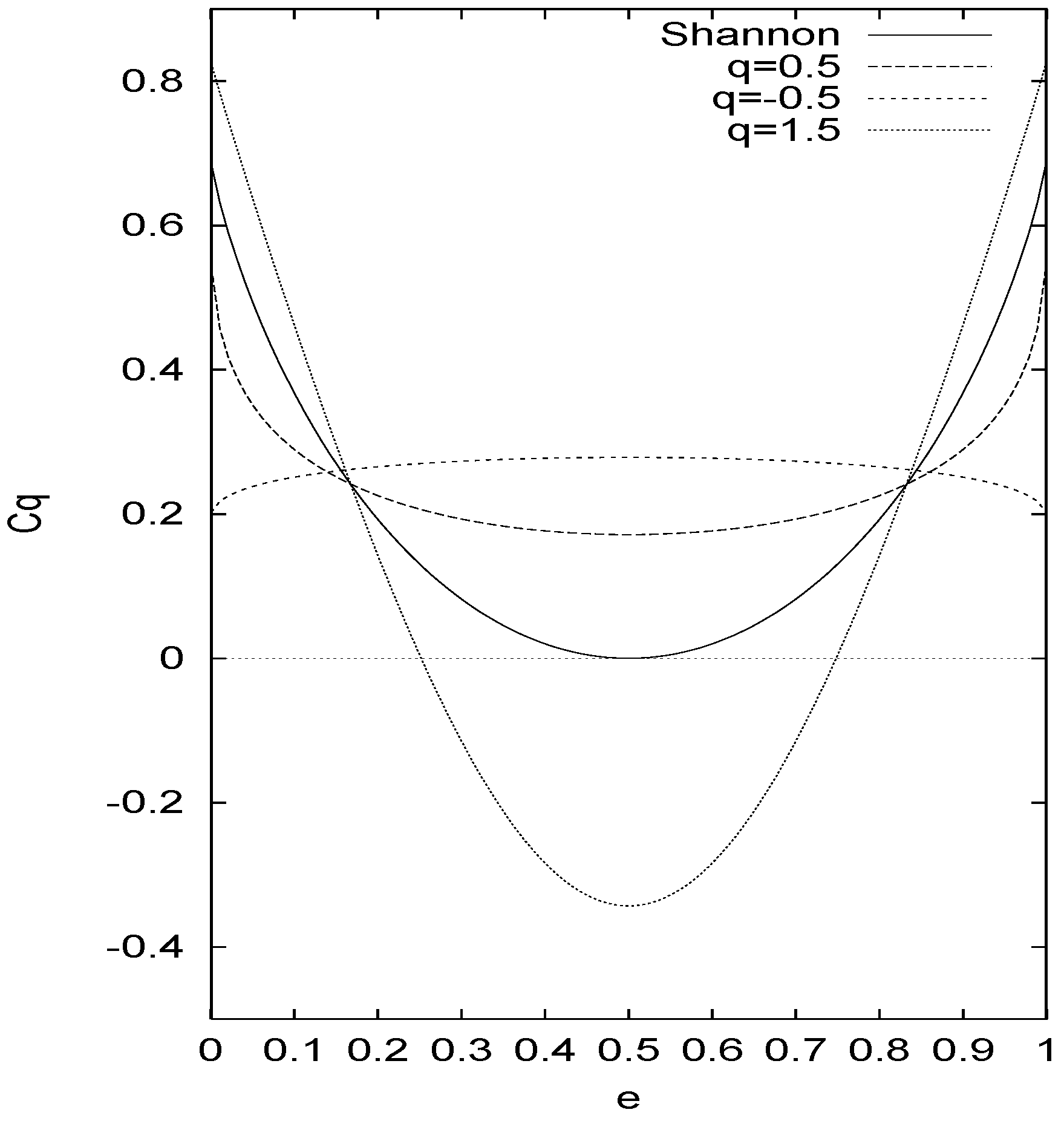
Fig.2 shows the channel capacity by Eq.(23) for some values of q and Shannon’s capacity as a reference. The zero capacity is achieved for all cases when e = 1/2. This capacity contrasts with the one by the first definition Eq(15); the negative capacity emerges for q < 0 and it goes beyond(underrun) the Shannon’s capacity when q > 1 (q < 1).

In conclusion, we have summarized the present developments of a possibility of extension of Shan- non’s information theory with a nonadditive information content. As far as the source coding theorem is concerned, we can successfully extend the theorem with nonadditive information con- tent of the form − ln_q p(x) with escortaverage. Moreover we have devised new possible definitions of the mutual information in nonadditive context. One of which is due to the entropy expression Eq.(15) that preserves the symmetry in the input and the output. The other has constructed by the generalized KL entropy. As an application of this, the behavior of the channel capacity of BSC has shown for different noise characteristics. The generalized channel capacity can entail negativ- ity for q > 1 in the former case and for q < 0 in the latter case. In the nonadditive context, we may allow the mutual information to be asymmetric, however, if we decide to take the standpoint that any generalization of mutual information has to retain symmetry, we would have to accept the modification of the intuitively reasonable property of Shannon’s capacity. On the other hand, the mutual information by the generalized KL entropy may suggest plausible definition in that the zero capacity is achieved for all q when e = 1/2. However the consistent definition of the generalized mutual information that both approaches give the same results would be welcomed. The necessity for investigation on whether or not the capacity based on the statistics which breaks the additivity can be valid for the real communication channel remains unchanged.

Figure 2. The channel capacity of BSC is plotted against the error probability for Shannon and some different values of q defined by Eq.(21)

Figure 2. The channel capacity of BSC is plotted against the error probability for Shannon and some different values of q defined by Eq.(21)